110___

1. Решение текстовых задач

2. Текстовые задачи

задачина характерные типы.
Все Текстовые
задачи разбиваются
Задачи одного типа решаются
одним и тем же приемом.
Например, выделяют задачи:
На движение;
На совместную работу;
На концентрацию и смеси;
На проценты;
На числовые зависимости (на сумму и
кратное сравнение, на нахождение трех чисел
по их суммам, взятым попарно, и т.д.)

3. Задачи на движение

Действие движения характеризуется
тремя компонентами: пройденный путь,
скорость и время, которые связаны
формулой
S = vt

4.

Пример 1.
Туристу до станции нужно было пройти 8 км.
Пройдя 7 км, он сделал привал на 15 мин и поэтому,
чтобы придти на станцию вовремя, увеличил скорость
на 2 км/ч.
Найдите скорость туриста после остановки.

5.

Так как фактически на один последний километр
турист затратил на 15 мин = ¼ часа меньше,
чем по плану, то
х≠0, х≠2
4х – 4(х – 2 )= х(х – 2 )
х2 – 2х – 8 = 0
х1 = -задачи
2; удовлетворяет
х2 = 4
Условию
только х = 4.
После остановки турист двигался со скоростью 4 км/ч
Ответ: 4 км/ч

6. Пример 2 (движение по воде)

Катер прошел 21 км п0 течению реки
и такой же путь обратно, затратив
на весь путь 1ч 45 мин .
Скорость течения реки равна 5 км/ч.
Найдите собственную скорость катера.

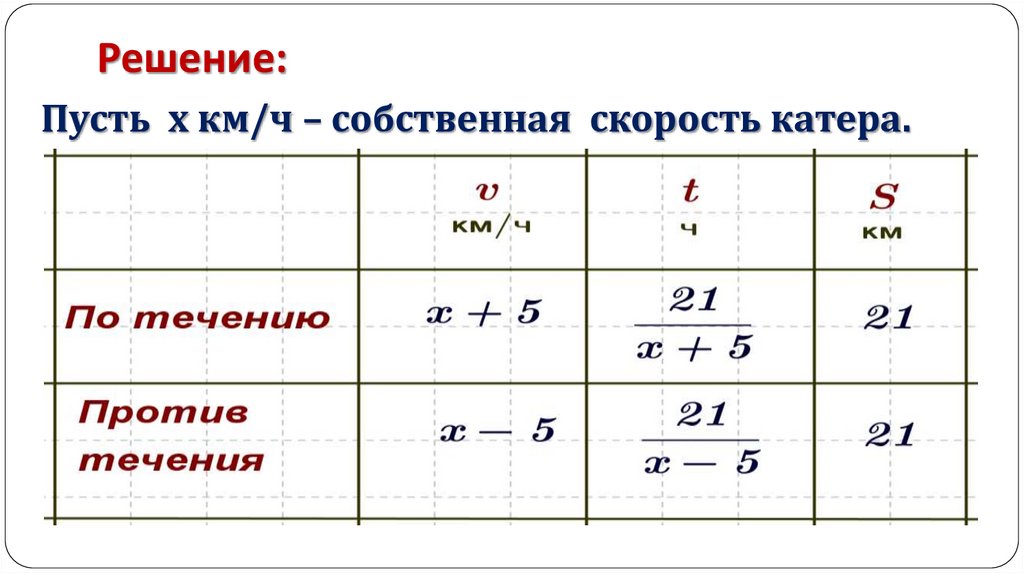
7. Решение:

Пусть х км/ч – собственная скорость катера.

8.

Так как на путь туда и обратно катер затратил
1 ч 45 мин =
то задаче соответствует уравнение:
х ≠ - 5, х ≠ 5.
12(х – 5) + 12(х + 5) = х2 – 25
х2 – 24х – 25 = 0
х1 = -1, х2 =только
25
Условию задачи удовлетворяет
х = 25. Значит
собственная скорость катера 25 км/ч.

9.

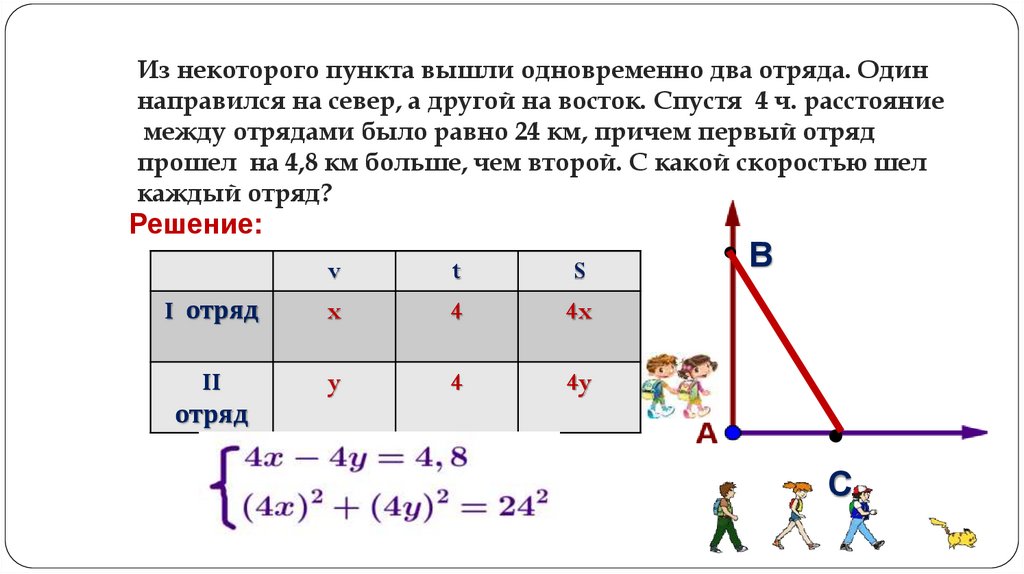
Из некоторого пункта вышли одновременно два отряда. Один
направился на север, а другой на восток. Спустя 4 ч. расстояние
между отрядами было равно 24 км, причем первый отряд
прошел на 4,8 км больше, чем второй. С какой скоростью шел
каждый отряд?
Решение:
v
t
S
I отряд
x
4
4x
II
отряд
y
4
4y
•В
С

10.

(не подходит по смыслу
задачи)
Значит скорость второго отряда 3,6 км/ч, тогда скорость
первого 4,8 км/ч
Ответ: скорость первого отряда 4,8 км/ч, скорость
второго - 3,6 км\ч.

11.

Пусть длина электрички х. Тогда ее путь пройденный
мимо товарного поезда х + 0,78 (км)
Ответ: 120 метров

12. Движение по окружности

Два тела двигаются по окружности длиной 1,2 м с
постоянными скоростями. Если они двигаются в
разных направлениях, то встречаются через каждые
15 с, если же они двигаются в одном направлении,
то одно тело догоняет другое через каждые 60с.
Найти скорости тел в м/мин.

13. Решение

15 с =
мин, 60 с = 1 мин
v1, v2 - скорости тел
________________________________
2v1 = 6
v1 = 3 м/мин, тогда v2 = 1,8 м/мин.

14. Решение задач на работу

15. Пример 1

16.

I
печник
II
печник
N
tч
A
х
2
2х
у
3
3у
Вместе
х+у
1/(х + у)
1
За 2 часа работы первого и 3 часа работы
второго печника было выполнено 20% работы.
2х + 3у = 0,2
Если они будут работать вместе, то всю
работу они выполнят за 1/ (х + у) часов,
что по условию равно 12 ч.
1/ (х + у) = 12

17.

Решим систему уравнений

18.

Значит производительность 1 печника
и значит, всю работу он может
за 20 часов.
Тогда производительность 2 печника
и значит, всю работу он выполнит
за 30 часов.
Ответ: 20 ч, 30 ч

19.

В.22 № 13
Решение:
Пусть производительности труда Игоря, Паши и Володи
соответственно равны х, y, z. (количество работы в
единицу времени) . Всю работу примем за 1. Тогда
Ответ: 10

20.

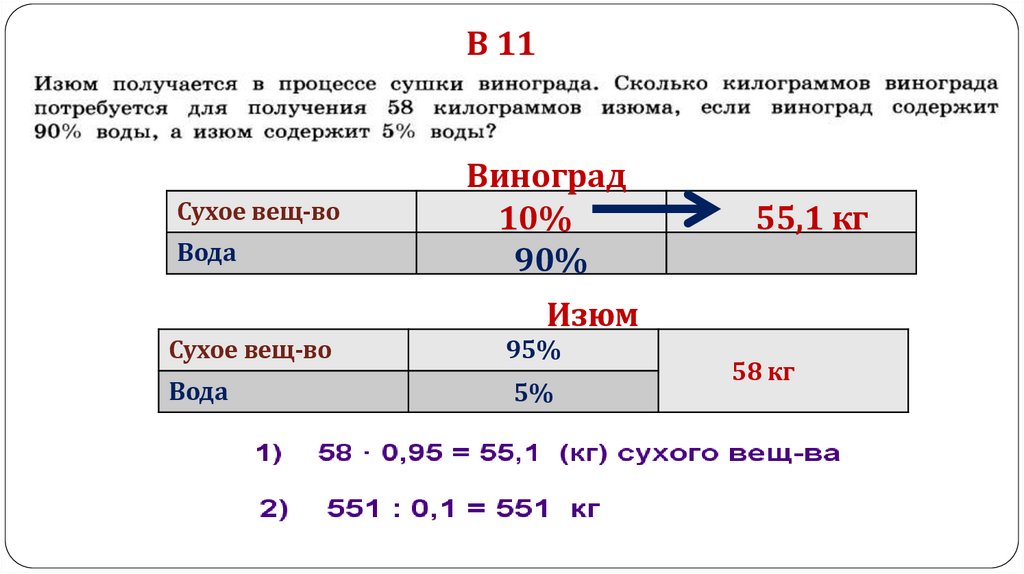
В 11
Сухое вещ-во
Вода
Виноград
10%
90%
55,1 кг
Изюм
Сухое вещ-во
95%
Вода
5%
58 кг

21.

Три одинаковых арбуза дороже дыни на 14 %.
На сколько процентов два таких же арбуза дешевле
дыни ?
Решение.
3х рублей – 3 арбуза - 114 %
х рублей – 1 арбуз
у рублей - 1 дыня
- 100 %
у рублей - 1 дыня
1. То есть
3х = 1, 14 у
2.
х = 1, 14 у : 3
2х = 0,38 у ∙2
х = 0,38 у
2х = 0,76 у
2х рублей – 2 арбуза
у рублей - 1 дыня
- 76 %
- 100 %
100% - 76% = 24%
Ответ: 24

22.

Семья состоит из мужа, жены и их сына – студента. Если
зарплата мужа увеличится вдвое, то общий доход семьи возрастет
на 50%. Если стипендия сына уменьшится в два раза, то общий
доход семьи снизится на 10%. Сколько процентов от общего дохода
составляет зарплата жены?
2x + y + z = 1,5 (x + y + z)
Решение:
Муж
x
Жена
Сын
y
z
x + y + 0,5 z = 0,9 (x + y + z)
100%
x + (x + y + z )= 1,5 (x + y + z)
x = 0,5 (x + y + z)
x + y = 0,8 (x + y + z)
y = 0,3 (x + y + z)
2x + 2 y + z = 1,8 (x + y + z)
x +x + y + y + z = 1,8 (x + y + z)