Симметрия в пространстве относительно плоскости Плоскости симметрий в многогранниках

1. Презентация на тему: «Симметрия в пространстве относительно плоскости. Плоскости симметрий в многогранниках»

Рубан Александр и Милько Кирилл, 10-А

2. Введение

Симметрия (от греч. symmetria -
соразмерность) — это свойство
фигуры сохранять свою форму и
положение при определённых
преобразованиях.
Плоскость симметрии — это
воображаемая плоскость, которая
делит фигуру на две части,
являющиеся зеркальным отражением
друг друга.

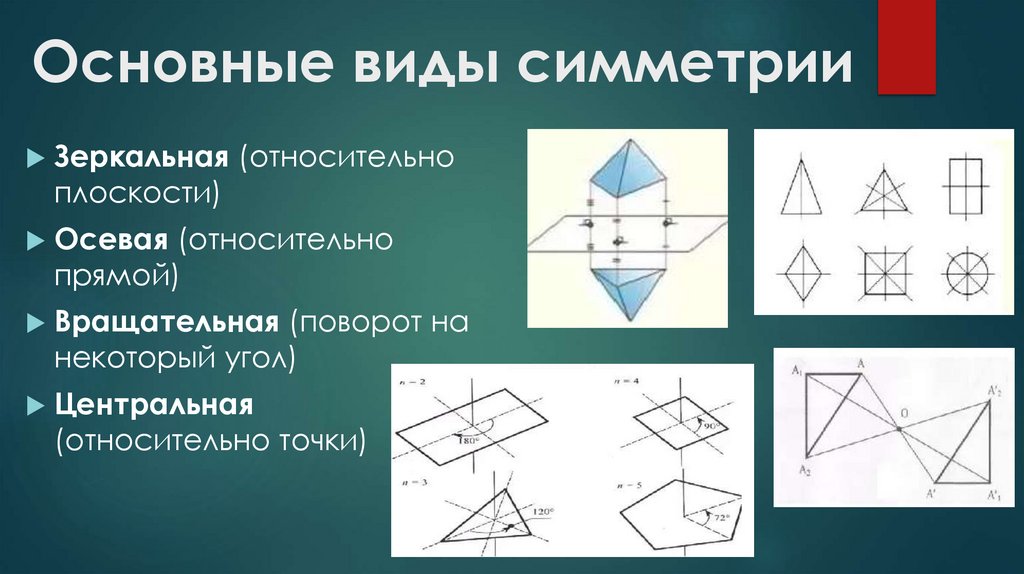
3. Основные виды симметрии

Зеркальная (относительно
плоскости)
Осевая (относительно
прямой)
Вращательная (поворот на
некоторый угол)
Центральная
(относительно точки)

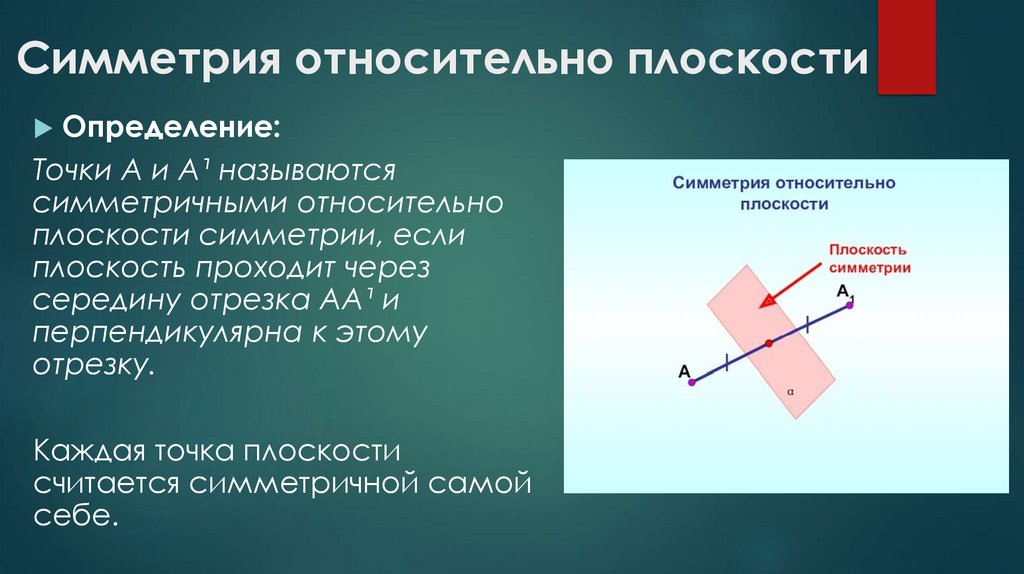
4. Симметрия относительно плоскости

Определение:
Точки А и А¹ называются
симметричными относительно
плоскости симметрии, если
плоскость проходит через
середину отрезка АА¹ и
перпендикулярна к этому
отрезку.
Каждая точка плоскости
считается симметричной самой
себе.

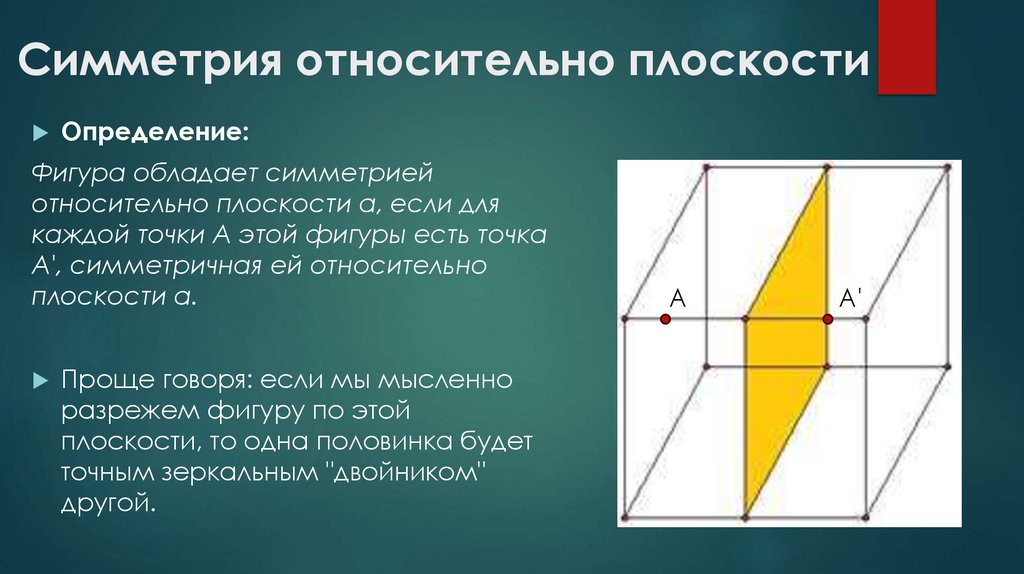
5. Симметрия относительно плоскости

Определение:
Фигура обладает симметрией
относительно плоскости α, если для
каждой точки А этой фигуры есть точка
А', симметричная ей относительно
плоскости α.
Проще говоря: если мы мысленно
разрежем фигуру по этой
плоскости, то одна половинка будет
точным зеркальным "двойником"
другой.
А
А'

6. Плоскости симметрии в простейших многогранниках

Куб имеет всего 9 плоскостей симметрии:
3 плоскости, проходящие через середины
параллельных рёбер (делят куб на две
равные призмы).
6 плоскостей, проходящие через
противоположные рёбра (диагональные
плоскости).
Также куб имеет центр симметрии,
который образуется при пересечении всех
его диагоналей.

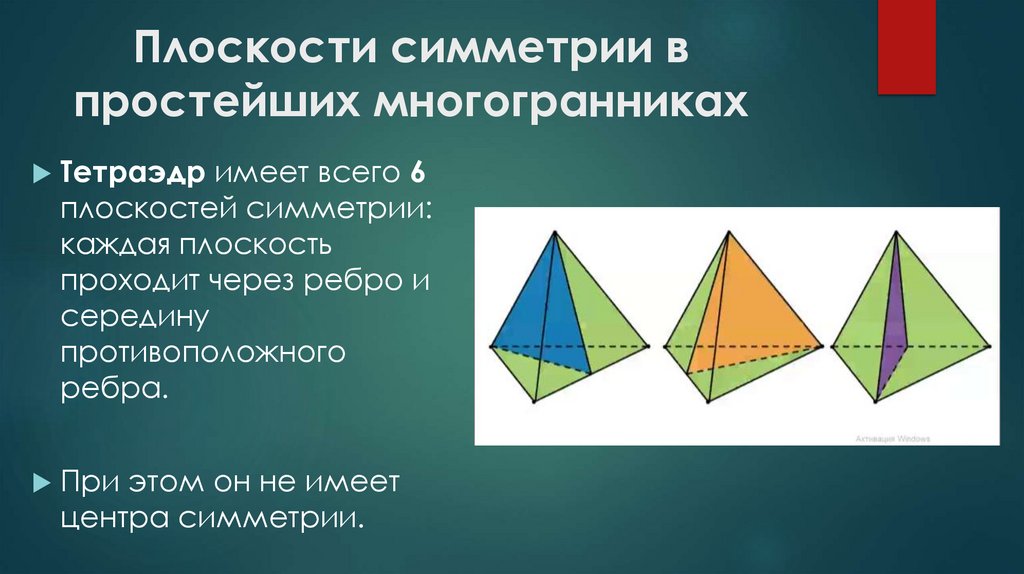
7. Плоскости симметрии в простейших многогранниках

Тетраэдр имеет всего 6
плоскостей симметрии:
каждая плоскость
проходит через ребро и
середину
противоположного
ребра.
При этом он не имеет
центра симметрии.

8. Плоскости симметрии в простейших многогранниках

Прямая треугольная призма (с правильным
треугольником в основании) имеет 4
плоскости симметрии:
Одна параллельна основаниям и проходит
через середины боковых рёбер.
3 вертикальные плоскости проходят через
боковое ребро и медиану
противоположной боковой грани.

9. Важные свойства

1. Количество плоскостей ― важная характеристика
многогранника, говорящая о степени его "правильности" и
гармоничности.
2. Правильные многогранники обладают наибольшим возможным
для их формы числом плоскостей симметрии.
3. Если многогранник имеет центр симметрии, то каждая его
плоскость симметрии обязательно проходит через этот центр.
4. Фигура может иметь плоскость симметрии, но не иметь центра
симметрии (как тетраэдр или пирамида).

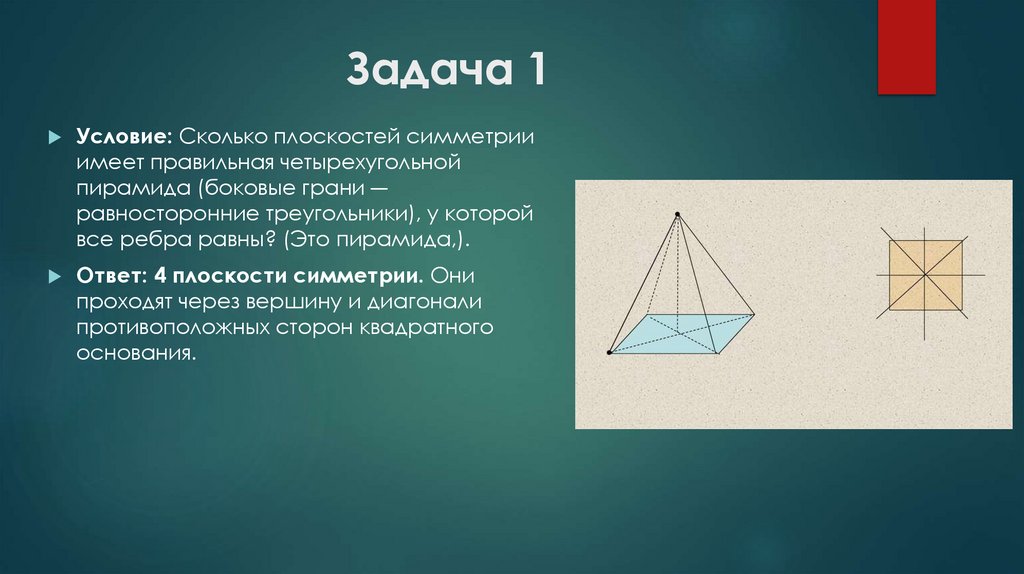
10. Задача 1

Условие: Сколько плоскостей симметрии
имеет правильная четырехугольной
пирамида (боковые грани ―
равносторонние треугольники), у которой
все ребра равны? (Это пирамида,).
Ответ: 4 плоскости симметрии. Они
проходят через вершину и диагонали
противоположных сторон квадратного
основания.

11. Задача 2

Условие: Сколько плоскостей симметрии имеет
цилиндр?
Ответ: бесконечное число плоскостей симметрии.
Все они проходят через диаметры оснований
цилиндра, а также ещё одна плоскость, которая
разделяет цилиндр на два равных.

12. Заключение

Как мы увидели, плоскость симметрии — мощный
инструмент для описания гармонии и
упорядоченности пространственных форм.
Изучение симметрии многогранников является
фундаментальным принципом в геометрии, который
помогает лучше понимать их геометрическую
сущность и находить неочевидные закономерности.