решение задач

1.

Презентация к уроку
Практикум по решению задач
по теме «Электростатика»

2.

+
+
+
+
+
+
+
+
+
+
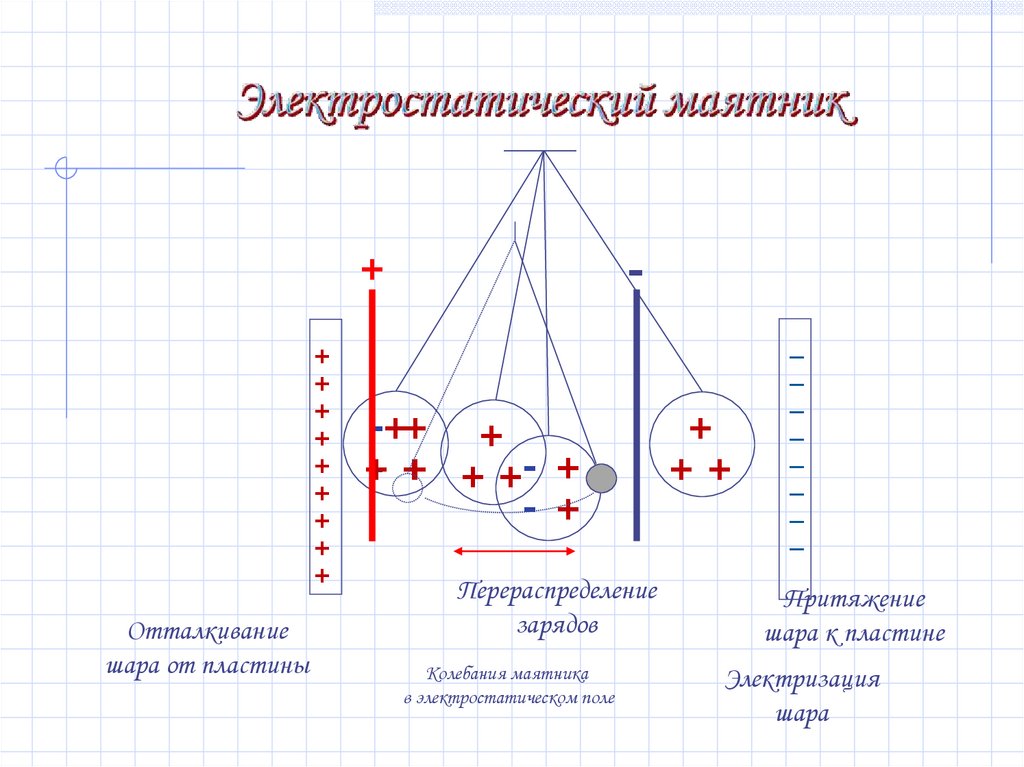
Отталкивание
шара от пластины
-
-++ +
+
- + + +- +
- +
Перераспределение
зарядов
Колебания маятника
в электростатическом поле
+
++
_
_
_
_
_
_
_
_
Притяжение
шара к пластине
Электризация
шара

3.

Проверь себя

4.

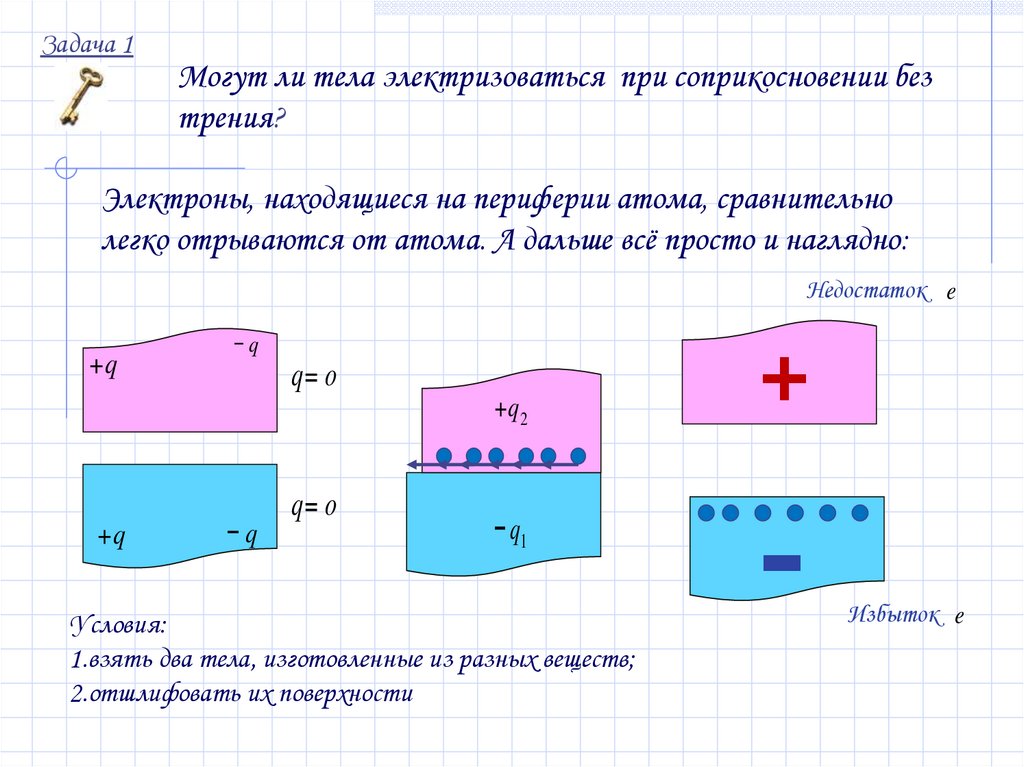
Задача 1
Могут ли тела электризоваться при соприкосновении без
трения?
Электроны, находящиеся на периферии атома, сравнительно
легко отрываются от атома. А дальше всё просто и наглядно:
Недостаток e
+q
−q
q= o
+q 2
+q
−q
q= o
− q1
Условия:
1.взять два тела, изготовленные из разных веществ;
2.отшлифовать их поверхности
+
-
Избыток e

5.

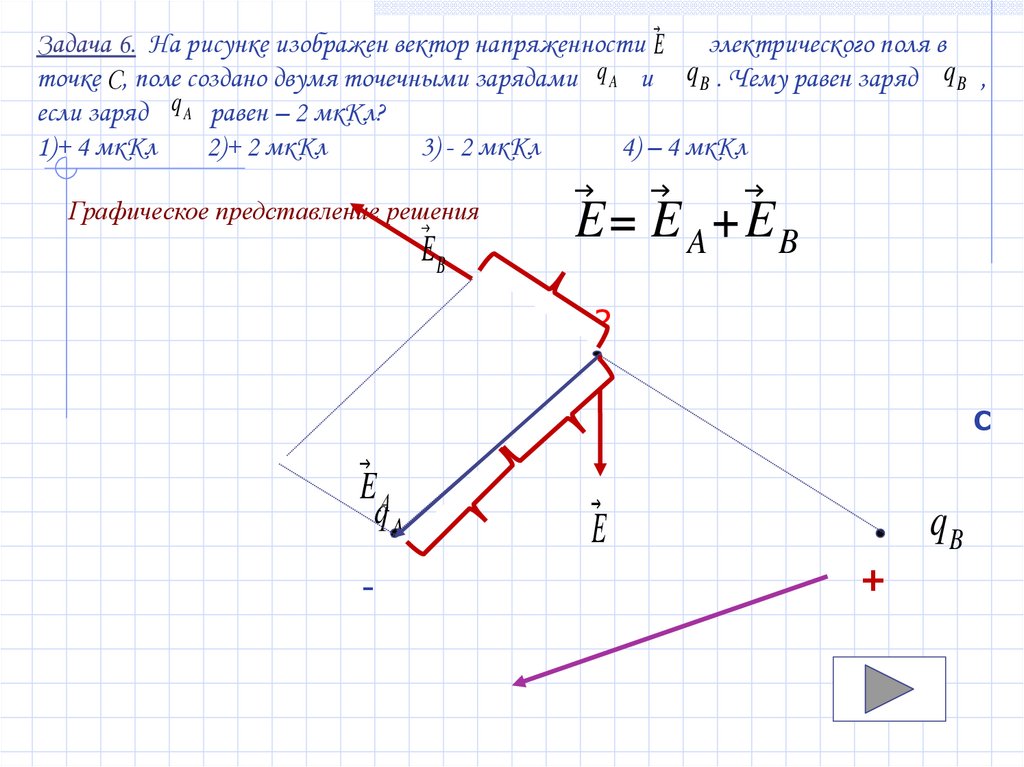
Задача 6. На рисунке изображен вектор напряженности ⃗E
электрического поля в
точке С, поле создано двумя точечными зарядами q A и q B . Чему равен заряд q B ,
если заряд q A равен – 2 мкКл?
1)+ 4 мкКл
2)+ 2 мкКл
3) - 2 мкКл
4) – 4 мкКл
Графическое представление решения
⃗E
B
⃗E = ⃗E + ⃗E
A
B
?
С
⃗E
qА A
-
⃗E
qB
+

6.

Математическая модель решения
В последнюю очередь обращаемся к математической модели
задачи:
qВ
Е В= k 2
⃗E
r
А
Е А = 2Е
⃗E
B
ЕА= k
qA
r2
EA qA
=
EB qB
⇒
q В= + 1 мкКл
Ответ: 1)

7.

Задача 7. Потенциал вершины равномерно заряженного куба равен 16 В.
Чему равен потенциал в центре куба?
16 В
q
Решение.
1 шаг. Потенциал вершины куба
можно
определить по формуле:
r
q
ϕ=k
r
4?В
шаг.Определим
Разобьём заряженный
куб
8 одинаковых
маленьких
кубиков.
ϕϕo навершины
324шаг.
потенциал
маленького
кубика:
шаг. Определим потенциал ц в центре куба, собрав все кубики в
qодин
↓ большой
в 8 разкуб:⇒ ϕ 0 = k 2q = k q ;
}
r ↓ в 2 раза
8r
ϕ ц = 8ϕ 0 = 32 В
4r
ϕ
ϕ o=
= 4B
4
Ответ: общий потенциал 8 вершин маленьких кубиков 32 В

8.

Задача 8 Пластины плоского конденсатора изолированы друг от друга слоем
диэлектрика. Конденсатор заряжен до разности потенциалов 1 кВ и отключён
от источника. Определите диэлектрическую проницаемость диэлектрика, если
при его удалении разность потенциалов между пластинами конденсатора
возрастает до 3 кВ.
Конденсатор отключён от источника
1 шаг. Анализ условия задачи:
q= const
q
C
С↓ ; q= const
С↓ ;
… U =
ε0 S
C 2=
d
εε0 S
C1 =
d
При удалении диэлектрика:
U↑
С1 1
= ;
С2 ε
U1 1
= ;
U2 ε
U 1 C2
=
;
U 2 C1
2 шаг. Математическая модель задачи:
ε=
U2
U1
q
q
U 1 = ;U 2 =
C1
C2
Ответ: 3

9.

Задача 9. Конденсатор подключен к аккумулятору. Как изменится энергия конденсатора
при раздвижении его пластин? Как согласуется это изменение с законом
сохранения энергии? Каким будет ответ в случае, если заряженный конденсатор
отключён от аккумулятора перед раздвижением пластин?
При раздвижении его (конденсатора) пластин
Конденсатор подключен к источнику тока
Анализ условия задачи:
ак изменится энергия конденсатора?
Как согласуется это изменение с законом сохранения энергии?

10.

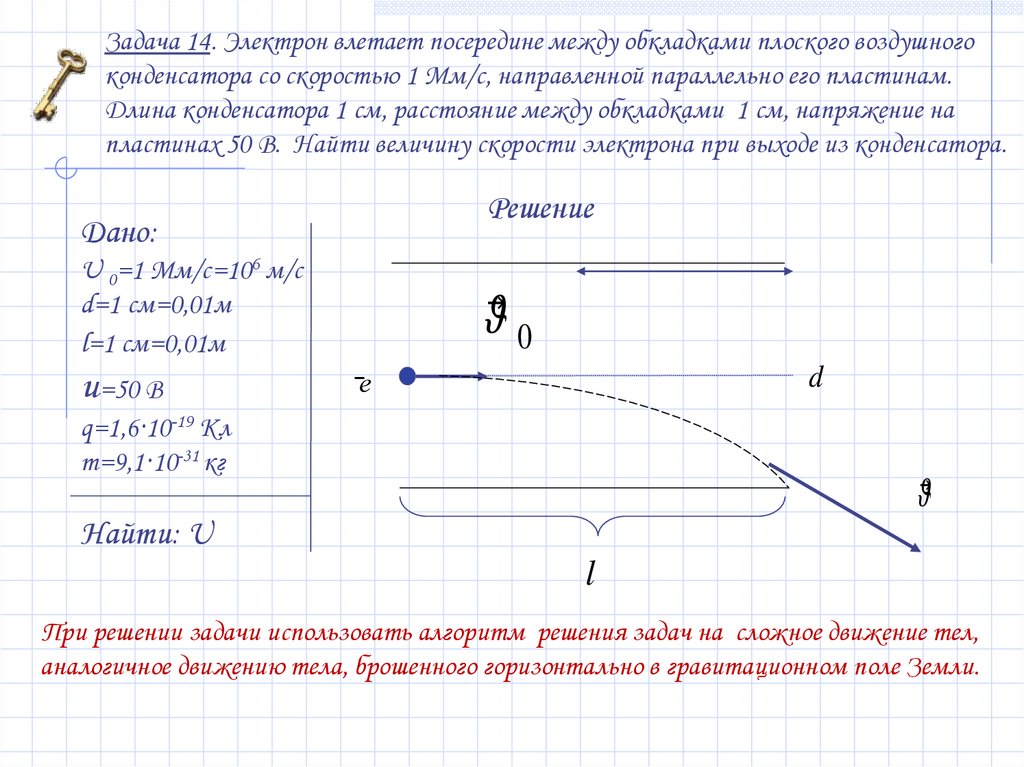
Задача 14. Электрон влетает посередине между обкладками плоского воздушного
конденсатора со скоростью 1 Мм/с, направленной параллельно его пластинам.
Длина конденсатора 1 см, расстояние между обкладками 1 см, напряжение на
пластинах 50 В. Найти величину скорости электрона при выходе из конденсатора.
Решение
Дано:
U 0=1 Мм/с=106 м/с
d=1 cм=0,01м
l=1 см=0,01м
u=50 В
ϑ⃗ 0
d
е̄
q=1,6·10-19 Кл
m=9,1·10-31 кг
ϑ⃗
Найти: U
l
При решении задачи использовать алгоритм решения задач на сложное движение тел,
аналогичное движению тела, брошенного горизонтально в гравитационном поле Земли.

11.

Домашняя контрольная работа по теме «Электрическое
поле» в виде теста