Tv_I_Ms_Chast_4

1. Теория вероятностей и математическая статистика (ТВиМС). Часть 4. Распределения дискретных и непрерывных случайных величин и их

числовые характеристики.

2. Введение. Дискретные и непрерывные случайные величины

• Определение: Случайной называют величину, которая в результате
испытания принимает значение единственное, заранее неизвестное т
зависящее от случайных причин, которые заранее не могут быть
учтены.
• Случайные величины (с.в.) принято обозначать большими буквами
латинского алфавита (X, Y, Z, …), а значения, ими принимаемые –
малыми (x, y, z, …). Например, если с.в. величина X принимает три
значения, их обозначают x1, x2, x3.
• Определение: Дискретной называют случайную величину (д.с.в.),
которая принимает отдельные, изолированные возможные значения с
определенными вероятностями. Число возможных значений д.с.в.
может быть конечным или счетным.
• Определение: Непрерывной называют случайную величину (н.с.в.),
которая принимает непрерывный ряд значений из некоторого
конечного или бесконечного промежутка. Число возможных значений
н.с.в. бесконечно и несчетно.

3. §1. Распределения дискретных случайных величин и их числовые характеристики

• Определение: Законом распределения дискретной случайной
величины (д.с.в.) называют соответствие между ее возможными
значениями и их вероятностями. Такое соответствие может быть
задано таблично, аналитически (в виде формулы), графически.
• Определение: Дискретным рядом распределения д.с.в. называется
таблица, в которой перечислены (как правило, упорядоченно) все
возможные значения д.с.в. и соответствующие им вероятности:
X
x1
x2
…
xn
iP(xi)
P(X)
p1
p2
…
pn
1
Прим. Значения д.с.в. не повторяются: xi xj при i j.
• Д.с.в. X принимает с необходимостью одно из множества значений
{x1, x2, …, xn}. События X = x1, X = x2, …, X = xn образуют полную
группу. Поэтому с необходимостью: p1 + p2 + … + pn = 1.

4. §1. … продолжение

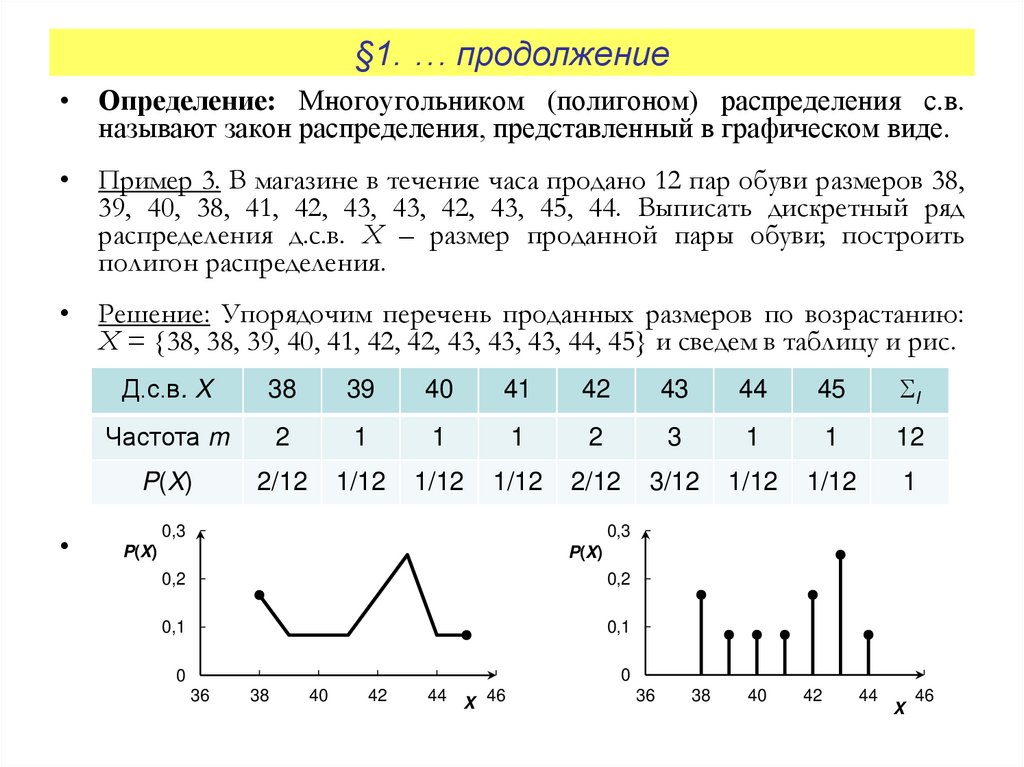
• Определение: Многоугольником (полигоном) распределения с.в.
называют закон распределения, представленный в графическом виде.
• Пример 3. В магазине в течение часа продано 12 пар обуви размеров 38,
39, 40, 38, 41, 42, 43, 43, 42, 43, 45, 44. Выписать дискретный ряд
распределения д.с.в. X – размер проданной пары обуви; построить
полигон распределения.
• Решение: Упорядочим перечень проданных размеров по возрастанию:
X = {38, 38, 39, 40, 41, 42, 42, 43, 43, 43, 44, 45} и сведем в таблицу и рис.
Д.с.в. X
38
39
40
41
42
43
44
45
I
Частота m
2
1
1
1
2
3
1
1
12
P(X)
2/12
1/12
1/12
1/12
2/12
3/12
1/12
1/12
1
0,3
0,3
P(X)
P(X)
0,2
0,2
0,1
0,1
0
0
36
38
40
42
44 X 46
36
38
40
42
44
X
46

5. §1. … продолжение

• Определение: Модой распределения называют значение
соответствующее максимуму закона (ряда) распределения.
xi ,
• Определение: Если (явно выделяющаяся) мода одна распределение
называют унимодальным; если моды две – бимодальным и т.д.
10
8
8
Отн. частота, %
Отн. частота, %
10
6
4
2
0
4
2
0
0
20
40
60
80
Баллы ЕГЭ-2008 (матем.)
6
100
0
20
40
60
80
100
Баллы ЕГЭ-2009 (матем.)
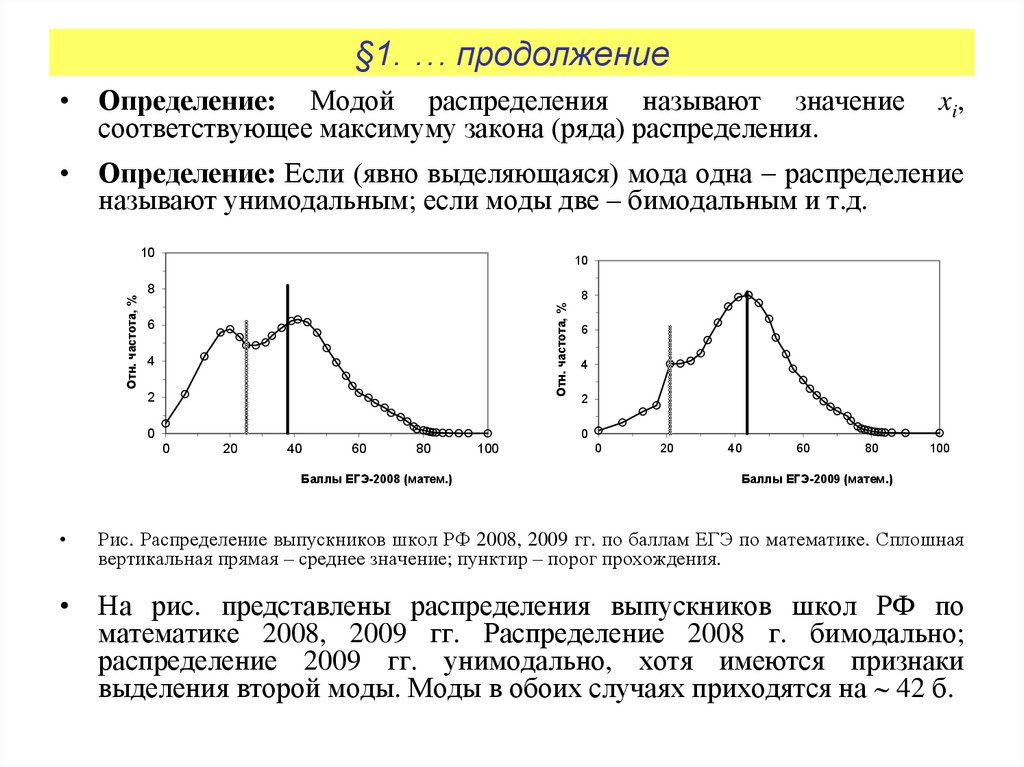
Рис. Распределение выпускников школ РФ 2008, 2009 гг. по баллам ЕГЭ по математике. Сплошная
вертикальная прямая – среднее значение; пунктир – порог прохождения.
• На рис. представлены распределения выпускников школ РФ по
математике 2008, 2009 гг. Распределение 2008 г. бимодально;
распределение 2009 гг. унимодально, хотя имеются признаки
выделения второй моды. Моды в обоих случаях приходятся на 42 б.

6. §1. … продолжение. Биномиальное распределение

• Определение: Биномиальным называют распределение вероятностей,
определяемое формулой Бернулли (0 k n, q = 1 – p):
• Pn(k) = Cnk pk qn k.
• В табличном виде ряд биномиального распределения есть:
X
x0
x1
x2
…
xk
…
xn
i
X=k
0
1
2
…
k
…
n
Pn(k)
qn
…
Cnk pk qn k
…
pn
1
P(X)
p0
…
pk
…
pn
1
npqn 1 ½n(n 1)p2qn 2
p1
p2
0,3
0,4
Pn(k)
(а)
0,3
Pn(k)
(б)
0,2
0,2
0,1
0,1
0
0
0
1
2
3
4
5
6 k7
0
2
4
6
8
10
12
k
14
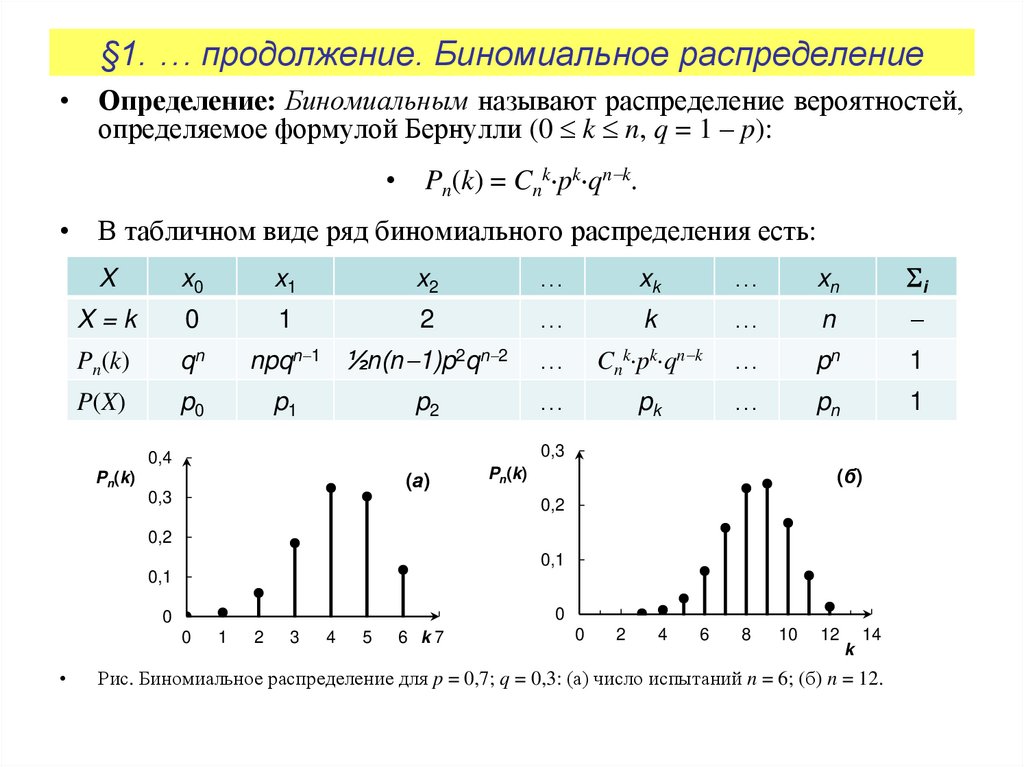
Рис. Биномиальное распределение для p = 0,7; q = 0,3: (а) число испытаний n = 6; (б) n = 12.

7. §1. … продолжение. Распределение Пуассона

• Определение: Распределением Пуассона называют распределение
вероятностей, определяемое формулой Пуассона (n p = = Const):
• Pn(k) = ( k/k!) e ,
k = 0, 1, 2, …
• В табличном виде ряд распределения Пуассона есть:
X=k
0
1
2
…
k
…
i
Pn(k)
e
e
( 2/2) e
…
( k/k!) e
…
1
0,3
0,3
(а)
Pn(k)
(б)
0,2
0,2
0,1
0,1
0
0
0
Pn(k)
2
4
6
8
k
10
0
2
4
6
8
k
10
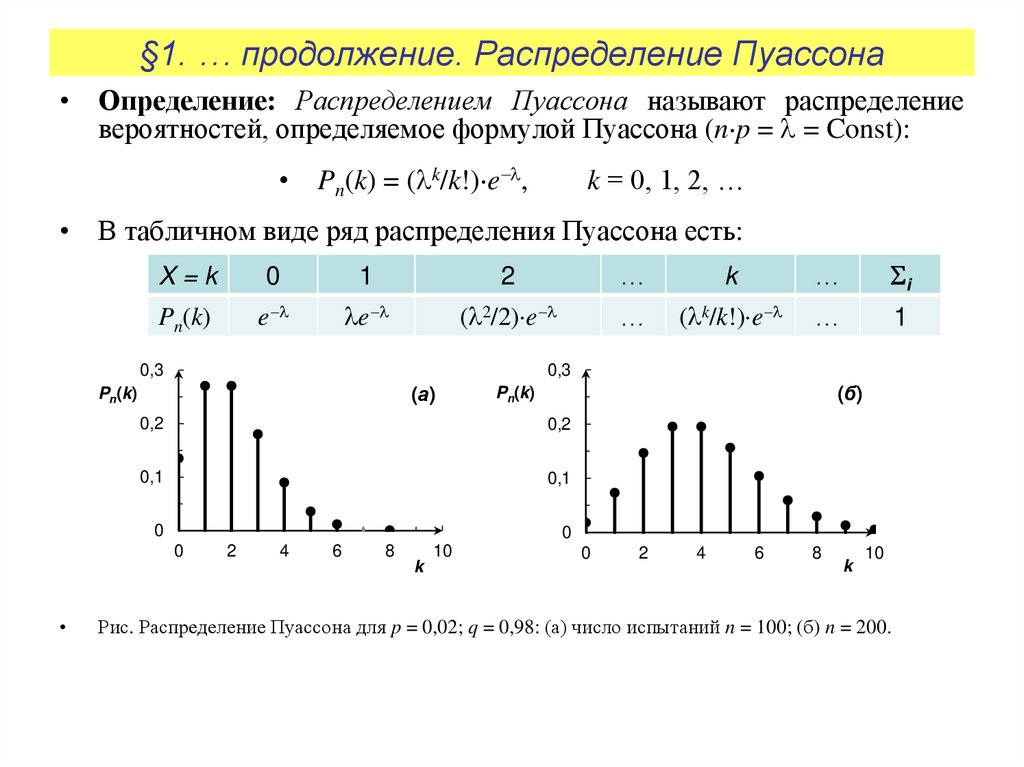
Рис. Распределение Пуассона для p = 0,02; q = 0,98: (а) число испытаний n = 100; (б) n = 200.

8. §1. … продолжение. Геометрическое распределение

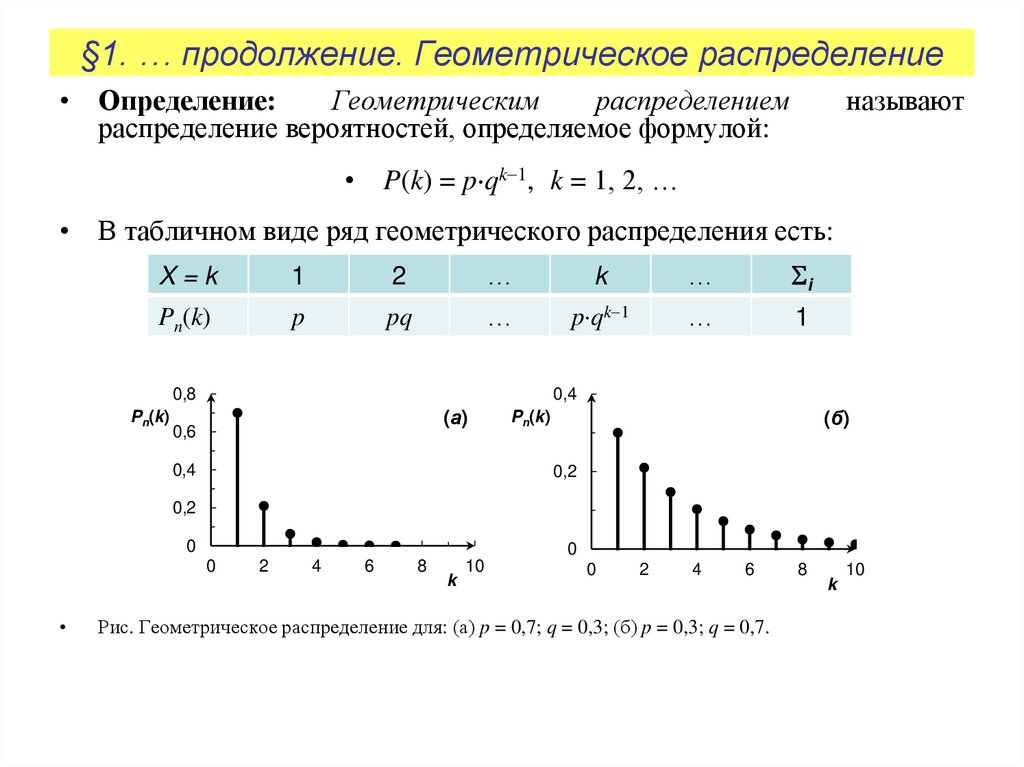
• Определение:
Геометрическим
распределением
распределение вероятностей, определяемое формулой:
называют
• P(k) = p qk 1, k = 1, 2, …
• В табличном виде ряд геометрического распределения есть:
X=k
1
2
…
k
…
i
Pn(k)
p
pq
…
p qk 1
…
1
0,8
Pn(k)
0,4
(а)
0,6
0,4
Pn(k)
(б)
0,2
0,2
0
0
0
2
4
6
8
k
10
0
2
4
6
Рис. Геометрическое распределение для: (а) p = 0,7; q = 0,3; (б) p = 0,3; q = 0,7.
8
k
10

9. §1. … продолжение. Числовые характеристики распределения дискретной случайной величины

• Определение: Числовыми характеристиками (распределения)
случайной величины называется набор чисел, обобщенно
характеризующих
закон
распределения
этой
с.в.
(мода,
математической ожидание, дисперсия, СКО и др.)
• Определение: Математическим ожиданием дискретной случайной
величины (д.с.в.) X называют сумму произведений всех ее возможных
значений на соответствующие вероятности:
• M(X) = i xi pi = x1 p1 + x2 p2 + …. + xn pn.
• Пример 4. Найти математическое ожидание числа очков, выпадающих
при бросании игральной кости.
• Решение: Закон распределения д.с.в. X – число выпавших очков при
бросании игральной кости является равномерным:
X
1
2
3
4
5
6
i
P(X)
1/6
1/6
1/6
1/6
1/6
1/6
1
• Математическое ожидание д.с.в. X равно:
• M(X) = i xi pi = 1 + 2 + 3 + 4 + 5 + 6 = 3,5.
• Ответ: M(X) = 3,5.

10. §1. … продолжение. Числовые характеристики распределения дискретной случайной величины

• Пример 5. Найти математическое ожидание
выпадающих при бросании пары игральных костей.
суммы
очков,
• Решение: Закон распределения д.с.в. X – сумма выпавших очков при
бросании пары игральных костей является треугольным (см. табл. и
рис.):
12
i
P(X) 1/36 2/36 3/36 4/36 5/36 7/36 5/36 4/36 3/36 2/36 1/36
1
X
2
3
4
5
6
7
8
9
10
11
0,3
P(X)
0,2
0,1
0
0
2
4
6
8
10
12
14
X
• Математическое ожидание д.с.в. X равно:
• M(X) = i xi pi = (1/36) (2 1 + 3 2 + 4 3 + … + 10 3 + 11 2 + 12 1) = 7.
• Ответ: M(X) = 7.

11. §1. … продолжение. Свойства математического ожидания

• Вероятностно-статистический смысл математического ожидания.
• Пусть произведено n испытаний, в которых д.с.в. X приняла m1 раз
значение x1, m2 раз значение x2, …, mk раз значение xk; при этом:
• m1 + m2 + … + mk = n.
• Определение: Средним арифметическим Xср д.с.в. X называют
величину:
• Xср = {x1 m1 + x2 m2 + … + xk mk},
• или
• Xср = x1 w1 + x2 w2 + … + xk wk,
• где относительные частоты есть w1 = m1/n; w2 = m2/n; …; wk = mk/n.
• При большом числе испытаний (n ) относительные частоты
стремятся к соответствующим вероятностям (закон больших чисел):
w1 p1; w2 m2; …; wk pk. Поэтому при больших n:
• Xср x1 p1 + x2 p2 + … + xk pk = M(X).
• Утверждение. Математическое ожидание приближенно равно (тем
точнее, чем больше n) среднему арифметическому наблюдаемых
значений д.с.в. В этом и состоит вероятностно – статистический
смысл математического ожидания.

12. §1. … продолжение. Свойства математического ожидания

• Свойство 1. Математическое ожидание (М.О.) постоянной величины
равно самой этой постоянной:
• M(C) = C.
• Док-во: СРС.
• Свойство 2. Постоянный множитель можно выносить за знак М.О.:
• M(CX) = CM(X).
• Док-во: СРС.
• Свойство 3. М.О. произведения двух независимых случайных
величин равно произведению их математических ожиданий:
• M(XY) = M(X) M(Y).
• Док-во: СРС.
• Свойство 4. М.О. суммы двух случайных величин равно сумме их
математических ожиданий:
• M(X + Y) = M(X) + M(Y).
• Док-во: СРС.

13. §1. … продолжение. Свойства дисперсии и среднеквадратического отклонения (СКО)

• Определение: Отклонением называют разность между с.в. X и ее
математическим ожиданием M(X) :
• X = X M(X).
• Для отклонения X закон распределения имеет вид:
X
x1 M(X)
x2 M(X)
…
xn M(X)
i
P( X)
p1
p2
…
pn
1
Прим. Величину X = X M(X) также называют центрированной величиной.
• Теорема. Математическое ожидание отклонения равно нулю:
• M( X) = M(X M(X)).
• Док-во: СРС.
• Определение: Дисперсией (рассеянием) D(X) случайной величины
называют математическое ожидание квадрата ее отклонения от
математического ожидания:
• D(X) = M( X2) = M((X M(X))2).

14. §1. … продолжение. Свойства дисперсии и среднеквадратического отклонения (СКО)

• Для квадрата отклонения X2 закон распределения имеет вид:
X2
(x1 M(X))2
(x2 M(X))2
…
(xn M(X))2
i
P( X2)
p1
p2
…
pn
1
• Дисперсия D(X) с.в. может быть найдена по формуле:
• D(X) = M((X M(X))2) =
• = p1 (x1 M(X))2 + p2 (x2 M(X))2 + … + pn (xn M(X))2.
• Теорема (формула вычисления дисперсии). Дисперсия равна
разности между М.О. квадрата с.в. X и квадратом ее математического
ожидания:
• D(X) = M(X2) (M(X))2 = M(X2) M2(X).
• Док-во: Для доказательства достаточно выписать цепочку равенств,
следующую из свойств математического ожидания:
• D(X) = M((X M(X))2) = M(X2 2X M(X) + M2(X)) = M(X2) M2(X), ч.т.д.

15. §1. … продолжение. Свойства дисперсии и среднеквадратического отклонения (СКО)

• Свойство 1. Дисперсия постоянной величины равна нулю:
• D(C) = 0.
• Док-во: СРС.
• Свойство 2. Постоянный множитель можно выносить за знак
дисперсии, возведя его в квадрат:
• D(CX) = C2 D(X).
• Док-во: Достаточно применить формулу вычисления дисперсии:
• D(CX) = M((СX)2) (M(СX))2 = M(С2X2) (СM(X))2 =
• = С2 M(X2) С2 (M(X))2 = С2 [M(X2) M2(X)] = C2 D(X), ч.т.д.
• Свойство 3. Дисперсия суммы двух независимых случайных величин
равна сумме их дисперсий:
• D(X + Y) = D(X) + D(Y).
• Док-во: По определению дисперсии:
• D(X + Y) = M((X + Y)2) (M(X + Y))2 = M(X2 +2XY + Y2) (M(X) + M(Y))2 =
= M(X2)+2M(XY ) + M(Y2) M2(X) + 2M(X) M(Y) + M2(Y) = D(X) + D(Y),
ч.т.д.

16. §1. … продолжение. Свойства дисперсии и среднеквадратического отклонения (СКО)

• Свойство 4. Дисперсия разности двух независимых случайных
величин равна сумме их дисперсий:
• D(X Y) = D(X) + D(Y).
• Док-во: По доказанным свойствам дисперсии:
• D(X Y) = D(X + ( 1) Y) = D(X)+ D(( 1) Y)) = D(X)+ D(( 1) Y)) =
• = D(X)+ ( 1)2 D(Y)) = D(X) + D(Y),
ч.т.д.
• Замечание: Дисперсия как мера разброса значений с.в. X не слишком
удобна, т.к. имеет размерность квадрата с.в. С этой точки зрения
более удобна величина, называемая средним квадратичным
(квадратическим) отклонением (СКО); в западной терминологии СКО
называют также стандартным отклонением.
• Определение: Средним квадратичным отклонением (СКО) случайной
величины X называют квадратный корень из дисперсии этой с.в.:
• (X) = D(X).
• Замечание: Свойства СКО (X) непосредственно вытекают из
соответствующих свойств дисперсии D(X) случайной величины X.

17. §1. … продолжение. Свойства дисперсии и среднеквадратического отклонения (СКО)

• Теорема. Среднее квадратичное отклонение суммы конечного числа
взаимно независимых случайных величин равно квадратному корню
из суммы квадратов СКО этих величин:
• (X1 + X2 + …+ Xn) = { 2(X1) + 2(X2) + … + 2(Xn)}.
• Док-во: По доказанным свойствам дисперсии:
• (X1 + X2 + …+ Xn) = D(X1 + X2 + …+ Xn) =
• = {D(X1) + D(X2) +…+ D(Xn)} = { 2(X1) + 2(X2) +…+ 2(Xn)}, ч.т.д.
• Теорема. Пусть имеется система из n независимых д.с.в. X1, X2, …, Xn,
которые имеют одинаковые распределения, т.е. равные М.О.,
дисперсии и СКО: a(X1) = a(X2) = … = a(Xn) = a; D(X1) = D(X2) = … =
D(Xn) = 2; (X1) = (X2) = … = (Xn) = . Тогда М.О., дисперсия и
СКО среднего арифметического этих с.в., соответственно, равны:
• M(Xср) = M[ (X1 + X2 + … + Xn)] = a;
• D(Xср) = D[ (X1 + X2 + … + Xn)] = 2;
• (Xср) = [ (X1 + X2 + … + Xn)] = / n.
• Док-во: СРС.

18. §2. Распределения непрерывных случайных величин и их числовые характеристики

• Определение: (Интегральной) функцией распределения называют
функцию F(X), определяющая вероятность того, что случайная
величина X в результате испытания примет значения, меньшее x, т.е.
• F(X) = P(X x).
• Определение: Непрерывной называют случайную величину (н.с.в.)
функция распределения которой является непрерывной, кусочногладкой функцией с кусочно-непрерывной производной.
• Свойство 1. Значения функции распределения принадлежат
промежутку [0; 1], т.е. F(x) изменяется в диапазоне 0 F(x) 1.
• Док-во: СРС.
• Свойство 2. Функции распределения является F(x) неубывающей:
• F(x1) F(x2) при x1 x2.
• Док-во: СРС.
• Следствие 1. Вероятность того, что с.в. X примет значения X [a; b]:
• P(a X < b) = F(b) F(a).
• Следствие 2. Вероятность того, что с.в. X примет конкретное
фиксированное значение X = a равна нулю.

19. §2. Продолжение …

• Свойство 3. Если возможные значения случайной величины
принадлежат (a; b), тo
• F(x) = 0 при x a
• Док-во: СРС.
F(x) = 1 при x b.
и
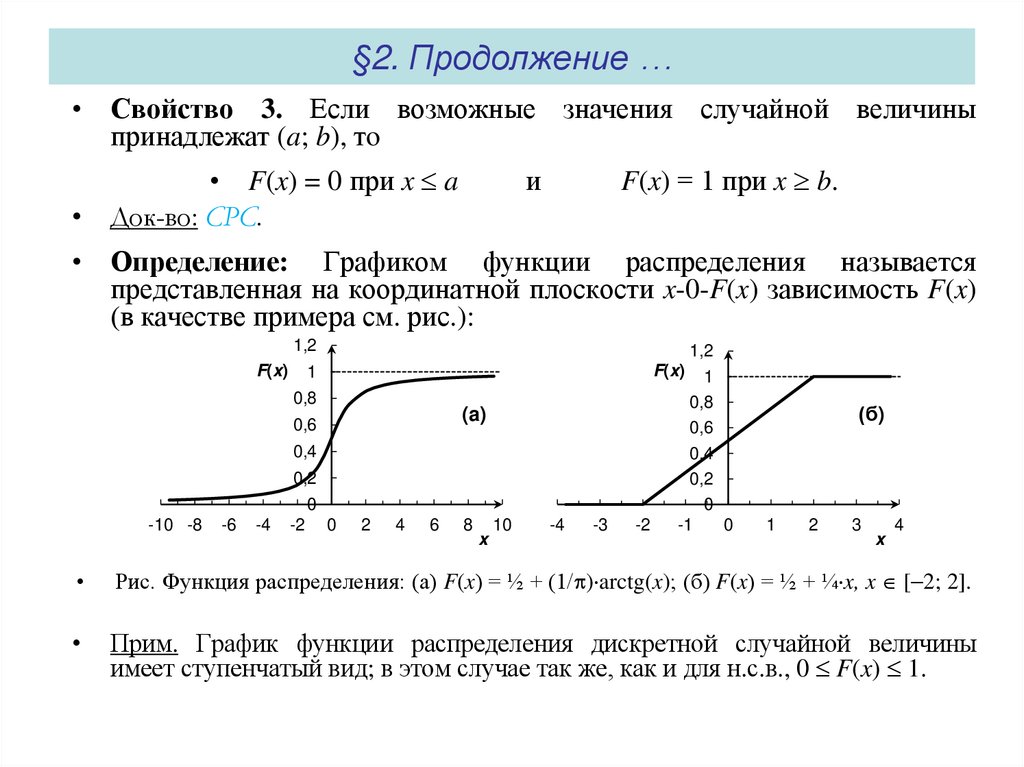
• Определение: Графиком функции распределения называется
представленная на координатной плоскости x-0-F(x) зависимость F(x)
(в качестве примера см. рис.):
1,2
F(x)
1
0,8
(a)
0,6
0,4
0,2
0
-10 -8
-6
-4
-2
0
2
4
6
8
x
10
-4
-3
1,2
F(x) 1
0,8
0,6
0,4
0,2
0
-2
-1
0
(б)
1
2
3
x
4
Рис. Функция распределения: (а) F(x) = ½ + (1/ ) arctg(x); (б) F(x) = ½ + ¼ x, x [ 2; 2].
Прим. График функции распределения дискретной случайной величины
имеет ступенчатый вид; в этом случае так же, как и для н.с.в., 0 F(x) 1.

20. §2. Продолжение …

• Определение.
Плотностью
функции
распределения
(ПФР)
вероятностей (дифференциальной функцией распределения) функцию
f(x) первую производную интегральной функции F(x):
• f(x) = F (x).
• Следствие. По плотности распределения f(x) путем интегрирования
можно восстановить функцию распределения F(x):
x
• F(x) = f(x)dx.
• Прим. Для дискретной случайной величины понятие плотности
функции распределения f(x) не определено.
• Теорема. Вероятность того, что н.с.в. X примет значения X [a; b]
может быть найдена интегрированием от a до b:
b
• P(a X < b) = f(x)dx.
a
• Прим. Геометрически это соответствует нахождению площади под
графиком ПФР f(x) на промежутке [a; b].

21. §2. Продолжение …

• Определение: График ПФР f(x) называют кривой распределения
(вероятностей).
• Сформулируем свойства плотности функции распределения f(x).
• Свойство 1. Плотность функции распределения f(x) неотрицательная
функция.
• Док-во: Функция распределения F(x) – неубывающая функция.
Поэтому ее производная F (x) неотрицательна, ч.т.д.
• Свойство 2. Несобственный интеграл от плотности распределения
f(x) в пределах от до + равен единице (условие нормировки):
+
f(x)dx = 1.
• Свойство 3 (вероятностный смысл плотности распределения).
Вероятность того, что случайная величина X примет значение,
принадлежащее интервалу (x; x + dx), равна произведению плотности
вероятности f(x) в точке x на ширину этого интервала dx:
• dP(X) = F(x + dx) F(x) = f(x)dx.

22. §2. Продолжение …

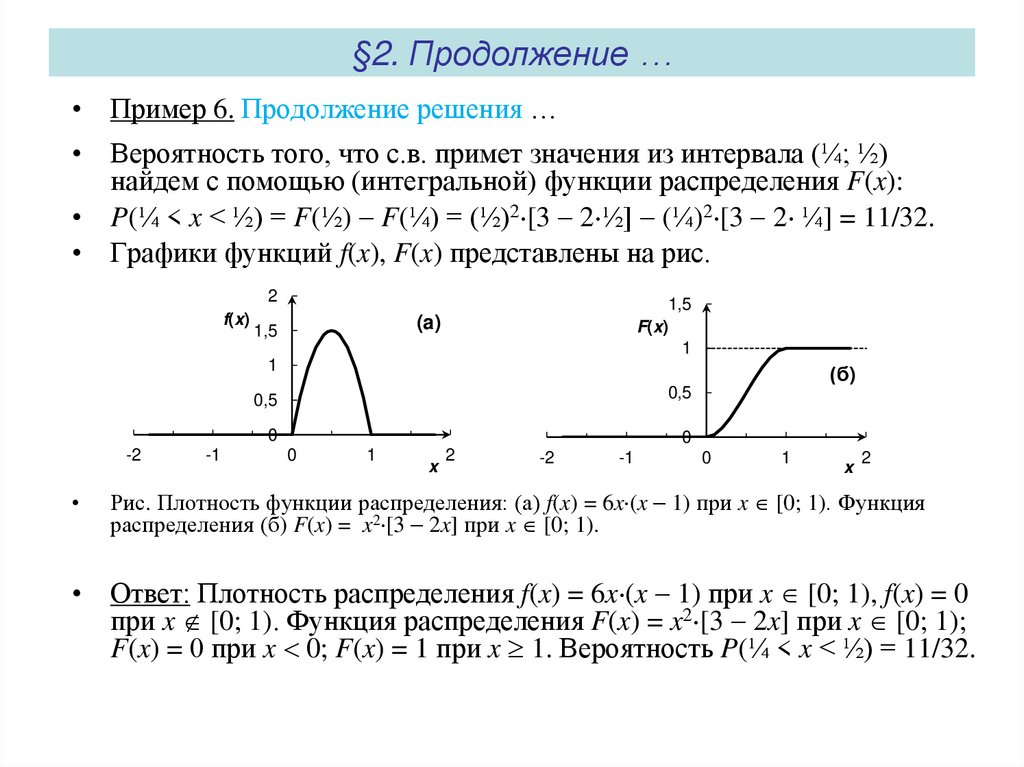
• Пример 6. Плотность распределения н.с.в. задана функцией
• f(x) = С x (x 1) при x [0; 1), f(x) = 0 при x [0; 1).
• Требуется: нормировать плотность функции распределения f(x);
найти функцию распределения F(x); найти вероятность того, что с.в.
примет значения из интервала (¼; ½). Построить графики f(x), F(x).
• Решение: Неизвестную постоянную (нормировочную константу) C
определим из условия нормировки:
• +
• f(x)dx = 1.
•
1
1
1
• В данном случае,‫׬‬0