физический смысл моя (1)

1. Физический (механический) и геометрический смысл производной

2. Определение

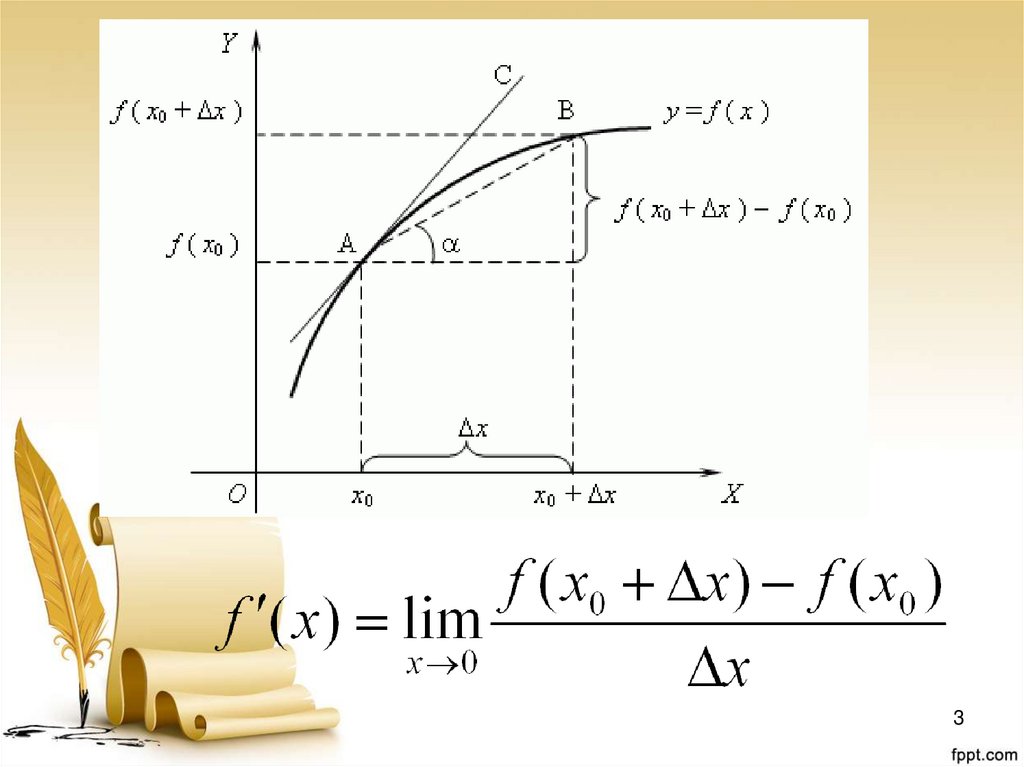
Физический и геометрический смысл
производной
Определение
• Производной функции в данной точке
называется предел отношения
приращения функции к приращению
аргумента при условии ,что приращение
аргумента стремится к нулю
2

3.

3

4.

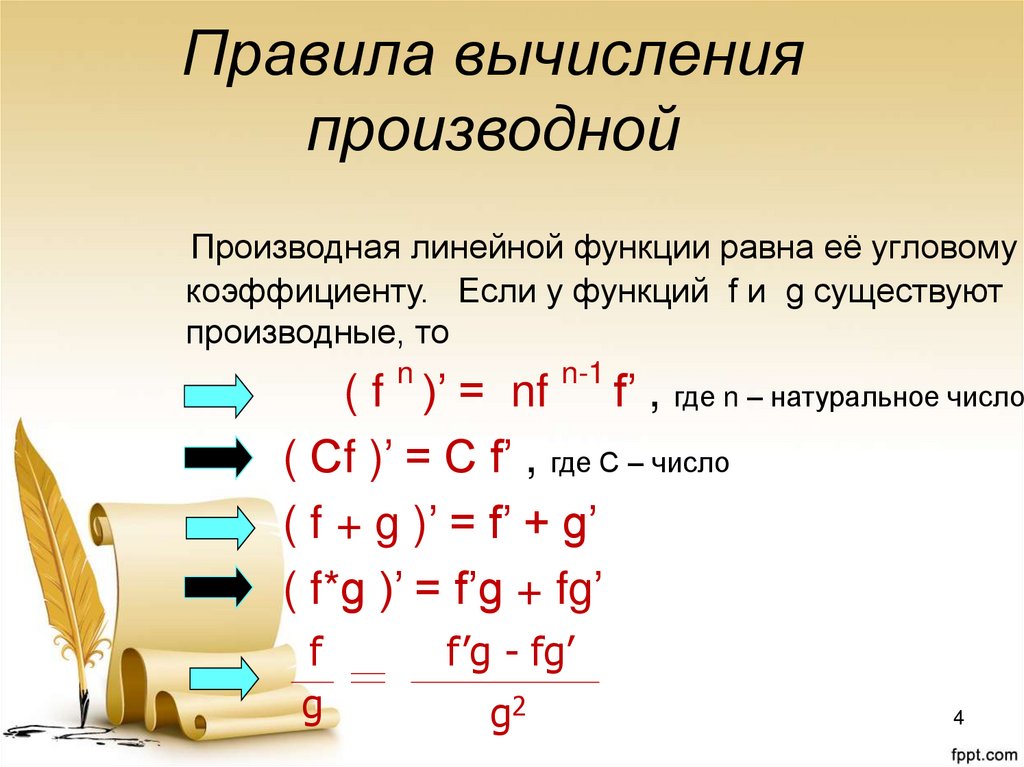
Правила вычисления
производной
Производная линейной функции равна её угловому
коэффициенту. Если у функций f и g существуют
производные, то
n
n-1
( f )’ = nf f’ , где n – натуральное число
( Сf )’ = C f’ , где С – число
( f + g )’ = f’ + g’
( f*g )’ = f’g + fg’
f
g
f’g - fg’
g2
4

5.

Вторая производная
Пусть
функция
f
имеет
производную
f’
во
всех
точках
промежутка X. Эта производная в свою
очередь является функцией от x. Если
функция f’ дифференцируема, то ее
производную
называют
второй
производной от f и обозначают f’’.
Таким образом, f’’ = (f’)’.
5

6.

Пример 1
Найти производную функции
y=x3+5x2+6x+4
Решение:
(y)’=(x3+5x2+6x+4)’=3x2+10x+ 6
Ответ: (y)’=3x2+10x+6
6

7.

Пример 2
Найти вторую производную от функции
y=x4+3x³+6x²+5x+1.
Решение
(y)’=4x3+9x2+12x+5.
(y)’’=12x2+18x+12.
Ответ: (y)”=12x2+18x+12.
7

8.

Физический смысл
производной
Если
уравнение
движения
задано функцией, то первая
производная этой функции
даст
скорость,
заданную
функцией,
а
вторая
производная даст ускорение,
заданное функцией.
8

9.

Физический смысл первой
производной
Мгновенная скорость в момент времени t0
прямолинейного движения, совершаемого по
закону x = f (t), равна значению производной
функции f при t = t0.
v = f’ (t)
Таким же образом определяют мгновенную скорость
других физических процессов: углового вращения,
радиоактивность распада и т. д.
9

10.

Задача 1
Материальная
точка
движется
по
закону y=x4-5x3+6x2+3x-7.
Найти ускорение и момент времени,
при котором ускорение равно 30.
Решение
1)Найдём скорость движения:
V=y’.
V=(x4-5x3+6x2+3x-7)’=4x3-15x2+12x+3.
10

11.

2) Найдём ускорение:
A=v’.
A=(4x3-15x2+12x+3)’=12x2-30x+12.
3)Найдём момент времени, при
котором ускорение равно 30.
12x2-30x+12=30
12x2-30x-18=0
D=1764
x=3.
Ответ: a=12x2-30x+12; x=3.
11

12.

Задача 2
Материальная точка движется по
закону y=2x3+6x2-11x-9. Найти
ускорение и момент времени, при
котором численные значения
скорости и ускорения равны.
Решение
1)Найдём скорость:
V=y’.
V=(2x3+6x2-12x-9)’=6x2+12x-12.
12

13.

2)Найдём ускорение
A=v’.
A=(6x2+12x-12)’=12x+12.
3)Находим момент времени, при
котором A=v.
6x2+12x-12=12x+12.
6x2-24=0.
x2-4=0.
x=2.
Ответ: a=12x+12; x=2.
13

14.

Домашнее задание
1. Материальная точка движется по прямой согласно уравнению
s(t) = t3 – 2t2 + 3,5t – 15 (м/с)
а) В какой момент времени ускорение будет равно 8 м/с2.
б) Какое ускорение будет в момент времени t = 2с?
2. Материальная точка движется прямолинейно по закону
(где x — расстояние от точки отсчета в метрах, t —
время в секундах, измеренное с начала движения). Найдите ее скорость (в
м/с) в момент времени t = 9 с.
3. Закон прямолинейного движения материальной точки равен
, где x – расстояние от точки отсчета
(м); t – время с начала движения (с). Найдите скорость точки в момент
времени t = 6 с. Ответ выразите в метрах в секунду.
4.

15.

Домашнее задание
1. Точка движется прямолинейно по закону
(s выражается в метрах, t – в секундах)
.
Найти скорость движения через 3 секунды
после начала движения.
2. Точка движется прямолинейно по закону
.
Найти
скорость
ускорение точки в момент t = 4с.
и