Похожие презентации:
Производная. Алгебра и начала анализа. 10 класс
1. Производная
Алгебра и начала анализа10класс.
Учитель Андреева Н.А.
2. Основные цели
Обобщить теоретические знания по теме:«Производная. Геометрический и физический
смысл производной»;
Закрепить правила дифференцирования;
Рассмотреть решение задач, связанных с
этой темой, базового и повышенного уровней
сложности;
Организовать работу учащихся по указанной
теме на уровне соответствующем уровню уже
сформированных у них знаний.
3. Какая из записей точно соответствует по определению производной?
Производной функции в данной точкеназывается предел отношения приращения
функции в этой точке к приращению
аргумента, когда приращение аргумента
стремится к нулю.
f ( x0 x) f ( x0 )
f ( x ) lim
x 0
x
4. В каком из перечисленных случаев можно говорить о физическом смысле производной?
Производная от перемещения по времениявляется мгновенная скорость.
Производная от скорости по времени является
ускорением.
Физический смысл
y f (x)
f ( x0 )
-скорость
f ( x0 )
-ускорение
5.
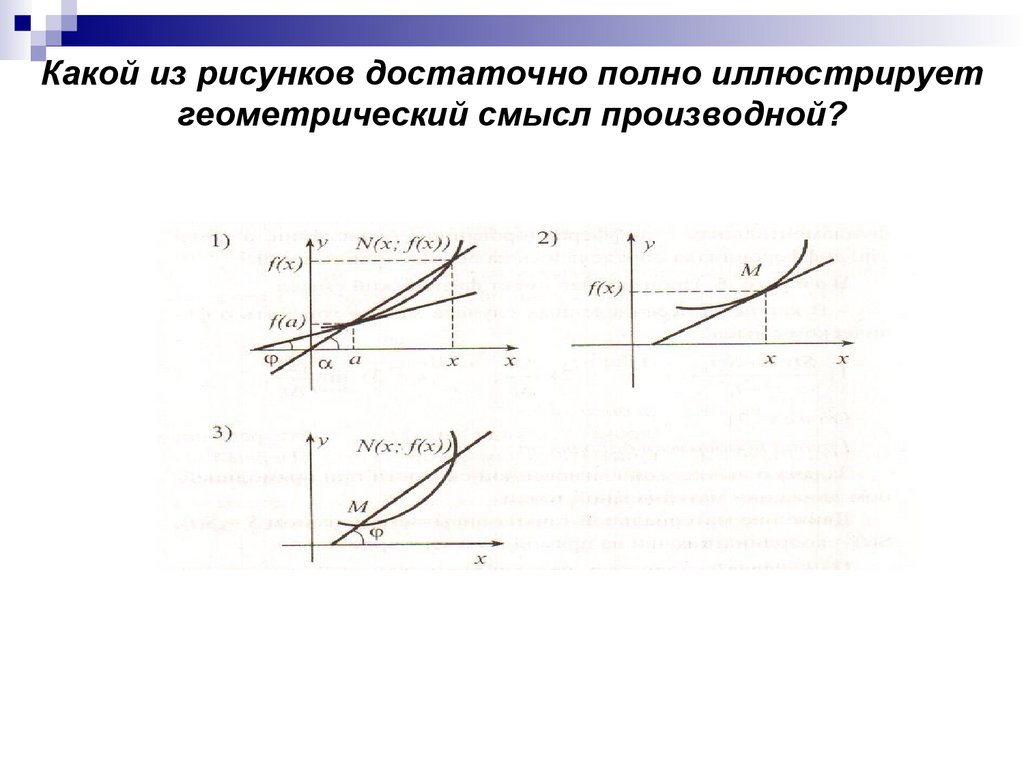
Какой из рисунков достаточно полно иллюстрируетгеометрический смысл производной?
6.
f ( x) k tgГеометрический смысл
производной состоит в том, что
значение производной функции
y=f(x) в точке x равно угловому
коэффициенту касательной к
графику функции в точке с
абсциссой x
7. Правила дифференцирования
uv
u v
uv
u v uv
c u c u , где
u u v uv
2
v
v
c const
8. Производная сложной функции
y f u x сложная функцияf внешняя функция ,
u помежуточная функция
f u x f u u x
Производная
от
произведению производной
функции
по
производную промежуточной
" сложной "
от
функции
внешней
промежуточной
на
по
основной
9. Таблица производных
n x n 1x
n
c 0, x 1
ax
b
a
1
1
2
x
x
x
2
1
x
10.
sin x cos xcos x sin x
1
tgx 2
cos x
1
ctgx 2
sin x
11.
arcsin xarccos x
1
2
1 x
1
1 x
1
arctgx
2
1 x
1
arcctgx
2
1 x
2
12. Вычислите устно. Найдите производную функции:
1. Найти производную функции1) x6 – x3 + 2x2
y(x) = x6 – x4 + 2x3 – 3
2) x6 – x4 + 6x3 – 3
3) 6x5 – 4x3 + 6x2
4) 6x5 – 4x3 + 6x2 – 3
13. Вычислите устно. Найдите производную функции:
2. Найти значение производной функцииy(x) = x2 – 3x в точке с абсциссой x0 = 1
Ответы:
1) –2
2) –1
3) 1
4) 2
14. Вычислите устно. Найдите производную функции:
у(х) = (1/5x – 7) 5Ответы:
1) y'(x) = (1/5x – 7) 4
2) y'(x) = (1/5x – 7) 3
3) y'(x) = 5(1/5x– 7) 4
4) y'(x) = 5x 4 – 7
15.
Вычислите устно.Точка движется прямолинейно по закону
S(t) = 2t 3 – 3t.
Вычислите скорость движения точки в
момент
t0 = 2c
Ответы:
1) 9
2) 13
3) 21
4) 18
16.
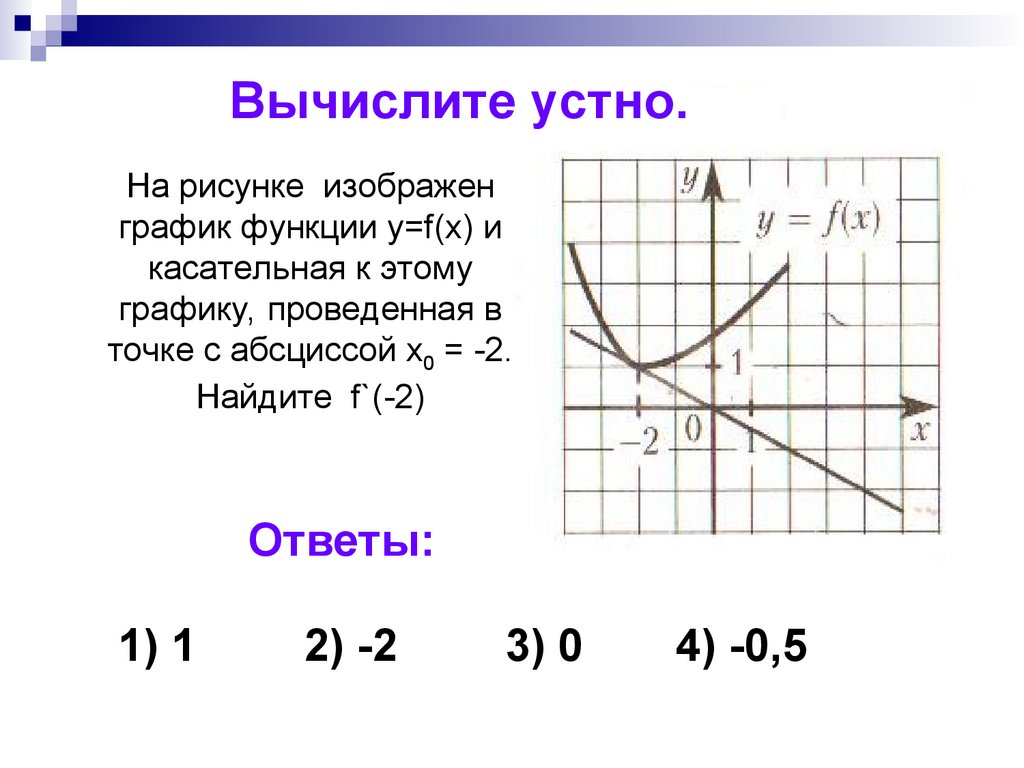
Вычислите устно.На рисунке изображен
график функции y=f(x) и
касательная к этому
графику, проведенная в
точке с абсциссой х0 = -2.
Найдите f`(-2)
Ответы:
1) 1
2) -2
3) 0
4) -0,5
17. Решение задач
1) f(x) = 6 Sin x – 3. Решите уравнение f`(x)=02) f(x) = (x2 + 5)
. Вычислить f`(x)
Задание 1 группе
1) f(x) = 4 Cos x +2. Решить уравнение f `(x)=0.
2) f(x) = (x5 – 3)
.Вычислить f `(x)
18.
Решение задачНайдите абсциссу точки графика функции
Х3 – 3х2 + 10х – 11, в которой
У=
3
касательная наклонена к оси х под углом 450
Задание 2 группе
Найдите абсциссу точки графика функции
3
Х
У=
– 2х2 + 5х +5, в которой касательная
3
параллельна оси х.
19.
Решение задачЗапишите уравнение всех
касательных к графику функции
Х-3
У=
Х–2,
параллельных прямой у = х + 100
Задание 3 группе
Запишите уравнение всех
касательных к графику функции
параллельных прямой у = -5х -40
Х +4
У=
Х–1,
20. Самостоятельная работа
21.
Бланки ответов22. Критерии оценивания самостоятельной работы:
Каждое задание уровня А оценивается в2 балла;
Каждое задание уровня В оценивается в
3 балла;
Каждое задание уровня С оценивается в
4 балла.
23.
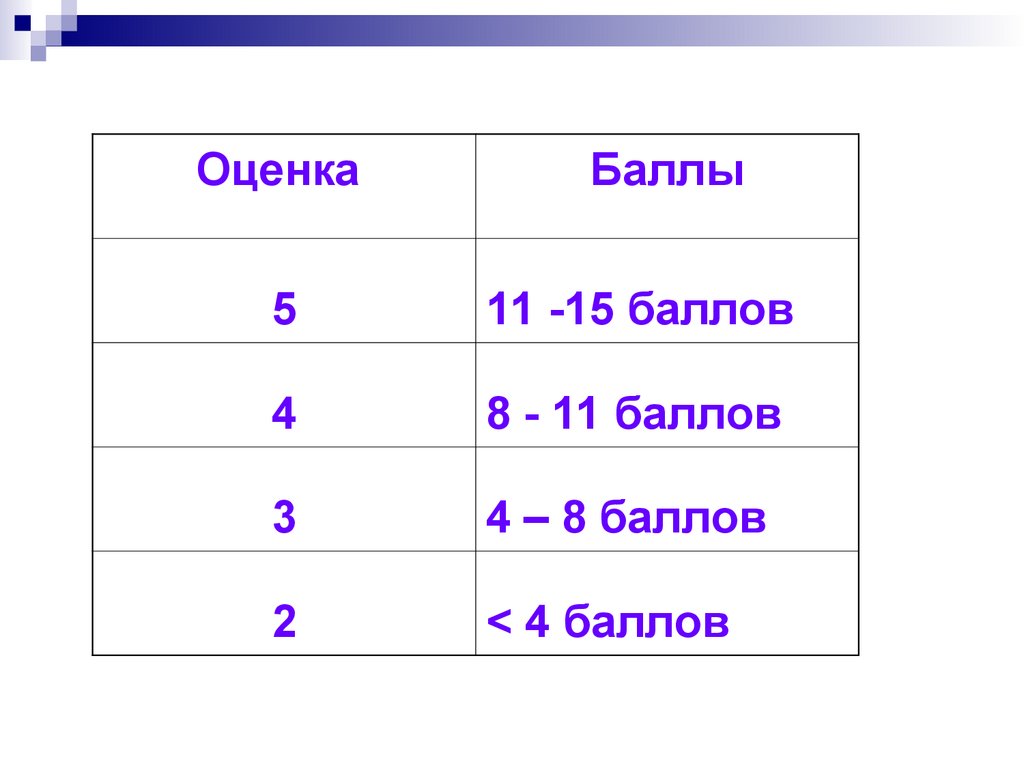
ОценкаБаллы
5
11 -15 баллов
4
8 - 11 баллов
3
4 – 8 баллов
2
< 4 баллов
24. Домашнее задание.
1. Пользуясь определением, найдите производную функции f(x)в точке х0:
2
x2
а) f(x)=
- х, х0=2;
б) f(x)=
+1, х0=-1.
x
4
2. Найдите производные функций:
4 2
2
а) f x x x 8 x ; б ) f x 3 4 x 1 .
x
3. Составьте и решите уравнение:
2
f x f 2 , если
f x
x 3x
.
x 4
4. Составьте и решите неравенство:
f x f x 0,
f x x 2 2 x 3.
если
25. Используемая литература:
Алгебра и начала анализа. 11 класс: Учеб. дляобщеобразоват. учреждений/[Ю.М. Колягин, Ю.В.
Сидоров, М.В. Ткачёва, Н.Е. Фёдорова и М.И.
Шабунин]. – М.: Мнемозина, 2002.- 240c.
2. Ершова А.П. Самостоятельные и контрольные работы
по алгебре и началам анализа для 10-11 классов.
[А.П.Ершова, В.В. Голобородько]. – М.: Илекса, 2005.
3. Ивлев Б.М. и др. Дидактические материалы по
алгебре и началам анализа для 11 класса./ [Б.М.
Ивлев, С.М. Саакян, С.И. Шварцбурд]. – М.:
Просвещение, 2003. – 192 c.
4. Дьячков А.К. Единый государственный экзамен.
Математика: Справочные материалы, контрольнотренировочные упражнения, задачи с развернутым
ответом; в 2-х частях.[Текст] /[ А.К.Дьячков, Н.И.
Иконникова, Е.В. Морозова, В.М.Казак ], под общ.
ред. А.К.Дьячкова. – Челябинск: Взгляд, 2006.
1.








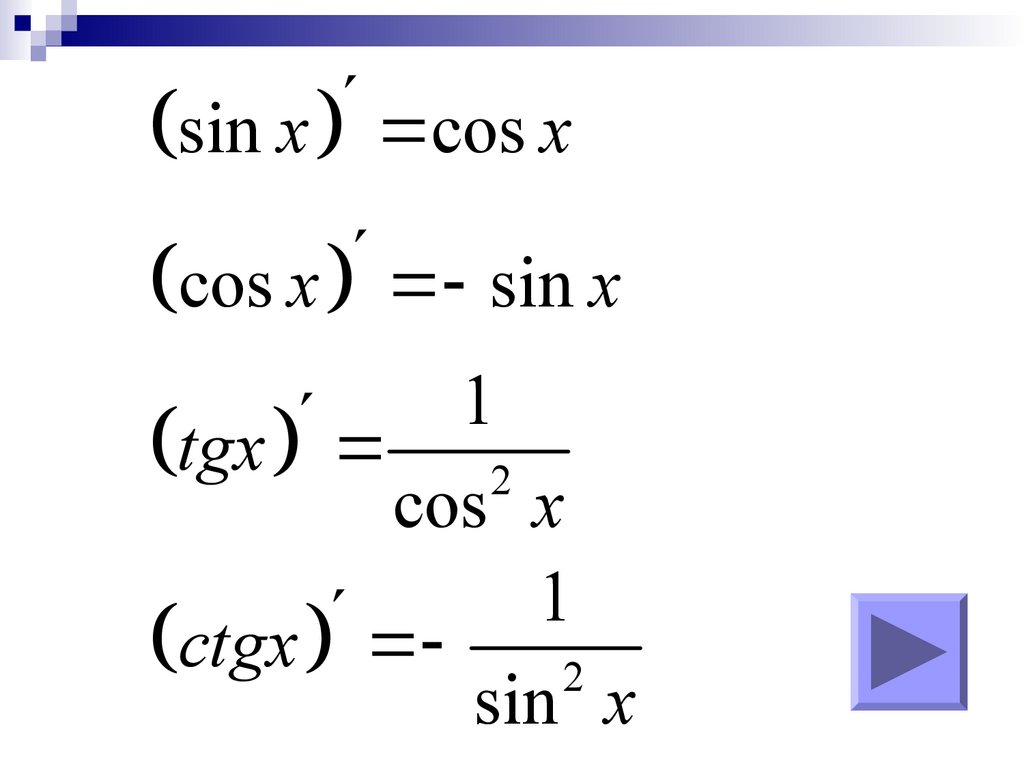
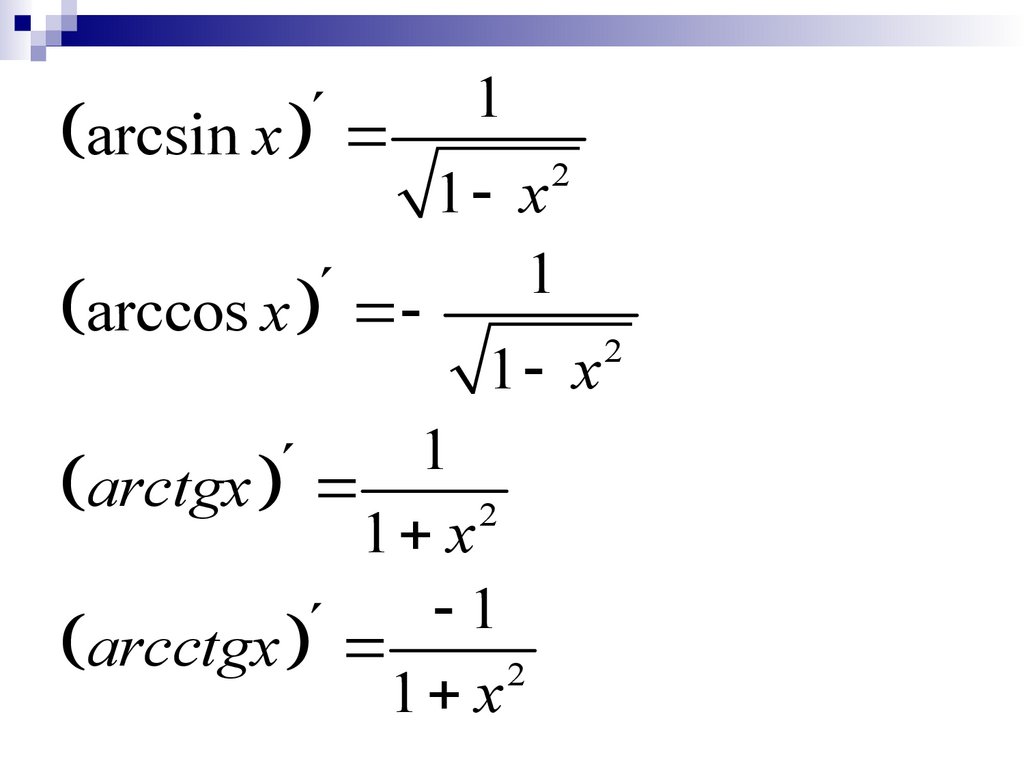












 Математика
Математика








