Похожие презентации:
4ef1cd38352114d5468b4133541ad69e
1. Приращение функции и аргумента. Производные простейших функций
2. Основные вопросы:
• Введение понятийи
• Определение производной.
• Касательная и секущая к графику
функции. Геометрический и
физический смысл производной.
2
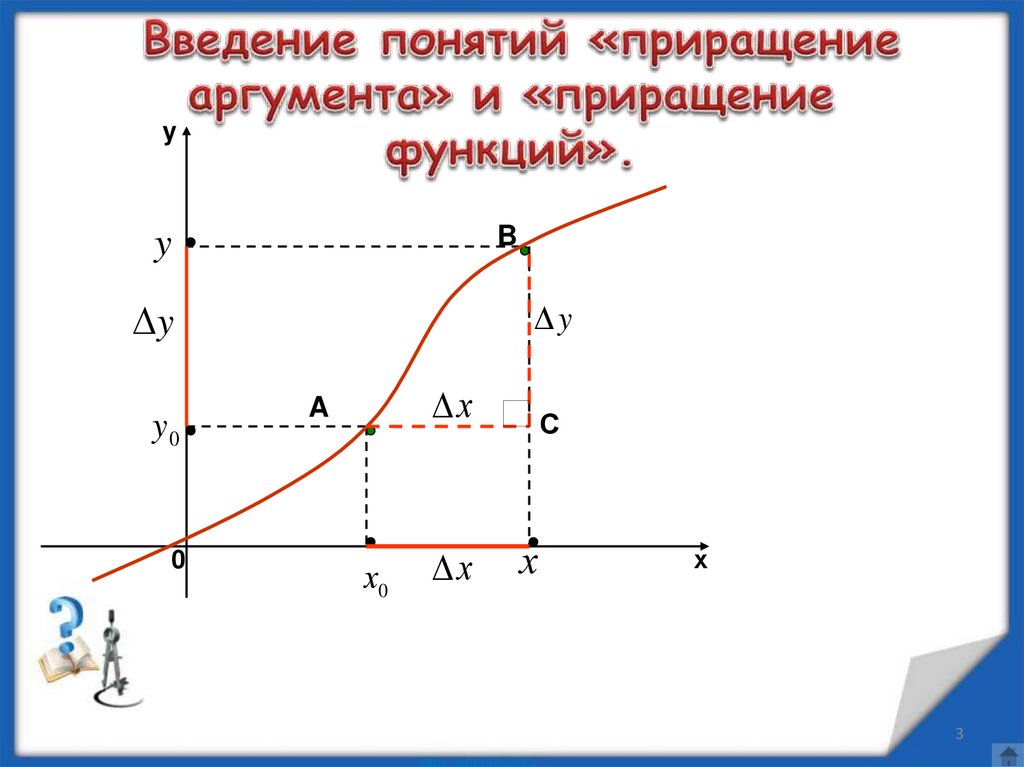
3. Введение понятий «приращение аргумента» и «приращение функций».
yB
y
y
y0
0
y
х
A
х0
х
С
х
х
3
4.
Определение 1: Пусть функция y f x определена вточках
х и x0 . Разность
называют
приращением аргумент а.
Определение 2: Разность
приращением функции.
Итак,
х х х0 , значит,
называют
х х0 х.
у у( х0 х) у( х0 )
4
5.
Предел отношения приращенияфункции у к приращению аргумента х
при условии, что - называется
производной данной функции и имеет
вид:
y
f ' ( x) lim
x 0 x
5
6.
67.
1. Даем аргументу Х приращение : Х + х2. Найдем наращенное значение функции, т.е. : у (х +
3. Вычисляем приращение функции:
х).
у у ( х х) у ( х)
4. Составляем отношение приращения функции к
приращению аргумента:
у у ( х х) у ( х)
х
х
у
5. Находим предел отношения
при
х
.
y
lim
y
x 0 x
х 0 :
7
8.
Дано : f ( x) x 2 1.Найдем f ( x) в точке х0 2, то есть f ( 2).
Решение
f ( x) f ( x0 x) f ( x0 )
f ( x0 x) f ( 2 x) ( 2 x) 2 1
4 4 x x 2 1 5 4 x x 2
f ( x0 ) ( 2) 2 1 4 1 5
f ( x) 5 4 x x 2 5 4 x x 2
f ( x) 4 x x 2
4 x
x
x
f ( x)
Если x 0, то
4, то есть f ( x) 4.
x
Ответ : f ( x) 4.
8
9.
910.
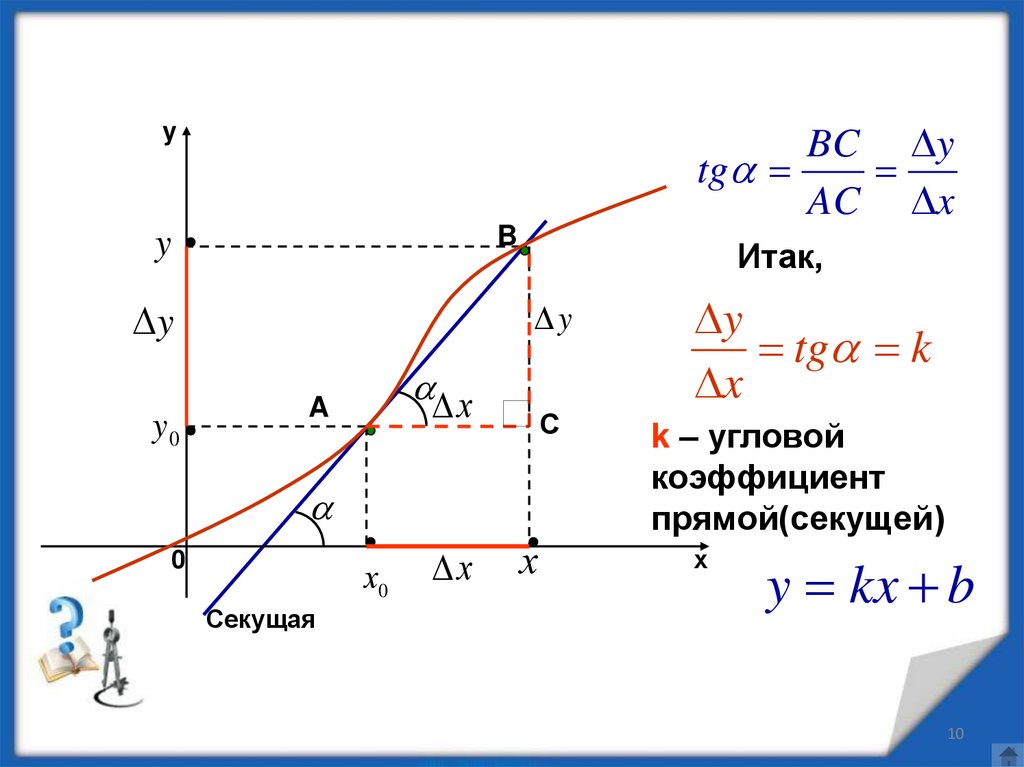
BC ytg
AC x
y
B
y
y
y0
Итак,
y
y
tg k
x
С
k – угловой
коэффициент
прямой(секущей)
х
A
0
х0
Секущая
х
х
х
y kx b
10
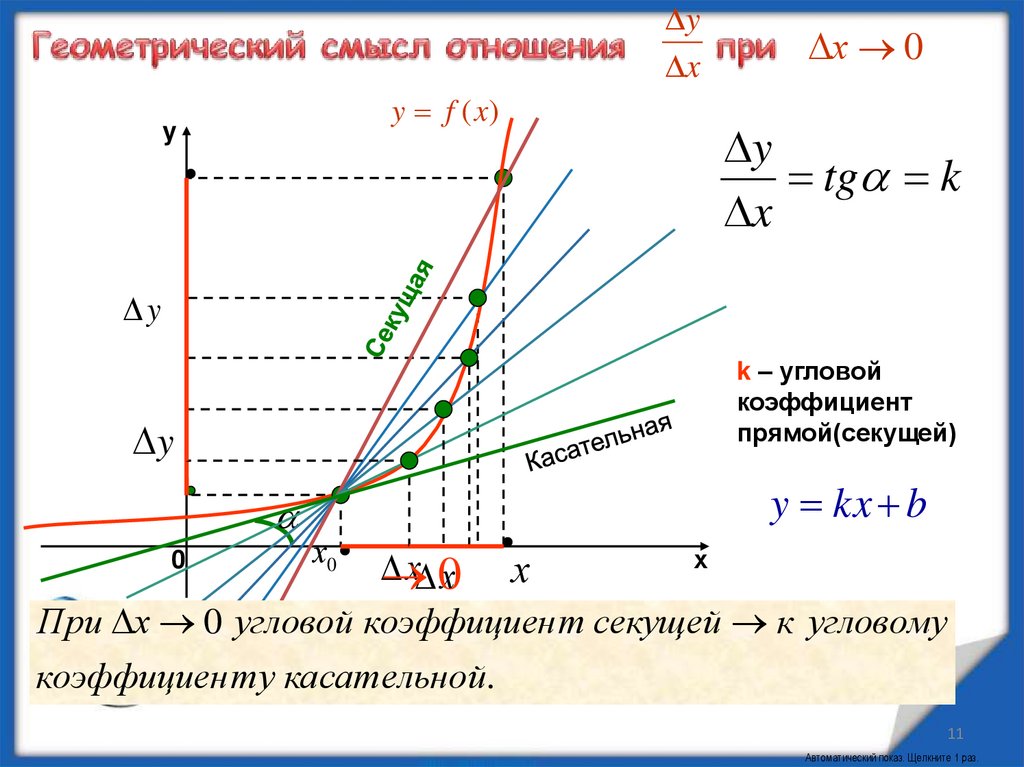
11. Геометрический смысл отношения при
yx
y f (x)
y
х 0
y
tg k
x
y
k – угловой
коэффициент
прямой(секущей)
y
y kx b
х0
х
х
х
0х
При
х стремится
0 угловойзанять
коэффициен
секущей Токесть,
угловому
Секущая
положениеткасательной.
касательная есть предельное положение секущей.
коэффициен ту касательной.
0
11
Автоматический показ. Щелкните 1 раз.
12.
y f (x)y
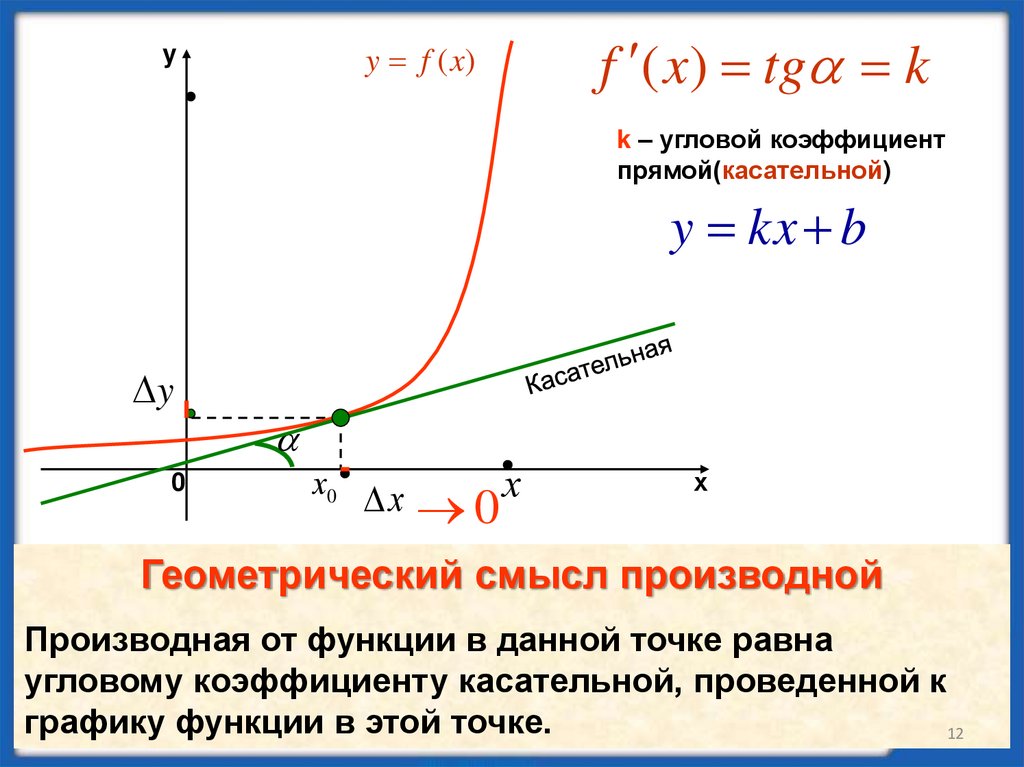
f ( x) tg k
k – угловой коэффициент
прямой(касательной)
y kx b
y
0
х0
х 0х
х
Геометрический смысл производной
Производная от функции в данной точке равна
угловому коэффициенту касательной, проведенной к
графику функции в этой точке.
12
13.
.и
,
13
14. Рассмотрим возможные типы задач на касательную
1415.
Ключевая задача 1.Решение. 1. Обозначим абсциссу точки касания а, тогда а=2.
2. Найдем f(a): f(a)=22–2·2–3, f(a)=-3.
3. Найдем f’ (x) и f’(a): f’(x)=2x–2, f’(a)=2.
4. Подставим найденные числа а, f(a), в общее
уравнение касательной у=f(a)+f’(a)(x–a): у=-3+2(х–2),
у=-3+2х–4, у=2х–7 – уравнение касательной.
15
16.
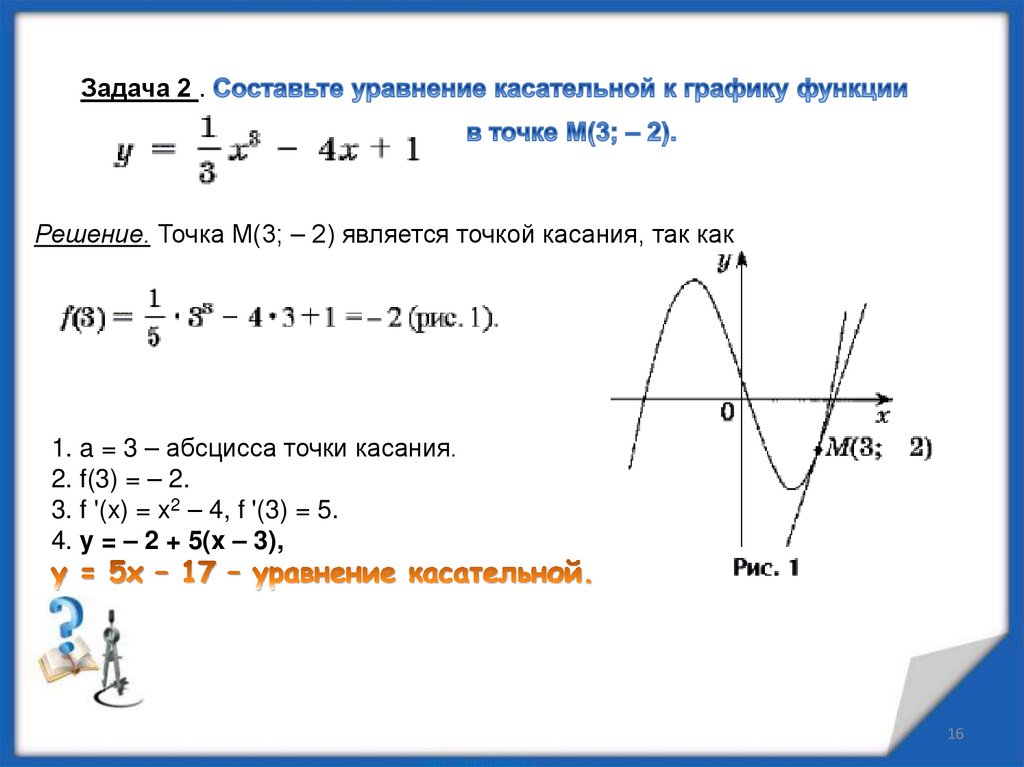
Задача 2 .Решение. Точка M(3; – 2) является точкой касания, так как
1. a = 3 – абсцисса точки касания.
2. f(3) = – 2.
3. f '(x) = x2 – 4, f '(3) = 5.
4. y = – 2 + 5(x – 3),
16
17. Физический смысл производной функции в данной точке
• Если материальная точка движется прямолинейно и ее координатаизменяется по закону
, то скорость ее движения
в момент
времени
равна производной
т.е.
x (t ),
(v(t ) x (t )).
a v (t ).
Ускорение движения
есть скорость изменения скорости, поэтому
ускорение движения в момент времени t равно производной v (t ).
a(t ) v (t ) x (t ).
17
18.
Точка движется прямолинейно по законуВычислите скорость движения точки:
а) в момент времени t;
б) в момент времени t=2с.
Решение.
S (t ) 2t 3t.
3
а)
V (t ) S (t ) (2t 3t ) 6t 3
б)
V (2) 6 * 2 3 21( м / с)
3
2
2
19.
Найдите скорость и ускорение для точки, движущейся позакону
S (t ) t 2 2t 3 :
а) в момент времени t;
б) в момент времени t=3с.
Решение.
2
а)V (t ) S (t ) (t 2t 3) 2t 2
a(t ) V (t ) S (t ) 2
б )V (3) 2 * 3 2 8( м / с)
a(3) 2( м / с )
2
20. Проблемная задача
• Две материальные точки движутся прямолинейно по законамS1 (t ) 2,5t 6t 1,
2
S
(
t
)
0
,
5
t
2
t
3
.
2
В какой момент времени скорости их равны, т.е.
2
V1 (t0 ) V2 (t0 ), t0 ?
21. Решение проблемной задачи
V1 (t ) ( 2,5t 6t 1) 5t 62
V1 (t 0 ) 5t 0 6
V2 (t ) (0,5t 2t 3) t 2
2
V2 (t 0 ) t 0 2
5t0 6 t 0 2
t0 2
22.
Домашнее задание:1. конспект лекции
2. Дадаян. гл.9,§9.1-9.4, №9.3,
9.5, 9.7
3. Колмогоров. гл.2,§4 п.1214,19, №178(б,в),193 (в,г), 194
(б,в) 195(б,г), 196 (б) №268
4. СВР: Подготовить
реферат на тему
«Производная и ее
применения»
22

















 Математика
Математика








