Плоское движение тела

1. ПЛОСКОПАРАЛЛЕНОЕ (ПЛОСКОЕ) ДВИЖЕНИЕ ТЕЛА

ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
КИНЕМАТИКА
ЛЕКЦИЯ 3

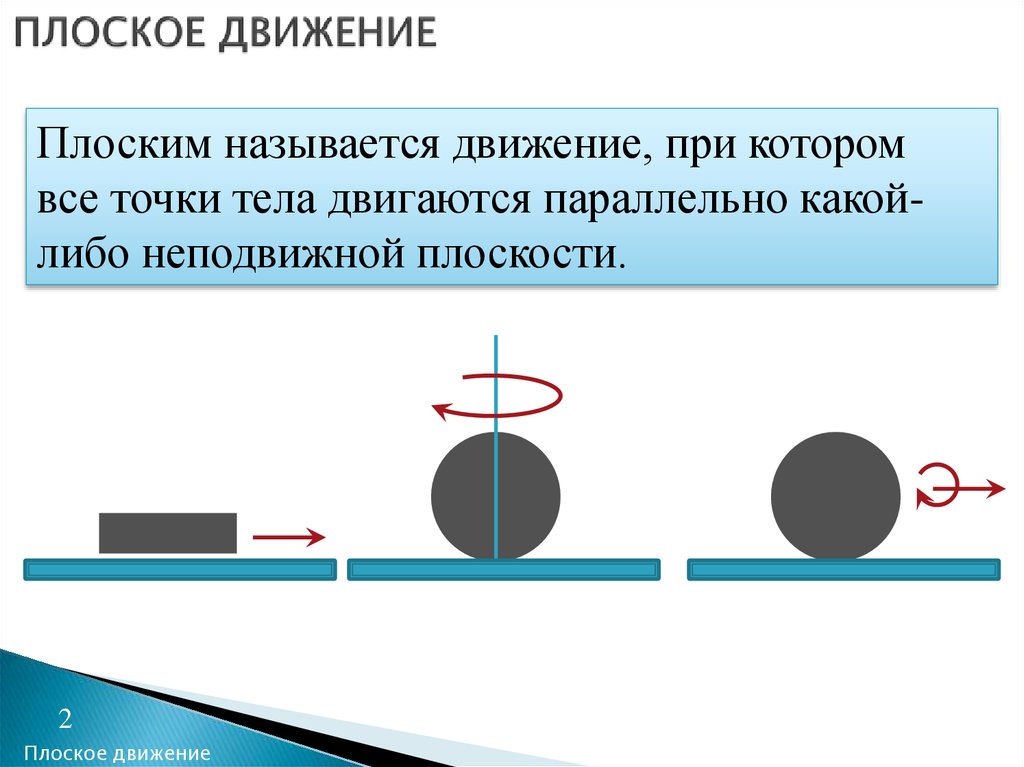
2. ПЛОСКОЕ ДВИЖЕНИЕ

Плоским называется движение, при котором
все точки тела двигаются параллельно какойлибо неподвижной плоскости.
2
Плоское движение

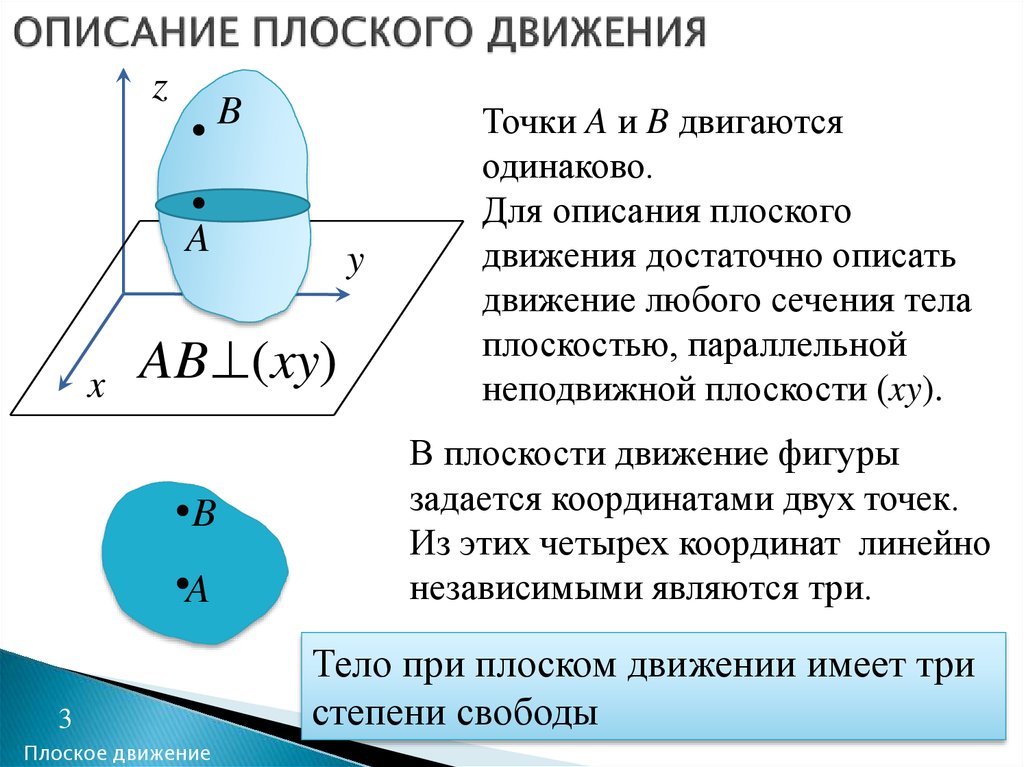
3. ОПИСАНИЕ ПЛОСКОГО ДВИЖЕНИЯ

z
B
A
x
y
AB (xy)
B
A
3
Плоское движение
Точки A и B двигаются
одинаково.
Для описания плоского
движения достаточно описать
движение любого сечения тела
плоскостью, параллельной
неподвижной плоскости (xy).
В плоскости движение фигуры
задается координатами двух точек.
Из этих четырех координат линейно
независимыми являются три.
Тело при плоском движении имеет три
степени свободы

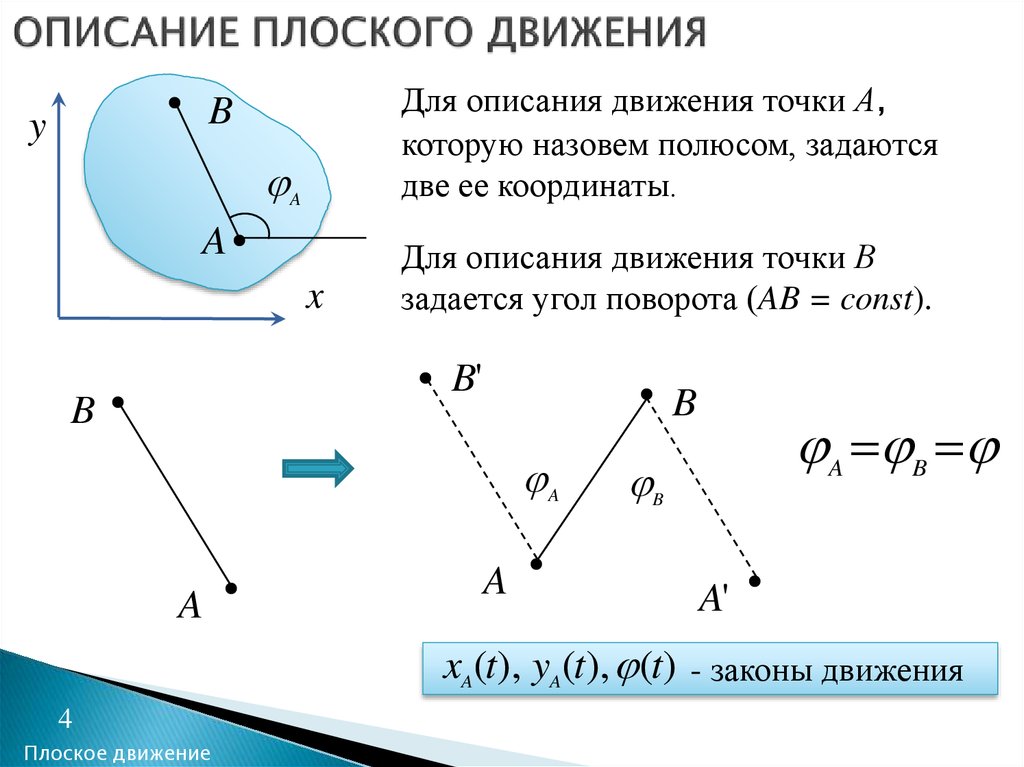
4. ОПИСАНИЕ ПЛОСКОГО ДВИЖЕНИЯ

Для описания движения точки А,
которую назовем полюсом, задаются
две ее координаты.
B
y
A
A
x
Для описания движения точки В
задается угол поворота (AB = const).
B'
B
B
A
A
A
A B
B
A'
xA(t), yA(t), (t) - законы движения
4
Плоское движение

5. ТЕОРЕМА О СЛОЖЕНИИ СКОРОСТЕЙ

Скорость любой точки тела в плоском движении
равна векторной сумме скорости в
поступательном движении тела вместе с полюсом
и скорости вращения точки вокруг полюса:
vB v A v A vBA
vB - скорость точки, v A - скорость полюса,
vBA - скорость вращение точки вокруг полюса.
5
Плоское движение

6. ТЕОРЕМА О СЛОЖЕНИИ СКОРОСТЕЙ

rB rA ;
z
B
rB
rA
O
x
drB drA d
dt
dt
dt
A
y
drB drA
vB ,
vA
dt
dt
d
Вектор описывает вращательное
?
движение точки В вокруг A.
dt
d
vBA
vBA AB; vBA AB
dt
6
Плоское движение
vB v A vBA

7. МГНОВЕННЫЙ ЦЕНТР СКОРОСТЕЙ (МЦС)

точка на системе отсчета, связанной с телом,
скорость которой в данный момент времени равна
нулю
Пример
Качение без
проскальзывания по
неподвижной поверхности
P
7
МЦС
Мгновенный центр
скоростей находится в точке
касания тела с неподвижной
поверхностью.

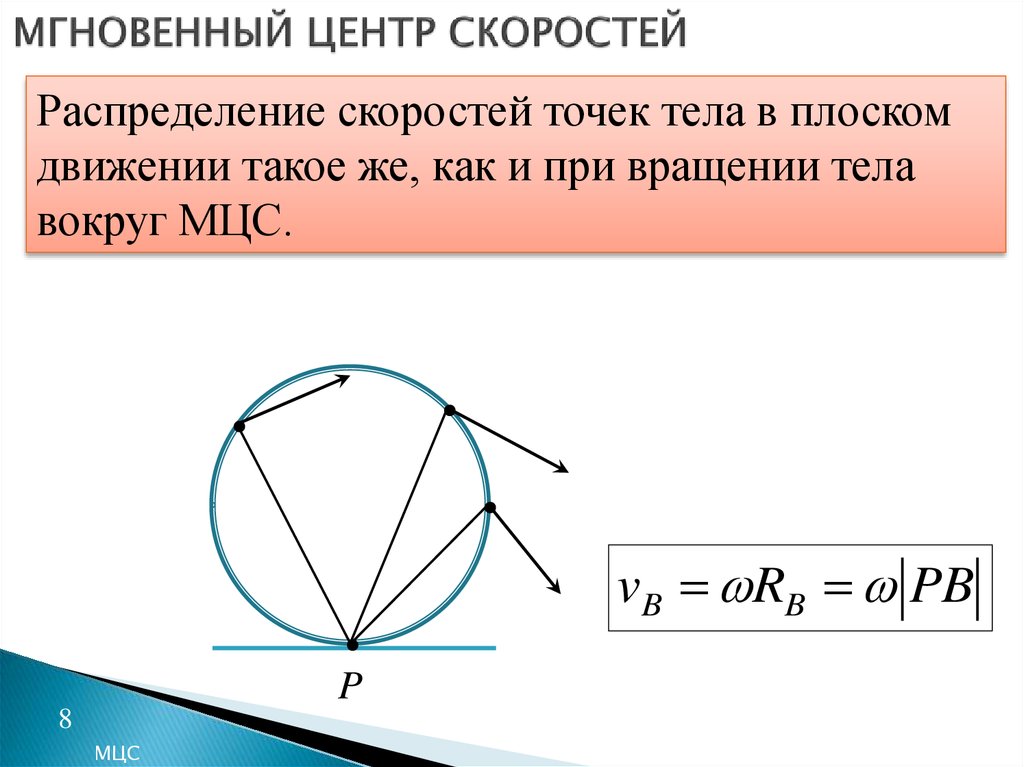
8. МГНОВЕННЫЙ ЦЕНТР СКОРОСТЕЙ

Распределение скоростей точек тела в плоском
движении такое же, как и при вращении тела
вокруг МЦС.
vB RB PB
P
8
МЦС

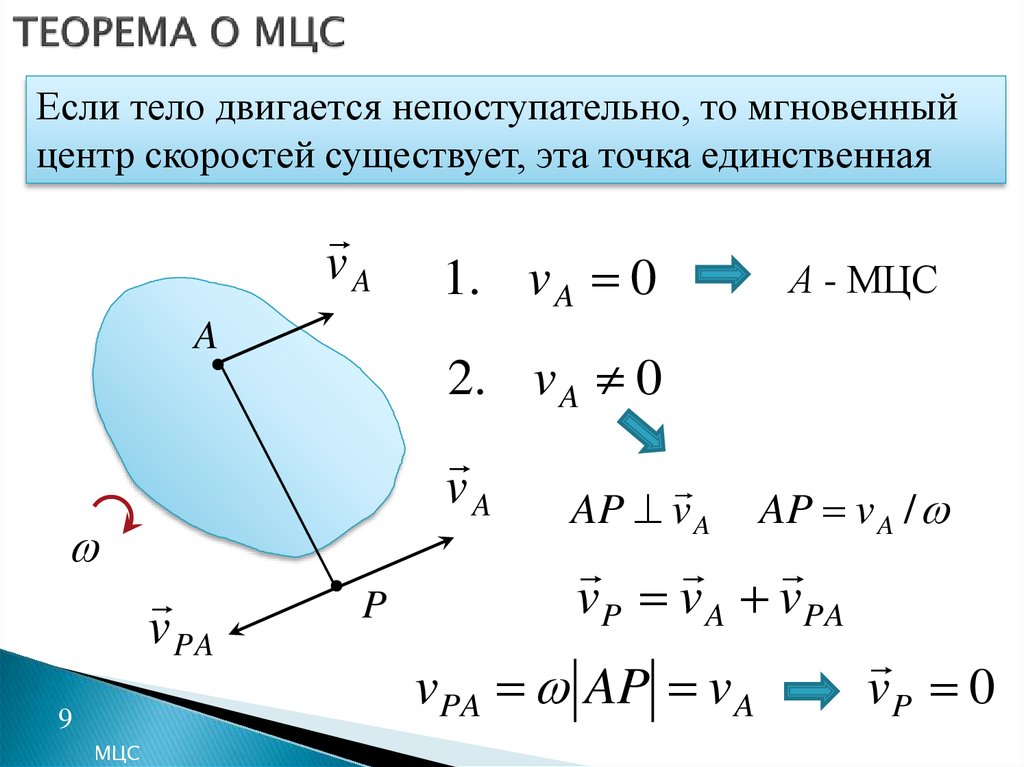
9. ТЕОРЕМА О МЦС

Если тело двигается непоступательно, то мгновенный
центр скоростей существует, эта точка единственная
vA
A
9
МЦС
v PA
P
1. v A 0
А - МЦС
2. v A 0
vA
AP v A AP v A /
vP v A vPA
vP 0
vPA AP v A

10. СПОСОБЫ НАХОЖДЕНИЯ МЦС

1. v A ,
Теорема о МЦС
2. Направлени е v A , vB
10
МЦС

11. ТЕОРЕМА О ПРОЕКЦИЯХ

Проекции скоростей двух точек плоской фигуры на
прямую, проходящую через эти точки, одинаковы
x
vA
vB v A vBA
vB
A
B
11
Теорема о проекциях
vB x vA x vBAx
v BA AB
vB x v A x