Лекция_3н

1. 4. МЕТОД ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ

2.

Метод гармонической линеаризации - является
приближенным
методом
исследования
режима
автоколебаний нелинейных систем. Этим методом можно
определить
условия
возникновения
и
параметры
автоколебаний как в системах второго порядка, так и в более
сложных системах
Метод заключается в замене существенного
наименьшего
элемента
с
характеристикой f(xH)эквивалентным линейным звеном с
коэффициентом kH. В замкнутой САУ, работающей в режиме
автоколебаний, условием эквивалентности служит равенство
амплитуд и фаз выходного сигнала реального нелинейного
элемента. При этом предлагается, что сигнал на входе
нелинейного элемента является синусоидальным. Такое
предположение справедливо во всех случаях, когда
линейная часть системы достаточно инерциальная и не
пропускает высокочастотные гармоники.

3.

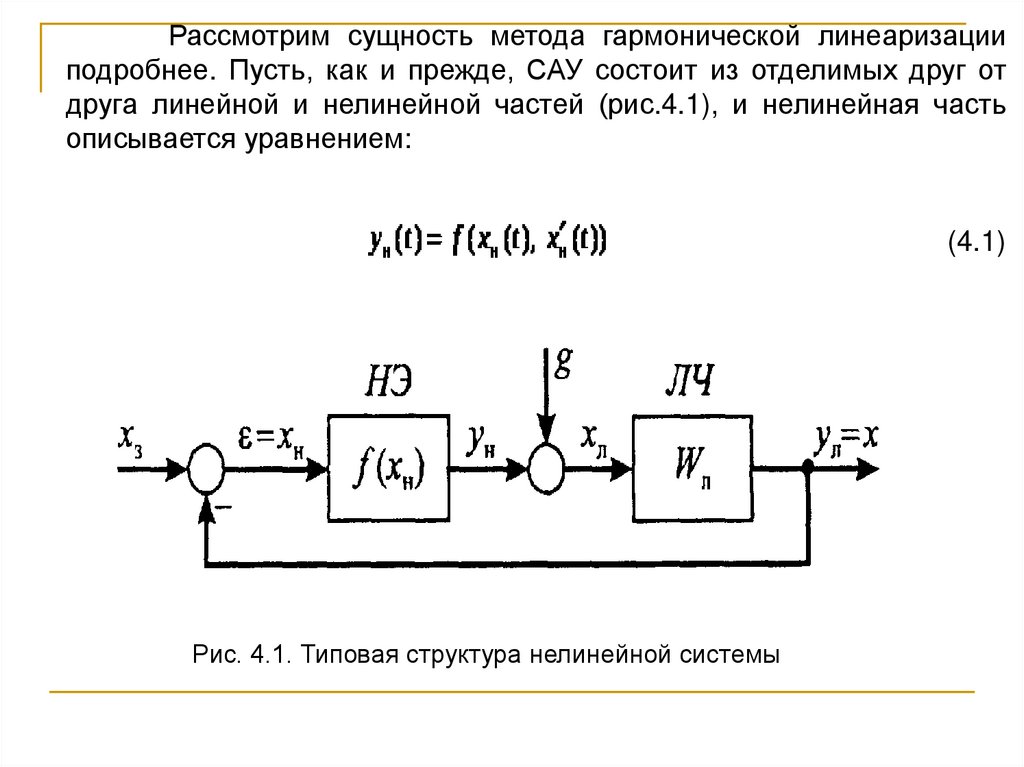
Рассмотрим сущность метода гармонической линеаризации
подробнее. Пусть, как и прежде, САУ состоит из отделимых друг от
друга линейной и нелинейной частей (рис.4.1), и нелинейная часть
описывается уравнением:
(4.1)
Рис. 4.1. Типовая структура нелинейной системы

4.

Предположим, что контур системы разомкнут (на выходе
линейной части) и что на входе нелинейного элемента действует
синусоидальный сигнал
(4.2)
При этом на выходе нелинейного элемента будет возникать
периодический сигнал
, форма которого зависит от характера
нелинейности и в общем случае существенно отличается от
синусоидальной.
Уравнение нелинейной части (4.1) при синусоидальном воздействии
(4.2) можно записать в таком общем виде:
(4.3)

5.

Периодический сигнал
Фурье
может быть разложен в ряд
где
- частота основной гармоники;
- частота k-той гармоники;
коэффициенты
и
определяются по формулам
, (k = 0, 1, 2,…)
(*)
, (k = 1, 2,…)
(**)

6.

k-тая гармоника выходного сигнала нелинейного элемента имеет
вид
(4.4)

7.

нелинейное уравнение может быть заменено линейным
уравнением. Эта операция называется гармонической
линеаризацией, а коэффициенты
и
коэффициентами гармонической линеаризации.
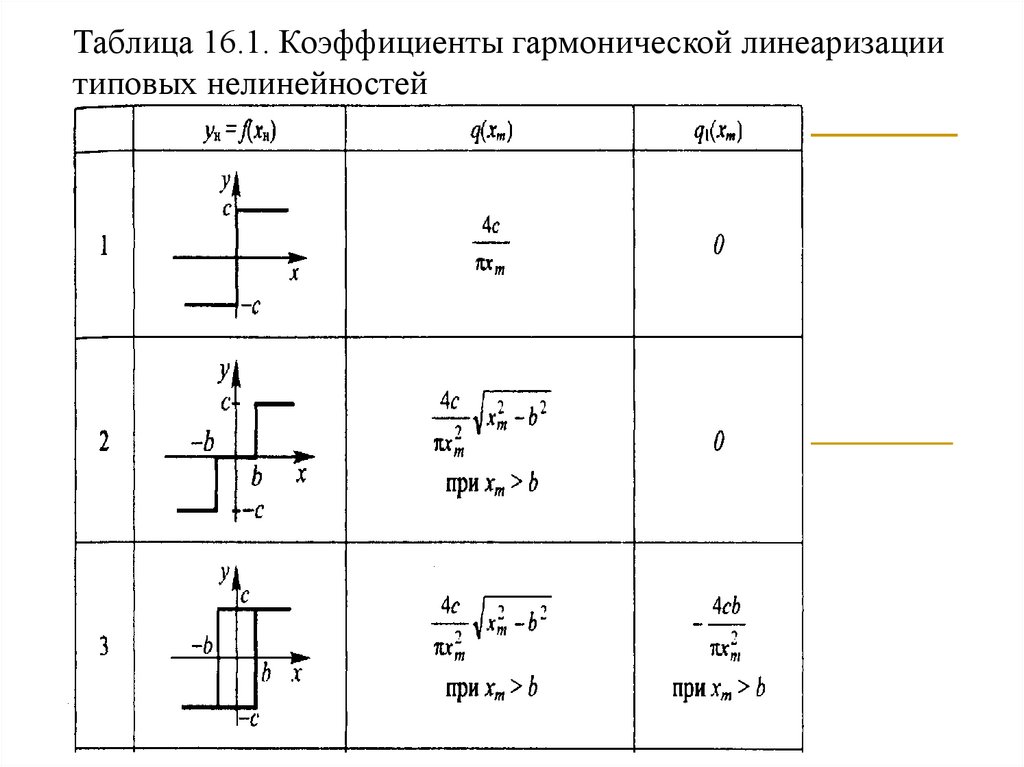
Коэффициенты гармонической линеаризации зависят от вида
нелинейности и могут быть определены по формулам.В таблице
16.1 приведены коэффициенты
и
для наиболее часто
встречающихся нелинейностей.
Гармоническая линеаризация принципиально отличается от
обычной линеаризации, т. к. коэффициенты гармонически
линеаризованного элемента непостоянны, а зависят от амплитуды
входного сигнала
. Однако при определенном режиме
периодических колебаний, когда значения
и хнт фиксированы,
коэффициенты гармонической линеаризации имеют также
постоянные значения. Благодаря этому для решения некоторых
задач анализа нелинейных систем могут быть использованы
понятия и методы теории линейных систем.

8.

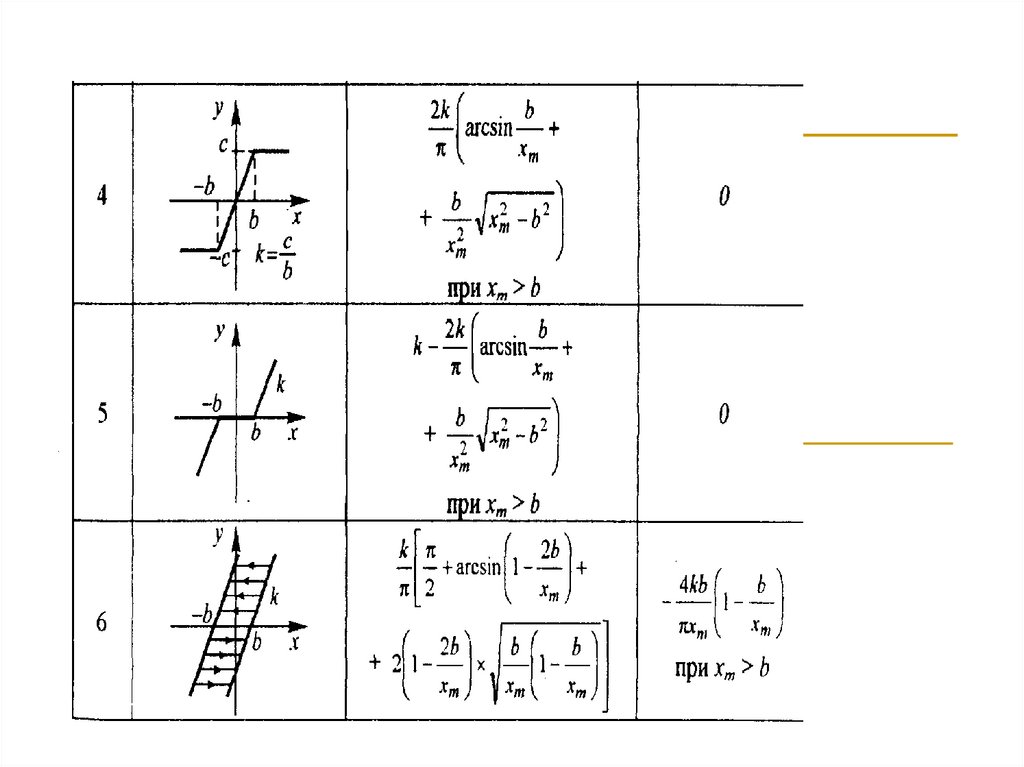
Таблица 16.1. Коэффициенты гармонической линеаризации
типовых нелинейностей

9.

10.

МЕТОДЫ УСТРАНЕНИЯ НЕГАТИВНОГО
ВЛИЯНИЯ
НЕЛИНЕЙНЫХ ЭЛЕМЕНТОВ

11.

Краткая характеристика методов.
Наличие существенно нелинейных элементов САУ, не предусмотренных
структурой, может вызвать ухудшение качества управления, а в ряде
случаев делает управление вообще невозможным. Это проявляется в росте
погрешности управления, увеличении времени протекания переходного
процесса и его колебательности, потере системой устойчивости в большом,
возможности возникновения автоколебательных режимов и др. В связи с
этим стремятся уменьшить вредное влияние нелинейных элементов
следующим образом:
1) улучшая конструкции функционально-необходимых элементов;
2) устраняя влияния нелинейного элемента путем изменения линейной
части системы за счет:
- изменения параметров и структуры линейной части системы;
- введения дополнительных линейных обратных связей (охват нелинейных
элементов линейными обратными связями);

12.

3) компенсируя влияние нелинейности путем:
- применения специальных компенсирующих нелинейных элементов,
обеспечивающих линейность системы;
- применения компенсирующих формирующих устройств,
осуществляющих введение дополнительного (компенсирующего) сигнала
управления по отклонению;
- используя вибрационную линеаризацию нелинейности.
Применительно к конкретной динамической системе можно применять
наиболее рациональные из указанных методов или их комбинации.

13.

Улучшение конструкции функционально необходимых элементов.
Тщательная конструктивная обработка, высокая точность изготовления
функционально необходимых элементов позволяют приблизить
характеристики этих элементом к линейным. Повышение запаса мощности
дает возможность увеличить линейный диапазон их работы без ограничения.
Увеличение коэффициента преобразования системы уменьшает влияние
зоны нечувствительности. Усложнение конструкции редуктора за счет
введения противолюфтовых шестерен и т. д. позволяет свести к минимуму
влияние люфта. Однако такой путь устранения вредного влияния
нелинейных элементов целесообразен до определенного предела, так как
ведет к возрастанию стоимости изготовления устройств и их эксплуатации.
Устранение в той или иной степени влияния сил сухого трения вызывает
уменьшение зоны нечувствительности и статических ошибок. Вместе с тем
уменьшение сил сухого трения, оказывающих стабилизирующее действие на
систему, может вызвать автоколебания. Целесообразным выбором
параметров системы можно добиться ослабления влияния различных
нелинейностей на качество и устойчивость САУ.

14.

Устранение вредного влияния нелинейного элемента за счет
изменения параметров линейной части САУ.
Изменение параметров и структуры линейной части САУ. С
помощью соответствующего выбора параметров линейной части можно
существенно ослабить или даже в некоторых случаях устранить влияние
нелинейных элементов на устойчивость и качество переходных процессов САУ.
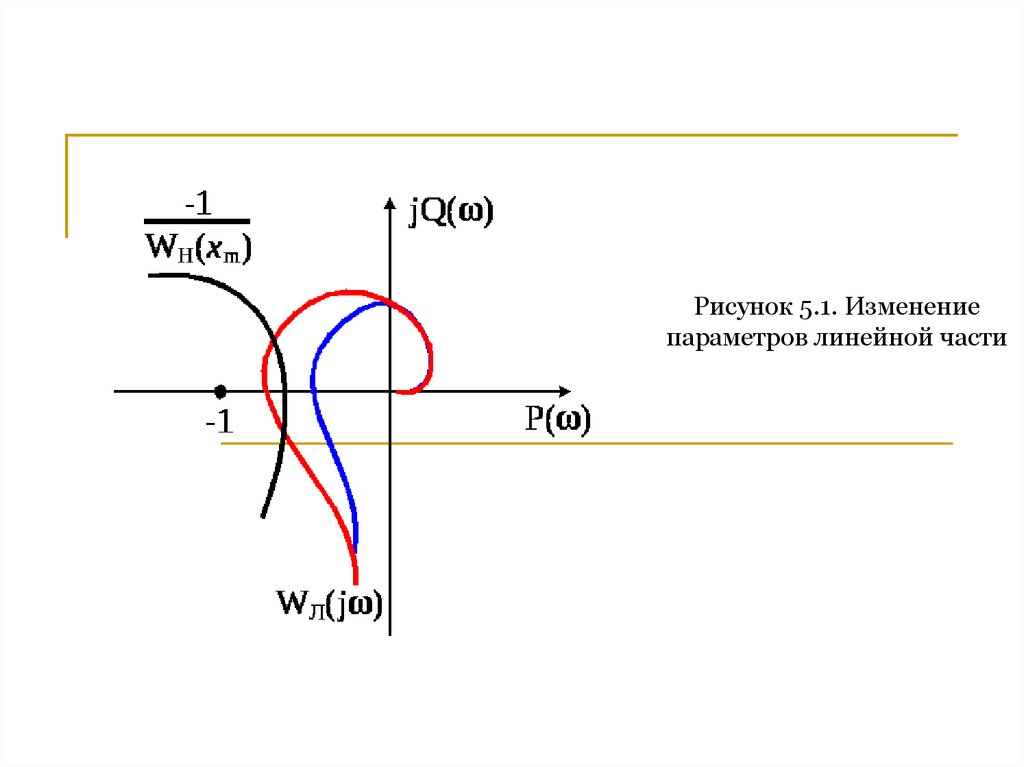
Изменяя параметры линейной части, можно добиться, чтобы
характеристики
и
не пересекались и условия гармонического
баланса (условия возникновения автоколебаний) не выполнялись (рис.5.1).

15.

Рисунок 5.1. Изменение
параметров линейной части

16.

Подбором параметров линейной части можно изменить параметры
возникающего автоколебательного режима
в нужном направлении.
Введение дополнительных обратных связей. Эффективный способ
уменьшения влияния нелинейных элементов применение обратных связей,
охватывающих те или иные нелинейные элементы. Если элемент с
,
имеющий нелинейность с эквивалентной
АФЧХ
охвачен стабилизирующей обратной связью, то
эквивалентная частотная характеристика определяется выражением
. (5.1)

17.

Можно так подобрать параметры стабилизирующей обратной
связи
, чтобы в рабочем диапазоне частот обеспечивалось
соотношение
. (5.2)
Тогда
и характеристика системы не зависит от свойств нелинейного элемента и
амплитуды действующих на систему сигналов. Данный способ достаточно
экономичен, эффективен и широко применяется на практике.

18.

Компенсация влияния нелинейностей.
Метод коррекции, основанный на применении обратных
нелинейностей.
Суть метода в том, что для компенсации влияния той или иной нелинейности в
цепь системы включается статическое звено, имеющее характеристику,
компенсирующую исходную. В результате суммарная характеристика линейна.
Здесь возможны последовательная и параллельная коррекции.
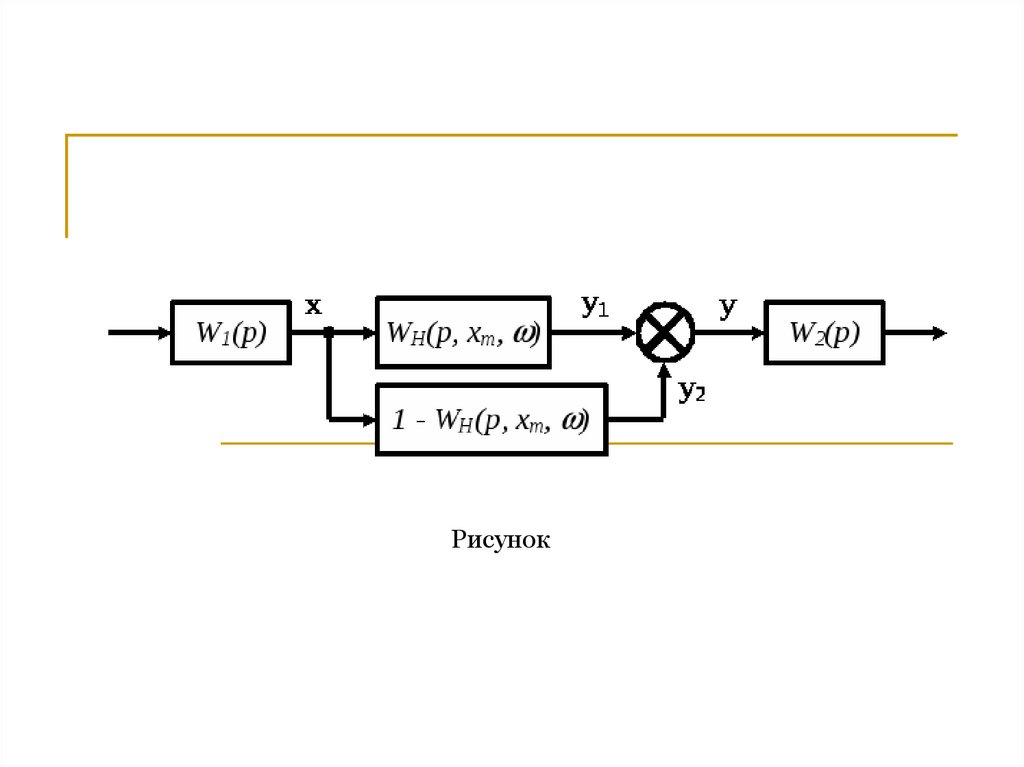
На рисунке показано, как осуществляется компенсация характеристики
нелинейного элемента
путем параллельного включения добавочного нелинейного элемента с
характеристикой
, выполняемого в виде модели.

19.

Рисунок

20.

Таким образом, если х — синусоидальный сигнал, то сигналы у1 и у2 в сумме
тоже должны давать синусоидальный сигнал у. Следовательно, эти
параллельно соединенные нелинейные элементы могут быть заменены
линейным элементом.

21.

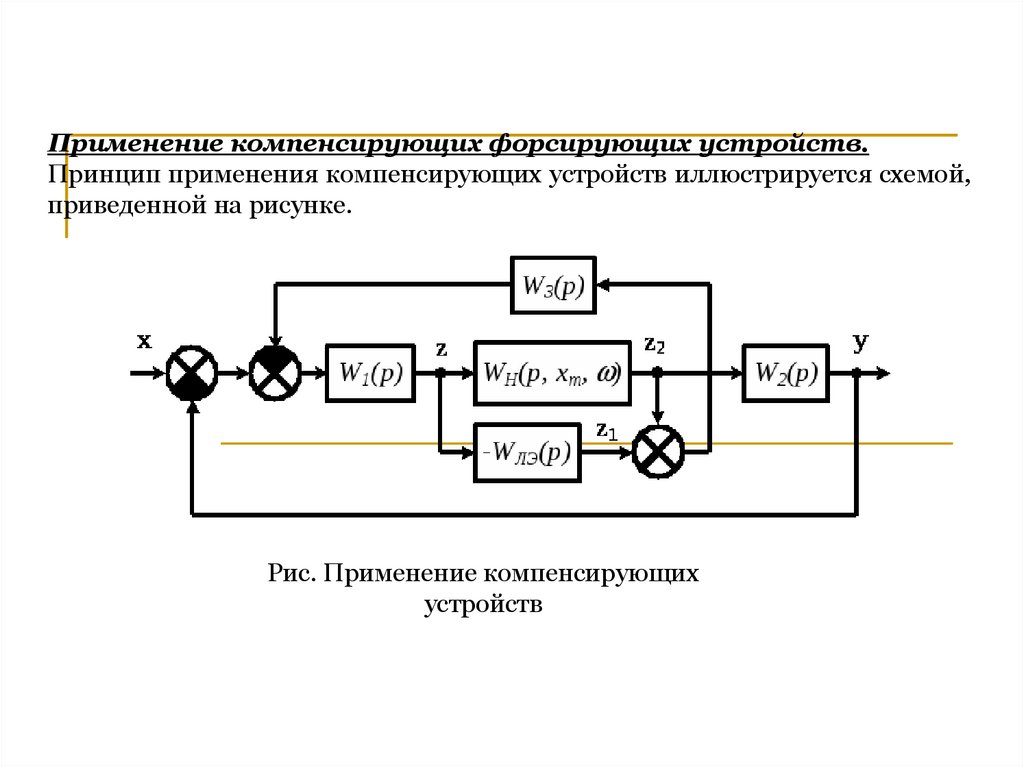
Применение компенсирующих форсирующих устройств.
Принцип применения компенсирующих устройств иллюстрируется схемой,
приведенной на рисунке.
Рис. Применение компенсирующих
устройств

22.

Параллельно нелинейному элементу включается модель линейного элемента
(– WЛЭ(p)) с желаемой характеристикой. Сигналы нелинейного элемента и
линейного элемента сравниваются и через форсирующий элемент
с W3(p) подаются в прямую цепь. Если
, то на вход схемы поступает
отрицательный сигнал, уменьшающий
; если
, то компенсирующий
сигнал – положительный, увеличивающий
. За счет компенсирующего
контура обеспечивается равенство
, т.е. устранение влияния
нелинейности на работу системы.
ПФ системы в разомкнутом состоянии без компенсации имеет вид

23.

При наличии цепи компенсации
При условии, что
нелинейный элемент влияния на
характеристики системы не оказывает, т. е.
Часто желательно иметь
, тогда

24.

Реализация таких систем вызывает ряд трудностей, и полная
компенсация влияния нелинейности, как правило, невозможна.
Действительно, элемент с характеристикой W3(p) должен быть
в общем случае дифференцирующим, что невозможно или
трудновыполнимо; кроме того, для устойчивой работы система
должна быть грубой.
Несмотря на указанные трудности, данный метод позволяет в
достаточной степени ослабить действие нелинейного элемента
типа зона нечувствительности, люфт и др.

25.

СТАТИЧЕСКИЕ И ПЕРЕХОДНЫЕ
ХАРАКТЕРИСТИКИ НЕЛИНЕЙНЫХ
СИСТЕМ

26.

Для нелинейных систем справедливы
все положения точности линейных САУ в
стационарных режимах, в частности,
положение о влиянии на точность САУ
величины коэффициента передачи системы,
порядка астатизма, компенсирующих
воздействий по внешним возмущениям.
Вместе с тем наличие нелинейностей в
системе создает определенные особенности
в стационарных режимах

27.

Статический режим САУ определяется
зависимостью статического значения выходной
величины Y системы от входного воздействия X
или внешнего возмущающего воздействия F. В
нелинейных системах наличие нелинейных
статических
характеристик
у
отдельных
звеньев приводит к тому, что зависимость Y(X)
получается также нелинейной, т.е. статизм
системы также является нелинейной функцией.

28.

Для приближенной оценки нелинейной
системы
можно
оперировать
максимальными отклонениями
выходной
величины Ymax , соответствующим
максимально возможному
изменению
входного воздействия Xmax , а также
диапазоном
изменения
крутизны
статической характеристики системы, т.е.
изменением величины статизма

29.

Статическая
характеристика
нелинейной
системы
строится
по
статическим
характеристикам
составляющих ее звеньев, исходя из их
соединения, определяемого структурной
схемой. Вначале по характеристикам
отдельных звеньев строят характеристики
групп последовательно и параллельно
соединенных звеньев, а также звеньев,
охваченных местными обратными связями.

30.

Для последовательного соединения
звеньев задаются рядом дискретных
значений входной величины X. Для каждого
их этих значений определяется
соответствующее значение выходной
величины каждого звена, являющего
входной величиной для следующего звена,
и так до получения значения выходной
величины всей цепочки Y.

31.

ПРИ ПАРАЛЛЕЛЬНОМ СОЕДИНЕНИИ
ЗВЕНЬЕВ ОРДИНАТА ИСКОМОЙ
ЗАВИСИМОСТИ Y определяется как сумма
ординат статических характеристик
отдельных звеньев