Похожие презентации:
Нелинейные системы автоматического управления
1. Нелинейные системы автоматического управления
Нелинейной системой автоматическогоуправления называется такая система,
которая содержит хотя бы одно звено
описываемое нелинейным уравнением
УГАТУ-2015
1
2.
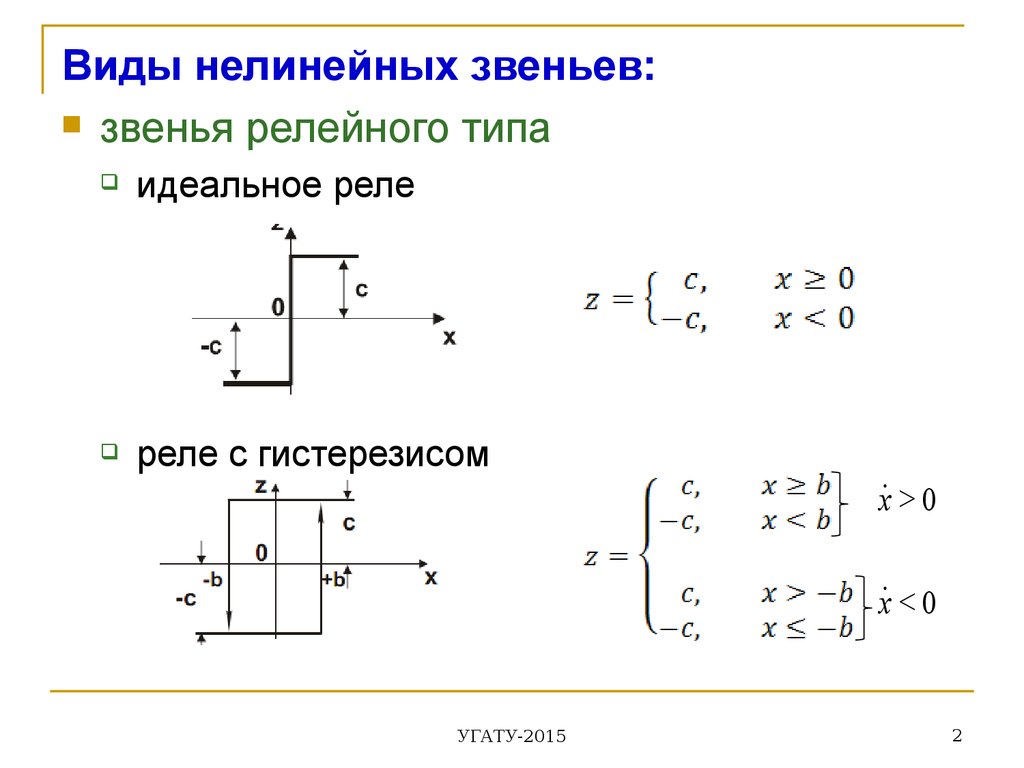
Виды нелинейных звеньев:звенья релейного типа
идеальное реле
реле с гистерезисом
x > 0
x < 0
УГАТУ-2015
2
3.
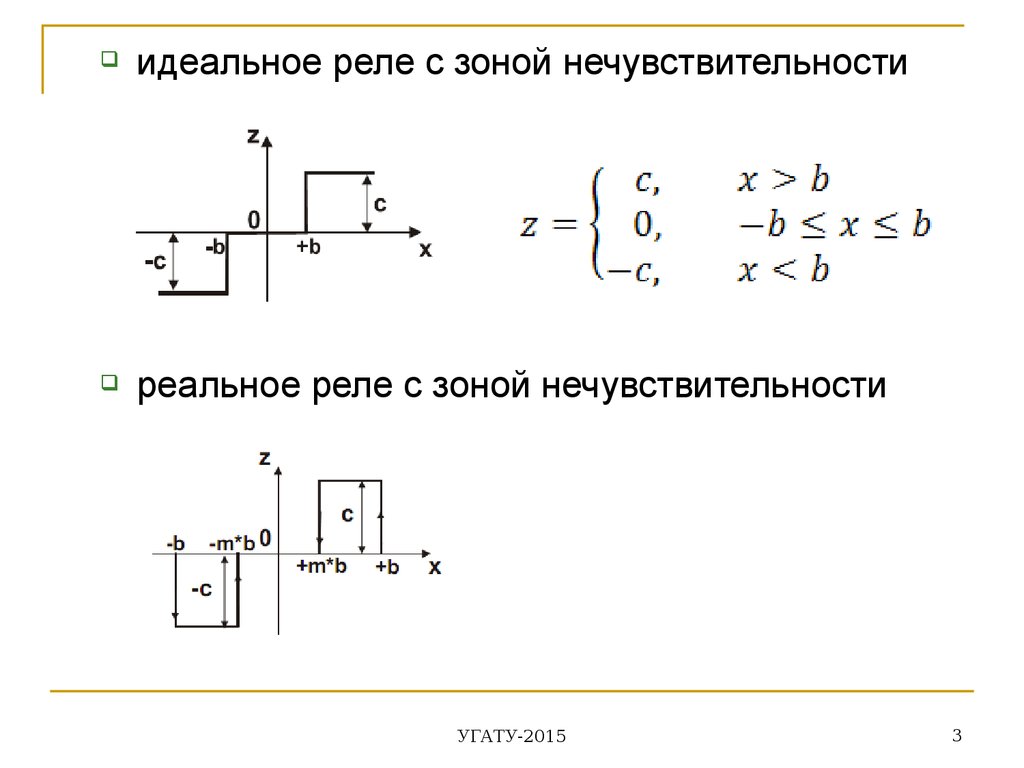
идеальное реле с зоной нечувствительностиреальное реле с зоной нечувствительности
УГАТУ-2015
3
4.
звено с кусочно-линейной характеристикойусилитель с ограничением
усилитель с зоной нечувствительности
УГАТУ-2015
4
5.
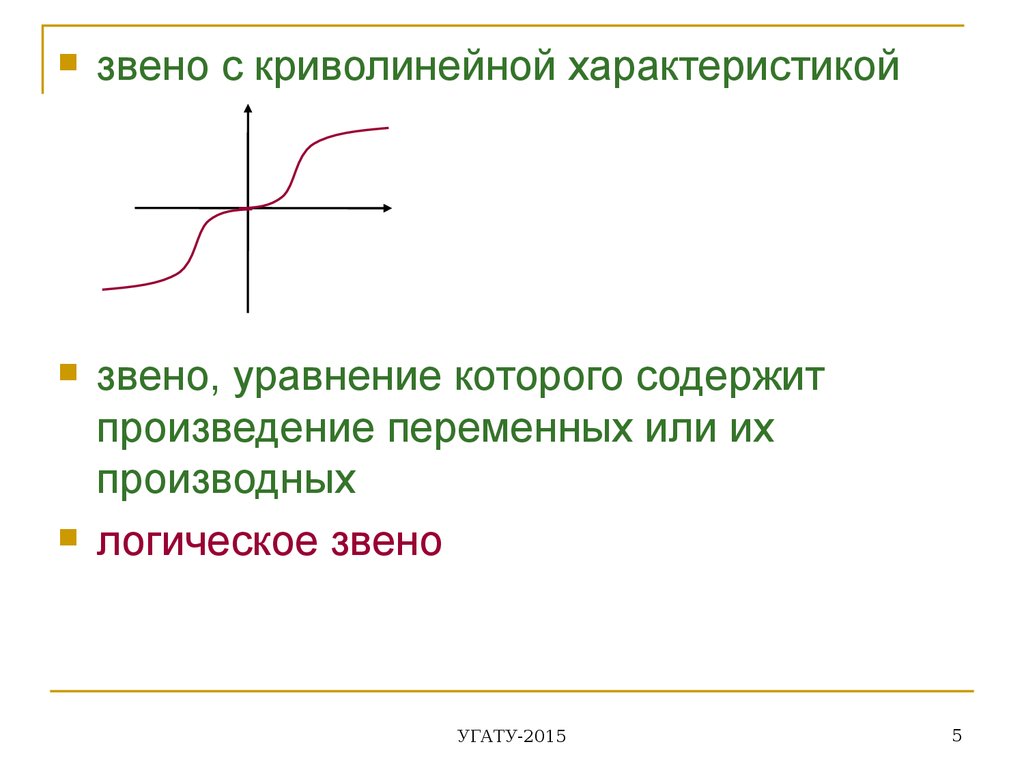
звено с криволинейной характеристикойзвено, уравнение которого содержит
произведение переменных или их
производных
логическое звено
УГАТУ-2015
5
6. Метод гармонической линеаризации
относится к приближенным методампрост и универсален
широко распространен в инженерной
практике
УГАТУ-2015
6
7.
Идея метода гармоническойлинеаризации. Условия применимости
Предполагается
в системе автоколебания с амплитудой ak и
частотой ωk.
*
*
x
(
t
)
x
sin t
Сигнал на входе НЗ
Сигнал
на выходе
НЗ
y
y (t )
0
2
yk sin(k k ),
t,
k 1
УГАТУ-2015
7
8.
предполагается,что сигнал y(t), пройдя через линейную
часть WЛ(jω), фильтруется ею в такой
степени, что в сигнале на x(t) на выходе
линейной части можно пренебречь высшими
гармониками x2(t), x3(t)…и считать, что
x(t ) x1 sin( t 1 )
Это предположение называется гипотезой
фильтра.
УГАТУ-2015
8
9.
yk WЛ ( jk )1
y1 WЛ ( j )
УГАТУ-2015
9
10.
x * (t ) x(t ) 00 x(t ) (t )
x * (t ) (t )
(1)
(2)
(3)
x* x1 - уравнение баланса амплитуд
- уравнение баланса фаз
гармонических колебаний
уравнения гармонического баланса
УГАТУ-2015
10
11. Решаются две группы задач:
исследование периодических движений внелинейных замкнутых системах
(определение условий устойчивости и
параметров ПД);
исследование условий отсутствия
моногармонических автоколебаний в
нелинейных замкнутых системах.
УГАТУ-2015
11
12. Гармоническая линеаризация нелинейностей
Пустьзаданная нелинейная функция
y F (x)
При
выполнении гипотезы фильтра
переменная x(t) a sin t sin .
Разложим периодический сигнал на выходе
НЗ в ряд Фурье:
1
y A0 A1 sin B1 cos A2 sin 2 B2 cos 2
2
УГАТУ-2015
12
13.
1y A0 A1 sin B1 cos A2 sin 2 B2 cos 2
2
Предполагаем
1 2
A0 F (a sin )d 0
0
x
sin
a
px
cos
a
где p=d/dt
q (a )
y q(a) x
px
где q(a) и q'(a) – коэффициенты гармонической
линеаризации
УГАТУ-2015
13
14.
A1 1 2q(a )
[ F (a sin ) sin ]d ,
a a 0
2
B1 1
q (a)
[
F
(
a
sin
)
cos
]
d
a a 0
Для однозначной нелинейной
характеристики F(x) коэффициент q'(a)=0.
Для неоднозначной характеристики типа
гистерезис q'(a)≠0 и q'(a)<0
УГАТУ-2015
14
15.
Замена исходного нелинейного уравненияприближенным уравнением для первой
гармоники называется гармонической
линеаризацией
y
q (a )
W Н (a, ) q (a)
p
x
передаточной функцией нелинейного
гармонически линеаризованного звена
УГАТУ-2015
15
16. Исследование устойчивости периодических движений методом гармонической линеаризации
Исследованиеустойчивости
периодических движений
методом
гармонической
Запишем уравнение
замкнутой гармонически
линеаризованной
нелинейной САУ в
линеаризации
операторной форме:
X ( s ) WЛ ( s )Y ( s )
Y ( s ) WH X ( s )
R
( s)
передаточная
функция линейной
WЛ ( s)
Q( s)
части, n[R(s)] m[Q(s)]
УГАТУ-2015
16
17.
Характеристическое уравнениегармонически линеаризованной нелинейной
САУ:
q
L( s ) Q( s ) R( s )(q
подставим
s) 0
в L(s) s=jωп
выделим
вещественную U(aп,ωп,) и мнимую
V(aп,ωп) части.
по
критерию Михайлова
U (aп , п ) 0,
М (aп , п ) 0.
УГАТУ-2015
17
18.
U (aп , п ) 0,М (aп , п ) 0.
определяются параметры ПД aп и ωп.
УГАТУ-2015
18
19.
Если при положительном приращенииамплитуды ∆a>0 кривая Михайлова займет
положение 1-1, а при отрицательном
приращении амплитуды ∆a<0 займет
положение 2-2, то исследуемые ПД с
параметрами (aп,ωп) устойчивы, т.е. в НС
имеют место автоколебания. В противном
случае ПД – неустойчивы, а сама
нелинейная САУ устойчива в малом.
УГАТУ-2015
19
20. Частотный метод исследования устойчивости ПД в НС Л. С. Голдфарба (1946 г.)
Основная идея1 WH (a) W Л ( s) 0
(4)
WН(a) комплексный коэффициент передачи НЭ
j Н ( a )
WН (a, ) q (a) jq (a ) WН (a ) e
УГАТУ-2015
20
21.
2WН (a, ) [q(a )] [q (a)]2 , Н (a) arctg
q (a )
q(a)
s=jω
решим полученное уравнение относительно
неизвестных aп и ωп .
Графоаналитическое решение
1
W Л ( j )
Z Н (a)
W Н (a)
1
Z Н (a )
W Н (a )
- инверсный коэффициент
гармонической линеаризации
УГАТУ-2015
21
22.
qУГАТУ-2015
q’
22
23.
УГАТУ-201523
24.
Оба годографа и строятся на однойкомплексной плоскости.
W Л ( j ) - АФХ линейной части определяет
частоту ωп ПД,
Z Н (a ) - амплитуду aп ПД.
ПД – устойчивы, если, двигаясь по
характеристике в сторону возрастания
амплитуды, переходим из неустойчивой в
устойчивую область D-разбиения при
устойчивой линейной части .
УГАТУ-2015
24
25.
УГАТУ-201525
26.
УГАТУ-201526
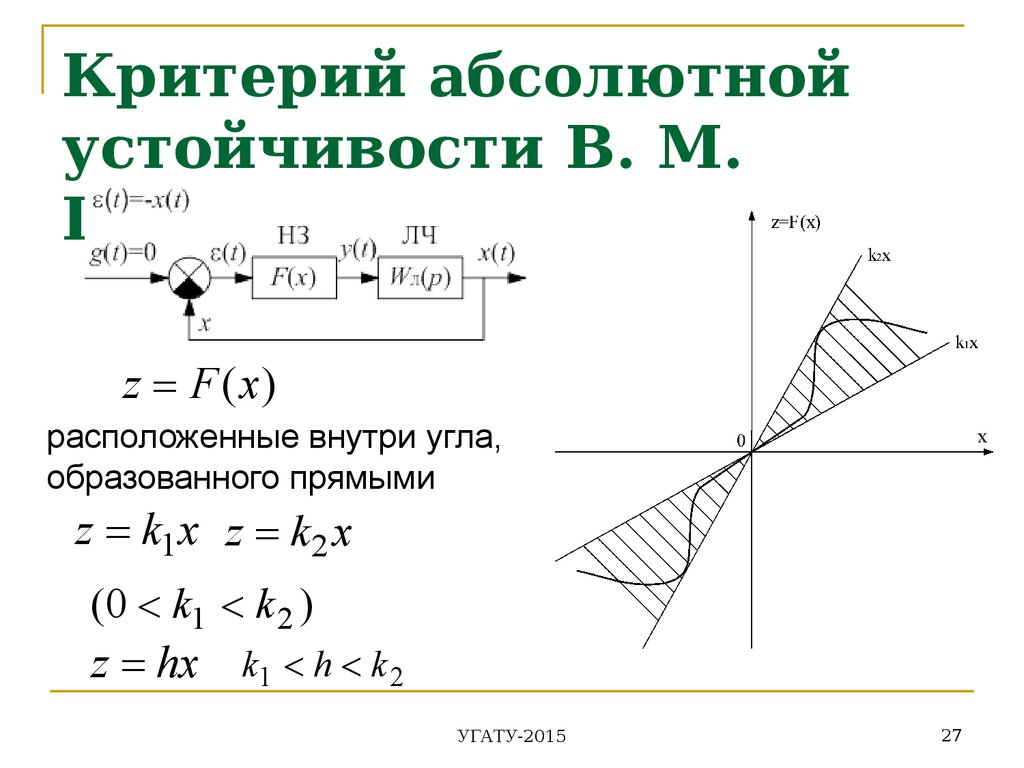
27. Критерий абсолютной устойчивости В. М. Попова
z F (x)расположенные внутри угла,
образованного прямыми
z k1x z k 2 x
(0 k1 k 2 )
z hx k1 h k 2
УГАТУ-2015
27
28.
F ( x)0
K
x
K1 0
линейная часть системы устойчива W Л (s)
Абсолютная устойчивость нелинейной САУ
предложена в 1959 г. в работе румынского
математика В. М. Попова.
УГАТУ-2015
28
29.
Теорема. Если замкнутая система состоитиз
устойчивой
линейной
части
с
передаточной
функцией,
все
полюсы
которой
располагаются
в
левой
полуплоскости, и нелинейного элемента с
характеристикой z F (x) , лежащей в угле
0 F ( x) / x K , то достаточным условием этой
системы является выполнение при всех 0
неравенства
1
Re 1 jq W Л ( j ) 0
k
(1)
где q – произвольное вещественное число
УГАТУ-2015
29
30.
Геометрическая интерпретация теоремы.введем видоизмененную частотную
характеристику W * ( j )
Re W * ( j ) Re W Л ( j )
ImW * ( j ) ImW Л ( j )
обозначим
Re W * ( j ) U * ( ) ImW * ( j ) V * ( )
1
1
Re 1 jq WЛ ( j ) ReWЛ ( j ) q ImWЛ ( j ) 0
K
K
(2)
(3)
(4)
1
U ( ) qV ( ) 0
K
1
U * ( ) qV * ( ) 0
K
*
*
УГАТУ-2015
30
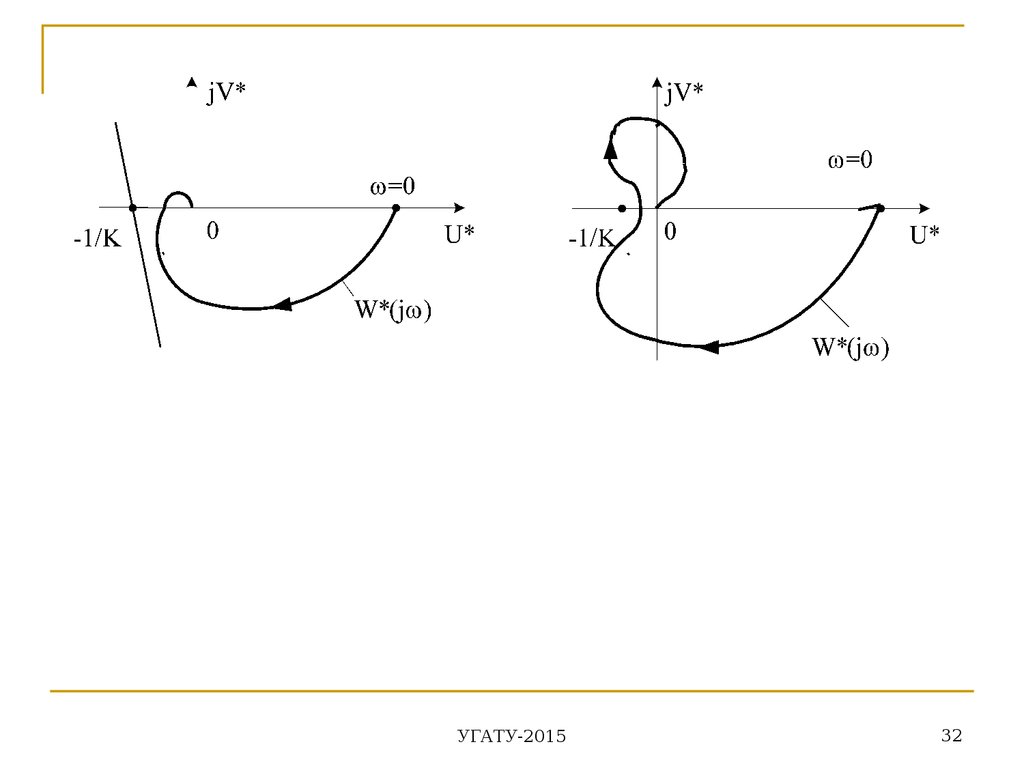
31.
(4) определяет собой прямую линию наплоскости W * ( j ) , которая проходит через
точку с координатами ( 1 , j 0)
K
1
с угловым коэффициентом, равным
.
q
Теорема. САУ будет абсолютно устойчива,
если на плоскости видоизмененной
частотной характеристики W * ( j ) линейной
части системы можно провести прямую через
точку так, чтобы
располагалась
W * ( j )
справа от этой прямой. Указанную прямую
принято называть прямой Попова.
УГАТУ-2015
31
32.
УГАТУ-201532
33. Второй метод Ляпунова
не требует нахождения решениядифференциального уравнения
основная идея
замена анализа решений нелинейных
уравнений произвольного порядка на
оценку свойств этих решений с помощью
дифференциального неравенства
УГАТУ-2015
33
34.
исследуется изменение «расстояния» впространстве состояний от текущей точки
системы до начала координат
В качестве оценки расстояния можно
использовать скалярную функцию,
которую обозначим через V(x)
фазовые траектории системы
x& f ( x),
x Î Rn ,
f (0) 0
устойчивое состояние равновесия
-«стягиваются»
УГАТУ-2015
34
35.
Суть второго метода Ляпунова сводится коценке изменения некоторой функции
координат состояния системы вдоль
траекторий движения
V(x) - называют функцией Ляпунова.
УГАТУ-2015
35
36.
xnxn
V
x (0 )
V
(8.14
x (0 )
x1
x1
а
б
Рис. 1. Изменение функции V в случае устойчивой (а) и неустойчивой (б)
систем
Функция V(x) называется положительно определенной
в области D, если выполняются свойства
V ( x) 0 "x Î D,
V (0) 0.
УГАТУ-2015
36
37.
Полной производной функции Ляпунова в силу системыназывается функция V&( x)
¶V
¶V
&
V ( x)= T x&= T f ( x)
¶x
¶x
¶V
¶V
=
,...,
– вектор-строка частных производных.
T
¶ xn
¶x
¶ x1
¶V
¶V
¶V
&
V ( x)
f1 ( x ) K
f n ( x)
¶ x1
¶ xn
УГАТУ-2015
в развернутой форме
37
38.
Теоремы второго метода ЛяпуноваСостояние равновесия системы является
асимптотически устойчивым, если для
положительно
определенной
функции
Ляпунова V(x) ее полная производная в силу
системы
есть
отрицательно
определенная
функция,
т.
е.
при
выполнении условий
V(x) > 0 " x ¹ 0, V(0)= 0,
&
&
0.
V(x) 0 " x ¹ 0, V(0)=
УГАТУ-2015
38
39.
Теорема о неустойчивостиСостояние равновесия системы является
неустойчивым, если для положительно
определенной функции Ляпунова V(x) ее
полная производная в силу системы
представляет собой также положительно
определенную функцию.
теоремы
дают только достаточные условия
устойчивости и неустойчивости
УГАТУ-2015
39
40.
Примерс помощью второго метода Ляпунова
оценить устойчивость системы, поведение
которой описывают следующие уравнения:
x&
1 x2 ,
x&2 x1 5 x2 u.
Полагаем u = 0 и рассмотрим автономную
систему x&1 x2 ,
x&2 x1 5 x2 .
УГАТУ-2015
40
41.
Выберем для нее в качестве функцииЛяпунова следующую функцию:
V ( x) x12 x22 0 "x ¹ 0,
V (0) 0.
Определим
теперь полную производную
функции Ляпунова вдоль траектории
движения автономной системы
2
2
&
V&( x) 2 x1 x&
2
x
x
2
x
x
2
x
x
10
x
10
x
1
2 2
1 2
1 2
2
2
обращается
в нуль не только в начале
координат, но и на всей оси .
УГАТУ-2015
41
42.
V ( x) x12 2 x1 x2 x22 0 "x ¹ 0, V (0) 0,V&( x) 2( x1 x2 ) x&
1 2( x1 x2 ) x&
2
V&( x) 2 x12 10 x1 x2 8 x22
полная производная новой функции
Ляпунова есть отрицательно
определенная функция.
Следовательно, исходная система
является асимптотически устойчивой.
УГАТУ-2015
42





































 Математика
Математика Физика
Физика








