Применение производной к исследованию функции

1. Применение производной к исследованию функций

ГБПОУ «Краевой политехнический колледж»
Применение производной
к исследованию
функций
Чернушка

2. План исследования функции и построение графика функции:

1. Найти область определения функции D (x);.
2. Найти область значения функции E(х);
3. Определить четность или нечетность функции,
периодичность функции;
4. Найти точки пересечения с осями координат;
5. Определить наибольшее или наименьшее значений
функций и периоды возрастания или убывания функций;
6. Определить значение функции в дополнительных точках;
7. Построить график данной функции.

3. План исследования функции и построение графика функции:

1. Найти область определения функции D (x):
Для этого необходимо определить все значения переменной х, при
которых выражение не имеет смысл. Например:
А)у=х+3, здесь нет ограничений, поэтому
D(x):(-∞;∞)
2х−8
Б) у=
, дробь не имеет значение, если знаменатель равен 0,
х+3
значит D(x):(-∞;-3)ꓴ(-3; ∞)
В) у= 5х + 1, подкоренное выражение имеет смысл, если
1
подкоренное выражение неотрицательное, значит D(x): (- ; ∞)
5

4. План исследования функции и построение графика функции:

2. Найти область значения функции E(х);
Область значение функции определяется по
переменной у.

5. План исследования функции и построение графика функции:

3. Определить четность или нечетность функции, периодичность функции;
Чтобы определить четность функции, необходимо проверить значение функции при
х и при –х.
Если f(x)=f(-x) функция четная, значит график симметричен относительно оси у.
Если f(x)= -f(-x) функция нечетная, значит график симметричен относительно начало
координат.
Если f(x)≠f(-x) функция ни четная ни нечетная.
Например:
А)у= х+3
у(х)=х+3, а у(-х)=-х+3. Видим, что у(х)≠у(-х) функция не является ни четной и ни
нечетной.
Б) у=х2, а у=(-х)2 .у(х)=у(-х) , функция четная.
В) у=х3, а у=(-х)3 .у(х)=-у(х) , функция нечетная.

6. План исследования функции и построение графика функции:

4. Найти точки пересечения с осями координат;
Чтобы найти точки пересечения графика с осью х,
надо функцию приравнять к 0 и решить
полученное уравнение. Например: f(x)=x2-9, точки
пересечения будут (3;0) и (-3;0).
А чтобы найти точки пересечения графика с осью
у, надо в функцию вместо х подставить 0 и
вычислить значение. Например: f(x)=x2-9, точка
пересечения будет (0;9)

7. План исследования функции и построение графика функции:

5. Определить наибольшее или наименьшее значений функций и
периоды возрастания или убывания функций;
Чтобы найти наибольшее или наименьшее значение функции,
необходимо:
1. Найти производную функцию;
2. Приравнять f ,(x) к нулю и решить получившееся уравнение.
3. Полученные корни отметьте на координатной прямой и
определите знаки на каждом промежутке.
4. В зависимости от знака в данном промежутке определить
возрастание или убывание функции
5. Все полученные результаты лучше оформить в виде таблицы.

8. Рассмотрим на конкретном примере

Найдите наименьшее и наибольшее значение
х3
функции у= -36х+9.
3
1. Найдем производную
f ,(x)=x2-36
2. x2-36=0
Х1=6 и Х2=-6
3. Отметим точки на прямой
-6
6

9.

Как мы видим точи -6 и 6 разделили прямую
на три промежутка (-∞; -6), (-6;6) и (6;∞).
Оформим в таблицу
(-∞; -6),
f, (x)
f (x)
-6
(-6;6) 6
(6;∞).

10.

Чтобы определить знаки на каждом
промежутке, надо выбрать любое число из
этого промежутка ( кроме концов), подставить
в производную функции и вычислить.
Например, из первого промежутка можно
взять число -10, вычислим
f ,(x)=(-10)2-36=100-36=64 >0, значит в таблице
проставляем +.

11.

(-∞; -6),
f, (x)
+
-6
(-6;6) 6
(6;∞).
-
+
f (x)
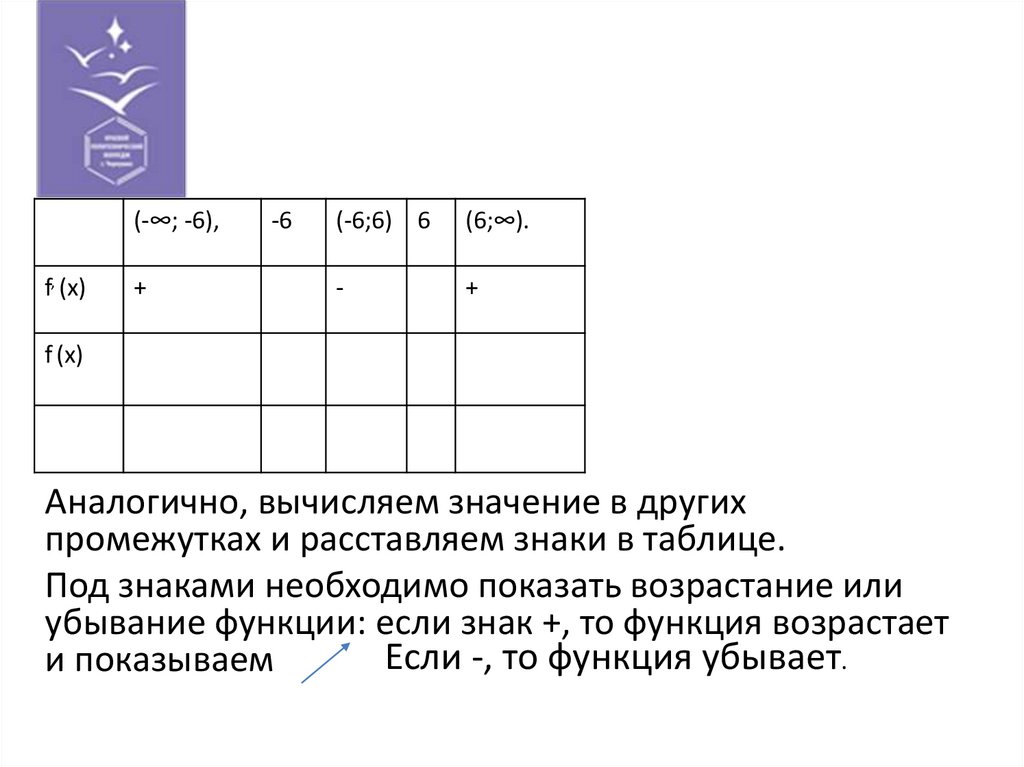
Аналогично, вычисляем значение в других
промежутках и расставляем знаки в таблице.
Под знаками необходимо показать возрастание или
убывание функции: если знак +, то функция возрастает
Если -, то функция убывает.
и показываем

12.

f, (x)
f (x)
(-∞; -6),
-6
(-6;6) 6
(6;∞).
+
0
-
+
153
0
-135
В столбцах где записаны числа надо вычислить конкретное
значение, для этого подставим эти числа:
f ,(x)=(-6)2-36=36-36=0
(−6)3
f(x)=
-36* (-6)+9=153
3
Аналогично, вычисляем с числом 6.

13.

f, (x)
f (x)
(-∞; -6),
-6
(-6;6) 6
(6;∞).
+
0
-
+
0
153
-135
max
min
Таким образом, наибольшее значение функции 153, наименьшее -135.
Число -6 это точка максимум (так как функция сначала возрастает, затем
убывает, получилась «горка») и значение в этой точке наибольшее.
Число 6 это минимум (так как функция сначала убывает, затем возрастает,
получилась «впадина»), значение функции наименьшее.

14.

Нахождение наибольшего и наименьшего
значения функций, точек минимума и максимума
называется исследование функций на
монотонность