Конференция_Графикон_Опарышев

1. «Геометрический алгоритм построения гладкого обвода на основе кривых двойного соприкосновения»

ФГБОУ ВО «Нижегородский государственный
архитектурно-строительный университет» (ННГАСУ)
«Геометрический алгоритм построения гладкого обвода
на основе кривых двойного соприкосновения»
Опарышев Вадим Павлович
2.5.1 – Инженерная геометрия и компьютерная графика.
Цифровая поддержка жизненного цикла изделий
Научный руководитель:
д. т. н., доцент
Конопацкий Евгений Викторович
Нижний Новгород, 2025

2.

Актуальность работы
Системы автоматизированного проектирования при всём
многообразии инструментов для решения задач, имеют ряд
ограничений, которые связаны с формообразованием геометрии
объектов, необходимые определить с нужными значениями кривизны
и в нужной параметризации. В большинстве своём они имеют
скудный инструментарий формообразующих элементов и
геометрических примитивов.
Таким образом, необходимо расширение инструментария при
исследовании и моделировании новых кривых
2

3.

Обзорная часть по теме исследований
При проектировании архитектурно-строительных сооружений важная роль
отводится начальному этапу проектирования, который предусматривает многовариантные
решения с целью учета ряда требований, предъявляемых к геометрической форме, что
возможно в интерактивном режиме при работе с ЭВМ.
Анализ данных по теме проводился в нескольких направлениях.
После сравнения существующих методов параметризации поверхностей по
средствам трудов Я.А. Кокарева, Е.В. Конопацкого, Ан. Алксдр. Бездитного, А.В. Замятина
и др., исследующие неизученные особенности её видов, необходимо было рассмотреть
существующие алгоритмы построения геометрических объектов. Для этого обратились к
научным исследованиям Т.М. Мясоедовой, К.Л. Панчука, Аюшеева Т.В, Балюбы И.Г,
Конопацкого Е.В., Иванова Г.С. и др.
3

4.

Сравнительный анализ методов параметризации поверхностей позволил сделать
ряд выводов:
- каждый из методов применим только для какой – то конкретной группы
моделей, относительно темы исследования более подходящий рассмотренный метод –
кинематический метод моделирования.
- все представленные методы имеют под собой базисный набор свойств, с
помощью которых возможно максимально детально реализовать имеющийся проект;
- все представленные методы без особых проблем «погружаются» в САПР для
практического применения.
Анализ существующих алгоритмов построения геометрических объектов позволил
установить, что кинематический метод наиболее лучшим образом будет реализован
геометрическим алгоритмом, а наиболее подходящий из геометрических объектов –
гладкий обвод
4

5.

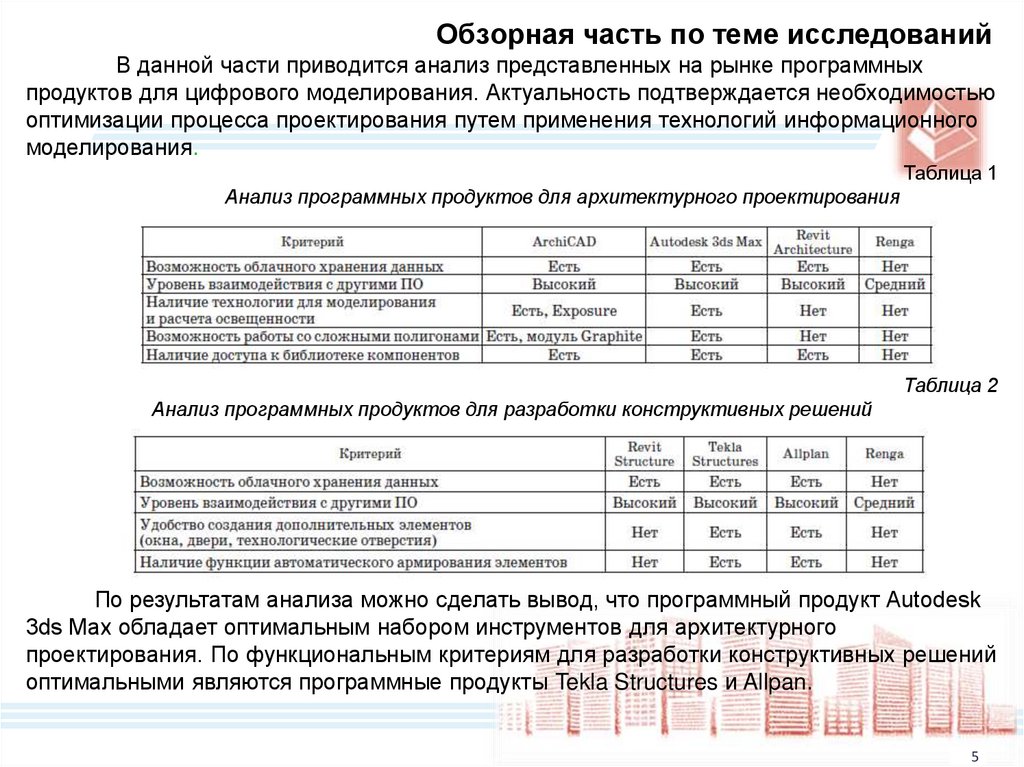
Обзорная часть по теме исследований
В данной части приводится анализ представленных на рынке программных
продуктов для цифрового моделирования. Актуальность подтверждается необходимостью
оптимизации процесса проектирования путем применения технологий информационного
моделирования.
Таблица 1
Анализ программных продуктов для архитектурного проектирования
Таблица 2
Анализ программных продуктов для разработки конструктивных решений
По результатам анализа можно сделать вывод, что программный продукт Autodesk
3ds Max обладает оптимальным набором инструментов для архитектурного
проектирования. По функциональным критериям для разработки конструктивных решений
оптимальными являются программные продукты Tekla Structures и Allpan.
5

6.

Моделирование дуги кривой 2-го порядка отношением на медиане
Как известно, кривая 2-го порядка однозначно определяется пятью
точками, пятью касательными или комбинациями точек и касательных (рис. 1).
Рисунок 1. Геометрическая схема определения кривой 2-го порядка с помощью инженерного дискриминанта
Уравнение кривой, которая является дугой обвода и может использоваться
для построения обводов первого порядка гладкости выглядят так:
M A C
kv 2
k 1 2v 2vv
2
B C
kv 2
k 1 2v 2vv
2
C.
6

7.

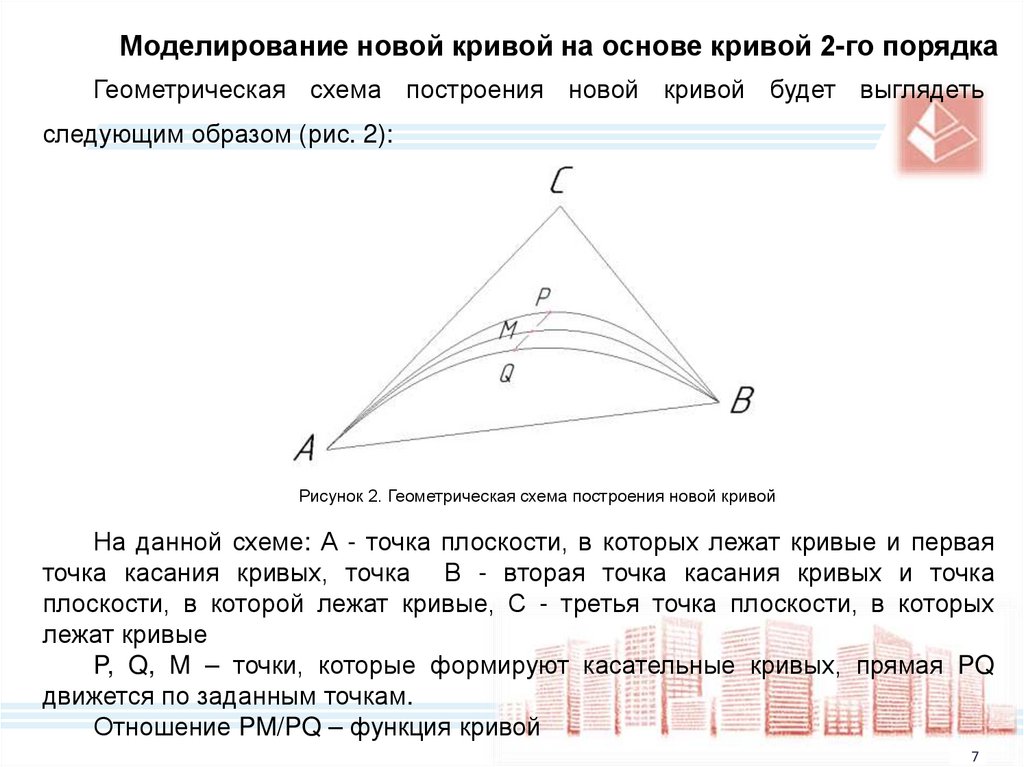
Моделирование новой кривой на основе кривой 2-го порядка
Геометрическая схема построения новой кривой будет выглядеть
следующим образом (рис. 2):
Рисунок 2. Геометрическая схема построения новой кривой
На данной схеме: А - точка плоскости, в которых лежат кривые и первая
точка касания кривых, точка В - вторая точка касания кривых и точка
плоскости, в которой лежат кривые, С - третья точка плоскости, в которых
лежат кривые
P, Q, M – точки, которые формируют касательные кривых, прямая PQ
движется по заданным точкам.
Отношение PM/PQ – функция кривой
7

8.

Аналитическое описание
Подставляя в отношения разные функции, мы управляем нелинейностью
пространства, изменения параметра функции на прямой
Уравнение кривых, которые лежат в заданной плоскости выглядят так:
P A C
Q A C
k pv 2
k p 1 2v 2vv
2
kq v 2
kq 1 2v 2vv
2
B C
B C
k pv2
k p 1 2v 2vv
2
kq v 2
kq 1 2v 2vv
2
C.
C.
k p kq 0.5
Для поискаM
кривой,
проходящей
через точку M необходимо, чтобы сумма
Pv Qv
.
функций, проходящих через точки P и Q были равны 1
функции
к ним представлены
Наиболее показательные
k p v 3 и графикиkqкривизны
v 2v
M слайдах
A C
2
2
на последующих
k p 1 2v 2vv
kq 1 2v 2vv
k p v 2v
kq v 3
C.
B C
2
2
k 1 2v 2vv k 1 2v 2vv
q
p
8

9.

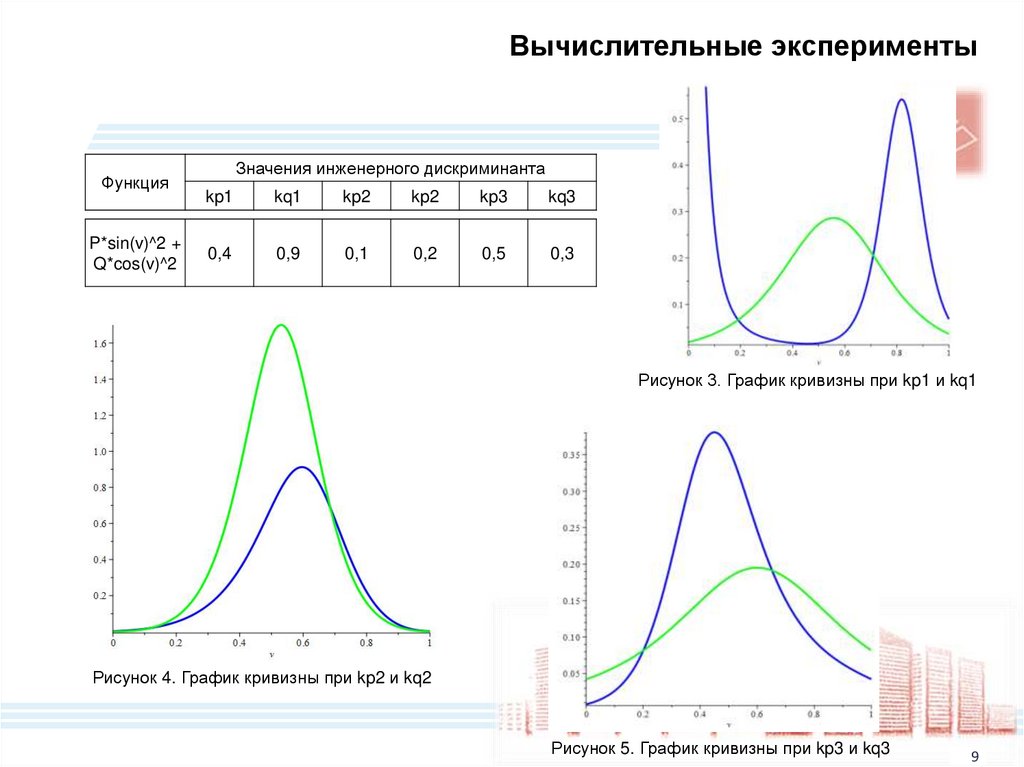
Вычислительные эксперименты
Функция
P*sin(v)^2 +
Q*cos(v)^2
Значения инженерного дискриминанта
kp1
kq1
kp2
kp2
kp3
kq3
0,4
0,9
0,1
0,2
0,5
0,3
Рисунок 3. График кривизны при kp1 и kq1
Рисунок 4. График кривизны при kp2 и kq2
Рисунок 5. График кривизны при kp3 и kq3
9

10.

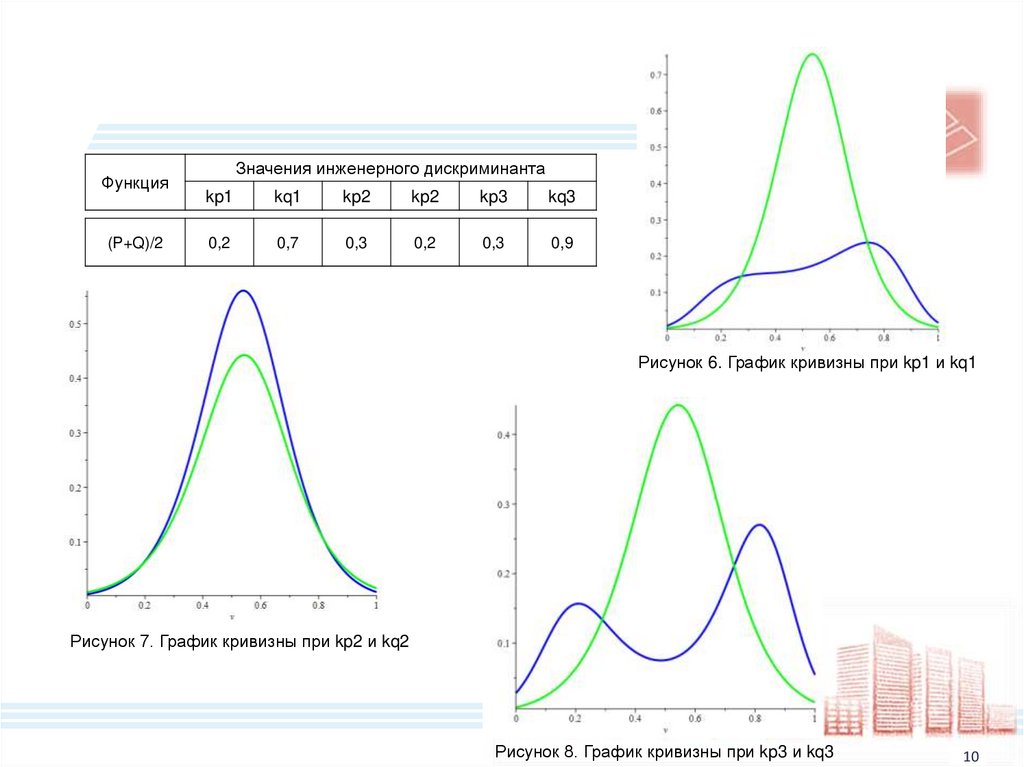
Функция
(P+Q)/2
Значения инженерного дискриминанта
kp1
kq1
kp2
kp2
kp3
kq3
0,2
0,7
0,3
0,2
0,3
0,9
Рисунок 6. График кривизны при kp1 и kq1
Рисунок 7. График кривизны при kp2 и kq2
Рисунок 8. График кривизны при kp3 и kq3
10

11.

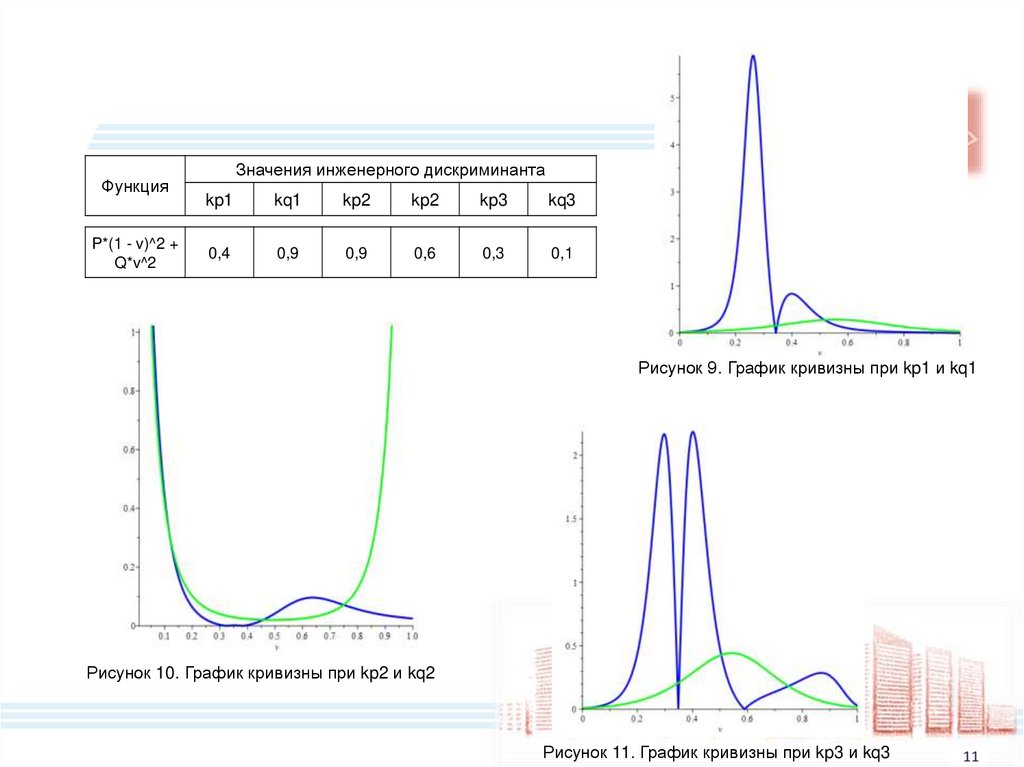
Функция
P*(1 - v)^2 +
Q*v^2
Значения инженерного дискриминанта
kp1
kq1
kp2
kp2
kp3
kq3
0,4
0,9
0,9
0,6
0,3
0,1
Рисунок 9. График кривизны при kp1 и kq1
Рисунок 10. График кривизны при kp2 и kq2
Рисунок 11. График кривизны при kp3 и kq3
11

12.

Моделирование обвода на основе дуг кривых 2-го порядка
Геометрическая схема построения обвода будет выглядеть следующим
образом (рис. 12):
Рисунок 12. Геометрическая схема построения обвода
На данной схеме: C0, C1, C2, C3 – узловые точки, с заданными
касательными в них, A0, A1, A2, - управляющие точки, t1, t2, t3, t4 – касательные,
C1, C2 – точки стыковки с равным значением кривизны
12

13.

Аналитическое описание
Для задания касательных и значения кривизны решим систему линейных
уравнений
для
нахождения
неизвестных
параметров
Обязательное условие: кол-во уравнений должно совпадать с кол-вом
неизвестных
При этом линии M01(v1) и М02 (v2) должны быть состыкованы в точке C1
по второму порядку гладкости. Для этого определим первые и вторые
производные из уравнений выше, после чего приравняем полученные
производные двух линий/
Т.о. получаем обвод из двух сегментов, составленных по второму порядку
гладкости с равным значением кривизны в точке стыка
Наиболее показательные функции и графики кривизны к ним
представлены на последующих слайдах
13

14.

Значения инженерного дискриминанта
Функция
kp1(М01) kq1(М01) kp2(М02) kq2(М02) kp1(М01) kq1(М01) kp2(М02) kq2(М02) kp1(М01) kq1(М01) kp2(М02) kq2(М02)
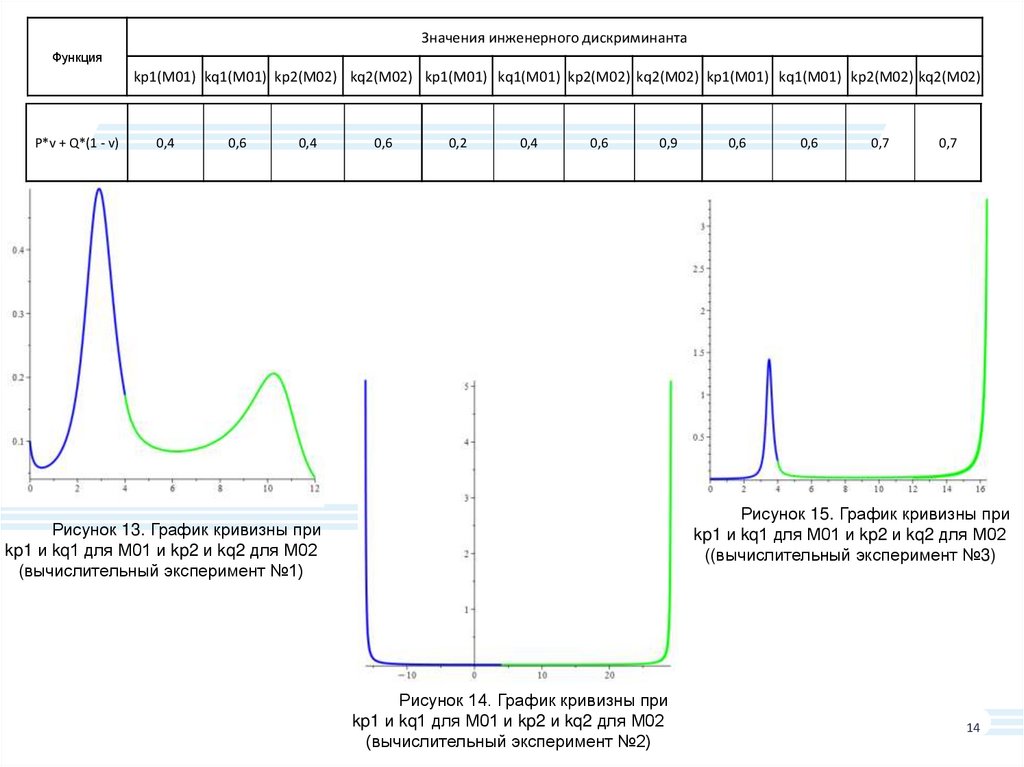
P*v + Q*(1 - v)
0,4
0,6
0,4
0,6
0,2
0,4
0,6
0,9
0,6
0,6
0,7
0,7
Рисунок 15. График кривизны при
kp1 и kq1 для М01 и kp2 и kq2 для М02
((вычислительный эксперимент №3)
Рисунок 13. График кривизны при
kp1 и kq1 для М01 и kp2 и kq2 для М02
(вычислительный эксперимент №1)
Рисунок 14. График кривизны при
kp1 и kq1 для М01 и kp2 и kq2 для М02
(вычислительный эксперимент №2)
14

15.

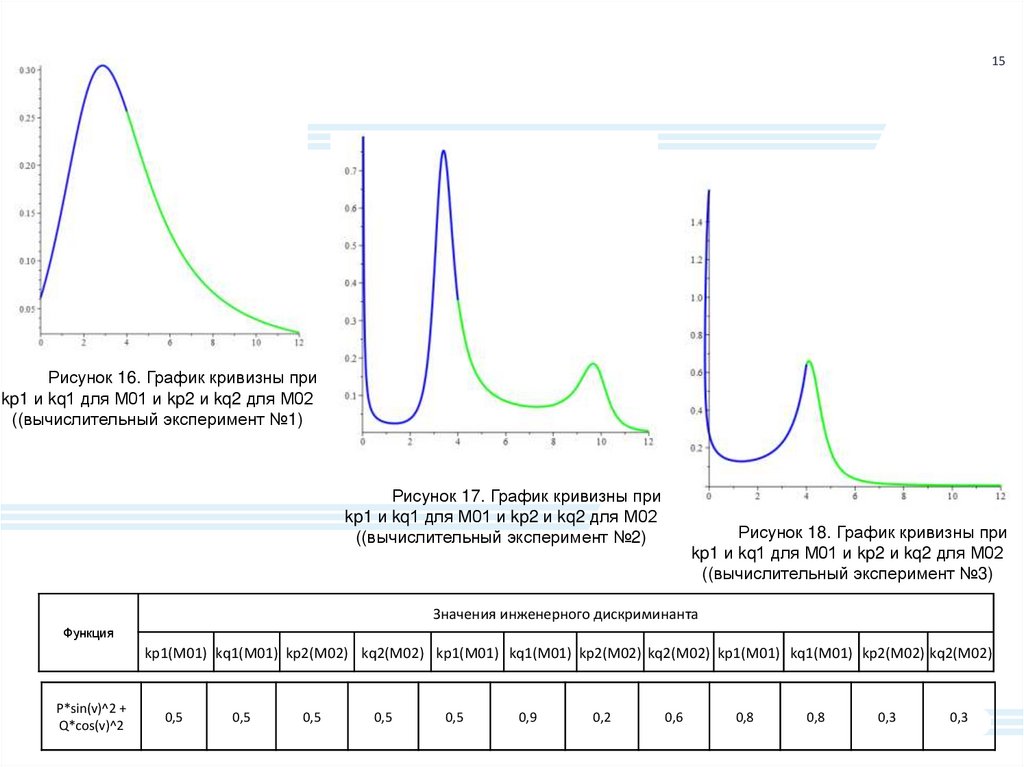
15
Рисунок 16. График кривизны при
kp1 и kq1 для М01 и kp2 и kq2 для М02
((вычислительный эксперимент №1)
Рисунок 17. График кривизны при
kp1 и kq1 для М01 и kp2 и kq2 для М02
((вычислительный эксперимент №2)
Рисунок 18. График кривизны при
kp1 и kq1 для М01 и kp2 и kq2 для М02
((вычислительный эксперимент №3)
Значения инженерного дискриминанта
Функция
kp1(М01) kq1(М01) kp2(М02) kq2(М02) kp1(М01) kq1(М01) kp2(М02) kq2(М02) kp1(М01) kq1(М01) kp2(М02) kq2(М02)
P*sin(v)^2 +
Q*cos(v)^2
0,5
0,5
0,5
0,5
0,5
0,9
0,2
0,6
0,8
0,8
0,3
0,3

16.

Значения инженерного дискриминанта
Функция
kp1(М01) kq1(М01) kp2(М02) kq2(М02) kp1(М01) kq1(М01) kp2(М02) kq2(М02) kp1(М01) kq1(М01) kp2(М02) kq2(М02)
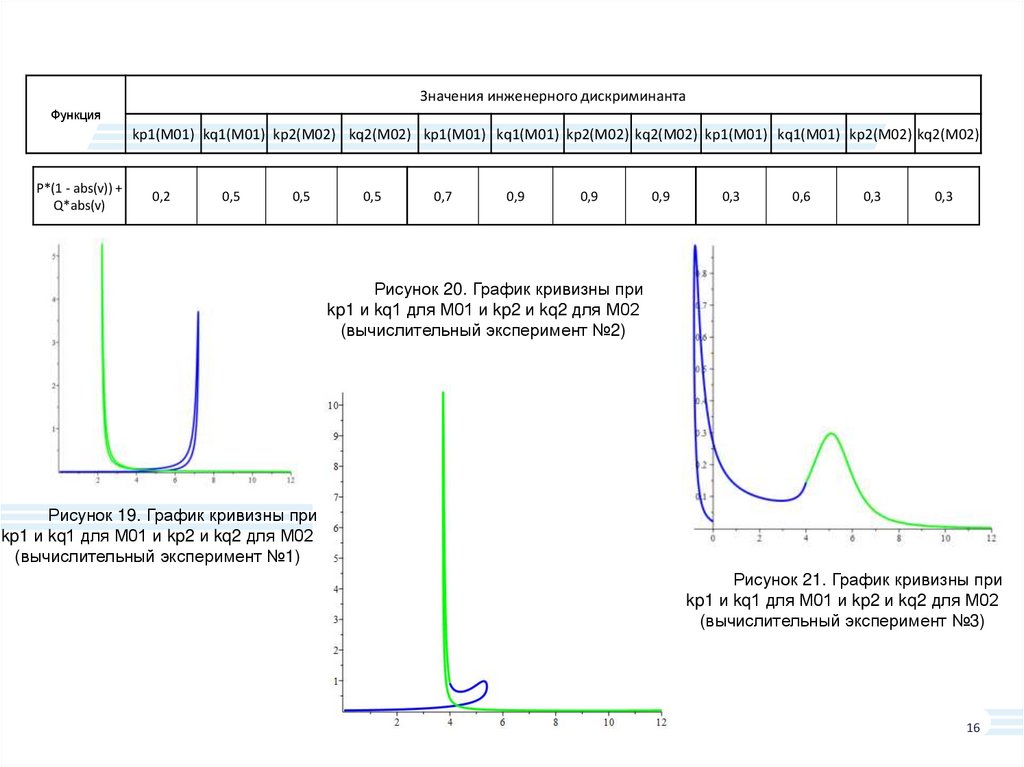
P*(1 - abs(v)) +
Q*abs(v)
0,2
0,5
0,5
0,5
0,7
0,9
0,9
0,9
0,3
0,6
0,3
0,3
Рисунок 20. График кривизны при
kp1 и kq1 для М01 и kp2 и kq2 для М02
(вычислительный эксперимент №2)
Рисунок 19. График кривизны при
kp1 и kq1 для М01 и kp2 и kq2 для М02
(вычислительный эксперимент №1)
Рисунок 21. График кривизны при
kp1 и kq1 для М01 и kp2 и kq2 для М02
(вычислительный эксперимент №3)
16

17.

Выводы
кривые при любых значениях инженерного дискриминанта будут
иметь две точки касания;
кривизна заданных функций зависит от значения инженерного
дискриминанта: на графике кривизны отсутствуют резкие скачки при
близких значениях дискриминанта;
попарные значения инженерного дискриминанта дают наилучшую
гладкость в точке стыковки двух кривых линий;
трансцендентные функции при любых комбинациях значений
инженерного дискриминанта обладают гладкостью в точке стыковки.
17

18. Спасибо, что уделили мне время

СПАСИБО, ЧТО УДЕЛИЛИ
МНЕ ВРЕМЯ
18