Похожие презентации:
Урок решения задач по разделу «Электростатика»
1.
Урок решения задачпо разделу «Электростатика»
2.
ОСНОВНЫЕ ПОНЯТИЯ И ЗАКОНЫ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ1.Сила взаимодействия двух неподвижных точечных зарядов q1 и q2 :
2
| q1 || q2 |
1
9 Н м
F
,k
9 10
2
4 0 r
4 0
Кл2
1
2. Напряженность электрического поля:
F
E
q
Напряженность поля точечного заряда q:
1
q
kq
E
2
2
4 0 r
r
3.Потенциал электрического поля:
A
q
Потенциал поля точечного заряда q:
1
q
kq
4 0 r
r
4.Принцип суперпозиции для напряженности и потенциала:
E Ei
i
3.
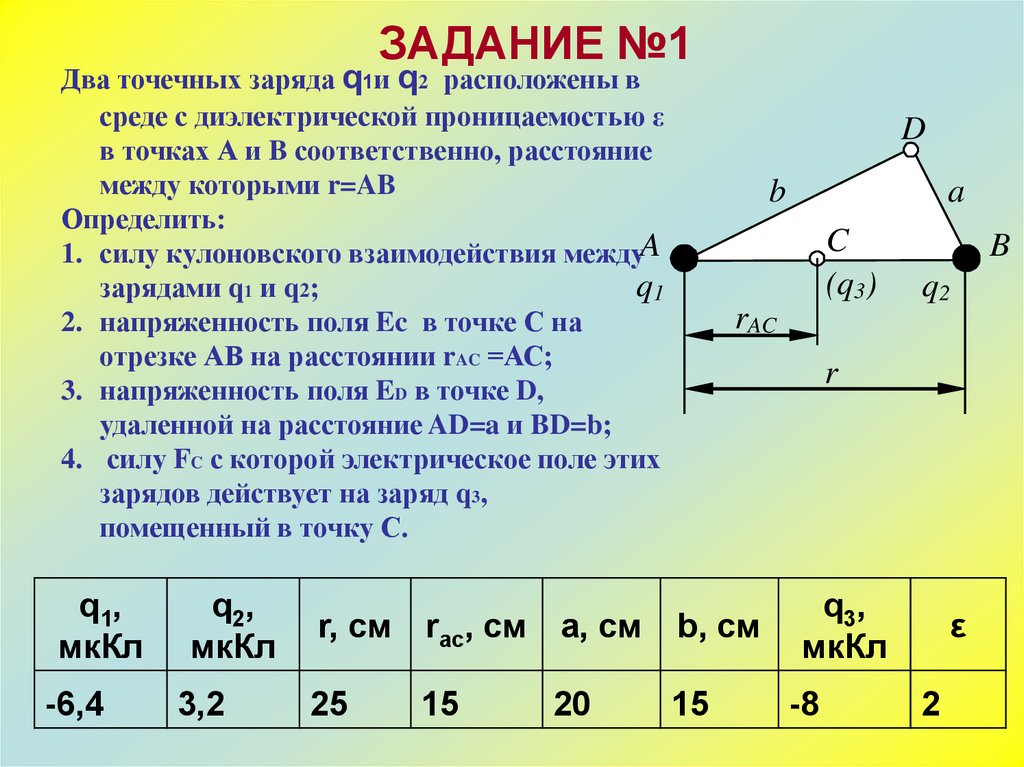
ЗАДАНИЕ №1Два точечных заряда q1и q2 расположены в
среде с диэлектрической проницаемостью ε
в точках А и B соответственно, расстояние
между которыми r=AB
Определить:
1. силу кулоновского взаимодействия междуA
q1
зарядами q1 и q2;
2. напряженность поля Ec в точке С на
отрезке АВ на расстоянии rAC =АС;
3. напряженность поля ED в точке D,
удаленной на расстояние AD=a и BD=b;
4. силу FC с которой электрическое поле этих
зарядов действует на заряд q3,
помещенный в точку С.
q1,
мкКл
-6,4
q2,
мкКл
3,2
D
b
C
(q3)
q2
r
b, см
25
15
20
B
rAC
r, см rac, см a, см
15
a
q3,
мкКл
-8
ε
2
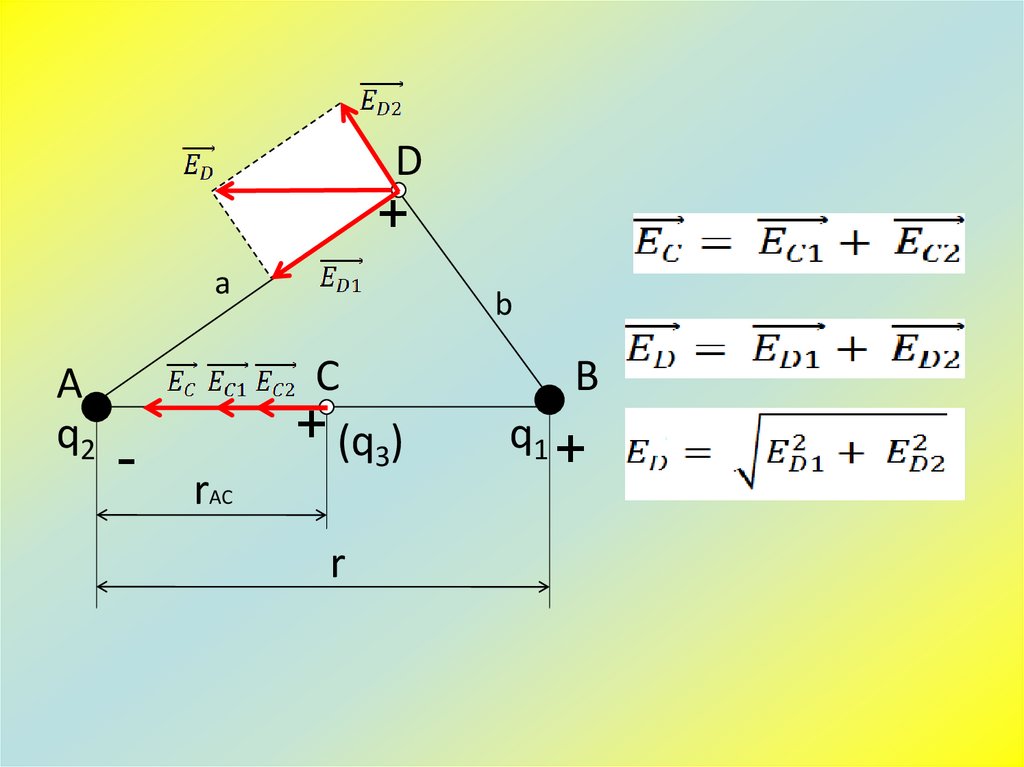
4.
D+
a
A
q2
-
rAC
b
C
+ (q3)
r
B
q1 +
5.
1.F1, 2 kq1 q2
r
2
6
6,4 10 3,2 10
F1, 2 9 10
2 2
2 (25 10 )
9
6
1,5H
2.EC EC1 EC 2
k | q1 | 9 10 6, 4 10
EC1
2
rAC
2(15 10 2 ) 2
9
кН
1280
Кл
6
k | q2 |
9 10 3, 2 10
кН
1440
2
2 2
(r rAC )
2((25 15) 10 )
Кл
9
EC 2
6
кН
EC 2720
Кл
6.
3.ED E 2 D1 ED 2 26
кН
720
Кл
9
6
кН
640
Кл
6
3
k | q1 | 9 10 6, 4 10
ED1
2
2 2
a
2(20 10 )
9
k | q2 | 9 10 3, 2 10
ED 2
2
2 2
b
2(15 10 )
кН
ED 963,3
Кл
4.FC | q3 | EC 8 10 2720 10 21,8H
7.
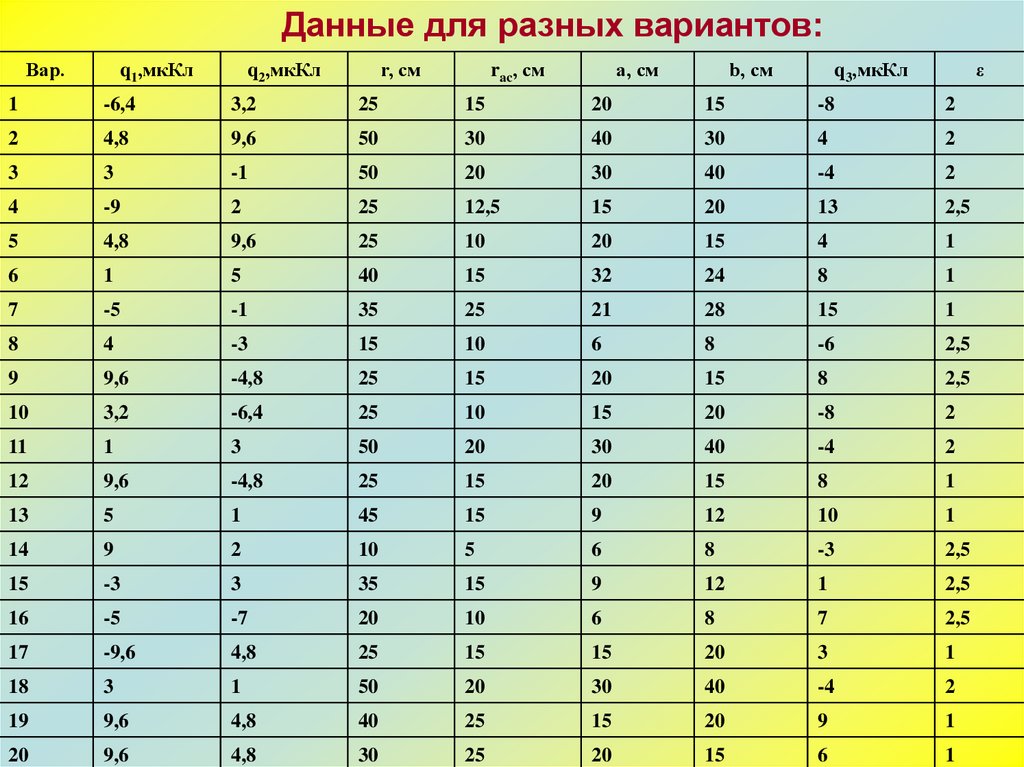
Данные для разных вариантов:Вар.
q1,мкКл
q2,мкКл
r, см
rac, см
a, см
b, см
q3,мкКл
ε
1
-6,4
3,2
25
15
20
15
-8
2
2
4,8
9,6
50
30
40
30
4
2
3
3
-1
50
20
30
40
-4
2
4
-9
2
25
12,5
15
20
13
2,5
5
4,8
9,6
25
10
20
15
4
1
6
1
5
40
15
32
24
8
1
7
-5
-1
35
25
21
28
15
1
8
4
-3
15
10
6
8
-6
2,5
9
9,6
-4,8
25
15
20
15
8
2,5
10
3,2
-6,4
25
10
15
20
-8
2
11
1
3
50
20
30
40
-4
2
12
9,6
-4,8
25
15
20
15
8
1
13
5
1
45
15
9
12
10
1
14
9
2
10
5
6
8
-3
2,5
15
-3
3
35
15
9
12
1
2,5
16
-5
-7
20
10
6
8
7
2,5
17
-9,6
4,8
25
15
15
20
3
1
18
3
1
50
20
30
40
-4
2
19
9,6
4,8
40
25
15
20
9
1
20
9,6
4,8
30
25
20
15
6
1
8.
ЗАДАНИЕ №2В вершинах квадрата со стороной а
находятся четыре заряда q1, q2, q3, q4.
Определите напряженность и его направление,
а также потенциал
электрического поля в центре квадрата.
Найдите силу, действующую на
q1
помещенный в центре квадрата
точечный заряд q0.
q4
q2
q3
9.
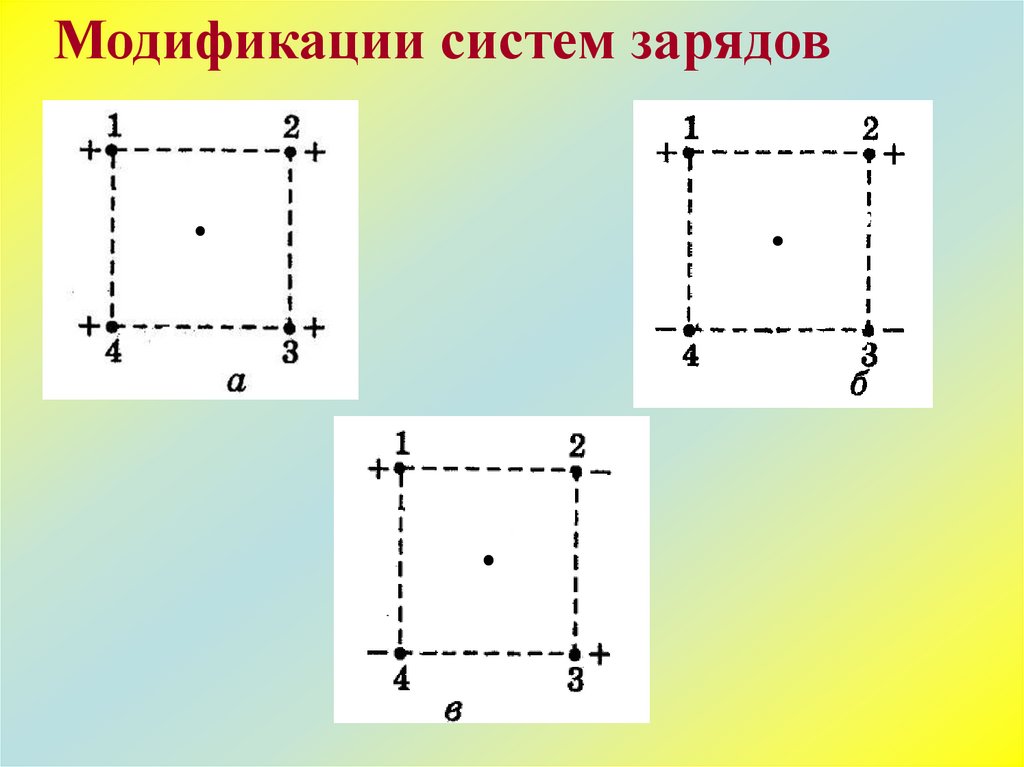
Модификации систем зарядов10.
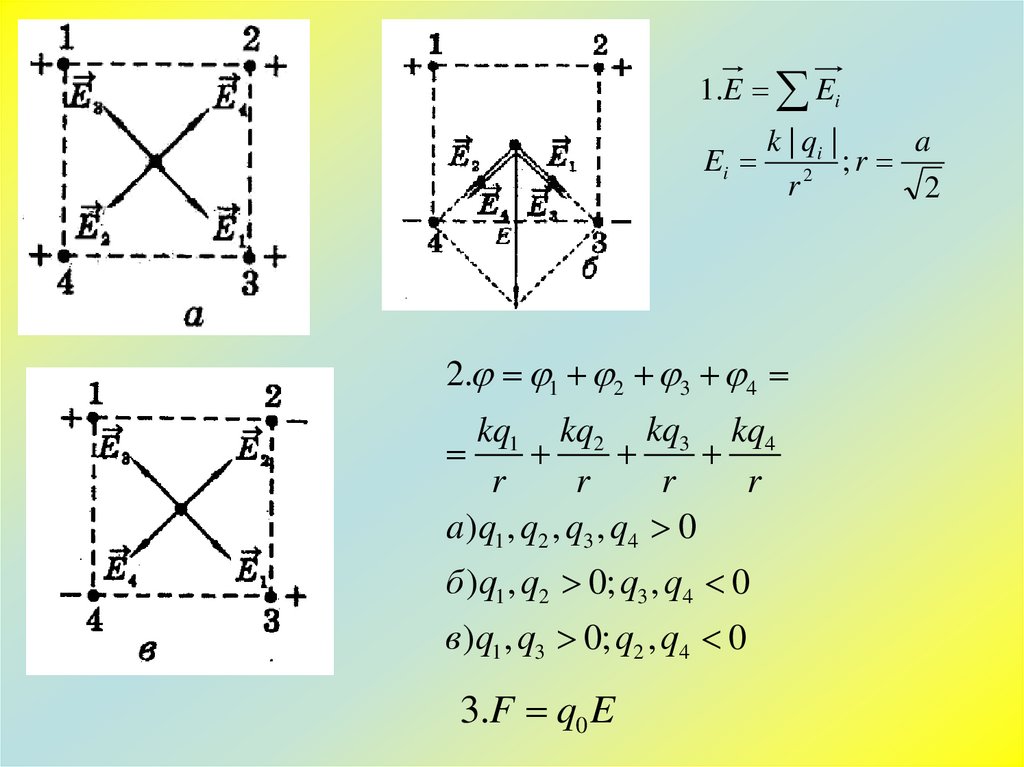
1 .E Eik | qi |
a
Ei 2 ; r
r
2
2. 1 2 3 4
kq1 kq2 kq3 kq4
r
r
r
r
a )q1 , q2 , q3 , q4 0
б )q1 , q2 0; q3 , q4 0
в )q1 , q3 0; q2 , q4 0
3.F q0 E
11.
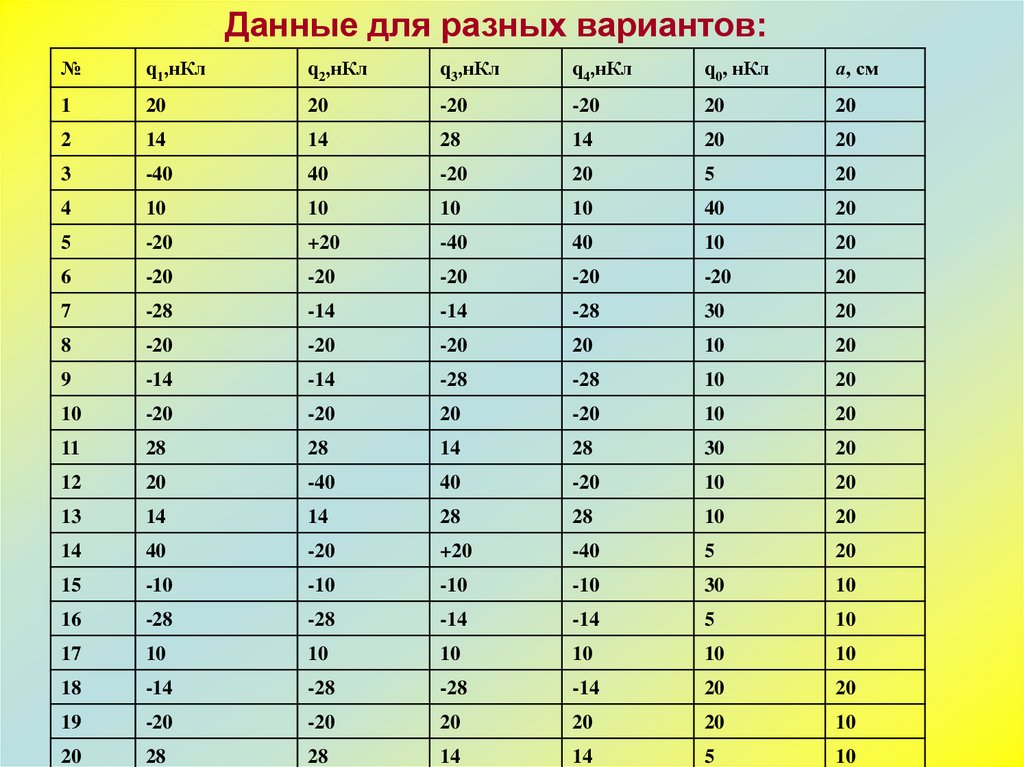
Данные для разных вариантов:№
q1,нКл
q2,нКл
q3,нКл
q4,нКл
q0, нКл
а, см
1
20
20
-20
-20
20
20
2
14
14
28
14
20
20
3
-40
40
-20
20
5
20
4
10
10
10
10
40
20
5
-20
+20
-40
40
10
20
6
-20
-20
-20
-20
-20
20
7
-28
-14
-14
-28
30
20
8
-20
-20
-20
20
10
20
9
-14
-14
-28
-28
10
20
10
-20
-20
20
-20
10
20
11
28
28
14
28
30
20
12
20
-40
40
-20
10
20
13
14
14
28
28
10
20
14
40
-20
+20
-40
5
20
15
-10
-10
-10
-10
30
10
16
-28
-28
-14
-14
5
10
17
10
10
10
10
10
10
18
-14
-28
-28
-14
20
20
19
-20
-20
20
20
20
10
20
28
28
14
14
5
10
12.
Вспомогательная задача:По тонкой сфере радиусом R
равномерно распределен заряд q.
Определите напряженность и
потенциал электрического
поля в точках А и В, находящихся
на расстояниях rA, rB от центра сферы.
1. Для точки А :
0 ≤ rA ≤ R
kq
E A 0; A
const
R
2. Для точки B: rB >R
kq
kq
EB 2 ; B
r B
rB
R
A
q
B
13.
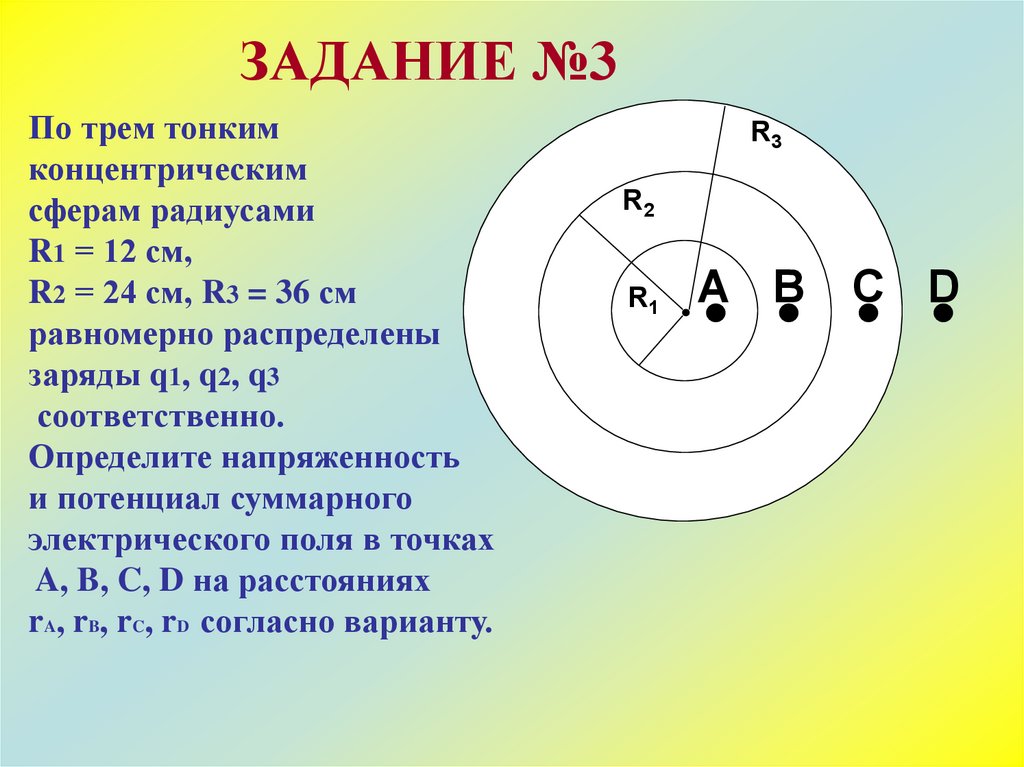
ЗАДАНИЕ №3По трем тонким
концентрическим
сферам радиусами
R1 = 12 см,
R2 = 24 см, R3 = 36 см
равномерно распределены
заряды q1, q2, q3
соответственно.
Определите напряженность
и потенциал суммарного
электрического поля в точках
A, B, C, D на расстояниях
rA, rB, rC, rD согласно варианту.
R3
R2
R1
A B
C D
14.
E E1 (r ) E2 (r ) E3 (r )1 (r ) 2 (r ) 3 (r )
1. Для точки А
0≤r≤R
E1 E2 E3 0
EA 0
1 (r )
R3
R2
R1
A
rA
kq
kq1
kq
; 2 (r ) 2 ; 3 (r ) 3
R1
R2
R3
kq1 kq2 kq3
A( r )
R1 R2
R3
R2
2. Для точки B
R ≤ r ≤ 2R
R1 rB
kq1
; E2 E3 0
kq3
kq1
kq2
2
(
r
)
;
(
r
)
;
(
r
)
r B
1
2
3
rB
R2
R3
kq
kq1 kq2 kq3
EB E1 2 1
(
r
)
B
r B
r
R
R
E1
B
R3
2
3
B
15.
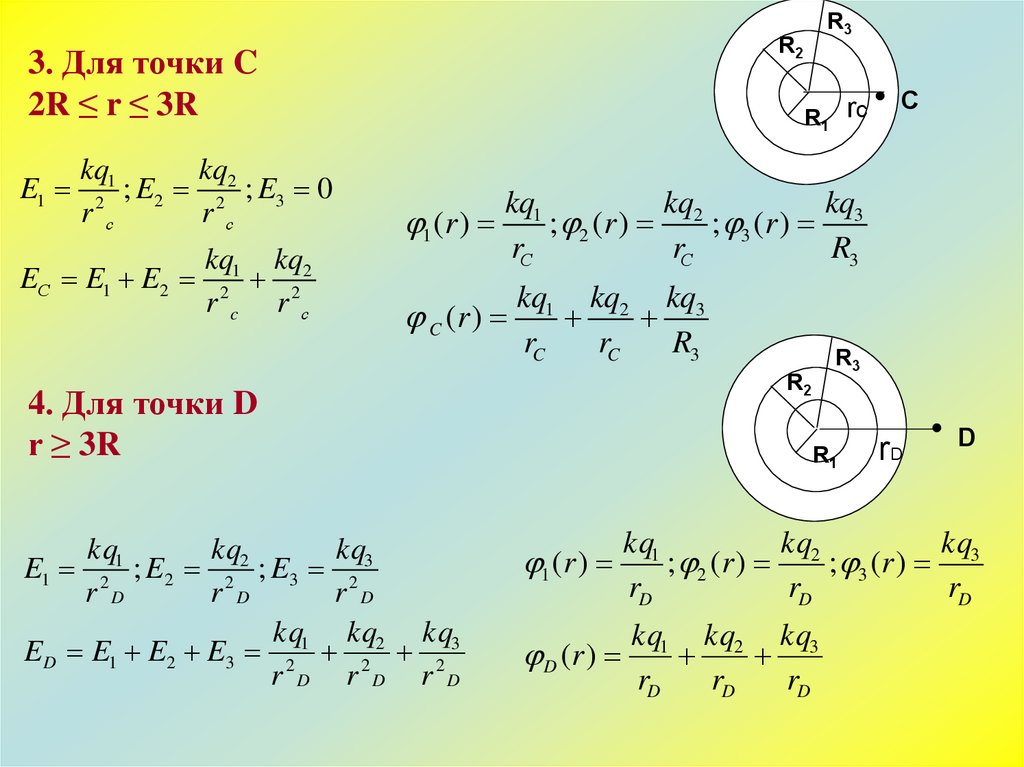
R23. Для точки C
2R ≤ r ≤ 3R
kq1
kq2
E1 2 ; E2 2 ; E3 0
r с
r с
EС E1 E2
kq1 kq2
2
2
r c r с
R3
rc
R1
C
kq3
kq1
kq2
1 (r )
; 2 (r )
; 3 ( r )
rС
rС
R3
C (r )
kq1 kq2 kq3
rC
rC
R3
R2
4. Для точки D
r ≥ 3R
kq
kq
kq
E1 2 1 ; E2 2 2 ; E3 2 3
r D
r D
r D
kq1 kq2 kq3
ED E1 E2 E3 2 2 2
r D r D r D
R3
R1
rD
D
1 (r )
kq
kq1
kq
; 2 (r ) 2 ; 3 (r ) 3
rD
rD
rD
D (r )
kq1 kq2 kq3
rD
rD
rD
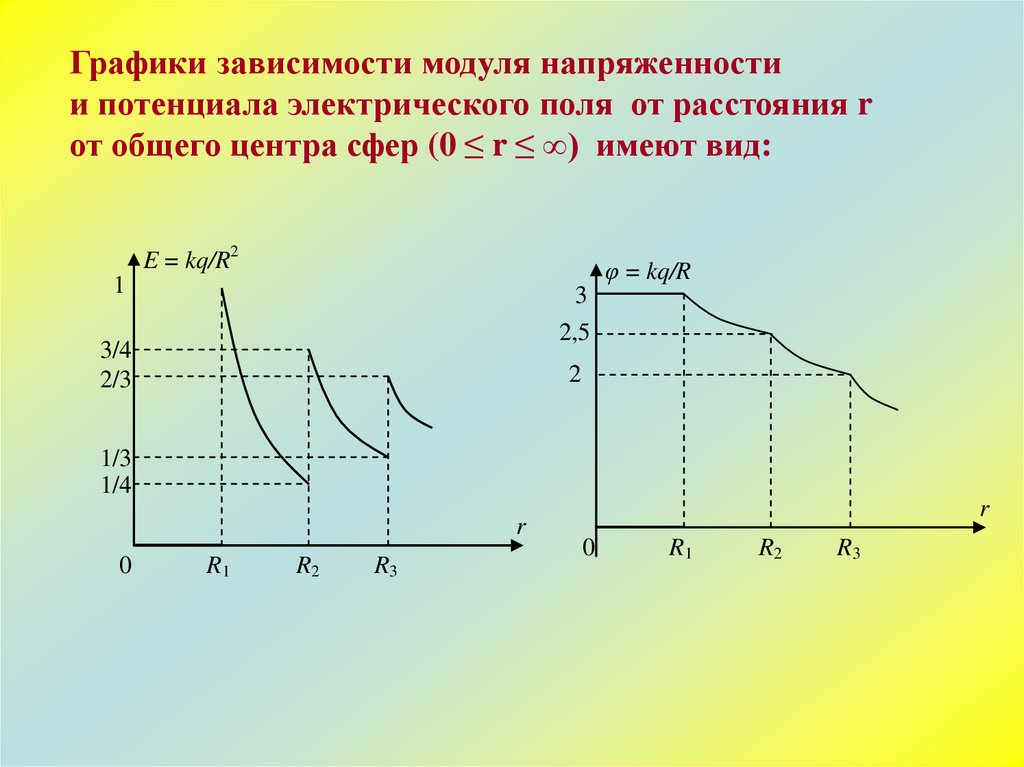
16.
Графики зависимости модуля напряженностии потенциала электрического поля от расстояния r
от общего центра сфер (0 ≤ r ≤ ∞) имеют вид:
E = kq/R2
φ = kq/R
1
3
2,5
3/4
12/3
1
2
1/3
1/4
1
1
0
r
R1
R2
R3
r
0
R1
R2
R3
17.
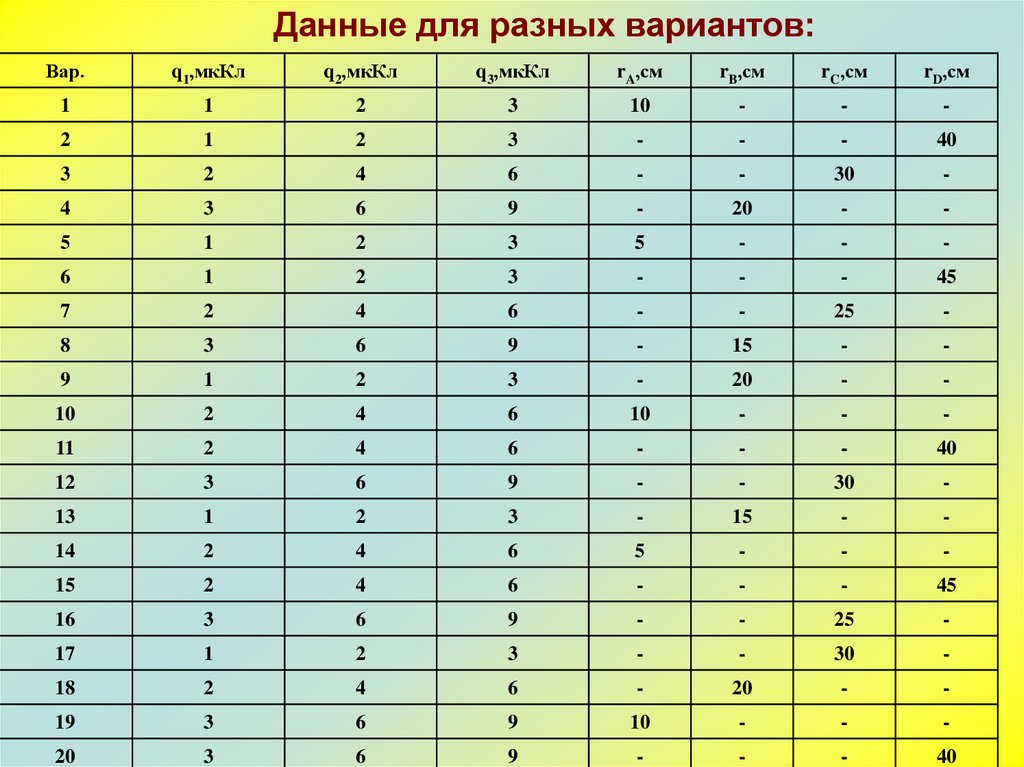
Данные для разных вариантов:Вар.
q1,мкКл
q2,мкКл
q3,мкКл
rA,см
rB,см
rC,см
rD,см
1
1
2
3
10
-
-
-
2
1
2
3
-
-
-
40
3
2
4
6
-
-
30
-
4
3
6
9
-
20
-
-
5
1
2
3
5
-
-
-
6
1
2
3
-
-
-
45
7
2
4
6
-
-
25
-
8
3
6
9
-
15
-
-
9
1
2
3
-
20
-
-
10
2
4
6
10
-
-
-
11
2
4
6
-
-
-
40
12
3
6
9
-
-
30
-
13
1
2
3
-
15
-
-
14
2
4
6
5
-
-
-
15
2
4
6
-
-
-
45
16
3
6
9
-
-
25
-
17
1
2
3
-
-
30
-
18
2
4
6
-
20
-
-
19
3
6
9
10
-
-
-
20
3
6
9
-
-
-
40


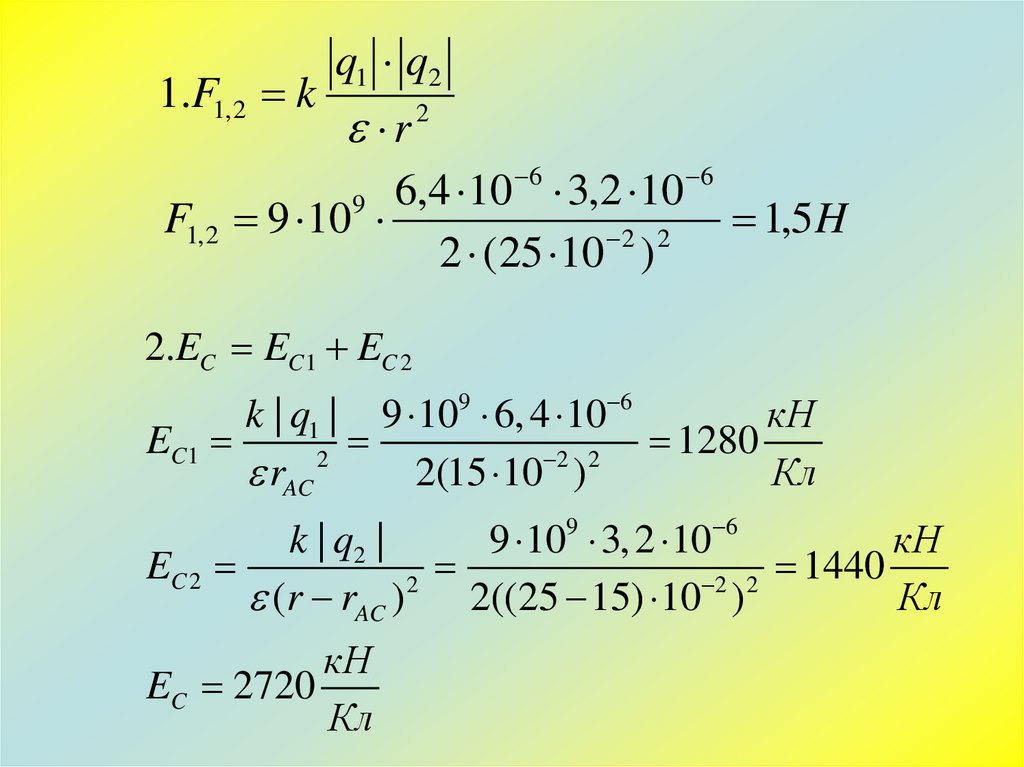
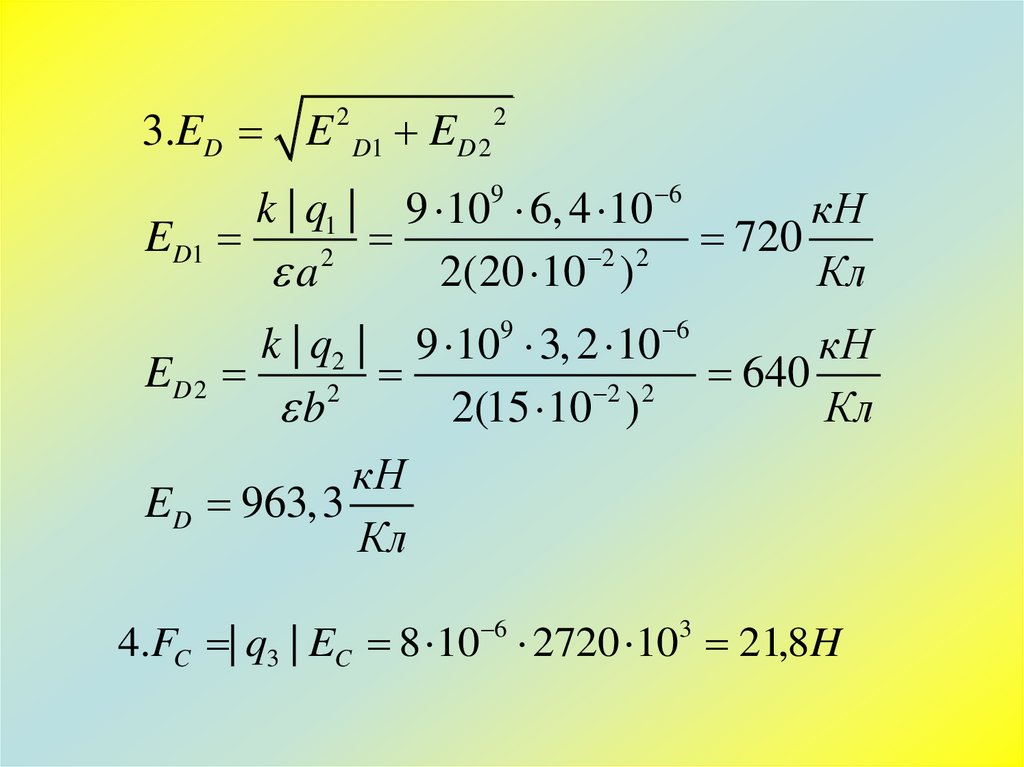


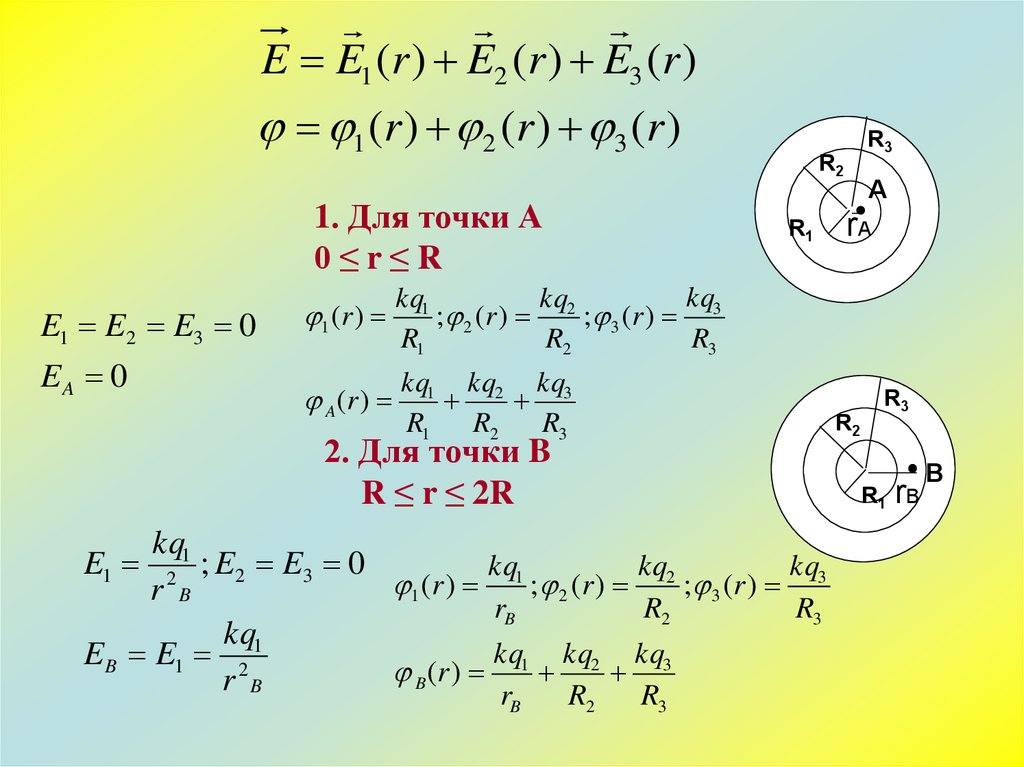
 Физика
Физика








