2d5aa2753e95498ea87ae0be80a58838

1.

2.

Заданиям с выбором ответа
А1. Найдите значение выражения 5
2) 37
1) 5
3) 3
log 2
А2. Вычислите
1) 0
2) - 1
4)
7
log5 37
3
1
1
log 1
4
8
2
3) 1
4) 5
log5 8
5
А3. Укажите значение выражения
log 8 2
1) 1
2) 3
3) 2
4) 24
2
f x log
2x x
А4. Найдите область определения функции
0,5
1) 0; 2
2) ; 0 2; 3) 0; 2
4) ; 0 2;
А5. Укажите промежуток, содержащий корень уравнения
log 7 2 x 5 2
1) (0;5)
2) (5;15)
3) (15;25)
4) (25;100)

3.

Заданиям с выбором ответа
А1. Найдите значение выражения
1) 10
3) log 2 10
2) 5
А2. Вычислите
1) 1
4) 20
1
2 log 6 3 log 6
4
2) 2
3) - 1
4) - 2
А3. Укажите значение выражения
1) lg 124
1 2 log 2 10
2
2) lg 32
3) 3,5
lg 128
lg 4
4) 4
А4. Найдите область определения функции f ( x) log 1 x 1 x 2
1) ; 2 1;
2) ; 2 1;
3) 2;1
4) 2;1
2
А5. Укажите промежуток, содержащий корень уравнения
lg log 3 log 5 x 0
1) (1;30)
2) (30;50)
3) (50;100)
4) (100;200)

4. Преобразование, приводящее к потере корней уравнения.

Задание 1.
Преобразование,
приводящее к потере
корней уравнения.
Преобразование, не
приводящее к потере
корней уравнения.
log 2 х 2 8,
log 2 х
2log 2 х
8,
log 2 х 4,
х 24 ,
х=16.
2
8,
2log 2 х
8,
log 2 х
4,
х 24 ,
х=16 или х = - 16.

5.

Свойст ва логарифмов.
log a b
2n
2n log a b , a 0, a 1, b 0, n N.
log а b c. log a b log a c , a 0, a 1, b c 0.
b
b
log а log a b log a c , a 0, a 1, 0.
c
c
1
log a 2 n b
log a b, a 1, b 0, n N .
2n

6.

Задание 2.
Решить уравнение
Решение.
2
log x 1 x x 6 4
2
2
log x 1 x x 6 4, используя свойство логарифмов
2
log a b2n 2n log a b , a 0, a 1, b 0, n N ,
получим:
2
2 log x 1 x 2 x 6 4, log x 1 x x 6 2.
По определению логарифма
x 2 x 6 x 1 2 , x 2 x 6 0,
x 1,
x 1 0,
или
x 0,
x 0,
x 2 x 6 x 2 2 x 1;
x 2 x 6 0;
Первая система решений не имеет,
решение второй системы:
Ответ: 1.
x 2 x 6 0,
x 1,
x 0,
x 2 x 6 x 2 2 x 1;
1 x 2,
x 0,
5
x , x 1;
2
X=1.

7.

Задание 3. Решите
уравнение
log 5 x 3 log 5 x
3
2
В ответе запишите число корней уравнения.
1
log x 5
Решение. Преобразуем уравнение с помощью свойств логарифма,
учитывая, что x 1, x 0.
log 5 x 3 log 5 x log 5 x,
3
2
log 5 x 3 log 5 x 2 log 5 x.
3
2
Перенесём все члены уравнения в левую часть и разложим на множители:
(log 5 x 3 log 5 x 2) log 5 x 0.
2
Корнями этого уравнения являются числа 1; 0,2 и 0,04. С учётом
области определения получаем ,что корнями уравнения являются
числа 0,2 и 0,04.
Ответ: 2.

8.

Задание 4. Представьте, что решая некоторое уравнение, вы на каком-то шаге
переходите от уравнения (1) к уравнению (2). Что произошло с корнями уравнения
(1) при этом переходе?
Поставьте в колонке I знак «+», если при переходе от (1) к (2) ни один из корней (1)
не потерялся, знак « - » - если потерялся;
в колонке II знак «+», если при переходе от (1) к (2) не появилось новых корней,
знак « - » - если они появились;
в колонке III знак «+», если уравнения (1) и (2) равносильны, знак « - » - в
противном случае.
1.
2.
(1)
(2)
log 2 x 2 log 2 3 x
x 2 3 x
lg x 1 lg 2x 3 x 1 2x 3
3.
ln x 1 ln 2 x 0 ln x 1 2 x 0
4.
log x 2 x 3 1
5.
2
log x 2 2 2 x 1 0 log x 2 2x 1 0
x 2x 3
6. log x x 9 log x 9 0 2 log x 9 0
2
2
2
x
7.
x 3 7 x
ln x 3 ln 7 x
8.
x 2 2 x 1
2 ln x x 1 ln 2
I
II
III

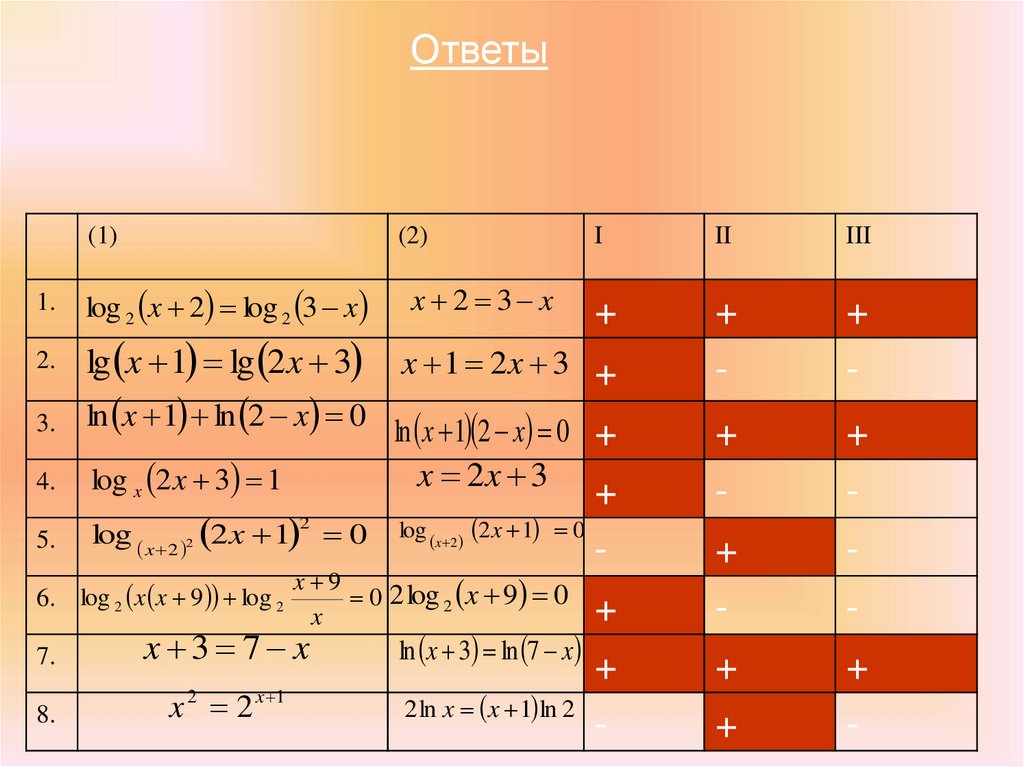
9.

Ответы
I
II
III
+
+
+
-
+
-
+
x 2x 3
4. log x 2 x 3 1
+
2
log
2
x
1
0 log 2 x 1 0
5.
x 2
x 9
0 2 log 2 x 9 0
6. log x x 9 log
+
x
x 3 7 x
ln x 3 ln 7 x
7.
+
x 2 2 x 1
2 ln x x 1 ln 2
8.
-
+
+
+
+
+
+
-
1.
(1)
(2)
log 2 x 2 log 2 3 x
x 2 3 x
2.
lg x 1 lg 2x 3
3.
ln x 1 ln 2 x 0 ln x 1 2 x 0
x 2
2
2
x 1 2x 3
2

10.

Проверь своё внимание!
1)
x 1
log 3
?
5
2)
f ( x) log 5 121 x 2 , 121 x 2 0, x 11, x 11.
3)
log 5 3
3 5, log 5 3 2 x, x
.
2
4)
5)
2x
9
2 log3 5
3
4 log3 5
4.
lg x 2 2 lg x.
5