DL-3 Intro to NN (1)

1.

03
Deep Learning
Введение в нейронные сети
2026

2.

План
❏
❏
❏
❏
❏
❏
Перцептрон и его ограничения
Многослойный перцептрон
Теоремы универсальной аппроксимации
Обучение нейронных сетей
Подходы к инициализации весов
Архитектуры для простейших задач

3.

Перцептрон

4.

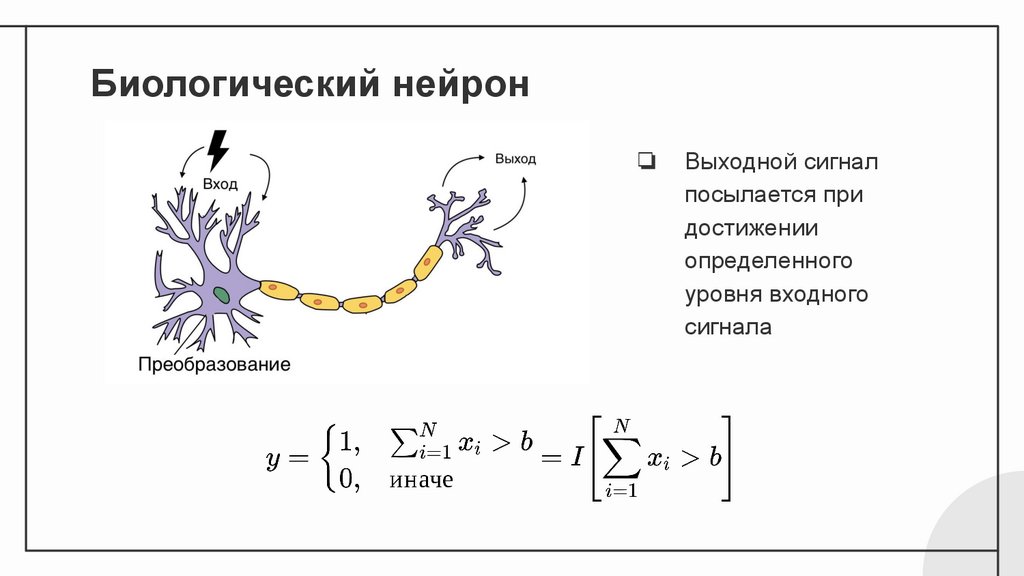
Биологический нейрон
❏
Выходной сигнал
посылается при
достижении
определенного
уровня входного
сигнала

5.

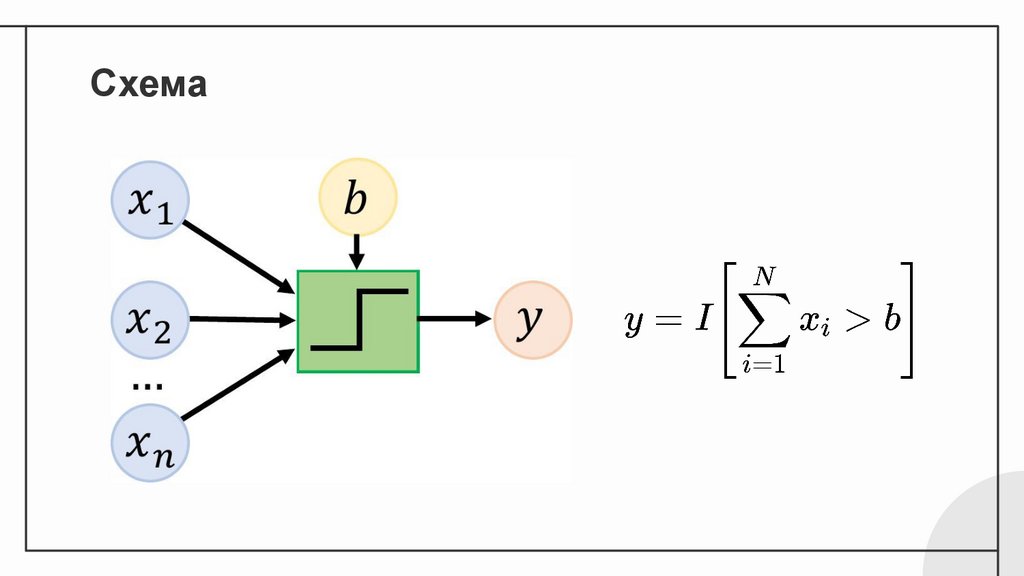
Схема

6.

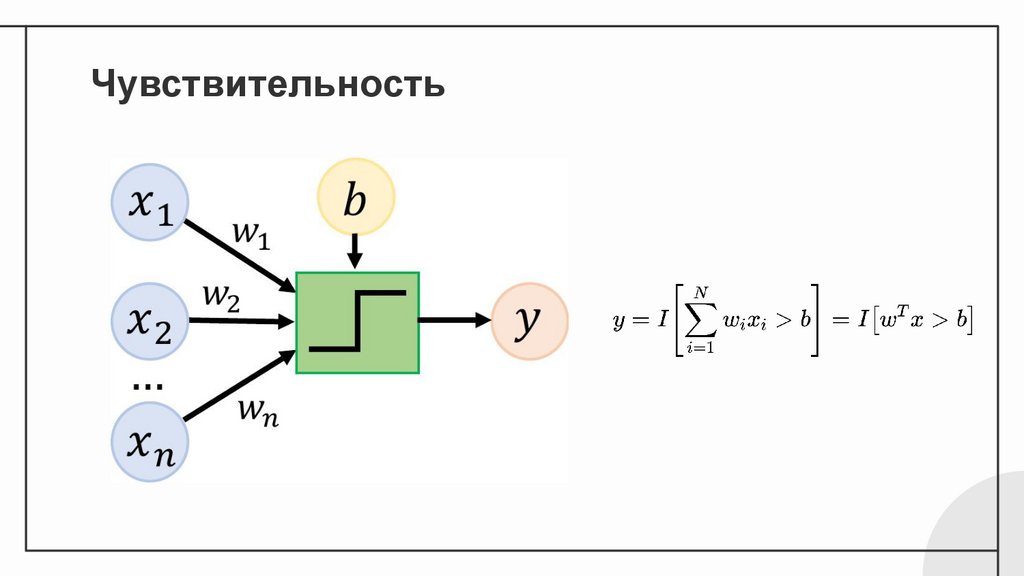
Чувствительность

7.

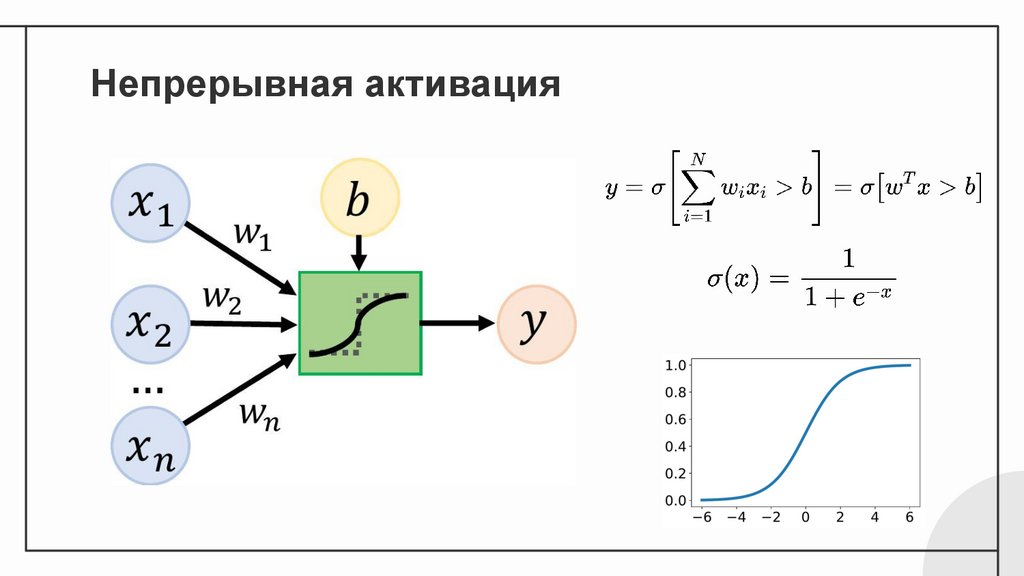
Непрерывная активация

8.

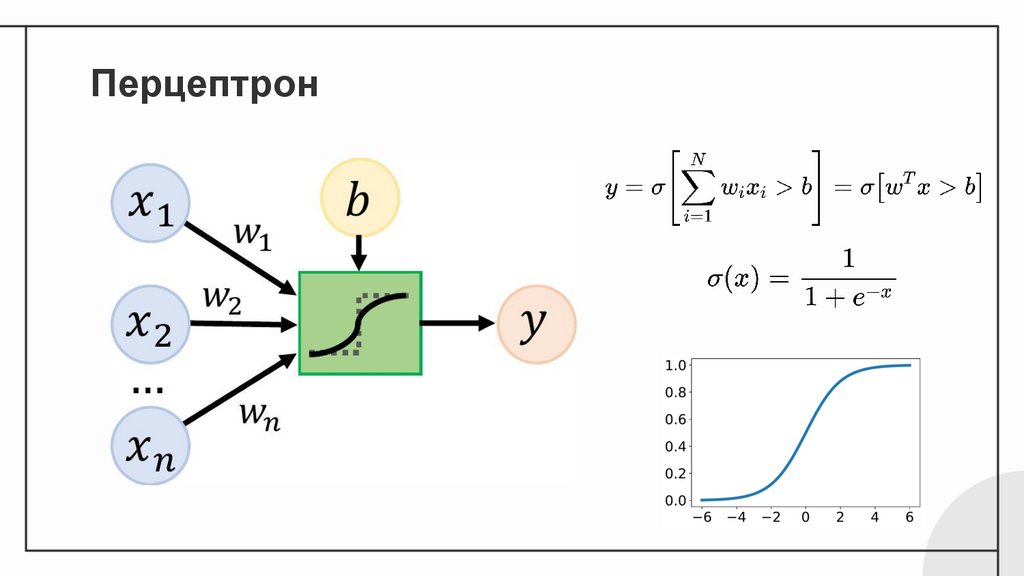
Перцептрон

9.

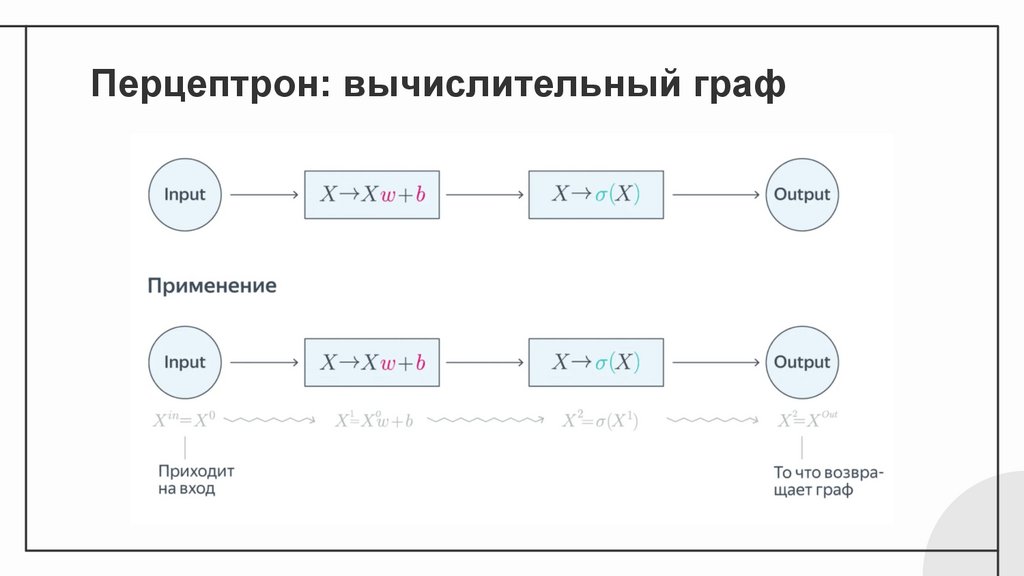
Перцептрон: вычислительный граф

10.

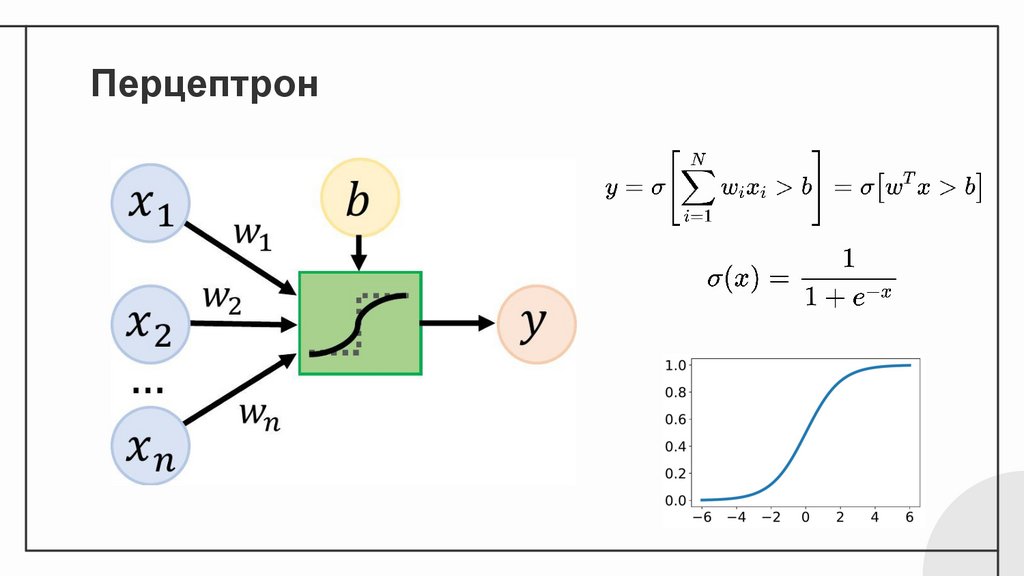
Перцептрон

11.

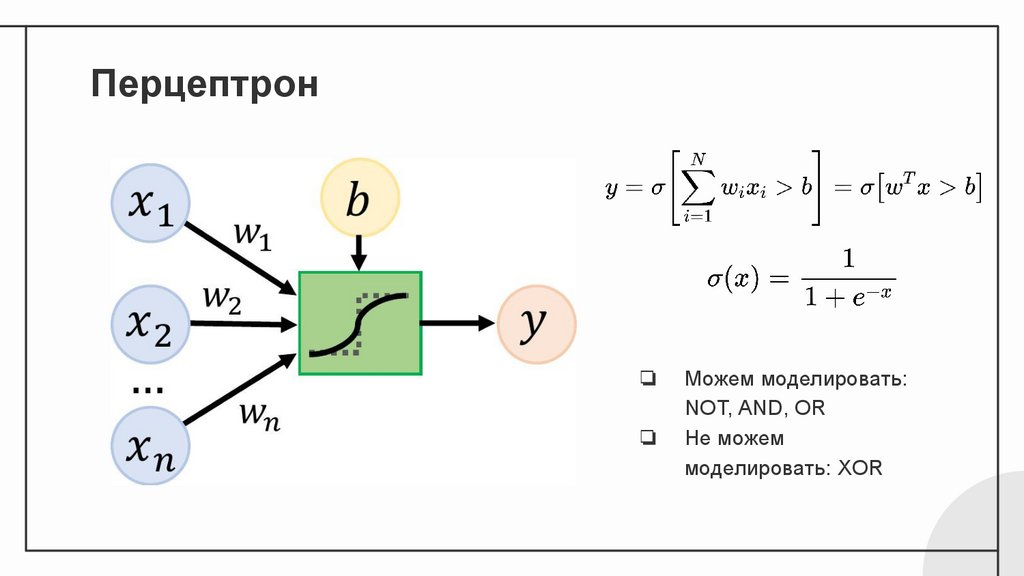
Перцептрон
❏
❏
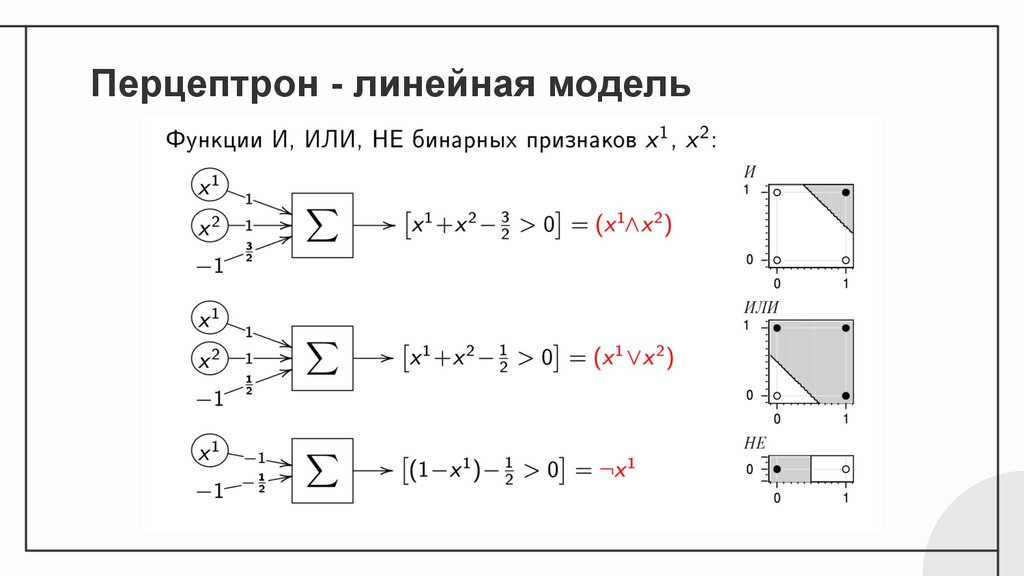
Можем моделировать:
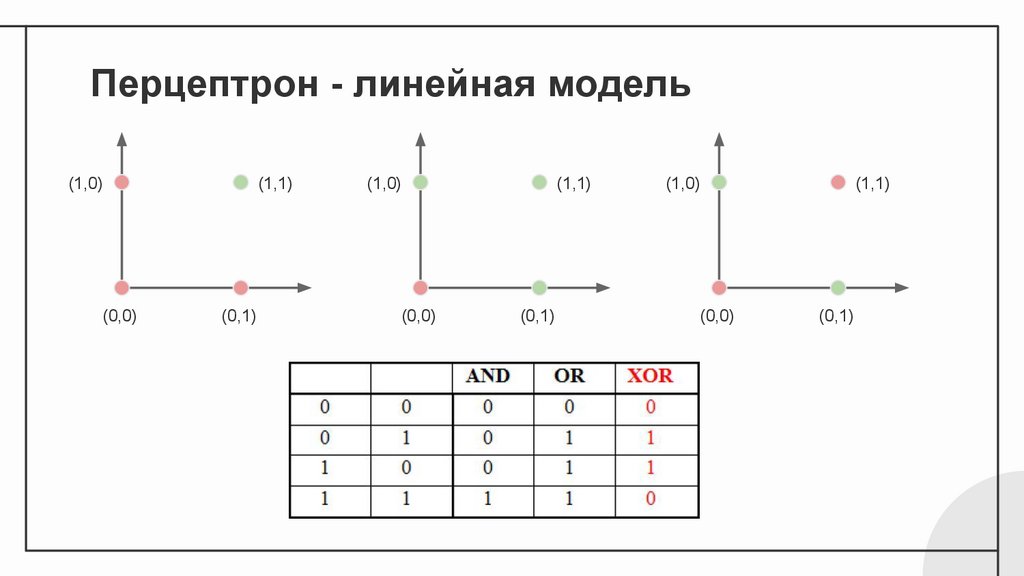
NOT, AND, OR
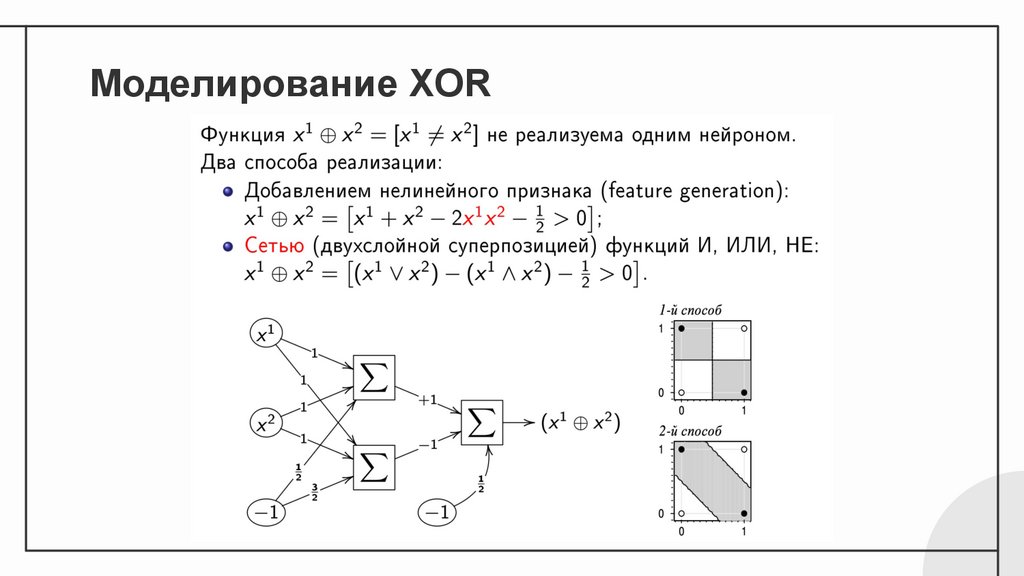
Не можем
моделировать: XOR

12.

Перцептрон - линейная модель
(1,0)
(0,0)
(1,1)
(0,1)
(1,0)
(0,0)
(1,1)
(0,1)
(1,0)
(0,0)
(1,1)
(0,1)

13.

Перцептрон - линейная модель

14.

Моделирование XOR

15.

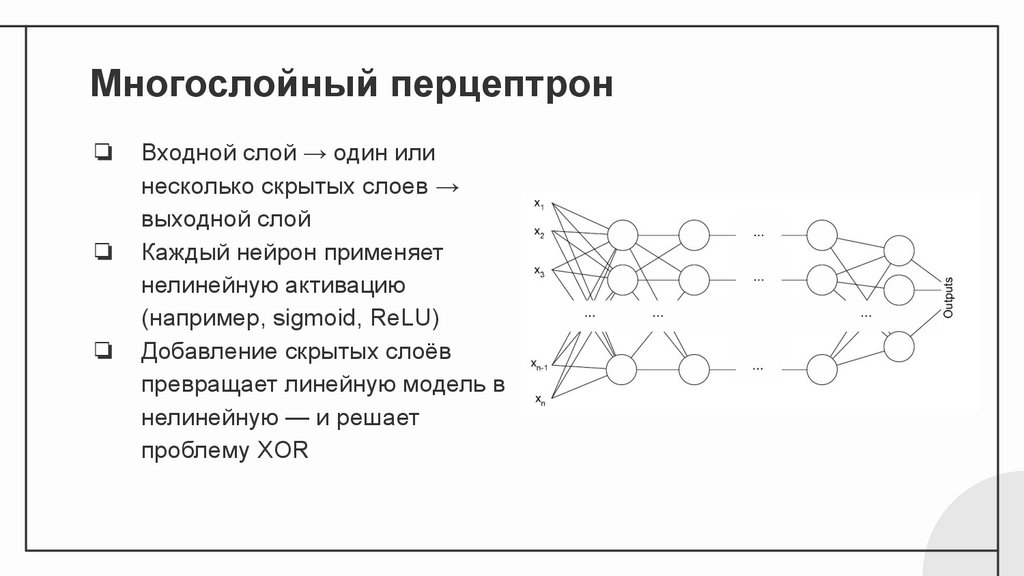
Многослойный перцептрон
❏
❏
❏
Входной слой → один или
несколько скрытых слоев →
выходной слой
Каждый нейрон применяет
нелинейную активацию
(например, sigmoid, ReLU)
Добавление скрытых слоёв
превращает линейную модель в
нелинейную — и решает
проблему XOR

16.

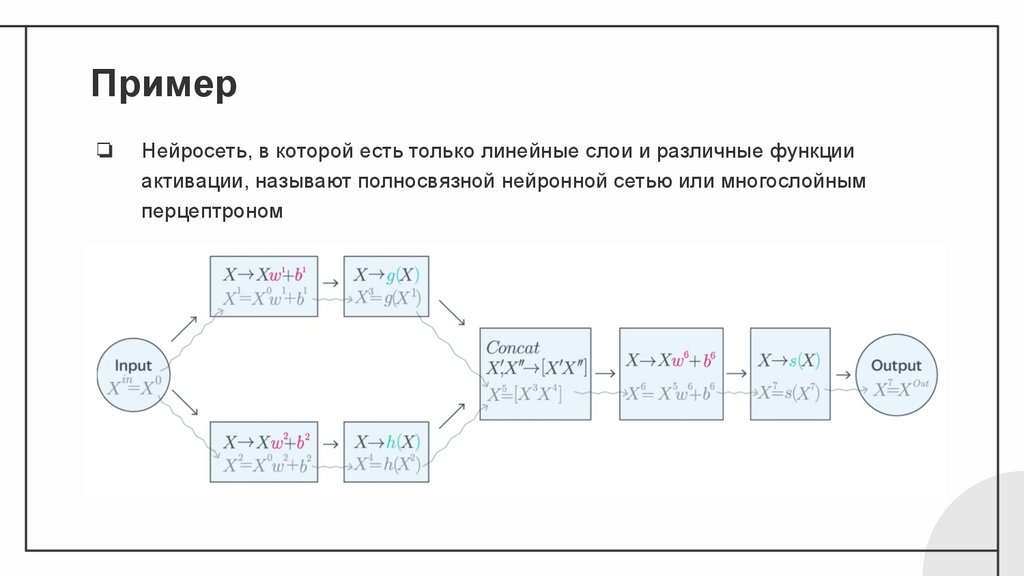
Пример
❏
Нейросеть, в которой есть только линейные слои и различные функции
активации, называют полносвязной нейронной сетью или многослойным
перцептроном

17.

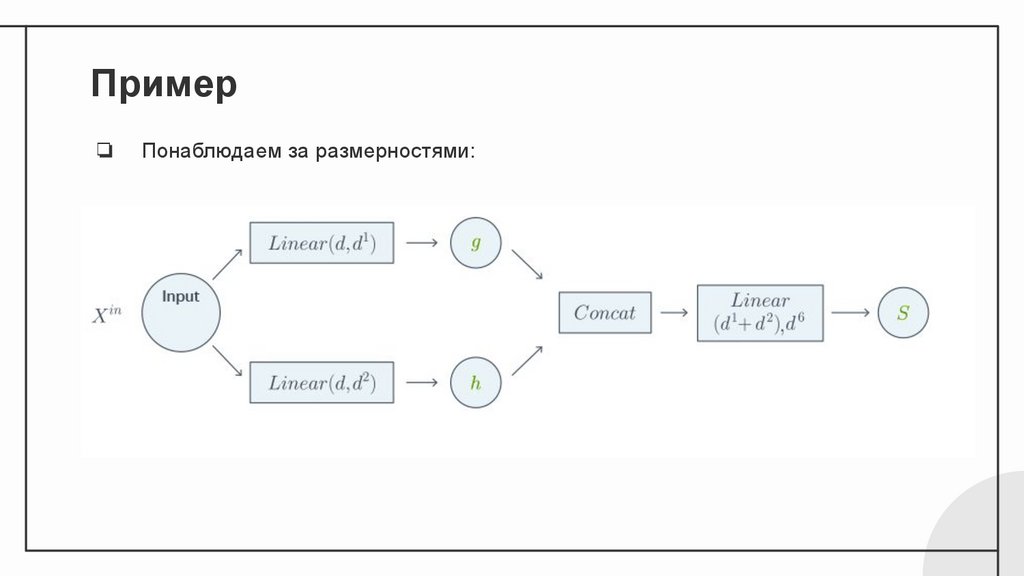
Пример
❏
Понаблюдаем за размерностями:

18.

Теоремы
универсально
й
аппроксимаци
и

19.

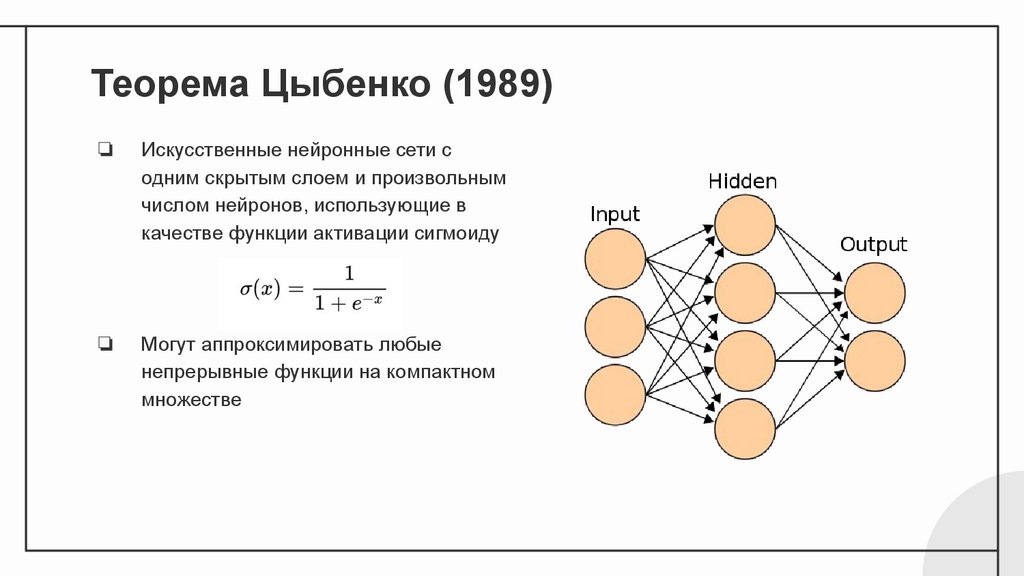
Теорема Цыбенко (1989)
❏
Искусственные нейронные сети с
одним скрытым слоем и произвольным
числом нейронов, использующие в
качестве функции активации сигмоиду
❏
Могут аппроксимировать любые
непрерывные функции на компактном
множестве

20.

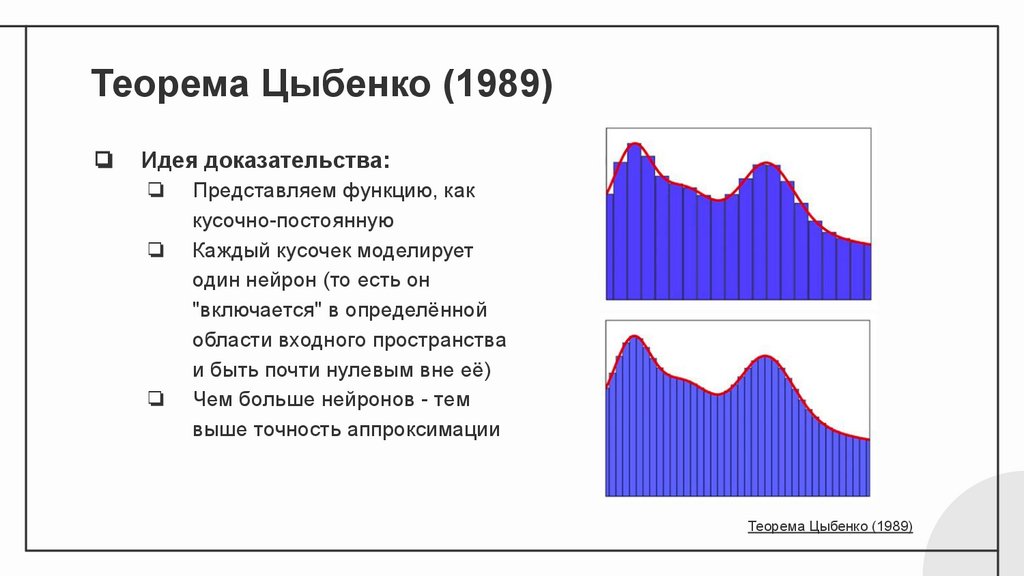
Теорема Цыбенко (1989)
❏
Идея доказательства:
❏
❏
❏
Представляем функцию, как
кусочно-постоянную
Каждый кусочек моделирует
один нейрон (то есть он
"включается" в определённой
области входного пространства
и быть почти нулевым вне её)
Чем больше нейронов - тем
выше точность аппроксимации
Теорема Цыбенко (1989)

21.

Другие теоремы универсальной аппроксимации
❏
❏
❏
Майоров и Пинкус (1999)
Нейронные сети с двумя скрытыми слоями и ограниченным числом нейронов в
каждом слое могут быть универсальными аппроксиматорами в пространстве
непрерывных функций на компактном множестве, если используются сигмоидные
функции активации
Теорема Хорника (1989) и Теорема Хорника (1991)
Курт Хорник и его коллеги расширили результаты Цыбенко на произвольное число
скрытых слоев. Они также доказали, что это свойство не зависит от конкретных
функции активации, если она является непрерывной, ограниченной, неконстантой и
неполиномиальной
Расширение Лешно и соавторов (1992)
Расширили результаты Хорника, ослабив требования к функции активации, позволяя
ей быть кусочно-непрерывной и лишь локально ограниченной, а также не являться
полиномом почти всюду, что позволяет включить часто используемые функции
активации, такие как ReLU, Mish, Swish (SiLU), GELU и другие

22.

Обучение
нейронных
сетей

23.

Как обучить нейронную сеть?
❏
Обучить нейронную сеть — подобрать значения
всех настраиваемых параметров
❏
Два этапа:
1. Задать функцию потерь
2. Подобрать параметры, которые будут ее
минимизировать
❏
Как подобрать параметры?
Любым методом оптимизации!

24.

Как обучить нейронную сеть?
❏
❏
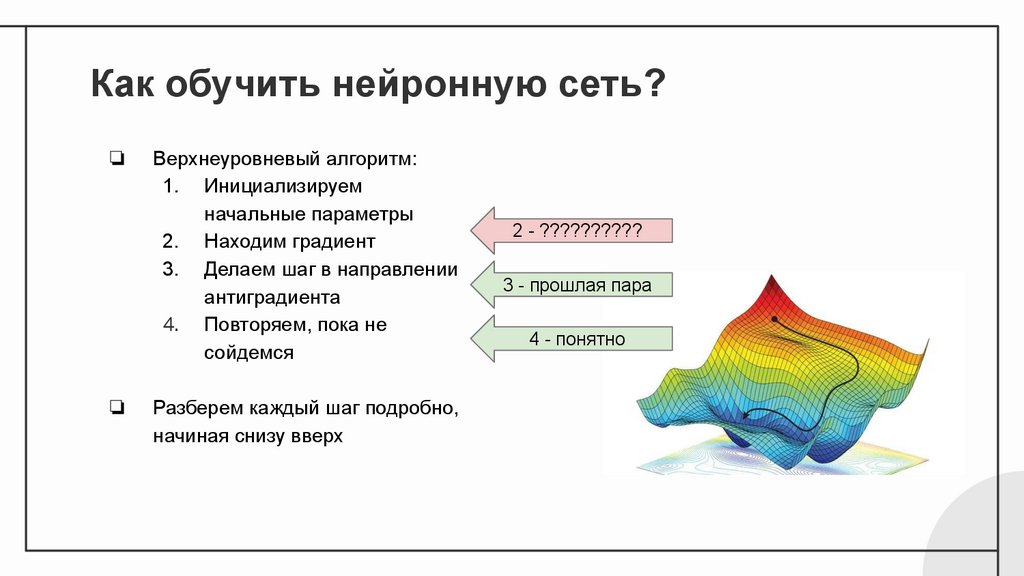
Верхнеуровневый алгоритм:
1. Инициализируем
начальные параметры
2. Находим градиент
3. Делаем шаг в направлении
антиградиента
4. Повторяем, пока не
сойдемся
Разберем каждый шаг подробно,
начиная снизу вверх
2 - ??????????
3 - прошлая пара
4 - понятно

25.

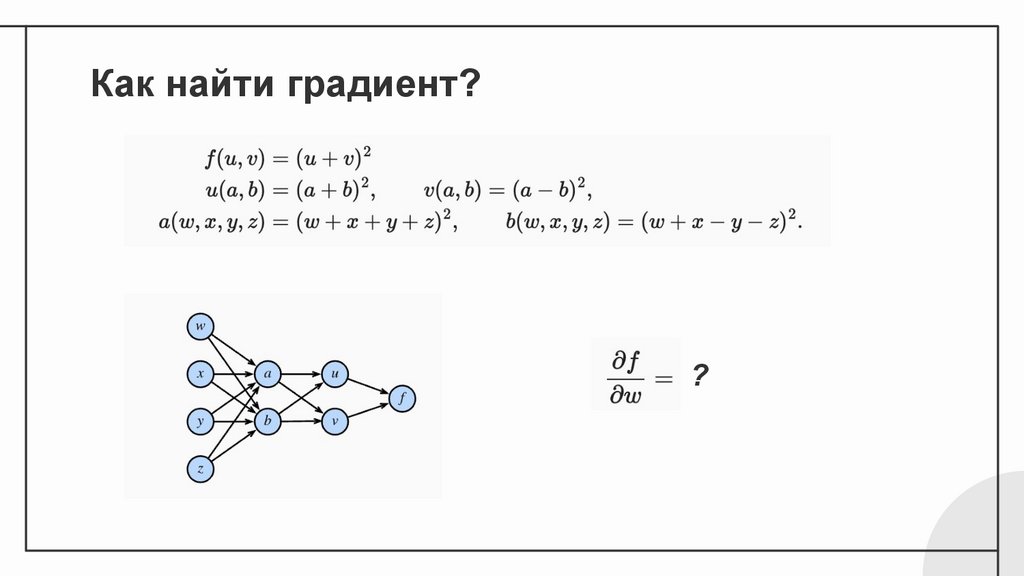
Как найти градиент?
?

26.

Как найти градиент?

27.

Multivariate Chain Rule

28.

Multivariate Chain Rule
❏
❏
Посчитали
Чтобы посчитать
❏
Мы увидели, как изменение w влияет на все остальные параметры
(dw оставляли)
В DL нам интересно другое: как каждый параметр влияет на
функцию потерь (нужно оставлять df)
Решение - поменять направление, в котором применяется цепное
правило!
❏
❏
надо проделать все заново - неприятно

29.

Multivariate Chain Rule
Было:
Стало:

30.

Backward pass
Стало:
❏
❏
Видим, как каждый параметр влияет на функцию потерь
Все считается за один проход

31.

Backward pass
Стало:
❏
❏
Видим, как каждый параметр влияет на функцию потерь
Все считается за один проход

32.

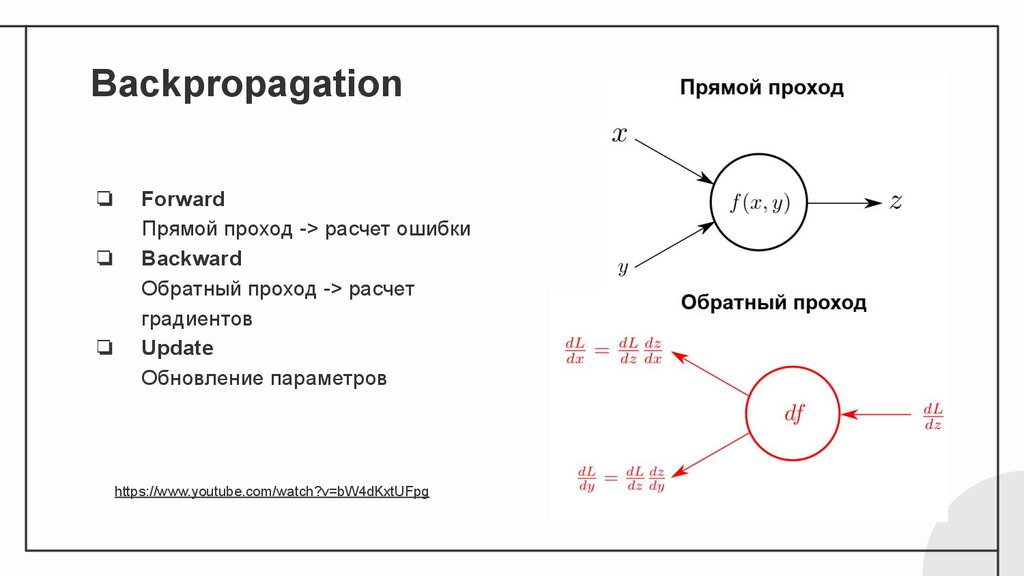
Backpropagation
❏
❏
❏
Forward
Прямой проход -> расчет ошибки
Backward
Обратный проход -> расчет
градиентов
Update
Обновление параметров
https://www.youtube.com/watch?v=bW4dKxtUFpg

33.

Как обучить нейронную сеть?
❏
❏
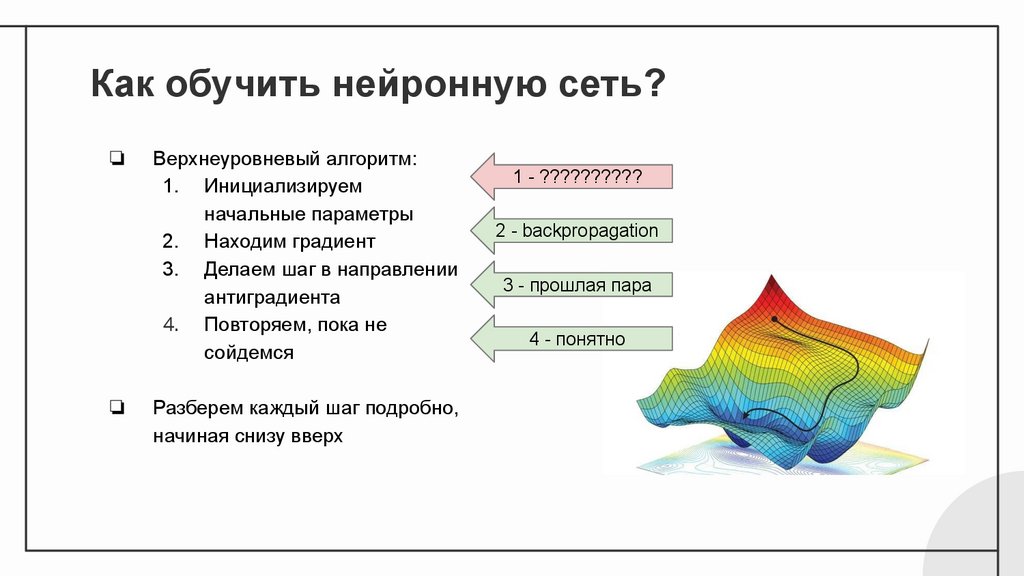
Верхнеуровневый алгоритм:
1. Инициализируем
начальные параметры
2. Находим градиент
3. Делаем шаг в направлении
антиградиента
4. Повторяем, пока не
сойдемся
Разберем каждый шаг подробно,
начиная снизу вверх
1 - ??????????
2 - backpropagation
3 - прошлая пара
4 - понятно

34.

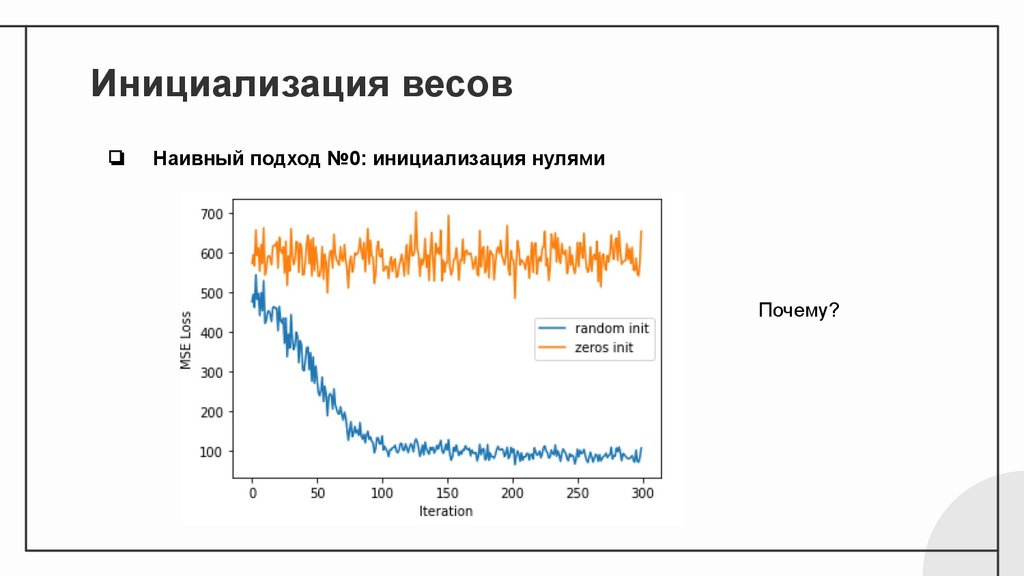
Инициализация весов
❏
Наивный подход №0: инициализация нулями
Почему?

35.

Инициализация весов
❏
Наивный подход №0: инициализация нулями

36.

Инициализация весов
❏
Подход №1: инициализация случайными числами

37.

Инициализация весов
❏
Подход №1: инициализация случайными числами
❏
Дисперсия результата линейно зависит от дисперсии входных
данных с коэффициентом

38.

Инициализация весов
❏
Подход №1: инициализация случайными числами
❏
Увеличение дисперсии промежуточных представлений с каждым новым
преобразованием (слоем) может вызвать численные ошибки или
насыщение функций активации
Снижение дисперсии может привести к почти нулевым промежуточным
представлениям -> ничего не будет учиться
Нужно использовать распределение, дисперсия которого позволила бы
сохранить дисперсию результата
❏
❏
Например:

39.

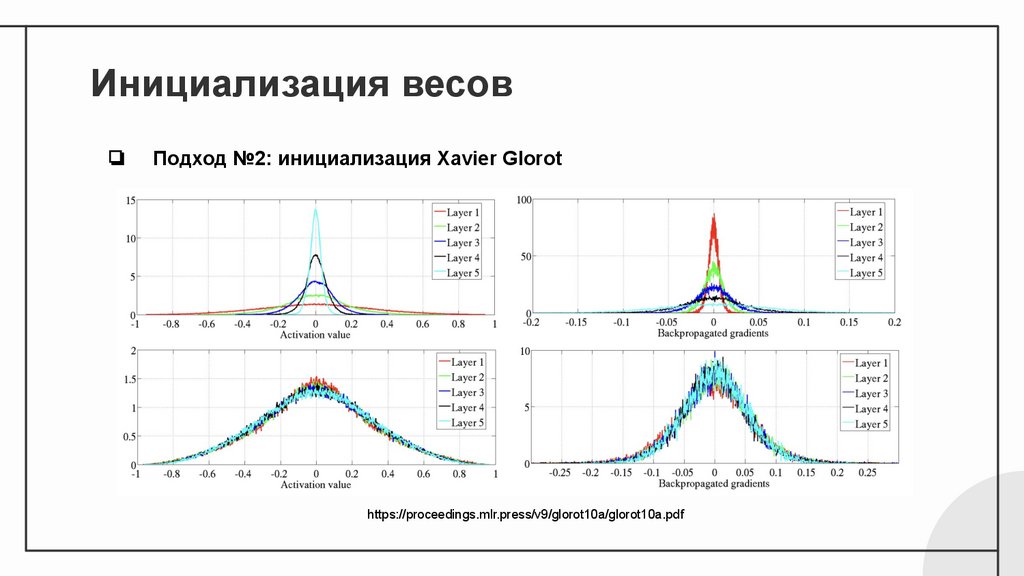
Инициализация весов
❏
Подход №2: инициализация Xavier Glorot
❏
Пусть хотя бы в среднем будет 1 ;)

40.

Инициализация весов
❏
Подход №2: инициализация Xavier Glorot
Компромисс:
-
хорошо работает для tanh
В случае использования равномерного распределения:

41.

Инициализация весов
❏
Подход №2: инициализация Xavier Glorot
https://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf

42.

Инициализация весов
❏
Подход №3: инициализация Kaiming He
❏
Область значений ReLU существенно смещена относительно нуля

43.

Инициализация весов
❏
Подход №3: инициализация Kaiming He

44.

Инициализация весов
❏
Подход №3: инициализация Kaiming He

45.

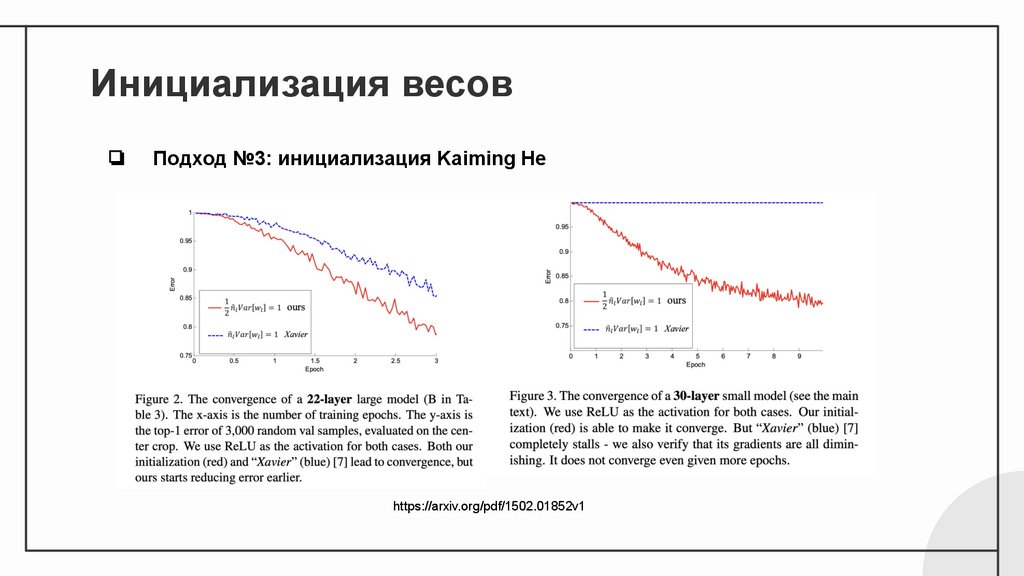
Инициализация весов
❏
Подход №3: инициализация Kaiming He
https://arxiv.org/pdf/1502.01852v1

46.

Архитектуры для
простейших задач

47.

Бинарная классификация
❏
Подойдёт любая архитектура,
на выходе у которой одно
число от 0 до 1,
интерпретируемое как
вероятность
❏
В качестве функции потерь
удобно брать log loss

48.

Многоклассовая классификация
❏
❏
❏
Нужно построить сеть, которая будет выдавать K
неотрицательных чисел, суммирующихся в 1 (где K — число
классов)
Им можно придать смысл вероятностей классов и
предсказывать тот класс, «вероятность» которого максимальна
Лосс - кросс энтропия:

49.

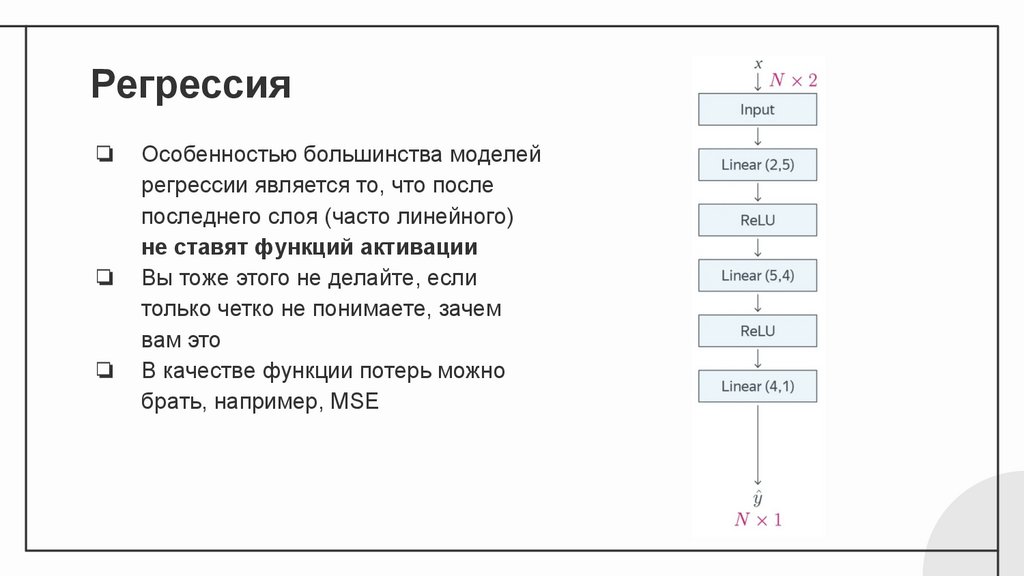
Регрессия
❏
❏
❏
Особенностью большинства моделей
регрессии является то, что после
последнего слоя (часто линейного)
не ставят функций активации
Вы тоже этого не делайте, если
только четко не понимаете, зачем
вам это
В качестве функции потерь можно
брать, например, MSE

50.

❏
❏
❏
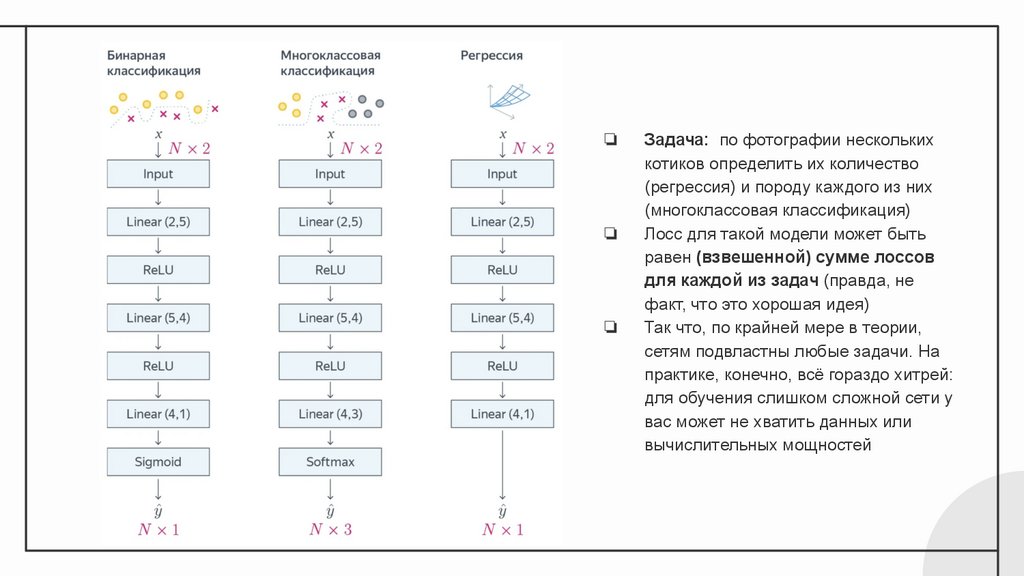
Задача: по фотографии нескольких
котиков определить их количество
(регрессия) и породу каждого из них
(многоклассовая классификация)
Лосс для такой модели может быть
равен (взвешенной) сумме лоссов
для каждой из задач (правда, не
факт, что это хорошая идея)
Так что, по крайней мере в теории,
сетям подвластны любые задачи. На
практике, конечно, всё гораздо хитрей:
для обучения слишком сложной сети у
вас может не хватить данных или
вычислительных мощностей