презенташка

1.

Самарский Государственный Технический
Университет
УЛУЧШЕНИЕ КАЧЕСТВА ВОССТАНОВЛЕНИЯ
ИЗОБРАЖЕНИЙ С ПОМОЩЬЮ ИНТЕРПОЛЯЦИИ
СПЛАЙНАМИ
Р.С. Олешко, студент СамГТУ,
С.А. Никулин, студент СамГТУ,
А.Г. Золин, к.т.н. доцент кафедры
ИТ, СамГТУ (Самара, Россия)

2.

В данной работе речь пойдет об исследовании способа аппроксимации
восстановленного изображения сплайнами, а так же о его результатах,
которые он способен показать.
Разложим изображение на ряд пикселей вида:
Где каждый xi - пиксель исходного изображения. После искажения
значения каждого пикселя, каждое новое значение xi′ представляет
собой среднеарифметическое i и i-1 значения :

3.

В результате изначальный ряд пикселей (1)принимает вид :
Где значения xi′ соответствуют (2).
При процессе обращения искажения изображения получаем исходное
изображение, но с рядом пикселей :
При этом, X0 - неизвестная константа с чередующимся знаком. Таким
образом, на каждом шаге будут накладываться помехи, которые в
конечном итоге исказят результат [1].
Если обозначить изначальную функцию, по которой строятся пиксели
как f(x,y) а итоговую как , то задача восстановления искаженного
изображения заключается в нахождении полного приближения
полученной функции к исходной.

4.

Перейдем к моделированию и практической проверки ситуации
устранения эффекта Гиббса в восстановлении изображений. Для
более точного восстановления смазанного изображения
воспользуемся сплайновыми функциями.
Для вычисления сплайн-функции, заданной на сетке X1<X2< …
<XN, требуется упорядоченная монотонно возрастающая
последовательность Xi..Это означает, что сплайнфункция y = y(x)
может быть построена только для однозначной функции.

5.

Кривая, построенная на основе сплайнов, описывается следующим
образом:
Где p(t) - радиус-вектор точек на кривой, Pi - вершины
аппроксимируемой ломаной (всего вершин n+1), а Nik - весовая
функция i-й нормализованной сплайн-базисной кривой порядка k (т. е.
степени k-1).

6.

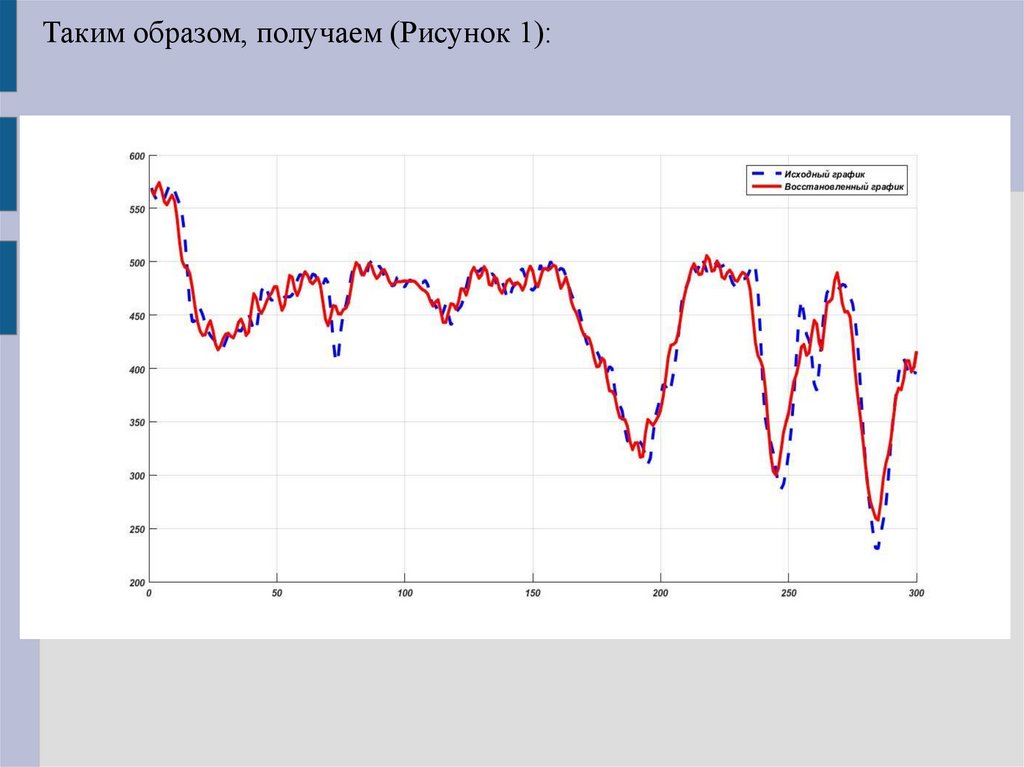
Таким образом, получаем (Рисунок 1):

7.

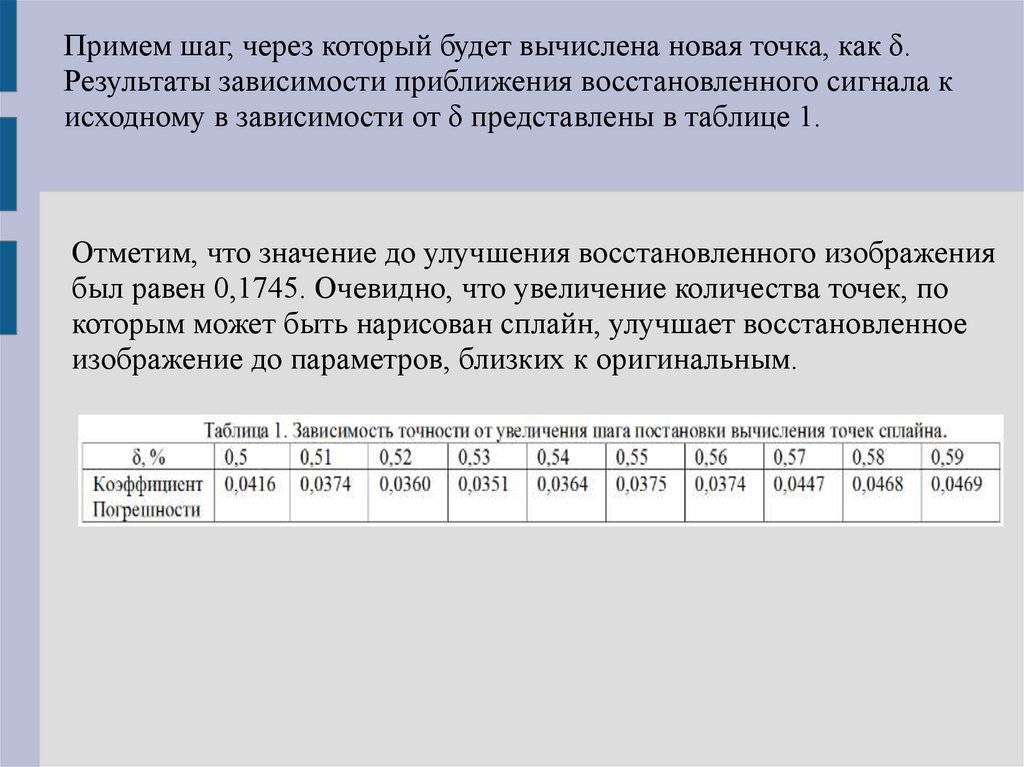
Примем шаг, через который будет вычислена новая точка, как δ.
Результаты зависимости приближения восстановленного сигнала к
исходному в зависимости от δ представлены в таблице 1.
Отметим, что значение до улучшения восстановленного изображения
был равен 0,1745. Очевидно, что увеличение количества точек, по
которым может быть нарисован сплайн, улучшает восстановленное
изображение до параметров, близких к оригинальным.

8.

Теперь проведем эксперимент, целью которого поставим выявление
того, насколько хорошо метод применим к более и менее смазанным
изображениям. Примем δ за 0,53. Результаты этого эксперимента
представлены в таблице 2:
В результате исследований был получен простой в реализации
алгоритм улучшения качества восстановленных смазанных
изображений. Малое значение погрешности восстановления говорит о
том, что данный метод позволяет на порядок улучшить качество
полученного восстановленного изображения. Погрешность
вычислялась по формуле:

9.

Улучшенное восстановленное изображение имеет лучшее
приближение к оригинальной, чем восстановленное, а
следовательно даст лучшие результаты в работе систем
видеонаблюдения. Отметим, что коэффициент приближения
достаточно высок. В настоящее время ведутся исследования по
результатам других методов улучшения качества, а так же по
возможности применения нескольких способов к одному
изображению последовательно.

10.

Список использованной литературы.
1. Гонсалес Р., Вудс Р. –«Цифровая обработка изображений»//
«Техносфера», Москва 2012 г.
2. В.И. Батищев, И.И. Волков, А.Г. Золин «Аппроксимационный
подход к решению обратных задач восстановления сигналов в базисе
экспоненциальных функций// Проблемы управления и моделирования
в сложных системах» :Труды XVI Международной конференции (30
июня – 03 июля 2014 г. Самара, Россия) / Под ред.: акад. Е.А.
Федосова, акад. Н.А. Кузнецова, проф. В.А. Виттиха. - Самара:
Самарский научный центр РАН, 2014. С. 678-682
3. http://www.keldysh.ru – Институт прикладной математики им. М.В.
Келдыша Российской академии наук