Информатика в задачах теплоэнергетики

1. Информатика в задачах теплоэнергетики

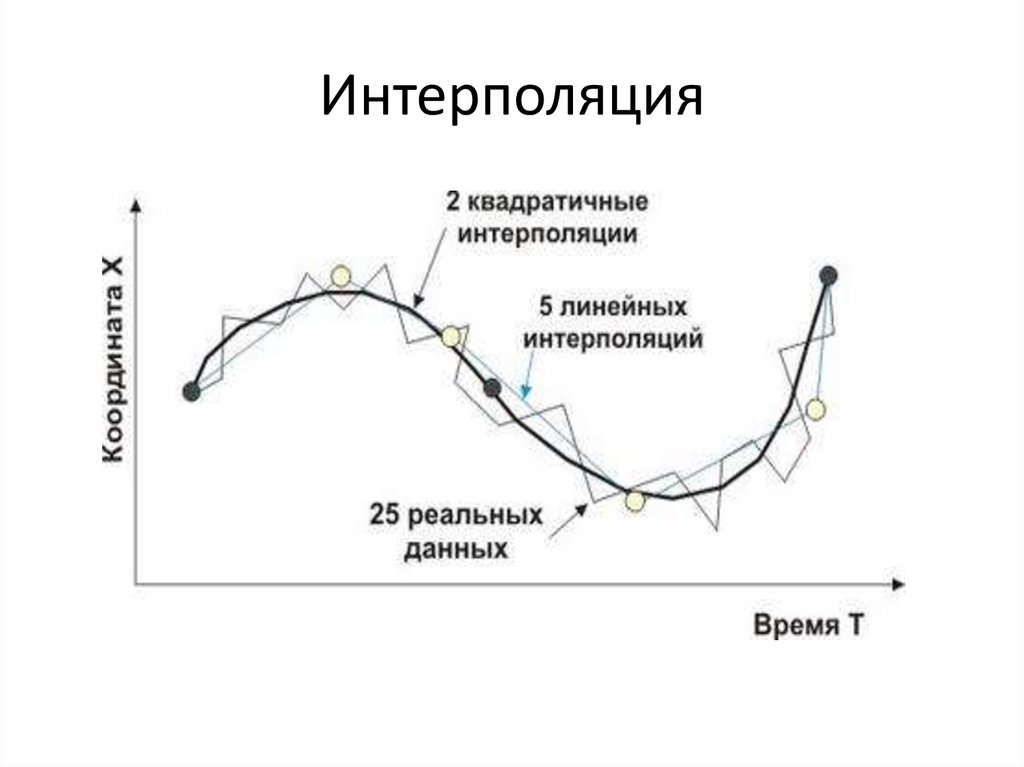
2. Интерполяция

Слово интерполяция (interpolatio)
переводится
с
латинского,
как
изменение или обновление. С точки
зрения математики, это определение
промежуточных значений какой либо
переменной величины по ряду соседних
известных её значений.

3. Интерполяция

Если задана функция y(x), то это означает, что
любому допустимому значению х сопоставлено
значение y. Но нередко оказывается, что
нахождение этого значения очень трудоемко.
Решение задач интерполяции обеспечивается
построением интерполяционной функции y(x)
приближенно заменяющей исходную φ(x)
заданную таблично, и проходящей через все
заданные точки – узлы интерполяции.

4. интерполяция

При интерполировании рассматриваются
три основные проблемы:
выбор интерполяционной функции y(x);
оценка погрешности интерполяции R(x);
размещение узлов интерполяции для
обеспечения наивысшей возможной
точности восстановления функции (х1, x2, х3,
х4 …хn).

5. Интерполяция

6. Интерполяция

Практически
все
интерполяционные
методы базирующиеся на использовании в
качестве
интерполяционной
функции
полиномов, дают одни и те же результаты, но
с разными затратами. Это объясняется тем,
что полином n-й степени, содержащий n+1
параметр и проходящий через все заданные
n+1 точки – единственный.

7. Интерполяция

Следует
отметить,
что
существует
очевидный
способ
построения
интерполяционной функции: из условия
прохождения функции через все точки
составляется система уравнений, из решения
которой
находятся
все
неизвестные
параметры. Однако, этот путь не всегда
эффективен, особенно при большом числе
точек.

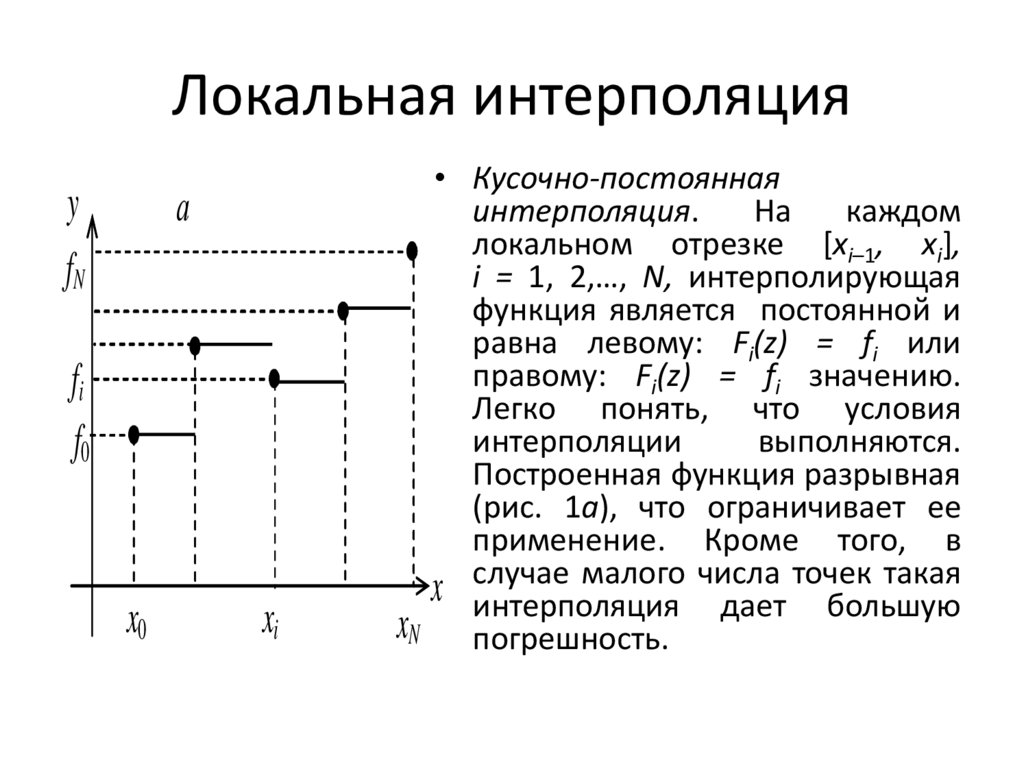
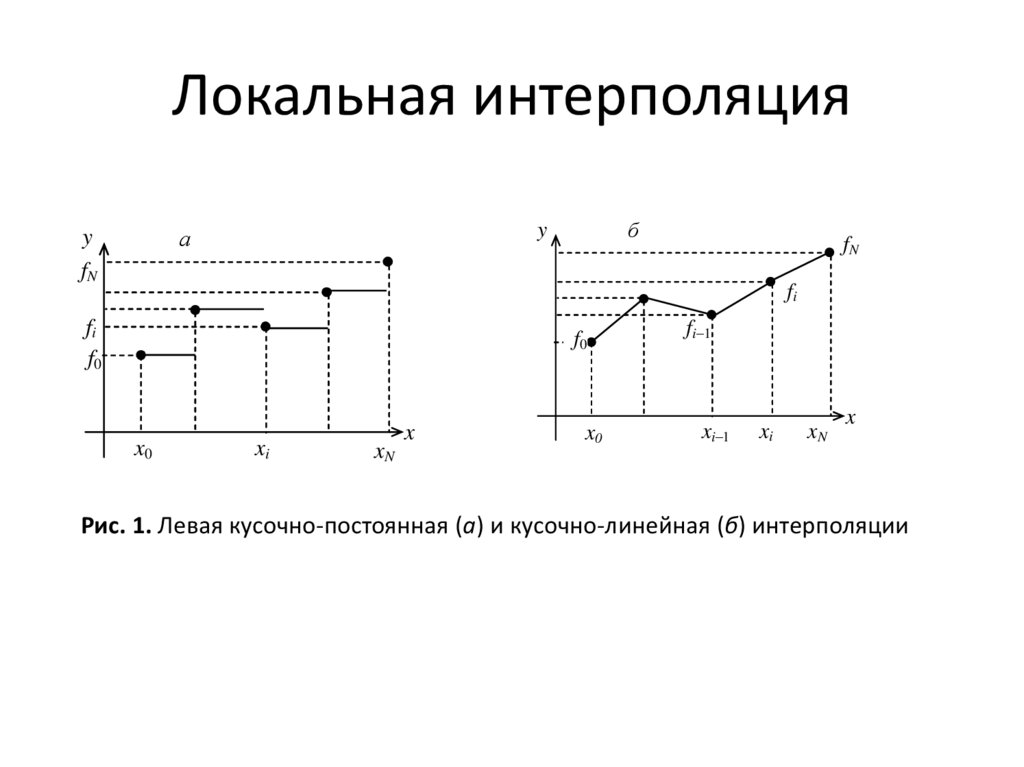
8. Локальная интерполяция

а
y
fN
fi
f0
x0
xi
• Кусочно-постоянная
интерполяция.
На
каждом
локальном отрезке [xi–1, xi],
i = 1, 2,…, N, интерполирующая
функция является постоянной и
равна левому: Fi(z) = fi или
правому: Fi(z) = fi значению.
Легко понять, что условия
интерполяции
выполняются.
Построенная функция разрывная
(рис. 1а), что ограничивает ее
применение. Кроме того, в
малого числа точек такая
x случае
дает большую
xN интерполяция
погрешность.

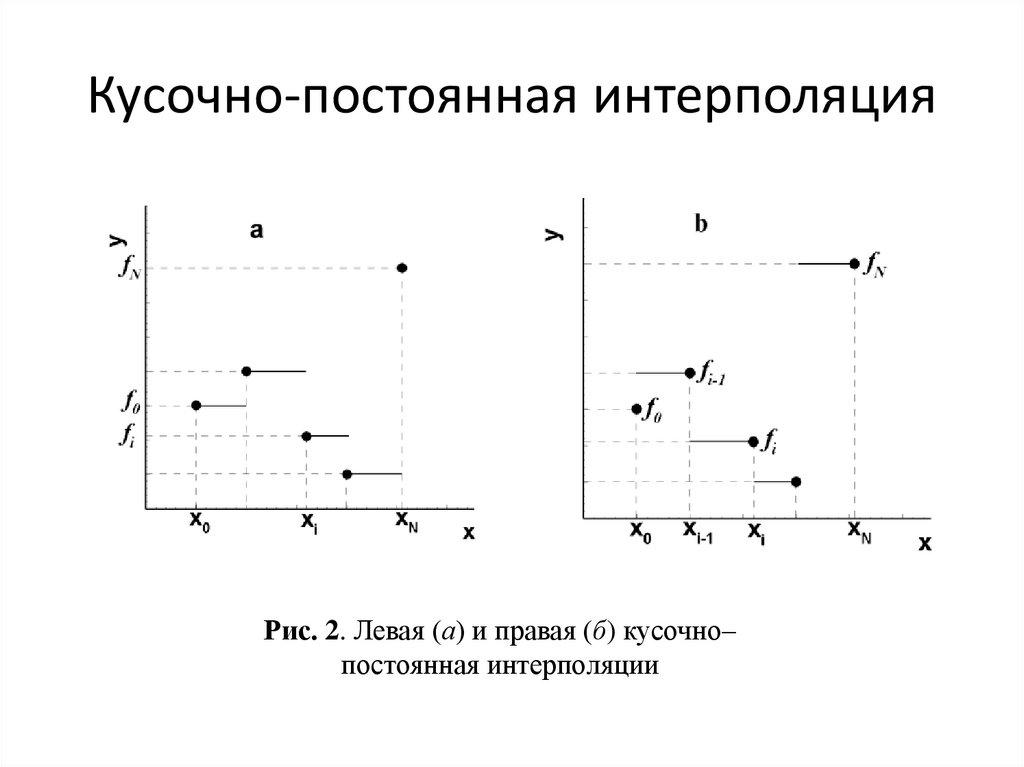
9. Кусочно-постоянная интерполяция

При кусочно-постоянной
каждом отрезке xi 1 , xi
значению функции.
интерполяции интерполяционный многочлен на
равен константе, а именно, левому или правому
Для левой кусочно-постоянной интерполяции
.
f 0 , x 0 x x1
f 1 , x1 x x 2
F x
...
f N 1 , x N 1 x x N
Для правой кусочно-постоянной интерполяции
f 1 , x 0 x x1
f 2 , x1 x x 2
F x
...
f N , x N 1 x x N
F x f i 1
если
xi 1 x xi
F x f i xi 1 x xi

10. Кусочно-постоянная интерполяция

Рис. 2. Левая (а) и правая (б) кусочно–
постоянная интерполяции

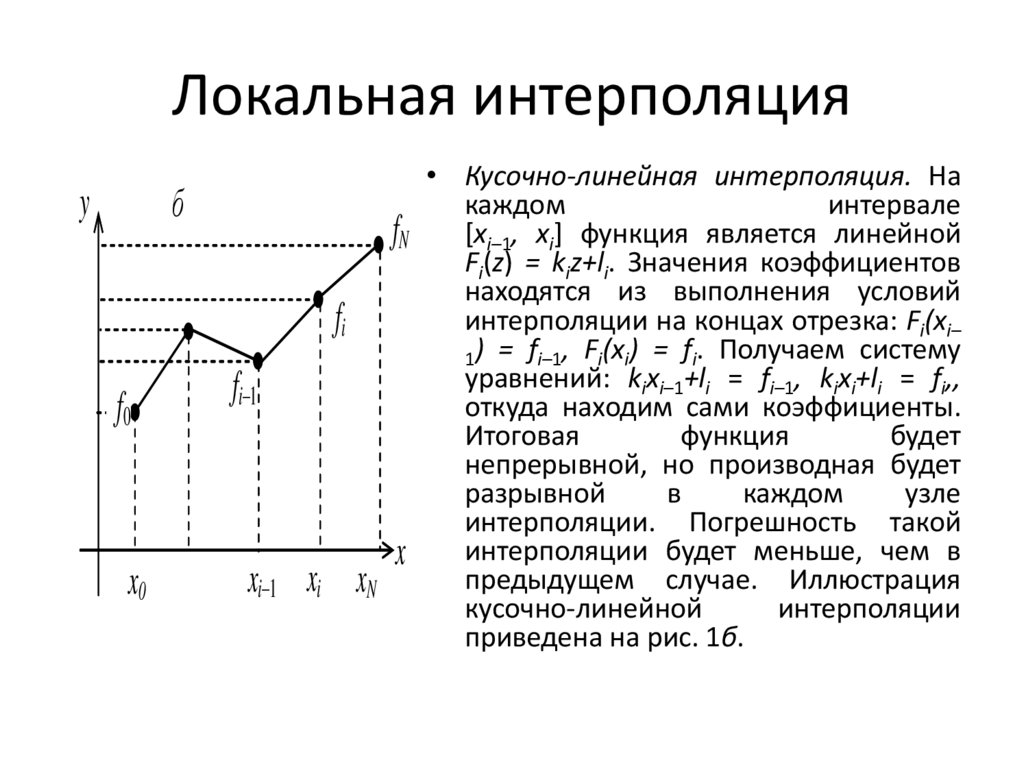
11. Локальная интерполяция

б
y
f0
x0
fi–1
xi–1
• Кусочно-линейная интерполяция. На
каждом
интервале
fN [xi–1, xi] функция является линейной
Fi(z) = kiz+li. Значения коэффициентов
находятся из выполнения условий
интерполяции на концах отрезка: Fi(xi–
fi
1) = fi–1, Fi(xi) = fi. Получаем систему
уравнений: kixi–1+li = fi–1, kixi+li = fi,,
откуда находим сами коэффициенты.
Итоговая
функция
будет
непрерывной, но производная будет
разрывной
в
каждом
узле
интерполяции. Погрешность такой
x интерполяции будет меньше, чем в
предыдущем случае. Иллюстрация
xi xN
кусочно-линейной
интерполяции
приведена на рис. 1б.

12. Кусочно-линейная интерполяция

k i xi 1 li f i 1
f i f i 1
ki
xi xi 1
k i xi li f i
f i f i 1
x xi f i
F x
xi xi 1
Т.е.
f i f i 1
li f i
xi
xi xi 1
если
xi 1 x xi
f1 f 0
x x0 f 0 , x0 x x1 ,
x1 x0
f 2 f1
x x1 f1 , x1 x x2
F x
x 2 x1
...
f f
N 1
N
x x N 1 f N 1 , x N 1 x x N
x N 1 x N 1
При использовании линейной интерполяции сначала нужно определить
интервал, в который попадает искомое значение аргумента, а затем
подставить его в формулу!

13. Локальная интерполяция

б
y
а
y
fN
fN
fi
fi
f0
f0
x0
xi
xN
x
x0
fi–1
xi–1
xi
xN
x
Рис. 1. Левая кусочно-постоянная (а) и кусочно-линейная (б) интерполяции

14. Пример вычисления кусочно-постоянной и кусочно-линейной интерполяции

Пример вычисления кусочно-постоянной и кусочнолинейной интерполяции

15. Метод Лагранжа

ЛАГРАНЖ, ЖОЗЕФ ЛУИ (Lagrange, Joseph Louis) (1736–
1813) (рис.1.2), французский математик и механик.
Родился 25 января 1736 в Турине. Учился в Туринском
университете. Стал профессором геометрии в
Артиллерийской школе Турина. Лагранж внес
существенный вклад во многие области математики,
включая
вариационное
исчисление,
теорию
дифференциальных уравнений, решение задач на
нахождение максимумов и минимумов, теорию
чисел (теорема Лагранжа), алгебру и теорию
вероятностей. В двух своих важных трудах – Теория
аналитических функций (Théorie des fonctions
analytiques, 1797) и О решении численных уравнений
(De la résolution des équations numériques, 1798) –
подытожил все, что было известно по этим вопросам
в его время, а содержавшиеся в них новые идеи и
методы были развиты в работах математиков 19 в.
Умер Лагранж в Париже 10 апреля 1813.

16. Метод Лагранжа

Пусть известны значения некоторой функции f(х)
в n+1 различных произвольных точках yi=f(xi),
i=0,…n. Для интерполирования (восстановления)
функции в какой либо точке х, принадлежащей
отрезку [х0, хn], необходимо построить
интерполяционный полином n-го порядка,
который в методе Лагранжа представляется
следующим образом:

17. Метод Лагранжа

Если раскрыть произведение всех скобок в числителе, то получим полином n-го
порядка от х, так как в числителе содержится n сомножителей первого порядка. Таким
образом, интерполяционный полином Лагранжа, не что иное, как обычный полином nго порядка, несмотря на форму записи.
максимальное значение (n+1)-й производной исходной функции f(x) на отрезке [х0, хn]:

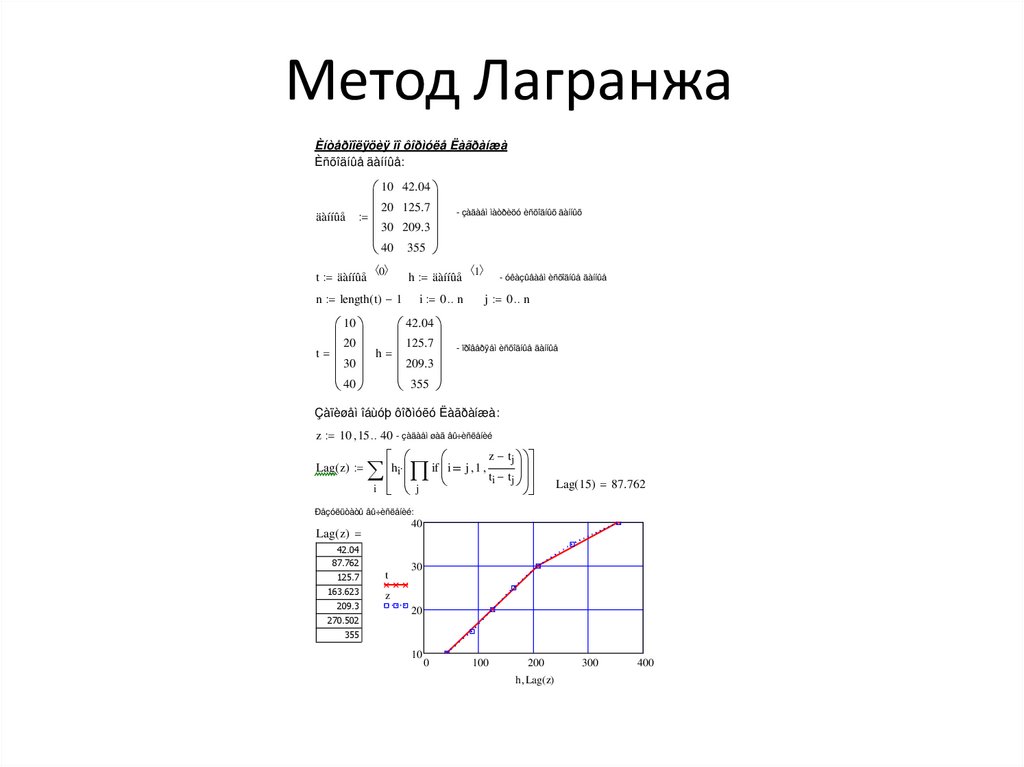
18. Метод Лагранжа

Дана таблично заданная функция (табл. 1.1.).
Требуется найти h(t) при t=15оС. В нашем
случае n=3.
Таблица 1.1.
Данные для интерполяции по методу Лагранжа
n
(кол-во точек)
оС
t,
h, кДж/кг
0
1
2
3
10
42,04
20
125,70
30
209,30
40
355,00
Решение:
Запишем функцию Лагранжа в развернутом виде:

19. Метод Лагранжа

Решение:
Запишем функцию Лагранжа в развернутом виде:

20. Метод Лагранжа

Попробуем найти значение функции h(t) при t=15оС при n=2. Для интерполяции выберем точки 0, 1 и 2.
Снова запишем функцию Лагранжа:

21. Метод Лагранжа

Èíòåðïîëÿöèÿ ïî ôîðìóëå Ëàãðàíæà
Èñõîäíûå äàííûå:
10
20
äàííûå
30
40
t äàííûå
42.04
125.7
- çàäàåì ìàòðèöó èñõîäíûõ äàííûõ
209.3
0
355
h äàííûå
n length ( t) 1
i 0 n
10
42.04
20 h 125.7
t
30
209.3
40
355
1
- óêàçûâàåì èñõîäíûå äàííûå
j 0 n
- ïðîâåðÿåì èñõîäíûå äàííûå
Çàïèøåì îáùóþ ôîðìóëó Ëàãðàíæà:
z 10 15 40 - çàäàåì øàã âû÷èñëåíèé
Lag( z)
i
hi
j
if i
z tj
j 1
ti tj
Lag( 15) 87.762
Ðåçóëüòàòû âû÷èñëåíèé:
40
Lag( z)
42.04
87.762
125.7
163.623
209.3
270.502
t
30
z
20
355
10
0
100
200
h Lag( z)
300
400

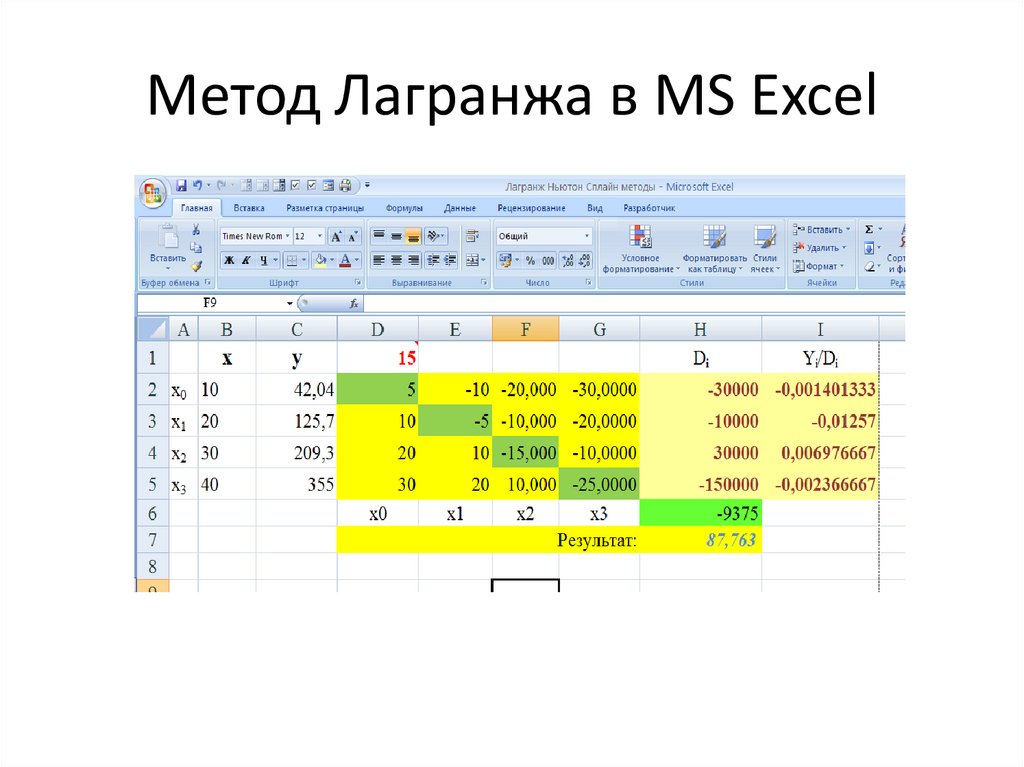
22. Метод Лагранжа в MS Excel

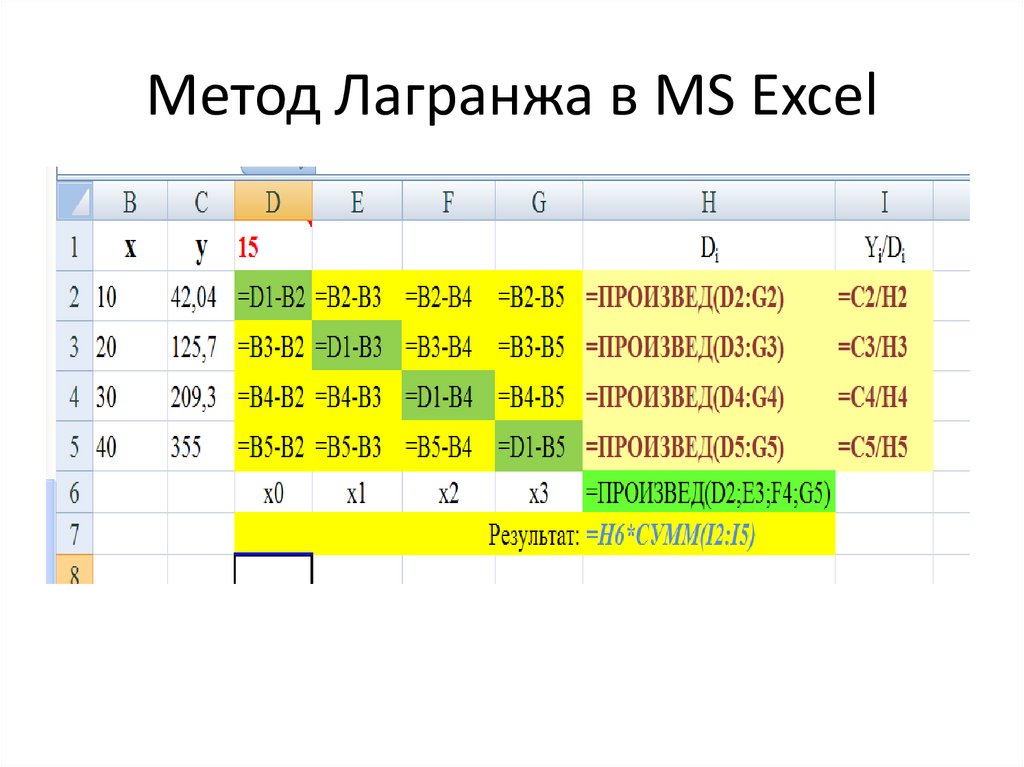
23. Метод Лагранжа в MS Excel

24.

25. Метод Ньютона

Английский математик, физик, алхимик и историк
Исаак Ньютон родился в местечке Вулсторп в
Линкольншире в семье фермера. Отец Ньютона
умер незадолго до его рождения; мать вскоре
вышла вторично замуж за священника из
соседнего городка и переехала к нему, оставив
сына с бабушкой в Вулсторпе.
В 1668 г. Ньютону была присвоена степень
магистра, а в 1669 г. Барроу передал ему физикоматематическую кафедру, которую Ньютон
занимал до 1701 г. В те же годы Ньютон
разрабатывал основы математического анализа, о
чем стало широко известно из переписки
европейских ученых, хотя сам Ньютон не
опубликовал тогда по этому поводу ни одной
строчки: первая публикация Ньютона об основах
анализа была напечатана лишь в 1704 г., а более
полное руководство – посмертно (1736).

26. Метод Ньютона

Интерполяция может производится для произвольно
и равномерно расположенных узлов интерполяции
Интерполяционный многочлен Ньютона записывается следующим
образом:

27. Метод Ньютона

Часто вводят безразмерную переменную q, показывающую
сколько содержится шагов от x0 до заданной точки x:
В этом случае выражение для интерполяционного полинома запишется в
следующем виде (первая интерполяционная формула Ньютона):

28. Метод Ньютона

Существует и вторая интерполяционная формула Ньютона (1687 год):
Погрешность интерполяции можно оценить по выражению:

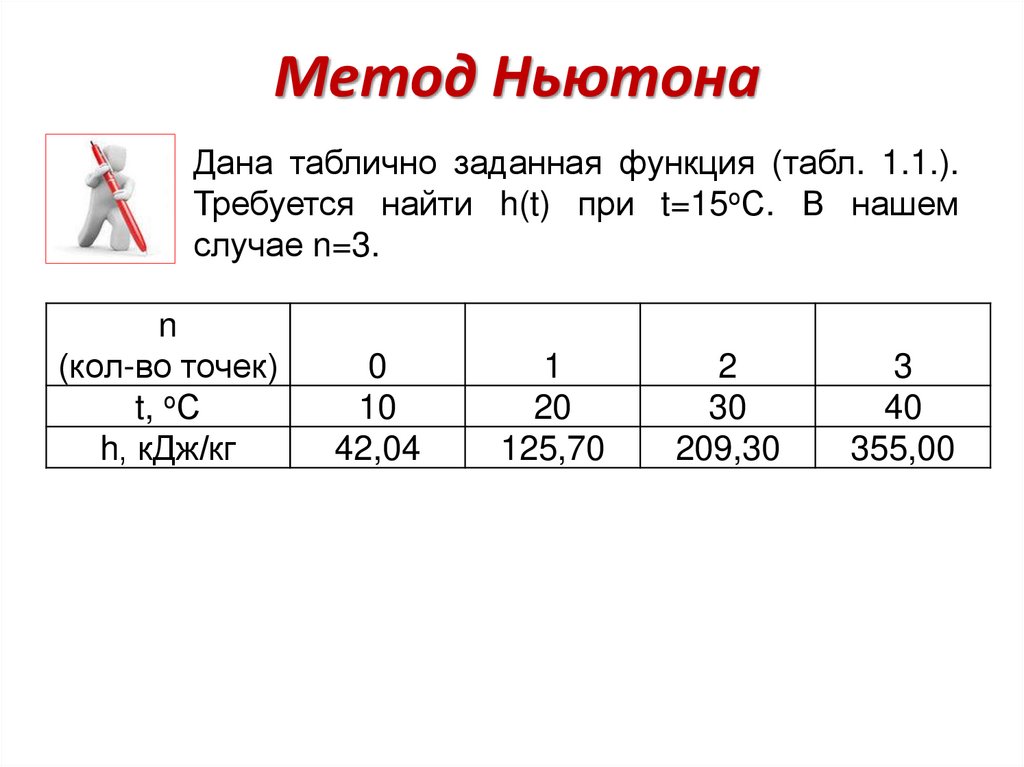
29. Метод Ньютона

Дана таблично заданная функция (табл. 1.1.).
Требуется найти h(t) при t=15оС. В нашем
случае n=3.
n
(кол-во точек)
t, оС
h, кДж/кг
0
10
42,04
1
20
125,70
2
30
209,30
3
40
355,00

30. Метод Ньютона

Для интерполяции будем использовать только первые три точки, а
остальные для оценки погрешности.
В нашем случае n=2. Определяем значение безразмерной
переменной q по известной формуле:

31. Метод Ньютона

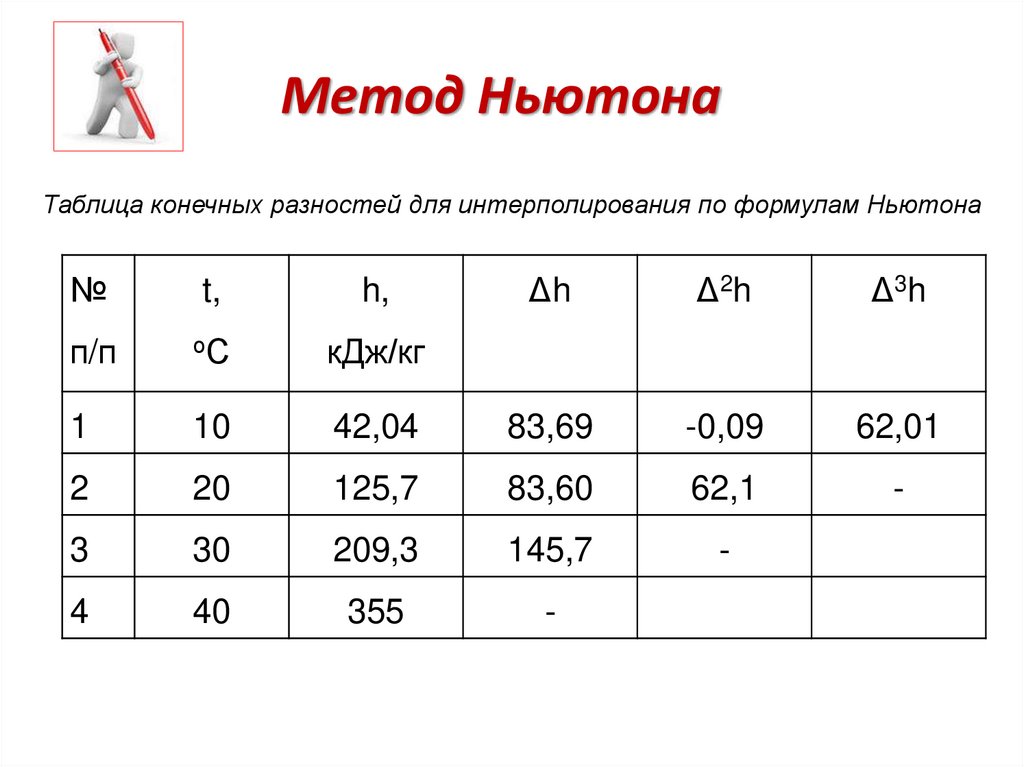
Таблица конечных разностей для интерполирования по формулам Ньютона
№
t,
h,
Δh
Δ 2h
Δ 3h
п/п
оС
кДж/кг
1
10
42,04
83,69
-0,09
62,01
2
20
125,7
83,60
62,1
-
3
30
209,3
145,7
-
4
40
355
-

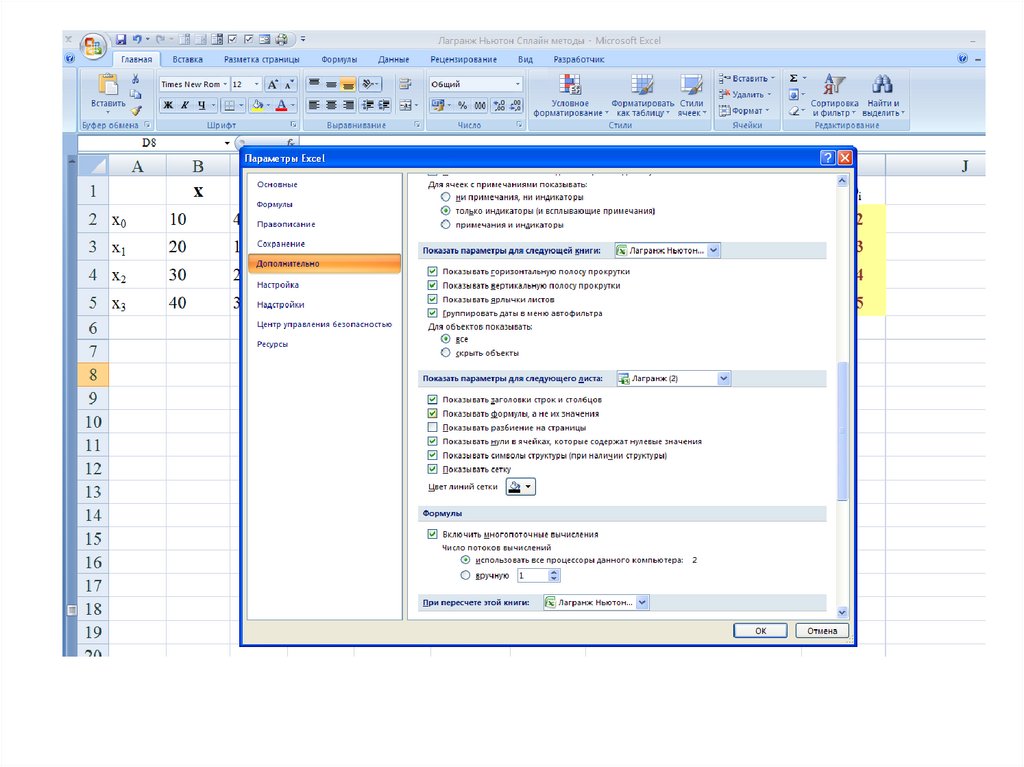
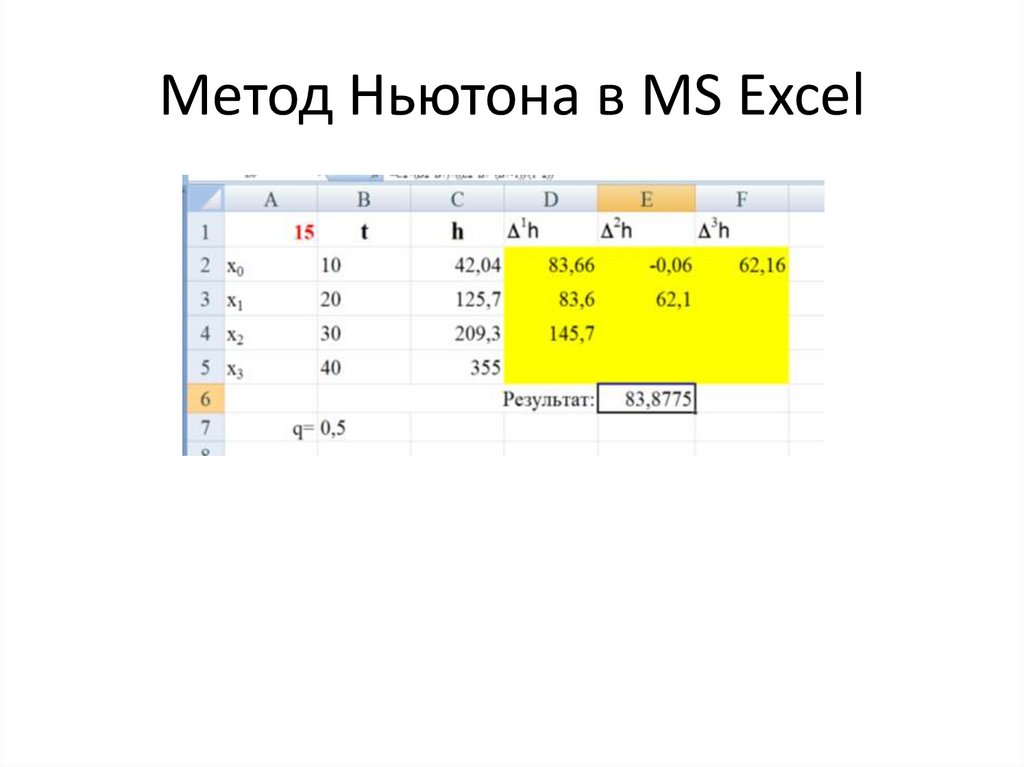
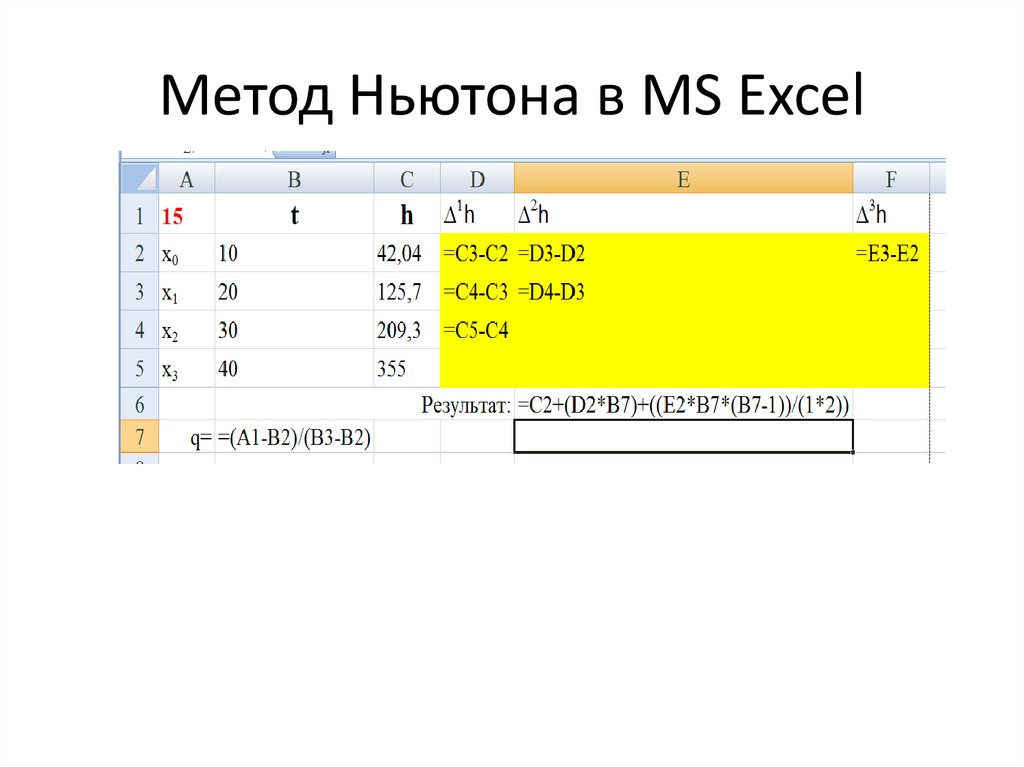
32. Метод Ньютона

Подставляем все необходимые значения в формулу Ньютона из нашей таблицы (лист 19),
получим:

33. Метод Ньютона в MS Excel

34. Метод Ньютона в MS Excel

35.

Пример Интерполирование по формулам Ньютона в программе Mathcad.
10
20
èñõäàí
30
40
42.04
x èñõäàí
125.7
209.3
355
q
42.04
125.7
y
209.3
355
0
y èñõäàí
x0 15
x0 x0 0.5
h x x 10
1
h
0
y 1 y 0 0.06
y y 62.1
2
1
y2
0
y2 0.06
0
0
y3 y2 y2
y1 y0
83.66
y y 2 y 1 83.6
y3 y2 145.7
y 42.04
y
1
83.66
y2 q ( q 1)
h15 y y q
0
0
0
2
83.8775
1
0
( 62.16 )

36. Метод сплайнов

Слово сплайн, происходящее от
английского слова spline, означает
гибкую линейку, используемую для
проведения гладких кривых через
заданные точки на плоскости.
Форма этого универсального лекала
на каждом отрезке описывается
кубической параболой. Сплайны
широко
используются
в
инженерных
приложениях,
в
частности,
в
компьютерной
графике, поскольку позволяют с
хорошей точностью задать кривые
в виде нескольких массивов
коэффициентов.

37. Метод сплайнов

На каждом отрезке [xi-1, xi], i=1,2,…N будем искать функцию
S(x)= Si(x) в виде полинома третьей степени:
S i x ai bi x xi ci
x xi 2
2
di
x xi 3
6
где а, b, c, d – коэффициенты, подлежащие
определению на всех n элементарных отрезках.
К важным достоинствам интерполяции кубическими
сплайнами
относится
получение
функции,
имеющей
минимальную возможную кривизну. К недостаткам сплайновой
интерполяции относится необходимость получения сравнительно
большого числа параметров.

38. Метод сплайнов

,
Неизвестные коэффициенты
находим из:
•условий интерполяции:
•непрерывности функции
ai , bi , ci , d i
S1 x 0 f 0
i 0,1,2,..., N
S i xi f i i 1,2,..., N
S i xi 1 S i 1 , xi 1 i 2,3,..., N
непрерывности первой и второй производной:
S i xi 1 S i 1 xi 1 S i xi 1 S i 1 xi 1
i 2,3,..., N
Учитывая, что
S i 1 x ai 1 bi 1 x xi 1 ci 1
x xi 1 2
2
d i 1
x xi 1 3
6

39. Метод сплайнов

.
Метод сплайнов
,
;
Для определения
4N
неизвестных получаем систему
ai f i
4N 2
i 1,2,..., N
hi2
hi3
bi hi ci
di
f i f i 1
2
6
d i hi2
bi bi 1 ci hi
2
d i hi ci ci 1
i 1,2,..., N
i 1,2,..., N
i 1,2,..., N
hi xi xi 1
Недостающие два уравнения выводятся из дополнительных условий:
S a S b 0
уравнений:

40. Метод сплайнов

Можно показать, что при этом
c0 c N 0
. Из системы можно исключить неизвестные
, получив систему
N 1
bi d i
линейных уравнений (СЛАУ) для определения коэффициентов
hi ci 1 2 hi hi 1 ci hi 1ci 1
i 1,2,..., N 1
ci
f i 1 f i
f i f i 1
6
hi
hi 1
После этого вычисляются коэффициенты b и d
ci ci 1
di
hi
ci hi d i h
f i f i 1
bi
2
6
hi
2
i
i 1,2,..., N

41. Метод сплайнов

В случае постоянной сетки
hi h
система уравнений упрощается:
f 2 2 f1 f 0
4c1 c 2 6
h2
f i 1 2 f i f i 1
ci 1 4ci ci 1 6
h2
i 2,3,..., N 2
f N 2 f N 1 f N 2
c N 2 4c N 1 c N 6
h2
cN 0

42. Метод сплайнов

Для вычисления значения в произвольной
точке отрезка необходимо решить систему
уравнений на коэффициенты сi, , затем найти
все коэффициенты bi и di, . Далее,
необходимо определить, на какой интервал
попадает эта точка, и, зная номер , вычислить
значение сплайна и его производных в точке.

43. Метод сплайнов

S z ai 0 bi 0 z xi 0 ci 0
z x i 0 2
S z bi 0 ci 0 z xi 0 d i 0
di0
2
z xi 0
S z ci 0 d i 0 z xi 0
2
2
z xi 0 3
6

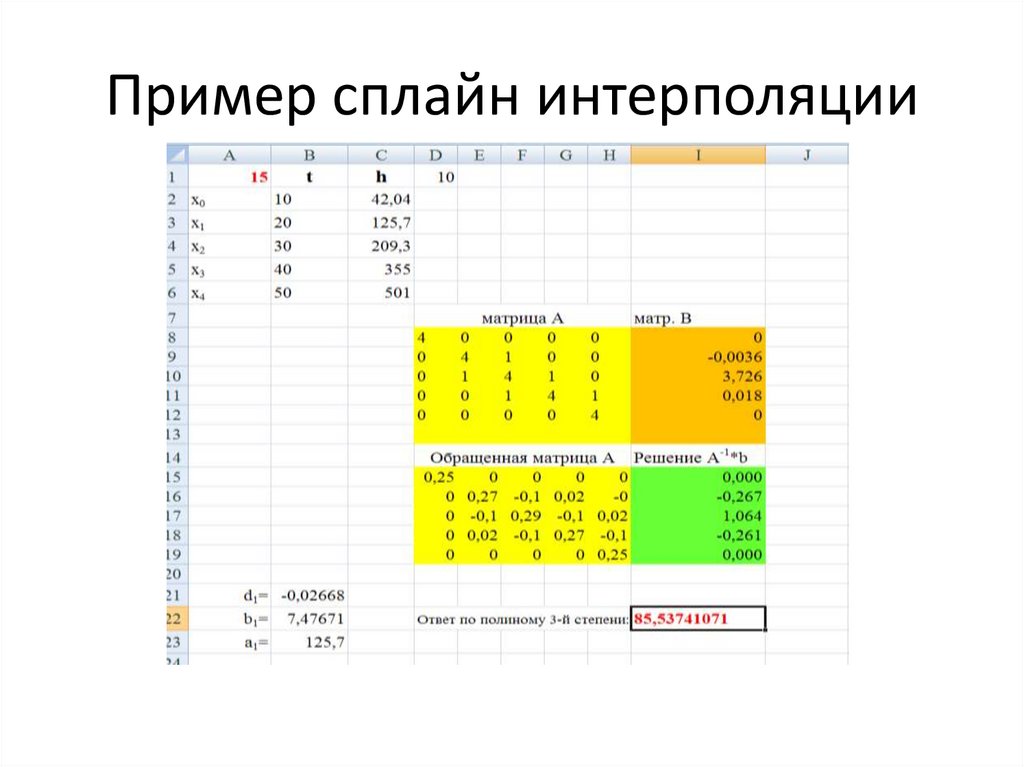
44. Пример сплайн интерполяции ручной способ

45. Пример сплайн интерполяции

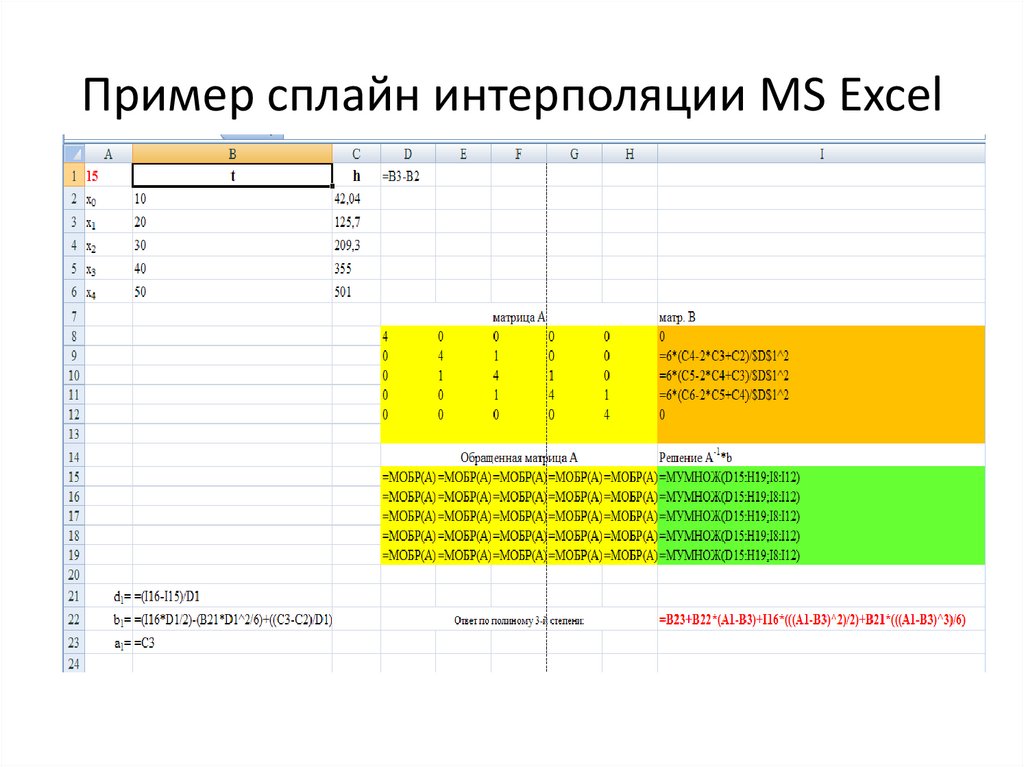
46. Пример сплайн интерполяции MS Excel

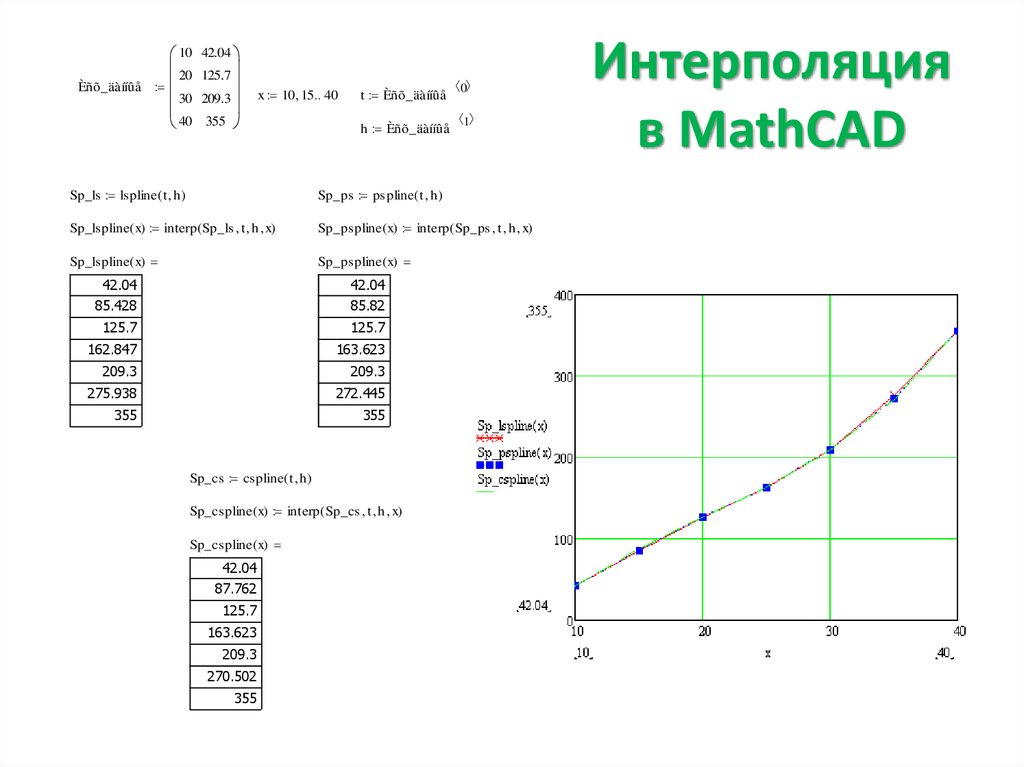
47. Интерполяция в MathCAD

Функции интерполяции определяют кривую, точно проходящую
через заданные точки. Из-за этого результат очень чувствителен к
ошибкам данных.
Кубическая сплайн-интерполяция позволяет провести кривую через
набор точек таким образом, что первые и вторые производные кривой
непрерывны в каждой точке. Эта кривая образуется путем создания ряда
кубических полиномов, проходящих через наборы из трех смежных
точек. Кубические полиномы затем состыковываются друг с другом,
чтобы образовать кривую.
MathCAD поставляется с тремя сплайн-функциями:
cspline(vx,vy) – генерирует кривую сплайна, которая может быть
кубическим полиномом в граничных точках;
pspline(vx,vy) – генерирует кривую сплайна, которая приближается к
параболе в граничных точках;
lspline(vx,vy) – генерирует кривую сплайна, которая приближается к
прямой в граничных точках.

48. Интерполяция в MathCAD

10
20
Èñõ_äàííûå
30
40
42.04
125.7
209.3
355
x 10 15 40
t Èñõ_äàííûå
h Èñõ_äàííûå
0
1
Sp_ls lspline( t h )
Sp_ps pspline( t h )
Sp_lspline( x) interp ( Sp_ls t h x)
Sp_pspline( x) interp ( Sp_ps t h x)
Sp_lspline( x)
Sp_pspline( x)
42.04
42.04
85.428
85.82
125.7
125.7
162.847
163.623
209.3
209.3
275.938
272.445
355
355
Sp_cs cspline( t h )
Sp_cspline( x) interp ( Sp_cs t h x)
Sp_cspline( x)
42.04
87.762
125.7
163.623
209.3
270.502
355
Интерполяция
в MathCAD