160919281

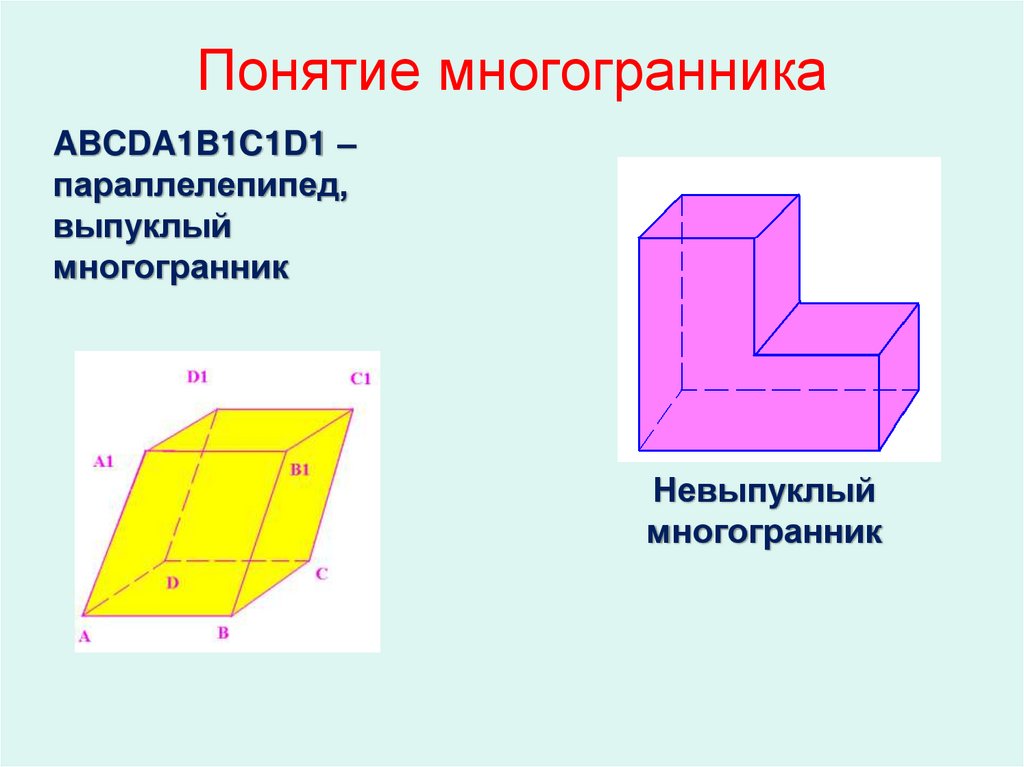
1. Понятие многогранника

ABCDA1B1C1D1 –
параллелепипед,
выпуклый
многогранник
Невыпуклый
многогранник

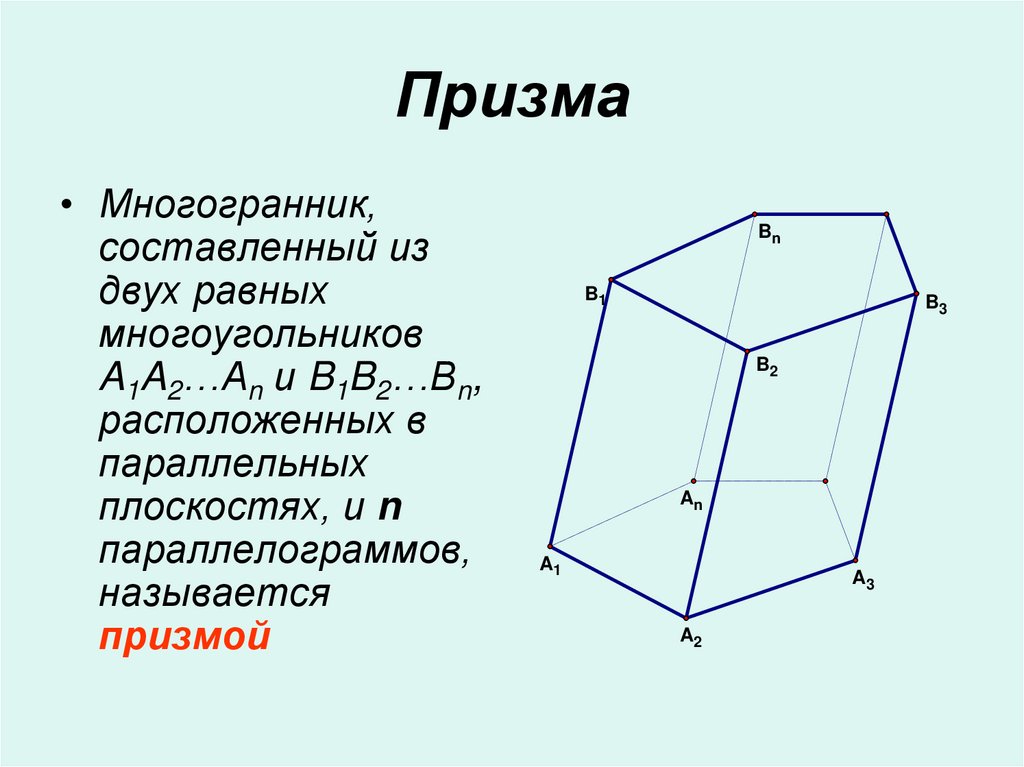
2. Призма

• Многогранник,
составленный из
двух равных
многоугольников
A1A2…An и B1B2…Bn,
расположенных в
параллельных
плоскостях, и n
параллелограммов,
называется
призмой
Bn
B1
B3
B2
An
A1
A3
A2

3.

Bn
B1
B3
B2
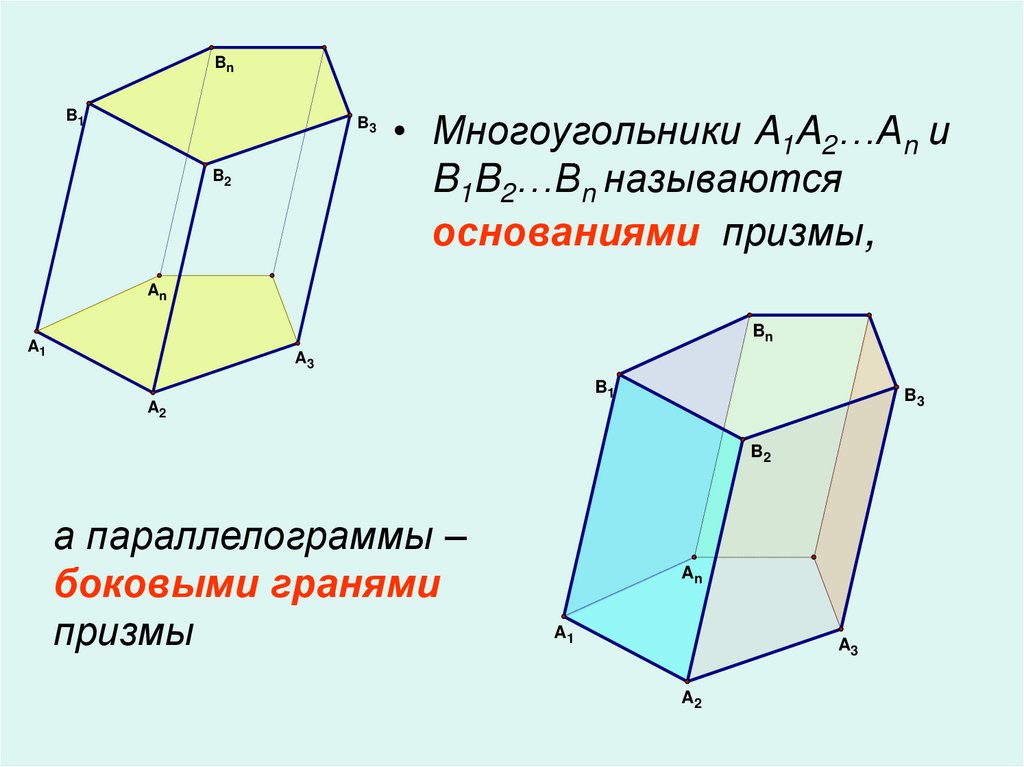
• Многоугольники A1A2…An и
B1B2…Bn называются
основаниями призмы,
An
Bn
A1
A3
B1
B3
A2
B2
а параллелограммы –
боковыми гранями
призмы
An
A1
A3
A2

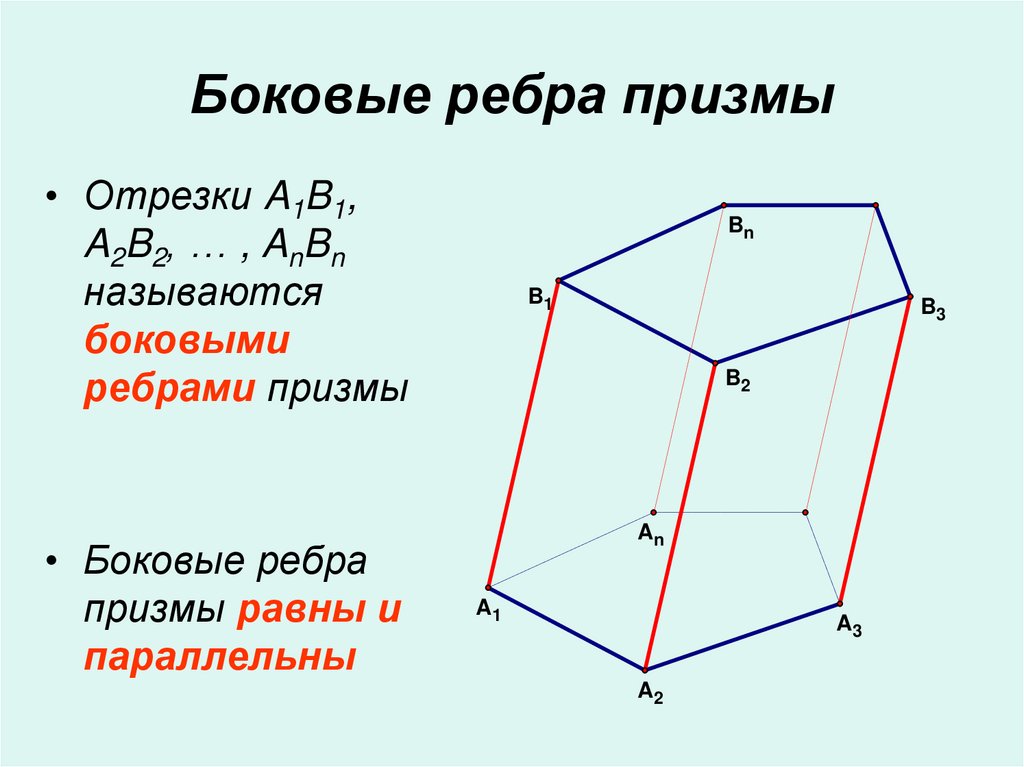
4. Боковые ребра призмы

• Отрезки A1B1,
A2B2, … , AnBn
называются
боковыми
ребрами призмы
• Боковые ребра
призмы равны и
параллельны
Bn
B1
B3
B2
An
A1
A3
A2

5.

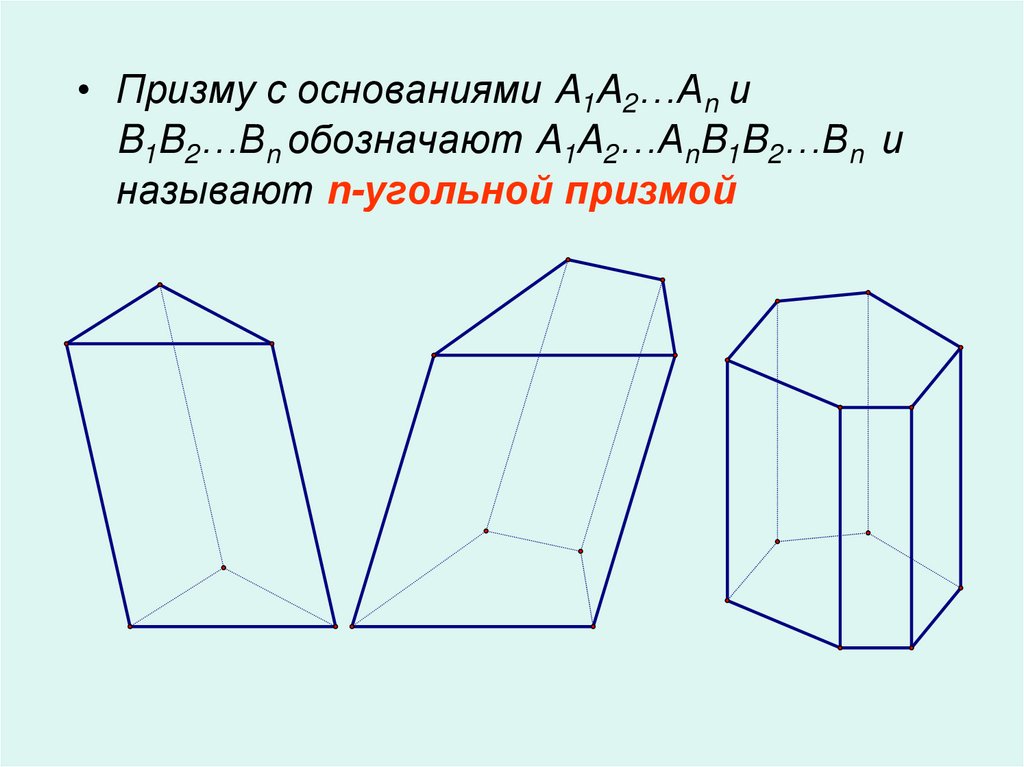
• Призму с основаниями A1A2…An и
B1B2…Bn обозначают A1A2…AnB1B2…Bn и
называют n-угольной призмой

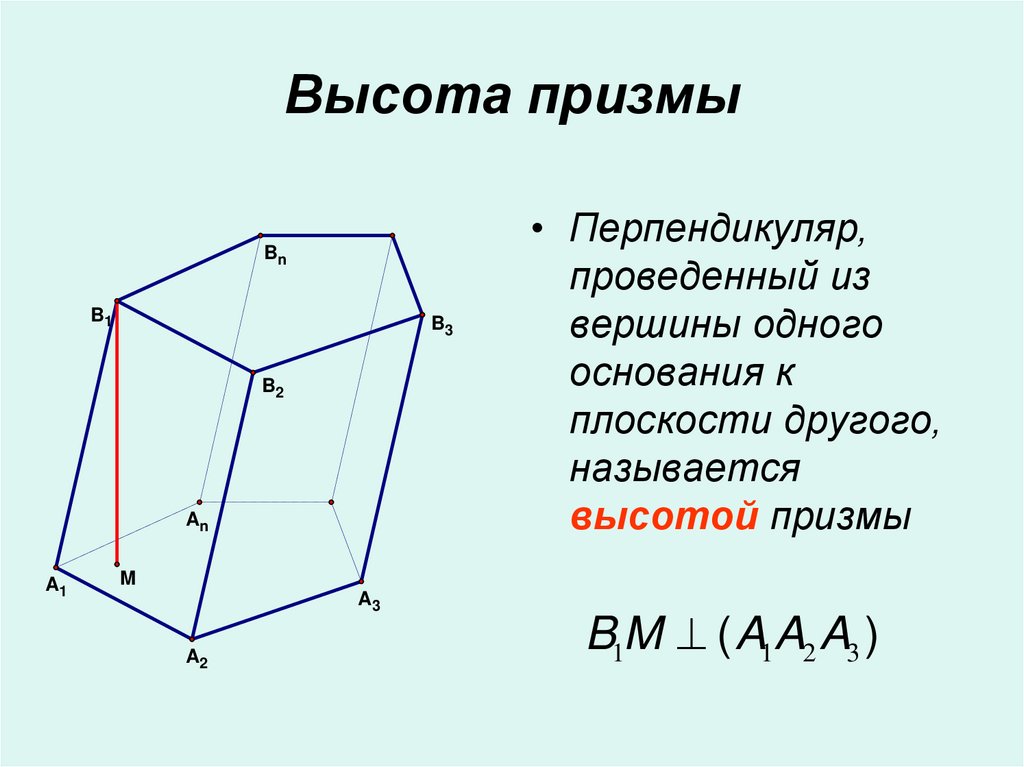
6. Высота призмы

Bn
B1
B3
B2
An
A1
• Перпендикуляр,
проведенный из
вершины одного
основания к
плоскости другого,
называется
высотой призмы
M
A3
A2
B1M ( A1A2 A3 )

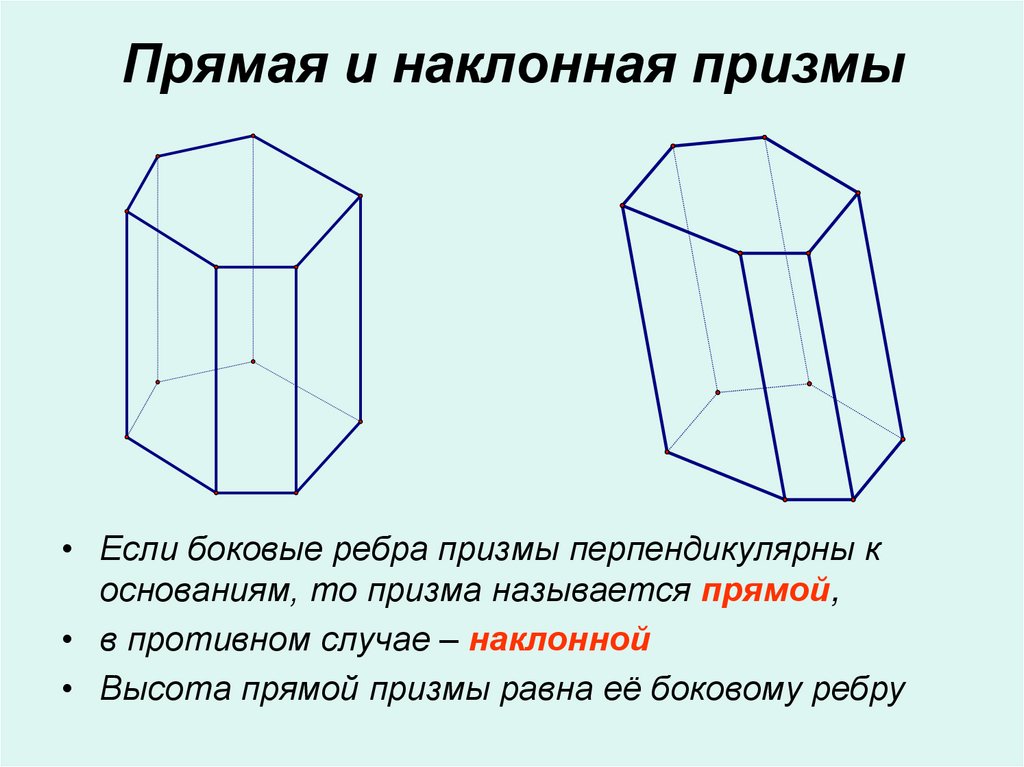
7. Прямая и наклонная призмы

• Если боковые ребра призмы перпендикулярны к
основаниям, то призма называется прямой,
• в противном случае – наклонной
• Высота прямой призмы равна её боковому ребру

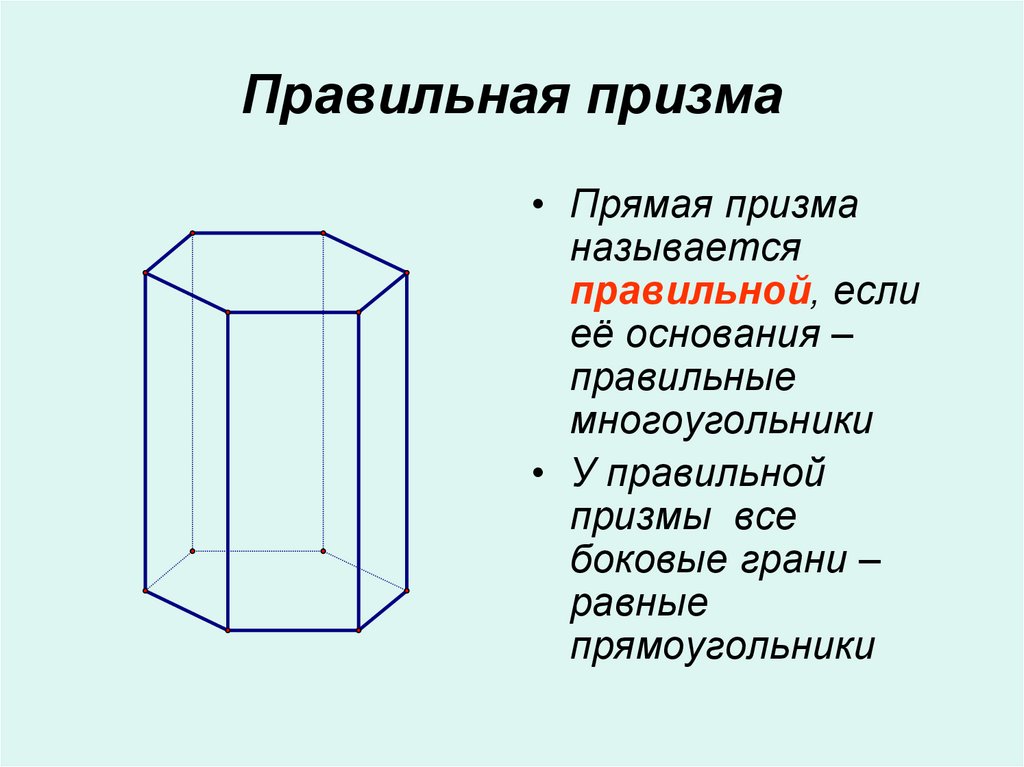
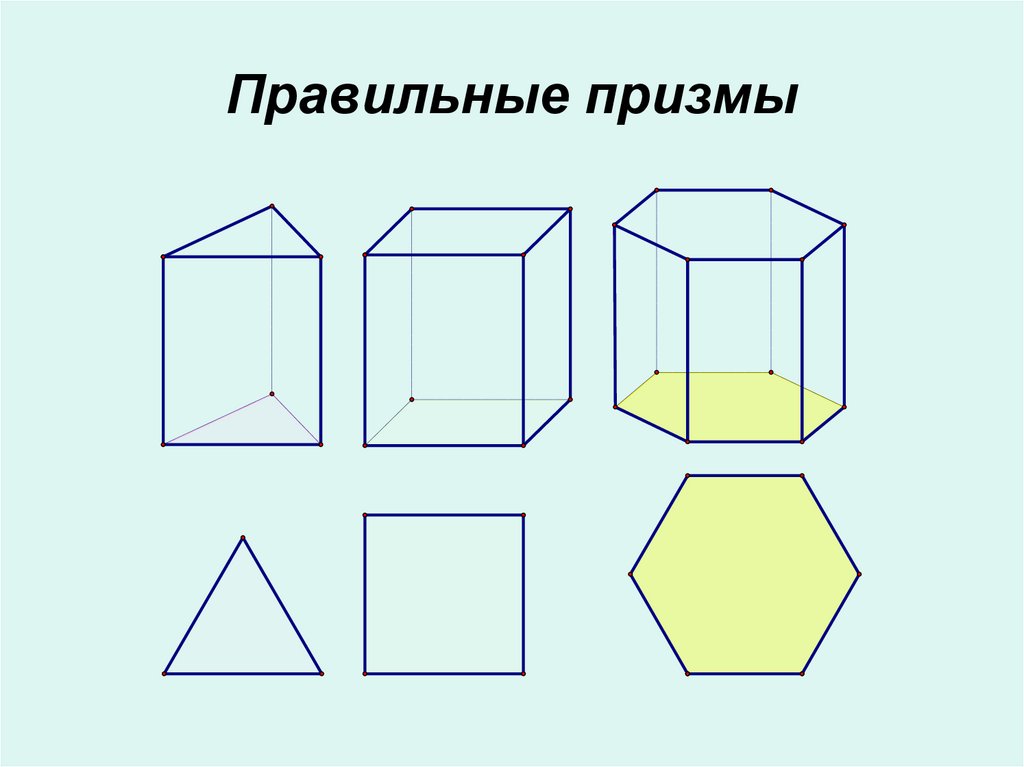
8. Правильная призма

• Прямая призма
называется
правильной, если
её основания –
правильные
многоугольники
• У правильной
призмы все
боковые грани –
равные
прямоугольники

9. Правильные призмы

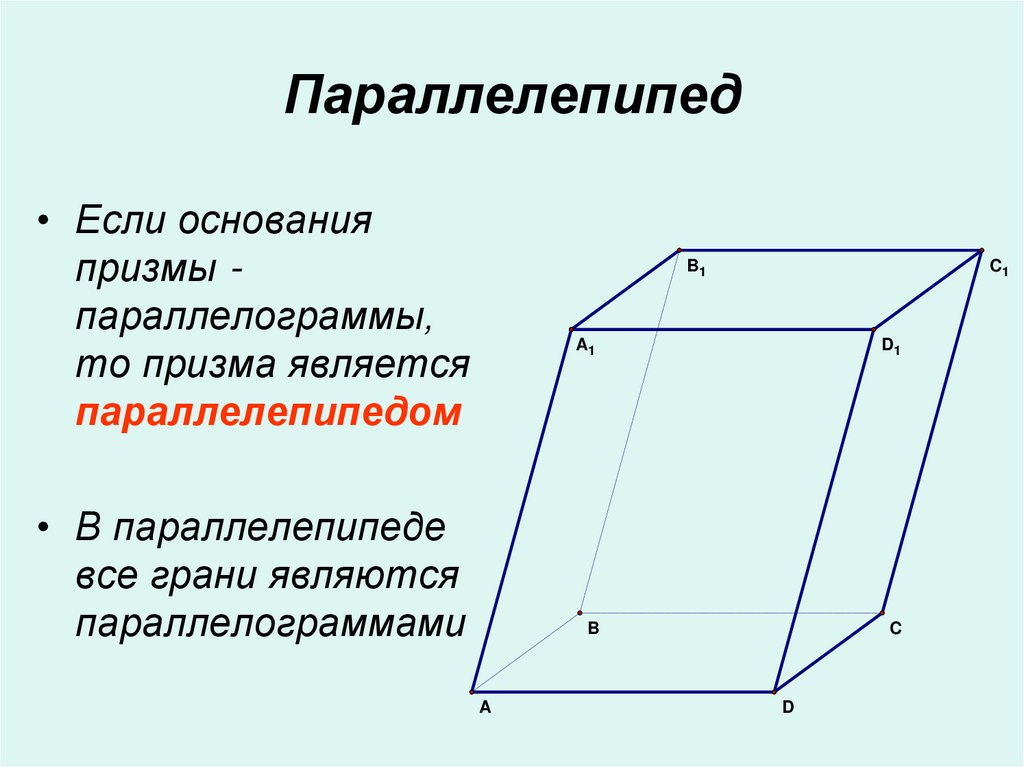
10. Параллелепипед

• Если основания
призмы параллелограммы,
то призма является
параллелепипедом
B1
• В параллелепипеде
все грани являются
параллелограммами
A
C1
A1
D1
B
C
D

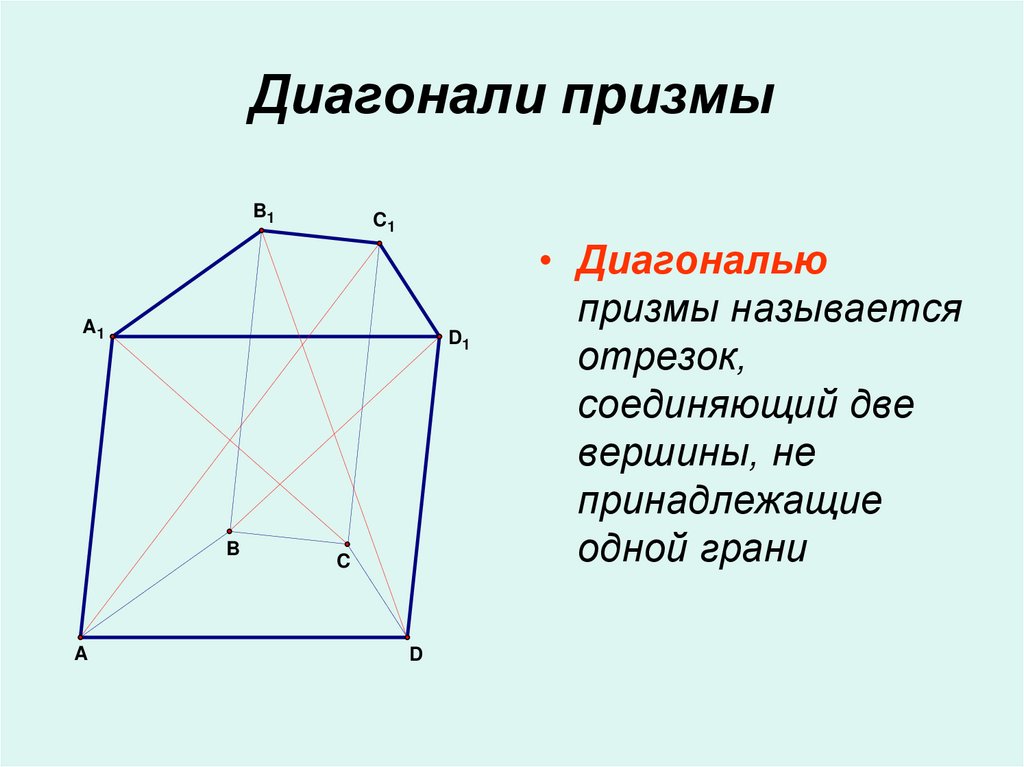
11. Диагонали призмы

B1
C1
A1
D1
B
A
C
D
• Диагональю
призмы называется
отрезок,
соединяющий две
вершины, не
принадлежащие
одной грани

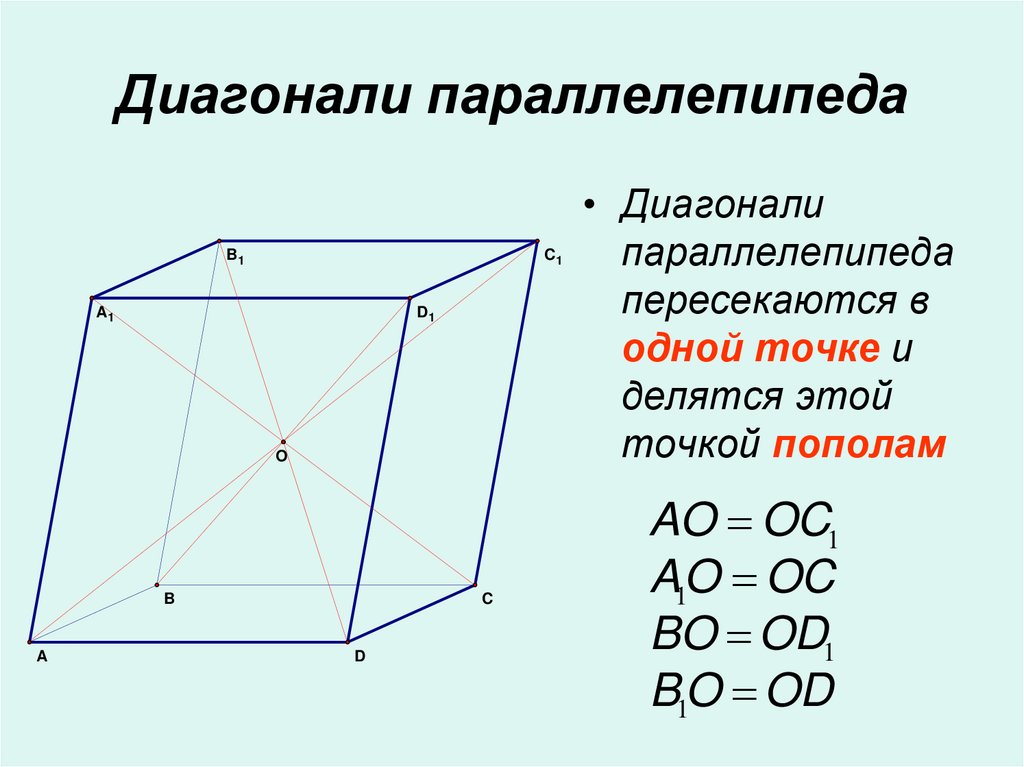
12. Диагонали параллелепипеда

B1
C1
A1
D1
O
B
A
C
D
• Диагонали
параллелепипеда
пересекаются в
одной точке и
делятся этой
точкой пополам
AO OC1
AO
OC
1
BO OD1
B1O OD

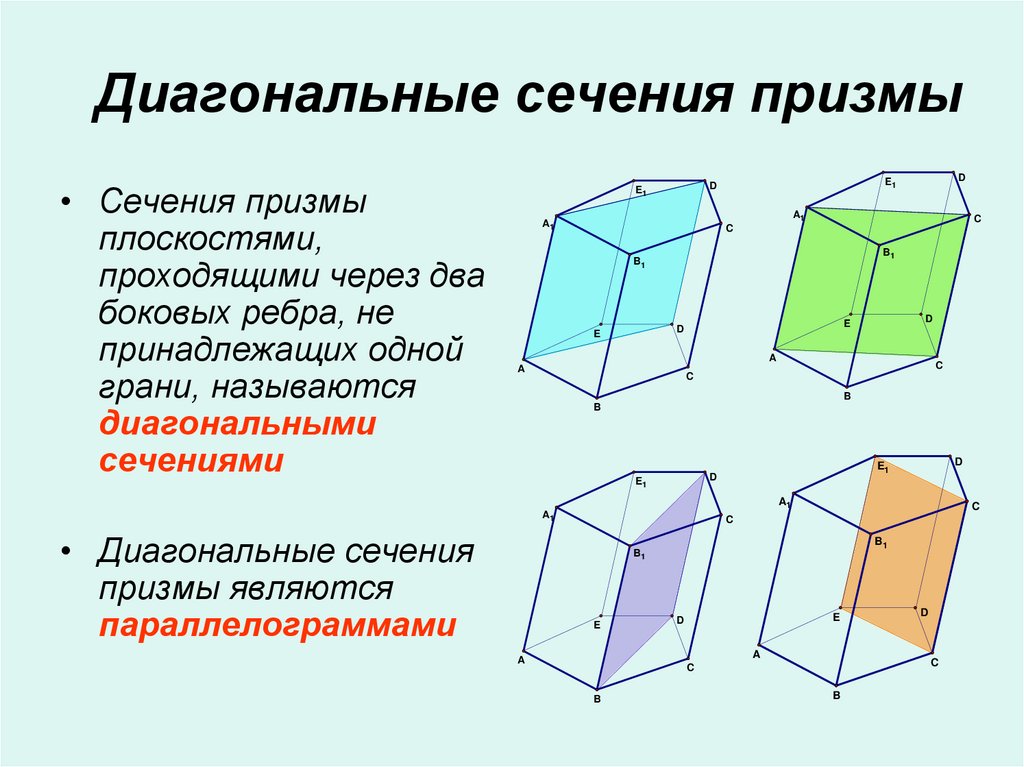
13. Диагональные сечения призмы

• Сечения призмы
плоскостями,
проходящими через два
боковых ребра, не
принадлежащих одной
грани, называются
диагональными
сечениями
D
E1
D
E1
A1
A1
C
C
B1
B1
D
E
D
E
A
A
C
C
B
B
E1
D
E1
D
A1
A1
• Диагональные сечения
призмы являются
параллелограммами
C
C
B1
B1
E
E
D
A
A
C
C
B
D
B

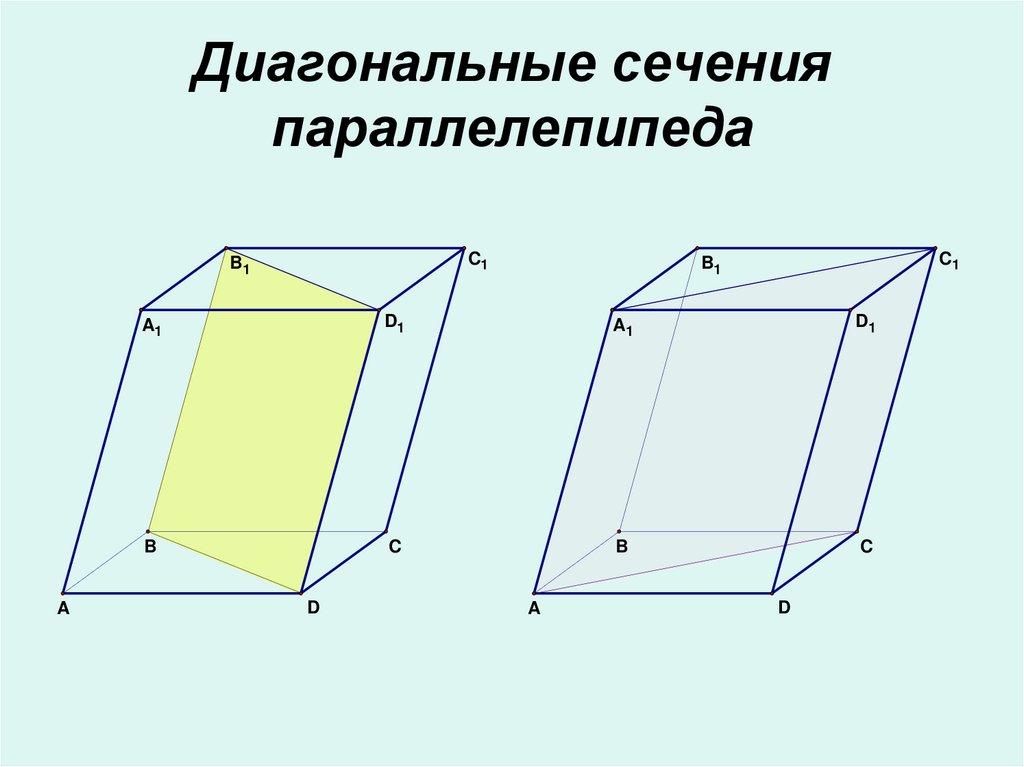
14. Диагональные сечения параллелепипеда

C1
B1
A
C1
B1
A1
D1
A1
D1
B
C
B
C
D
A
D

15. Площадь поверхности призмы

• Площадью полной поверхности
призмы называется сумма площадей
всех её граней Sполн
• Площадью боковой поверхности
призмы называется сумма площадей
её боковых граней Sбок
Sполн Sбок 2Sосн

16. Теорема о площади боковой поверхности прямой призмы

Теорема.
Площадь боковой поверхности прямой
призмы равна произведению периметра
основания на высоту призмы
Sбок Pосн H

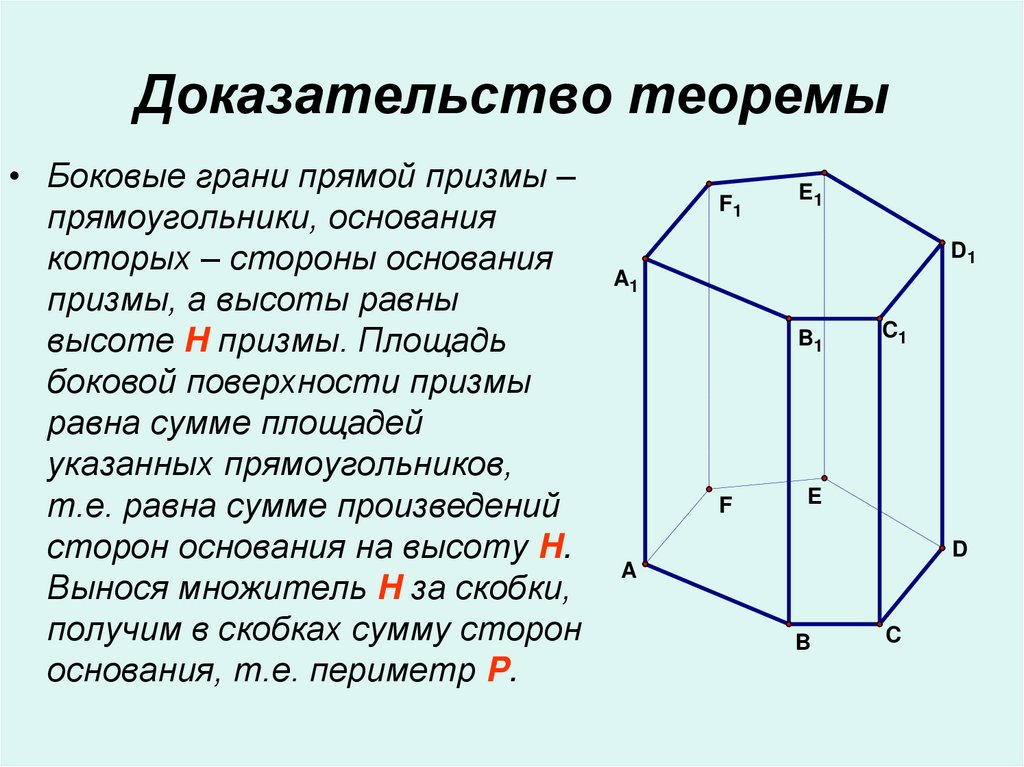
17. Доказательство теоремы

• Боковые грани прямой призмы –
прямоугольники, основания
которых – стороны основания
призмы, а высоты равны
высоте H призмы. Площадь
боковой поверхности призмы
равна сумме площадей
указанных прямоугольников,
т.е. равна сумме произведений
сторон основания на высоту H.
Вынося множитель H за скобки,
получим в скобках сумму сторон
основания, т.е. периметр P.
F1
E1
D1
A1
B1
F
C1
E
D
A
B
C

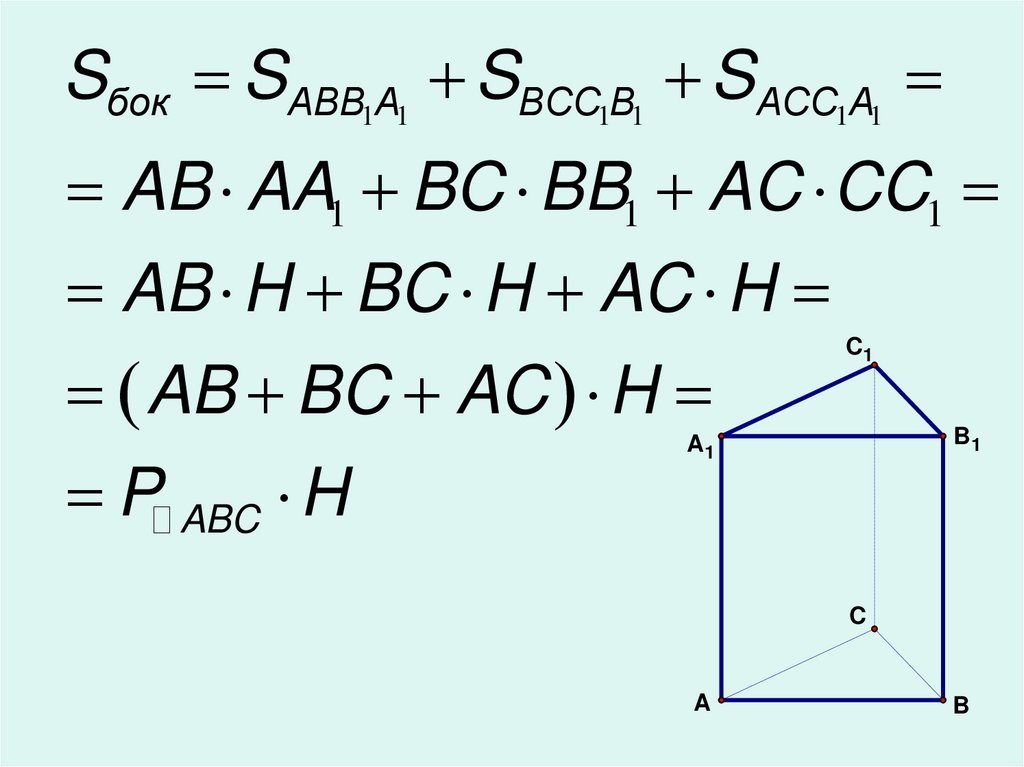
18.

Sбок SABB1A1 SBCC1B1 SACC1A1
AB AA1 BC BB1 AC CC1
AB H BC H AC H
AB BC AC H
P ABC H
C1
B1
A1
C
A
B

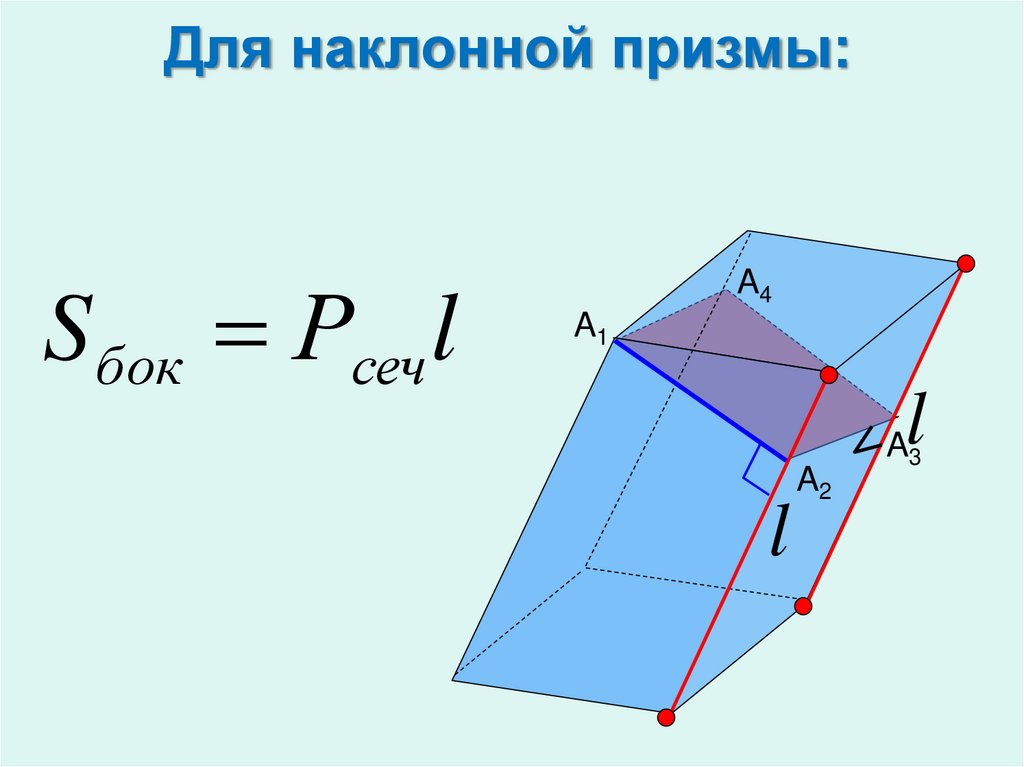
19.

Для наклонной призмы:
Sбок Рсеч l
A4
A1
l
l
A2
A3

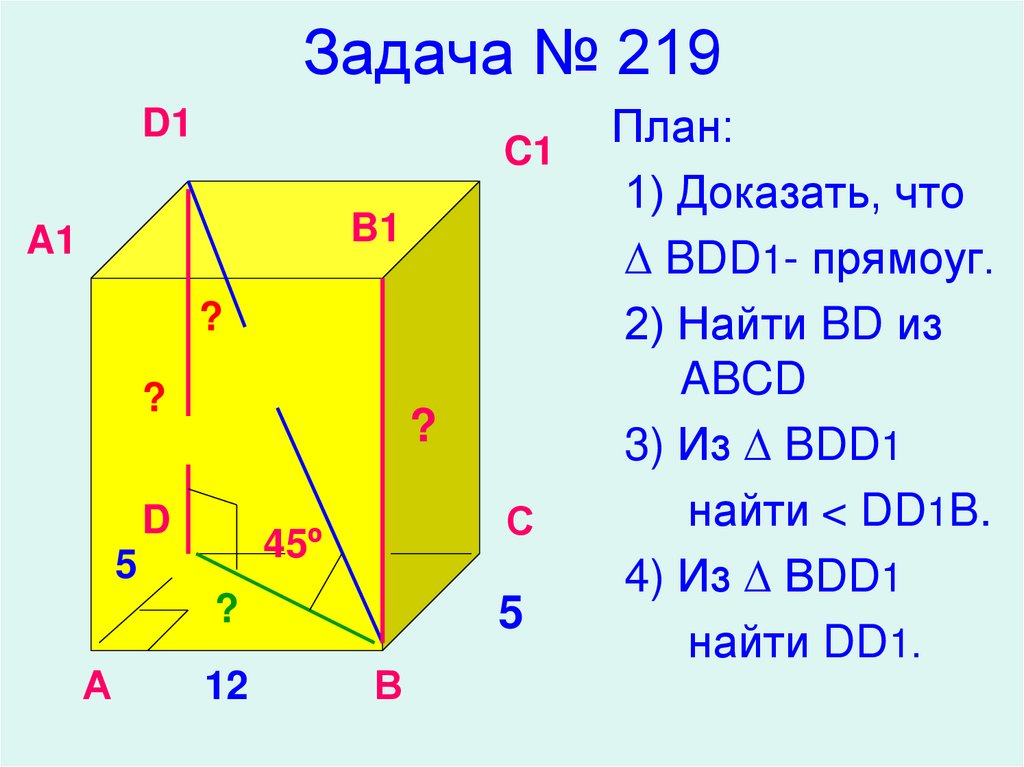
20. Задача № 219

D1
C1
B1
A1
?
?
?
D
С
45º
5
?
А
12
5
В
План:
1) Доказать, что
∆ BDD1- прямоуг.
2) Найти BD из
ABCD
3) Из ∆ BDD1
найти < DD1B.
4) Из ∆ ВDD1
найти DD1.

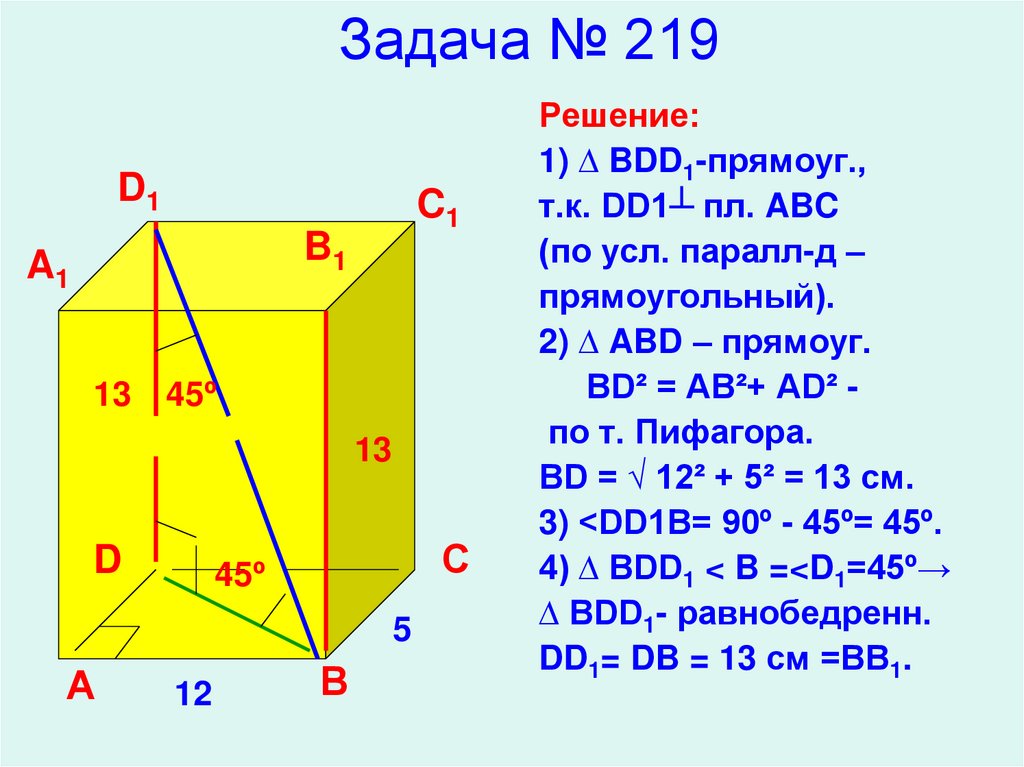
21. Задача № 219

D1
C1
B1
A1
13
45º
13
D
С
45º
5
А
12
В
Решение:
1) ∆ BDD1-прямоуг.,
т.к. DD1┴ пл. ABC
(по усл. паралл-д –
прямоугольный).
2) ∆ ABD – прямоуг.
BD² = AB²+ AD² по т. Пифагора.
BD = √ 12² + 5² = 13 см.
3) <DD1B= 90º - 45º= 45º.
4) ∆ BDD1 < B =<D1=45º→
∆ BDD1- равнобедренн.
DD1= DB = 13 см =ВВ1.

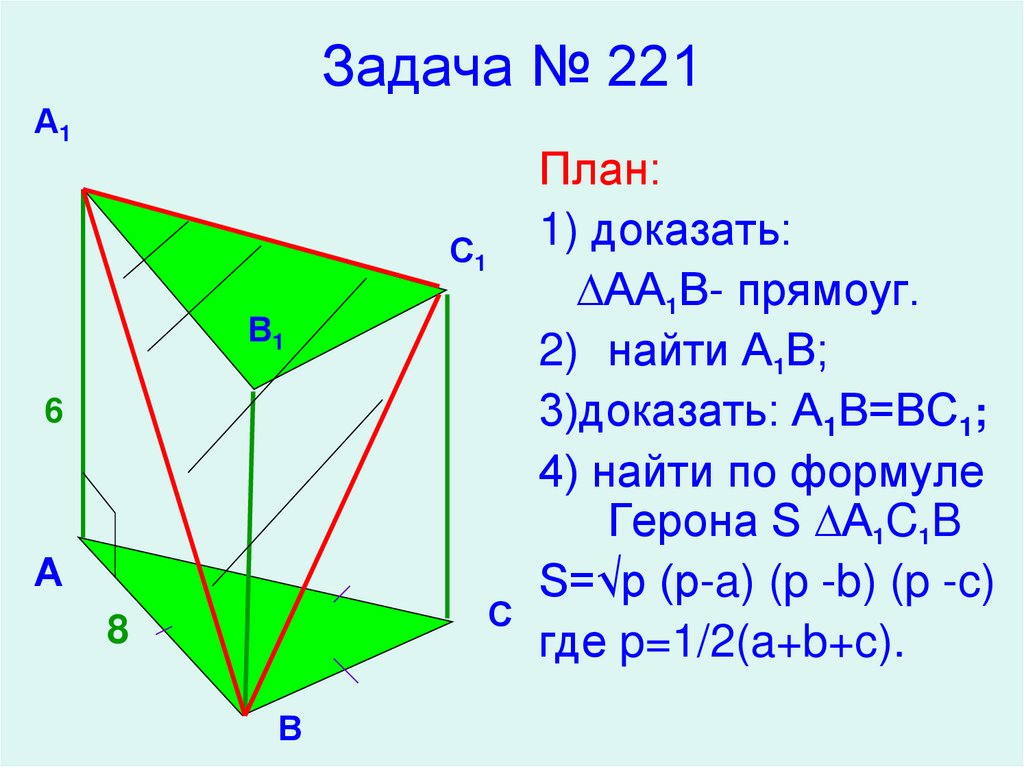
22. Задача № 221

А1
В1
6
А
8
В
План:
1) доказать:
С1
∆АА1В- прямоуг.
2) найти А1В;
3)доказать: А1В=ВС1;
4) найти по формуле
Герона S ∆A1C1B
S=√p (p-a) (p -b) (p -c)
С
где p=1/2(a+b+c).

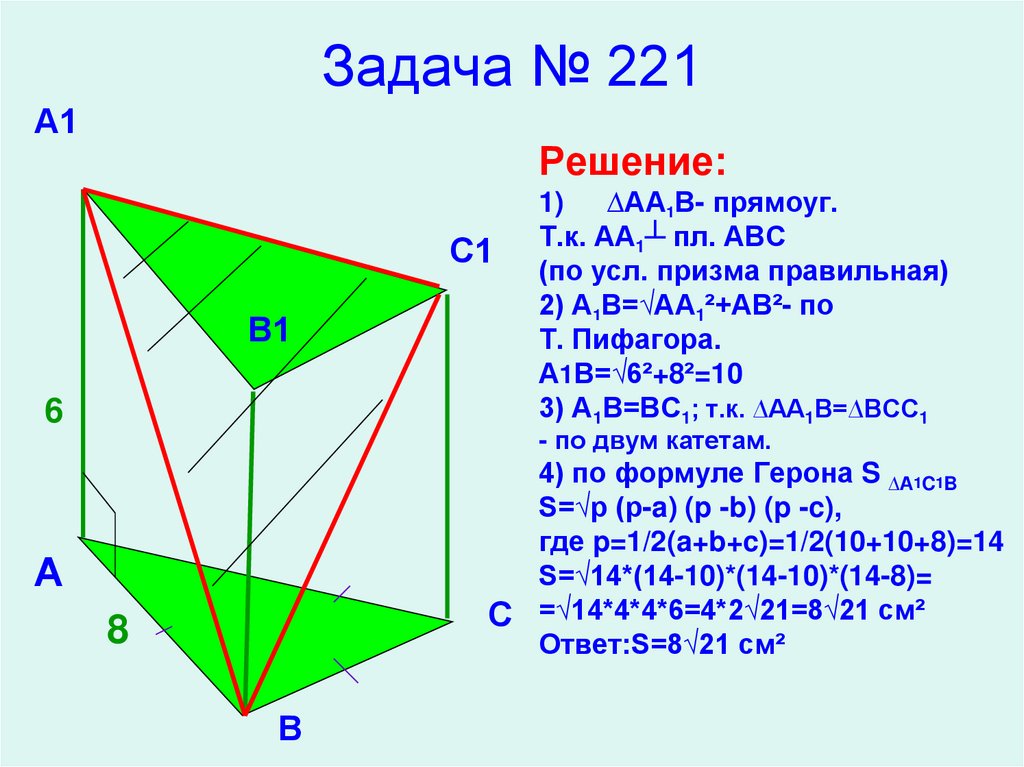
23. Задача № 221

А1
Решение:
С1
В1
6
1)
∆АА1В- прямоуг.
Т.к. АА1┴ пл. АВС
(по усл. призма правильная)
2) А1В=√АА1²+АВ²- по
Т. Пифагора.
А1В=√6²+8²=10
3) А1В=ВС1; т.к. ∆АА1В=∆ВСС1
- по двум катетам.
4) по формуле Герона S ∆A1C1B
S=√p (p-a) (p -b) (p -c),
где p=1/2(a+b+c)=1/2(10+10+8)=14
S=√14*(14-10)*(14-10)*(14-8)=
С =√14*4*4*6=4*2√21=8√21 см²
Ответ:S=8√21 см²
А
8
В