Обыкновенные дифференциальные уравнения

1. Обыкновенные дифференциальные уравнения

2.

Физический смысл дифференциальных уравнений
Скорость
многих
процессов
зависит
от
того,
насколько далеко уже «продвинулось» развитие этих
процессов за предшествующее время.
Если
x(t)—зависимость
результата
некоторого
процесса х от времени, то производная этой функции
по времени х'(t) характеризует скорость этого
процесса.
Поскольку скорость процесса часто находится в
зависимости от его результата, в одном уравнении
оказываются как x(t), так и x'(t).

3.

Использование дифференциальных уравнений в медицинских приложениях:
Для определения скорости кровотока, скорости движения клапанов и стенок сердца,
определения вязкости крови и других параметров гемодинамики.
Для описания медико-биологических приложений ультразвука: эхоэнцефалограмма,
УЗИ, ультразвуковая физиотерапия, ультразвуковая локация и кардиография.
Для описания процессов физиологической акустики, которая изучает устройство и
работу звуковоспринимающих и звуковоспроизводящих органов человека и животных.
Для определения функции изменения численности популяции микроорганизмов в
зависимости от времени.

4.

Обыкновенные дифференциальные уравнения
Обыкновенные дифференциальные уравнения (ОДУ) — это уравнения, которые содержат
неизвестную (искомую) функцию одной переменной и её производные. Этим они отличается от
уравнений в частных производных, где неизвестная — функция нескольких переменных
Общая форма ОДУ:
F(x, y, y', y'', ...) = 0,
где x — независимая переменная, y — зависимая переменная, а y', y'' и т. д. обозначают
производные первого, второго и более высокого порядка от y по отношению к x.

5.

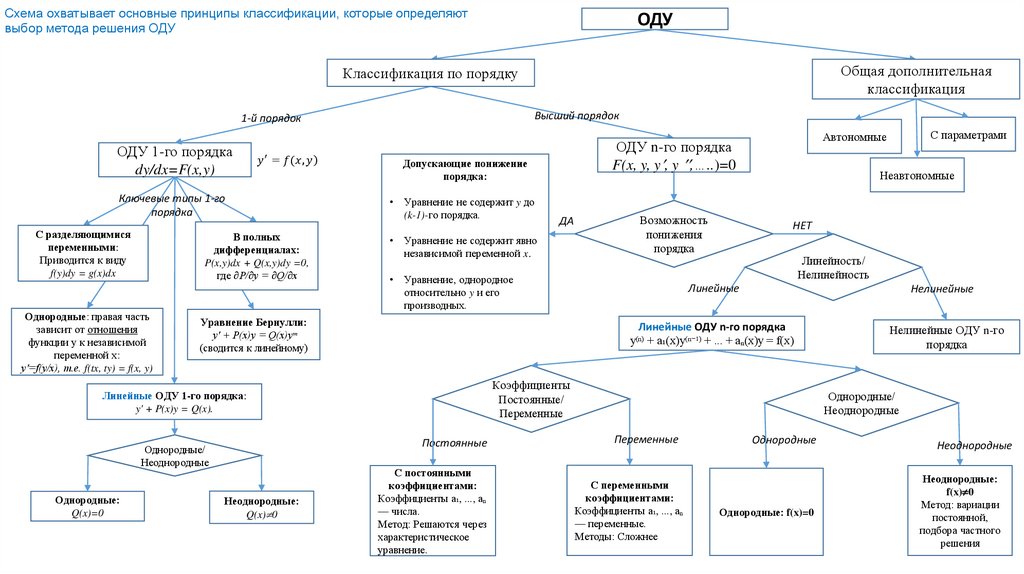
Виды обыкновенных дифференциальных уравнений
Некоторые виды ОДУ по порядку производной:
Первого порядка — содержат только первую производную неизвестной функции.
Высших порядков — включают производные n-го порядка (например, уравнение для
движения тела под действием силы тяжести − линейное однородное дифференциальное
уравнение второго порядка с постоянными коэффициентами. Его решение – это знакомая из
физики формула