Дифференциальные уравнения как средство описания динамических систем. Лекция 4

1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ КАК СРЕДСТВО ОПИСАНИЯ ДИНАМИЧЕСКИХ СИСТЕМ Основные понятия и определения

Математическое моделирование

2.

Схема математического моделирования
допущение
неудовл.
алгоритм
удовл.
Результат
2

3.

Многие задачи физики, химии, механики, экономики
и других наук сводятся к решению
дифференциальных уравнений и их систем.
Поэтому решение ДУ является одной из важнейших
математических задач.
К обыкновенным дифференциальным
уравнениям приходят в тех случаях, когда состояние
зависящей от времени динамической системы,
связаны с ее предшествующими состояниями. Тогда
систему удается описать аналитической
зависимостью между некоторыми параметрами, т.е.
построить математическую модель.
3

4.

Опр. Дифференциальным уравнением (ДУ)
называется равенство, содержащее производные
или дифференциалы неизвестной функции
dy
f (x),
dx
где:
f (x)
- известная функция,
y y (x)
- функция независимой переменной x, которую надо найти.
dy
d2y
2( y 3); 2 t 1; y x 2 ; xdy y 3 dx
dx
dt
Если неизвестная функция зависит только от одного
аргумента, то ДУ называется обыкновенным ДУ.
4

5.

Порядком ДУ называется наивысший порядок
входящей в уравнение производной.
y 3 xy x 3 y 2 0 второго порядка
3
d S
2 dS
tS
5 третьего
3
dt
dt
Обыкновенное ДУ n-го порядка в общем случае
содержит независимую переменную (x), неизвестную
функцию (y) и ее производные до n-го порядка
включительно y , y , y ,..., y ( n) и имеет вид:
( n)
F ( x, y, y , y , y ,..., y ) 0
5

6.

Функция, удовлетворяющая ДУ, т.е. обращающая его в
тождество, называется интегралом (или решением)
этого уравнения. Процесс нахождения решения ДУ
уравнения называется интегрированием уравнения.
x y 2 xy 2 y 0 дифференциальное
уравнение
y 2 x его решение, интеграл
2
y 2, y 0
x2 0 2 x 2 2 2 x 0
4x 4x 0
6

7.

Интеграл ДУ называется общим, если он содержит
столько независимых произвольных постоянных, каков
порядок уравнения, а функции, получаемые из общего
интеграла при различных числовых значениях
произвольных постоянных, называются частными
интегралами (частными решениями) этого уравнения.
Пример:
решением ДУ
y 2 x является любая первообразная для функции
y x
все первообразные для функции 2 x
например решением будет
2x
2
и, следовательно, все решения ДУ даются формулой:
y x2 C
С – произвольная постоянная
Получили бесконечное множество решений ДУ, т.к. каждому конкретному
числовому значению С соответствует свое решение. В частности при С=0,
2
получаем частное решение
y x
7

8.

График решения ОДУ называется интегральной
кривой этого уравнения.
Геометрически общее решение ДУ представляет
собой семейство интегральных кривых этого
уравнения.
y x2 C
Решение описывает
бесконечное семейство
интегральных кривых, а
частному решению
соответствует одна кривая из
этого семейства.
8

9.

Итак,
решением ДУ
F ( x, y, y , y , y ,..., y ( n) ) 0
называется всякая функция y (x)
которая при подстановке ее в уравнение превращает
его в тождество.
Общее решение ОДУ n-го порядка содержит n
произвольных постоянных С1 , С 2 ,..., С n
то есть общее решение имеет вид
y ( x, C1 , C2 ,..., Cn )
Частное решение ДУ получается из общего, если
произвольным постоянным придать определенные
значения.
9

10.

Как получить конкретные значения произвольных постоянных?
Задать дополнительные условия, которым должно
удовлетворять искомое решение.
могут задаваться значения искомой функции и ее
производных при некоторых значениях независимой
переменной, то есть в некоторых точках
Задача Коши
условия задаются в
одной точке
(начальные условия,
начальная точка)
Краевая задача
дополнительные
условия задаются в
более чем одной
точке (граничные
условия, начальная
и конечная точки)
10

11.

МЕТОДЫ РЕШЕНИЯ ОДУ
1. Графические (используют геометрические построения)
2. Аналитические (изучаются в курсе Мат. анализа)
3. Приближенные (используют различные упрощения,
разложение в ряд по малому параметру)
4. Численные (основной инструмент решения ОДУ)
Метод конечных разностей
Область непрерывного аргумента (отрезок) заменяется
дискретными значениями (узлами). Эти узлы составляют
разностную сетку.
Искомая функция заменяется функцией дискретного
аргумента на заданной сетке (сеточной функцией).
ДУ заменяется разностным уравнением относительно
сеточной функции. Аппроксимация на сетке
11

12.

Общая формулировка задачи Коши
( n)
( n 1)
y
f
(
x
,
y
,
y
,...,
y
)
Задача Коши для ДУ n-го порядка
заключается в отыскании функции y y (x ),
удовлетворяющей этому уравнению и начальным
условиям y ( x0 ) y0 , y ( x0 ) y0 ,..., y ( n 1) ( x0 ) y0( n 1) ,
где
x0 , y 0 , y 0 ,..., y
( n 1)
0
заданные числа
Пример постановки задачи Коши для ОДУ:
y
y x 2 0, y (1) 2, y (1) 0
x
Форма записи ДУ, когда старшая производная выражена в явном
виде называется уравнением, разрешенным относительно
старшей производной или уравнением в нормальной форме
y
y x 2 , y (1) 2, y (1) 0
x
12

13.

РЕШЕНИЕ ОБЫКНОВЕННЫХ
ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ
первого порядка
Метод Эйлера
13

14.

Задача Коши для ОДУ первого порядка
или
(1)
(2)
Решением дифференциального уравнения (ДУ) (2)
на интервале [a,b] называется функция y=y(x),
которая после ее подстановки в уравнение
превращает его в тождество на данном интервале.
Постановка задачи:
Требуется найти функцию y=y(x), удовлетворяющую ДУ
y’=f(x,y) (2) и принимающую при x=x0 заданное
значение y0, т.е. y(x0)=y0.
Для определенности будем считать, что решение
нужно получить для x>x0. Считаем, что условия
существования, единственности и гладкости решения
задачи выполнены.
14

15.

Для решения задачи Коши применим
конечно-разностный метод
Введем последовательность точек x0,x1,...,xi ,xn и шаги
изменения hi = xi+1 – xi = const.
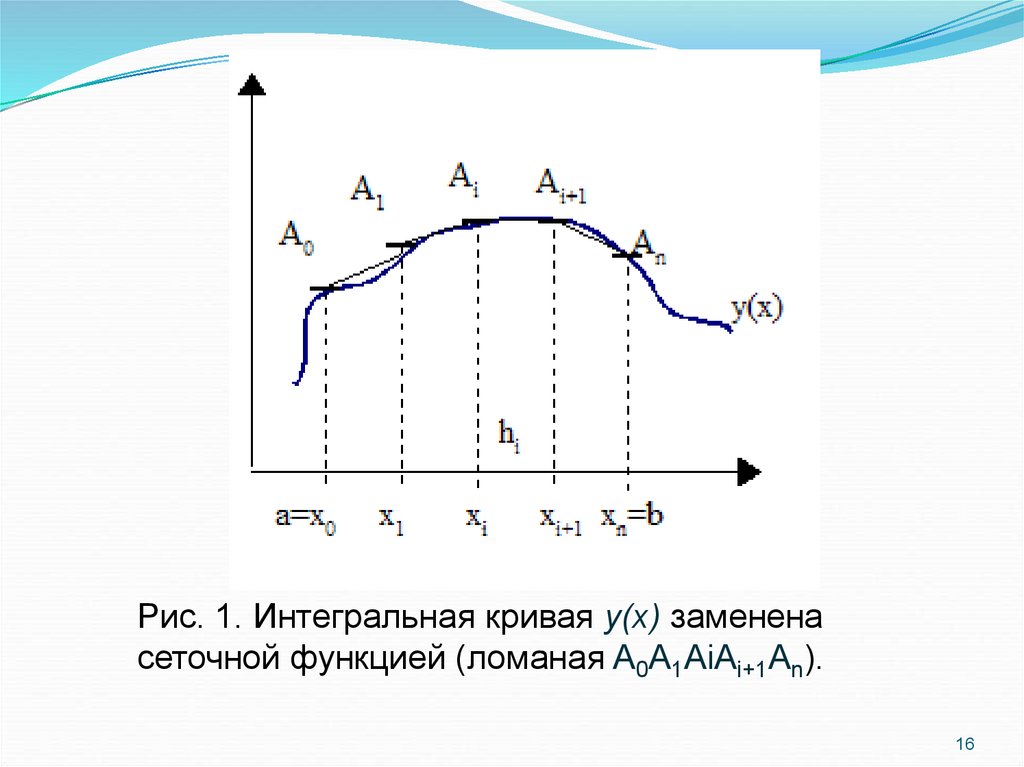
Интегральную кривую y=y(x) приближенно заменим
ломаной A0A1AiAi+1An. В каждой точке xi, называемой
узлом, вместо значения функции y(xi) вводятся числа yi,
аппроксимирующие точное решение y(x) на заданном
множестве точек. Функцию, заданную в виде таблицы
{xi,yi} называют сеточной функцией.
15

16.

Рис. 1. Интегральная кривая y(x) заменена
сеточной функцией (ломаная A0A1AiAi+1An).
16

17.

Заменяя значения производной в уравнении (2)
отношением конечных разностей, осуществляем
переход от дифференциальной задачи y’=f(x,y),
y(x0)=y0 относительно y к разностной задаче
относительно функций
:
(3)
(4)
k-шаговый метод:
при k=1 – одношаговый,
при k=2 – двухшаговый и т.д.
17

18.

Одношаговые методы.
Метод Эйлера
Постановка задачи Коши: Требуется найти функцию y=y(x),
удовлетворяющую ДУ (2) и принимающую при x=x0 заданное значение y0,
т.е.
y(x0)=y0 . (2а)
Для определенности будем считать, что решение нужно получить для
значений x>x0. Считаем, что условия существования, единственности и
гладкости решения задачи (2)-(2а) выполнены.
Метод Эйлера
(5)
18

19.

Метод Эйлера
Заменим значение функции y в узлах xi значениями
сеточной функции
. полагаем, что
(6)
Учитывая введенные обозначения (6) и,
пренебрегая вкладами порядка O(h2) и выше, из
равенства (5) получаем:
(7)
Таким образом, получим
(2а)
19

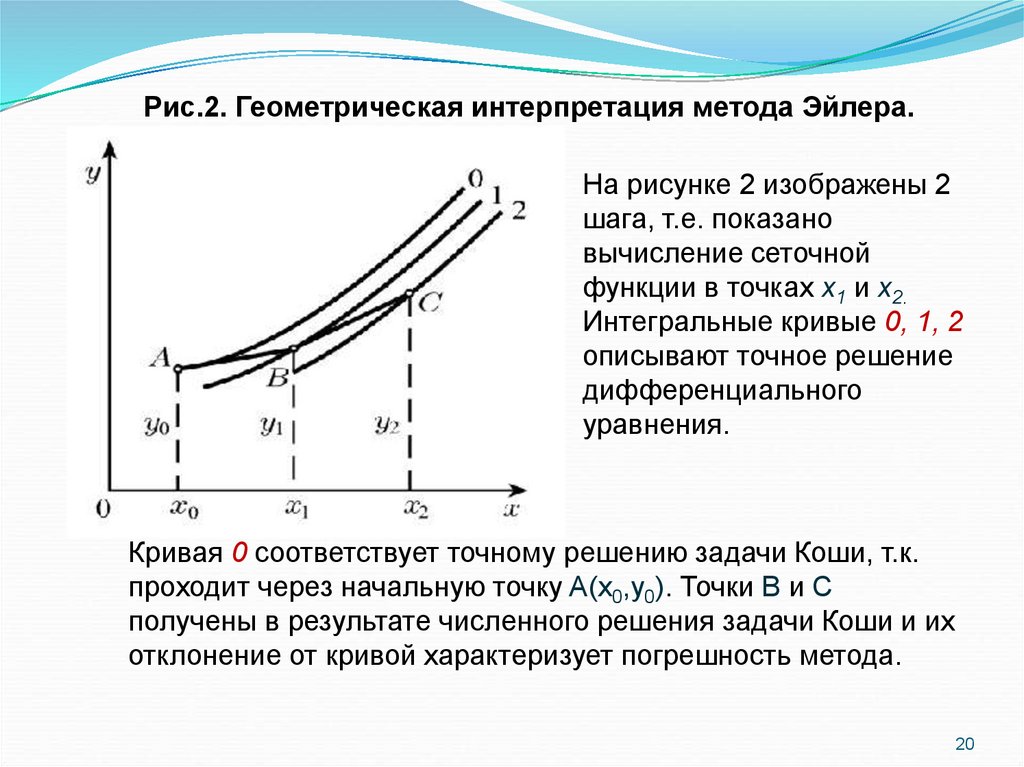
20.

Рис.2. Геометрическая интерпретация метода Эйлера.
На рисунке 2 изображены 2
шага, т.е. показано
вычисление сеточной
функции в точках x1 и x2.
Интегральные кривые 0, 1, 2
описывают точное решение
дифференциального
уравнения.
Кривая 0 соответствует точному решению задачи Коши, т.к.
проходит через начальную точку A(x0,y0). Точки B и C
получены в результате численного решения задачи Коши и их
отклонение от кривой характеризует погрешность метода.
20

21.

Отрезок AB — это отрезок касательной к кривой 0 в точке
A. Ее наклон равен значению производной y'0 = f(x0,y0).
Касательная BC проводится уже к другой интегральной
кривой 1.
Формула (7) соответствует уравнению касательной к
интегральной кривой y(xi) в точках (xi,yi) вида
y = yi + (x-xi)k. Т.е. вычисления по формуле Эйлера
состоят в том, что на каждом шаге заново находится
касательная к семейству решений (интегральных
кривых), выполняется приращение и т.д. В результате
траекторией движения будет ломаная АВС.
21

22.

Погрешность метода Эйлера
Пусть на конечном отрезке [x0,xi] с постоянным шагом
h посчитаны значения yhi , а при проходе того же
участка с половинным шагом h/2 — значения yh/2i .
Тогда для вычисления погрешности решения
применимо правило Рунге:
(8)
Для метода Эйлера k=1, выражение (8) упрощается
(9)
22

23.

Модифицированный метод Эйлера
Значения правой части уравнения y’=f(x,y) - функцию f(x,y)
возьмем равной среднему значению между f(xi,yi) и
f(xi+1,yi+1), т.е. вместо разностной схемы (7) запишем:
(10)
Считая
(i=0) начальным приближением, вычисляем первое
приближение
по формуле Эйлера (7):
Найденное значение
подставляем вместо
часть уравнения (10) и находим окончательно:
в правую
Такой алгоритм можно записать в виде одного соотношения:
(11)
23

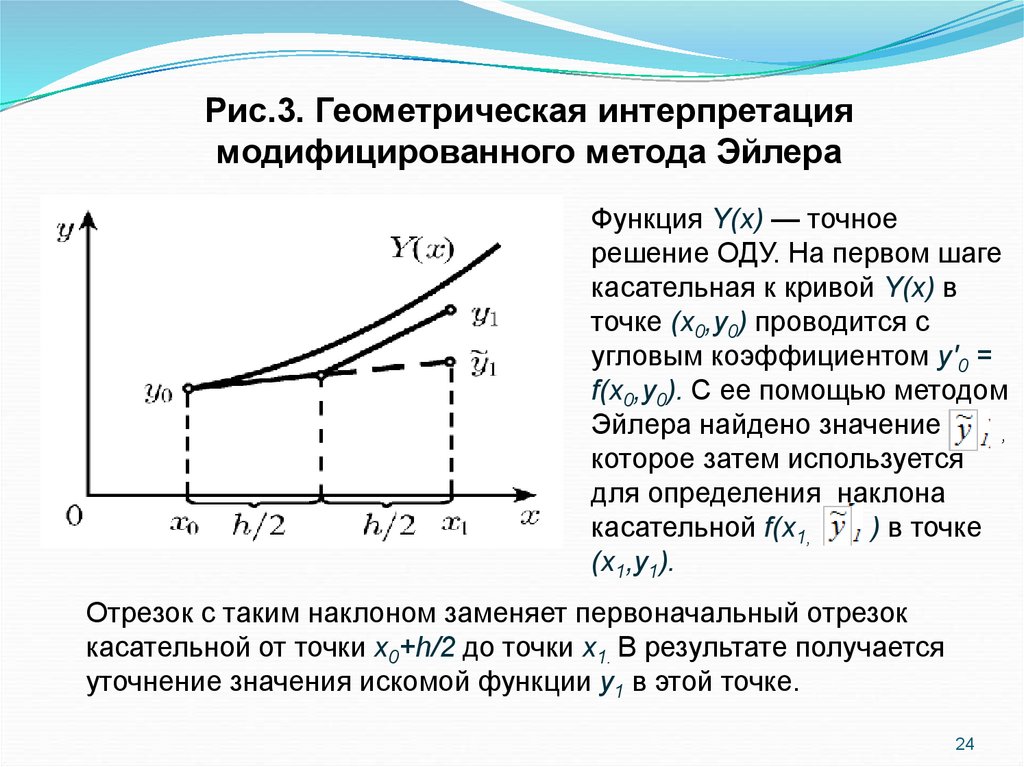
24.

Рис.3. Геометрическая интерпретация
модифицированного метода Эйлера
Функция Y(x) — точное
решение ОДУ. На первом шаге
касательная к кривой Y(x) в
точке (x0,y0) проводится с
угловым коэффициентом y'0 =
f(x0,y0). С ее помощью методом
Эйлера найдено значение
,
которое затем используется
для определения наклона
касательной f(x1,
) в точке
(x1,y1).
Отрезок с таким наклоном заменяет первоначальный отрезок
касательной от точки x0+h/2 до точки x1. В результате получается
уточнение значения искомой функции y1 в этой точке.
24