Презентация_к_уроку_алгебры_на_тему_Экстремумы_функции_11_класс

1. 11 класс Алгебра Экстремумы функции

2.

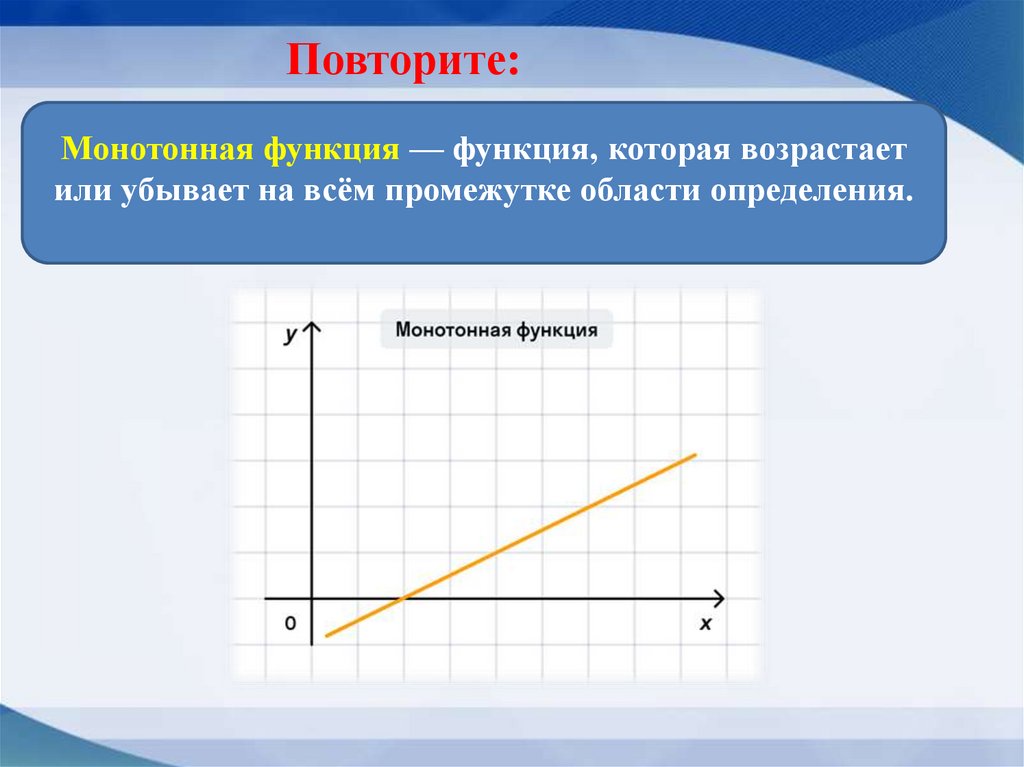
Повторите:
Монотонная функция — функция, которая возрастает
или убывает на всём промежутке области определения.

3. Повторите:

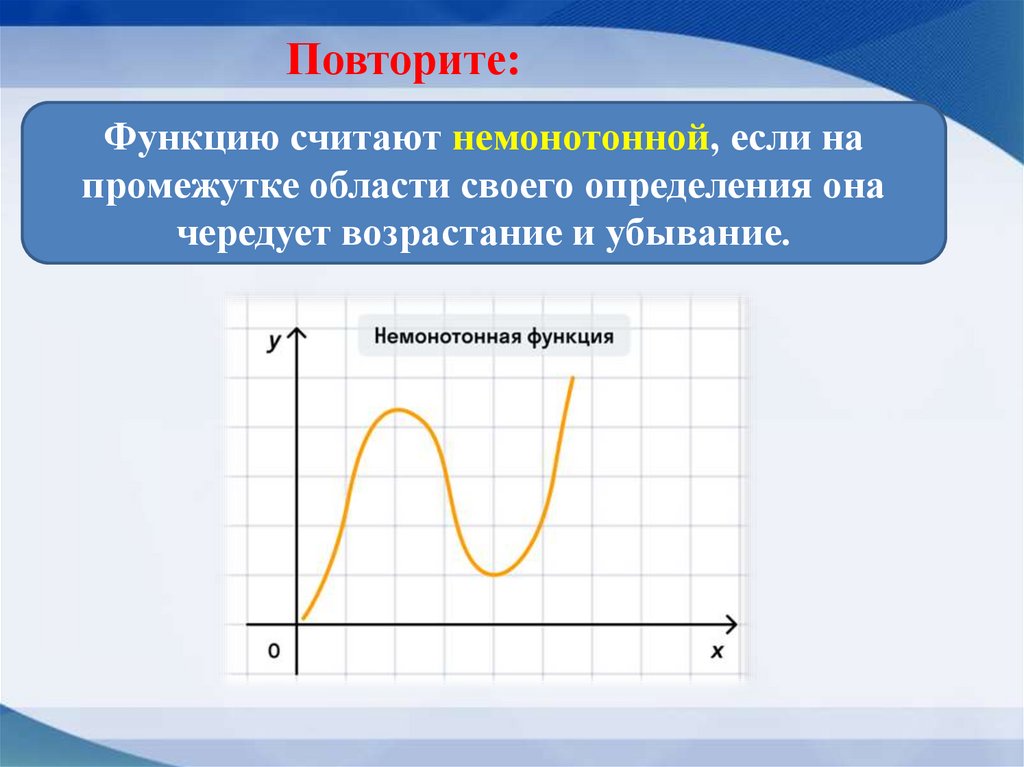
Функцию считают немонотонной, если на
промежутке области своего определения она
чередует возрастание и убывание.

4. Повторите:

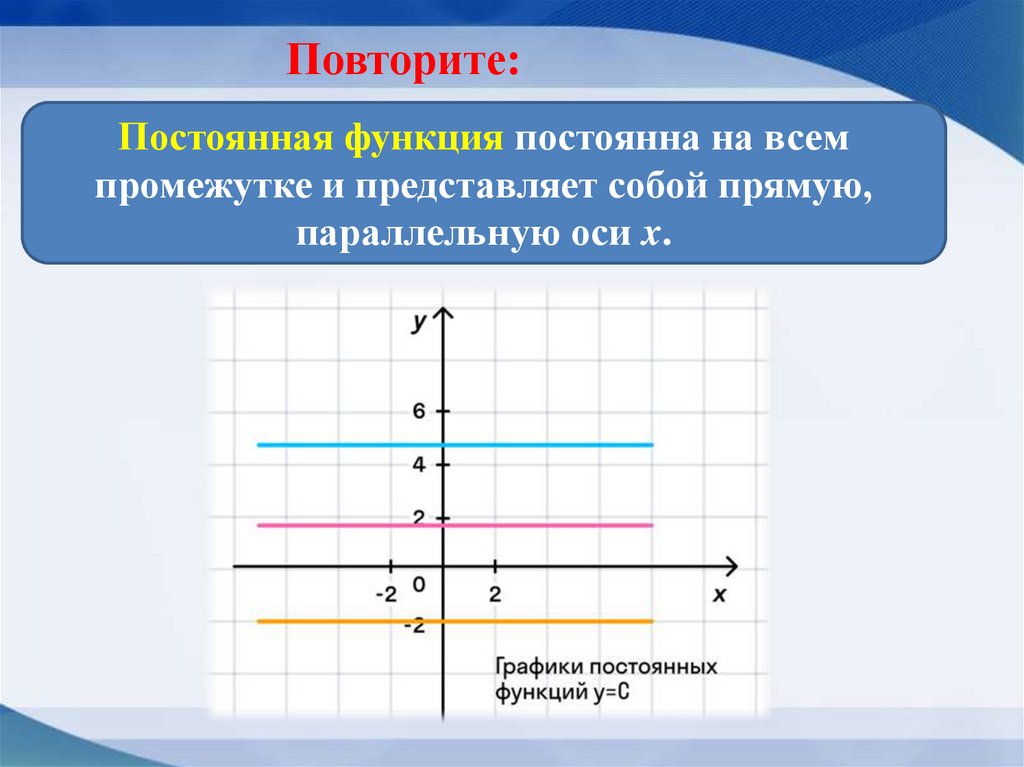
Постоянная функция постоянна на всем
промежутке и представляет собой прямую,
параллельную оси x.

5. Повторите:

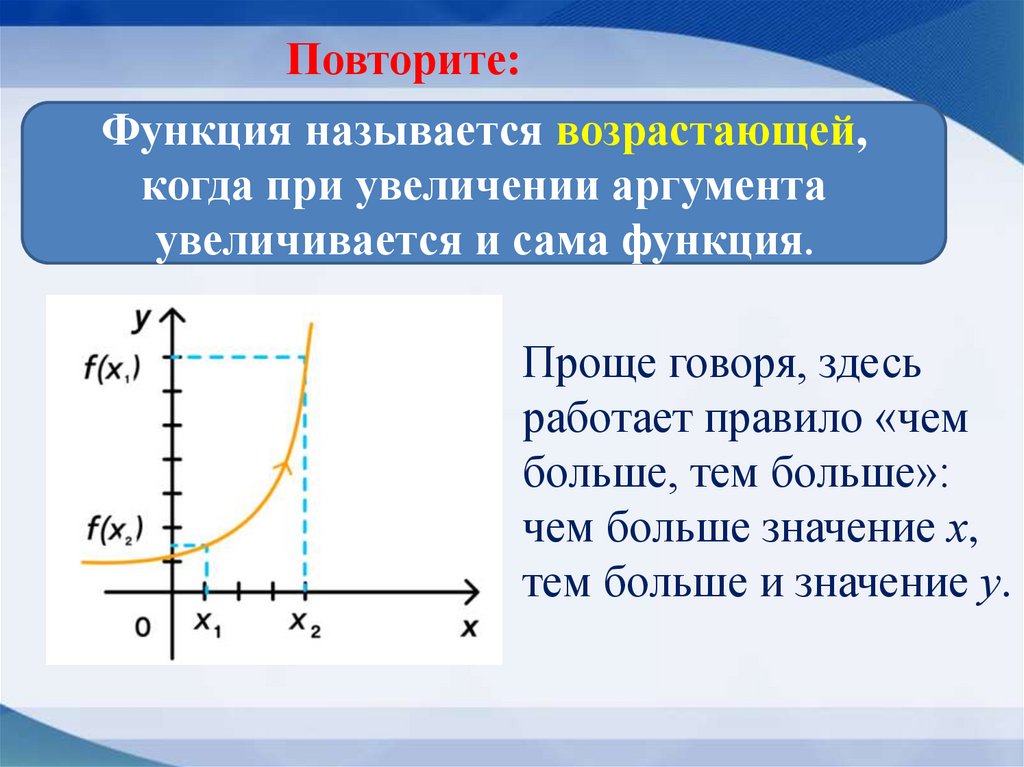
Функция называется возрастающей,
когда при увеличении аргумента
увеличивается и сама функция.
Проще говоря, здесь
работает правило «чем
больше, тем больше»:
чем больше значение х,
тем больше и значение у.

6. Повторите:

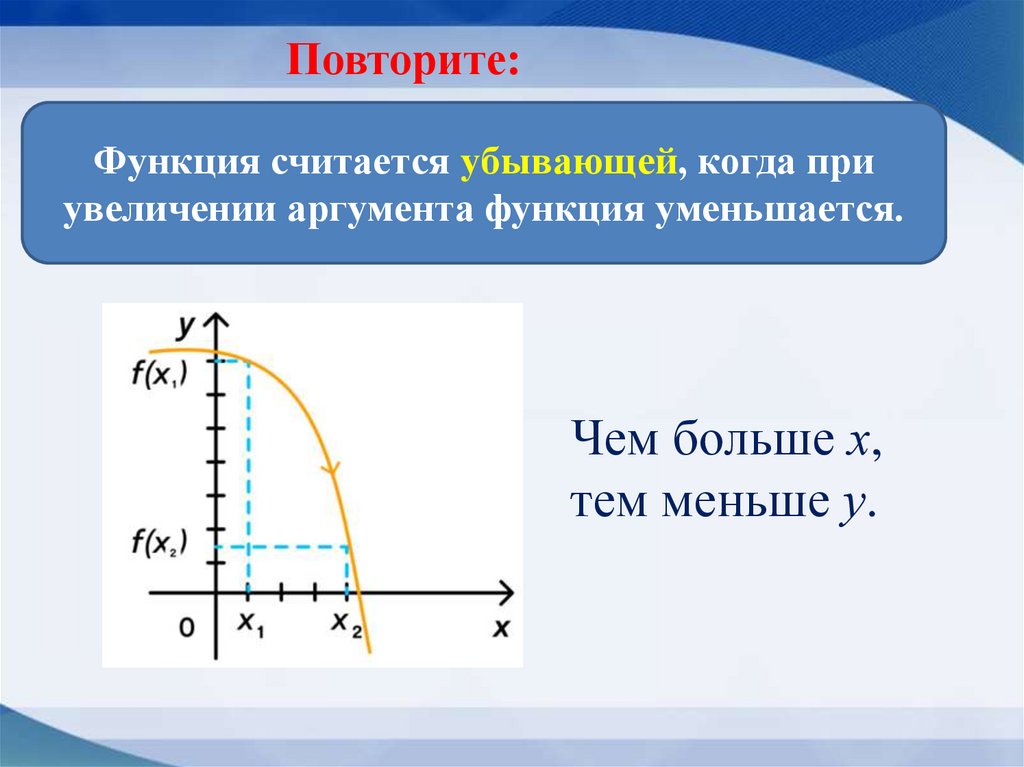
Функция считается убывающей, когда при
увеличении аргумента функция уменьшается.
Чем больше х,
тем меньше у.

7.

Повторите:

8.

Повторите:
Промежутки возрастания и убывания
функции называют промежутками
монотонности этой функции.

9. Повторите алгоритм нахождения промежутков возрастания (убывания) функции y=f(x):

1.Найти область определения функции.
2.Найти производную функции f´(x).
3.Решить уравнение f´ (x) =0.
4.На области определения функции отметить точки, в которых
производная равна нулю или не существует, обозначить интервалы, на
которые эти точки разбивают область определения.
5. Найти знак производной на каждом интервале.
6. Согласно признаку возрастания (убывания) функции, найти промежутки
возрастания и убывания функции.

10.

Запишите и выучите определение:
Экстре́мум (лат. extremum — крайний) —
максимальное или минимальное значение
функции на заданном множестве.

11.

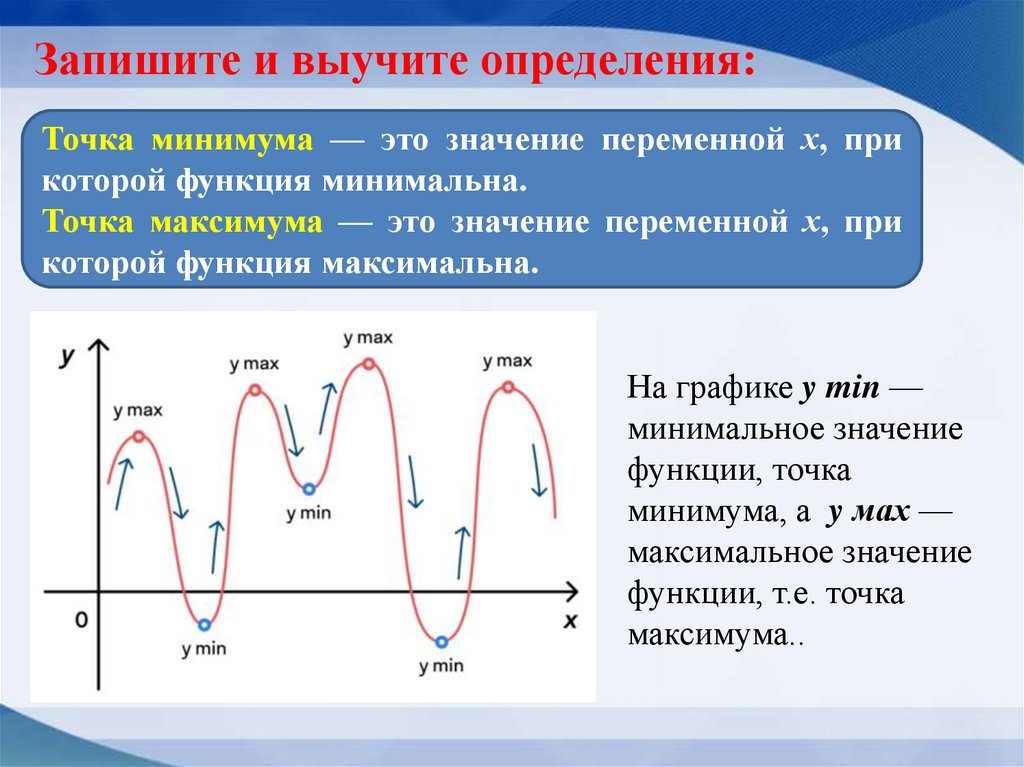
Запишите и выучите определения:
Точка минимума — это значение переменной х, при
которой функция минимальна.
Точка максимума — это значение переменной х, при
которой функция максимальна.
На графике y min —
минимальное значение
функции, точка
минимума, а y мах —
максимальное значение
функции, т.е. точка
максимума..

12. Иначе точки минимума и максимума в математике принято называть точками экстремума, а значения функции, которые соответствуют

точкам экстремума
— экстремумами функции.

13.

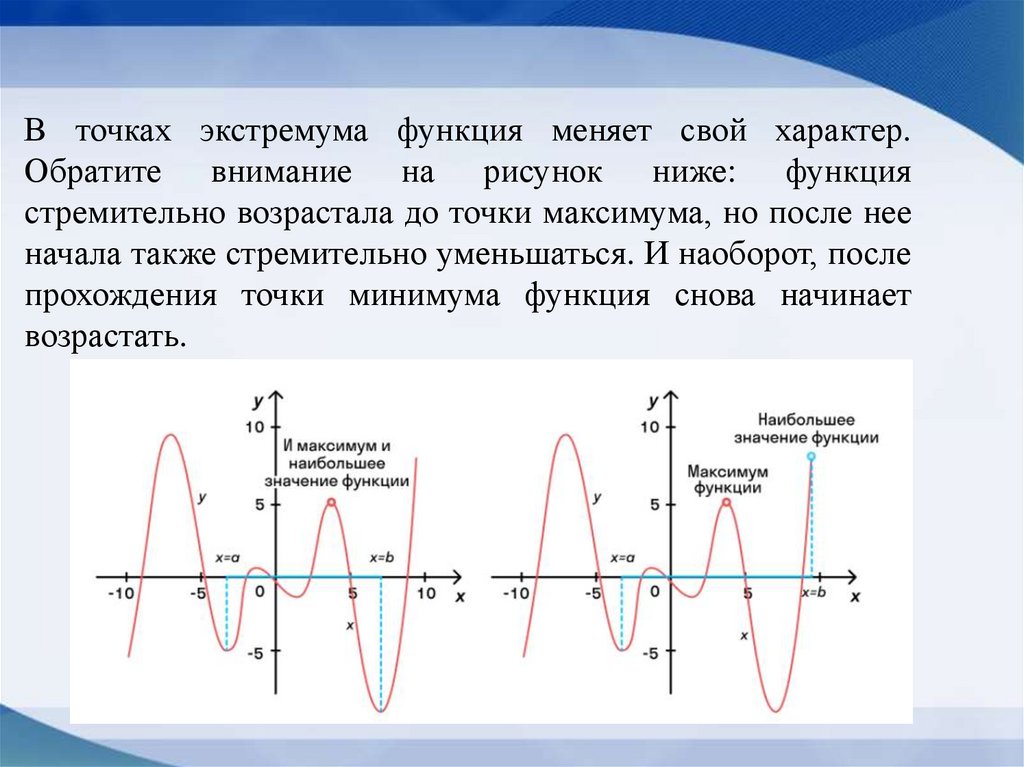
В точках экстремума функция меняет свой характер.
Обратите внимание на рисунок ниже: функция
стремительно возрастала до точки максимума, но после нее
начала также стремительно уменьшаться. И наоборот, после
прохождения точки минимума функция снова начинает
возрастать.

14.

Здесь вам может стать интересно:
наибольшее/наименьшее значение функции на
промежутке — это то же самое или нет?
К сожалению, нет. Эти значения иногда могут
совпадать, но часто определяются разными
точками.

15.

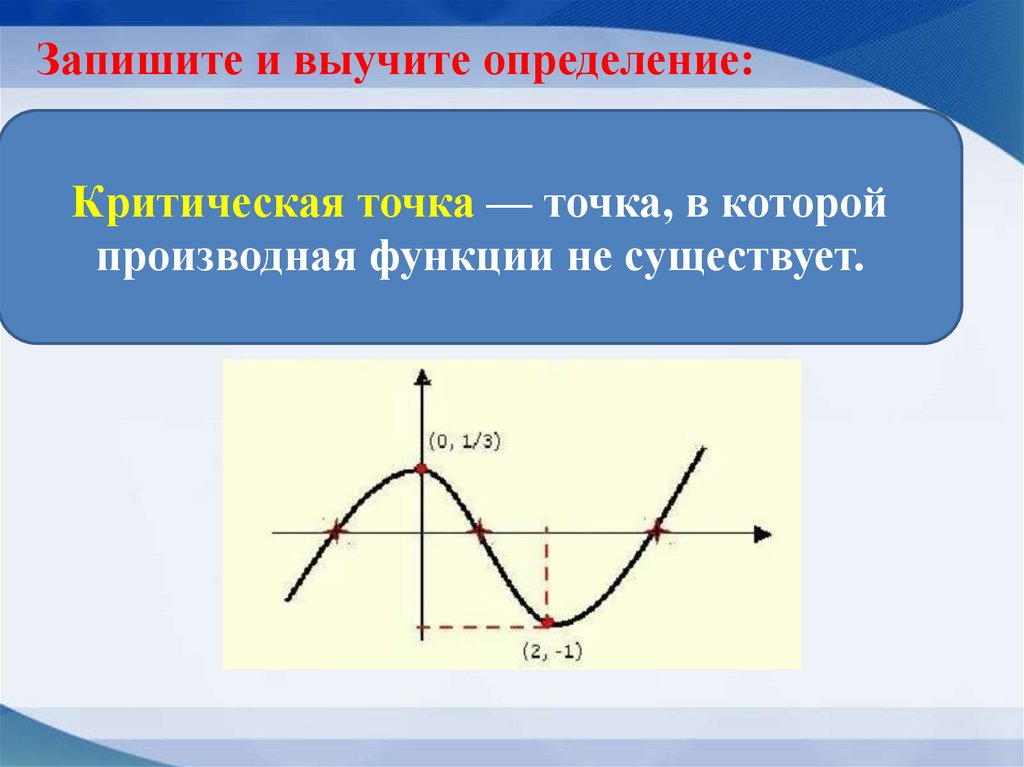
Запишите и выучите определение:
Критическая точка — точка, в которой
производная функции не существует.

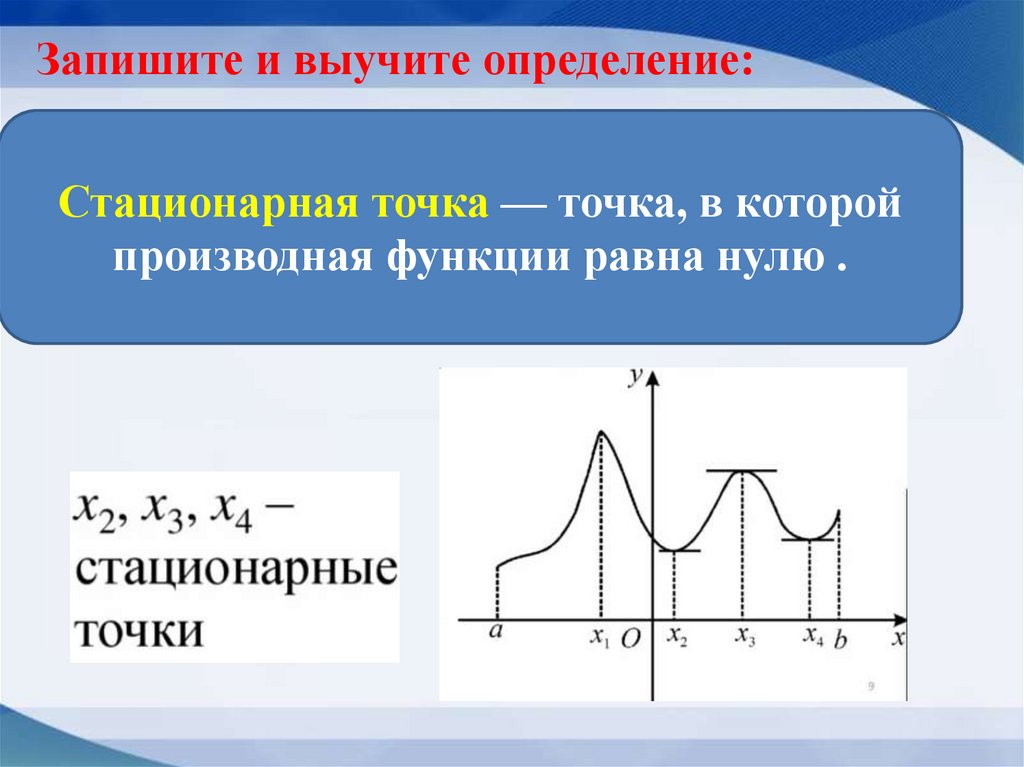
16.

Запишите и выучите определение:
Стационарная точка — точка, в которой
производная функции равна нулю .

17.

Теорема о достаточных
условиях экстремума функции.
Пусть непрерывная функция y = f(x) имеет стационарную x0. Тогда
возможен один из 3-х случаев.
1. Точка x0 является точкой минимума функции, если существует
такая окрестность этой точки, что в ней для любого x < x0 выполняется неравенство f '(x) < 0, а при x > x0 неравенство f '(x) > 0.
2. Точка x0 является точкой максимума функции, если существует
такая окрестность этой точки, что в ней для любого x < x0 выполняется неравенство f '(x) > 0, а при x > x0 неравенство f '(x) < 0.
3. В точке x0 экстремума нет, если существует такая окрестность
этой точки, что в ней для любого x ≠ x0 знаки производной
одинаковы.

18.

Алгоритм нахождения экстремумов функции
Пусть имеется непрерывная функция y = f(x), которую необходимо
исследовать на предмет наличия экстремумов. Для этого следует
выполнить последовательность действий:
1. Найти производную f '(x) заданной функции.
2. Найти критические точки. Для этого необходимо исследовать, в
каких точках производная функции f '(x) не существует, и найти
нули производной функции, т. е. решить уравнение f '(x) = 0.
3. Отметить критические точки на числовой прямой область
определения функции y = f(x)
4. Определить знаки производной функции f '(x) на получившихся
промежутках.
5. Опираясь на теорему о достаточных условиях экстремума
функции, сделать выводы о наличии или отсутствии точек
экстремума функции.

19.

Пример использования алгоритма нахождения
экстремумов функции.
Исследовать функцию y = 3x4 − 16x3 + 24x2 − 11 на наличие экстремумов.
1. Производная функции y' = 12x3 − 48x2 + 48x.
2. Производная функции y' существует при любом x. Далее решим
уравнение y' = 0.
12x3 − 48x2 + 48x = 0,
12x(x2 − 4x + 4) = 0,
12x(x − 2)2 = 0.
x1 = 0 и x2 = 2.
3. Изображаем числовую прямую, на которой отмечены критические
точки.
4. Получено 3 числовых промежутка. Определяем и отмечаем знак
производной функции на каждом промежутке. Для этого берём из каждого
промежутка любое значение аргумента, отличное от критических точек, и
подставляем в производную
5. На основании теоремы о достаточных условиях экстремума функции
приходим к выводу о том, что точка x1 = 0 является точкой минимума
функции, а точка x2 = 2 не является точкой экстремума функции.

20. №914 (2)