ВиС 13.02

1.

Случайная величина. Распределение
вероятностей. Диаграмма распределения.
Выполнили:
Ученицы 10А класса
Старостина Екатерина и Потапова Анастасия

2.

СЛУЧАЙНАЯ ВЕЛИЧИНА

3.

Случайной называется величина, которая может в результате опыта принимать то или иное
числовое значение, заранее неизвестно, какое именно.
Случайные величины обозначаются X, Y, Z, а их возможные значения х, у, z.
Случайные величины бывают двух типов: дискретные и
непрерывные.
Дискретная — принимает конечное или счётное множество значений.
Например, число выпавших очков на игральном кубике.
Непрерывная — принимает любое значение из некоторого числового промежутка.
Например, время ожидания автобуса на остановке.

4.

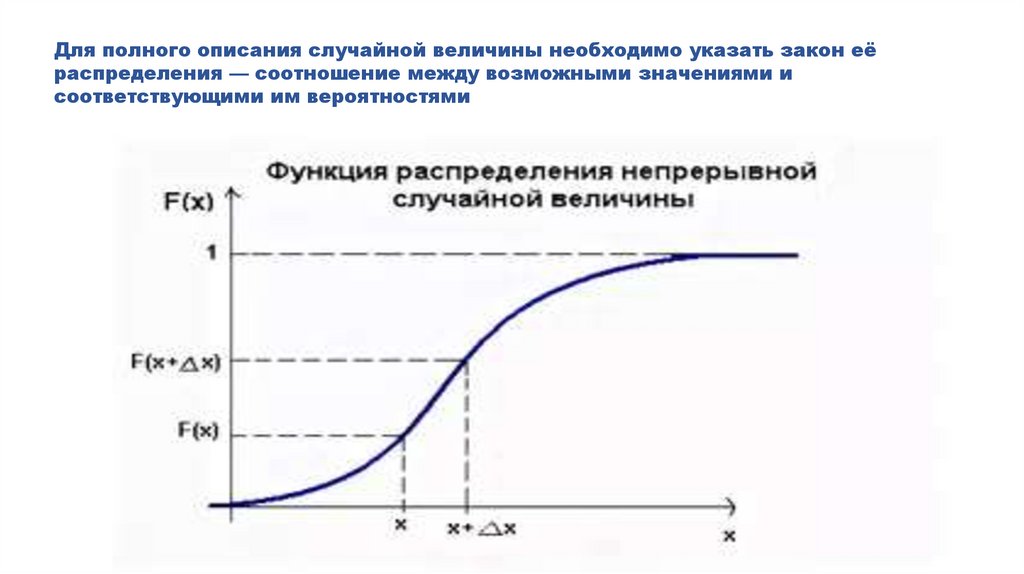
Для полного описания случайной величины необходимо указать закон её
распределения — соотношение между возможными значениями и
соответствующими им вероятностями

5.

Характеристика
Некоторые числовые характеристики случайных величин:
Математическое ожидание — характеризует среднее значение случайной величины, равно сумме
произведений всех возможных её значений на соответствующие им вероятности.
Дисперсия — отражает степень разброса значений случайной величины относительно
математического ожидания, равна математическому ожиданию квадрата отклонения случайной
величины от её математического ожидания.
Среднее квадратическое отклонение — характеризует среднюю величину рассеяния отдельных
значений случайной величины относительно её математического ожидания, равно квадратному
корню из дисперсии.
Мода — для дискретной случайной величины — её наиболее вероятное значение, для
непрерывной — значение, в котором плотность вероятности максимальна.

6.

Закон распределения случайной величины
может быть задан разными способами:
В виде таблицы (ряд распределения). В первой строке
перечислены в порядке возрастания все возможные значения
случайной величины, во второй — соответствующие им
вероятности.
Графически. Графическое изображение ряда распределения
называется многоугольником (полигоном) распределения. Для
его построения возможные значения случайной величины
откладываются по оси абсцисс, а вероятности — по оси
ординат; точки с координатами (xi, pi) соединяются отрезками.
Аналитически. Аналитическим выражением закона
распределения может быть, например, формула Бернулли (в
случае биноминального распределения), формула Пуассона (в
случае распределения Пуассона), формула геометрической
прогрессии (в случае геометрического распределения).

7.

РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ

8.

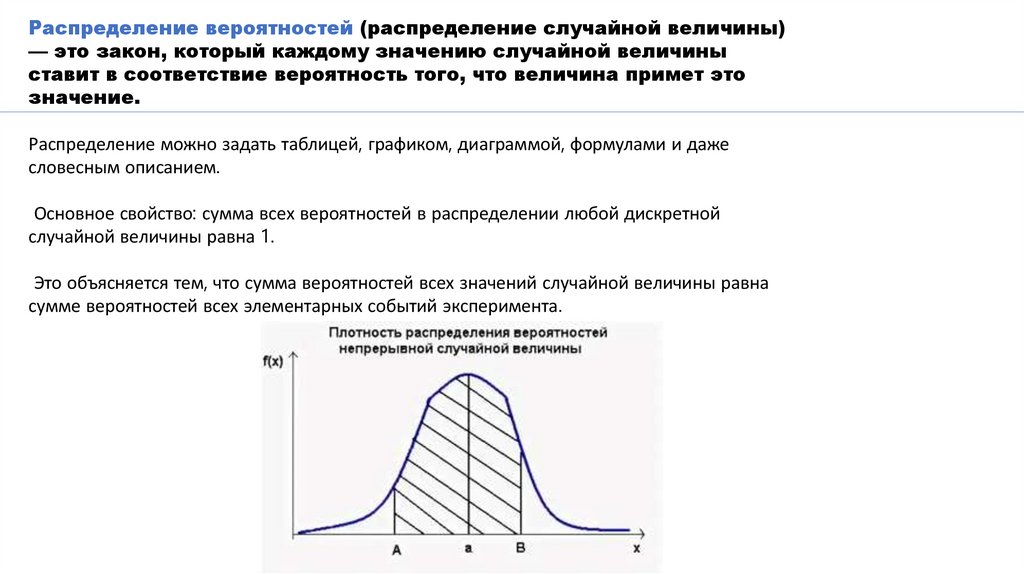
Распределение вероятностей (распределение случайной величины)
— это закон, который каждому значению случайной величины
ставит в соответствие вероятность того, что величина примет это
значение.
Распределение можно задать таблицей, графиком, диаграммой, формулами и даже
словесным описанием.
Основное свойство: сумма всех вероятностей в распределении любой дискретной
случайной величины равна 1.
Это объясняется тем, что сумма вероятностей всех значений случайной величины равна
сумме вероятностей всех элементарных событий эксперимента.

9.

Выделяют два фундаментальных класса распределений:
Дискретные
Непрерывные
Равномерное — у всех исходов одинаковая
вероятность. Например, при бросании монеты
вероятность выпадения орла или решки равна 0,5
Нормальное (гауссово) распределение — данные
распределяются по форме колокола, большинство
значений сгруппированы вокруг среднего.
Биномиальное — используется для моделирования
числа успешных исходов в серии независимых
испытаний с двумя возможными исходами: успех
или неудача. Пример: вероятность того, что при
бросании монеты орёл выпадет 3 раза из 5.
Экспоненциальное распределение — форма
гауссова распределения, в которой данные
описывают время между событиями, которые
происходят с постоянным средним интервалом.
Пуассоновское — применяется для определения
вероятности того, сколько раз произойдёт
определённое событие за фиксированный период
времени или в определённом пространстве. Пример
— сколько звонков поступит в колл-центр за час.

10.

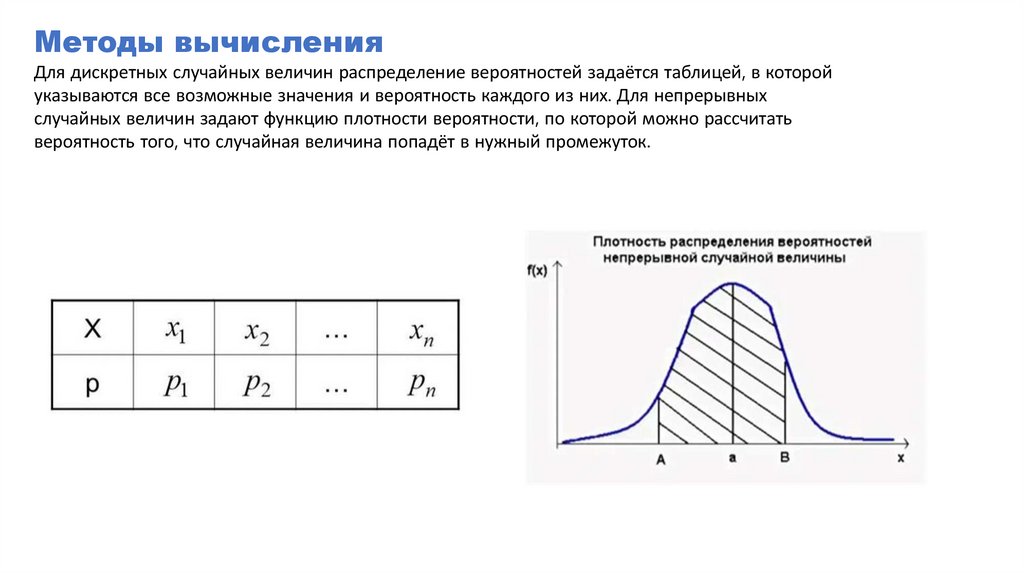
Методы вычисления
Для дискретных случайных величин распределение вероятностей задаётся таблицей, в которой
указываются все возможные значения и вероятность каждого из них. Для непрерывных
случайных величин задают функцию плотности вероятности, по которой можно рассчитать
вероятность того, что случайная величина попадёт в нужный промежуток.

11.

ДИАГРАММА РАСПРЕДЕЛЕНИЯ

12.

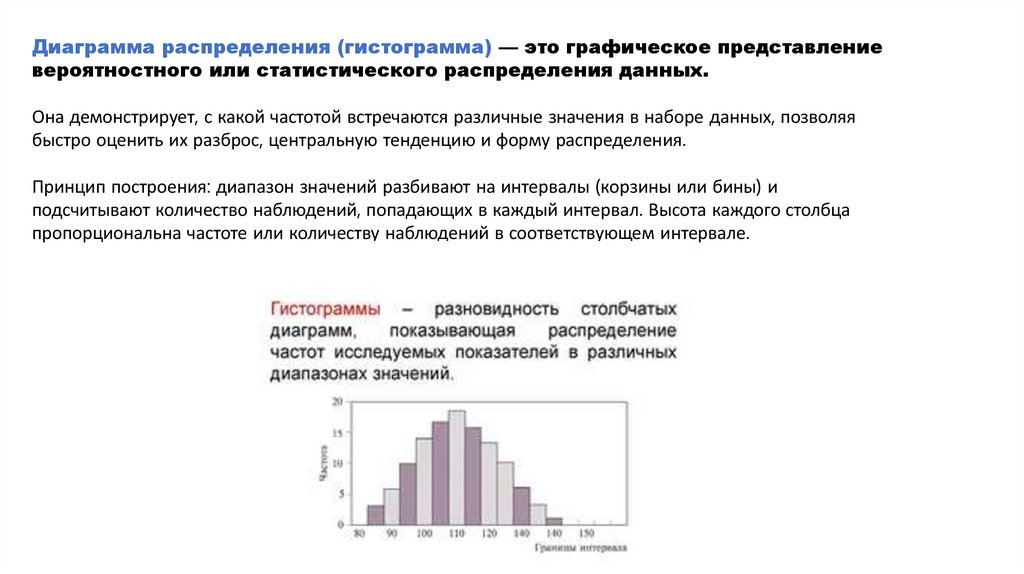
Диаграмма распределения (гистограмма) — это графическое представление
вероятностного или статистического распределения данных.
Она демонстрирует, с какой частотой встречаются различные значения в наборе данных, позволяя
быстро оценить их разброс, центральную тенденцию и форму распределения.
Принцип построения: диапазон значений разбивают на интервалы (корзины или бины) и
подсчитывают количество наблюдений, попадающих в каждый интервал. Высота каждого столбца
пропорциональна частоте или количеству наблюдений в соответствующем интервале.

13.

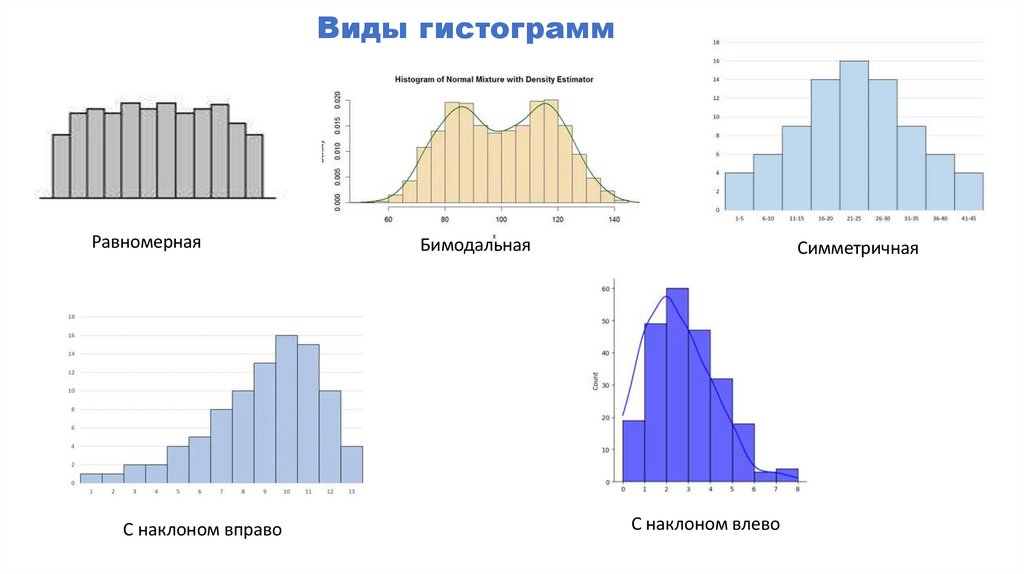
Виды гистограмм
Равномерная
С наклоном вправо
Бимодальная
Симметричная
С наклоном влево

14.

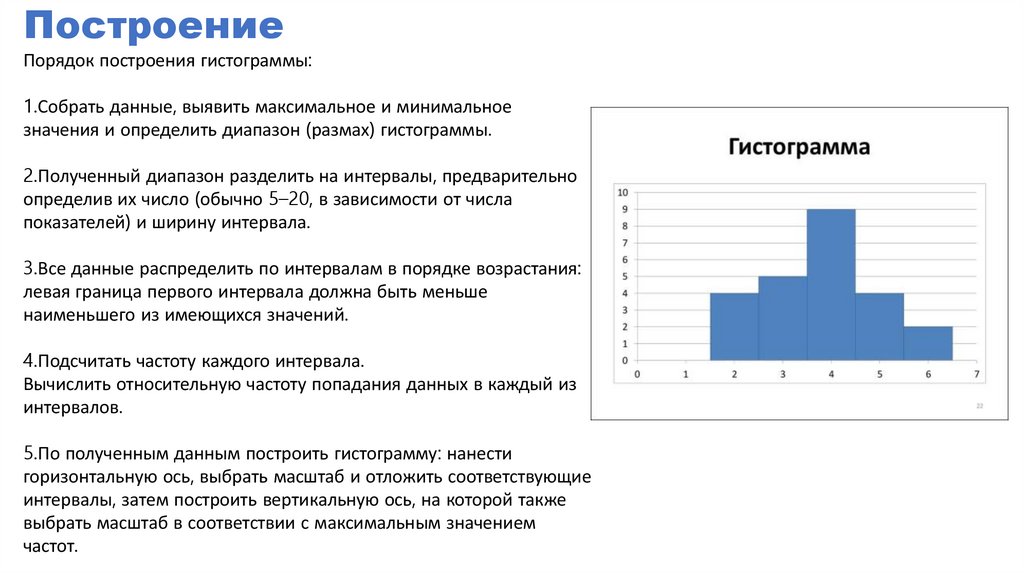
Построение
Порядок построения гистограммы:
1.Собрать данные, выявить максимальное и минимальное
значения и определить диапазон (размах) гистограммы.
2.Полученный диапазон разделить на интервалы, предварительно
определив их число (обычно 5–20, в зависимости от числа
показателей) и ширину интервала.
3.Все данные распределить по интервалам в порядке возрастания:
левая граница первого интервала должна быть меньше
наименьшего из имеющихся значений.
4.Подсчитать частоту каждого интервала.
Вычислить относительную частоту попадания данных в каждый из
интервалов.
5.По полученным данным построить гистограмму: нанести
горизонтальную ось, выбрать масштаб и отложить соответствующие
интервалы, затем построить вертикальную ось, на которой также
выбрать масштаб в соответствии с максимальным значением
частот.

15.

ЗАКЛЮЧЕНИЕ
Понятие случайной величины является фундаментом современной теории
вероятностей и статистики. Оно позволяет перевести неопределенность реального
мира на язык математики. Распределение вероятностей дает исчерпывающую
характеристику случайной величины, указывая не только возможные значения, но и
то, насколько часто они могут возникать. В свою очередь, диаграмма распределения
служит незаменимым инструментом визуализации, который позволяет наглядно
оценить характер случайного процесса, выявить его закономерности и наиболее
вероятные исходы. Освоение этих понятий необходимо для анализа данных и
принятия обоснованных решений в условиях неопределенности.

16.

СПАСИБО ЗА ВНИМАНИЕ