Похожие презентации:
Статистические методы обработки медико-биологических данных. Нормальный закон распределения
1.
Статистическиеметоды обработки
медико-биологических
данных
Нормальный закон
распределения
2.
Тема: Статистические методыобработки медико-биологических
данных
Нормальный закон распределения.
План лекции:
•Понятие случайных дискретных и
непрерывных величин.
•Распределения и характеристики
случайных величин.
•Нормальный закон распределения.
Кривая Гаусса и ее особенности.
Правило «трёх сигм».
3.
В медицине необходимо вести учет, анализи прогноз различных массовых явлений. В
целом, массовым явлениям присущи свои
особые закономерности. К доктору
обращаются пациенты с различными
заболеваниями. Болезнь конкретного
человека - случайное событие у врача. Но
случайные события предсказуемы,
например, в период эпидемии гриппа
наиболее часто встречаются заболевания
гриппом.
4.
Закономерности массовыхслучайных событий статистических данных,
отражающих эти события, изучаются с помощью
математической статистики.
5.
Типичная задача математическойстатистики - это приближенная
оценка неизвестной вероятности
случайного события по
результатам наблюдений,
экспериментов, когда событие
может происходить или не
осуществляться.
6.
Случайной величинойназывается переменная
величина, значение
которой зависит от исхода
некоторого испытания.
.
Дискретная
Непрерывная
7.
Дискретной называетсяслучайная величина, которая
может принимать значения
некоторой конечной или
бесконечной числовой
последовательности (число
слов в тексте, студентов в
аудитории, больных в
клинике...)
8.
Непрерывной называетсяслучайная величина,
которая может принимать
любые значения внутри
некоторого интервала
(масса, температура,
рост...)
9.
Дискретная ? илиНепрерывная?
10.
Статистический ряд – результаты измеренийдля статистического исследования,
записанные последовательно по порядку их
получения. Удобнее представить в таблице.
Х1, Х2, Х3………Хn
Х1
…
…..
….
Х2,
…
…
…
Х3
…
…..
..
…
…
…
…
…
…
…
…
…
…
…
…
…
…
….
….
…
…
…
Хn
11.
Распределение дискретнойслучайной величины
.
Дискретная случайная величина считается
заданной, если указаны ее возможные
значения и соответствующие им
вероятности
12.
Совокупность X и Р называетсяраспределением дискретной
случайной величины.
Дискретные X1 X2 X3 X4 X5 X6
случайные
величины xi
Вероятность pi P1 P2 P3 P4 P5 P6
13.
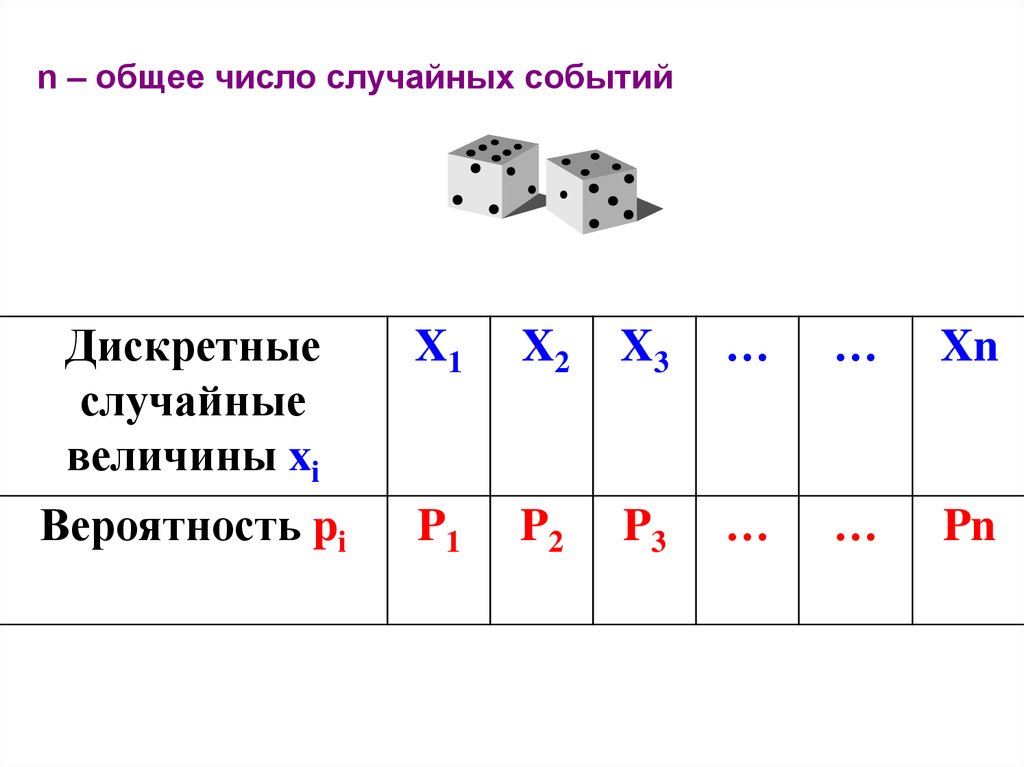
n – общее число случайных событийДискретные
случайные
величины xi
X1
X2
X3
…
…
Xn
Вероятность pi
P1
P2
P3
…
…
Pn
14.
Дискретные X1 X2 X3 X4 X5 X6случайные
1 2 3 4 5 6
величины
xi
Вероятность pi P1 P2 P3 P4 P5 P6
1/6
n
p
i 1
i
1/6
1
1/6
1/6
1/6
условие
нормировки
дискретных
случайных
величин
1/6
15.
Различные распределения1. Биномиальное
распределение
(позволяет определить
вероятность того, что
событие А произойдет m paз
при n испытаниях).
16.
2. Распределение Максвелла(распределение молекул газа по
скоростям, кинетическим
энергиям). График - кривая
Максвелла.
17.
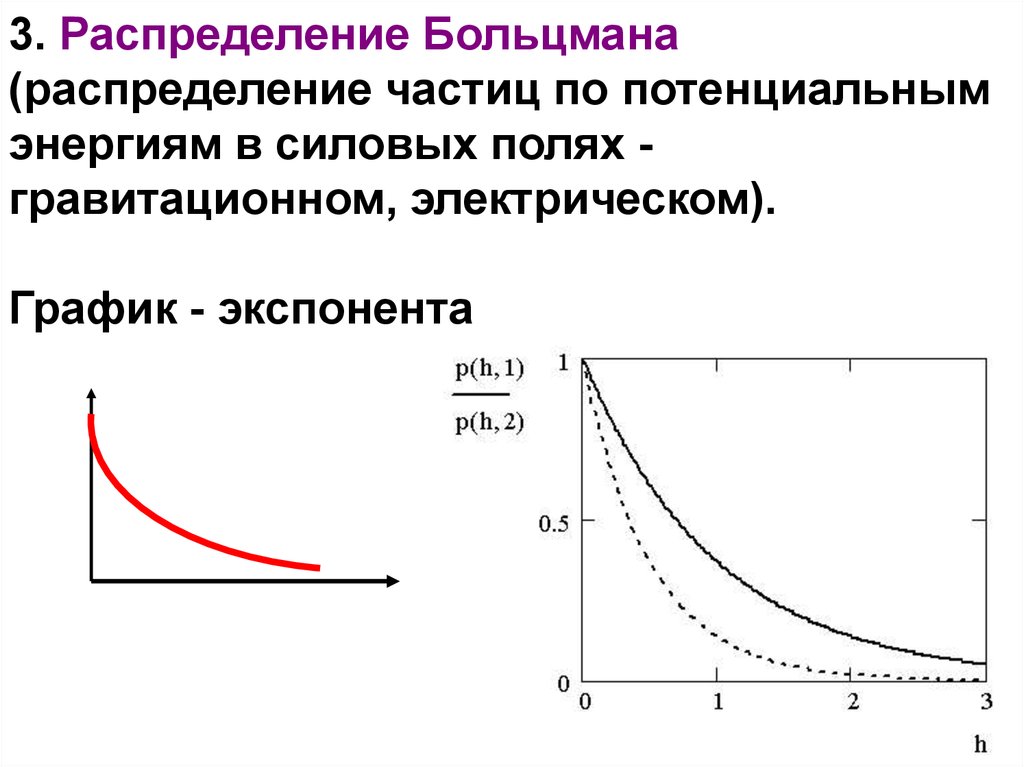
3. Распределение Больцмана(распределение частиц по потенциальным
энергиям в силовых полях гравитационном, электрическом).
График - экспонента
18.
4. Нормальное распределение(график - кривая Гаусса)
19.
5. Распределение Пуассона идр. ...
20.
Нормальный закон распределенияимеет важное практическое
значение в естественных науках.
Оказывается, распределение
роста, массы новорожденных и
много других случайных событий
физической и биологической
природы описываются
нормальным законом
распределения и графически
иллюстрируются кривой Гаусса.
21.
Числовые характеристикидискретных случайных
величин.
22.
1.Математическое ожиданиеслучайной величины есть сумма
произведений всех возможных ее
значений на вероятности этих
значений:
n
М ( х) xi pi
i 1
М ( х) х1 р1 х2 р2 .... хn pn
23.
2. Среднее арифметическое значениеm1 x1 m2 x2 m3 x3 m4 x4 ... ...mn xn
Х
n
mn
m1
x1 ... xn p1 x1 ... p n xn
n
n
n – число измерений
.
24.
Х<Х>
Если n велико , то относительные частоты
m/n = р,
а среднее арифметическое значение
практически равно математическому
ожиданию.
<Х> = М(х)
Математическое ожидание часто
отождествляют со средним значением
25.
3. Дисперсия случайнойвеличины – это математическое
ожидание квадрата отклонения
случайной величины от ее
математического ожидания;
D( x) M ( x ) [M ( x)]
2
D( x) M x M ( x)
2
2
26.
Дисперсия характеризуетрассеяние случайных
величин относительно
математического ожидания.
120
120
125
130
150
180
27.
Размерность дисперсии квадрат размерностислучайной величины, поэтому
введена величина
D(x)
4. σ - среднеквадратическое
отклонение, которое имеет
размерность случайной
величины.
28.
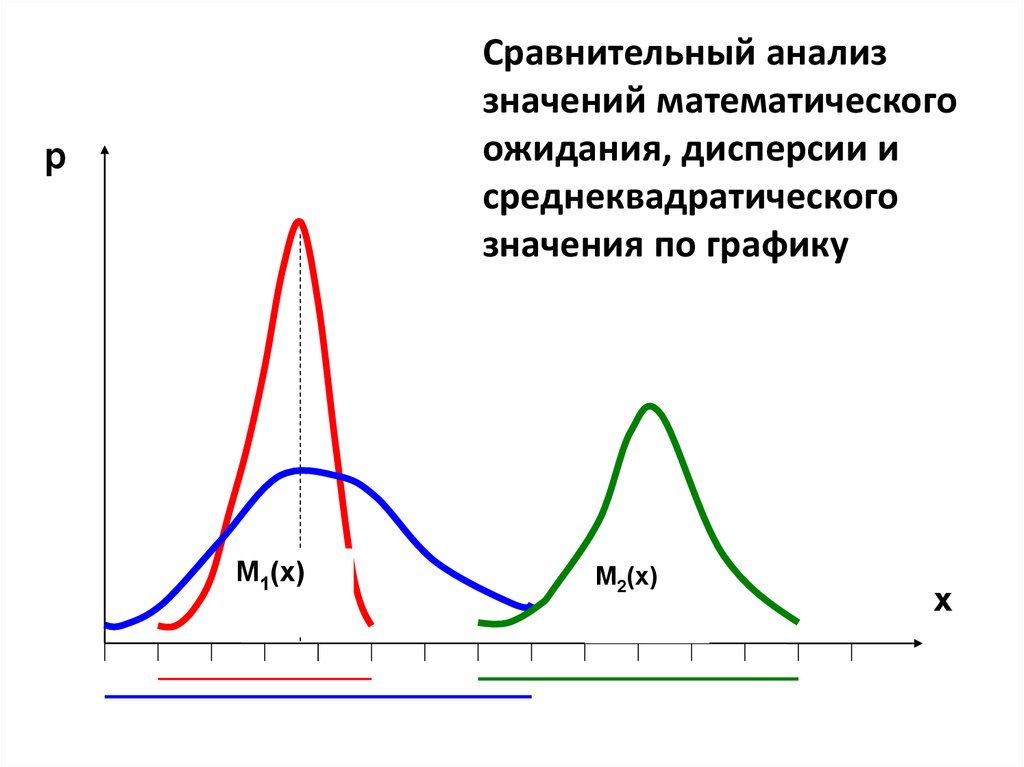
Сравнительный анализзначений математического
ожидания, дисперсии и
среднеквадратического
значения по графику
p
M1(x)
M2(x)
x
29.
Числовыехарактеристики
непрерывных случайных
величин.
30.
непрерывная случайная величинаX принимает значения между х и
х± Δх
dP =f(x)dx
х – Δх
х
х+ Δх
dP =f(x)dx, где f(x) - плотность
вероятности или функция
распределения вероятности.
31.
функция распределения вероятностипоказывает, как изменяется
вероятность, отнесенная к интервалу
dx случайной величины в
зависимости от значения самой этой
величины: f (х) = dP/dx
b
Pab f ( x)dx
a
32.
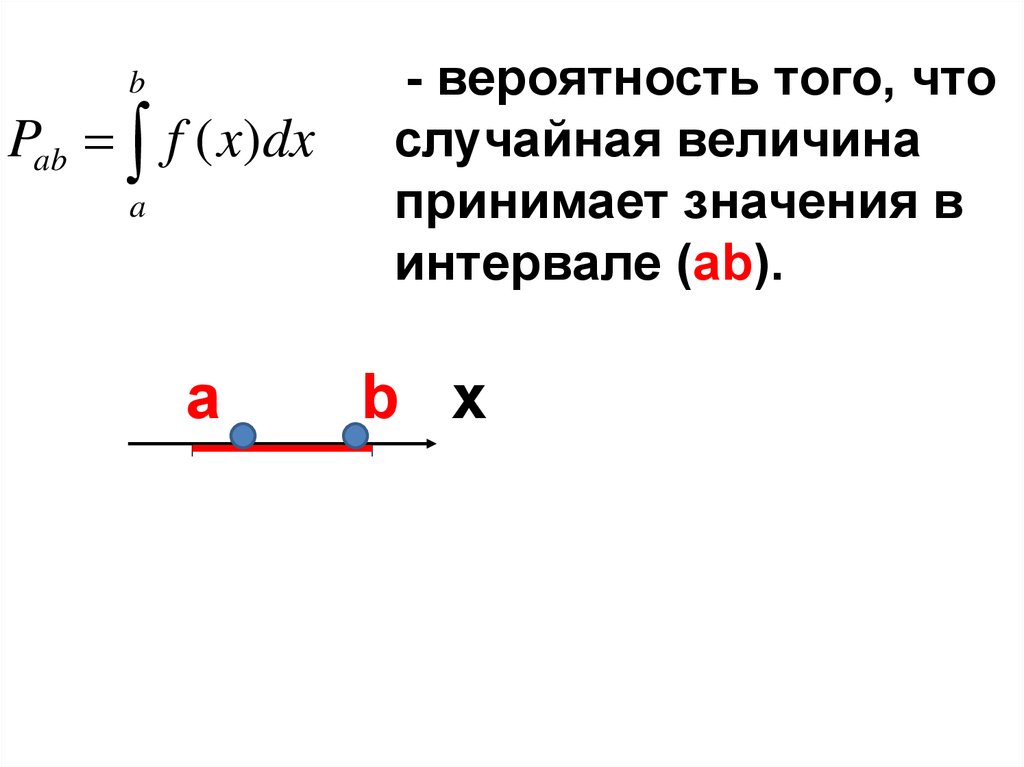
bPab f ( x)dx
a
a
- вероятность того, что
случайная величина
принимает значения в
интервале (аb).
b x
33.
-∞+∞
х
Какова вероятность того, что
случайная величина находится в
данном интервале?
34.
-f ( x)dx 1
условие нормировки
для непрерывной
случайной величины
35.
1. Математическое ожиданиеМ(х):
М ( х)
x
f
(
x
)
dx
36.
2. Дисперсия D(x) :D( x) [ x M ( x)] f ( x)dx
2
37.
3.Среднеквадратическое
отклонение,
которое имеет размерность
случайной величины.
D(x)
38.
Нормальный законраспределения:
2
1
( x M ( x )
f ( x)
exp
2
2
2
ехр - экспонента;
е±x= ехр(±х);
39.
График нормальногозакона - кривая Гаусса.
40.
Учитывая, чтоD
41.
21
x M ( x )
f ( x)
exp
;
2
2
2
x M ( x )
1
f ( x)
exp
2 D
2D
2
42.
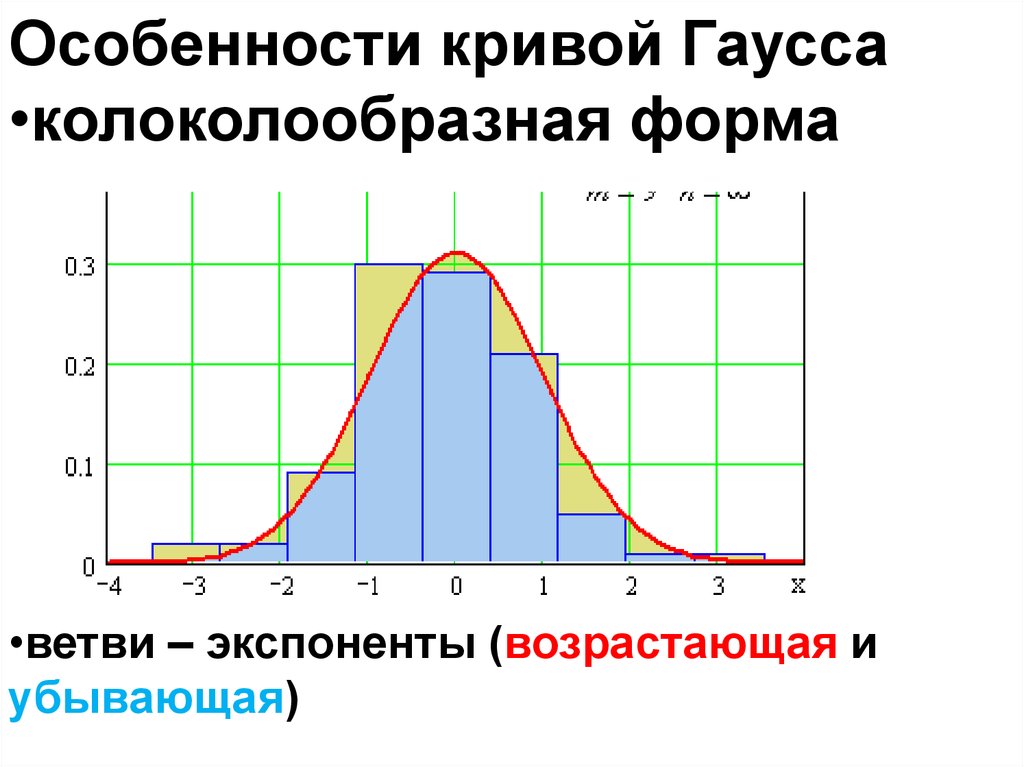
Особенности кривой Гаусса•колоколообразная форма
•ветви – экспоненты (возрастающая и
убывающая)
43.
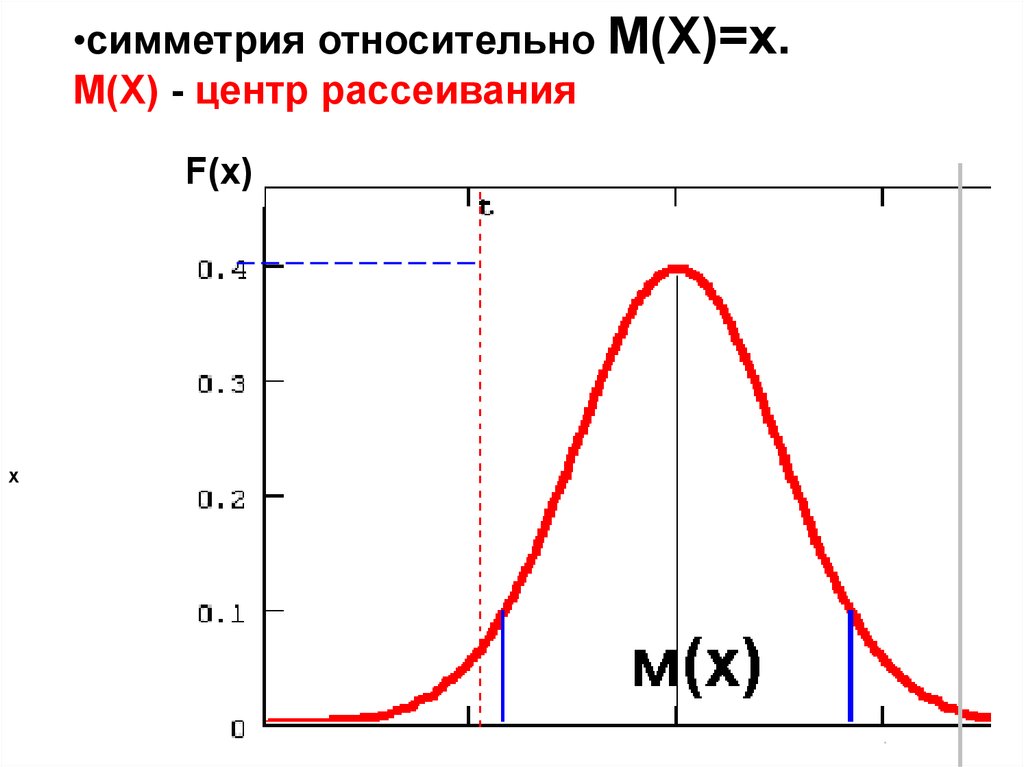
•симметрия относительно М(Х)=х.М(Х) - центр рассеивания
F(x)
х
44.
по данной формуле определяемкоординаты вершины кривой Гаусса,
когда х = М(х).
45.
Вершина графикаf ( x) max
1
2
46.
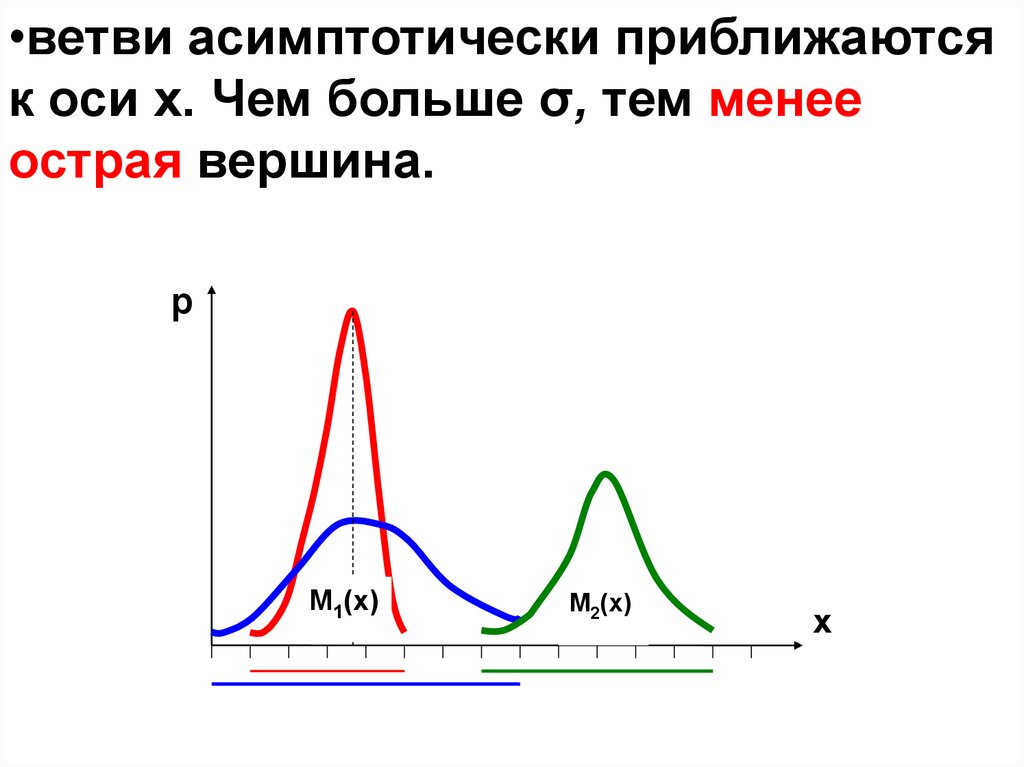
•ветви асимптотически приближаютсяк оси х. Чем больше σ, тем менее
острая вершина.
p
M1(x)
M2(x)
x
47.
•изменение математическогоожидания М(Х) сдвигает влево
или вправо вершину кривой
Гаусса
p
M1(x)
M2(x)
x
48.
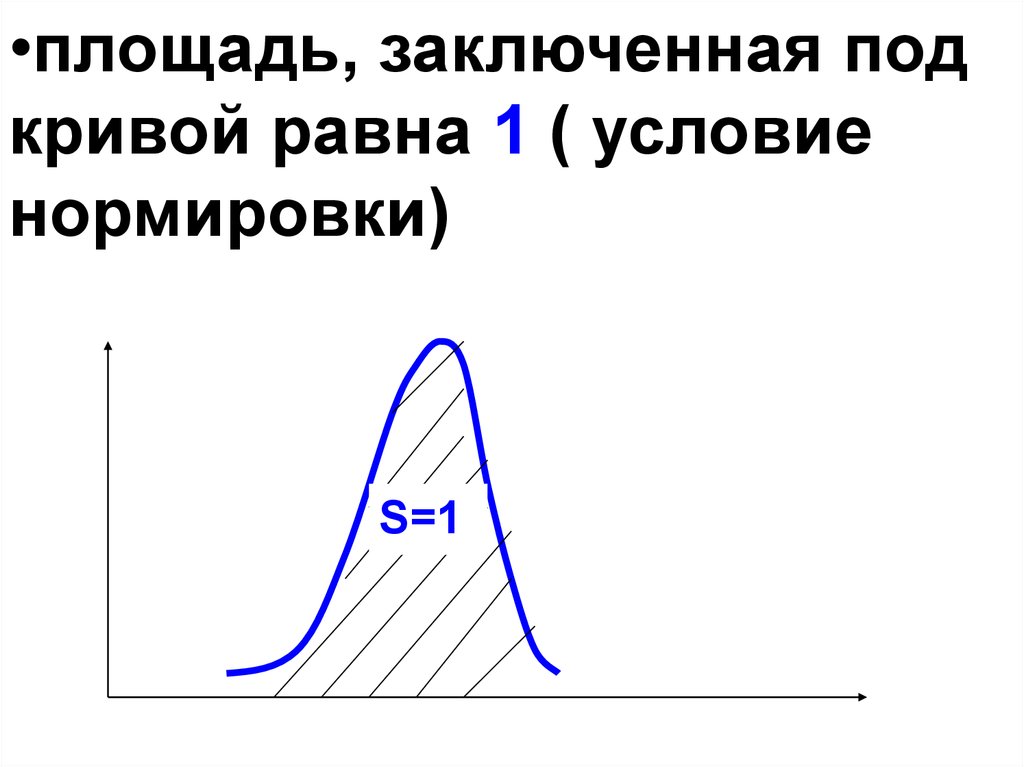
•площадь, заключенная подкривой равна 1 ( условие
нормировки)
S=1
49.
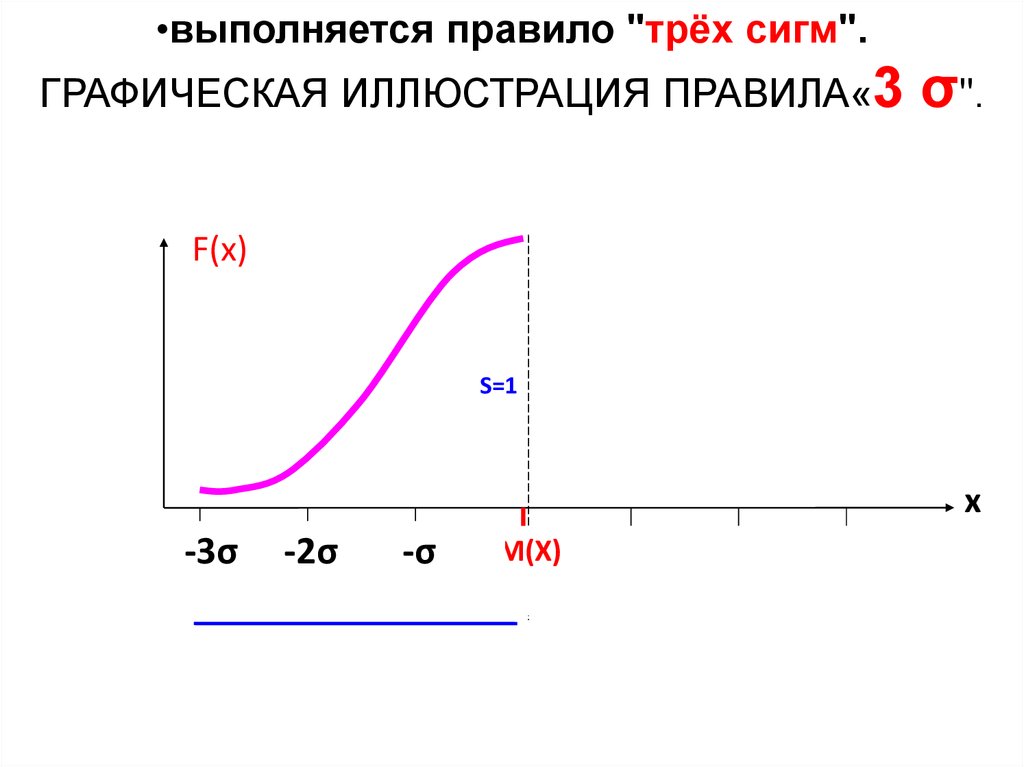
•выполняется правило "трёх сигм".ГРАФИЧЕСКАЯ ИЛЛЮСТРАЦИЯ ПРАВИЛА«3
σ".
F(x)
S=1
x
-3σ
-2σ
-σ
M(X)
50.
•Вероятность появления случайнойвеличины в интервале значений M(X)±3σ
равна 99,97% Это соответствует условию
нормировки - площадь под кривой равна 1,
т.е - практически все случайные величины нормального
распределения находятся под кривой Гаусса.
51.
•Вероятность появления случайной величины винтервале значений М(х)±σ равна 68%
М(х)±σ
F(x)
S=68%
-3σ
-2σ
-σ M(X) +σ
+2σ
+3σ
x
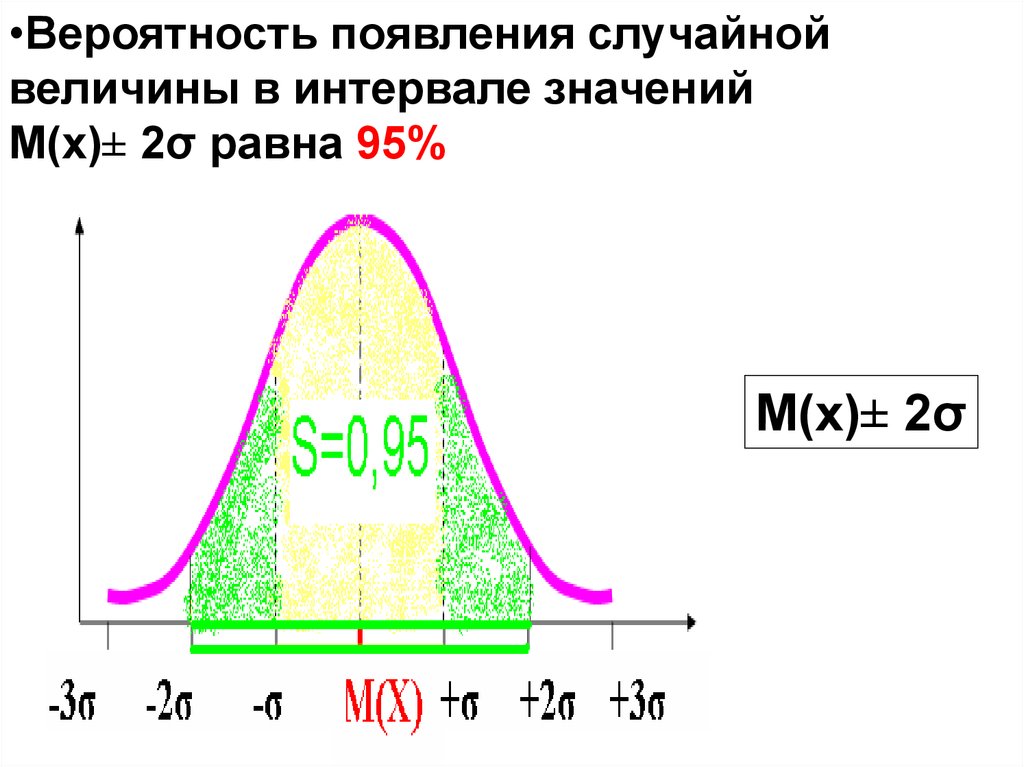
52.
•Вероятность появления случайнойвеличины в интервале значений
М(х)± 2σ равна 95%
М(х)± 2σ
53.
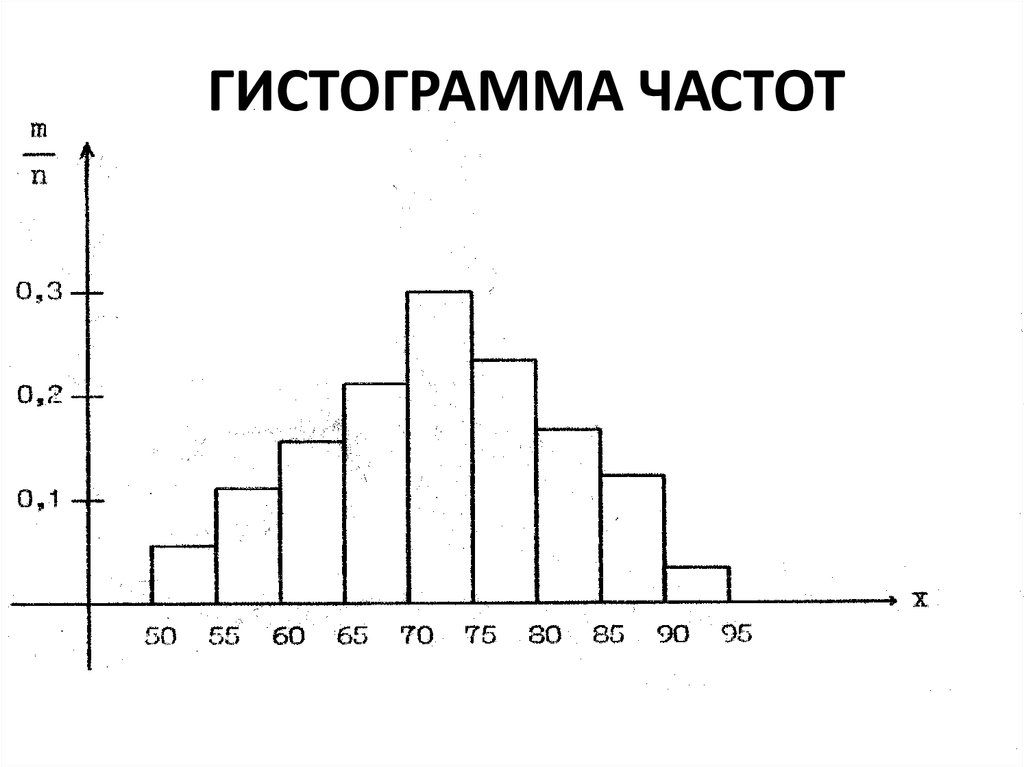
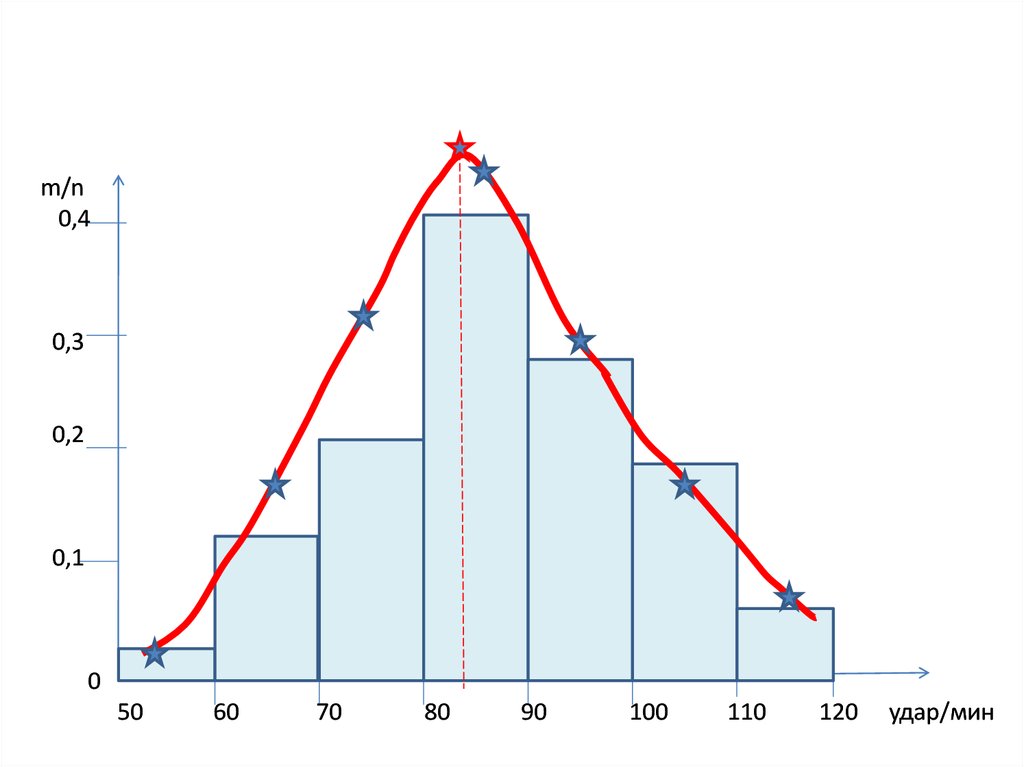
Для нормального закона распределенияхарактерен симметричный вид
гистограммы
•Гистограмма частот - совокупность
смежных прямоугольников,
построенных на одной прямой линии.
Основания прямоугольников
одинаковы.
Высоты прямоугольников равны
относительной частоте m/n
(вероятности).
54.
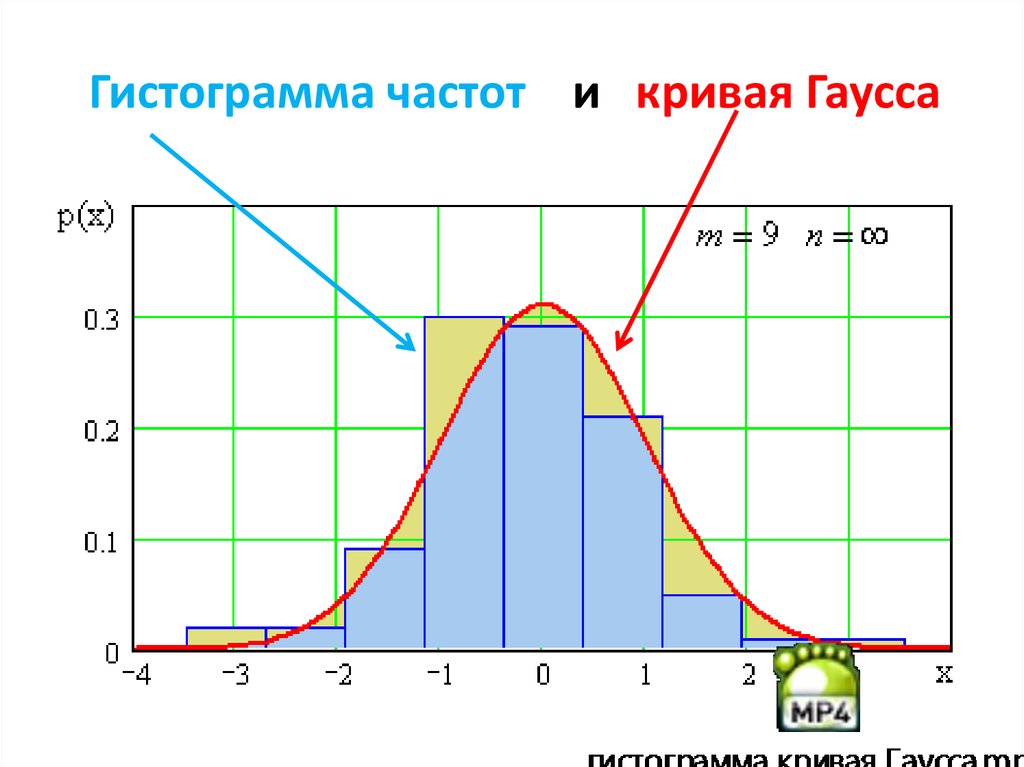
ГИСТОГРАММА ЧАСТОТ55.
m/n0,4
0,3
0,2
0,1
0
50
60
70
80
90
100
110
120
удар/мин






























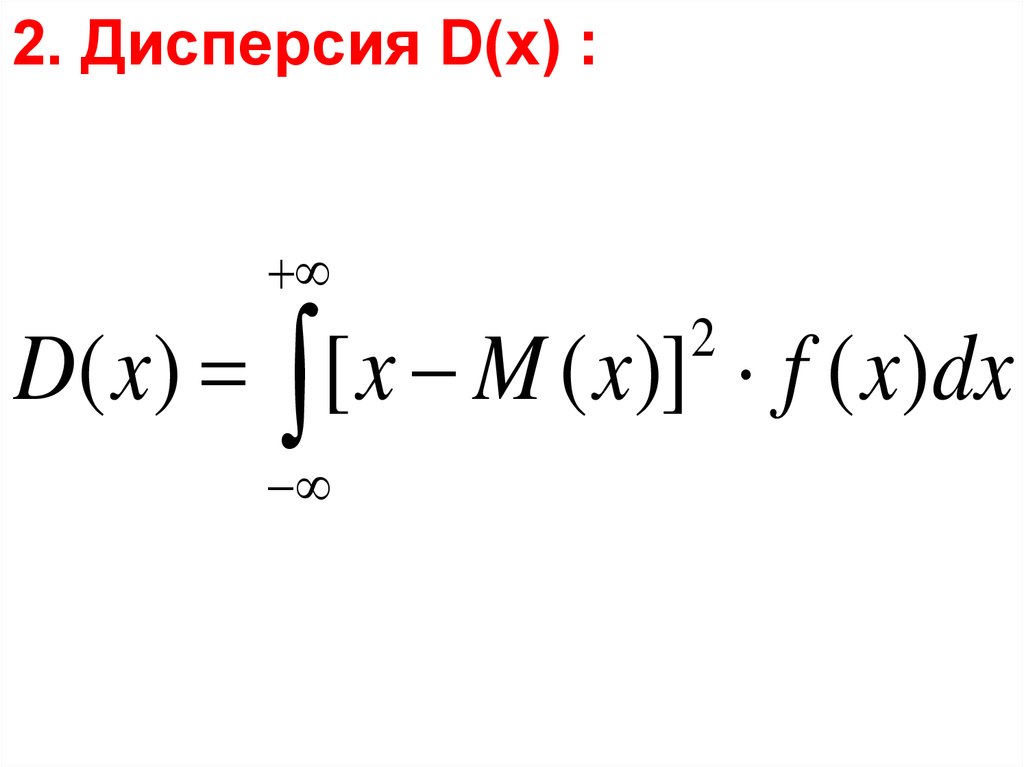



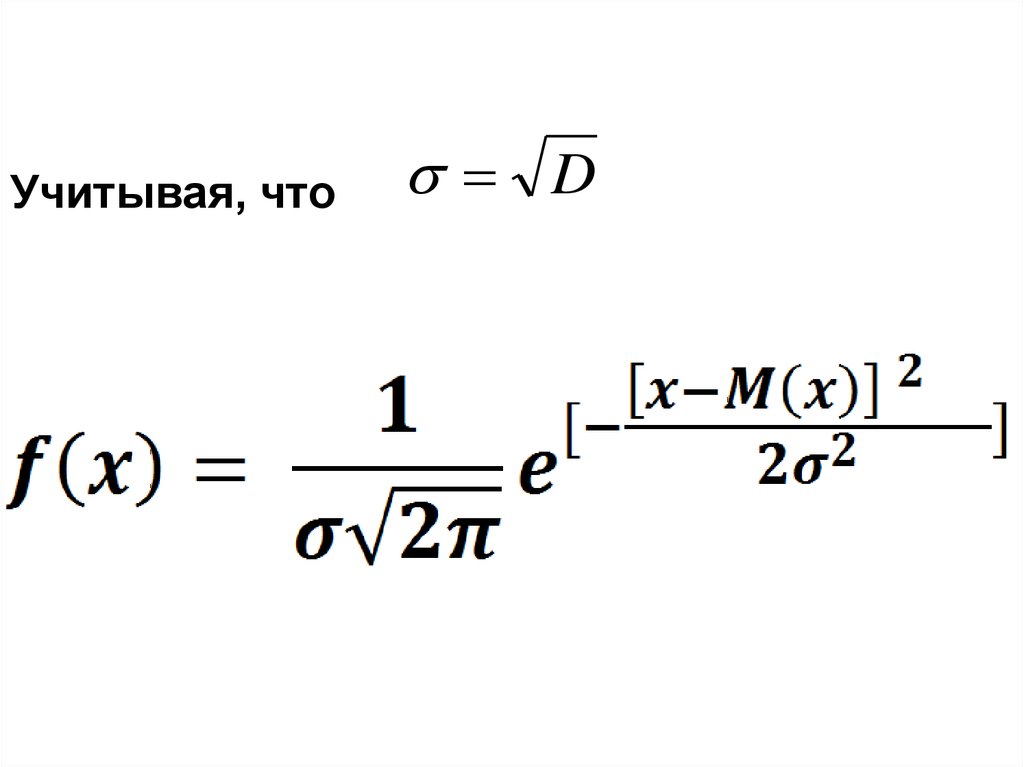
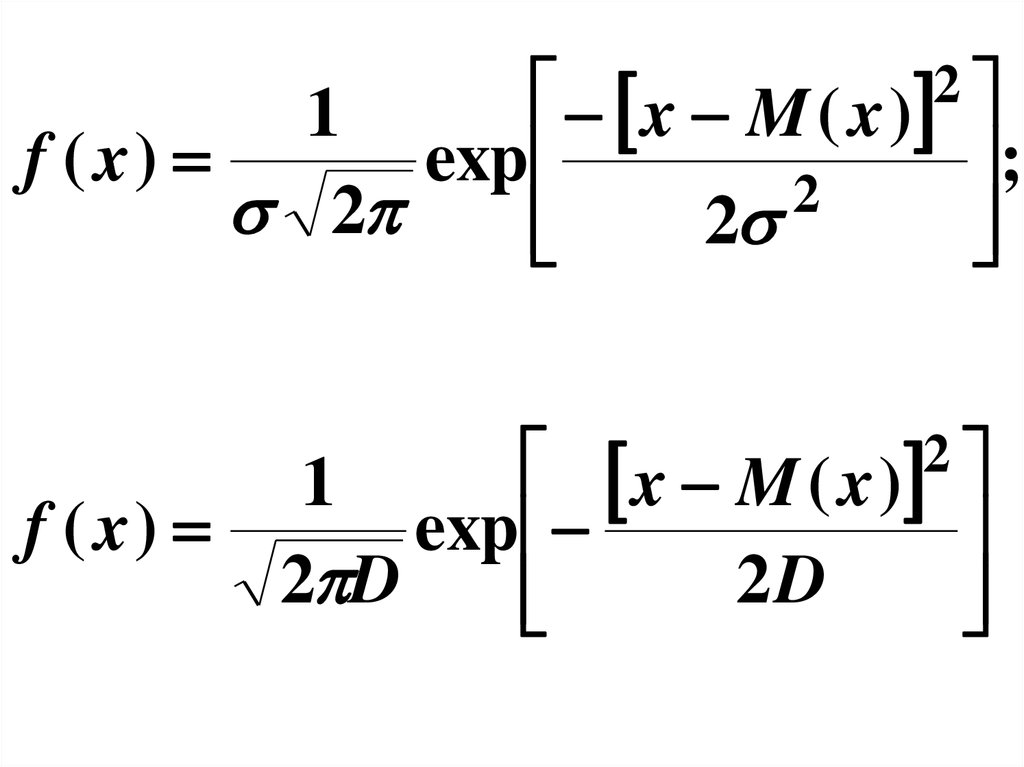

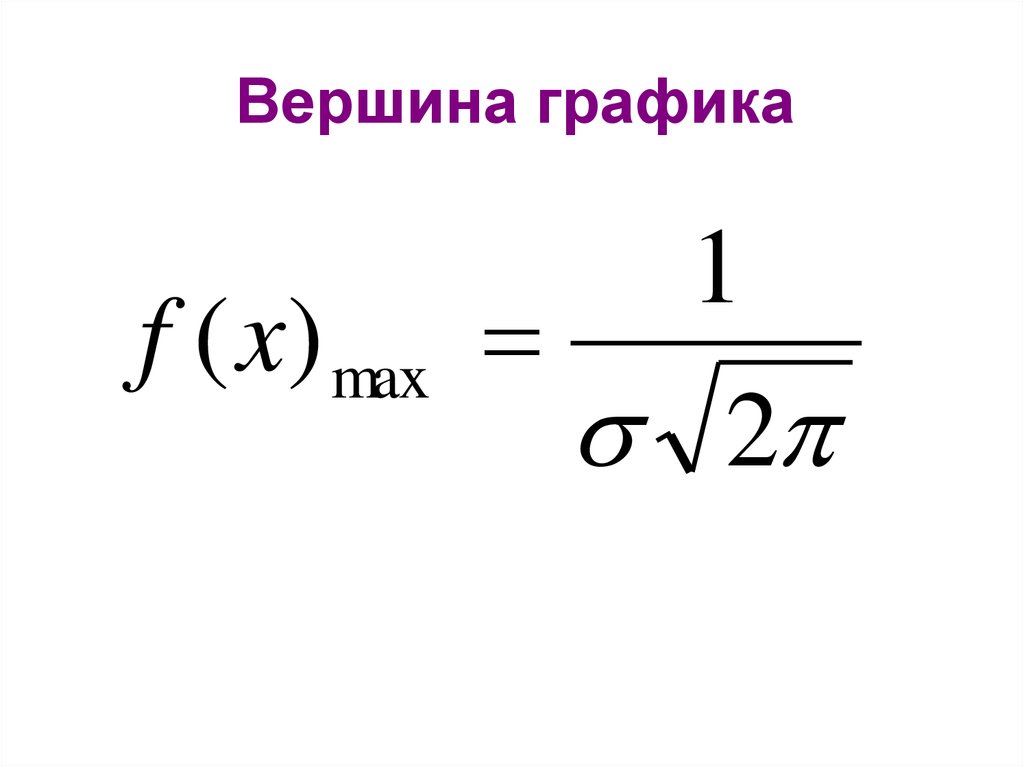




 Математика
Математика Медицина
Медицина








