Похожие презентации:
Начертательная геометрия
1. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Нижегородский государственный технический университетим. Р.Е. Алексеева
Кафедра «Инженерная графика»
И.Ю. Скобелева, И.А. Ширшова
Комплекс демонстрационных материалов
для чтения лекций по начертательной геометрии
2. Основоположники начертательной геометрии
Альберти (Alberti) Леон Баттиста(18.2.1404 - 25.4.1472)
Основатель теоретической перспективы.
Гаспар Монж (1746-1818)
Систематизировал и обобщил накопленный годами
опыт геометрических построений, систематизировал
метод проекций, ввел понятие "комплексный
чертёж".
3. Основоположники начертательной геометрии
Севастьянов Яков Александрович (1796 - 1849)Первым начал читать лекции на русском языке. Им же издан первый
на русском языке курс начертательной геометрии на русском языке.
Курдюмов Валериан Иванович (1853 - 1904)
Издал полный курс начертательной геометрии,
по обширной программе, со включением
проекций кривых линий и поверхностей и
метода аксонометрических проекций.
4. Лекция 1 Методы проецирования
Центральный метод проецированияП’ – плоскость проекций;
S – центр проекций;
[SA) и [SB) – проецирующие лучи;
A’ и B’– центральные проекции точек A и B на плоскость П’
5.
Параллельный метод проецированияП’ – плоскость проекций;
s – направление проецирования;
[SA), [SB) и [SC) – проецирующие лучи;
A’, B’ и C’ – параллельные проекции точек A, B и C на плоскость П’ в
направлении s
6. Ортогональное проецирование
Направление проецирования перпендикулярно плоскости проекцийs П ,
A B AB AB cos α
7. Ортогональное проецирование на три плоскости проекций
x12 Π1 Π 2 ;y13 Π1 Π 3 ;
z 23 Π 2 Π 3
П1- горизонтальная плоскость проекций;
П2- фронтальная плоскость проекций;
П3- профильная плоскость проекций
8. Проецирование точки на три плоскости проекций
А1- горизонтальная проекция точки А;А2- фронтальная проекция точки А;
А3- профильная проекция точки А
9. Трехкартинный комплексный чертеж точки (эпюр монжа)
z 23A 23
A2
A3
zA
x 12
A 12
xA
O123
A 31
y3
yA
A1
A 13
y1
A0
k 123
Чертеж на трех совмещенных плоскостях проекций называется
трехкартинным комплексным чертежом
10. Лекция 2 Прямая линия
Способы задания прямойДвумя точками.
Точкой и направлением.
Линией пересечения двух плоскостей.
Своими проекциями.
11. Классификация прямых
ПрямаяОбщего положения
Частного положения
Линии уровня
Горизонталь
Фронталь
Профильная
прямая
Горизонтальнопроецирующая
прямая
Проецирующие
прямые
Фронтальнопроецирующая
прямая
Профильнопроецирующая
прямая
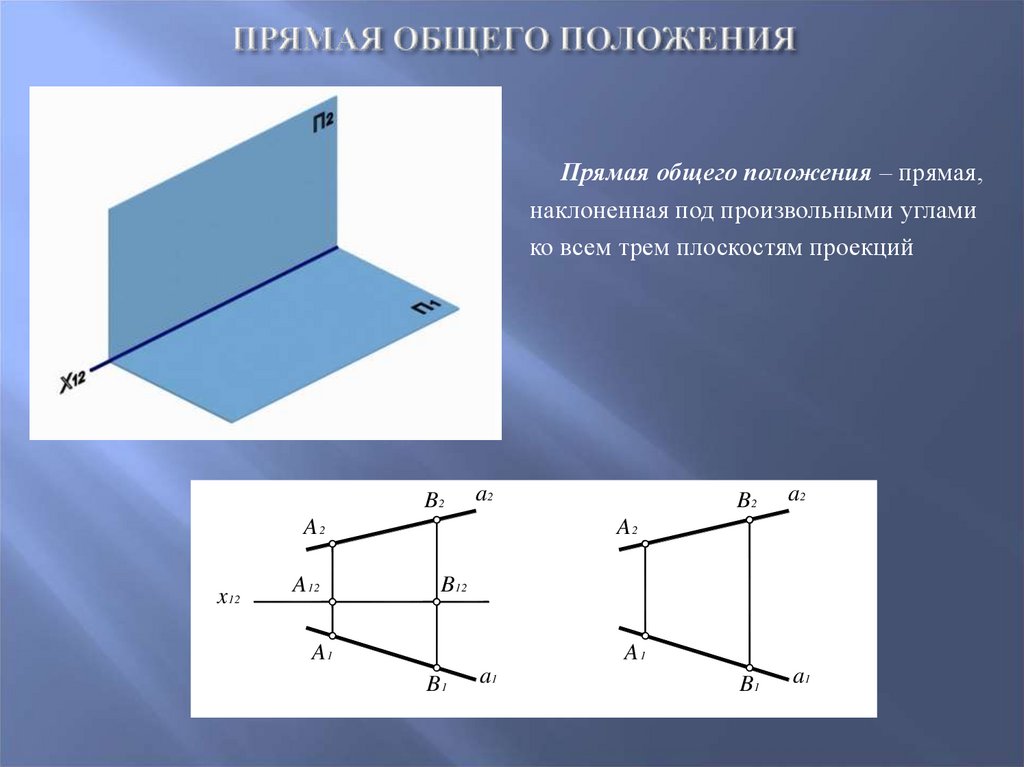
12. Прямая общего положения
– прямая,наклоненная под произвольными углами
ко всем трем плоскостям проекций
B2
a2
A2
x 12
A 12
B2
a2
B1
a1
A2
B12
A1
A1
B1
a1
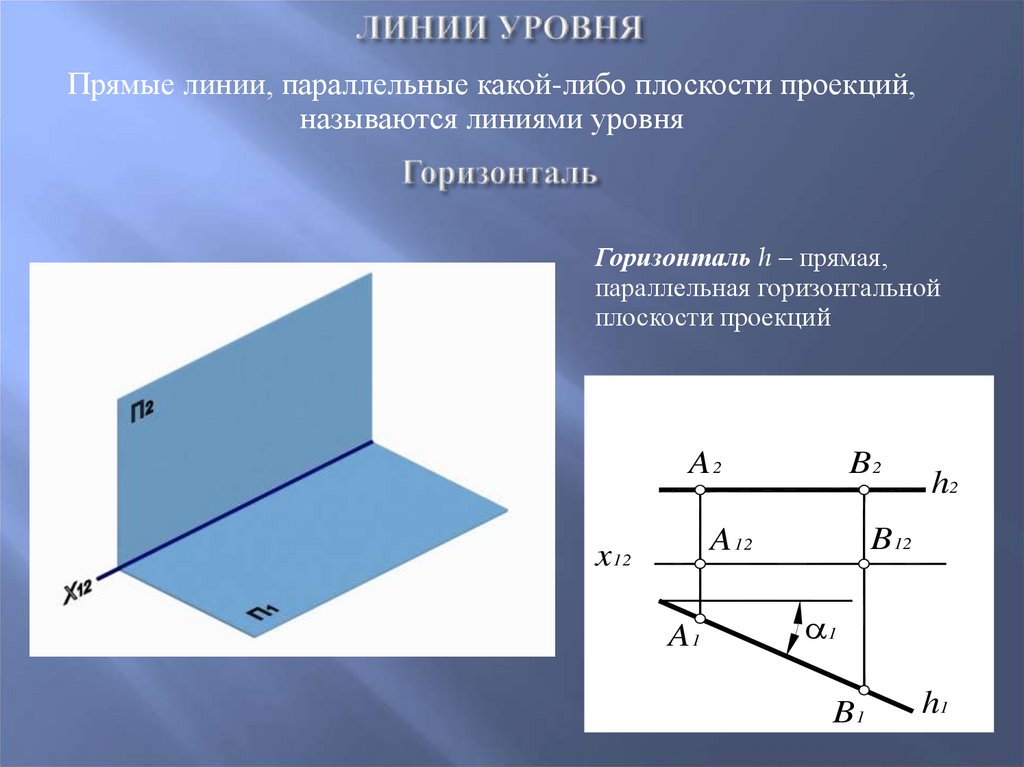
13. Линии уровня
Прямые линии, параллельные какой-либо плоскости проекций,называются линиями уровня
Горизонталь h – прямая,
параллельная горизонтальной
плоскости проекций
A2
B2
A 12
B12
x 12
A1
h2
1
B1
h1
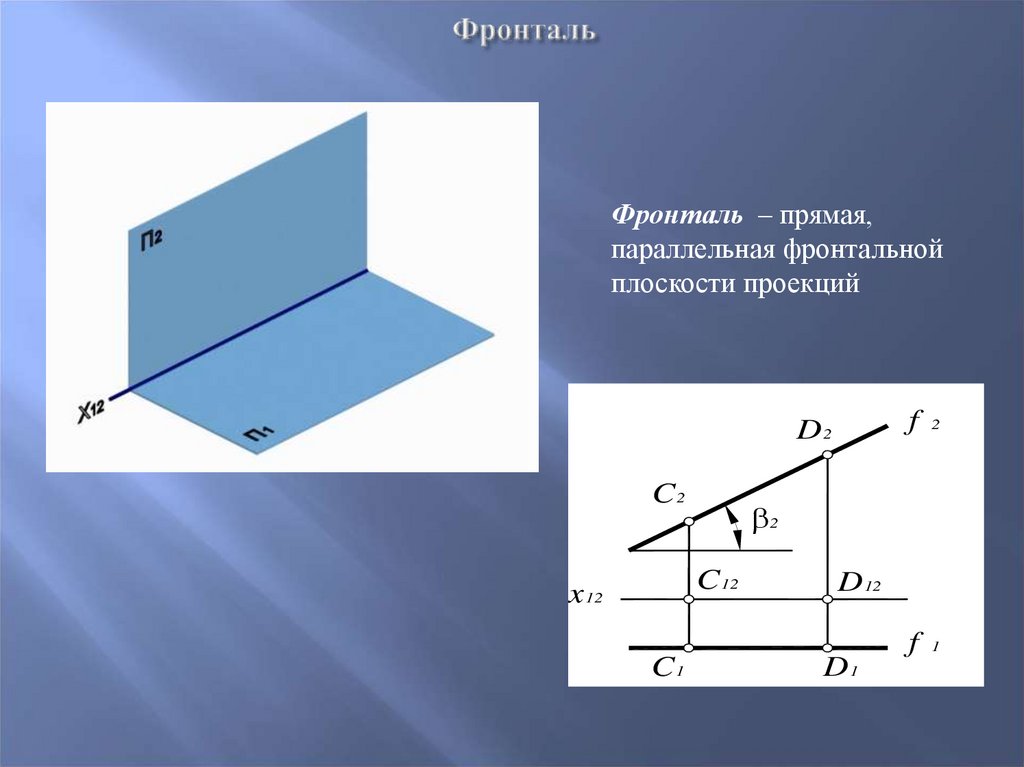
14. Фронталь
– прямая,параллельная фронтальной
плоскости проекций
f 2
D2
C2
2
C 12
x 12
C1
D 12
D1
f 1
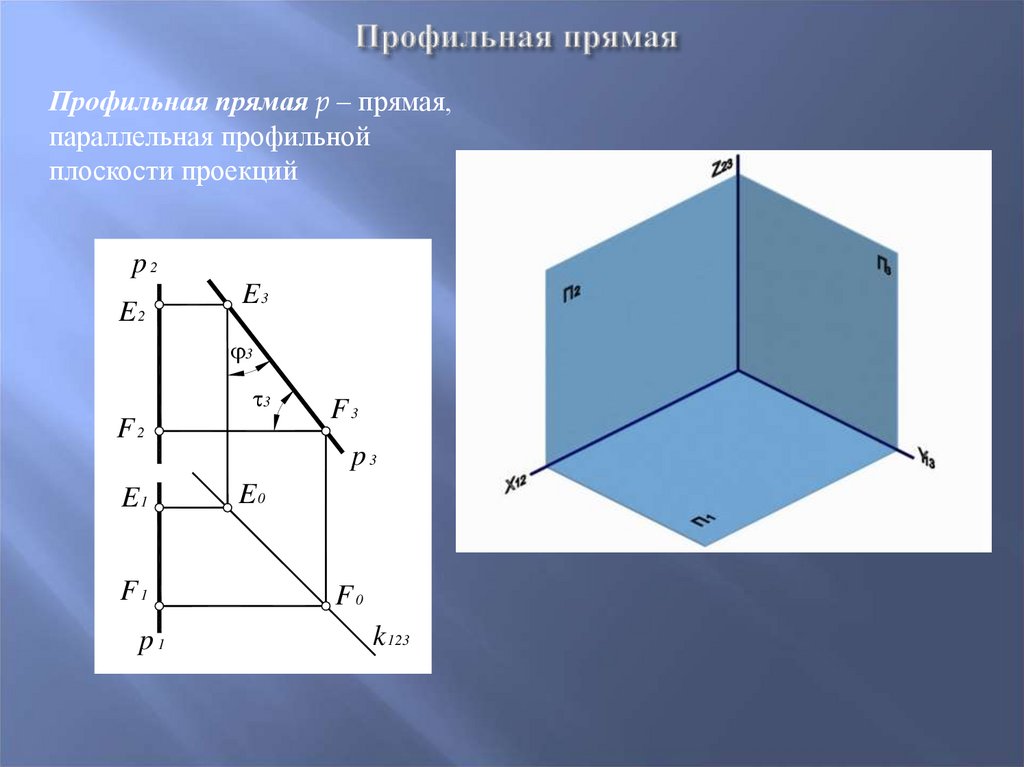
15. Профильная прямая
p – прямая,параллельная профильной
плоскости проекций
p2
E2
E3
3
3
F2
F3
p3
E1
F1
p1
E0
F0
k 123
16. Проецирующие прямые
Прямые линии, перпендикулярные какой-либо плоскости проекций,называются проецирующими
Горизонтально-проецирующая прямая – прямая, перпендикулярная
горизонтальной плоскости проекций
a2
x 12
a1
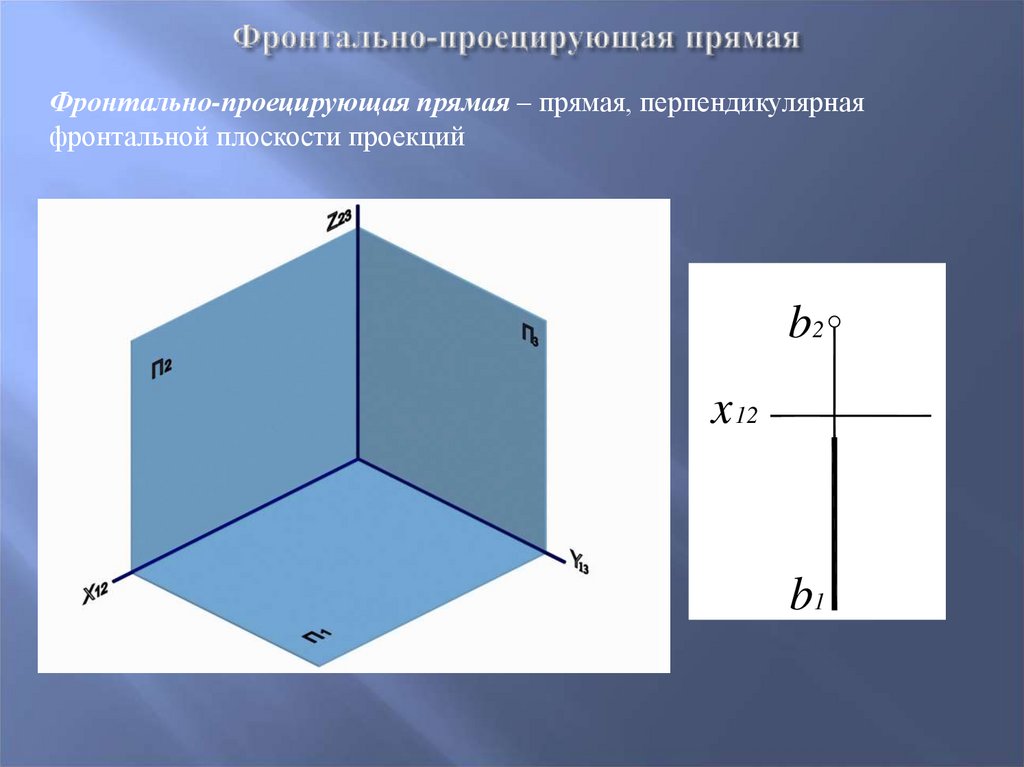
17. Фронтально-проецирующая прямая
– прямая, перпендикулярнаяфронтальной плоскости проекций
b2
x 12
b1
18. Профильно-проецирующая прямая
– прямая, перпендикулярнаяпрофильной плоскости проекций
c2
c3
c1
k 123
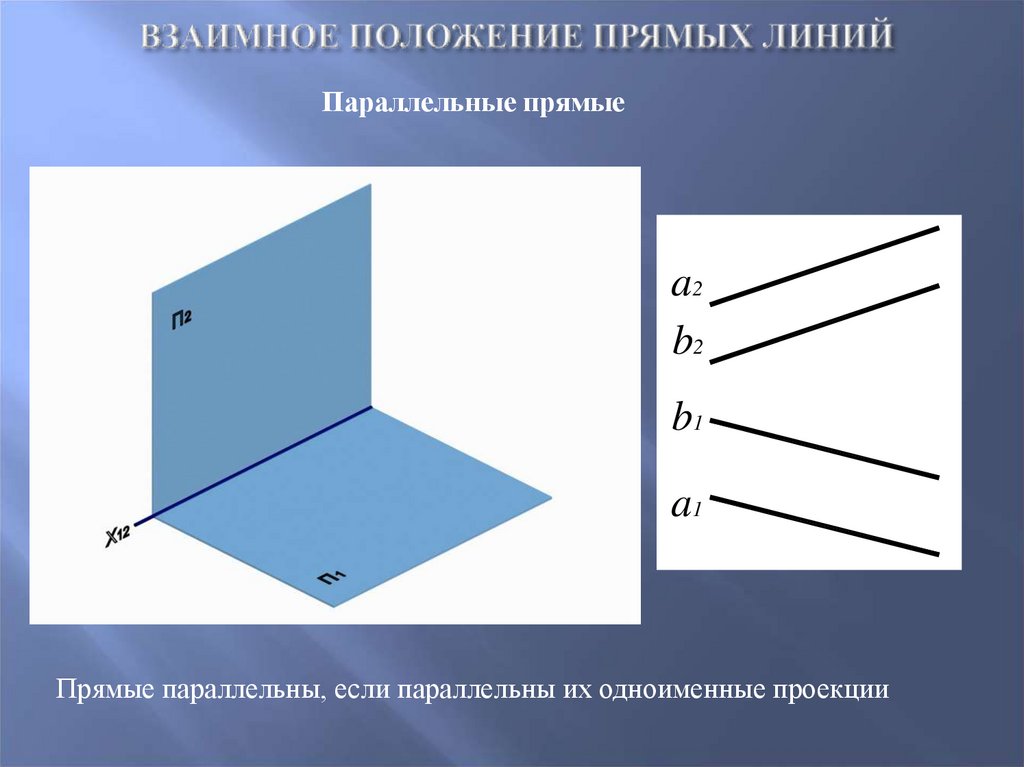
19. Взаимное положение прямых линий
Параллельные прямыеa2
b2
b1
a1
Прямые параллельны, если параллельны их одноименные проекции
20.
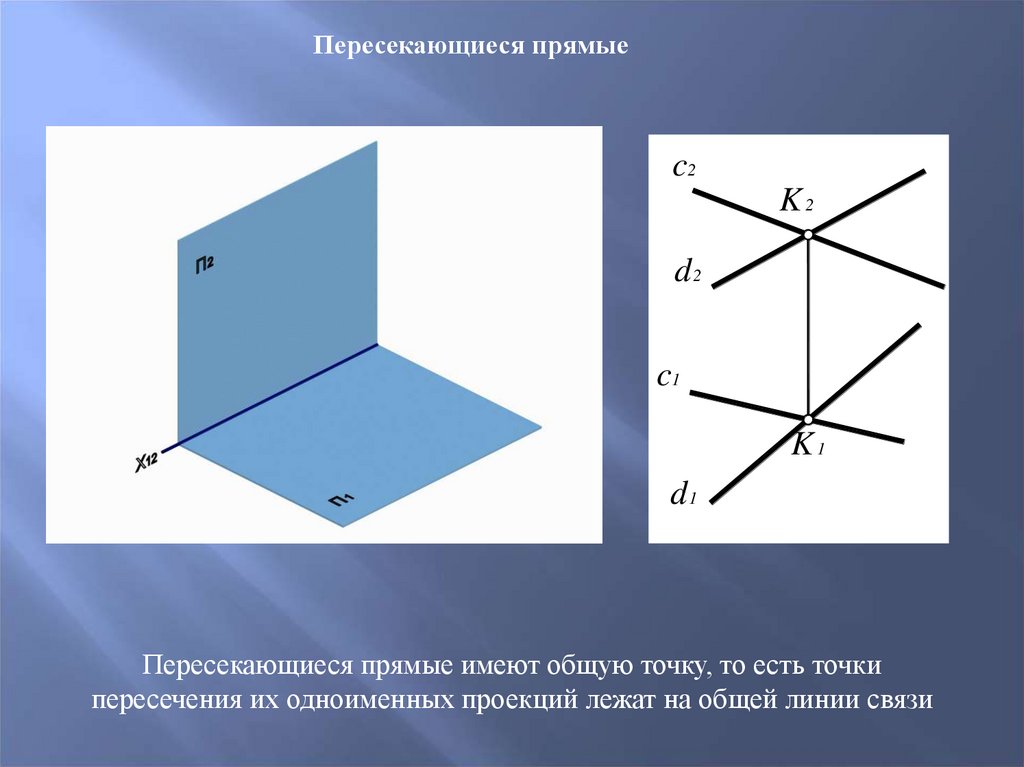
Пересекающиеся прямыеc2
K2
d2
c1
K1
d1
Пересекающиеся прямые имеют общую точку, то есть точки
пересечения их одноименных проекций лежат на общей линии связи
21.
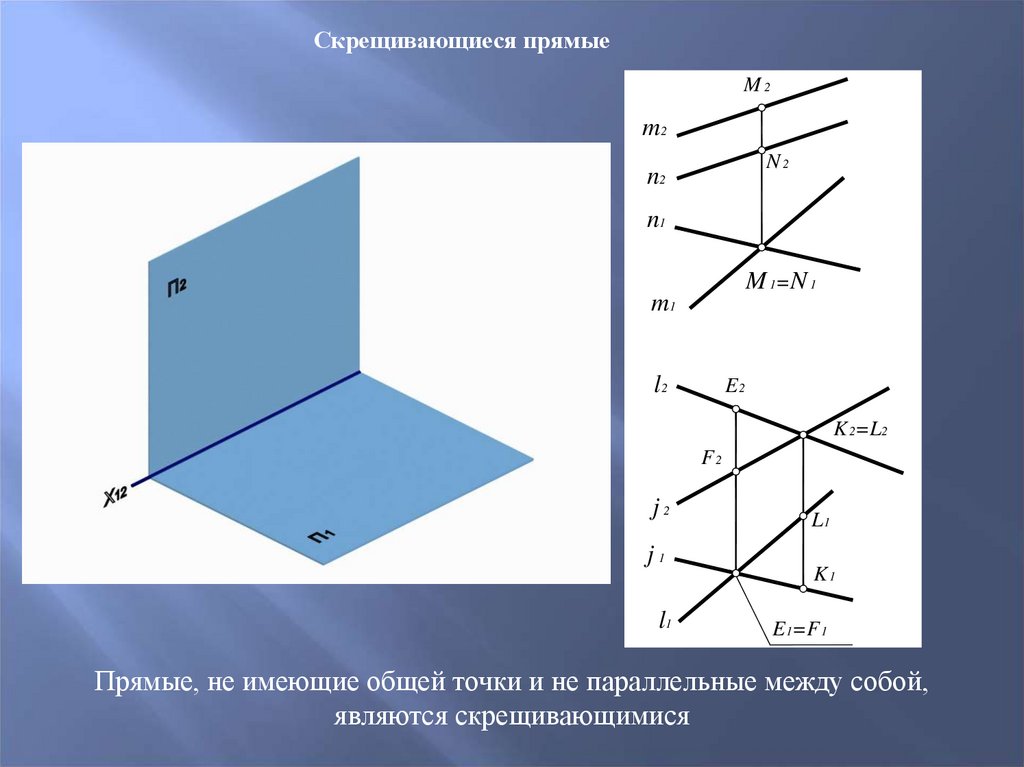
Скрещивающиеся прямыеM2
m2
N2
n2
n1
M 1= N 1
m1
l2
E2
K 2=L2
F2
j2
j1
l1
L1
K1
E 1=F 1
Прямые, не имеющие общей точки и не параллельные между собой,
являются скрещивающимися
22. Принадлежность точки прямой линии
K2a2
K a K1 a1 и K 2 a2
x 12
K K x
K 12
1
2
12
K1
a1
Точка принадлежит прямой, если ее проекции принадлежат
соответствующим (одноименным) проекциям прямой
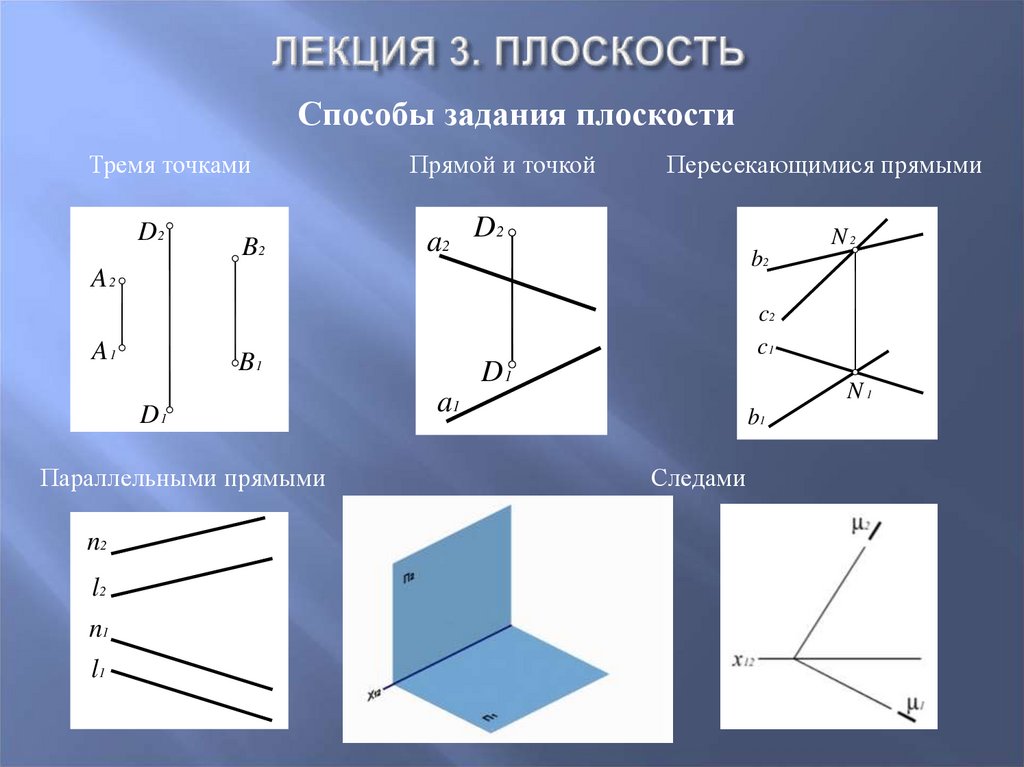
23. Лекция 3. Плоскость
A1c2
c1
B1
N1
D1
Способы задания
плоскости
Тремя точками
b2A 2
D2
N2
cA
2
1
c1
B2
B1
D1
N1
b1
Параллельными прямыми
D2
na2 2
l2
n1
l1a1
Прямой и точкой
b2
c2
c1
a2 N 2D 2
D2
Пересекающимися прямыми
B2
n2
N2
b2
A2
l2
A1
n1
D1
B1
D1
a1 N 1
c2
c1
l1
N1
b1
b1
a2
D2
Следами n2
n2
l2
l2
n1
n1
D1
b1
l1
D1
a1
l1
24. Классификация плоскостей
ПлоскостьОбщего положения
Частного положения
Плоскости уровня
Горизонтальная
плоскость
уровня
Фронтальная
плоскость
уровня
Профильная
плоскость
уровня
Горизонтальнопроецирующая
плоскость
Проецирующие
плоскости
Фронтальнопроецирующая
плоскость
Профильнопроецирующая
плоскость
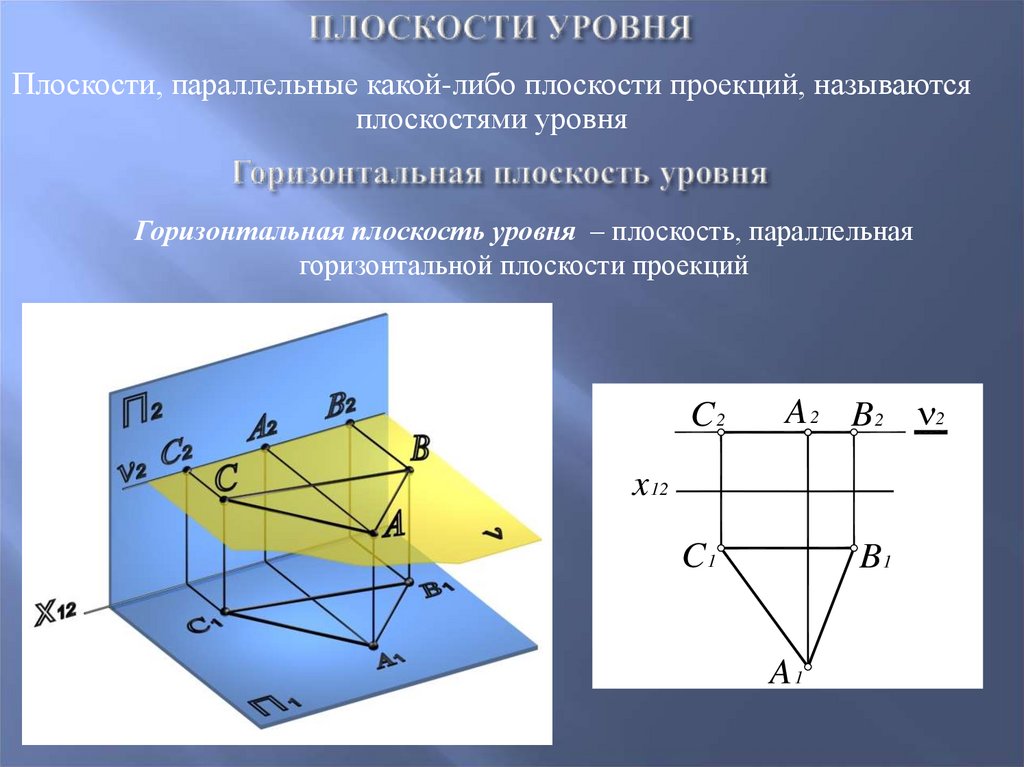
25. Плоскости уровня
Плоскости, параллельные какой-либо плоскости проекций, называютсяплоскостями уровня
Горизонтальная плоскость уровня – плоскость, параллельная
горизонтальной плоскости проекций
C2
A 2 B 2 2
C1
B1
x 12
A1
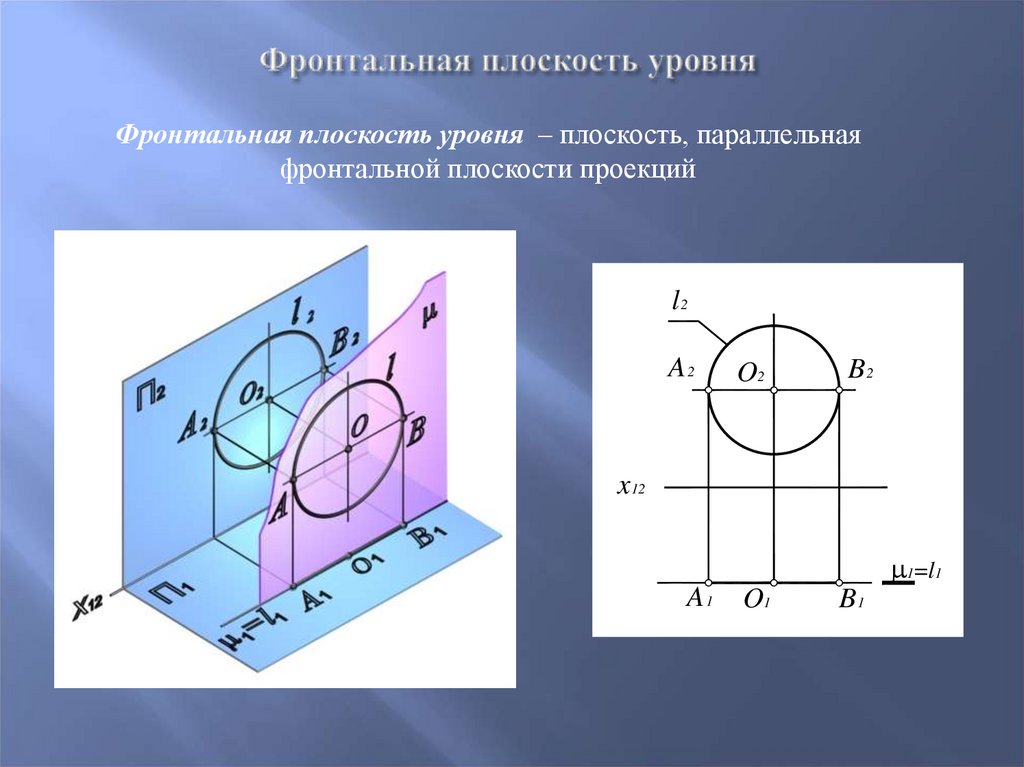
26.
Фронтальная плоскость уровня – плоскость, параллельнаяфронтальной плоскости проекций
l2
A2
O2
B2
x 12
1=l1
A1
O1
B1
27.
Профильная плоскость уровня – плоскость, параллельнаяпрофильной плоскости проекций
A2
A3
B2
B3
B1
A1
1
k 123
28. Проецирующие плоскости
Плоскости, перпендикулярные какой-либо плоскости проекций,называются проецирующими
Горизонтально-проецирующая плоскость – плоскость, перпендикулярная
горизонтальной плоскости проекций
B2
A2
x12
A1
1
1
B1
1
29.
Фронтально-проецирующая плоскость – плоскость, перпендикулярнаяфронтальной плоскости проекций
2=m2
x 12
m1
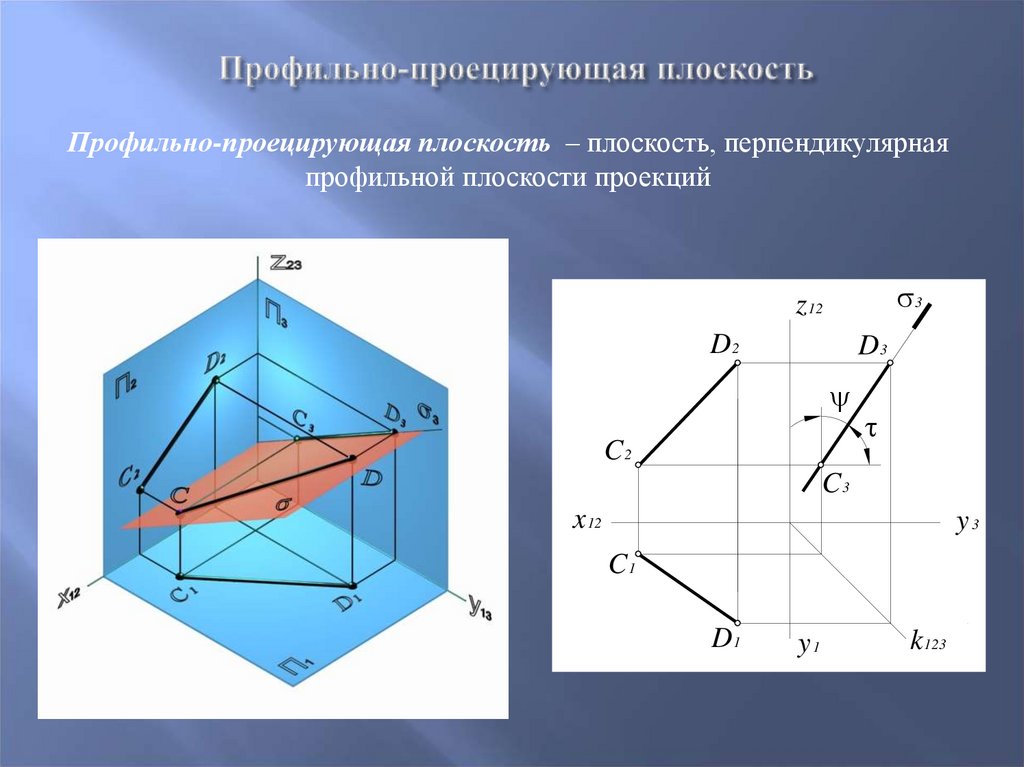
30.
Профильно-проецирующая плоскость – плоскость, перпендикулярнаяпрофильной плоскости проекций
3
z 12
D2
D3
C2
C3
x 12
y3
C1
D1
y1
k 123
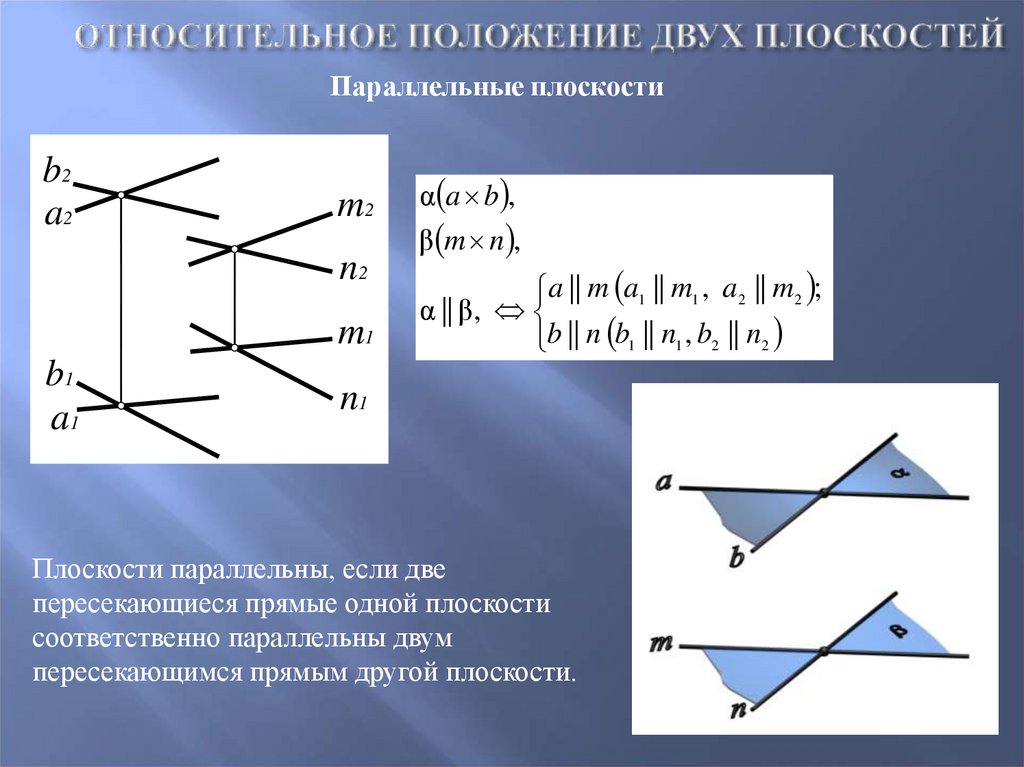
31. Относительное положение двух плоскостей
Параллельные плоскостиb2
a2
m2
n2
m1
b1
a1
α a b ,
β m n ,
a || m a1 || m1 , a2 || m2 ;
α || β,
b || n b1 || n1 , b2 || n2
n1
Плоскости параллельны, если две
пересекающиеся прямые одной плоскости
соответственно параллельны двум
пересекающимся прямым другой плоскости.
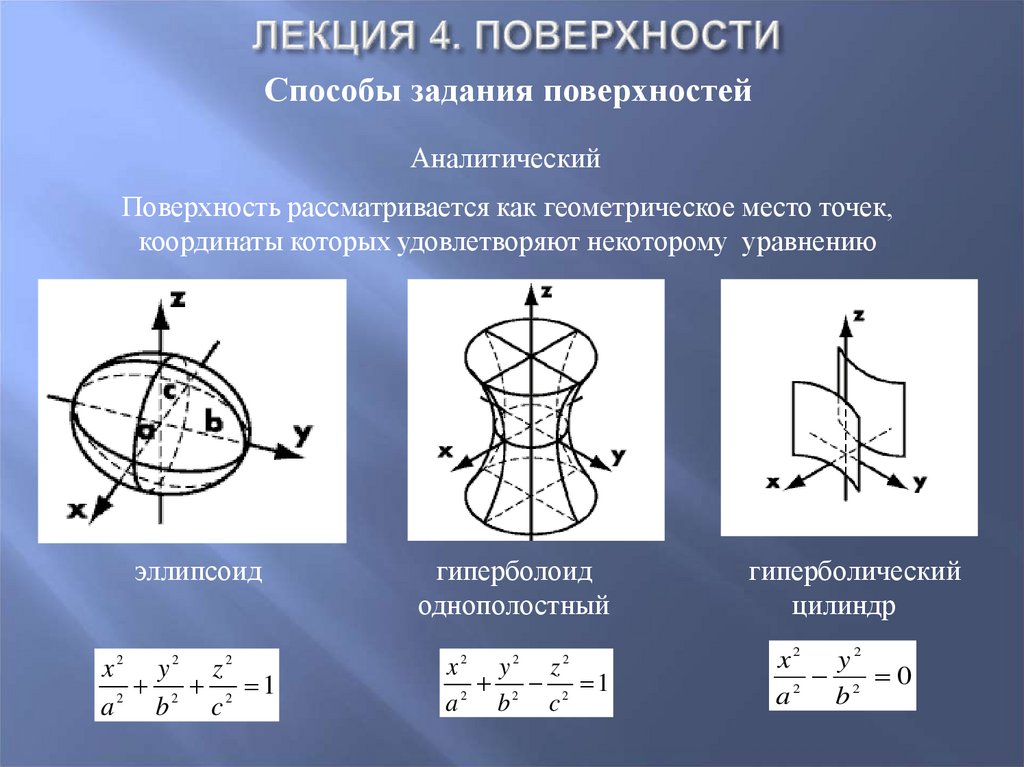
32. Лекция 4. Поверхности
Способы задания поверхностейАналитический
Поверхность рассматривается как геометрическое место точек,
координаты которых удовлетворяют некоторому уравнению
эллипсоид
гиперболоид
однополостный
гиперболический
цилиндр
x2 y2 z2
2 2 1
2
a
b
c
x2 y2 z2
1
a2 b2 c2
x2 y2
0
a2 b2
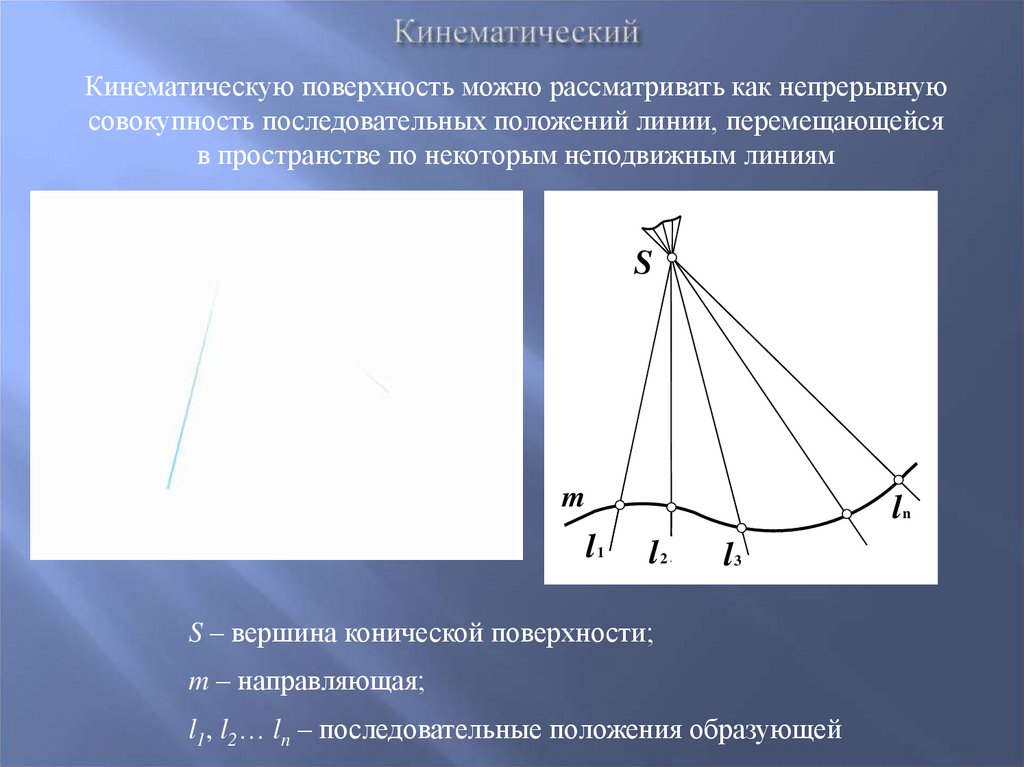
33. Кинематический
Кинематическую поверхность можно рассматривать как непрерывнуюсовокупность последовательных положений линии, перемещающейся
в пространстве по некоторым неподвижным линиям
S
m
ln
l1
l2
l3
S – вершина конической поверхности;
m – направляющая;
l1, l2… ln – последовательные положения образующей
34. Каркасный
Такие поверхности обычно задают достаточно плотной сетью линий иточек, принадлежащих этим поверхностям. Совокупность таких линий
называется каркасом поверхности. При этом точки, лежащие между
линиями каркаса, определяются приближенно
35. Классификация поверхностей
По способу задания• аналитические;
• кинематические;
• скульптурные
По закону движения образующей
• с поступательным движением образующей;
• с вращательным движением образующей;
• с винтовым движением образующей
По виду образующей
• поверхности с прямолинейной образующей или линейчатые поверхности;
• поверхности с криволинейной образующей
По закону изменения формы образующей
• поверхности с образующей постоянного вида;
• поверхности с образующей переменного вида
По признаку развертывания
• развертывающиеся поверхности – можно совместить с плоскостью без
разрывов и складок;
• неразвертывающиеся – нельзя совместить с плоскостью без разрывов и
складок
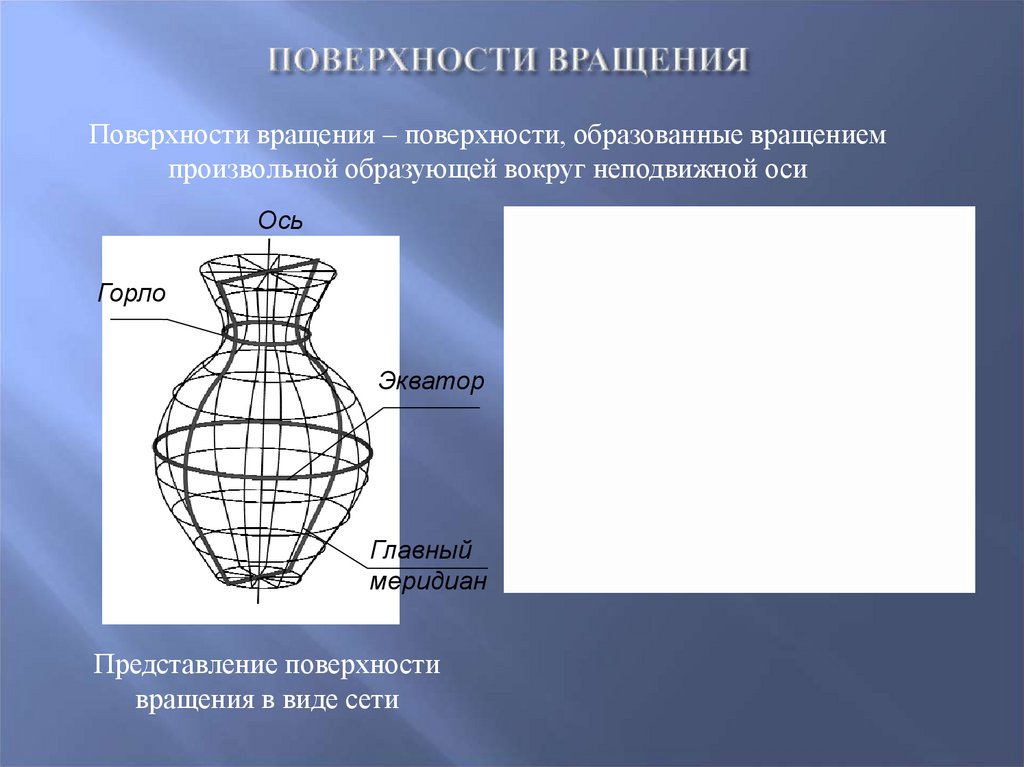
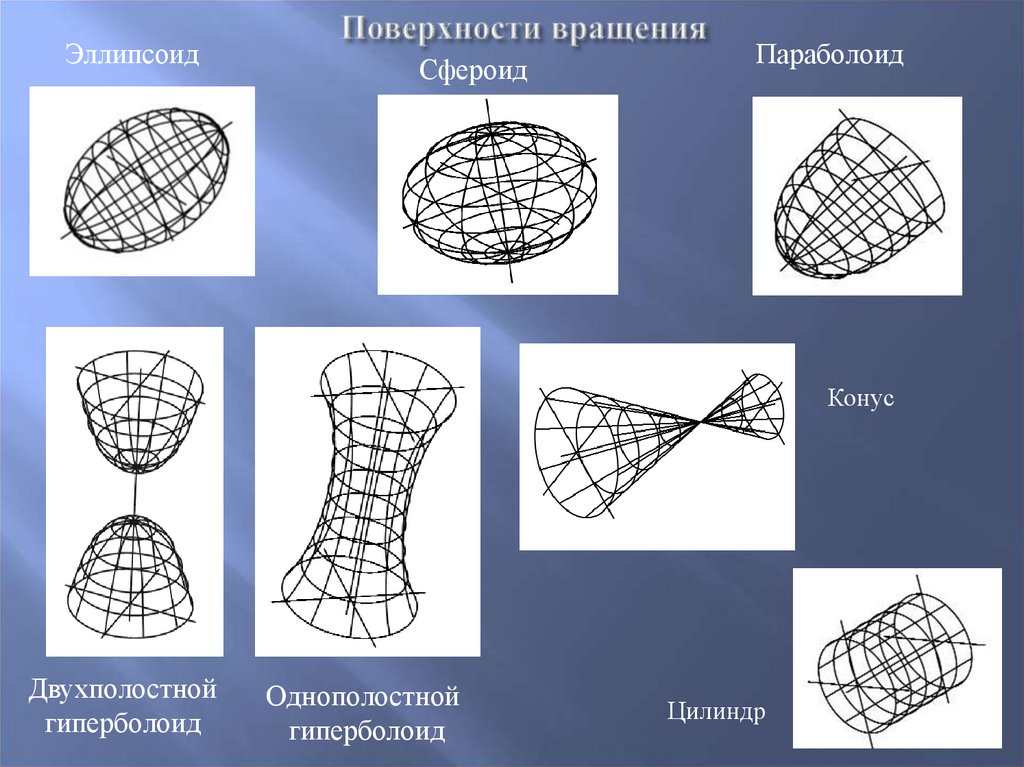
36.
Поверхности вращения – поверхности, образованные вращениемпроизвольной образующей вокруг неподвижной оси
Ось
Горло
Экватор
Главный
меридиан
Представление поверхности
вращения в виде сети
37.
Торовые поверхности – поверхности, образованные вращениемокружности или дуги окружности
Сфера
Открытый тор
Закрытый тор
Глобоид
38.
ЭллипсоидСфероид
Параболоид
Конус
Двухполостной
гиперболоид
Однополостной
гиперболоид
Цилиндр
39.
На комплексном чертеже изображается очерк поверхности, а такженаиболее важные линии и точки на поверхности
Точки касания поверхности и проецирующих лучей образуют линию l,
называемую контурной линией. Совокупность проецирующих лучей
образует проецирующую цилиндрическую поверхность, проекция которой и
представляет собой очерк l′ данной поверхности.
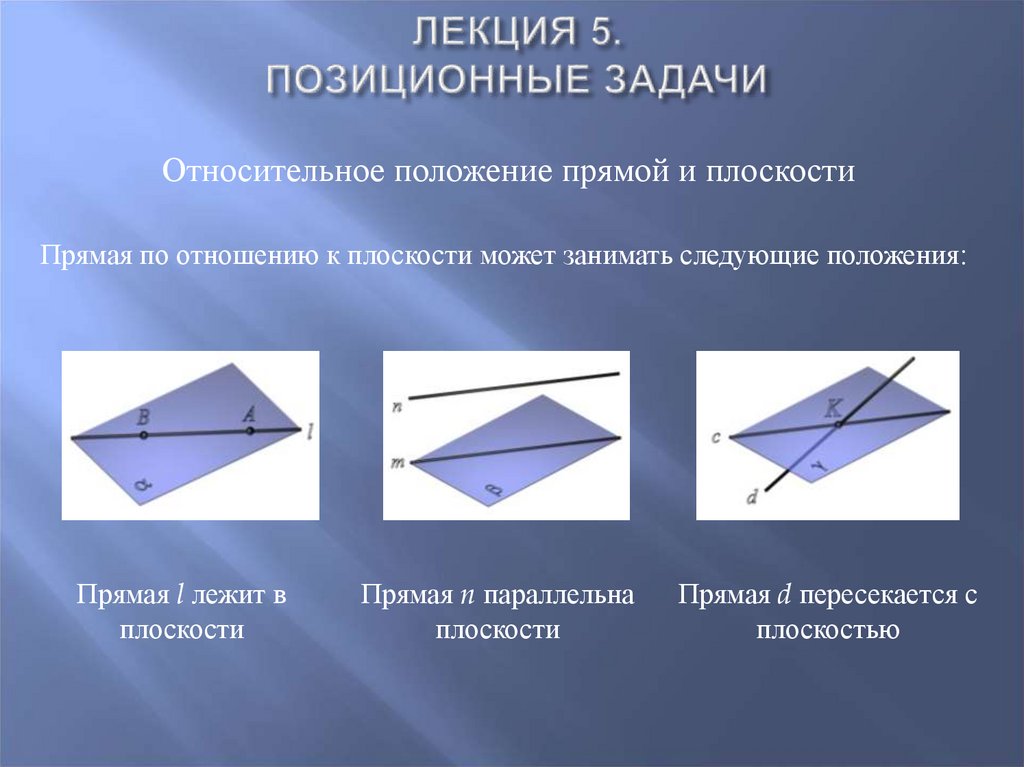
40. Лекция 5. Позиционные задачи
Относительное положение прямой и плоскостиПрямая по отношению к плоскости может занимать следующие положения:
Прямая l лежит в
плоскости
Прямая n параллельна
плоскости
Прямая d пересекается с
плоскостью
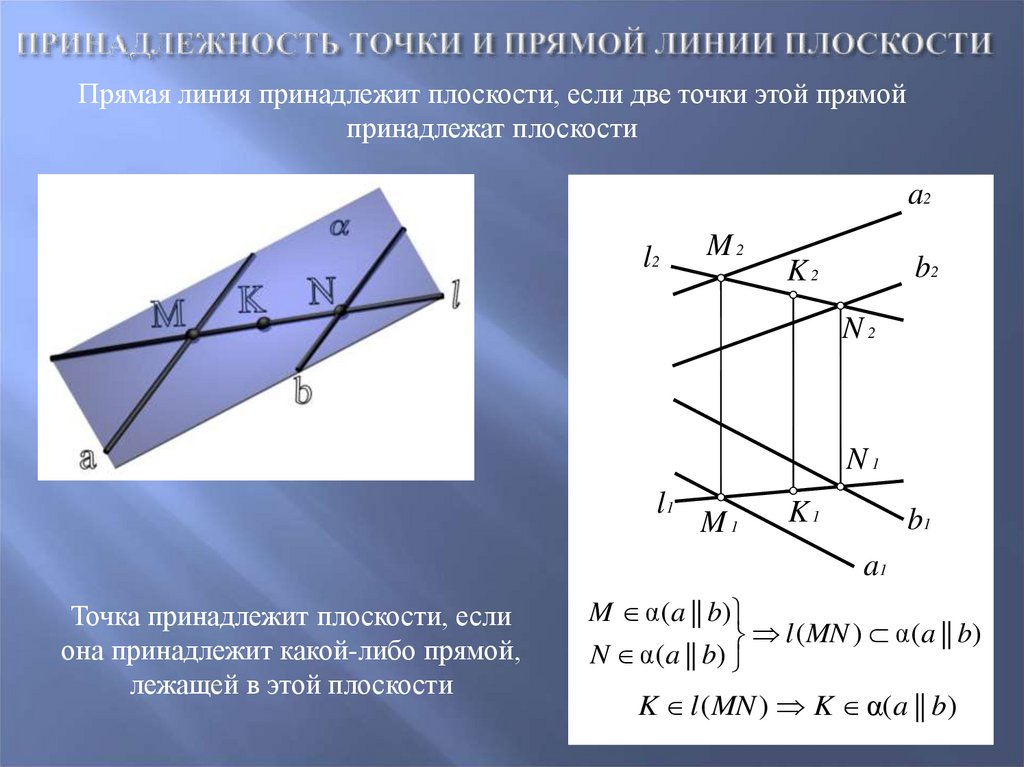
41. Принадлежность точки и прямой линии плоскости
Прямая линия принадлежит плоскости, если две точки этой прямойпринадлежат плоскости
a2
l2
M2
b2
K2
N2
N1
l1
M1
K1
b1
a1
Точка принадлежит плоскости, если
она принадлежит какой-либо прямой,
лежащей в этой плоскости
M α(a || b)
l ( MN ) α(a || b)
N α(a || b)
K l ( MN ) K α(a || b)
42. Параллельность прямой и плоскости
Прямая параллельна плоскости, если она параллельна какой–либо прямой,лежащей в этой плоскости
a2
1 b 1 α(a b)
m α ( a b)
2 a 2 α(a b)
b2
22
n2
12
m2
n1
21
m 1 11
b1
n1 || m1
n || m
n || α(a b)
n2 || m2
43. Линии уровня плоскости
;Прямые, лежащие в данной плоскости и параллельные одной из плоскостей
;
проекций, называются линиями уровня плоскости.
;
;
;
;
;
Прямая, лежащая в данной плоскости и параллельная горизонтальной
плоскости проекций П1, называется горизонталью плоскости.
Все горизонтали плоскости параллельны между собой.
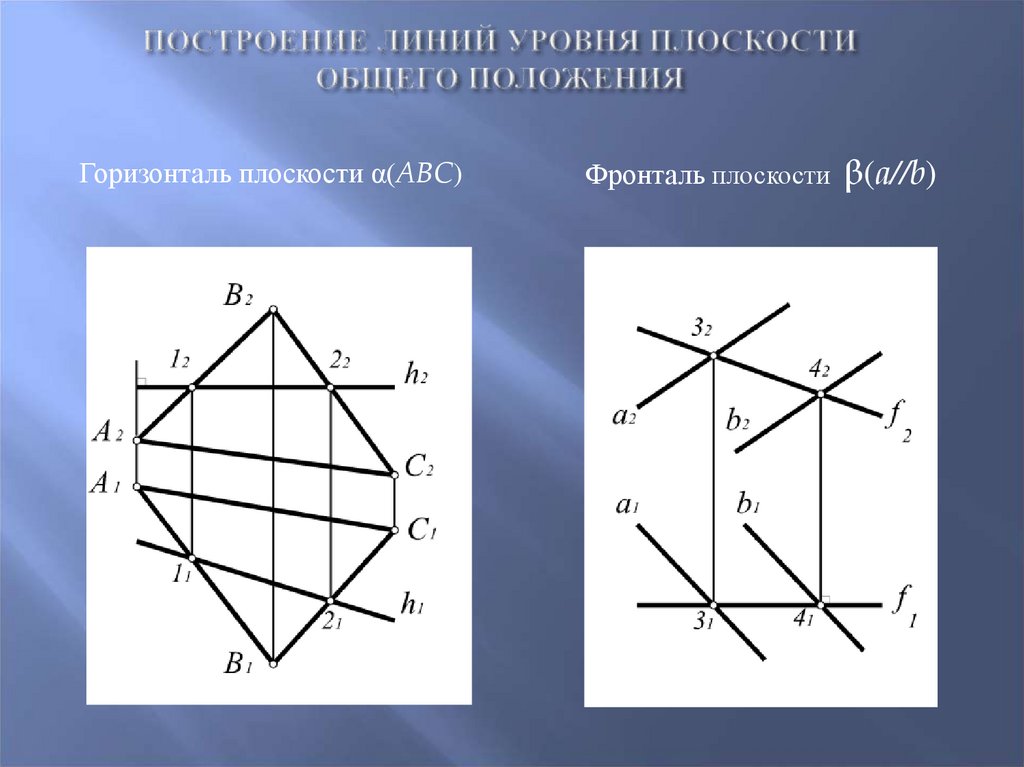
44. Построение линий уровня плоскости общего положения
Горизонталь плоскости α(ABC)Фронталь плоскости β(a//b)
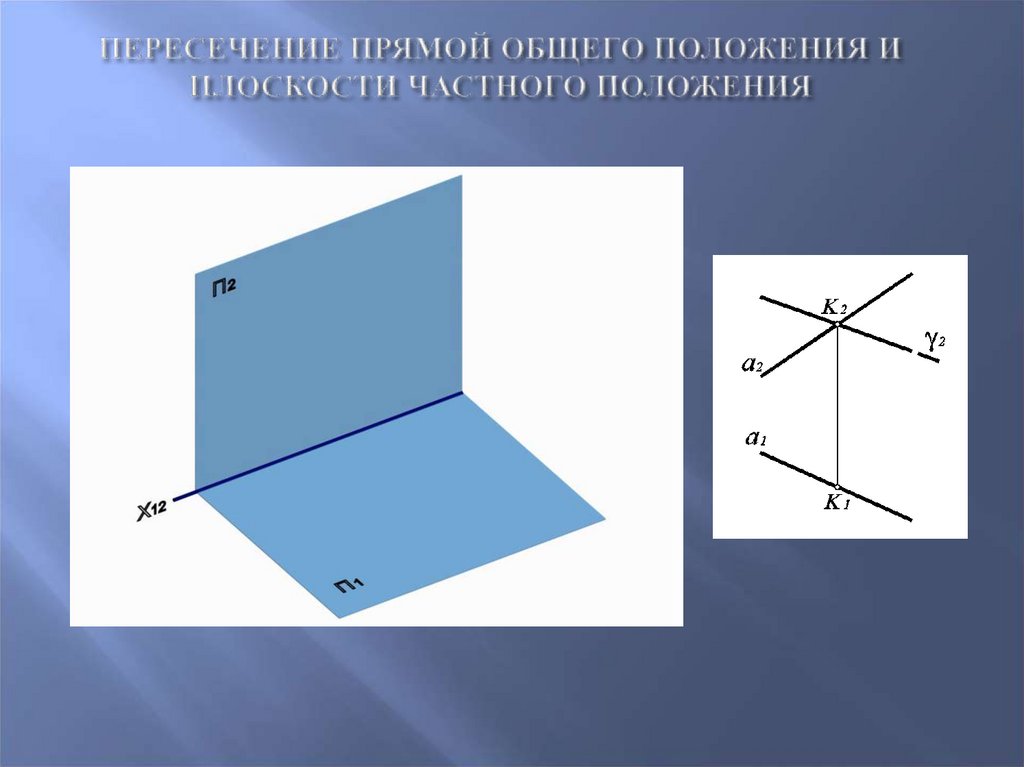
45. Пересечение прямой общего положения и плоскости частного положения
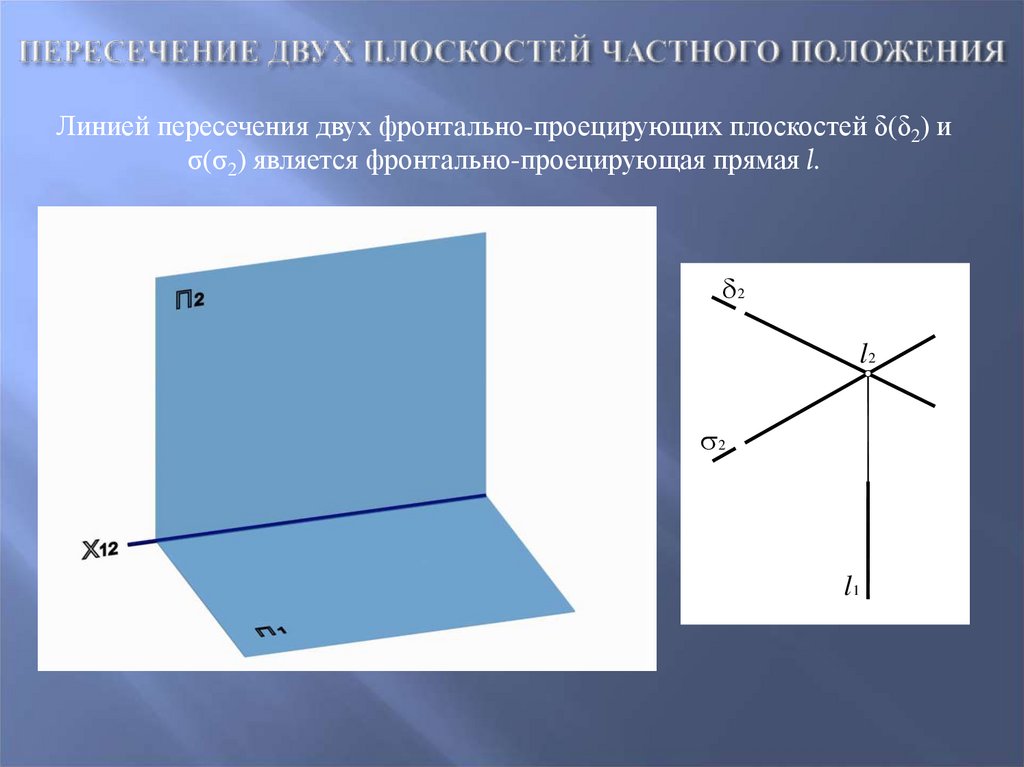
46. Пересечение двух плоскостей частного положения
Линией пересечения двух фронтально-проецирующих плоскостей δ(δ2) иσ(σ2) является фронтально-проецирующая прямая l.
2
l2
2
l1
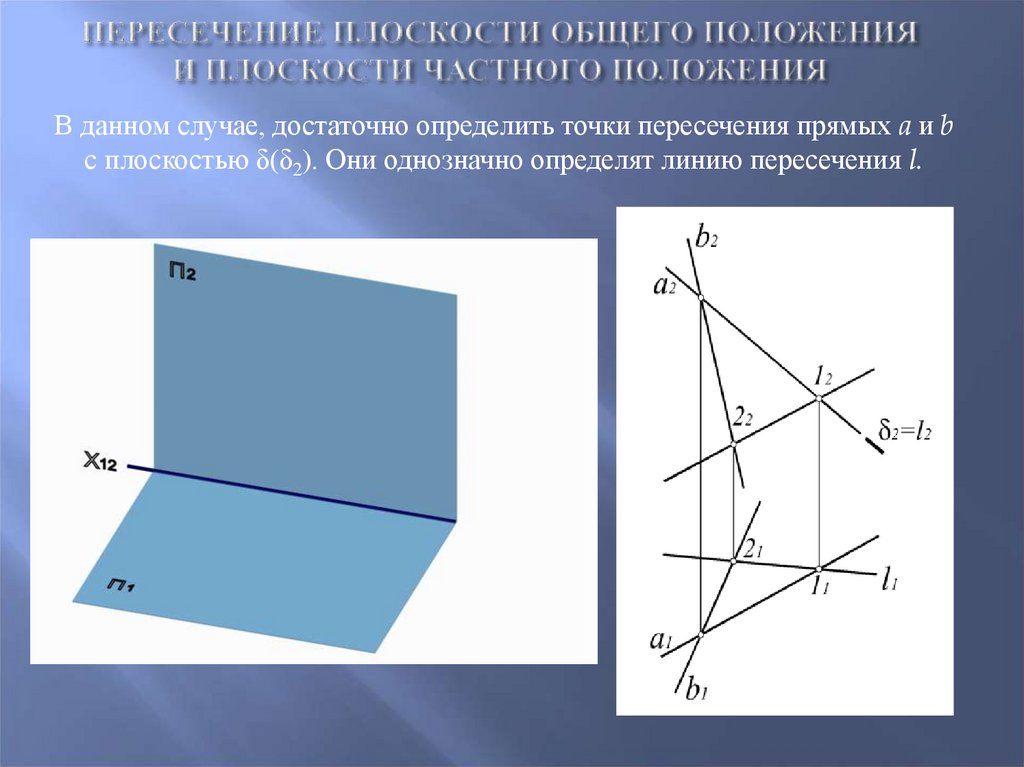
47. Пересечение плоскости общего положения и плоскости частного положения
В данном случае, достаточно определить точки пересечения прямых a и bс плоскостью δ(δ2). Они однозначно определят линию пересечения l.
48. Пересечение плоскости общего положения и прямой общего положения. Первая позиционная задача
Дано:α(ABC) – плоскость общего положения;
a(a1,a2) – прямая общего положения.
Определить:
K=a×α(ABC).
Решение:
1. Прямую заключить во вспомогательную плоскость частного
положения: a β.
2. Определить линию l как линию пересечения вспомогательной и
заданной плоскостей l=α(ABC) β.
3. Определить точку пересечения K=a l , которая является искомой
точкой пересечения прямой а с плоскостью α(ABC).
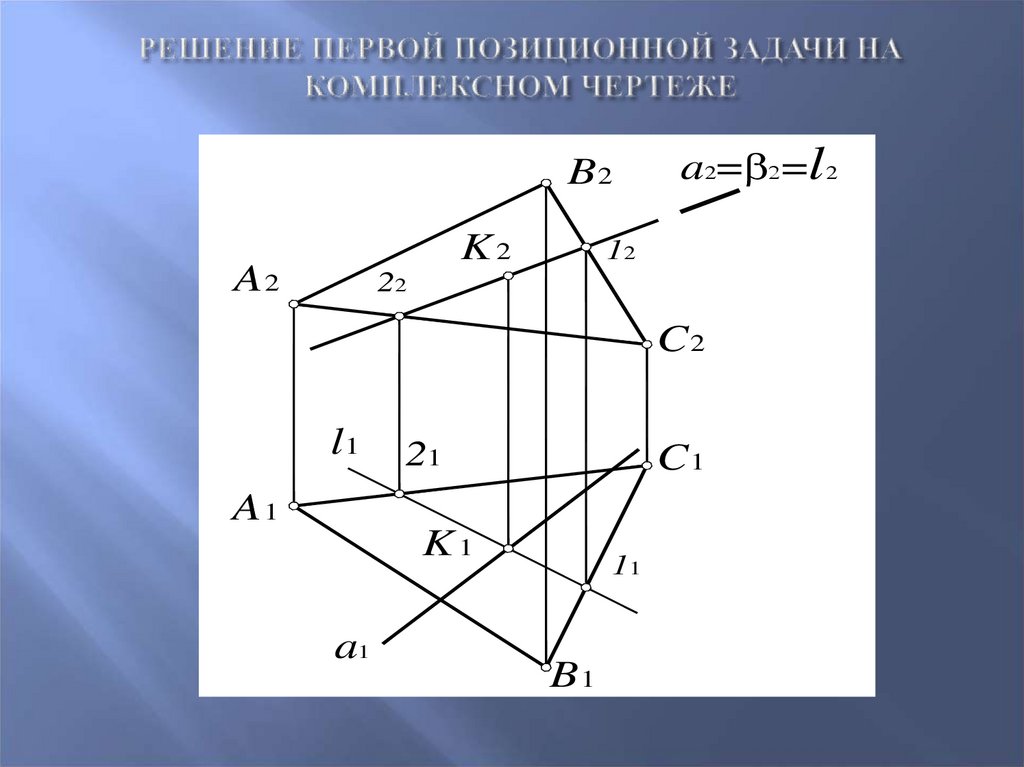
49. Решение первой позиционной задачи на комплексном чертеже
B2K2
A2
a2= =l 2
12
22
C2
l1
21
C1
A1
K1
a1
11
B1
50. Определение видимости. Метод конкурирующих точек
Определение видимости относительно горизонтальной плоскостипроекций:
B2
52
A2
42
a2
K2
C2
C1
A1
41=51
a1
K1
B1
Точки, конкурирующие на П1 : 4 – на прямой a и 5 – на прямой (AB).
Высота точки 5 больше, следовательно, на П1 видима прямая (AB), то
есть плоскость, а прямая a – невидима.
51.
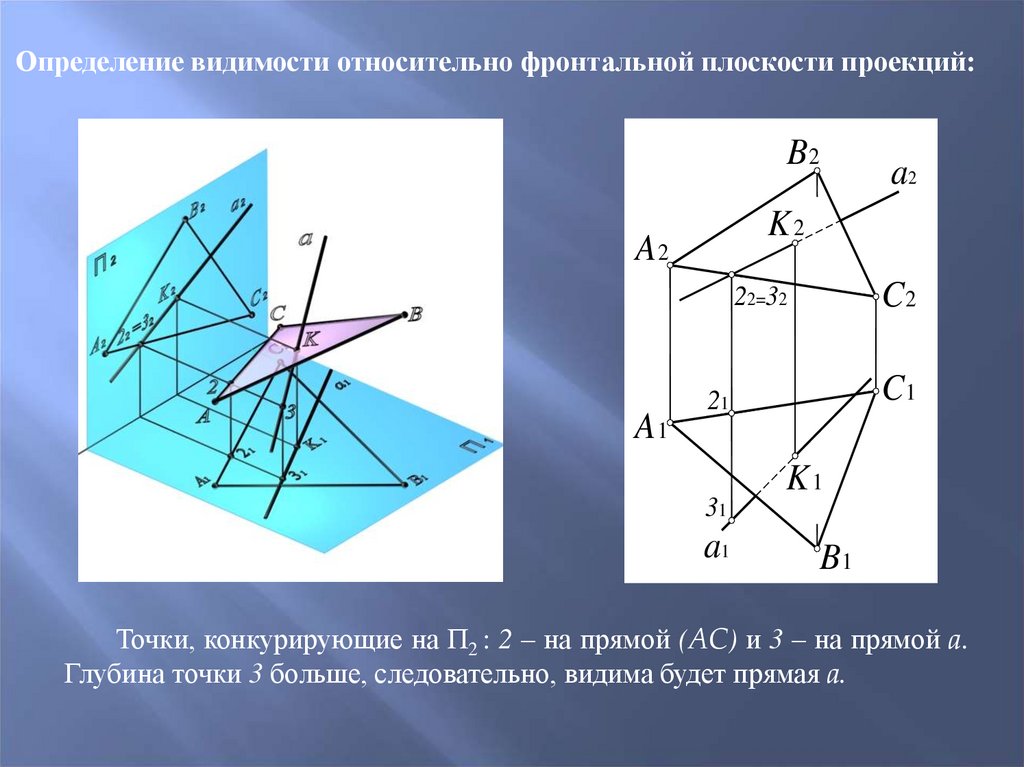
Определение видимости относительно фронтальной плоскости проекций:B2
a2
K2
A2
C2
22=32
A1
C1
21
31
a1
K1
B1
Точки, конкурирующие на П2 : 2 – на прямой (AC) и 3 – на прямой a.
Глубина точки 3 больше, следовательно, видима будет прямая a.
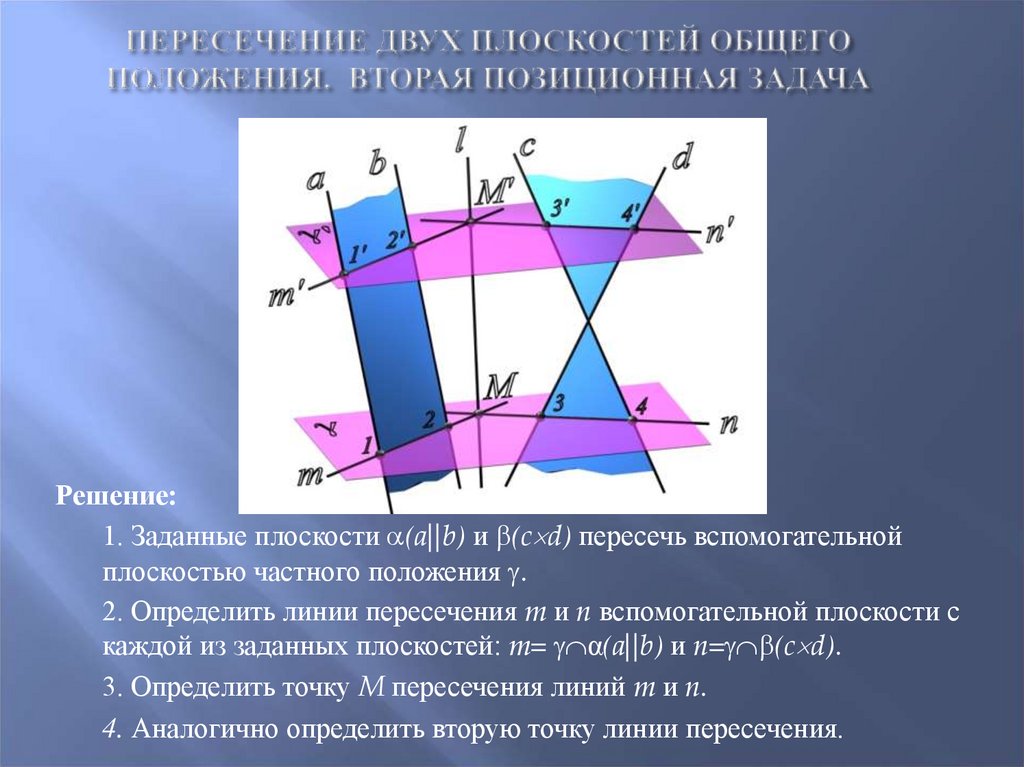
52. Пересечение двух плоскостей общего положения. Вторая позиционная задача
Решение:1. Заданные плоскости (a||b) и (c d) пересечь вспомогательной
плоскостью частного положения .
2. Определить линии пересечения m и n вспомогательной плоскости с
каждой из заданных плоскостей: m= α(a||b) и n= (c d).
3. Определить точку M пересечения линий m и n.
4. Аналогично определить вторую точку линии пересечения.
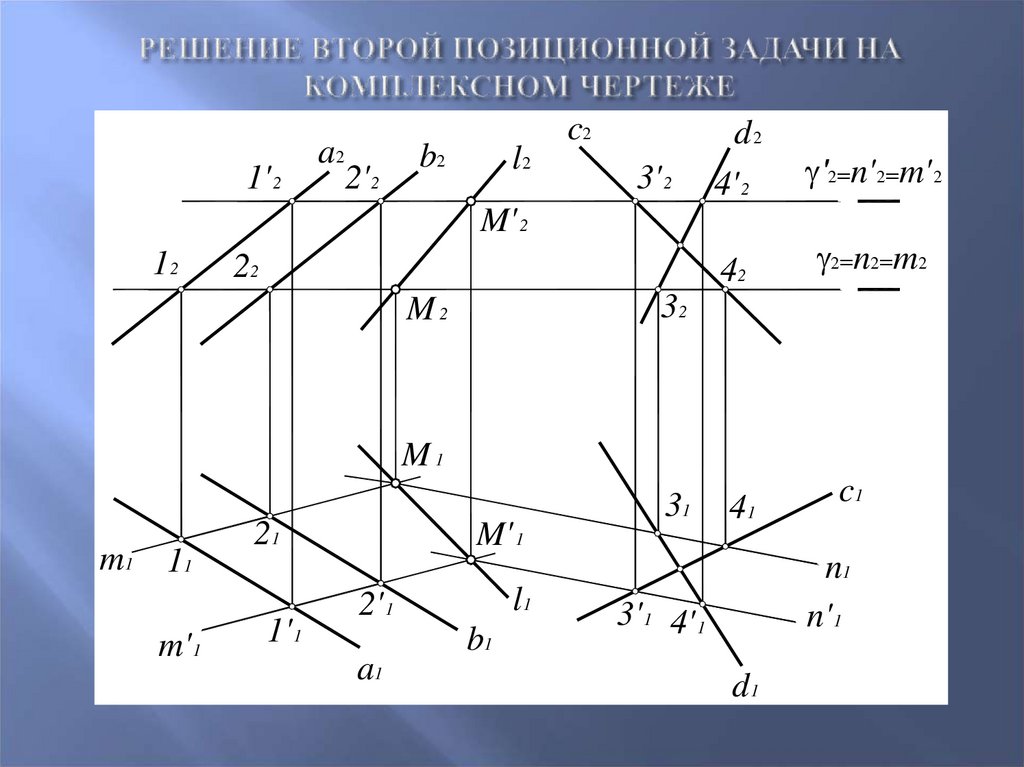
53. Решение второй позиционной задачи на комплексном чертеже
1' 2a2
2' 2
b2
l2
c2
3' 2
d2
4' 2
' 2 n' 2 m' 2
42
2 n 2 m 2
41
c1
M' 2
12
22
32
M2
M1
m 1 11
m' 1
21
1' 1
M' 1
l1
2' 1
a1
b1
31
n1
n' 1
3' 1 4' 1
d1
54. Лекция 6. Точка на поверхности
l ФсфA l A Фсф
Точка принадлежит поверхности, если она принадлежит какой-либо
линии на этой поверхности
55. Точка на поверхности конуса
На поверхности конуса можно получить как окружности, так ипрямые линии. В сечении конуса плоскостью, проходящей через его
вершину, получаются прямые линии
2=m2=m' 2
S2
S2
A 2=A' 2
A2
l2
12
32=42
m' 1
41
A' 1
S1
S1
A1
11
1=l1
m1
A1
31
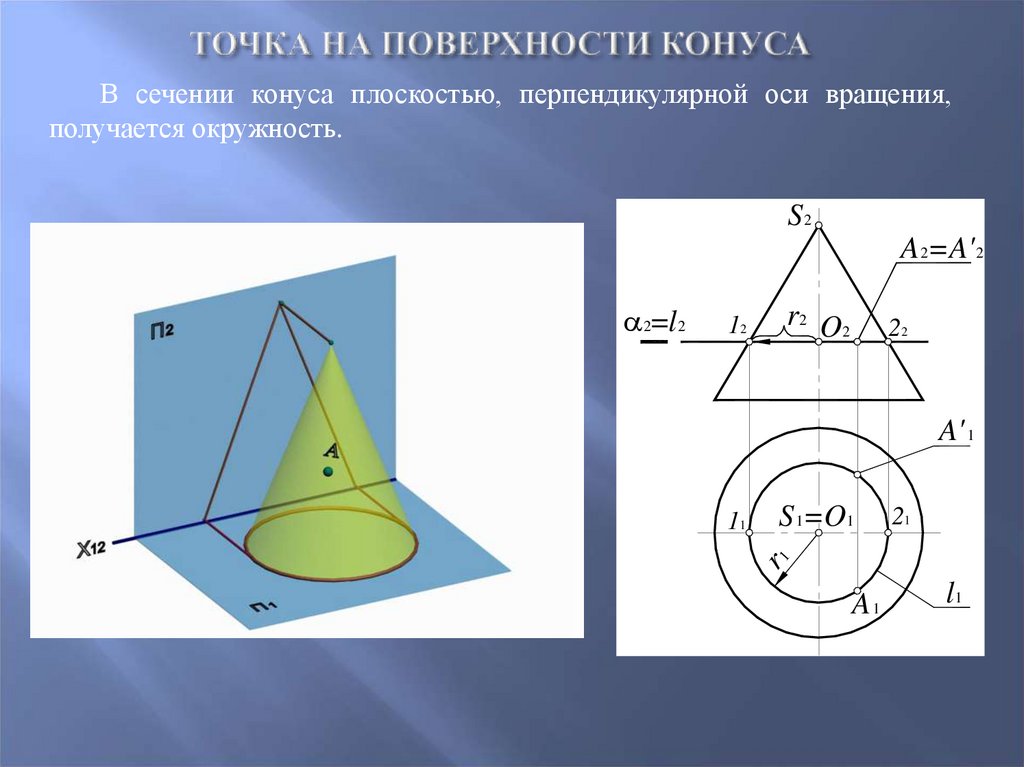
56. Точка на поверхности конуса
В сечении конуса плоскостью, перпендикулярной оси вращения,получается окружность.
S2
A 2=A' 2
12
r 2 O2
22
A' 1
11
S 1=O1
21
r1
2=l2
A1
l1
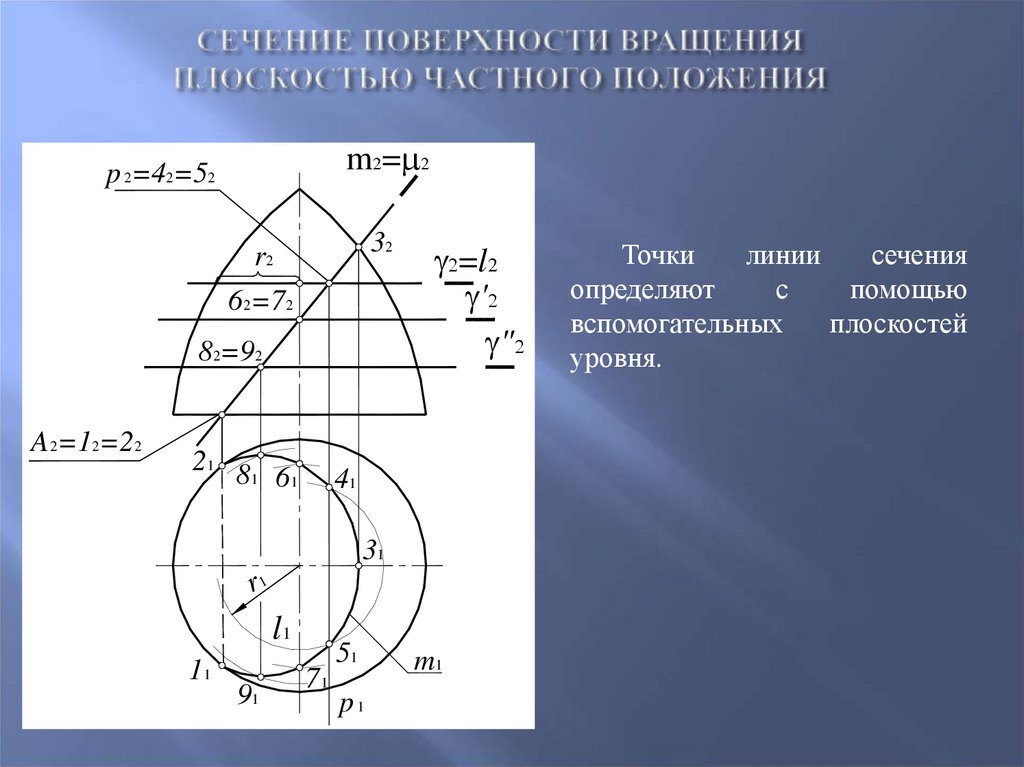
57. Сечение поверхности вращения плоскостью частного положения
m 2= 2p 2=42=52
32
r2
62=72
82=92
A 2=12=22
2 1 81
61
=l2
'
"
41
31
r1
l1
11
91
71
51
p1
m1
Точки
линии
сечения
определяют
с
помощью
вспомогательных
плоскостей
уровня.
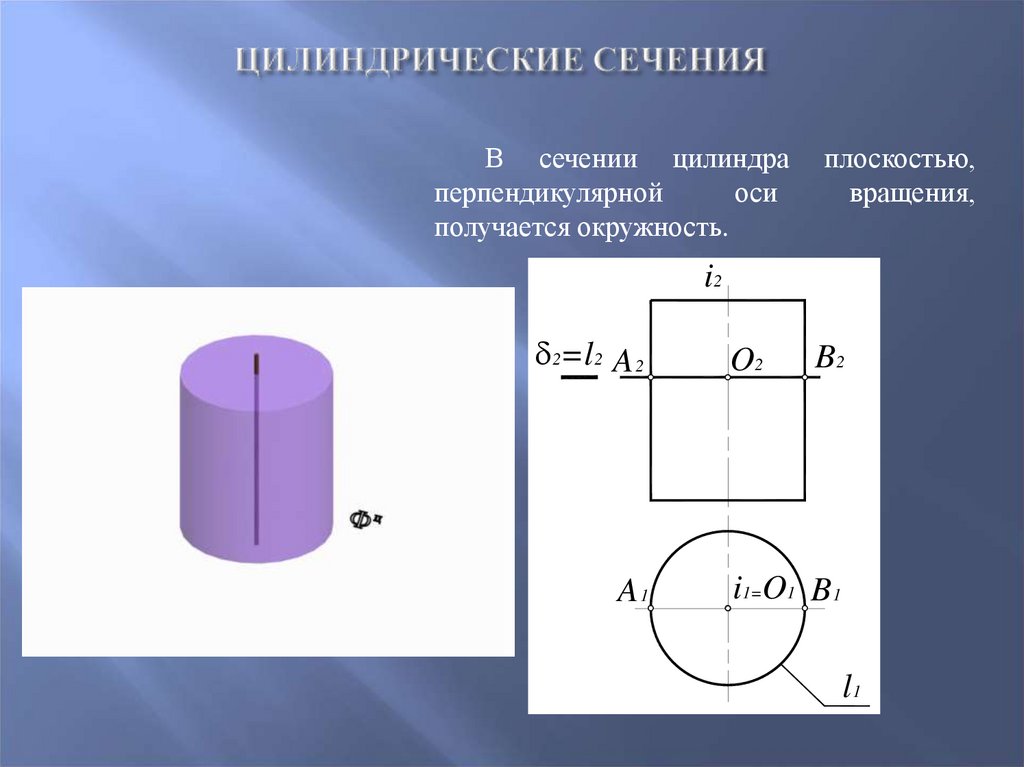
58. Цилиндрические Сечения
В сечении цилиндраперпендикулярной
оси
получается окружность.
плоскостью,
вращения,
i2
2=l2 A 2
A1
O2
B2
i1=O1 B1
l1
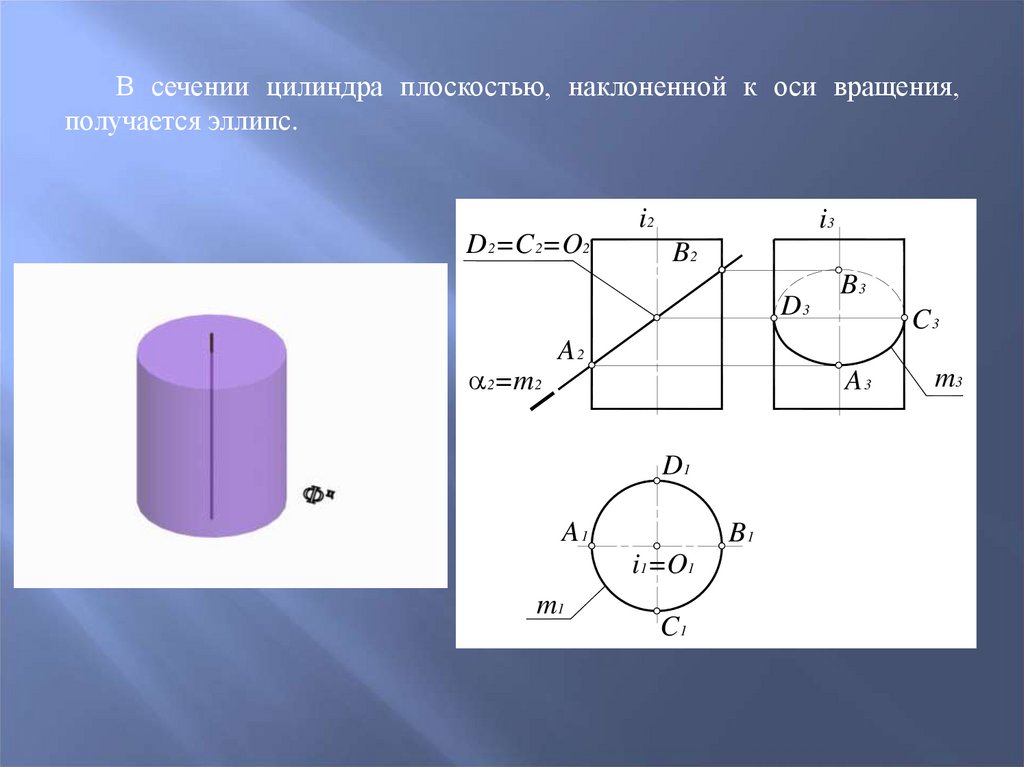
59.
В сечении цилиндра плоскостью, наклоненной к оси вращения,получается эллипс.
i2
D 2=C 2=O2
i3
B2
D3
2=m2
B3
C3
A2
A3
D1
A1
B1
i1=O1
m1
C1
m3
60.
В сечении цилиндра плоскостью, параллельной оси вращения,получаются параллельные прямые.
2=n2=n' 2
i3
i2
n3
n' 3
12=22
2 1= n 1
23
i1
21=n' 1
13
61. Конические Сечения
В сечении конуса плоскостью, перпендикулярной оси вращения,получается окружность.
i2
S2
2=t2 12
22
32=42
41
21
11
i1=S 1
t1
31
62.
CВ
сечении
конуса
плоскостью, наклоненной к оси
вращения, получается эллипс.
B
F
O
F'
A
D
B2
F2
A2
F' 2
O2=C 2=D2=m2
D1
O1
F' 1
A1
C1
m1
F 1 B1
63.
=g =dd
2
2
2
g
K
S2
D
F
M
d2
K2
W
F2
N
M 2=N 2
N1
d1
K1
S1
F1
M1
g1
В
сечении
конуса
плоскостью, параллельной
одной
из
образующих,
получается парабола.
64.
aL'
H'
2=s2=s' 2 2
=a2=a' 2
a'
s'
F'
L' 2=H' 2
12=22
G'
O
F' 2
s
G
L
S2
O2
F
K2
R
F2
H
L 2=H 2
a' 1
H' 1
H1
11
s1
G1 G' 1
F1
O1
S1
F' 1
L' 1
L1
a1
s' 1
21
В
сечении
конуса
плоскостью, пересекающей
образующие по обе стороны
от вершины, получается
гипербола.
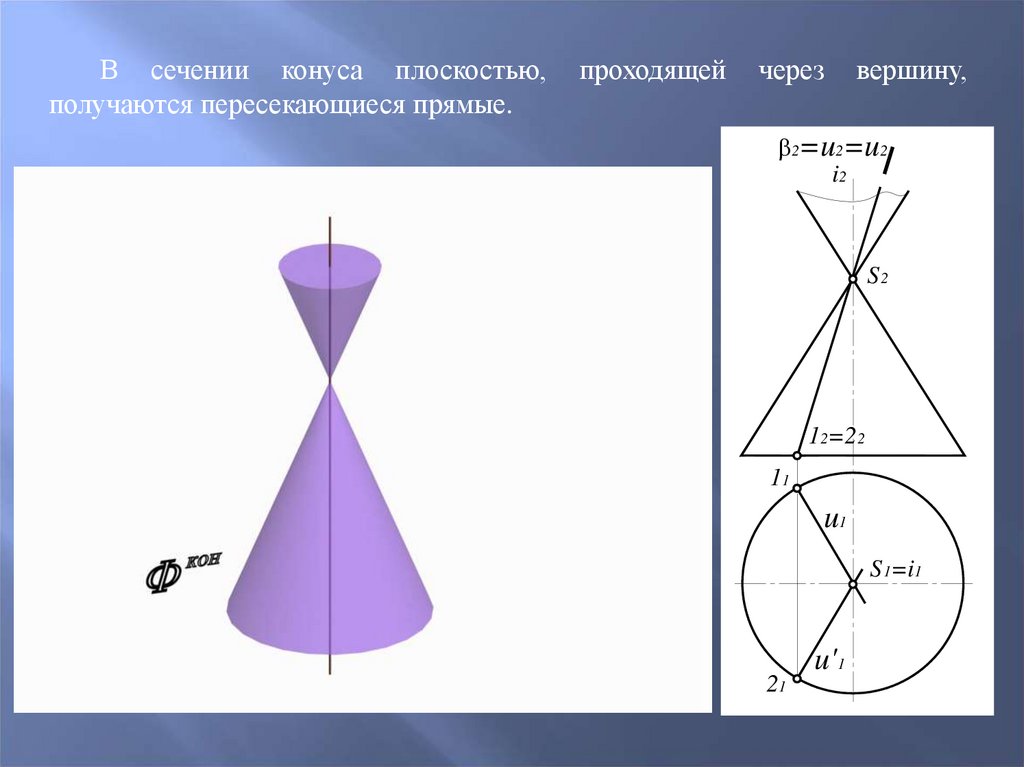
65.
В сечении конуса плоскостью,получаются пересекающиеся прямые.
проходящей
через
вершину,
2=u2=u2
i2
S2
12=22
11
u1
S 1=i1
21
u' 1
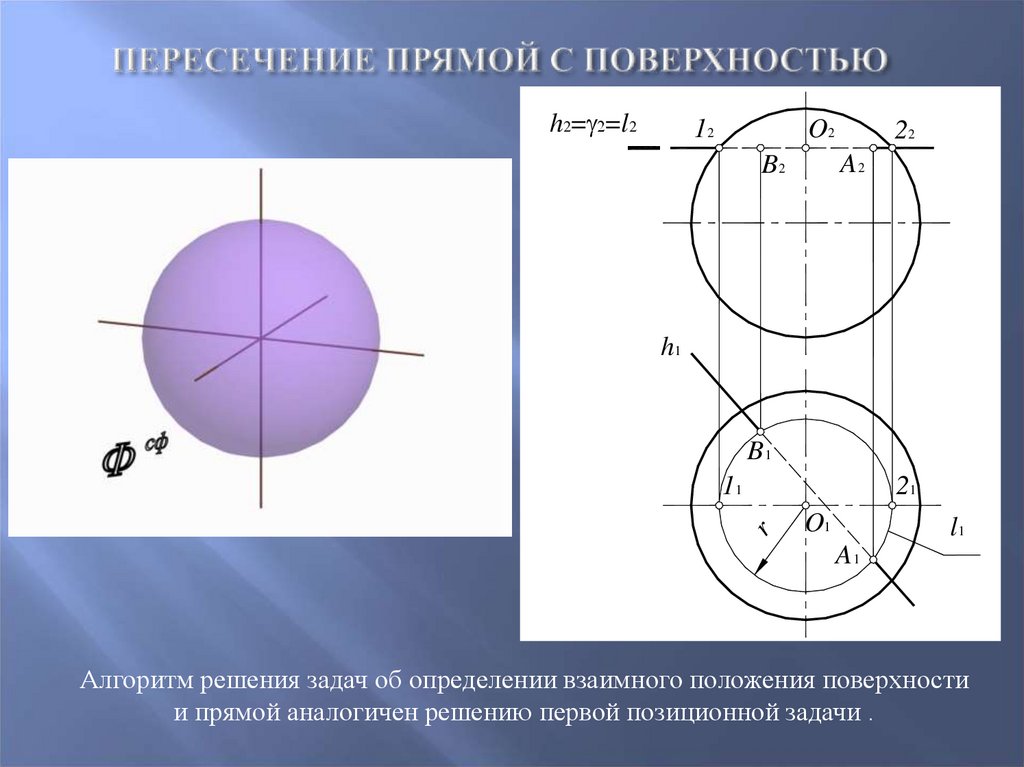
66. Пересечение прямой с поверхностью
h2= =l212
O2
22
A2
B2
h1
B1
21
r
11
O1
l1
A1
Алгоритм решения задач об определении взаимного положения поверхности
и прямой аналогичен решению первой позиционной задачи .
67. Лекция 7. Пересечение поверхностей
1. Обе заданные поверхности Ф' и Ф “ рассекают третьей, вспомогательнойплоскостью или поверхностью .
2. Определяют линии пересечения каждой заданной поверхности со
вспомогательной: Ф' × P =l', Ф'' × P =l''.
3. Определяют точки пересечения полученных линий l'×l'' = I и II и
соединяют лекальной кривой, которая и является искомой линией
пересечения поверхностей.
4. Определяют видимость поверхностей и линии их пересечения.
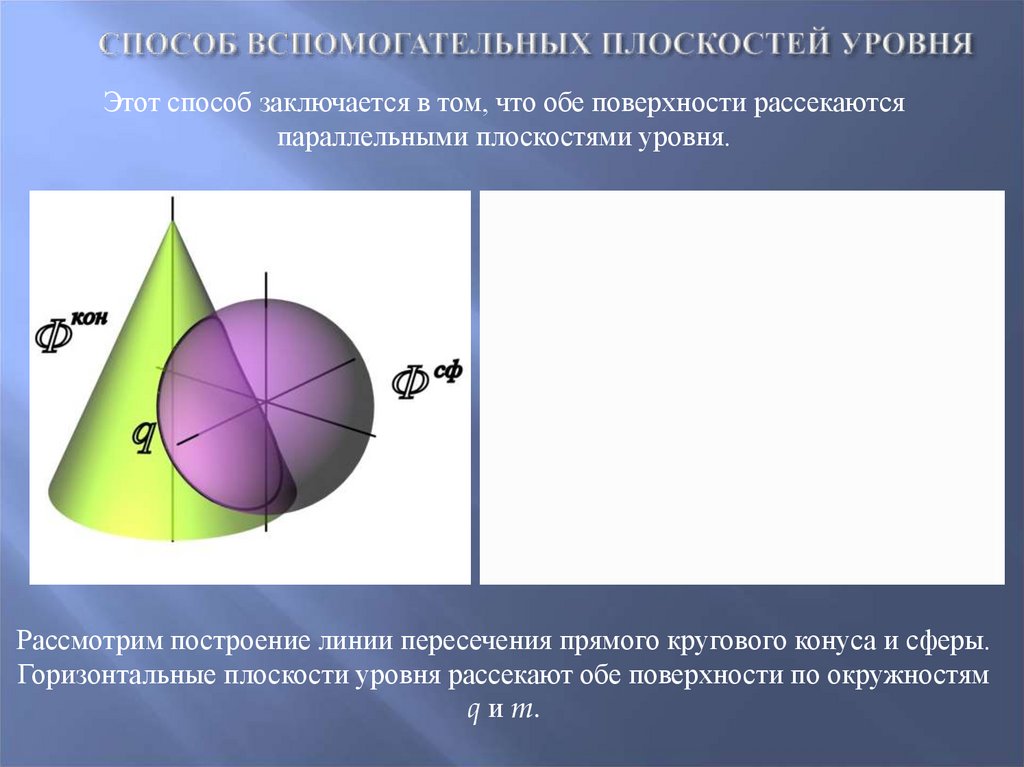
68. Способ вспомогательных плоскостей уровня
Этот способ заключается в том, что обе поверхности рассекаютсяпараллельными плоскостями уровня.
Рассмотрим построение линии пересечения прямого кругового конуса и сферы.
Горизонтальные плоскости уровня рассекают обе поверхности по окружностям
q и m.
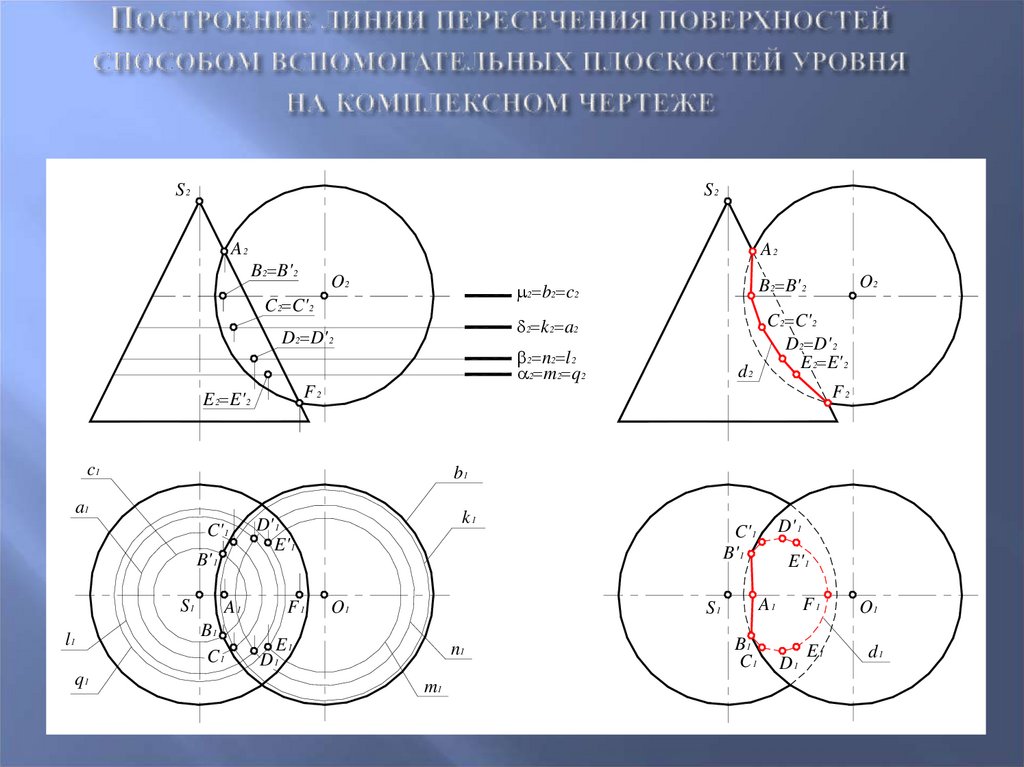
69. Построение линии пересечения поверхностей способом вспомогательных плоскостей уровня на комплексном чертеже
S2S2
A2
A2
B2 B' 2
O2
C 2 C' 2
D 2 D' 2
2 k 2 a2
C 2 C' 2
D 2 D' 2
E 2 E' 2
2 n2 l2
2 m2 q2
d2
O2
F2
c1
b1
a1
C' 1
B' 1
S1
q1
B2 B' 2
F2
E 2 E' 2
l1
2 b2 c2
A1
B1
C1
k1
D' 1
E' 1
F1
O1
n1
m1
E' 1
A1
S1
E1
D1
D' 1
C' 1
B' 1
B1
C1
D1
F1
O1
E1
d1
70. Способ концентрических сфер
Этот способ применяется для построения линии пересеченияповерхностей вращения произвольного вида, при условии, что оси этих
поверхностей пересекаются.
Окружности
Сфера
O2
Свойство сферы с центром на оси какой-либо поверхности:
если центр сферы находится на оси какой-нибудь поверхности вращения, то
сфера соосна с поверхностью вращения и в их пересечении получатся
окружности
71. Построение линии пересечения поверхностей вращения с пересекающимися осями
Точка пересечения осей поверхностейвспомогательных концентрических сфер.
принимается
за
центр
Вспомогательная сфера пересекает поверхность цилиндра по окружности l, а
поверхность конуса – по окружности m. Точки пересечения окружностей l и m
являются точками пересечения поверхностей.
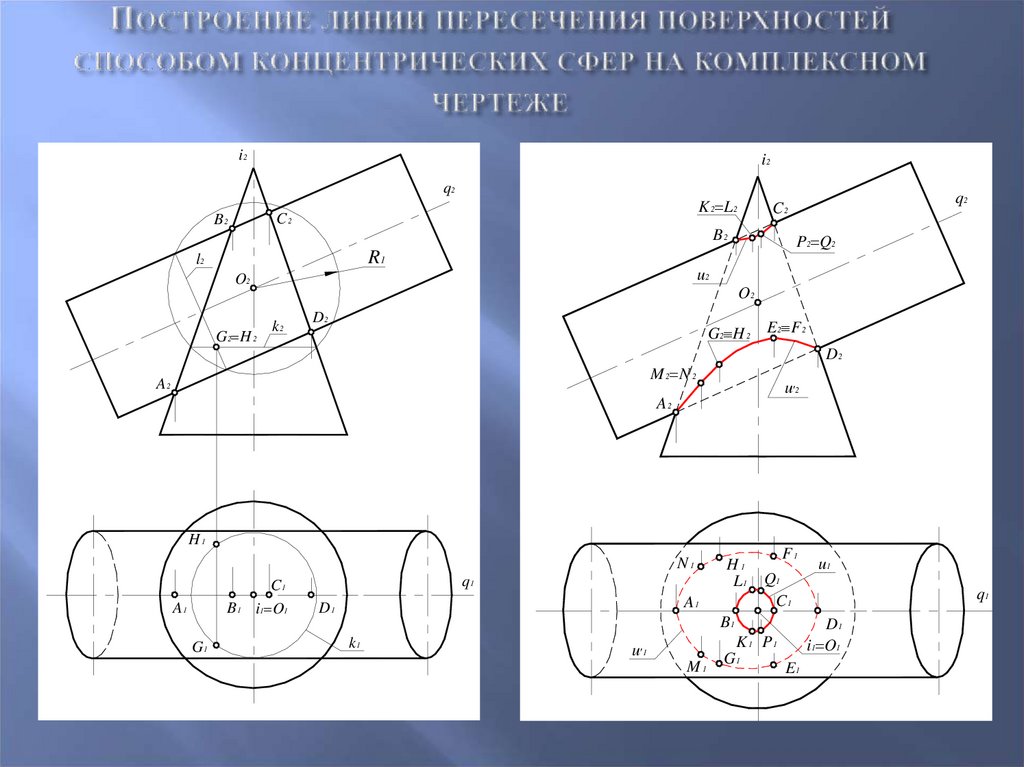
72. Построение линии пересечения поверхностей способом концентрических сфер на комплексном чертеже
i2i2
q2
K 2 L 2
C2
B2
B2
P 2 Q2
R1
l2
q2
C2
u2
O2
O2
G2 H 2
k2
D2
G2 H 2 E 2 F 2
D2
M 2 N 2
A2
u 2
A2
H1
N1
A1
B1
G1
C1
i1 O1
q1
H1
L1
A1
D1
F1
B1
k1
u 1
M1
u1
Q1
C1
K 1 P1
G1
q1
D1
i1 O1
E1
73. Способ эксцентрических сфер
основан на том, что около всякойокружности можно описать бесчисленное множество сфер, геометрическим
местом центров которых является прямая, проходящая через центр
окружности и перпендикулярная плоскости окружности.
Обязательным является наличие общей плоскости симметрии.
Рассмотрим способ на примере построения линии пересечения
поверхностей конуса и кольца, оси которых - скрещивающиеся прямые
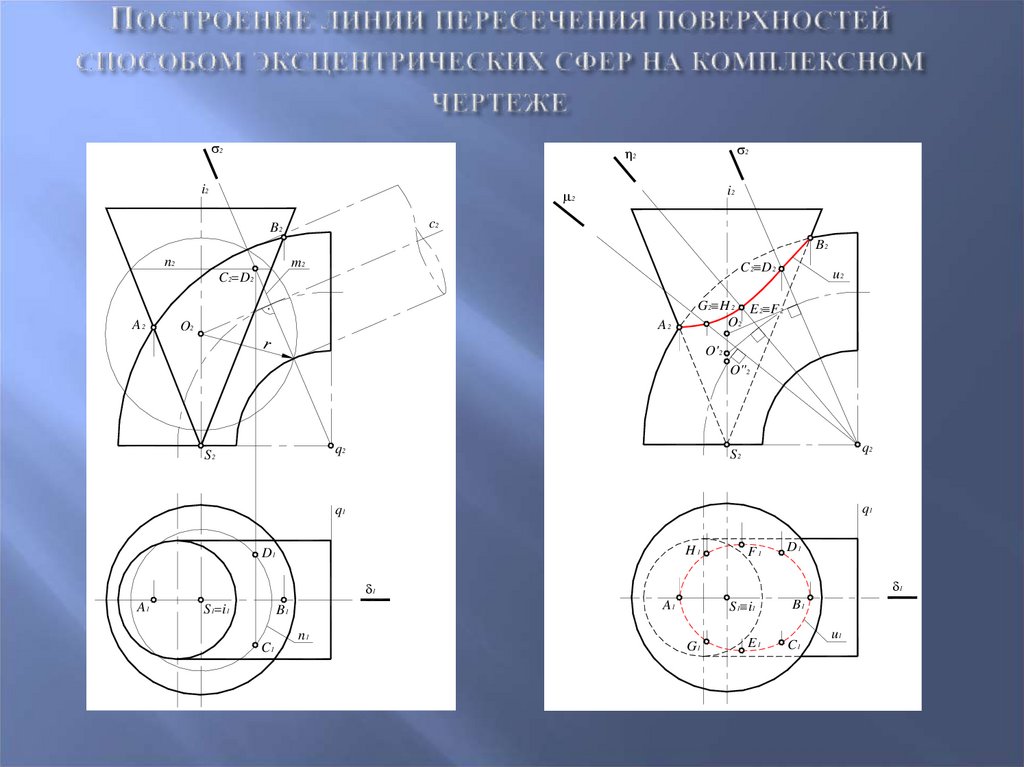
74. Построение линии пересечения поверхностей способом эксцентрических сфер на комплексном чертеже
22
2
i2
i2
2
c2
B2
B2
n2
A2
m2
C 2 D 2
C 2 D 2
A2
O2
u2
G2 H 2 E 2 F 2
O2
r
O' 2
O'' 2
q2
S2
q2
S2
q1
q1
H1
D1
F1
D1
S 1 i1
B1
E1
C1
1
1
A1
S 1 i1
A1
B1
C1
n1
G1
u1
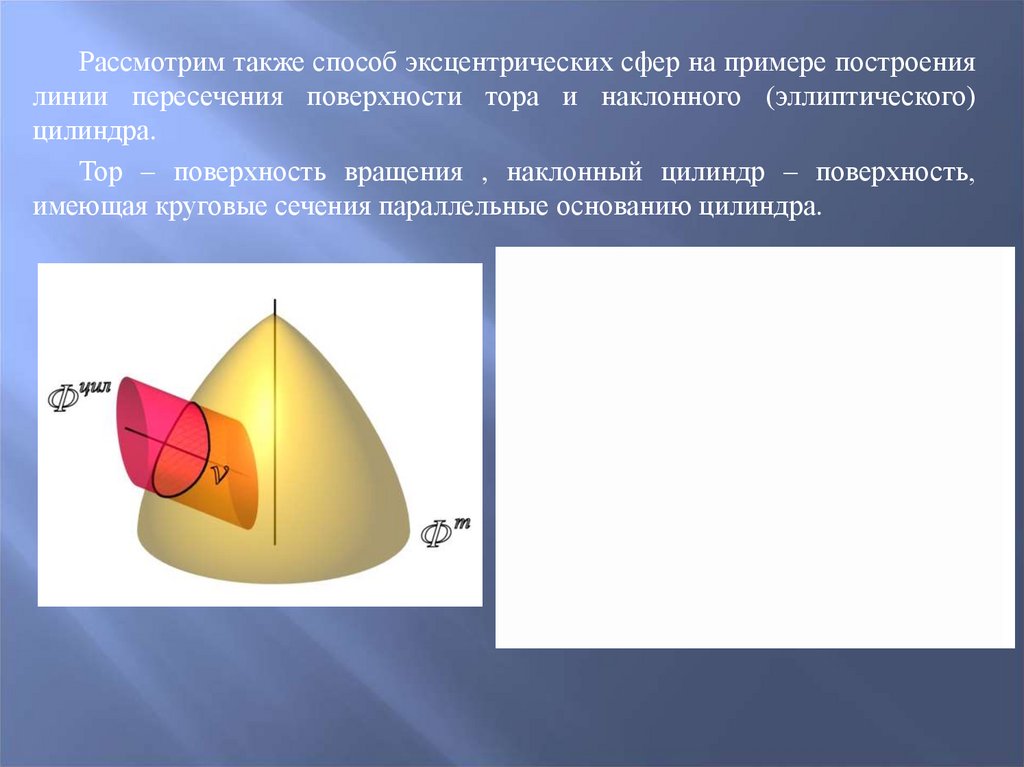
75.
Рассмотрим также способ эксцентрических сфер на примере построениялинии пересечения поверхности тора и наклонного (эллиптического)
цилиндра.
Тор – поверхность вращения , наклонный цилиндр – поверхность,
имеющая круговые сечения параллельные основанию цилиндра.
76. Построение линии пересечения поверхностей способом эксцентрических сфер на комплексном чертеже
22
2 2
m2
i2
i2
A2
K2
A2
q2
d2
q2
S 2 P 2
v2
G2 H 2
L2
l2
C 2 D 2
B2
C 2 D 2
B2
O 2
O ' 2
E 2 F 2
O2
O2
l1
P1
F1
D1
D1
q1 1
i2
A1
B1
C1
H1
v1
q1 1
i2
B1
A1
C1
E1
G1
S1
77. Лекция 8. Метрические задачи
Задачи, в которых определяются различные геометрические величины –расстояния между объектами, длины отрезков, углы, площади и т.д.
называются метрическими.
Прямой угол проецируется на плоскость без искажения, если одна из
его сторон параллельна этой плоскости
Дано: BAC = 90º; AB П‘
Доказать, что С'A' A'B‘
Доказательство:
если AB П', то A'B' AB, но AA' П'
AA' A'B' значит AB AA' AB
плоскости , тогда и A'B' CAA'C'.
Следовательно, C'A' A'B'.
78. Перпендикулярные прямые
На основании теоремы о проекциях прямого угла две взаимноперпендикулярные прямые (пересекающиеся или скрещивающиеся)
проецируются на П1 в виде взаимно перпендикулярных прямых, если одна
из них горизонталь, на П2 – если одна из них фронталь.
Пересекающиеся прямые
Скрещивающиеся прямые
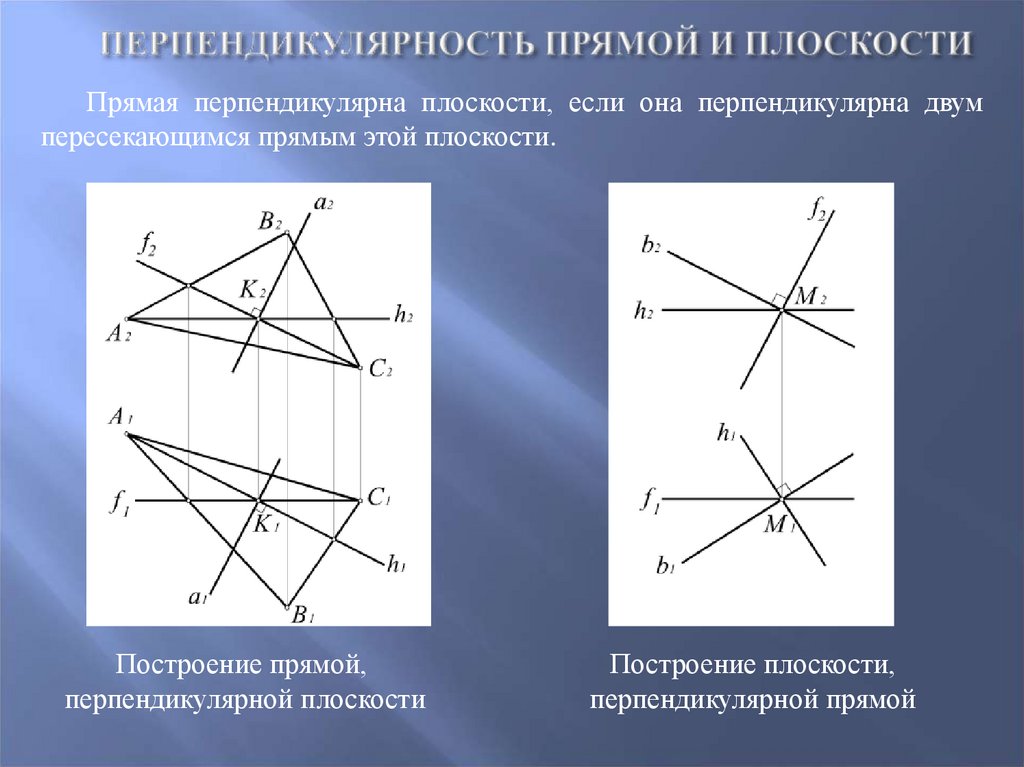
79. Перпендикулярность прямой и плоскости
Прямая перпендикулярна плоскости, если она перпендикулярна двумпересекающимся прямым этой плоскости.
Построение прямой,
перпендикулярной плоскости
Построение плоскости,
перпендикулярной прямой
80. Взаимная Перпендикулярность плоскостей
Две плоскости взаимно перпендикулярны, если одна из них проходитчерез перпендикуляр к другой.
Дано:
α h f ; A A1 , A2
Построить:
A β α
Решение:
A n;
n1 h1
n α h f
n2 f 2
m1 || n1 ; m2 || n2 ;
β n m α f h .
81. Преобразования комплексного чертежа
Способы преобразования комплексного чертежа позволяют переходитьот произвольных положений пространственных объектов к частным.
Способ
замены
плоскостей проекций состоит
в том, что проецируемый
объект
остается
неподвижным, а одна из
плоскостей проекций П1, П2
или П3 заменяется новой,
расположенной так, чтобы
проецируемый объект по
отношению
к
новой
плоскости
занял частное
положение.
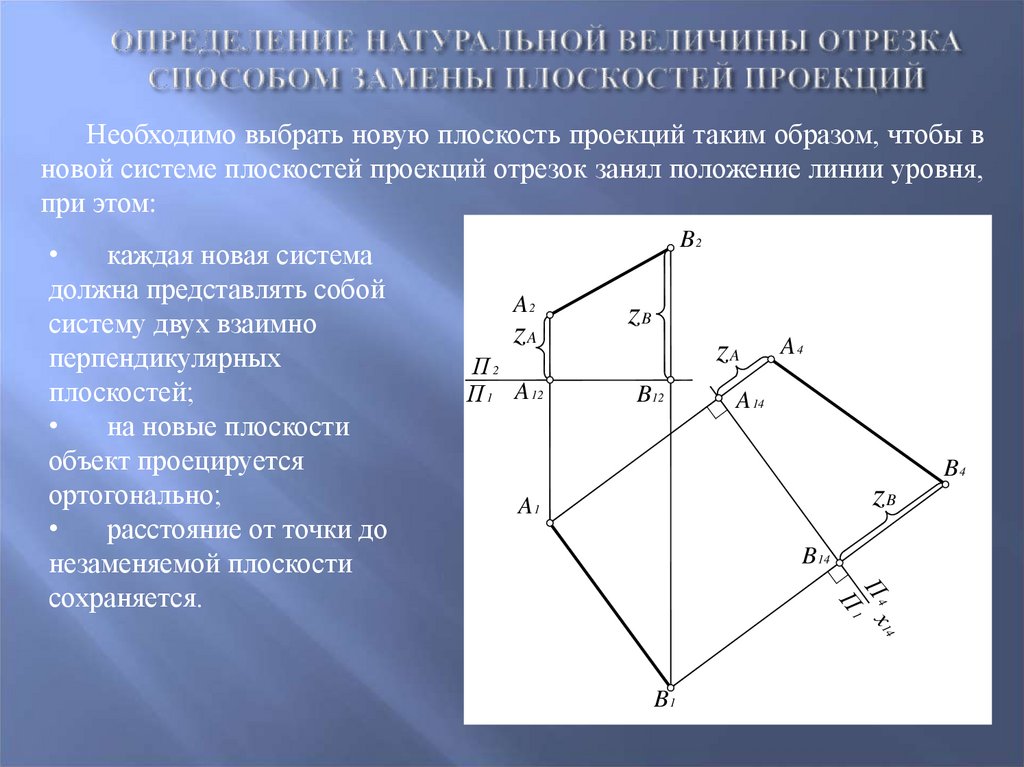
82. Определение натуральной величины отрезка способом замены плоскостей проекций
Необходимо выбрать новую плоскость проекций таким образом, чтобы вновой системе плоскостей проекций отрезок занял положение линии уровня,
при этом:
B2
A2
zA
x 12 П 2
П 1 A 12
zB
zA
B12
A4
A 14
B4
zB
A1
B14
4
П 1x
П
каждая новая система
должна представлять собой
систему двух взаимно
перпендикулярных
плоскостей;
на новые плоскости
объект проецируется
ортогонально;
расстояние от точки до
незаменяемой плоскости
сохраняется.
14
B1
83. Способ плоскопараллельного движения
Плоскопараллельным движением объекта в пространстве называетсятакое его перемещение, при котором все точки объекта перемещаются в
плоскостях, параллельных между собой.
Теорема. Если объект
совершает плоскопараллельное
движение относительно
плоскости проекций П1, то
фронтальные проекции его
точек будут двигаться по
прямым, перпендикулярным к
линиям связи; при этом
горизонтальная проекция
объекта движется по
плоскости проекций,
оставаясь равной самой себе.
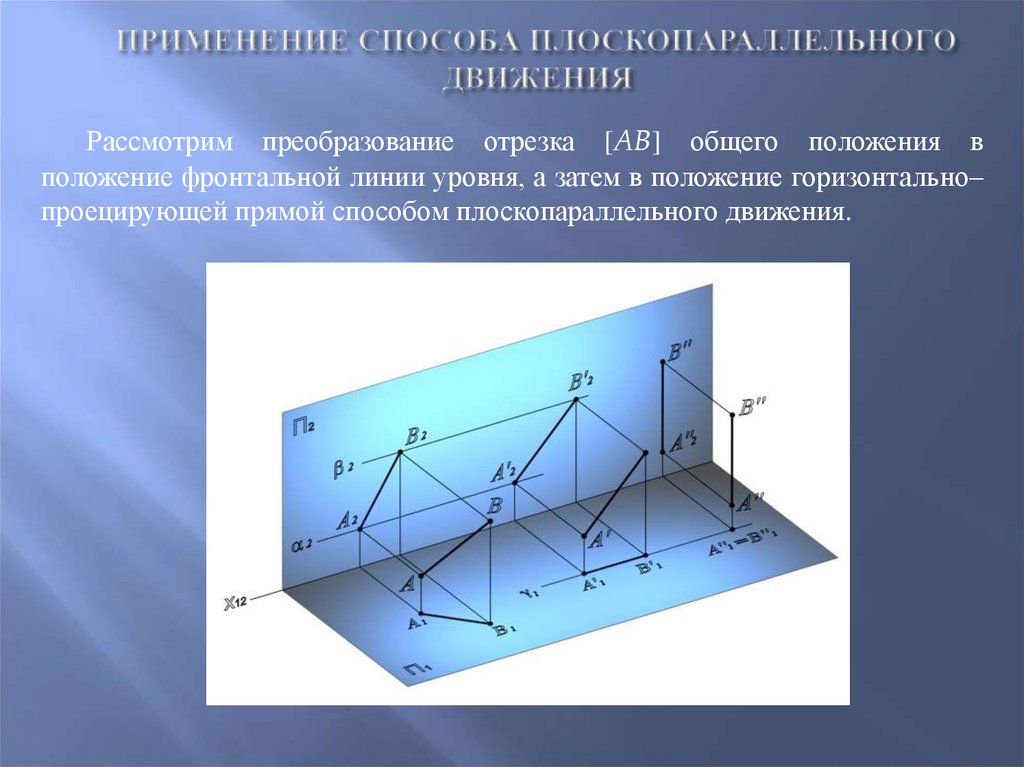
84. Применение способа плоскопараллельного движения
Рассмотрим преобразование отрезка [AB] общего положения вположение фронтальной линии уровня, а затем в положение горизонтально–
проецирующей прямой способом плоскопараллельного движения.
85. Преобразование отрезка общего положения на комплексном чертеже
Плоскопараллельным движением относительно П1 отрезок [AB] общегоположение переводится в положение фронтали, затем, плоскопараллельным
движением относительно П2 - в положение горизонтально-проецирующей
прямой
2
2
B2
B' 2
B'' 2
A' 2
A2
A'' 2
1
A1
A' 1
B1
B' 1
A'' 1 B'' 1
86. Вращение
– это движение по окружности вокруг некоторой оси. Припреобразовании комплексного чертежа способом вращения плоскости
проекций остаются неизменными, а проецируемый объект перемещается
таким образом, чтобы он занял какое-либо частное положение.
Элементы вращения:
Ось вращения – прямая, вокруг которой осуществляется вращение.
Плоскость вращения – плоскость, проходящая через вращаемую точку и
перпендикулярная оси вращения (плоскость окружности, которую
описывает точка при вращении).
Центр вращения – точка пересечения оси вращения и плоскости вращения.
Радиус вращения – кратчайшее расстояние от вращаемой точки до центра
(оси) вращения. Радиус всегда перпендикулярен оси вращения.
Угол поворота – угол между начальным и конечным положением радиуса
вращения.
87. Вращение вокруг проецирующей прямой
При вращении вокруг горизонтально-проецирующей прямойA1
перемещается по окружности l1 с центром в точке О1 и радиусом
r=r1= O1A1 , A2 перемещается по фронтальному следу плоскости γ2 в
пределах отрезка [12,22].
Элементы вращения:
i2
2=l2
O2 A' 2
A2
12
22
i1=O1
11
r1
A1
21
A' 1
l1
i(i1 i2) П1 – ось вращения ;
( 2) i – плоскость вращения;
O=i(i1 i2) ( 2) – центр
вращения;
R=O1A1 – радиус вращения;
l – траектория вращения.
88.
Способом вращения вокруг проецирующей прямой можно совместитьточку с плоскостью или поверхностью. Рассмотрим совмещение точки с
поверхностью прямого кругового конуса, поставленного основанием на
плоскость
Фк
i2
O2
M2
M' 2 M'' 2
2=l2=n2
M'' 1
r1
i1=O1
M' 1
n1
M1
l1
89. Лекция 9. аксонометрические проекции
z'e' z
L'
E'
F'
z
S
ez
П'
K'
e' x
A'
x'
C'
D'=O'
L
E
B'
e' y
y'
K
D=O
F
A
x
C
ex
ey
B
y
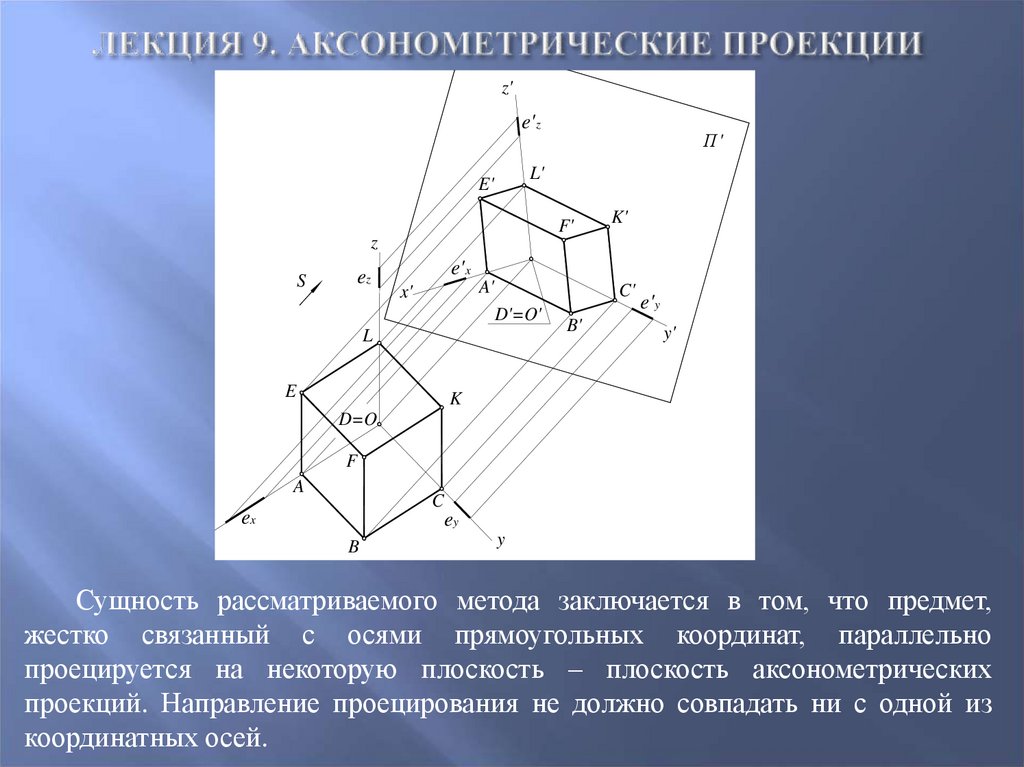
Сущность рассматриваемого метода заключается в том, что предмет,
жестко связанный с осями прямоугольных координат, параллельно
проецируется на некоторую плоскость – плоскость аксонометрических
проекций. Направление проецирования не должно совпадать ни с одной из
координатных осей.
90. Виды аксонометрических проекций
Показателем искажения называют отношение аксонометрическогомасштаба к соответствующему натуральному:
по оси x: u=ex'/ex;
по оси y: v=еy'/ey;
по оси z: w=еz'/еz.
В зависимости от соотношения показателей искажения различают три
вида аксонометрических проекций:
1. Изометрия - все три показателя искажения равны между собой:
u=v=w;
2. Диметрия - два показателя искажения одинаковы:
u=w≠v;
3. Триметрия - все три показателя искажения различны:
u≠w≠v.
91. Прямоугольные (ортогональные) аксонометрические проекции
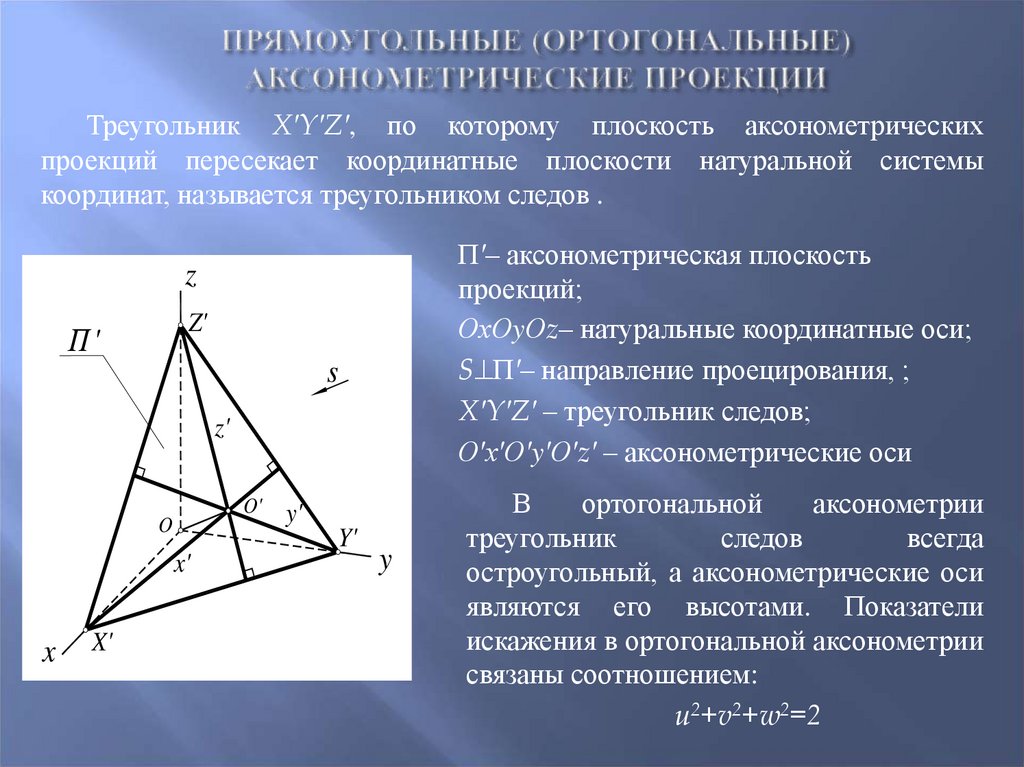
Треугольник X′Y′Z′, по которому плоскость аксонометрическихпроекций пересекает координатные плоскости натуральной системы
координат, называется треугольником следов .
П′– аксонометрическая плоскость
проекций;
ОхОyОz– натуральные координатные оси;
S П′– направление проецирования, ;
X′Y′Z′ – треугольник следов;
О′х′О′y′О′z′ – аксонометрические оси
z
Z'
П'
s
z'
O'
O
Y'
x'
x
X'
y'
y
В
ортогональной
аксонометрии
треугольник
следов
всегда
остроугольный, а аксонометрические оси
являются его высотами. Показатели
искажения в ортогональной аксонометрии
связаны соотношением:
u2+v2+w2=2
92. Прямоугольная изометрическая проекция
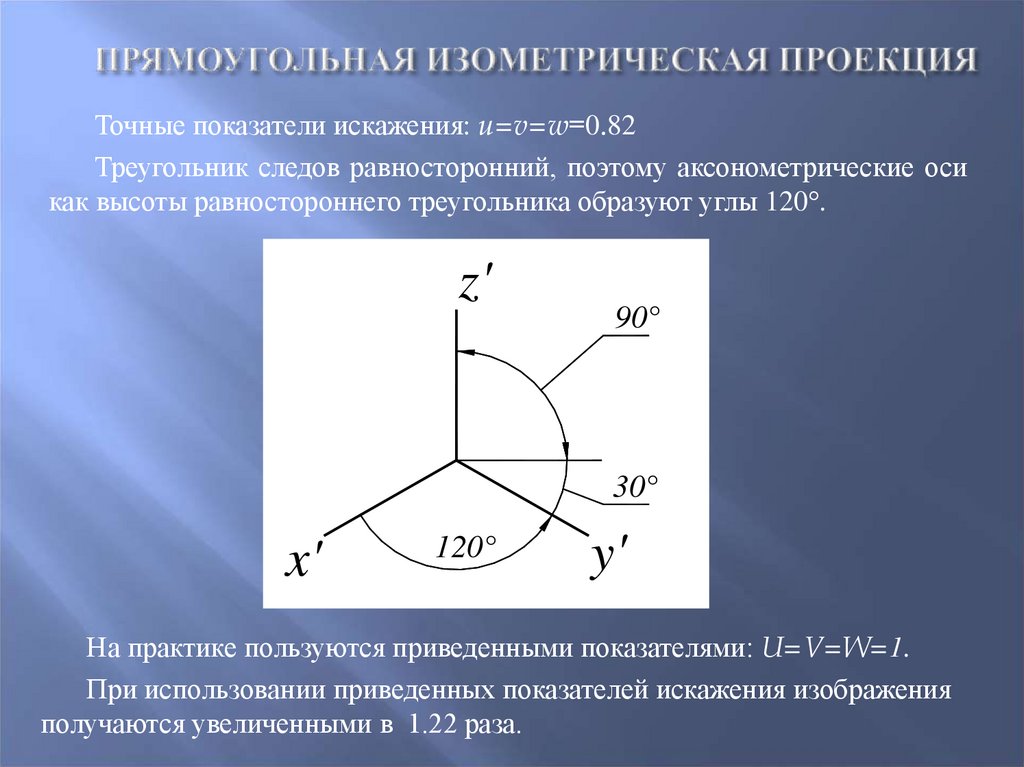
Точные показатели искажения: u=v=w=0.82Треугольник следов равносторонний, поэтому аксонометрические оси
как высоты равностороннего треугольника образуют углы 120 .
z'
z'
90°
7°10'
30°
x'
120°
x'
y'
На практике пользуются приведенными показателями: U=V=W=1.
При использовании приведенных показателей искажения изображения
получаются увеличенными в 1.22 раза.
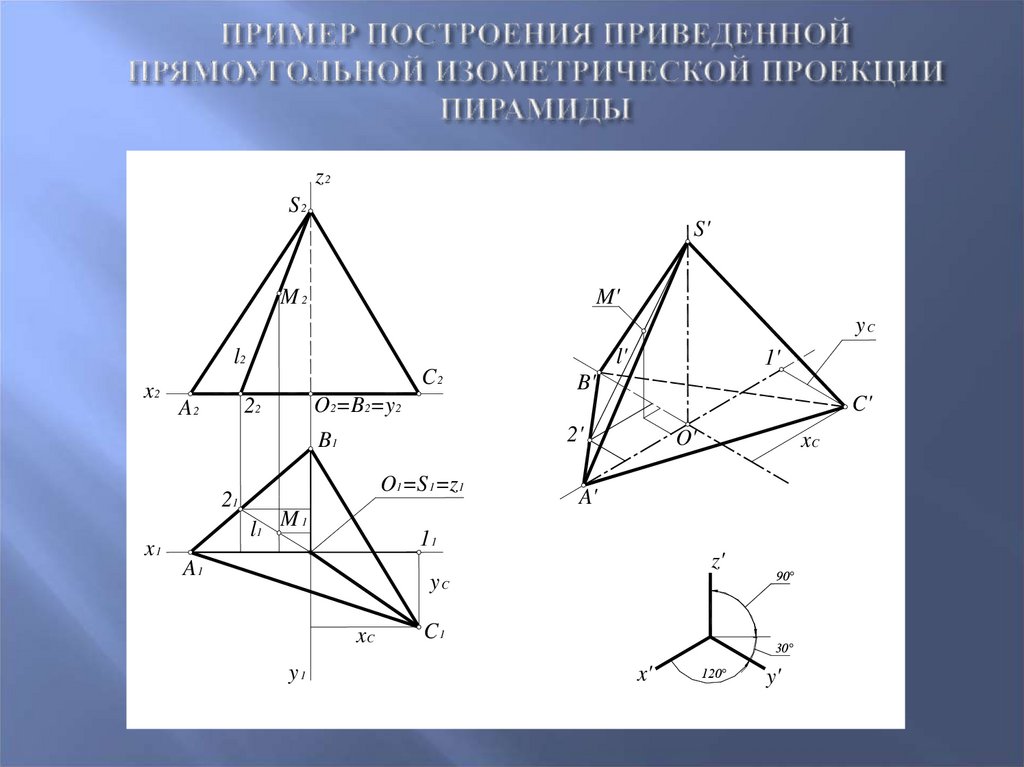
93. Пример построения приведенной Прямоугольной изометрической проекции пирамиды
z2S2
S'
M2
M'
yC
l2
x2
C2
x1
B'
C'
2'
B1
21
1'
O2=B2=y2
22
A2
l'
O1=S 1=z1
l1 M 1
O'
xC
A'
11
z'
A1
yC
xC
y1
C1
90°
30°
x'
120°
y'
94. Прямоугольная диметрическая проекция
°Точные показатели искажения: u=w=0.94; v=0.47.
z'
90°
90°
7°10'
30°
y'
x'
41°25'
y'
На практике пользуются приведенными показателями:. U=W=1; V=0.5.
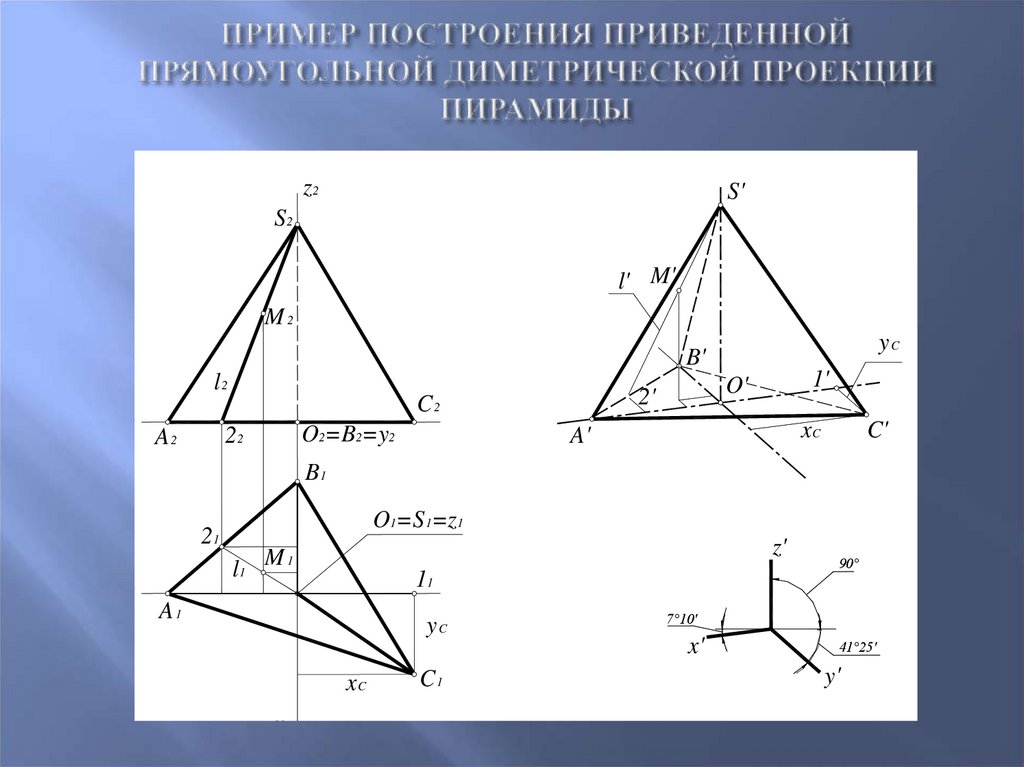
95. Пример построения приведенной Прямоугольной диметрической проекции пирамиды
z2S'
S2
l' M'
M2
yC
B'
l2
x2
C2
O2=B2=y2
22
A2
1'
O'
2'
xC
A'
C'
B1
O1=S 1=z1
21
x1
l1
z'
M1
11
A1
yC
xC
y1
C1
90°
7°10'
x'
41°25'
y'
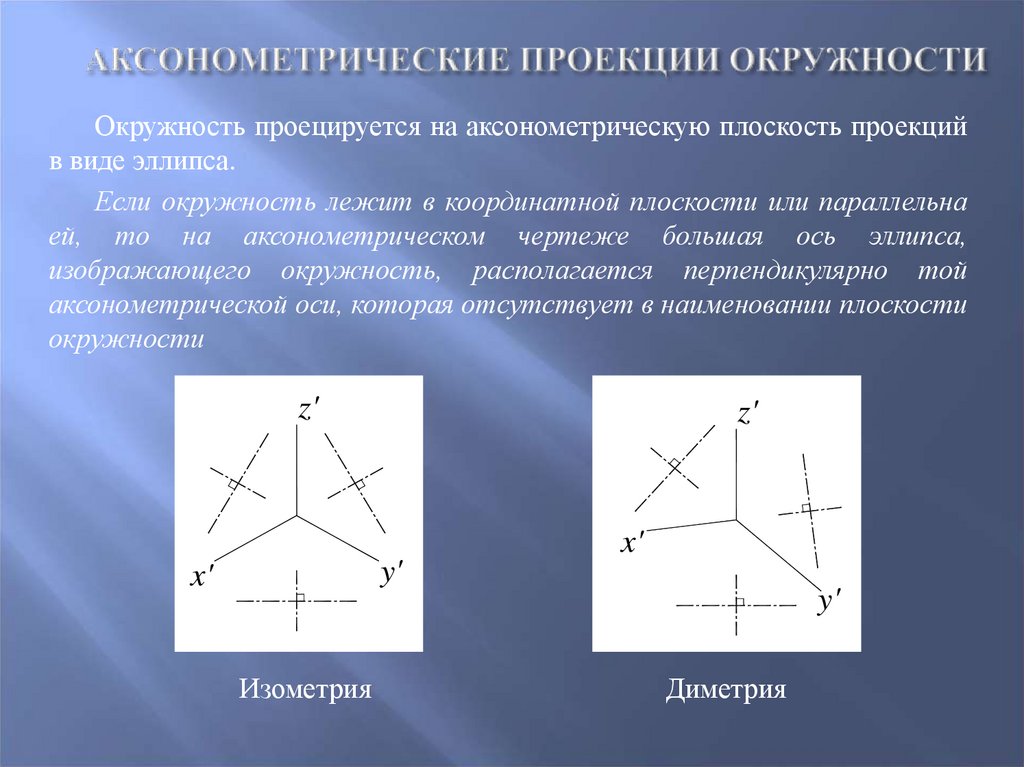
96. Аксонометрические проекции окружности
Окружность проецируется на аксонометрическую плоскость проекцийв виде эллипса.
Если окружность лежит в координатной плоскости или параллельна
ей, то на аксонометрическом чертеже большая ось эллипса,
изображающего окружность, располагается перпендикулярно той
аксонометрической оси, которая отсутствует в наименовании плоскости
окружности
z'
x'
x'
Изометрия
z'
y'
z'
x'
y'
z'
x'
y'
Диметрия
y'
97. Размеры осей эллипса в прямоугольных приведенных изометрии и диметрии (d – диаметр окружности).
ИзометрияДиметрия
в плоскостях П1 и
во всех плоскостях
в плоскости П2
П3
БОЭ
МОЭ
БОЭ
МОЭ
БОЭ
МОЭ
1.22d
0.72d
1.06d
0.35d
1.06d
0.95d
z'
C'
3'
2'
B'
A'
O'
1'
МОЭ
D'
4'
БОЭ
А′В′=1,22d – большая ось
эллипса;
С′D′=0,7d – малая ось эллипса;
1′-2′ – размер по оси x, равный
диаметру окружности d;
3′-4′ – размер по оси y, равный
диаметру окружности d
98.
МО
z'
3'
B'
C'
2'
3' C'БОЭ
2'
B'
2'
2'
БОЭ
O' A'
B' x'1'
O'
x'
D' 4'1' y'
D' 4' y'
x'
1'
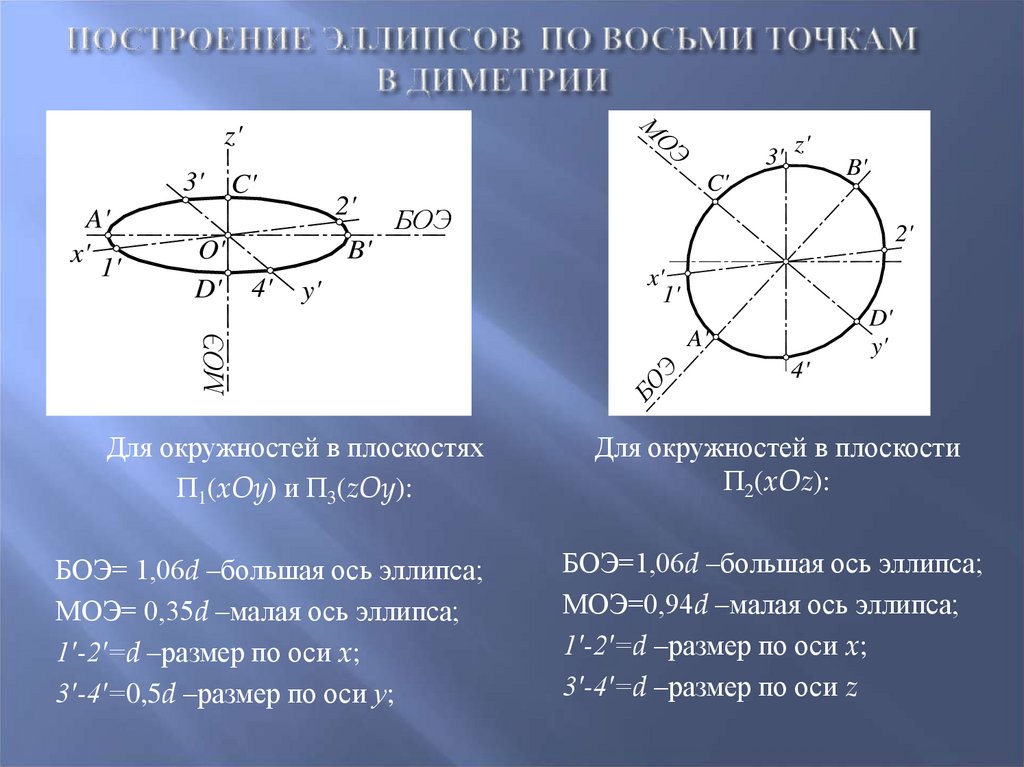
Для окружностей в плоскостях
П1(xOy) и П3(zOy):
БОЭ= 1,06d –большая ось эллипса;
МОЭ= 0,35d –малая ось эллипса;
1′-2′=d –размер по оси x;
3′-4′=0,5d –размер по оси у;
Э
БО
БО
Э
A'
МОЭ
МОЭ
B' z'
Э
A'
x'
1'
C'
C'
z'
О
3'
М
Э
z'
3'
A'
D'
y'
4'
4'
D'
y'
Для окружностей в плоскости
П2(xOz):
БОЭ=1,06d –большая ось эллипса;
МОЭ=0,94d –малая ось эллипса;
1′-2′=d –размер по оси x;
3′-4′=d –размер по оси z


















































 Математика
Математика Инженерная графика
Инженерная графика








