Похожие презентации:
Сечения призмы
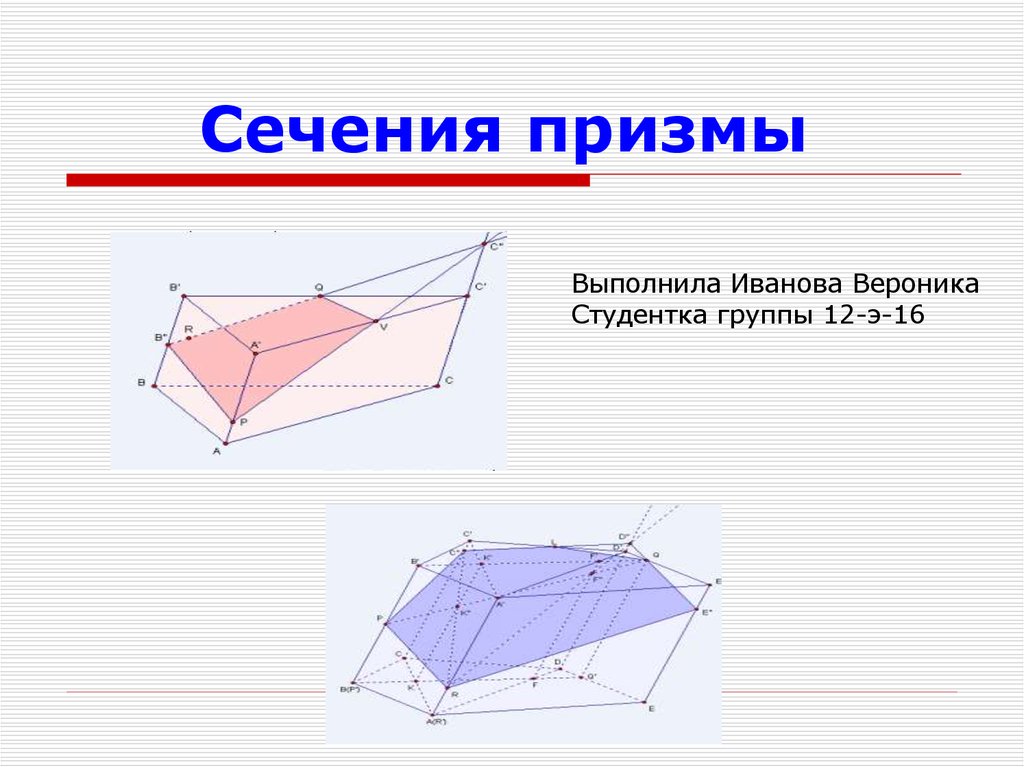
1. Сечения призмы
Выполнила Иванова ВероникаСтудентка группы 12-э-16
2.
Для решения многих геометрическихзадач, необходимо уметь строить
сечения призмы различными
плоскостями
3. Плоская фигура, образовавшаяся при пересечении какой-либо плоскости с пространственной фигурой, называется плоским сечением или просто с
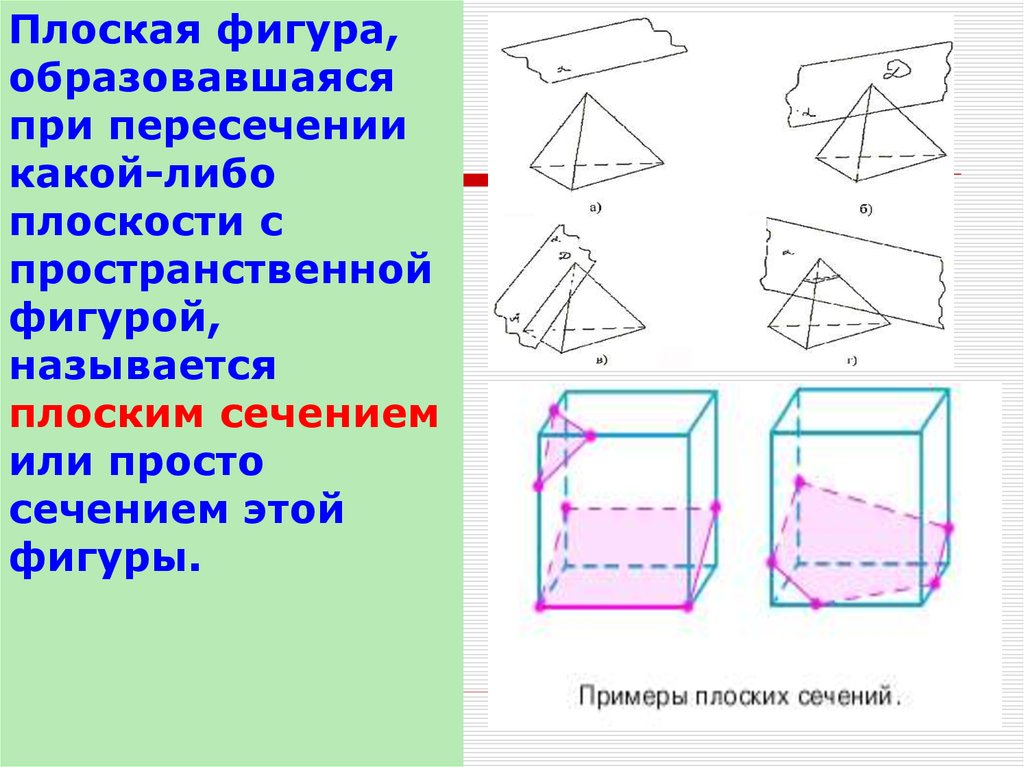
Плоская фигура,образовавшаяся
при пересечении
какой-либо
плоскости с
пространственной
фигурой,
называется
плоским сечением
или просто
сечением этой
фигуры.
4.
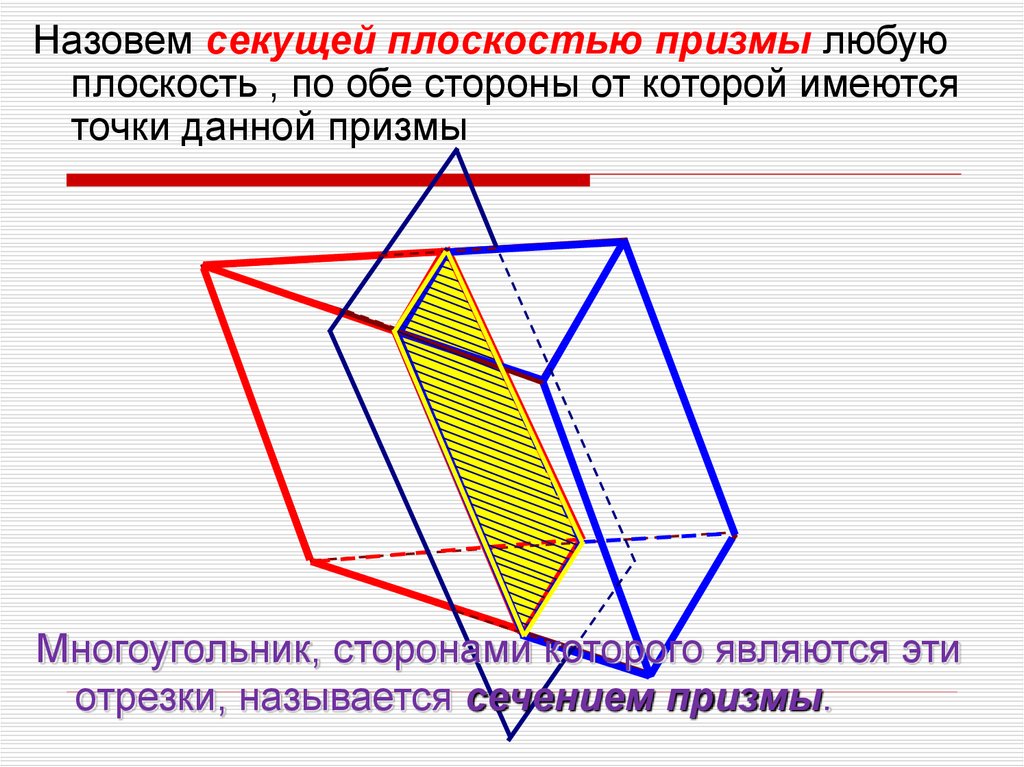
Назовем секущей плоскостью призмы любуюплоскость , по обе стороны от которой имеются
точки данной призмы
Многоугольник, сторонами которого являются эти
отрезки, называется сечением призмы.
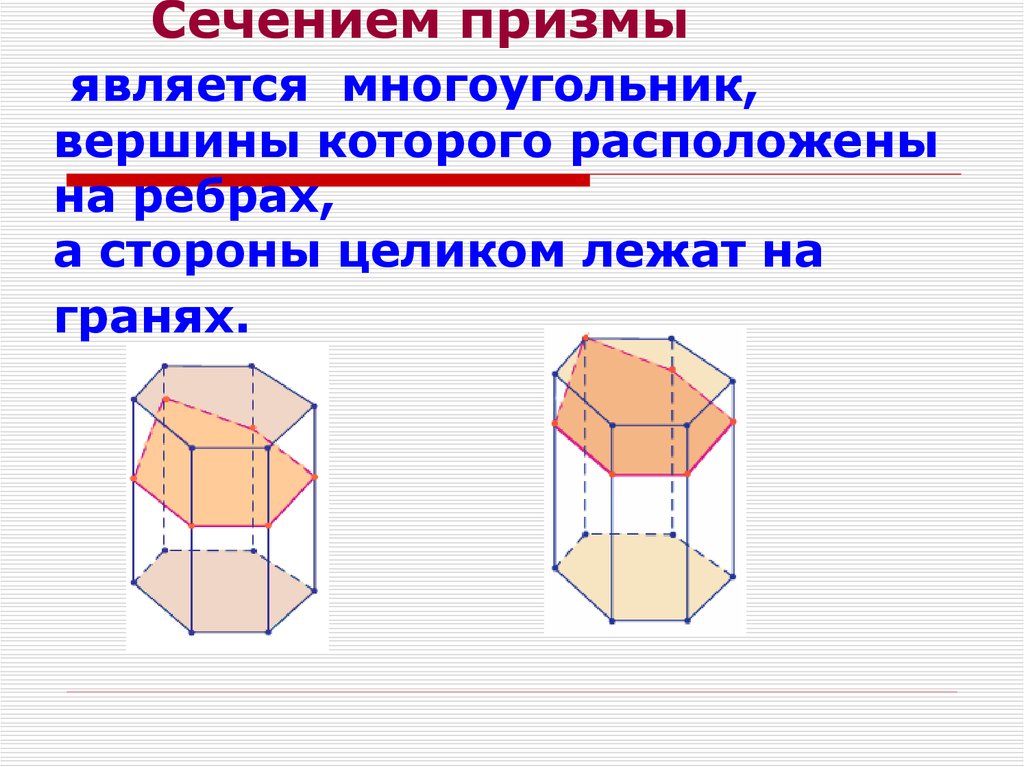
5. Сечением призмы является многоугольник, вершины которого расположены на ребрах, а стороны целиком лежат на гранях.
6. Вид сечения зависит от расположения плоскости
7.
Сечения призмы плоскостями, параллельнымибоковым ребрам, являются параллелограммами
В частности параллелограммами являются диагональные
сечения. Это сечения плоскостями, проходящими через два
боковых ребра, не принадлежащей одной грани.
8.
Построить сечение призмы плоскостью –означает:
В плоскости каждой пересекаемой грани
многогранника указать 2-е точки,
принадлежащие сечению;
Соединить их прямой;
Найти точки пересечения прямой с ребрами
призмы.
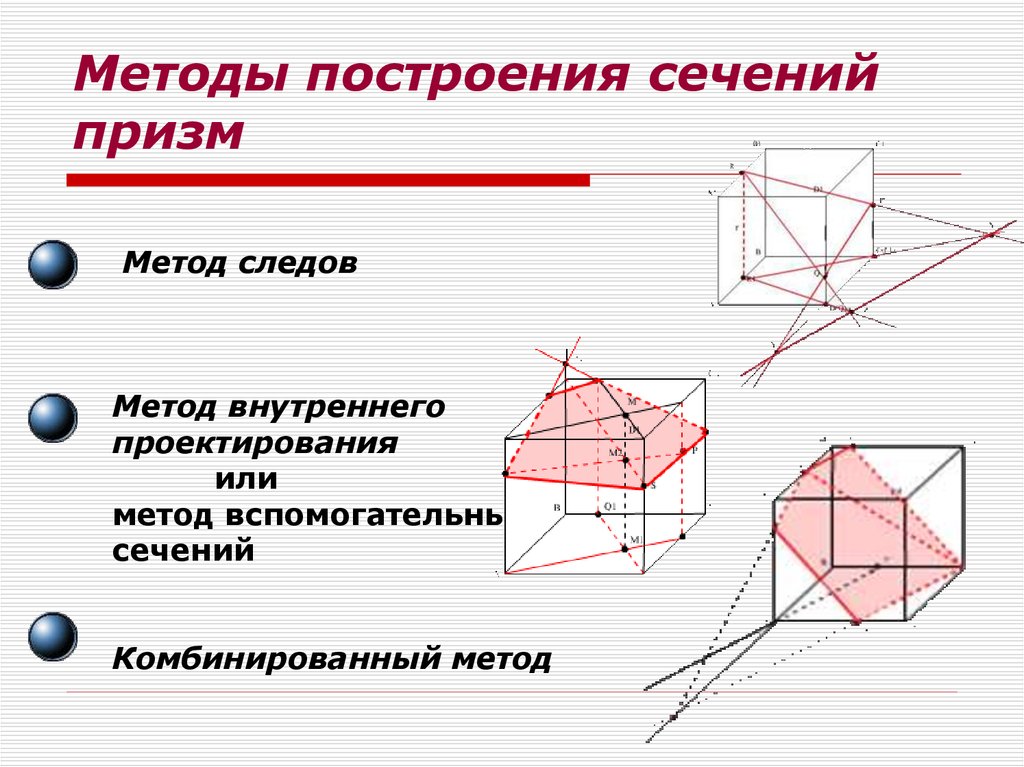
9. Методы построения сечений призм
Метод следовМетод внутреннего
проектирования
или
метод вспомогательных
сечений
Комбинированный метод
10. Метод следов
Если плоскостьпересекает
плоскость
по прямой S, то
прямую S называют следом
плоскости
на плоскость
11. Метод следов
Метод следов включает триважных пункта:
Строится линия пересечения (след)
секущей плоскости с плоскостью
основания многогранника.
Находим точки пересечения
секущей плоскости с ребрами
многогранника.
Строим и заштриховываем сечение.
12.
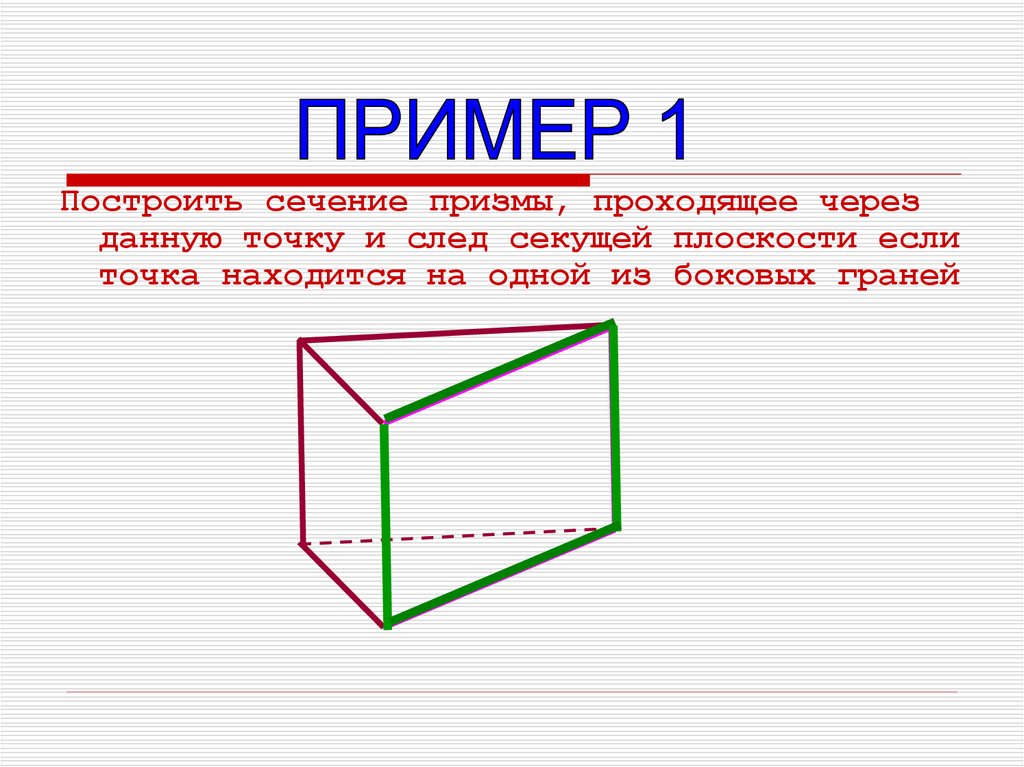
Построить сечение призмы, проходящее черезданную точку и след секущей плоскости если
точка находится на одной из боковых граней
13.
Построим призму14.
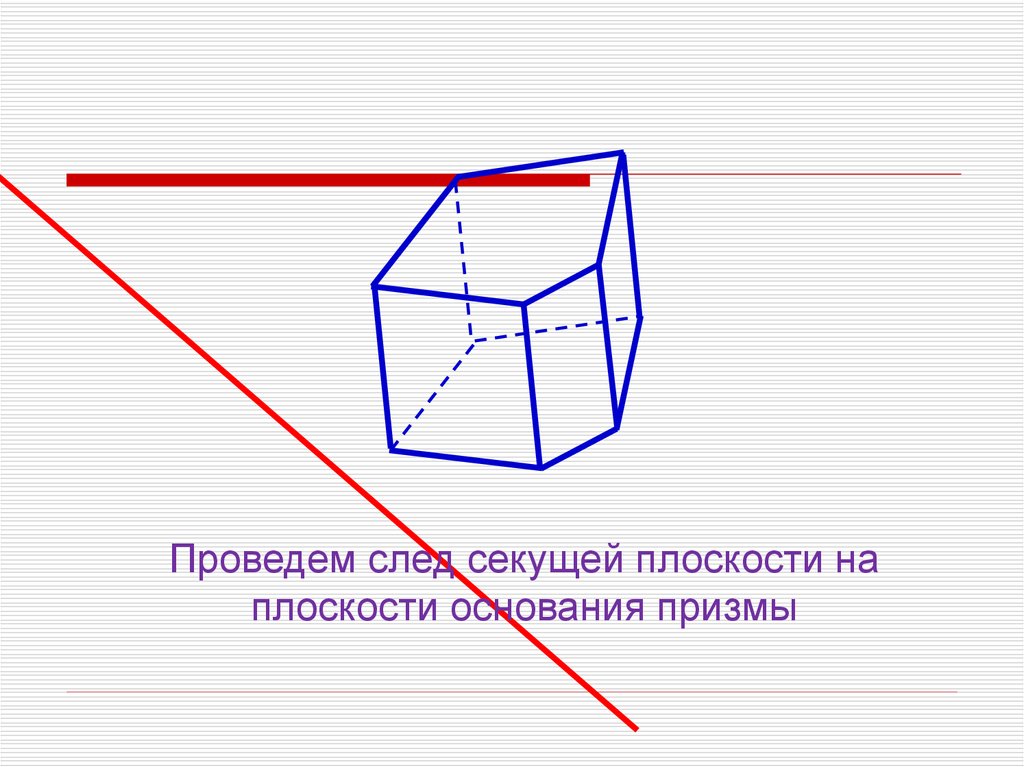
Проведем след секущей плоскости наплоскости основания призмы
15.
АПусть точка А принадлежащая сечению
находится на боковой грани
16.
АСначала строится отрезок, по которому
сечение призмы пересекает грань, на которой
находится данная точка А.
17.
АДля этого построим прямую, по которой
плоскость данной грани
18.
АДля этого построим прямую, по которой
плоскость данной грани
пересекает плоскость основания
19.
АD
пересекает
Эта прямая пересекает след секущей
плоскость основания
плоскости в точке D.
20.
АD
Проведем прямую через точку А и D.
Эта прямая пересекает след секущей
плоскости в точке D.
21.
АС
В
D
Проведем прямую через точку А и D.
22.
Отрезок ВС прямой АD на рассматриваемойграни и есть пересечение этой грани с секущей
плоскостью.
С
А
В
D
Концы отрезка ВС принадлежат и соседним
граням. Поэтому описанным способом можно
построить пересечение и остальных граней с
нашей секущей плоскостью.
23.
Построить сечение призмы, проходящее черезданную точку и след секущей плоскости если
данная точка находится на верхнем
основании
24.
Пусть точка принадлежащая сечению находится на верхнемосновании
Тогда линия пересечения секущей плоскости с верхним основанием
будет параллельна следу секущей плоскости
Проведем след секущей плоскости призмы
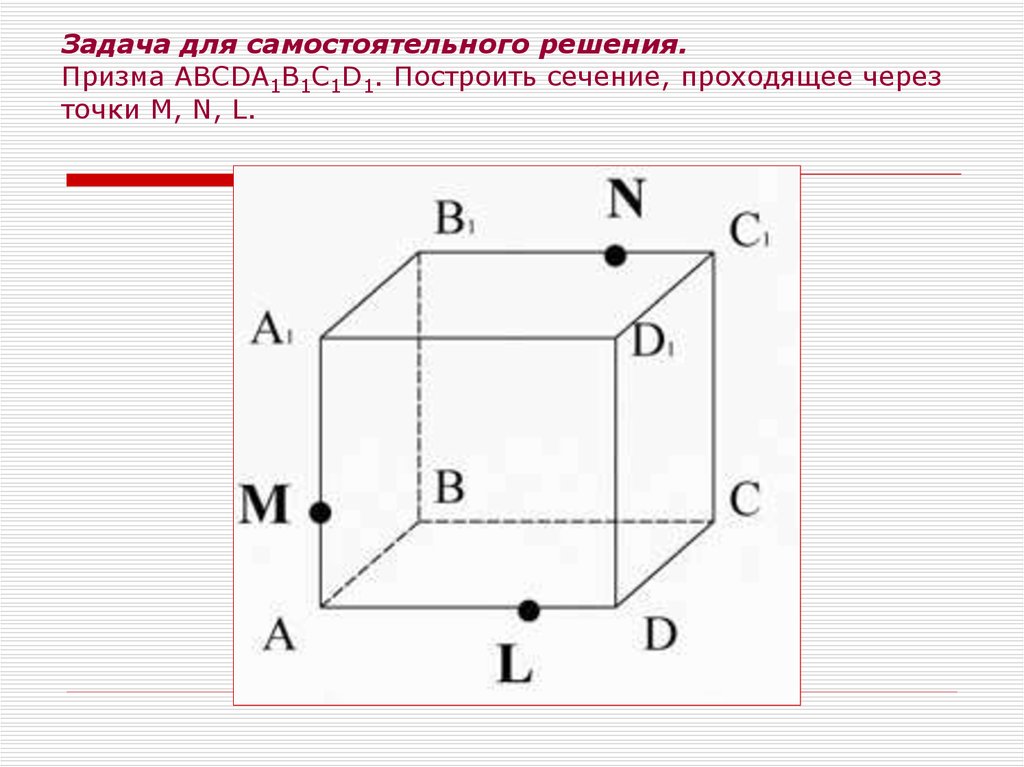
25. Задача для самостоятельного решения. Призма ABCDA1B1C1D1. Построить сечение, проходящее через точки M, N, L.
26.
MKNTPL - искомое сечение.N
B1
X2
C1
K
T
X1
D1
A1
B
C
P
M
A
L X3
D
27.
Найдите площадь поверхности прямойпризмы, в основании которой лежит ромб с
диагоналями, равными 25 и 60, и боковым
ребром, равным 25.
28.
29.
Найдите боковое ребро правильнойчетырехугольной призмы, если
сторона ее основания равна 15, а
площадь поверхности равна 930.























 Математика
Математика








