Оценочная и сравнительная классификация алгоритмов

1. Введение в Машинное обучение

Лекционные слайды по курсу
Введение в
Машинное обучение
ETHEM ALPAYDIN
© The MIT Press, 2004
[email protected]
http://www.cmpe.boun.edu.tr/~ethem/i2ml

2.

Глава 14:
Оценочная и сравнительная
классификация алгоритмов

3. Введение

Вопросы:
Оценка ожидаемой ошибки обучающего
алгоритма: будет ли погрешность метода
ближайшего соседа (k-NN) при k=1 (1-NN) менее
2%?
Сравнение ожидаемых ошибок двух алгоритмов:
метод ближайшего соседа (k-NN) более точен чем
многослойный персептрон (MLP) ?
Обучение/проверка/тестирование выборки
Методы ресамплинга: Кросс-валидация по K блокам
(K-fold cross-validation)
3
Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V1.1)

4. Предпочтение алгоритма

Критерии (зависимые от применения):
Ошибка неверной классификации, или риск
(функции потерь)
Время обучения/ уровень сложности
Время тестирования/ уровень сложности
Интерпретируемость
Лёгкая программируемость
Обучение с учетом издержек классификации (Costsensitive learning)
4
Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V1.1)

5. Ресамплинг и кросс-валидация по K блокам

Необходимость многократного обучения/ оценки
выборки {Xi,Vi}i: Обучения/оценки выборка из i
блоков
Кросс-валидация по K блокам: разделение X на k
блоков, Xi, i=1,...,K
V1 X1
T 1 X2 X3 X K
V2 X2
T 2 X1 X 3 X K
VK X K T K X1 X2 X K 1
Ti делится на K-2 частей
Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V1.1)
5

6. Кросс-валидация 5×2

Кросс-валидация: 5 раз по 2 блока (Dietterich, 1998)
T 1 X1 1
V1 X1 2
2
1
T 2 X1
V2 X1
T 3 X2 1
V3 X2 2
T 4 X2 2
V4 X2 1
T 9 X5 1
2
T 10 X5
V9 X5 2
1
V10 X5
6
Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V1.1)

7. Выборка с возвратом (Bootstrapping)

Возьмём образцы из выборки с последующим их
возвратом
Вероятность того, что мы не выберем образец после
N попыток
N
1
1
1 e 0.368
N
то есть, только 36.8% образцов являются новыми!
7
Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V1.1)

8. Ошибки измерения

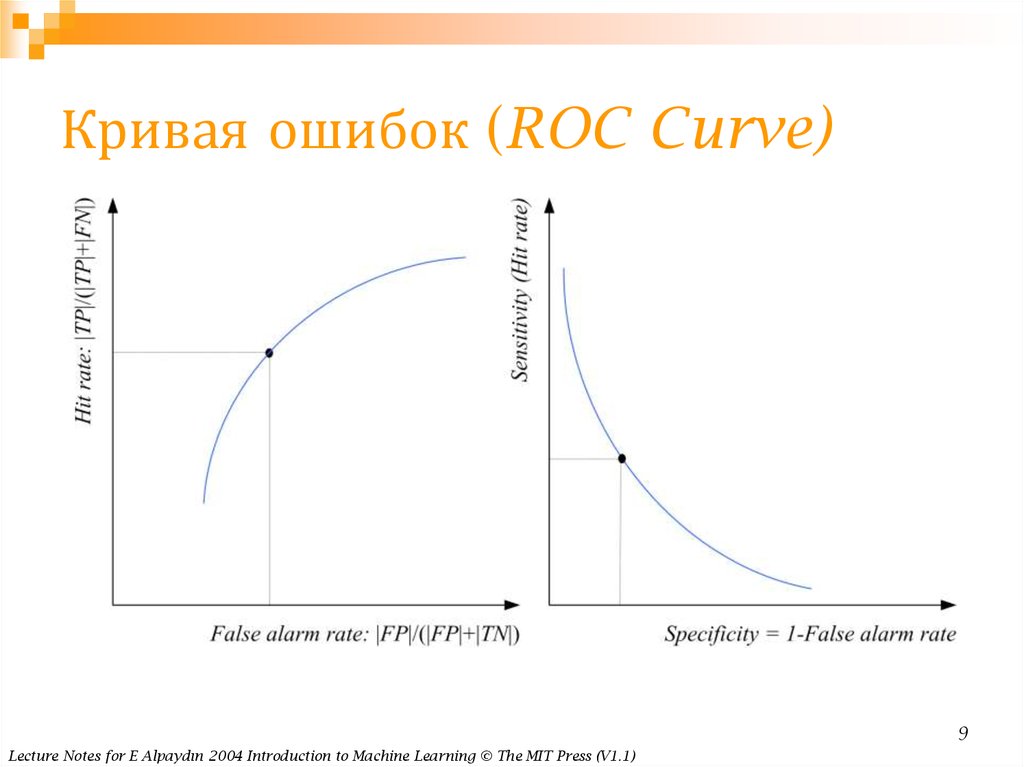
Уровень ошибки = (FN+FP) / N
Возврат = TP / (TP+FN) = чувствительность =
коэффициент совпадений
Точность = TP / (TP+FP)
Определенность = TN / (TN+FP)
Частота ложных тревог = FP / (FP+TN) = 1 - Specificity
8
Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V1.1)

9. Кривая ошибок (ROC Curve)

9
Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V1.1)

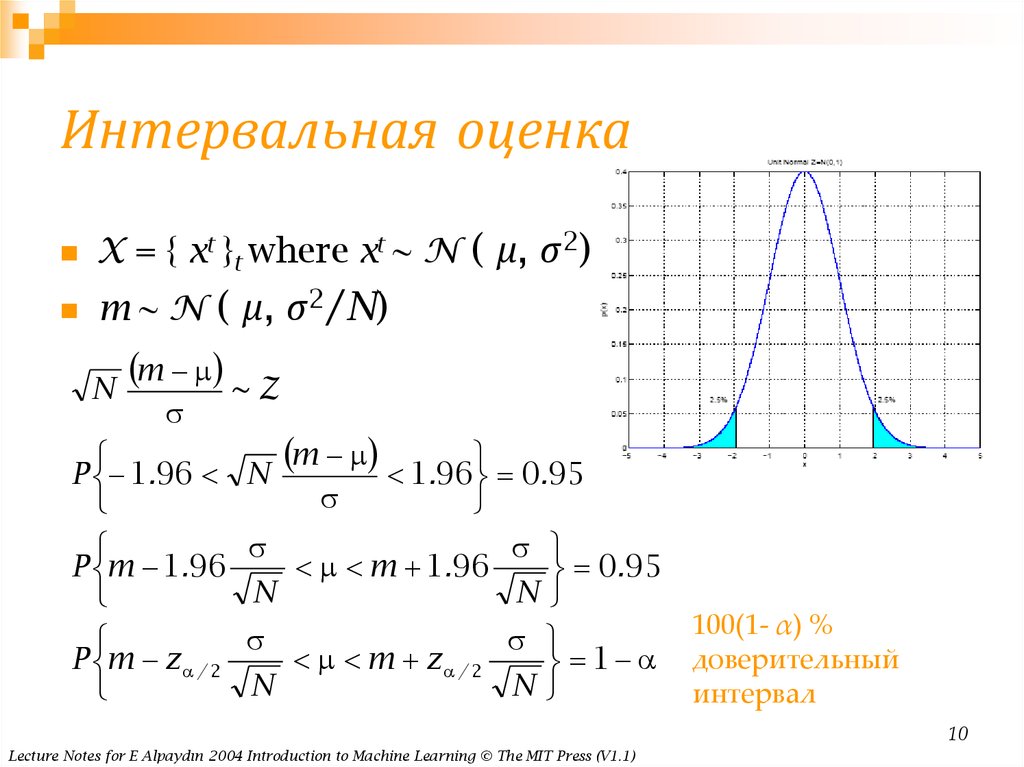
10. Интервальная оценка

X = { xt }t where xt ~ N ( μ, σ2)
m ~ N ( μ, σ2/N)
N
m ~ Z
m
P 1.96 N
1.96 0.95
P m 1.96
m 1.96
0.95
N
N
P m z / 2
m z / 2
1
N
N
100(1- α) %
доверительный
интервал
10
Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V1.1)

11.

m
P N
1.64 0.95
P m 1.64
0.95
N
P m z
1
N
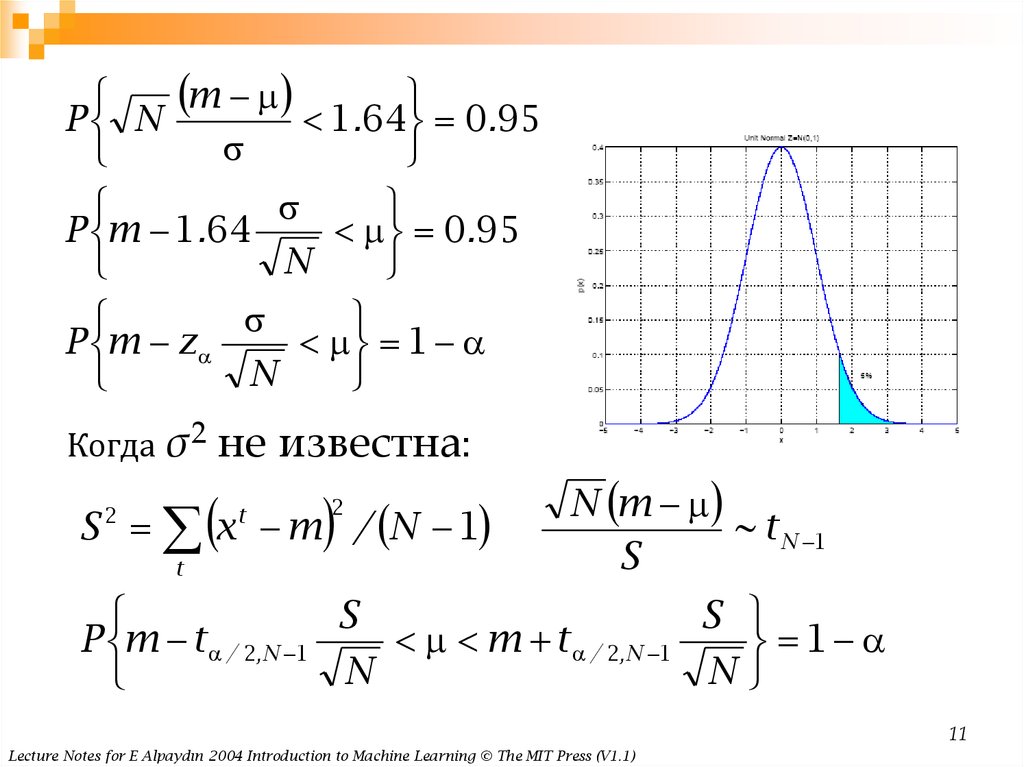
Когда
σ2 не известна:
S x m / N 1
2
t
t
2
N m
~ t N 1
S
S
S
P m t / 2,N 1
m t / 2,N 1
1
N
N
11
Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V1.1)

12. Проверка гипотезы

Отклоняем недостоверную гипотезу если она не
подкреплена выборкой с достаточной
достоверностью
X = { xt }t где xt ~ N ( μ, σ2)
H0: μ = μ0 или H1: μ ≠ μ0
Принимаем H0 с уровнем значимости α если μ0
находится в N
100(1 m α)
доверительном интервале
0
z / 2 , z / 2
Двусторонний тест
12
Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V1.1)

13.

Односторонняя проверка: H0: μ ≤ μ0 или H1: μ > μ0
Принимаем если
N m 0
, z
Дисперсия неизвестна: используем t, вместо z
Принимаем H0: μ = μ0 если
N m 0
t / 2,N 1 ,t / 2,N 1
S
13
Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V1.1)

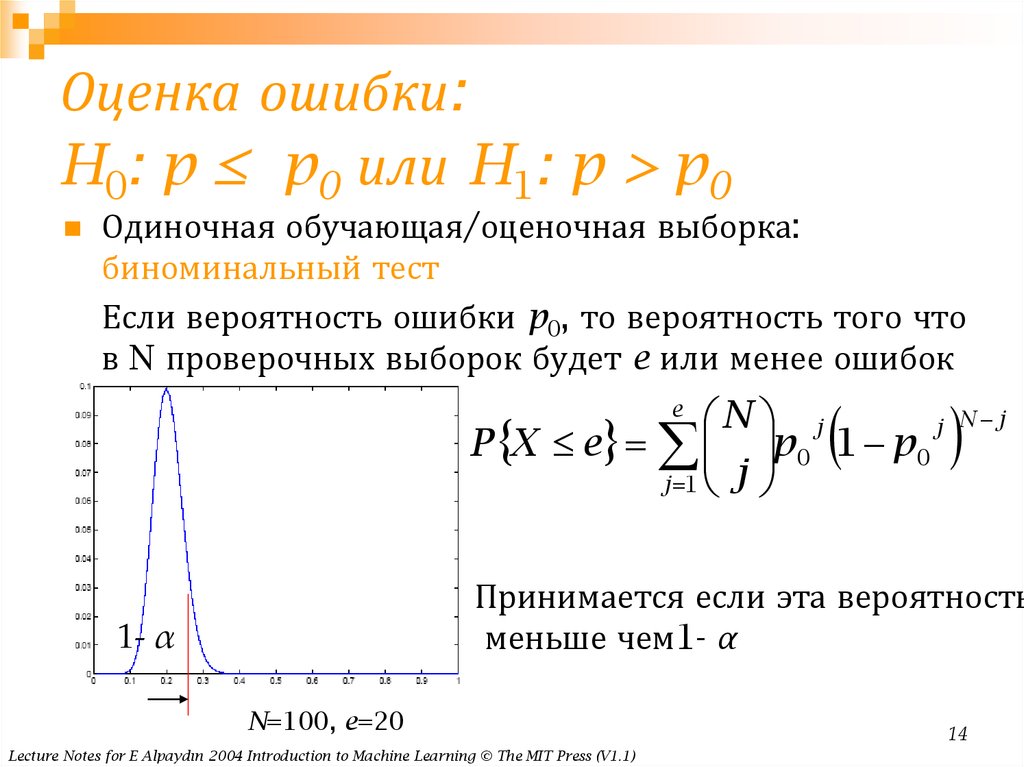
14. Оценка ошибки: H0: p ≤ p0 или H1: p > p0

Оценка ошибки:
H0: p ≤ p0 или H1: p > p0
Одиночная обучающая/оценочная выборка:
биноминальный тест
Если вероятность ошибки p0, то вероятность того что
в N проверочных выборок будет e или менее ошибок
N j
j
P X e p 0 1 p 0
j 1 j
e
N j
Принимается если эта вероятность
меньше чем1- α
1- α
N=100, e=20
Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V1.1)
14

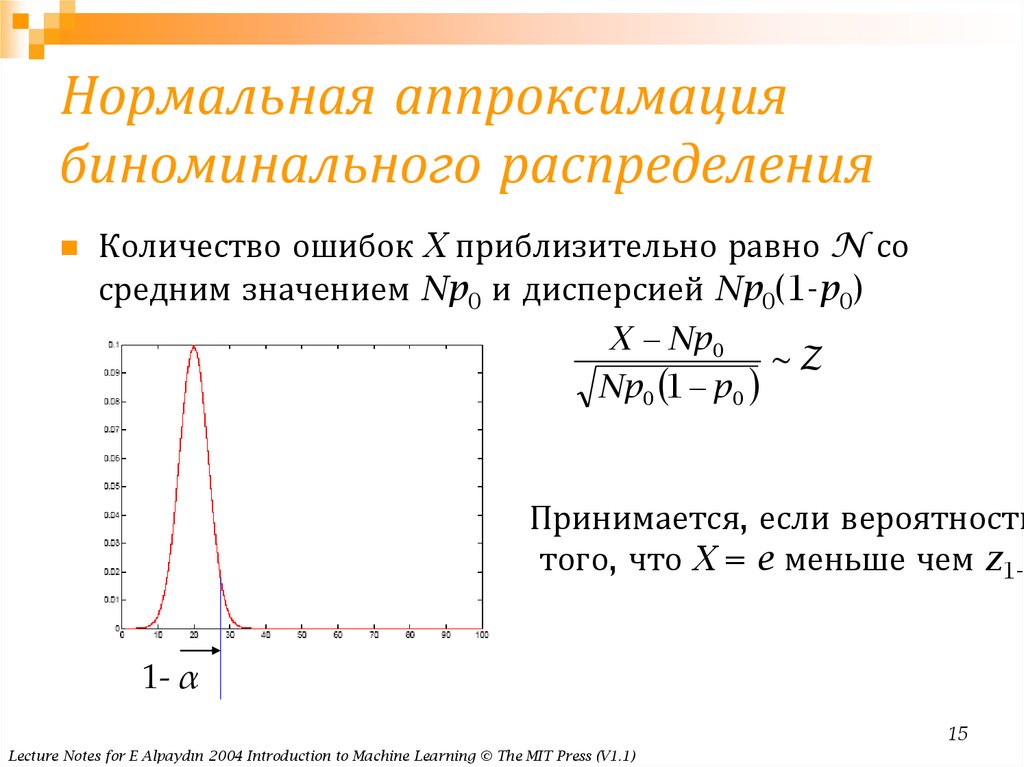
15. Нормальная аппроксимация биноминального распределения

Количество ошибок X приблизительно равно N со
средним значением Np0 и дисперсией Np0(1-p0)
X Np 0
~Z
Np 0 1 p 0
Принимается, если вероятность
того, что X = e меньше чем z1-α
1- α
15
Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V1.1)

16. t-тест для парных выборок

Многократное обучение/оценка выборки
xti = 1 если объект t неверно классифицирован на
N
свертке i
t
x
t 1 i
Уровень ошибки на свертке i:pi
N
С помощью m и s2 - математического ожидания и
дисперсии pi мы принимаем p0 или меньшую ошибку
если
K m p 0
~ t K 1
S
меньше чем tα,K-1
16
Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V1.1)

17. Сравнительные классификаторы: H0: μ0 = μ1 или H1: μ0 ≠ μ1

Однократное обучение/оценка выборки: тест МакНимара
Под H0, мы понимаем e01= e10=(e01+ e10)/2
e
Принимаем если< X2α,1
e10 1
2
01
e01 e10
~ X12
17
Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V1.1)

18. Кросс-валидация по K блокам CV t-тест для парных выборок

Используем кросс-валидацию по K блокам cv чтобы
получить K обучающих/оценочных блоков
pi1, pi2:Ошибки функции классификации 1 и 2 на
блоке i
pi = pi1 – pi2 : спаренное различие на блоке i
Нулевая гипотеза это имеет ли pi среднее значение,
равное 0
18
Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V1.1)

19. Кросс-валидация 5×2 cv t-тест для парных выборок

Используем 5×2 cv чтобы получить 2 блока из 5
обучений/оценок репликаций (Dietterich, 1998)
pi(j) : разница между ошибками 1 и 2 на блоках j=1,
2 репликации i=1,...,5
1
2
pi pi pi
/ 2
2
i
1
s pi pi
p1 1
2
s
i 1 i / 5
5
p
2
2
i
pi
2
~ t5
Двусторонняя проверка: принимаем H0: μ0 = μ1 если
находится в интервале (-tα/2,5,tα/2,5)
Односторонняя проверка: принимаем H0: μ0 ≤ μ1
если < tα,5
Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V1.1)
19

20. Кросс-валидация 5×2 cv F-тест для парных выборок

p
2 s
j
5
2
i 1
i
j 1
5
2
i 1 i
2
~ F10 ,5
Двусторонняя проверка: Принимаем H0: μ0 = μ1 если < Fα,10,5
20
Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V1.1)

21. Сравнение L>2 алгоритмов: анализ отклонений (Дисперсионный анализ)

Сравнение L>2 алгоритмов:
анализ отклонений
(Дисперсионный анализ)
H 0 : 1 2 L
Ошибки L алгоритмов на K блоках
X ij ~ N j , 2 , j 1,..., L, i 1,..., K
Мы строим две оценочные функции для σ2 .
Первая действительна если H0 истина, другая
действительна всегда.
Мы отклоняем H0 если две оценочные функции не
совпадают.
21
Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V1.1)

22.

22
Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V1.1)

23.

23
Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V1.1)

24. Другие тесты

Оценка диапазона (Ньюмена-Койлса):145 23
Непараметрические тесты (Критерий знаков,
Крускала — Уоллиса)
Противопоставление: Проверить отличаются ли 1 и 2
от 3,4, и 5
Множественные сравнения требуют Поправки
Бонферрони если для достижения уровня α есть m
гипотез, то каждая из них должна иметь значение
α/m.
Регрессия: Центральная предельная теорема
утверждает что сумма независимых одинаково
распределённых случайных величин переменных
любого распределения есть величина
приблизительно нормальная и к ней могут быть
24
применены
предшествующие
методы
Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V1.1)