Похожие презентации:
Элементы корреляционного анализа. Элементы корреляционного анализа
1. Пример записи решения задания РГР №3
ПРИМЕР ЗАПИСИ РЕШЕНИЯ ЗАДАНИЯРГР №3
Часть I. Элементы корреляционного анализа
Задание:
1.
Вычислить
коэффициент
корреляции
для
сгруппированных
данных
методом
условных
вариант.
2. Вычислить ошибку коэффициента корреляции.
Часть II. Элементы регрессионного анализа
Задание:
1. Составить уравнения регрессии y(x) и x(y).
2. Построить корреляционное поле и линию регрессии
y(x).
3. Сделать общий по двум частям вывод.
2.
Исходные данные:Корреляционная таблица зависимости между
числом эритроцитов (X в млн.) и
содержанием гемоглобина (Y в %) в крови
Y
X
42
32-52
62
52-72
82
72-92
nx
Аx 1,8
0,8
1,8
2,8
0,3-1,3
2
1,3-2,3
2
2,3-3,3
ny
4
4
1
5
1
1
2
n=10
2
Аy 62
6
hx 1
hy 20
3.
Часть I. Элементы корреляционного анализа1. Вычислим коэффициент корреляции для сгруппированных
данных методом условных вариант.
а). Переходим к условным вариантам
xi Ax
ui
hx
Аx 1,8
hx 1
vi
u
и
v:
yi Ay
Аy 62
hy
hy 20
0,8 1,8
u1
1
1
1,8 1,8
u2
0
1
42 62
v1
1
20
62 62
v2
0
20
2,8 1,8
u3
1
1
82 62
v3
1
20
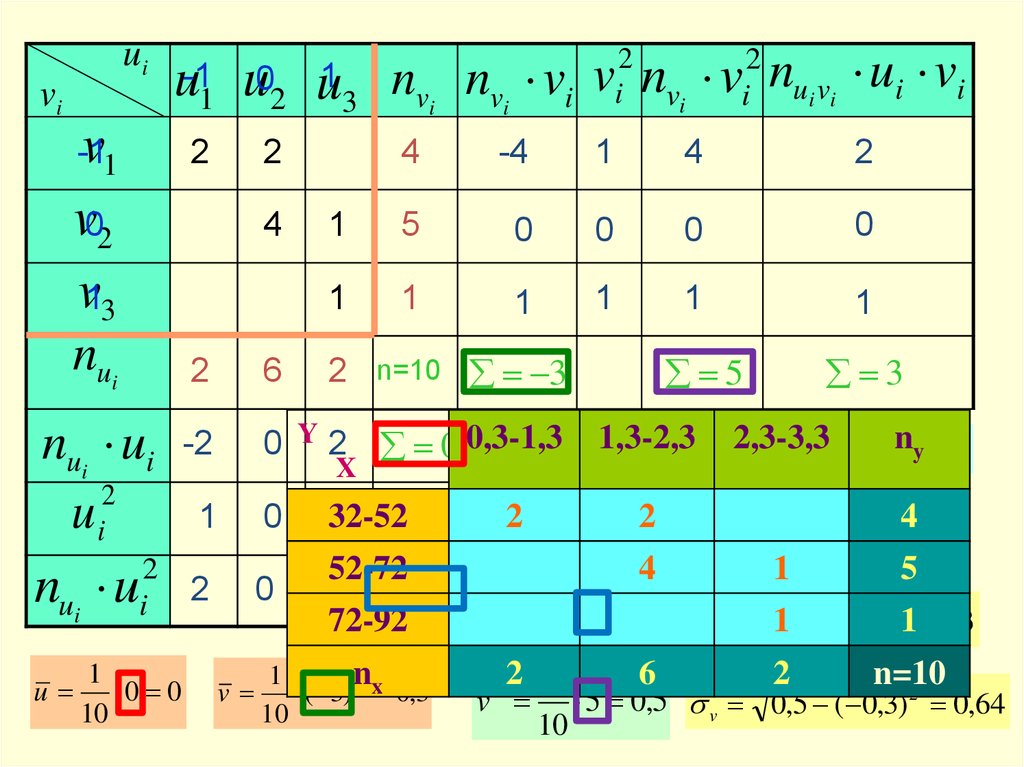
б). Вычислим основные статистические характеристики
,
, u , v :
u v
4.
uivi
u-1
1
u02
2
2
v1
-1
v02
v13
nui
nui ui
2
ui
2
nui ui
u
1
0 0
10
4
u1
3
nvi nvi vi v nvi v nui vi ui vi
2
i
4
-4
1
4
2
1
5
0
0
0
0
1
1
1
1
1
1
2 n=10 3
2
6
-2
0 Y 2 0 0,3-1,3
X
1
0
2
0
v
2
i
32-52
1
2
5
3
1,3-2,3
2 ( 1)2,3-3,3
( 1) 2 0n (y 1)
24 0 0 1 1 0
4
52-72
41 1 1
1
5
2 4 2 1
u 4 0,4 u 10,4 (0)2 1 0,63
72-92
n
1
( 3) x 0,3
10
10
2 1
6
2
n=10
2
v 5 0,5 v 0,5 ( 0,3)2 0,64
10
5.
в). Вычислим коэффициент корреляции:3 10 0 ( 0,3)
3
r
0,74
10 0,63 0,64
4,03
2. Вычислим ошибку коэффициента корреляции:
1 0,742
0,45
Sr
0,24
10 2
8
6.
Часть II. Элементы регрессионного анализа1. Составим уравнения регрессии y(x) и x(y).
by
b
x
а). Вычислим коэффициенты регрессии
и
:
y
b x 0,74
y
0,63 1
0,74 0,05 0,04
0,64 20
0,64 20
b y 0,74
0,74 20,32 15,04
0,63 1
x
б). Вычислим выборочные средние
x
и
y:
x 1,8 0 1 1,8
y 62 ( 0,3) 20 56
x
7.
в). Составим уравнения регрессии:ax 1,8 0,04 56 0,44
x 0,44 0,04 y - уравнение регрессии X от Y
a y 56 15,04 1,8 28,93
y 28,93 15,04 x - уравнение регрессии Y от X
8.
2. Построим корреляционное поле и линию регрессии y(x).Для построения линии регрессии y(x) возьмем два
произвольных значения x и вычислим соответствующие
значения y.
x
1
2
y
44
59
yi
80
60
40
20
0
1
2
3
xi
9.
3. ВыводКоэффициент корреляции r = 0,74 ± 0,24 свидетельствует
о сильной тесноте взаимосвязи между рассматриваемыми
признаками. Положительное значение коэффициента
корреляции говорит о прямой взаимосвязи, то есть с
увеличением числа эритроцитов содержание гемоглобина
в крови также увеличивается и наоборот. По уравнению
регрессии Y от X можно прогнозировать содержание
гемоглобина
в
крови
по
числу
эритроцитов.
Коэффициент регрессии Y на X равен 15,04, то есть при
увеличении числа эритроцитов на 1млн, содержание
гемоглобина в крови увеличится на 15,04 %.








 Математика
Математика








