Похожие презентации:
Корреляционный анализ данных. Лекция 9
1. Математика, часть 2
Кафедра маркшейдерского делаМатематика, часть 2
Корреляционный анализ данных
Лекция № 9
2. Система двух и более случайных величин
Кафедра маркшейдерского делаСистема двух и более
случайных величин
Данные, содержащими две или n случайных величин называются
– двумерными
– n - мерными
(Х, Y) - Обозначение двумерной случайной величины
Х, Y – составляющие или компоненты случайной величины (Х, У).
Примеры ДСВ:
геологическая проба руды, содержащая золото – Х и серебро – Y
результаты геохимического опробования образцов железорудного
месторождения, где кроме содержания железа определяется содержание
марганца, титана, висмута, ванадия и других компонентов.
Необходимо различать
– дискретные случайные величины
– непрерывные случайные величины
Z
3. Изображение системы из двух случайных ведичин
Кафедра маркшейдерского делаИзображение системы из
двух случайных ведичин
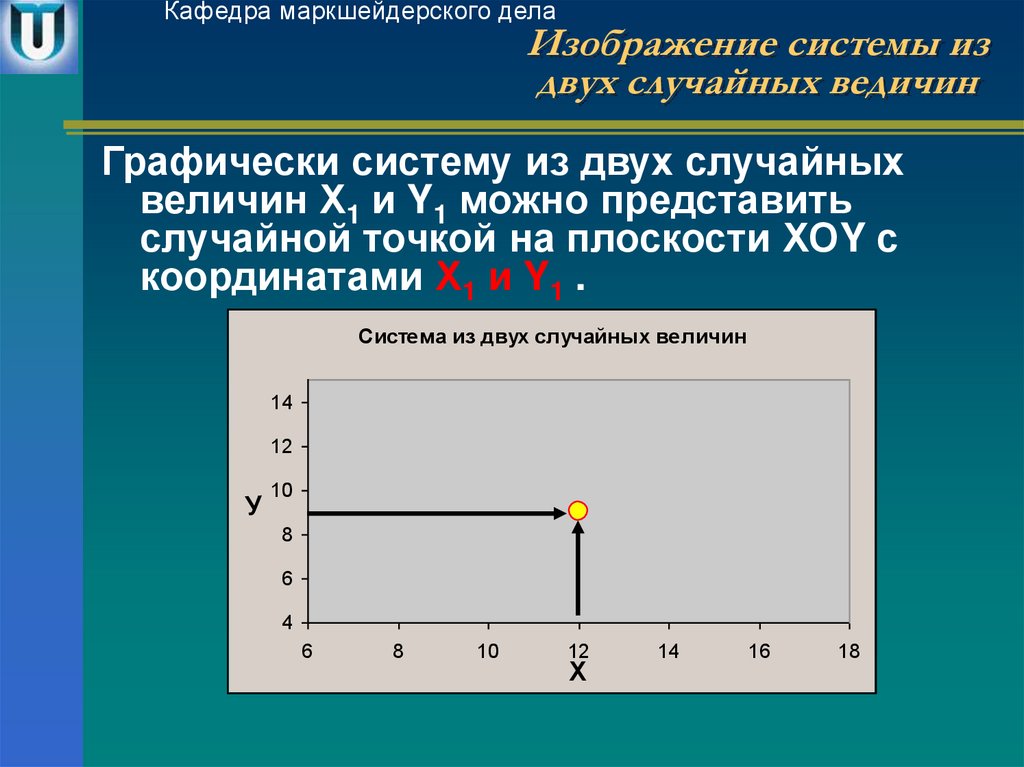
Графически систему из двух случайных
величин Х1 и Y1 можно представить
случайной точкой на плоскости ХОY с
координатами Х1 и Y1 .
Система из двух случайных величин
14
12
У
10
8
6
4
6
8
10
12
Х
14
16
18
4. Изображение системы из трёх случайных величин
Кафедра маркшейдерского делаИзображение системы из
трёх случайных величин
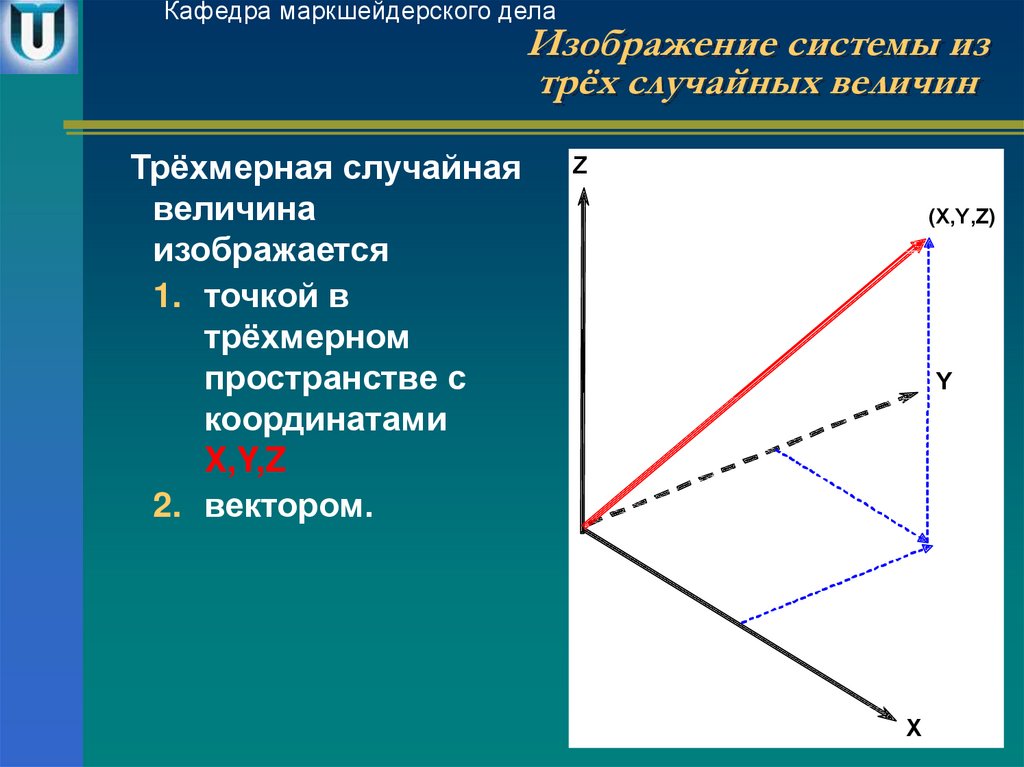
Трёхмерная случайная
величина
изображается
1. точкой в
трёхмерном
пространстве с
координатами
X,Y,Z
2. вектором.
Z
(X,Y,Z)
Y
X
5. 2 задачи корреляционного анализа
Кафедра маркшейдерского дела2 задачи корреляционного анализа
Зольность, %
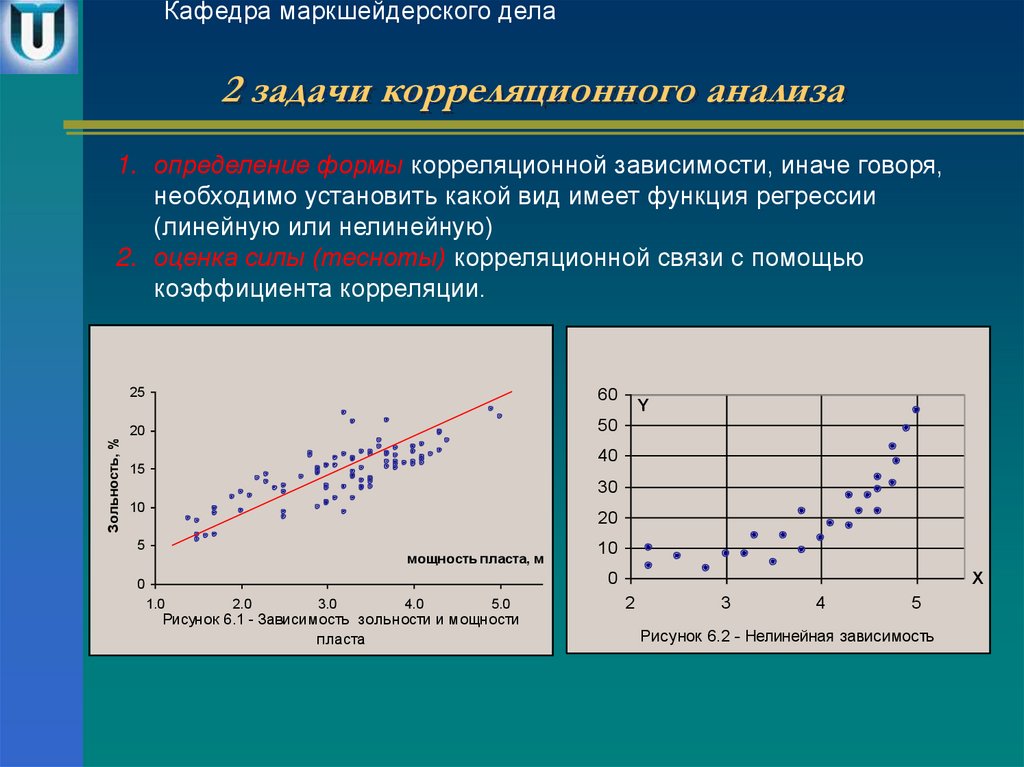
1. определение формы корреляционной зависимости, иначе говоря,
необходимо установить какой вид имеет функция регрессии
(линейную или нелинейную)
2. оценка силы (тесноты) корреляционной связи с помощью
коэффициента корреляции.
25
60
20
50
Y
40
15
30
10
20
5
мощность пласта, м
10
0
0
1.0
2.0
3.0
4.0
5.0
Рисунок 6.1 - Зависимость зольности и мощности
пласта
X
2
3
4
5
Рисунок 6.2 - Нелинейная зависимость
6. Закон распределения дискретной двумерной СВ
Кафедра маркшейдерского делаЗакон распределения
дискретной двумерной СВ
1. Законом распределения дискретной двумерной случайной
величины называют перечень возможных значений этой величины
(т. е. пар чисел (xi и у j ) и их вероятностей p(xi , уj ) (i=l, 2, ..., n; j=1,
2, ..., т). Обычно закон распределения задают в виде таблицы с
двойным входом
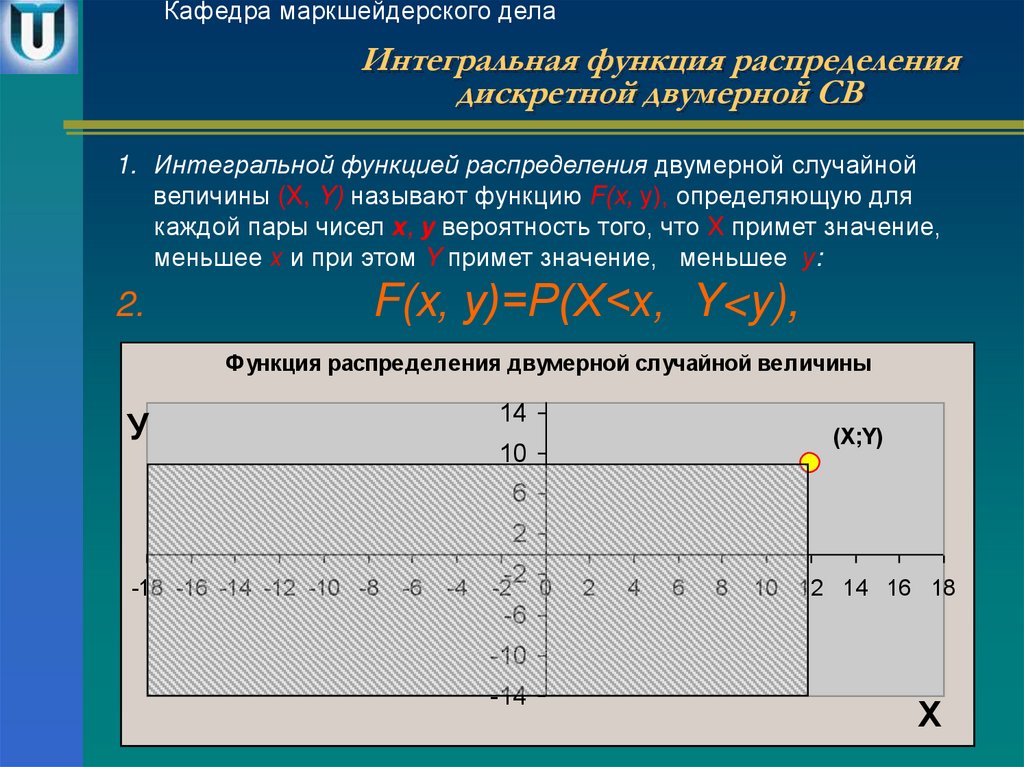
7. Интегральная функция распределения дискретной двумерной СВ
Кафедра маркшейдерского делаИнтегральная функция распределения
дискретной двумерной СВ
1. Интегральной функцией распределения двумерной случайной
величины (X, Y) называют функцию F(x, у), определяющую для
каждой пары чисел х, у вероятность того, что X примет значение,
меньшее х и при этом Y примет значение, меньшее у:
2.
F(x, у)=Р(Х<х, Y<y),
Функция распределения двумерной случайной величины
14
У
(X;Y)
10
6
2
-18 -16 -14 -12 -10 -8
-6
-4
-2
-2
0
2
4
6
8
10 12 14 16 18
-6
-10
-14
Х
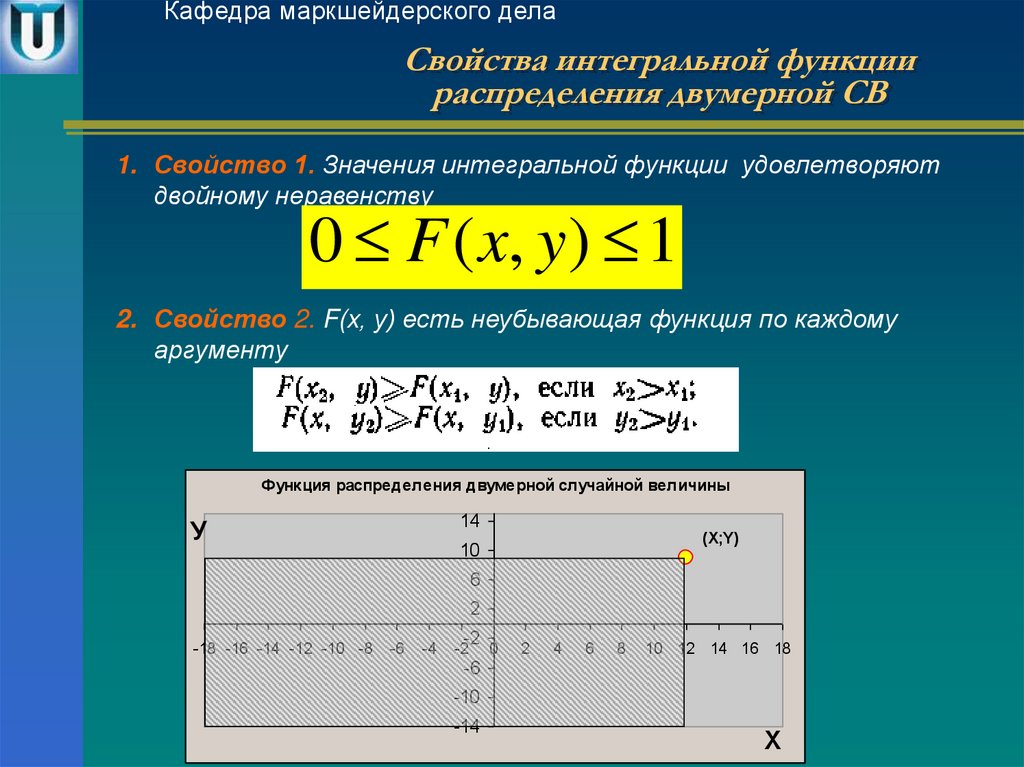
8. Свойства интегральной функции распределения двумерной СВ
Кафедра маркшейдерского делаСвойства интегральной функции
распределения двумерной СВ
1. Свойство 1. Значения интегральной функции удовлетворяют
двойному неравенству
0 F ( x, y) 1
2. Свойство 2. F(x, у) есть неубывающая функция по каждому
аргументу
Функция распределения двумерной случайной величины
14
У
(X;Y)
10
6
2
-18 -16 -14 -12 -10 -8
-6
-4
-2
-2
0
2
4
6
8
10 12 14 16 18
-6
-10
-14
Х
9. Свойства интегральной функции распределения двумерной СВ
Кафедра маркшейдерского делаСвойства интегральной функции
распределения двумерной СВ
3. Свойство 3. Имеют место предельные соотношения:
Функция распределения двумерной случайной величины
14
У
(X;Y)
10
6
2
-18 -16 -14 -12 -10 -8
-6
-4
-2
-2
0
2
4
6
8
10 12 14 16 18
-6
-10
-14
4. Свойство 4.
а) При y= интегральная функция системы становится
интегральной функцией составляющей X:
F(x, )=F1 (x).
б) При х= интегральная функция системы становится
интегральной функцией составляющей Y:,
Х
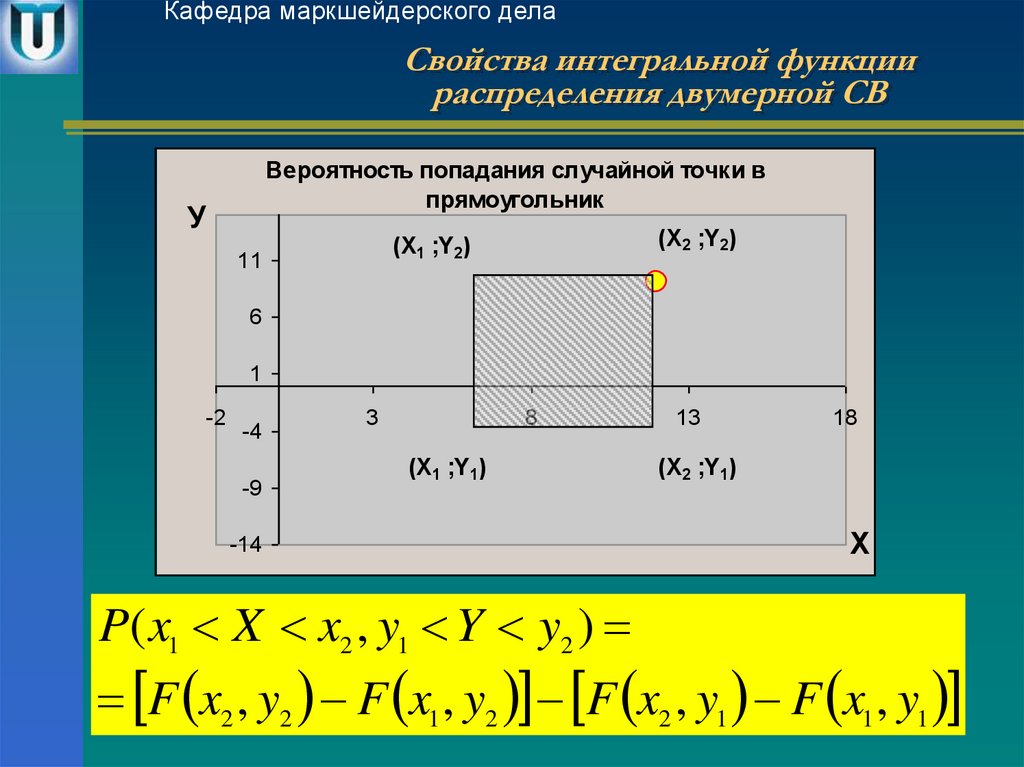
10. Свойства интегральной функции распределения двумерной СВ
Кафедра маркшейдерского делаСвойства интегральной функции
распределения двумерной СВ
Вероятность попадания случайной точки в
прямоугольник
У
(X2 ;Y2)
(X1 ;Y2 )
11
6
1
-2
-4
-9
3
8
(X1 ;Y1)
-14
P( x1 X x2 , y1 Y y2 )
13
18
(X2 ;Y1)
Х
F x2 , y2 F x1 , y2 F x2 , y1 F x1 , y1
11. Двумерная плотность вероятности
Кафедра маркшейдерского делаДвумерная плотность вероятности
Дифференциальной функцией распределения f(x, у)
двумерной непрерывной случайной величины (X, Y)
называют вторую смешанную частную производную
от интегральной функции:
F ( x, y )
f x, y
x y
2
Геометрически эту функцию можно истолковать как поверхность,
которую называют поверхностью распределения.
Зная дифференциальную функцию f(x, у), можно найти интегральную
функцию F(x, у) по формуле
12. Свойства дифференциальной функции распределения
Кафедра маркшейдерского делаСвойства дифференциальной функции
распределения
1.
Свойство 1. Дифференциальная функция
неотрицательна:
2.
Свойство 2. Двойной несобственный интеграл с
бесконечными пределами от дифференциальной
функции равен единице:
13. Отыскание дифференциальных функций
Кафедра маркшейдерского делаОтыскание дифференциальных функций
14. Зависимые и независимые СВ
Кафедра маркшейдерского делаЗависимые и независимые
СВ
две случайные величины называются независимыми, если закон
распределения одной из них не зависит от того, какие возможные
значения приняла другая величина.
Теорема. Для того чтобы случайные величины X и У были
независимыми, необходимо и достаточно, чтобы интегральная
функция системы (X, Y) была равна произведению интегральных
функций составляющих:
Следствие. Для того чтобы непрерывные случайные величины X
и У были независимыми, необходимо и достаточно, чтобы
дифференциальная функция системы (X, Y) была равна
произведению дифференциальных функций составляющих:
15. Корреляционный момент
Кафедра маркшейдерского делаКорреляционный момент
Корреляционным моментом μxy случайных величин X и Y называют
математическое ожидание произведения отклонений этих величин:
Для вычисления корреляционного момента дискретных величин
пользуются формулой
а для непрерывных
Теорема. Корреляционный момент двух независимых случайных
величин X и Y равен нулю.
16. Коэффициент корреляции. Зависимые СВ
Кафедра маркшейдерского делаКоэффициент корреляции.
Зависимые СВ
Две случайные величины могут быть связаны между собой
функциональной зависимостью, статистической либо независимыми между
собой.
Строгая функциональная зависимость случайных величин X и Y
встречается крайне редко и может быть записана, например, в виде:
Y aX b
(6.1)
Эта запись означает, что каждому значению Х соответствует только одно
значение У. Функциональную зависимость можно ещё назвать теоретической.
Как правило, случайные величины подвержены влиянию не одного
фактора, а целого набора случайных факторов. В результате одному значению
X соответствует не одно, а множество значений Y . Это множество называется
законом распределения случайной величины Y . В таком случае говорят о
статистической (корреляционной) зависимости, при которой изменение
случайной величины X вызывает изменение некоторых параметров
распределения другой - Y , в частности, среднего значения Y .
17. Пример корреляционной зависимости
Кафедра маркшейдерского делаПример корреляционной
зависимости
Пример случайной величины Y , которая не связана с величиной X
функционально, а связана корреляционно.
Одинаковые по форме образцы руды с одинаковым содержанием
полезного компонента X характеризуются разной
плотностью. Это
объясняется тем, что на плотность образца породы, кроме удельного веса
полезного компонента, влияют такие случайные факторы, как разная
пористость, разное количество включений других минералов и др.
Таким образом,
конкретная плотность Y руды не связана
функционально с конкретным содержанием полезных компонентов. Однако
практика показывает, что на полиметаллических месторождениях (свинцовоцинковых) в среднем на плотность руды Y влияет суммарное содержание
свинца и цинка в пробе X , т.е. плотность Y связана с X корреляционной
зависимостью.
18. Условные средние
Кафедра маркшейдерского делаУсловные средние
Условным средним y x называют среднее арифметическое значений Y ,
соответствующих значению случайной величины X x .
Допустим, что в процессе эксперимента мы отобрали 3 образца с
одинаковым значением содержания и определили плотность каждого из них.
Так для содержания x1 35% получены три значения плотности y1 3.30 т/м3,
y 2 3.26 т/м3 , y 3 3.28 т/м3. Среднее арифметическое значение плотности
определяется по формуле 3.2 и будет равно:
3.30 3.26 3.28
y 35
3.28 .
3
Число y 35 называется условным средним, чёрточка над буквой служит
обозначением
среднего
арифметического,
цифра
35
означает,
что
рассматриваются только те значения плотности Y , которые соответствуют
содержанию полезных компонентов в образце породы x1 35% .
19. Корреляционная зависимость
Кафедра маркшейдерского делаКорреляционная
зависимость
Если каждому значению x соответствует одно значение условной средней
y x , то считается, что случайная величина Y зависит от X корреляционно.
Корреляционной зависимостью Y от X называют функциональную
зависимость условной средней y x от x :
yx f ( x ) ,
(5.1)
а уравнение (5.1) уравнением регрессии Y по X . Функция f ( x ) называется
регрессией Y по X , а её график - линией регрессии Y по X .
Поскольку случайные величины X ,Y связаны корреляционно, то по
аналогии можно определить корреляционную зависимость X по Y . Все
вышеприведённые определения будут справедливы для данного случая, если в
определениях поменять местами случайные величины X ,Y .
20. Числовые характеристики СВ
Кафедра маркшейдерского делаЧисловые характеристики
СВ
Начальным моментом порядка k , s называется математическое ожидание
произведения соответствующих степеней случайных величин:
mk ,s M X k Y s
(6.13)
Для дискретных случайных величин выражение 6.13 имеет вид:
m k ,s
i
x k y s pi , j
,
(6.14)
j
где: pi , j P X xi Y y j - вероятности.
Для непрерывных случайных величин начальный момент порядка
k , s запишется:
mk ,s x k y s f ( x , y )dxdy
(6.15)
где: f ( x , y ) - плотность распределения системы двух случайных величин.
21. Числовые характеристики СВ
Кафедра маркшейдерского делаЧисловые характеристики
СВ
Центральным моментом порядка k , s называется математическое
ожидание соответствующих степеней центрированных случайных величин
X ,Y :
k ,s M X Y
k
s
M X m Y m
2
1,0
2
0 ,1
,
(6.16)
где: m1,0 , m0,1 - математические ожидания случайных величин X ,Y .
(второй смешанный центральный момент).
11 K xy m11 m10 m01 ,
(6.17)
и далее – коэффициент корреляции:
rxy
11
20 02
m11 m10 m01
,
x y
где: 20 - дисперсия случайной величины X ;
02 - дисперсия случайной величины Y ;
x , y - стандарты СВ X ,Y ; x 20 , y 02 .
(6.18)
22. Числовые характеристики СВ
Кафедра маркшейдерского делаЧисловые характеристики
СВ
Дисперсия для случайных величин X ,Y вычисляется по следующим
формулам:
2
20 m 20 m10
(6.19)
2
02 m02 m01
(6.20)
Сила связи между
X ,Y
оценивается при помощи выборочного
коэффициента корреляции rxy :
11
rxy
x y
,
где: 11 - второй смешанный центральный (корреляционный) момент;
x , y - стандарты (СКО) по x и y соответственно
(6.2)
23. Числовые характеристики СВ
Кафедра маркшейдерского делаЧисловые характеристики
СВ
Корреляционный момент K xy , или его ещё называют моментом связи,
вычисляется по одной их двух равноценных формул:
N
K xy 11
x
i
x y i y
i 1
(6.3)
N
N
x y
i
K xy 11
i 1
N
i
x y .
(6.4)
Выборочное уравнение регрессии ( Y по X ) имеет вид:
y x y rxy
y
x
x x .
(6.5)
24. Уравнение регрессии
Кафедра маркшейдерского делаУравнение регрессии
Обычно в таком виде уравнение 6.5 не применяется, поэтому его
приводят к линейному виду 6.1. Угловой коэффициент a и свободный член
b можно определить из выражений:
a rxy
y
x
(6.6)
y
b y rxy x
x
(6.7)
Окончательно уравнение регрессии ( Y по X ): y x ax b . Выборочное
уравнение регрессии ( X по Y ) представлено формулой 6.8, но его, как и
выражение 6.5, тоже приводят к линейному виду x y a' y b' .
x
y y
x y x rxy
y
(6.8)
25. Погрешность коэффициента корреляции
Кафедра маркшейдерского делаПогрешность
коэффициента корреляции
Погрешность определения коэффициента корреляции r зависит от
объёма выборки из генеральной совокупности. С увеличением объёма выборки
погрешность будет уменьшаться. Эта зависимость выражается следующей
формулой:
r
Надёжность коэффициента
следующего отношения:
1 rxy2
.
N
корреляции
(6.9)
оценивается
при
помощи
rxy
r
.
(6.10)
Если 3 то, согласно теореме Ляпунова с вероятностью Р=0,997 можно
утверждать, что связь между изучаемыми случайными величинами надёжная и
наоборот.
26. Числовые характеристики СВ
Кафедра маркшейдерского делаЧисловые характеристики
СВ
Чтобы оценить точность уравнения регрессии определяют среднее
квадратичное отклонение предсказанных значений y x от исходных y i . Это
можно выполнить по одной из двух формул:
y
N
y/ x
i 1
i
y xi
N
y/ x y 1
2
,
(6.11)
2
rxy .
(6.12)
27. Корреляционный анализ при большом числе данных
Кафедра маркшейдерского делаКорреляционный анализ
при большом числе данных
xmax xmin
x
1 3.2 lg N
ymax ymin
y
1 3.2 lg N
1.
2.
3.
4.
5.
6.
7.
Вычисляют классовый
интервал по формуле
Стержеса
Строят корреляционную решётку
Заносят все пары исходных
данных в корреляционную
решётку
Находят суммы, суммы
произведений
Вычисляют средние и стандарты
для Х и У, корреляционный
момент и коэффициент
корреляции
Рассчитывают уравнения
регрессии, СГО
Выполняют оценку точности
найденного уравнения регрессии
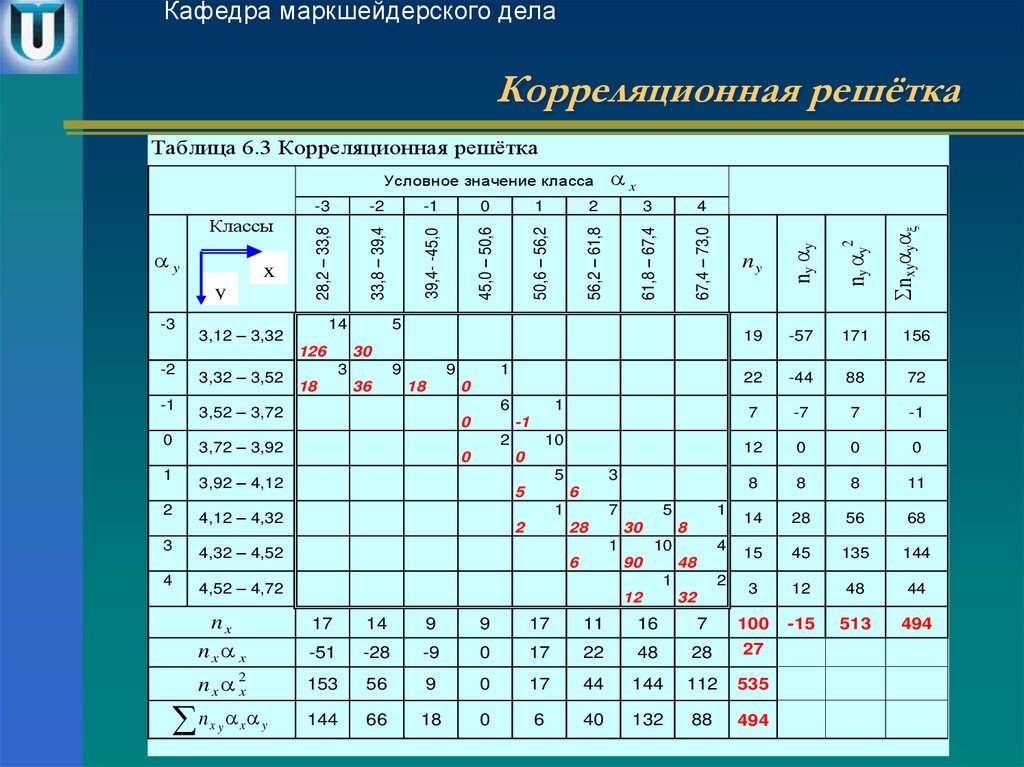
28. Корреляционная решётка
Кафедра маркшейдерского делаКорреляционная решётка
Таблица 6.3 Корреляционная решётка
3
4
56,2 – 61,8
61,8 – 67,4
67,4 – 73,0
14
3,12 – 3,32
126
-2
-1
0
1
2
3
4
3,32 – 3,52
5
ny
19
-57
171
156
22
-44
88
72
7
-7
7
-1
12
0
0
0
8
8
8
11
14
28
56
68
15
45
135
144
3
12
48
44
-15
513
494
30
3
18
9
36
9
18
1
0
6
3,52 – 3,72
0
1
-1
2
3,72 – 3,92
0
10
0
5
3,92 – 4,12
5
3
6
1
4,12 – 4,32
2
7
28
5
30
1
4,32 – 4,52
6
1
8
10
90
4
48
1
4,52 – 4,72
12
2
32
nx
nx x
17
14
9
9
17
11
16
7
100
-51
-28
-9
0
17
22
48
28
27
n x 2x
153
56
9
0
17
44
144
112
535
144
66
18
0
6
40
132
88
494
n
x y x y
nxy y
2
ny y2
1
ny y
-3
0
50,6 – 56,2
y
-1
45,0 – 50,6
x
-2
39,4- -45,0
y
-3
33,8 – 39,4
Классы
x
28,2 – 33,8
Условное значение класса
29. Расчёт начальных моментов
Кафедра маркшейдерского делаРасчёт начальных моментов
Средние значения для случайных величин X и Y определяются из
выражений:
'
m10 x 0 m10
x
(6.21)
m01 y 0 m'01 y
(6.22)
Первые условные начальные моменты вычисляются по следующим
формулам:
'
m10
n
x
N
x
m'01
,
n
y
N
y
,
(6.23)
где: N – количество пар значений X ,Y .
Чтобы получить
n
x
x
, необходимо умножить число попавших
значений n x в класс на его условное значение x и просуммировать.
30. Расчёт вторых условных начальных моментов
Кафедра маркшейдерского делаРасчёт вторых условных
начальных моментов
Вторые условные начальные моменты в соответствии с их определением
найдутся из следующих выражений:
m'20
2
nx x
,
N
m'02
2
ny y
(6.24)
N
Дисперсию и стандарты (СКО) удобнее вычислять через вторые
условные центральные моменты:
Dx 20
m'20
' 2
m10
x ,
2
x Dx ,
D y 02
m'02
y Dy
' 2
m01
y
2
. (6.25)
(6.26)
31. Расчёт вторых условных начальных моментов
Кафедра маркшейдерского делаРасчёт вторых условных
начальных моментов
Коэффициент корреляции для принятого способа обработки вычисляют
через условные начальные моменты и условные стандарты 'x , 'y по формуле:
rxy
'
'
m11
m10
m'01
'
'
x y
,
(6.27)
'
где: m11
- второй смешанный условный начальный момент:
'
m11
n
xy x y
N
.
(6.28)
32. Пример
Кафедра маркшейдерского делаПример
Вычислим коэффициент корреляции по данным табл. 6.3.
494 27 15
rxy 100 100 100 0.959
2.30 2.26
Погрешность и значимость коэффициента корреляции определим по
формулам 6.9, 6.10:
r 1 0.959 2 / 100 0.008
0.959 / 0.008 120
На основании этих расчётов делаем следующие выводы:
Зависимость
между
существенная, так как rxy
содержанием
железа
и
плотностью
0.5 ;
Коэффициент корреляции вычислен надёжно, поскольку
3;
руды
33. Пример
Кафедра маркшейдерского делаПример
Можно составить уравнение регрессии
yx f ( x ).
0.45
x 49.37 .
y x 3.79 0.959
12.86
После упрощений и преобразований будем иметь:
y x 0.033707 x 2.12602
(6.29)
Уравнение регрессии X по Y получим из выражения 6.8:
x y 27.30377 y 54.1153
(6.30)


























 Математика
Математика