Перенос изображения сквозь толщу мутной среды

1. Перенос изображения сквозь толщу мутной среды

Будак Владимир Павлович,
Московский энергетический институт (ТУ)
кафедра светотехники
Tomoyuki Nishita (Fukuyama University), Eihachiro
Nakamae (Hiroshima Prefectural University)
: +7 (095) 763-5239
[email protected]

2. ФРТ и ОПФ слоя мутной среды

Выражения для мощности сигналов от подложки и объекта:
Pпл 0 E (r ) E (r r )d 2 r , Pпс 0 (r ) E (r ) E (r r )d 2 r
E ( )
1 ˆ
ˆl ) dˆl , E (r ) 1 (r , ˆl )e( z, r r, ˆl ) d 2 r dˆl
(
,
l
)
(
z
,
,
По определению ФРТ системы есть реакция на точечный объект – δ(r):
Pпс 0 (r r0 ) E (r ) E (r r )d 2 r 0 E (r0 ) E (r r0 ) h(r r ) E (r ) E (r r )
• Система не является инвариантной к сдвигу- нельзя ввести ОПФ
• В наиболее реализуемых схемах №1 и 2 диаграммы направленности источника и
приемника несопоставимы друг с другом определяется ОПФ (на примере №2):
h(r r ) E (0) E (r r ) H ( ) E (0) F {E (r )}
T ( )
H ( )
, H (0) пс E (r ) E (r r )d 2 r E ( ) E ( ) d 2 , Pпс ( ) 0 пс ( )T ( ), Pпл пс 0
H (0)
Для определение ОПФ и ФРТ необходимо знать решение УПИ
для случая ТД источника

3. Яркость дымки – помеха обратного рассеяния (ПОР)

D( z , r, ˆl ) 0 l ( z; r , ˆl r, ˆl ) (r , ˆl ) d 2 r dˆl
(nˆ , nˆ S )
Представим весь слой в виде совокупности слоев,
отражающих по закону Lambert (Johann, 26.08.1728 25.09.1777). Тогда яркость дымки от слоя можно
представить в виде
(nˆ , nˆ R )
z
x dz dD( z , r, ˆl )
x 0 E (r ) E (r r )d 2 r dz
4
4
Тогда общая яркость дымки (помехи) обратного рассеяния:
D( z, r, ˆl )
x 0 E (r ) E (r r )d 2 r dz
4
z1
Последнее выражение можно получить более строго из теории возмущений.
Яркость дымки (помехи) обратного рассеяния на основе теории
возмущений так же выражается через решение для ТД

4. Решение УПИ для ТД-источника в среде с сильно анизотропным рассеянием

• Сильно анизотропное рассеяние - малоугловое приближение (МУП)
• МУП – разновидность параксиального приближения в оптике мутных сред
• В параксиальном приближении и МУП sinα α, cosα 1
• При этом поле ТД эквивалентно полю ТИ источника
В случае ТИ-источника УПИ принимает вид
L( r, ) 1 2 L
L
(
r
,
)
(ˆl, r )
r
r
4
ˆ
L(r, l ) L( r, ),
:
r
1
L( r , )
(rˆ ˆl )
r 0
2
4 r
x(ˆl, ˆl ) L(r, )dˆl
• Наиболее общее форма МУП – Goudsmit-Saunderson
• Решение для ТД получено только в форме Компанеец-Moliére-Snyder-Scott
• В 80-х удалось обобщить Goudsmit-Saunderson – МСГ: малоугловая модификация
метода сферических гармоник
МСГ является обобщением МУП в форме Goudsmit-Saunderson
и основывается на методе СГ

5. Малоугловая модификация метода сферических гармоник

Представим все угловые зависимости в УПИ в виде рядов по сферическим функциям:
L ( r , )
2k 1
4 r 2
k 0
Ck (r ) Pk ( ), x(ˆl, ˆl )
1 g2
k 0
(1 g 2 2 g )3 2
(2k 1) xk Pk (ˆl ˆl ), x( )
(2k 1) g k Pk ( )
k 0
что после преобразований в соответствии с СГ приведет к бесконечной системе
обыкновенных дифференциальных уравнений
1 d
k ( k 1)
Ck 1 (r ) Ck 1 ( r ) (1 xk )Ck (r )
(k 1)Ck 1 ( r ) kCk 1 ( r )
2k 1 dr
(2k 1)r
Тело яркости сильно анизотропная по углу функция:
-1
• Наличие особенностей по углу: δ-особенность в прямом излучении, θ – в первой
и логарифмической во второй
• Кратности выше третьей являются гладкими функциями по анизотропии близкими
к индикатрисе – сильная анизотропия рассеяния
• Коэффициенты Ck очень медленно меняются с номером k
Определим непрерывную функцию C(k,r) в целочисленных
точках k равную значениям коэффициентов Ck(r)

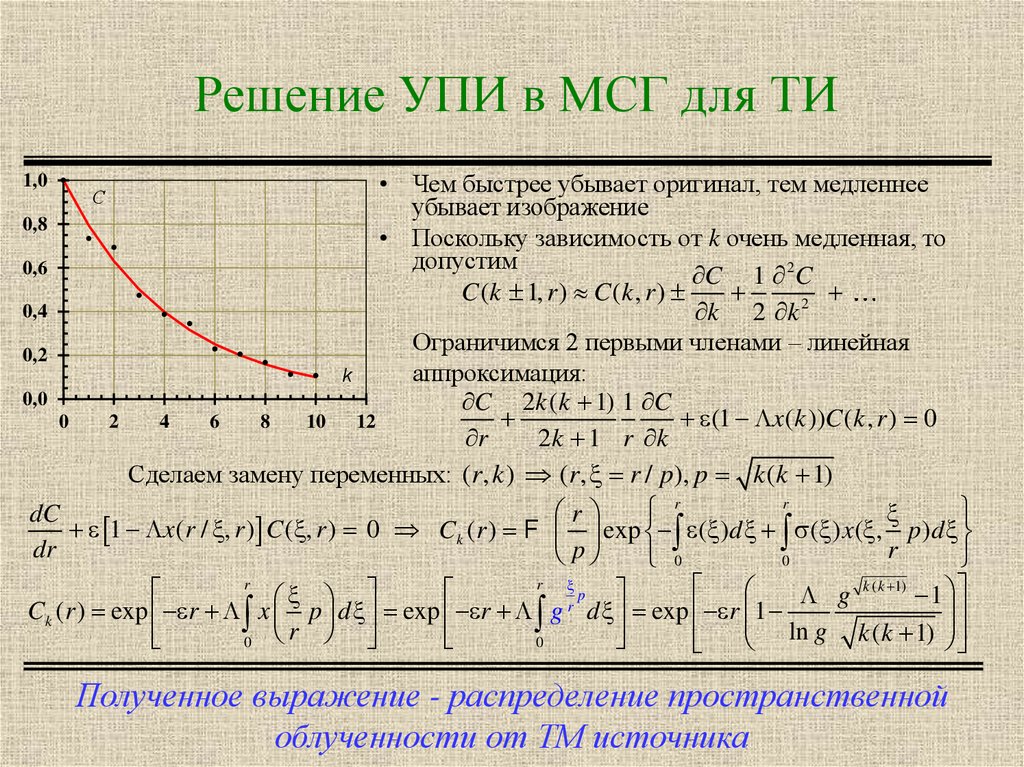
6. Решение УПИ в МСГ для ТИ

• Чем быстрее убывает оригинал, тем медленнее
убывает изображение
0,8
• Поскольку зависимость от k очень медленная, то
допустим
0,6
C 1 2C
C (k 1, r ) C (k , r )
2
0,4
k 2 k
Ограничимся 2 первыми членами – линейная
0,2
аппроксимация:
k
0,0
C 2k ( k 1) 1 C
(1 x ( k ))C ( k , r ) 0
0
2
4
6
8
10
12
r
2k 1 r k
Сделаем замену переменных: (r, k ) (r, r / p), p k (k 1)
r
r
r
dC
1 x ( r / , r ) C ( , r ) 0 Ck (r ) F exp ( )d ( ) x( , p)d
dr
r
p
0
0
r
r
k ( k 1)
p
g
1
r
Ck (r ) exp r x p d exp r g d exp r 1
r
ln
g
k
(
k
1)
0
0
1,0
С
Полученное выражение - распределение пространственной
облученности от ТМ источника

7. Сигнал от подложки

Распределение облученности от точечного прожектора
E
k
1 ˆ
2k 1
2
(r) (r , l )e( z, r r, ˆl )d r dˆl
Ck ( r)
2
k
k 0 4 r
Если прожектор имеет распределение Gauss (Carl Friedrich, 30.04.1777-06.03.1855) по
углу, то
2
1
(ˆl, ˆl )
exp
2
02
0
2
2( 1) e 2 0
2
1
k ( k 1) 2
exp
exp
k exp
0
2
2
2
2
4
0
0
0
0
Еще раз используя теорему сложения для полиномов Legendre (Adrien Marie, 18.09.175210.01.1833, 1783 - полиномы):
1 2k 1
пс
k k Ck2 ( z ) Pk (nˆ R nˆ S )
2
k 0 4 z
(nˆ nˆ ) 1
R S
1 2k 1
k k Ck2 ( z )
2
k 0 4 z
Многократные интегралы сведены к однократной сумме по
полиномам Legendre

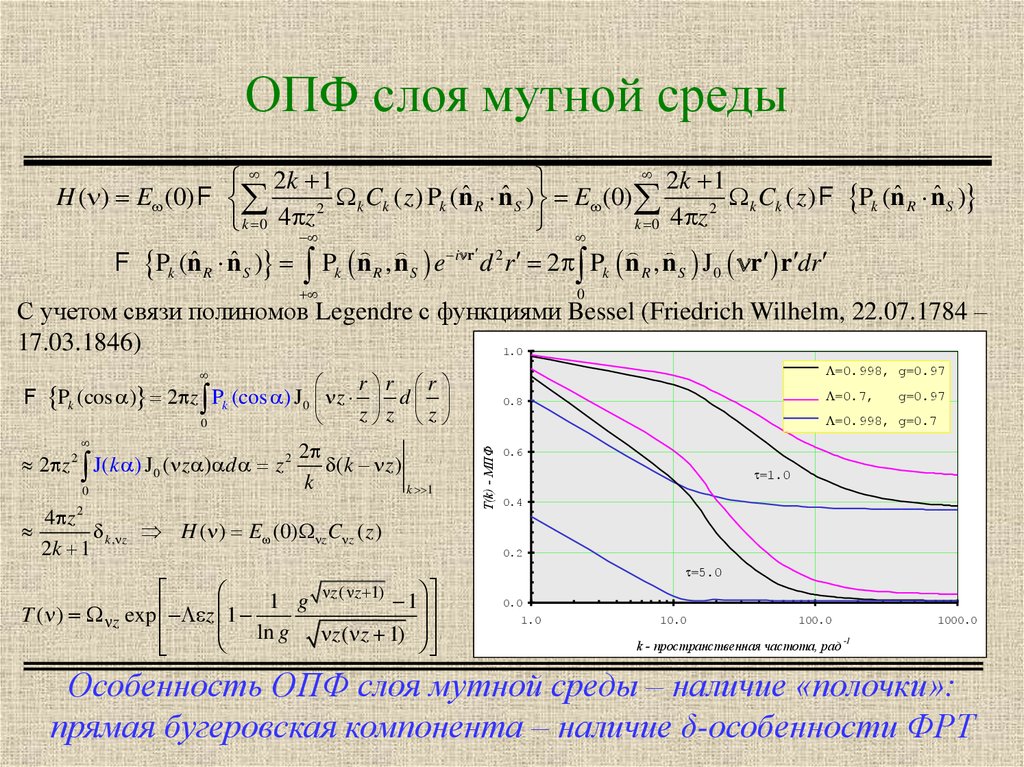
8. ОПФ слоя мутной среды

2k 1
2k 1
ˆ
ˆ
H ( ) E (0) F
C
(
z
)
P
(
n
n
)
E
(0)
k Ck ( z ) F Pk (nˆ R nˆ S )
k k
k
R
S
2
2
z
k 0 4 z
k 0 4
F Pk (nˆ R nˆ S )
Pk n R , n S e i r d 2 r 2 Pk n R , n S J 0 r r dr
0
С учетом связи полиномов Legendre с функциями Bessel (Friedrich Wilhelm, 22.07.1784 –
17.03.1846)
1.0
=0.998, g=0.97
r r r
F Pk (cos ) 2 z Pk (cos ) J 0 z d
z z z
0
2 z
2
J( k ) J 0 ( z ) d z
0
2
( k z )
k
k 1
4 z
k , z H ( ) E (0) z C z ( z )
2k 1
2
z ( z 1)
1
g
1
T ( ) z exp z 1
ln g z( z 1)
g=0.97
=0.998, g=0.7
T(k) - МПФ
2
=0.7,
0.8
0.6
t=1.0
0.4
0.2
t=5.0
0.0
1.0
10.0
100.0
k - пространственная частота, рад
1000.0
-1
Особенность ОПФ слоя мутной среды – наличие «полочки»:
прямая бугеровская компонента – наличие δ-особенности ФРТ

9. Яркость ПОР

2k 1
Pпор(nˆ R , nˆ S )
x 0
k k
4
4
k 0
z2 2
Ck ( z )
dz
2
z
z1
z2
z1
1 g k ( k 1)
exp 2 z 1
ln g
k (k 1)
z2
1
z2
z1
Ck2 ( z )
z2
dz Pk (nˆ R nˆ S )
z2
exp 2 zf k
1
1
dz
dz E1 (2 zf k z1 ) E1 (2 zf k z2 )
z1
z2
z2
z1
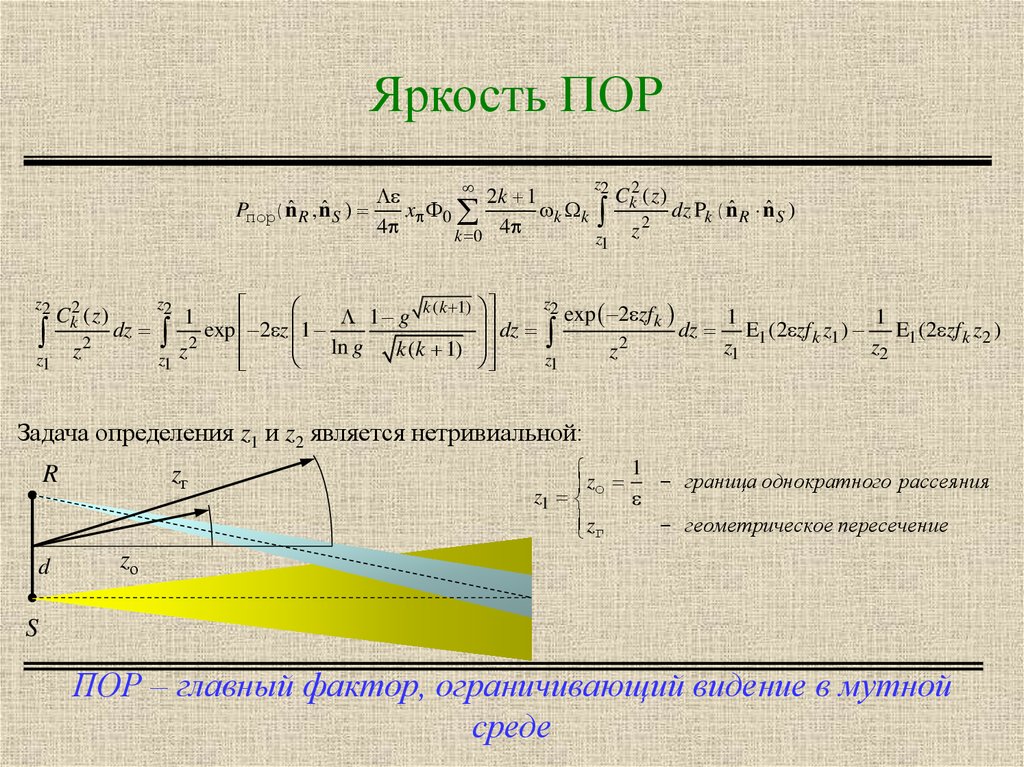
Задача определения z1 и z2 является нетривиальной:
R
d
zг
1
- граница однократного рассеяния
zо
z1
zг
- геометрическое пересечение
zо
S
ПОР – главный фактор, ограничивающий видение в мутной
среде

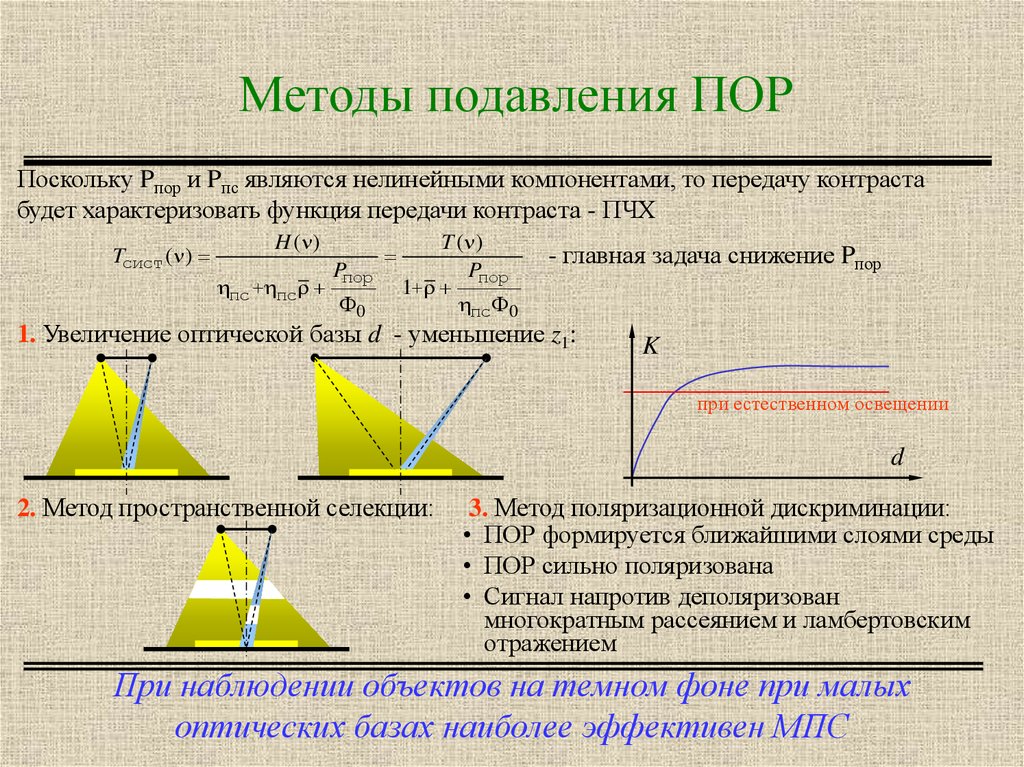
10. Методы подавления ПОР

Поскольку Pпор и Pпс являются нелинейными компонентами, то передачу контраста
будет характеризовать функция передачи контраста - ПЧХ
Tсист ( )
H ( )
пс + пс
Pпор
0
T ( )
Pпор
1+
пс 0
- главная задача снижение Pпор
1. Увеличение оптической базы d - уменьшение z1:
K
при естественном освещении
d
2. Метод пространственной селекции:
3. Метод поляризационной дискриминации:
• ПОР формируется ближайшими слоями среды
• ПОР сильно поляризована
• Сигнал напротив деполяризован
многократным рассеянием и ламбертовским
отражением
При наблюдении объектов на темном фоне при малых
оптических базах наиболее эффективен МПС