Готовимся к ЕГЭ

1.

2.

1 способ
На рисунке изображены график функции у =f(x) и касательная к
этому графику, проведенная в точке с абсциссой х0. Найдите
значение производной функции у =f(x) в точке х0.
Решение: 1). Угол, который составляет касательная с положительным
направлением оси Ох, тупой. Значит, значение производной в точке х0
отрицательно.
2). Найдем тангенс смежного угла.
Для этого подберем треугольник с
катетами-целыми числами. Этот
треугольник не подойдет.
Можно найти несколько удобных
треугольников с целочисленными
8
катетами, например,….
tga =
2
Еще удобный треугольник…
3). Найдем тангенс угла a – это
отношение 4:1. Тангенс тупого,
смежного угла равен – 4.
В8
- 4
3
10 х
х
у
х0
a
х
1
O
-3
8
aa -7
2
у =f(x)

3.

2 способ
В данных заданиях всегда есть удобные точки.
Этим можно воспользоваться.
Решение:
Уравнение прямой у = kx + b.
В этом уравнении угловой коэффициент k - искомая величина.
f/(xo)=k
у = kх + b
k=tgα
у
у =f(x)
Подставим координаты удобных
точек в уравнение прямой.
–
– 7 = b.
х
– 3 = – 1k + b.
х0
–4=k
O
(-1; -3)
-3
k=–4
Систему можешь решить и своим способом.
В8
- 4
3
10 х
х
(0; -7) -7

4.

1 способ
На рисунке изображены график функции у =f(x) и касательная к
этому графику, проведенная в точке с абсциссой х0. Найдите
значение производной функции у =f(x) в точке х0.
Решение: 1). Угол, который составляет касательная с
положительным направлением оси Ох, острый (хотя он и не
помещается в пределах чертежа). Значит, значение производной в
у
точке х0 положительно.
2). Найдем тангенс этого угла.
Для этого подберем треугольник
с катетами-целыми числами.
3
Можно найти несколько удобных
12
х
треугольников, например,….
a
O 1
х0
3). Найдем тангенс угла – это
отношение 3:12.
3
tga = 12
4). Переведем дробь 1
в десятичную запись: 4
В8
0 , 25
3
10 х
у =f(x)
х

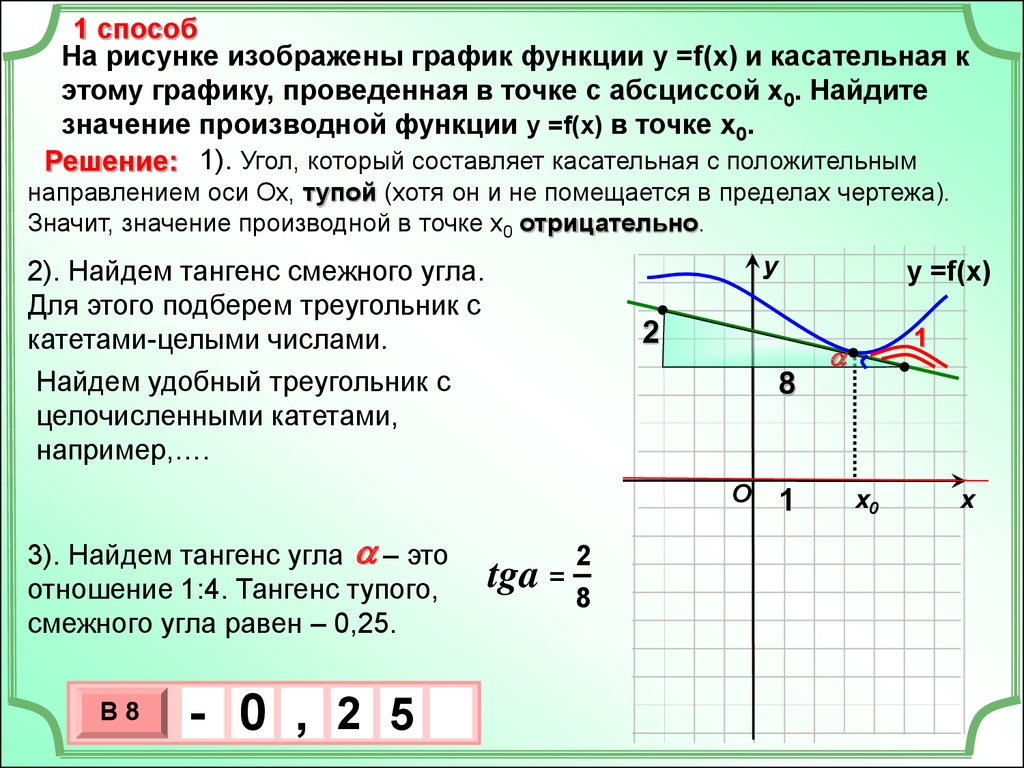
5.

2 способ
В данных заданиях всегда есть удобные точки.
Этим можно воспользоваться.
Решение:
Уравнение прямой у = kx + b.
В этом уравнении угловой коэффициент k - искомая величина.
f/(xo)=k
у = kх + b
k=tgα
у
Подставим координаты удобных
точек в уравнение прямой.
2 = –5k + b.
–
5 = 7k + b.
(7; 5)
(-5; 2)
х
O
– 3 = – 12k
12k = 3
х0
:12
k= 3
12
В8
1
0 , 25
3
10 х
х
у =f(x)
3
tga = 12

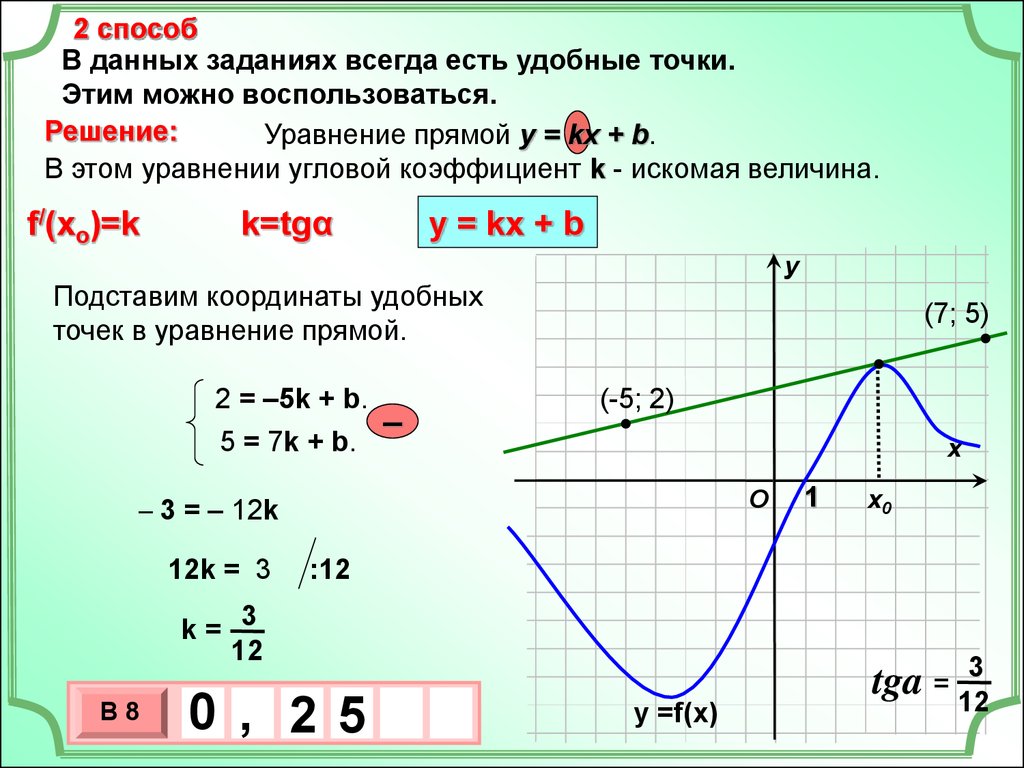
6.

1 способ
На рисунке изображены график функции у =f(x) и касательная к
этому графику, проведенная в точке с абсциссой х0. Найдите
значение производной функции у =f(x) в точке х0.
Решение: 1). Угол, который составляет касательная с положительным
направлением оси Ох, тупой (хотя он и не помещается в пределах чертежа).
Значит, значение производной в точке х0 отрицательно.
2). Найдем тангенс смежного угла.
Для этого подберем треугольник с
катетами-целыми числами.
Найдем удобный треугольник с
целочисленными катетами,
например,….
3). Найдем тангенс угла a – это
отношение 1:4. Тангенс тупого,
смежного угла равен – 0,25.
В8
- 0 , 2 5
3
10 х
х
у
a
tga
1
a
2
=
8
у =f(x)
1
O
a 8
х0
х
2

7.

2 способ
На рисунке изображены график функции у =f(x) и касательная к
этому графику, проведенная в точке с абсциссой х0. Найдите
значение производной функции у =f(x) в точке х0.
Решение: Решать подобные задания можно другим способом.
Уравнение прямой у = kx + b.
В этом уравнении угловой коэффициент k - искомая величина.
f/(xo)=k
у
у = kх + b
k=tgα
Подставим координаты известных
точек в уравнение прямой.
– 3 = 6k + b.
–
1
– 1 = –2k + b.
– 2 = 8k
k=–
В8
O
(-2; -1)
:8
1
4
у =f(x)
- 0 , 2 5
3
10 х
х
х0
х
(6; -3)

8.

1 способ
На рисунке изображены график функции у =f(x) и касательная к
этому графику, проведенная в точке с абсциссой х0. Найдите
значение производной функции у =f(x) в точке х0.
Решение: 1). Угол, который составляет касательная с положительным
направлением оси Ох, тупой (хотя он и не помещается в пределах чертежа).
Значит, значение производной в точке х0 отрицательно.
у
2). Найдем тангенс смежного угла.
Для этого подберем треугольник с
катетами-целыми числами.
Найдем удобный треугольник с
целочисленными катетами,
например,….
2
В8
- 0 , 2 5
3
10 х
х
1
a
8
O
3). Найдем тангенс угла a – это
отношение 1:4. Тангенс тупого,
смежного угла равен – 0,25.
у =f(x)
tga
2
=
8
1
х0
х

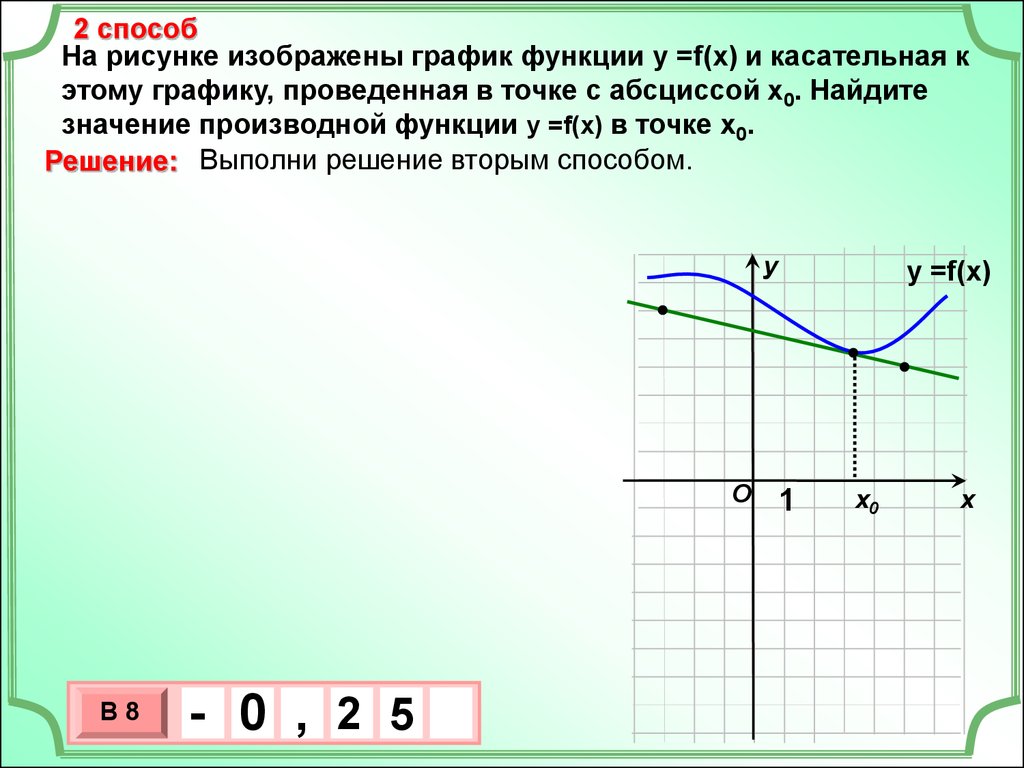
9.

2 способ
На рисунке изображены график функции у =f(x) и касательная к
этому графику, проведенная в точке с абсциссой х0. Найдите
значение производной функции у =f(x) в точке х0.
Решение: Выполни решение вторым способом.
у
O
В8
- 0 , 2 5
3
10 х
х
у =f(x)
1
х0
х