Элементы релятивистской механики. (Лекция 10)

1. Лекция 10 (2 сем). Элементы релятивистской механики-1

Курс физики для студентов 1-2 курса БГТУ
Кафедра физики БГТУ
доцент Крылов Андрей Борисович
Часть I.
ОСНОВНЫЕ
ЗАКОНЫ
РЕЛЯТИВИСТСКОЙ
МЕХАНИКИ
Лекция 10 (2 сем).
Элементы релятивистской механики-1
1. Границы применимости классической механики.
2. Постулаты Эйнштейна.
3. Преобразования Лоренца.
4. Следствия из преобразований Лоренца.
5. Теорема сложения скоростей в СТО
2017
1
+6

2. Границы применимости классической механики

Классическая механика (иначе механика Ньютона) покоится на прочном
фундаменте экспериментальных фактов, однако все они относятся к медленным
движениям макроскопических тел.
Под медленными или нерелятивистскими движениями понимают движения,
скорости которых очень малы по сравнению со скоростью света в вакууме с =
300 000 км/с.
Движения, скорости которых приближаются к скорости света в вакууме, называют
быстрыми или релятивистскими.
В этом смысле движение спутника или космического корабля со скоростью
= 8 км/с является еще очень медленным.
Механика Ньютона не может быть применима к движениям частиц, скорости
которых близки к скорости света в вакууме.
На основе теории относительности была создана новая механика, применимая не
только к медленным, но и к сколь угодно быстрым движениям.
Она называется релятивистской механикой.
2
+5

3. Ограничения классической механики

Первый вопрос: существует ли предельная скорость движения
Согласно механике Ньютона скорость, до которой можно ускорить тело из состояния покоя, в
принципе ничем не ограничена.
По релятивистской механике значение скорости тела не может перейти через определенный
предел, равный скорости света в вакууме с. В этом смысле скорость света с является предельной.
Скорость тела не может ее достигнуть, но в принципе может подойти к ней сколь угодно
близко.
Механика Ньютона предназначена только для макроскопических тел, т.к. классический подход к
изучению явлений микромира очень ограничен.
Адекватное описание явлений микромира (применимое, конечно, также в каких-то пределах)
дает квантовая механика, существенно отличающаяся от механики классической.
Движение в микромире является более сложной формой движения, чем механическое
перемещение тел в пространстве.
Вывод: Механика Ньютона имеет очень широкую и практически важную область
применимости.
Но вне области ее применимости механика Ньютона приводит к неверным или
недостаточно точным результатам.
Примеры задач вне применимости механики Ньютона:
задача о движении заряженных частиц в ускорителях, где надо пользоваться релятивистской
механикой.
задачи о движении электронов в атомах, которые надо решать с помощью квантовой механики.
3
+4

4. Принцип неопределенностей Гейзенберга

В классической механике состояние движения частицы в любой момент времени
характеризуется положением (координатой х при одномерном движении) и скоростью .
Вместо скорости можно пользоваться также импульсом, т. е. величиной р = m , равной
произведению массы частицы m на ее скорость .
Образом частицы является геометрическая точка, описывающая с течением времени
непрерывную траекторию.
В квантовой механике показано, что такой способ описания движения имеет
принципиальные границы применимости.
Согласно квантовой механике состояние частицы в каждый момент времени нельзя
характеризовать точными значениями ее координаты и импульса в этот момент времени.
Если в каком-либо состоянии координата известна с неопределенностью х, а импульс
− с неопределенностью δр, то обе эти величины одновременно не могут быть сделаны
сколь угодно малыми.
Они связаны соотношением:
где h − универсальная постоянная, называемая постоянной Планка в честь немецкого
физика-теоретика Макса Планка (1858−1947).
Это соотношение называется принципом (соотношением) неопределенностей
Гейзенберга по имени немецкого физика-теоретика Вернера Гейзенберга (1901−1976).
4
+2

5. Принципиальный предел точности одновременного измерения координаты и импульса частицы

Макс Планк (1858−1947)
Вернер Гейзенберг (1901−1976)
Принципиальный предел точности одновременного
измерения координаты и импульса частицы
Принцип (соотношение) неопределенностей Гейзенберга
Это соотношение определяет принципиальный предел точности одновременного
измерения координаты и импульса частицы, который не может быть превзойден
никаким усовершенствованием приборов и методов измерения.
Мгновенные состояния движения реальных частиц не могут быть
охарактеризованы классически − точными значениями координат и
импульсов.
Частицы ведут себя более сложно, чем материальные точки классической
механики.
5
+3х

6. Мгновенное состояние движения частицы

Классическая картина движения по непрерывным траекториям лишь
приближенно соответствует законам природы.
Границы
ее
применимости
определяются
соотношением
неопределенностей Гейзенберга.
Из него следует, что мгновенное состояние движения частицы нельзя также
характеризовать абсолютно точными значениями координаты и скорости.
Неопределенности этих величин должны удовлетворять условию:
Вывод:
Применимость классической механики имеет следующие границы:
1) классическая механика применима для описания механических систем, в
которых скорость составляющих ее объектов намного меньше скорости света
( << с);
2) классическая механика применима для описания только тех объектов, для
которых динамические величины с размерностью действия намного больше
постоянной Планка (h=6,63*10-34 Дж*c).
6
+4

7. Постулаты Эйнштейна

В основе специальной теории относительности А. Эйнштейна лежат два постулата, смысл
которых можно выразить так:
1. При одинаковых условиях, реализованных по отдельности в двух системах отсчета некоторой
инерциальной системы К (I) и системы К' (II), движущейся равномерно и прямолинейно
относительно системы I любые физические процессы в этих системах отсчета протекают
одинаково, а описывающие их математические соотношения не изменяют своего вида при
переходе из одной системы в другую.
Этот постулат является обобщением механического принципа относительности Галилея на
все без исключения физические явления.
2. В природе существует предельная (максимальная) скорость распространения физических
сигналов (взаимодействий), одна и та же во всех инерциальных системах отсчета.
Эта максимальная скорость совпадает со скоростью света в вакууме, она не зависит от
движения источника и приемника света и равна с = 300 000 км/с .
Скорость света есть инварианта (c = inv), т.е. не зависящая ни от чего константа.
Из первого принципа следует:
если для данной задачи (некоторого класса задач) найдена инерциальная система отсчета I, то
для этой задачи существует и бесчисленное множество инерциальных систем типа II,
движущихся равномерно прямолинейно относительно I. Скорости всех систем II меньше с.
Системы отсчета необходимо связывать с телами, а скорости тел не могут равняться или
превосходить максимальную скорость света в вакууме, равную с. Скорости тел строго
меньше максимальной.
Развитие науки показало, что оба принципа Эйнштейна подтверждаются всей совокупностью
экспериментальных и теоретических знаний современной физики.
7
+5

8. 3. Преобразования Лоренца и их следствия

y
y
A
V0t
O
O
V0
x
x
x
z
z
y = y
Эйнштейн показал, что в соответствии с двумя постулатами
теории относительности связь между координатами и
временем в двух инерциальных системах отсчета К и К
выражается не преобразованием Галилея:
x
а преобразованием Лоренца:
z = z
или
где
В основу вывода этих формул было положено условие равноправности всех систем отсчета,
согласно которому преобразования должны быть линейными.
Из преобразования Лоренца, следует, что при 0 << c оно совпадает с преобразованием Галилея .
Т.е. преобразование Галилея - частный случай преобразования Лоренца (более общее!!!), которое
основано на постулатах теории относительности и составляет основу релятивистской
кинематики.
8
+3

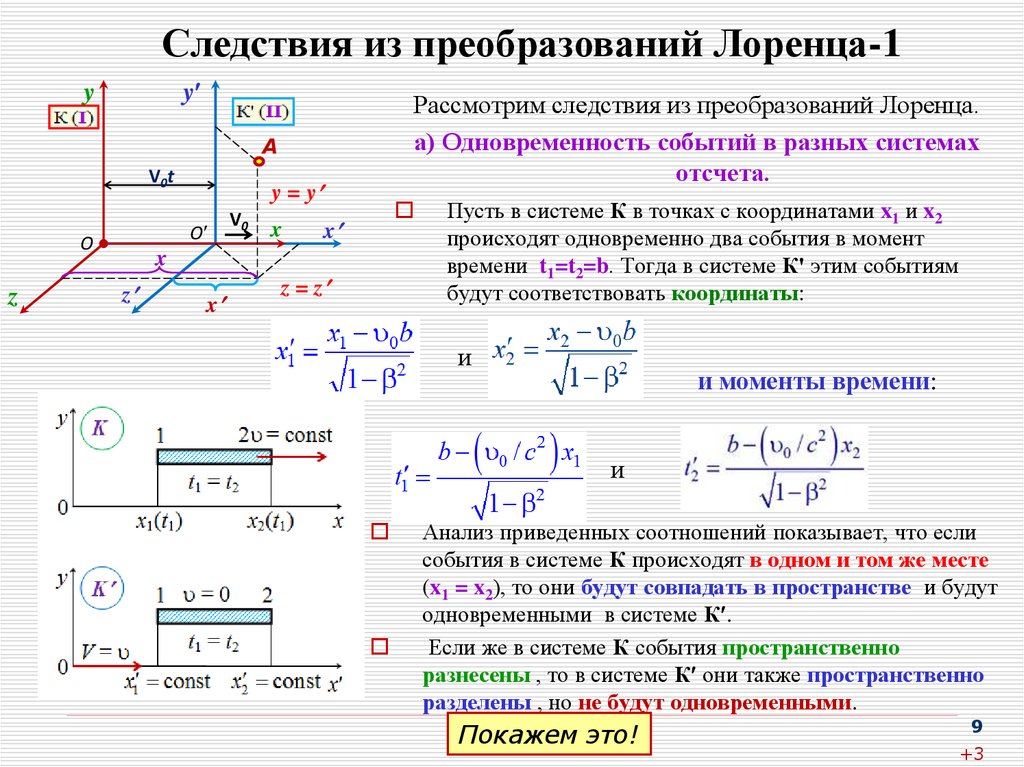
9. Следствия из преобразований Лоренца-1

y
y
Рассмотрим следствия из преобразований Лоренца.
а) Одновременность событий в разных системах
отсчета.
A
V0t
O
O
z
y = y
V0
x
x
x
z
x
z = z
Пусть в системе К в точках с координатами x1 и x2
происходят одновременно два события в момент
времени t1=t2=b. Тогда в системе К' этим событиям
будут соответствовать координаты:
и
и моменты времени:
и
Анализ приведенных соотношений показывает, что если
события в системе К происходят в одном и том же месте
(x1 = x2), то они будут совпадать в пространстве и будут
одновременными в системе К .
Если же в системе К события пространственно
разнесены , то в системе К они также пространственно
разделены , но не будут одновременными.
Покажем это!
9
+3

10. Следствия из преобразований Лоренца-1 (продолжение)

Рассмотрим следствия из преобразований Лоренца.
а) Одновременность событий в разных системах
отсчета.
Имеем:
и
Итак, тезис:
Хотя
Наблюдаем
но ,
в момент времени
t1=t2=b.
Если в системе К события пространственно разнесены ,
то в системе К они также пространственно разделены,
но не будут одновременными.
если
, то
относительность одновременности
10
+3

11. Следствия из преобразований Лоренца-2

б) Длина тел в различных системах.
Пусть стержень расположен вдоль оси х и покоится
относительно системы К .
Длина его в этой системе равна:
где х´1 и х´2 - не изменяющиеся со временем t координаты
концов стержня.
Относительно системы К стержень движется со скоростью 0.
Для определения его длины в этой системе отметим
координаты концов x1 и x2 в один и тот же момент времени
t1 = t2 = b
Тогда длина стержня в системе К равна:
Из преобразований Лоренца следует:
и
11
+3

12. Следствия из преобразований Лоренца-2 (продолжение)

б) Длина тел в различных системах.
в один и тот же момент времени t1 = t2 = b
и
Тогда, длина стержня в системе К равна:
Так как
, то
Таким образом, длина стержня l, измеренная в системе, относительно которой он движется,
отказывается меньше длины l0, измеренной в системе, относительно которой стержень
покоится:
Отметим, что в направлении осей у и z размеры стержня одинаковы во всех системах отсчета.
Сокращение длины движущихся тел
12
+5

13. Следствия из преобразований Лоренца-3

в) Длительность событий в различных системах.
Пусть в точке, неподвижной относительно системы К ,
происходит событие длительностью:
Поскольку событие происходит в точке, то
Относительно системы К точка, в которой происходит событие
перемещается со скоростью 0.
Согласно преобразованиям Лоренца началу и концу события в
системе К соответствуют моменты времени t1 и t2, которые
равны:
и
Временной интервал между событиями в этой системе равен:
Обозначим t2
– t1 = t.
Тогда:
13
+5

14. Следствия из преобразований Лоренца-3

в) Длительность событий в различных системах.
Из формулы следует, что t, определенное по часам, движущимся относительно
покоящейся системы, больше t0 , измеренной по часам, неподвижным
относительно неподвижной (покоящейся) системы.
Согласно формуле t0 < t, откуда следует, что движущиеся часы идут
медленнее, чем покоящиеся часы.
Время t0 , отсчитанное по часам, движущимся вместе с телом, называется
собственным временем этого тела.
Собственное время одинаково во всех инерциальных системах.
Замедление времени у движущихся тел
14
+4

15. 4. Закон сложения скоростей в релятивистской механике

y
y
A
V0t
V0
x
x
x
z
z
y = y
O
O
Положение материальной точки в неподвижной системе
координат К в каждый момент времени t определяется
значением x, y, z.
Проекции вектора скорости на координатные оси равны:
x
z = z
В системе К положение точки в момент времени t
определяется координатами x , y , z .
Проекция на оси x , y , z вектора скорости относительно
систем К :
Вспомним преобразования Лоренца:
Тогда формула преобразования скорости vx в релятивистской механике:
После дифференцирования:
, где
15
+5

16. 4. Закон сложения скоростей в релятивистской механике-2

, где
, где
Если 0 << c, то эти
соотношения переходят в
формулы
сложения скоростей в
классической механике.
, где
Если тело движется параллельно оси х, его скорость относительно системы К совпадает с
x и равна:
Пусть равна с. Тогда скорость по формуле равна:
Полученное соотношение утверждает, что скорость тела равна скорости света с, что подтверждает
второй постулат Эйнштейна.
16
+7

17. Спасибо за внимание!

Курс физики для студентов 1 курса БГТУ
Кафедра физики БГТУ
доцент Крылов Андрей Борисович
Часть I.
ОСНОВНЫЕ ЗАКОНЫ
РЕЛЯТИВИСТСКОЙ
МЕХАНИКИ
Спасибо за внимание!
Эйнштейн Альберт (1879−1955)
Лоренц Хендрик (1853−1928)
17