Элементы релятивистской механики (продолжение). Лекция № 9

1. Лекция № 9

ЭЛЕМЕНТЫ
РЕЛЯТИВИСТСКОЙ
МЕХАНИКИ
(продолжение)

2. Преобразования Лоренца

Преобразования Лоренца при переходе
от K- к K΄-СО (Лекция № 8, ф-ла (8.5а)):
x x ut
z z
y y
xu
t t 2 ,
c
где
1
1 u c
2
2

3.

При обратном переходе от K΄- к K-системе
отсчета (Лекция № 8, ф-ла (8.5б)):
x x ut
y y
z z
x u
t t 2
c

4. Кинематические следствия из преобразований Лоренца

Сокращение длин отрезков, параллельных u ,
относительно неподвижного наблюдателя t2 t1 :
l0 x2 x1 x2 x1 l
Замедление часов: В точке с координатой x΄
K΄-СО протекает процесс, длительность
которого в этой системе t 0 t 2 t1
(собственное время процесса). Длительность
этого процесса в K- системе, относительно
которой K΄-система движется
t t2 t1 t2 t1 t0

5. Релятивистский закон сложения скоростей

В K-системе движется частица со скоростью ,
проекции которой υx, υy и υz. В K΄-СО
d x d x d t
x
d t d t d t
d y d t
d
y
y
d t d t d t
d z d z d t
z
d t d t d t

6.

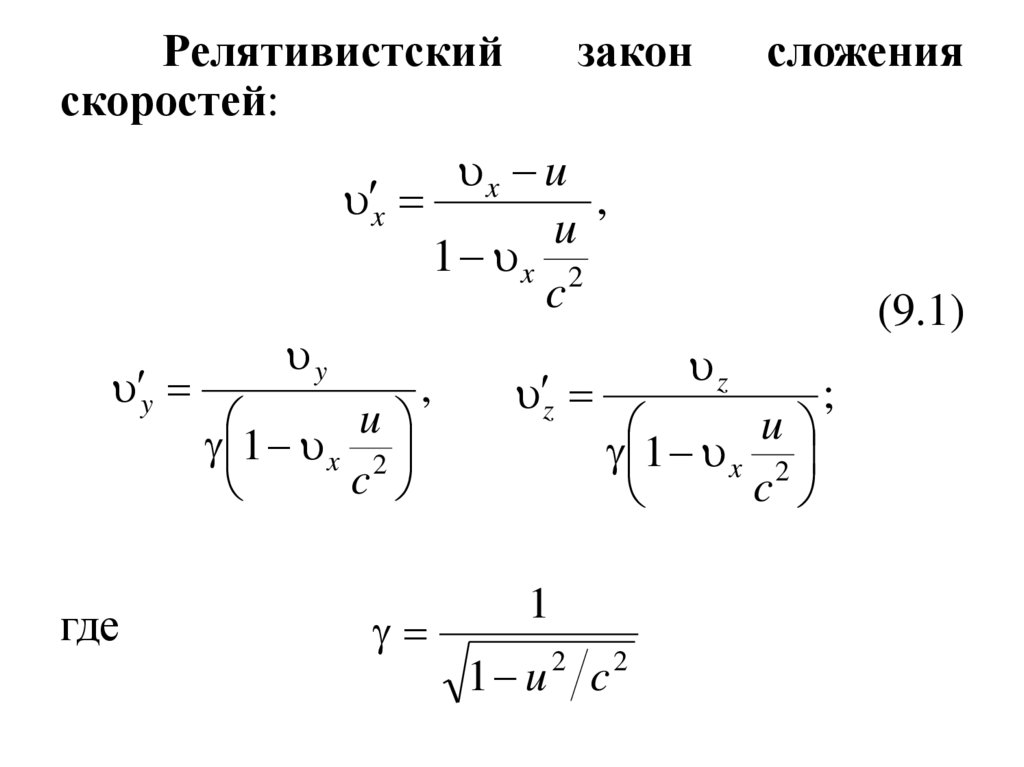
Релятивистский
скоростей:
закон
сложения
x u
x
,
u
1 x 2
c
y
где
y
u
1 x 2
c
,
z
(9.1)
z
u
1 x 2
c
1
1 u c
2
2
;

7.

Аналогично находим обратные зависимости,
для вычисления скорости в K-СО, если она
известна в K΄-СО:
x u
x
,
u
1 x 2
c
(9.2)
y
z
y
, z
u
u
1 x 2
1 x 2
c
c

8. Интервал

В релятивистской механике физический
процесс – это последовательность событий.
Понятие события включает место, где
оно произошло (его координаты x, y, z) и
момент времени t, когда оно произошло.
Интервал между двумя событиями (S12 ):
2
S12
2 2
c t12
2
l12
inv
t12 – промежуток времени между событиями,
l12 – расстояние между точками 1 и 2, в
которых происходят данные события.

9.

Во всех ИСО интервал
между
событиями 1 и 2 одинаков: S S inv
12
Типы интервалов:
1) пространственноподобный
l12 ct12
2) времениподобный
l12 ct12
3) светоподобный
l12 ct12
12

10.

Для (1) – пространственноподобного
интервала всегда можно найти такую K΄систему в которой оба события происходят
одновременно (t΄12 = 0):
2 2
c t12
2
l12
l12
2
Для (2) – времениподобного интервала
всегда можно найти такую K΄-СО, в к-рой оба
события происходят в одной точке (l΄12 = 0):
2 2
c t12
2
l12
2
c t12
2

11.

Существуют причинно связанные и
причинно не связанные события.
В случае пространственноподобных
интервалов (l12 > ct12) ни в одной СО события
не могут оказать влияния друг на друга, даже
если связь между событиями осуществлялась
со скоростью c = 3·108 м/с .
Такие события не причинно-связаны
(сигнал не может дойти).
События, разделенные времениподобными
и светоподобными интервалами (l12 ≤ ct12)
могут быть причинно-связанными друг с
другом, т.к. сигнал может дойти из т. 1 в т. 2
со скоростью с.

12. Элементы релятивистской динамики

Релятивистская масса частицы
m
m0
1 c
2
m0
2
(9.3)
m0 – масса (покоя) частицы, υ – скорость
движения частицы.
Релятивистский импульс
p m
m0
1 c
2
2
m0
(9.4)

13. Основное уравнение релятивистской динамики

частицы в ИСО при любых возможных
скоростях υ < c
d p d m
(9.5)
F
dt
dt

14. ЗАКОН ВЗАИМОСВЯЗИ МАССЫ И ЭНЕРГИИ

Кинетическая энергия
релятивистской частицы
Как и в ньютоновской механике,
приращение кинетической
энергии частицы
под действием силы F
d Ek F
dt
dr

15.

Согласно (9.5)
F d t d m d m m d ,
2
d Ek d m m d d m m d ,
где d d
Упростим это выражение, используя (9.3):
m
m0
1 c
2
2

16.

Возведем (9.3) в квадрат
2
2
m 1 2 m02
c
m c m
2 2
m0 c
m c m
2 2
m0 c
2 2
2 2
2
2
2
2
c
2
Найдем дифференциал этого выражения,
учитывая, что m0 и c – постоянные:
2mc d m 2m d m 2m d
2
2
2

17.

Если разделить это равенство на 2m, то его
правая часть совпадет с выражением для dEk
d E k c d m
2
(9.6)
Кинетическая энергия покоящейся частицы
равна нулю, а ее релятивистская масса m m0
Ek
d Ek
0
m
c dm c
2
m
dm
2
m0
m0
Кинетическая
энергия
движущейся со скоростью υ:
E k m m0 c
2
частицы,
(9.7)

18.

Перепишем (9.7) в форме:
mc m0 c E k
(9.8)
0 m0 c
(9.9)
2
2
Здесь
2
– энергия покоя частицы
внутренняя энергия тела),
mc
2
(это
общая
(9.10)
– полная энергия частицы.
0 Ek
(9.11)

19. Связь между импульсом и энергией релятивистской частицы

Полная энергия ε и импульс p частицы
имеют разные значения в разных СО. Однако
существует некоторая комбинация ε и p,
которая является инвариантной т.е. имеет
одно и то же значение в разных СО:
p c inv
2
2 2
(9.12)
Убедимся в правильности (9.12) подставив в
неё (9.10) и p m :
2 4
m
c
2 4
2 2 2
2
2 2
2
2
0
p c m c m c
1 c
2
2
1 c

20.

Уравнение связи энергии и импульса
частицы
p c
2
2 2
2 4
m0 c
2
0
(9.13)
Правая часть (9.13) не зависит от скорости
частицы, а следовательно, и от СО.
Из (9.11) и (9.13) получаем
2
2
0
0 0 p c
2 2
Ek
Ek 2 0
pc E k E k 2m0 c
2
(9.14)