Расширение пара на рабочих лопатках

1. 3.5. Расширение пара на рабочих лопатках

Закон сохранения энергии для рабочих лопаток (G=1 кг/с)
h1 , p1
Ru
c12
c22
h1 h2 Lu
2
2
c1
u
h2 , p2
2
h1
w2t 2
w22t
2
t0
c12
c22
c12 c22 w22 w12
h1 h2
2
2
2
w12
w22
h1
h2
2
2
c2
Для идеального процесса расширения на рабочих
лопатках:
w12
p0
p1w
h
w12
2
p1
p2
h1 H 0 p
H c
h2t
h1 h2t w12
h2t
2H 0 p
2
p2
p1w
h2t
s

2.

Для действительного процесса расширения на
рабочих лопатках:
w2
w2t
w12
w22
h1
h2
2
2
p0
t0
p1w
h
1 р
р 1 2
w2 w2t
H p
w22t
w22
2
p2
h1
H c
Частный случай:
H0 p 0
p1
w12
2
1
2
w22t
w22
w22t
1 2
2
w22t
h2
h2 h2t
H p
h2t
h2t
0
h2 t h1
w2t w1
w2 w1
s

3. 3.6. Работа (мощность) 1 кг газа в ступени ( по уравнению сохранения энергии )

p0
0 : H 0 р 0;
t0
h0
p1 p2
По уравнению сохранения энергии работа
(мощность) 1 кг газа на лопатках ступени:
h
Lu Hu H 0 H c H p
- располагаемая энергия ступени:
H 0c
p1
H0
h1t
H 0 H 0c H 0 p
Hu
H c
- располагаемая энергия на соплах:
p2
H0 p
h2t
?
H р
c12t
H 0c
2
- располагаемый теплоперепад на
рабочих лопатках:
H0 p
s
w22t w12
2

4.

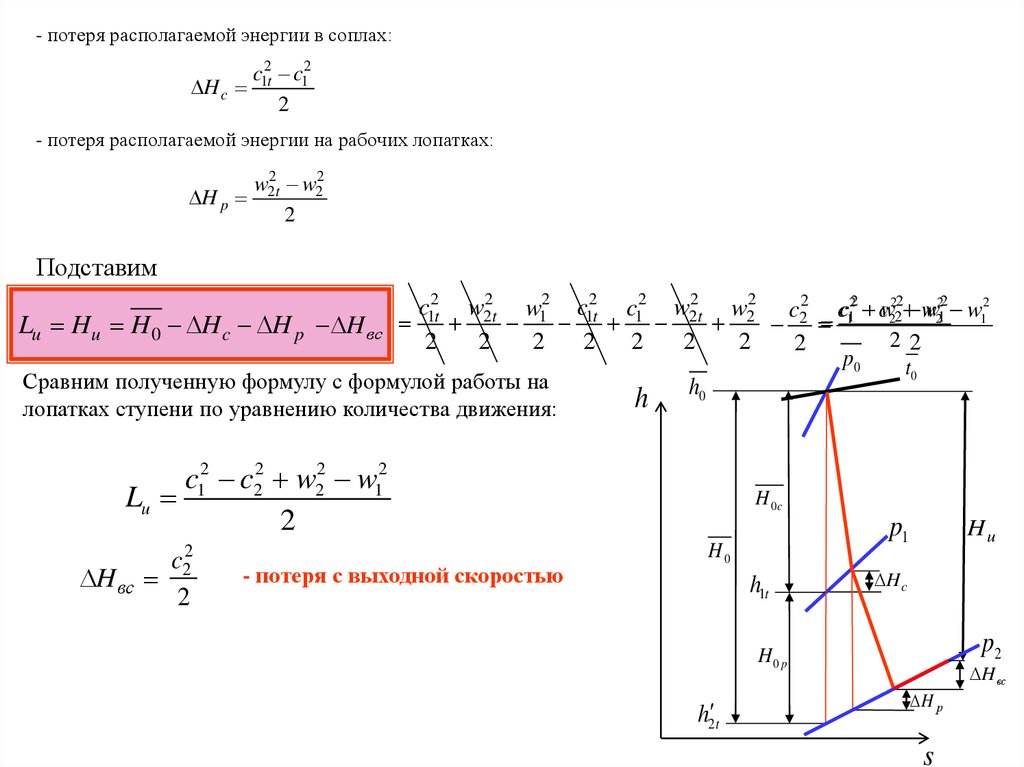
- потеря располагаемой энергии в соплах:
c12t c12
H c
2
- потеря располагаемой энергии на рабочих лопатках:
w22t w22
H p
2
Подставим
c12t w22t w12 c12t c12 w22t w22 c22 c1122 cw2222 ww2212 w12
Lu Hu H 0 H c H p H вс
22
2
2
2
2
2
2
2
2
p0
t0
Сравним полученную формулу с формулой работы на
h0
h
лопатках ступени по уравнению количества движения:
c12 c22 w22 w12
Lu
2
H вс
c22
2
- потеря с выходной скоростью
H 0c
p1
H0
h1t
Hu
H c
p2
H0 p
h2t
H вс
H р
s

5.

3.7. Процессы расширения в hs – диаграмме для ступеней с
различной степенью реактивности
0
0
p0
t0
h0
t0
h0
h
h
p1
p2 p1
H0
Hu
Hu
H0
H c
h1t
t0
h0
h
H 0c
Hu
H 0 H 0c
0 p0
p0
p2
p2
H 0c
H вс
H вс
H р
h2t
H р
h2t
H c
H вс
H0 p
H р
h2t
H0 p
H0 p 0
s
H0 p H0
p1
s
w12
Hc c H0c ; H p p H 0 p
2
с22
H вc
;
2
H c
s
H0 p 0

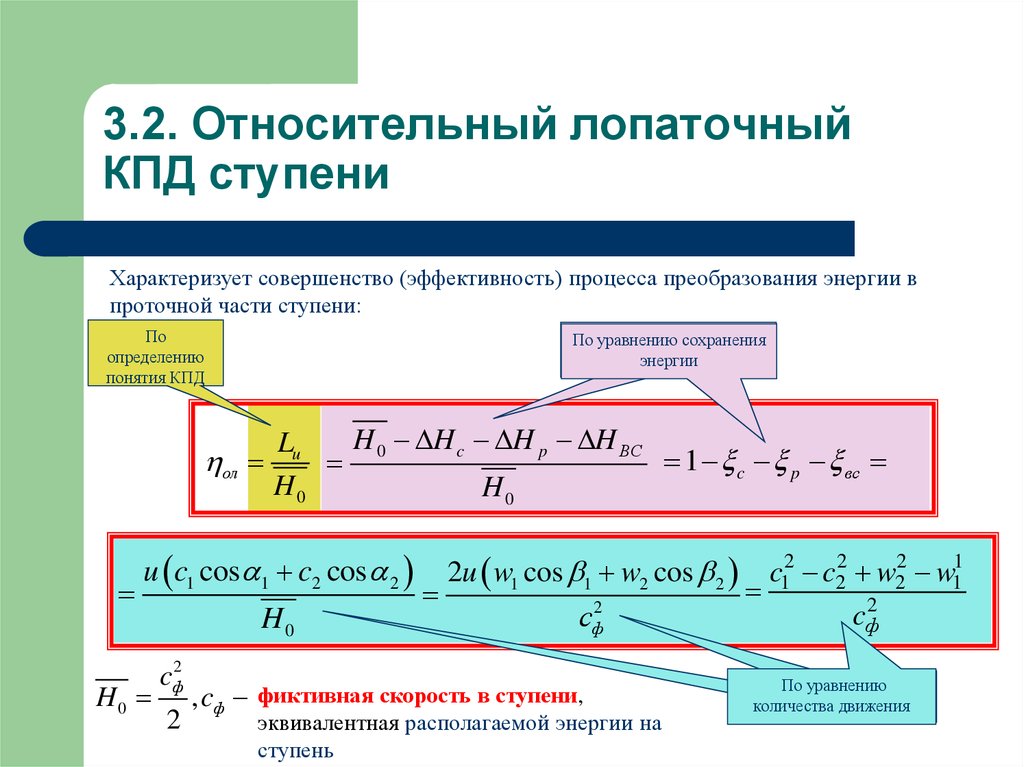
6. 3.2. Относительный лопаточный КПД ступени

Характеризует совершенство (эффективность) процесса преобразования энергии в
проточной части ступени:
По
определению
понятия КПД
По уравнению сохранения
энергии
H 0 H c H p H ВС
Lu
1 c p вс
ол
H0
H0
u c1 cos 1 c2 cos 2
H0
H0
cф2
2
2u w1 cos 1 w2 cos 2
сф2
, cф фиктивная скорость в ступени,
эквивалентная располагаемой энергии на
ступень
c12 c22 w22 w11
cф2
По уравнению
количества движения

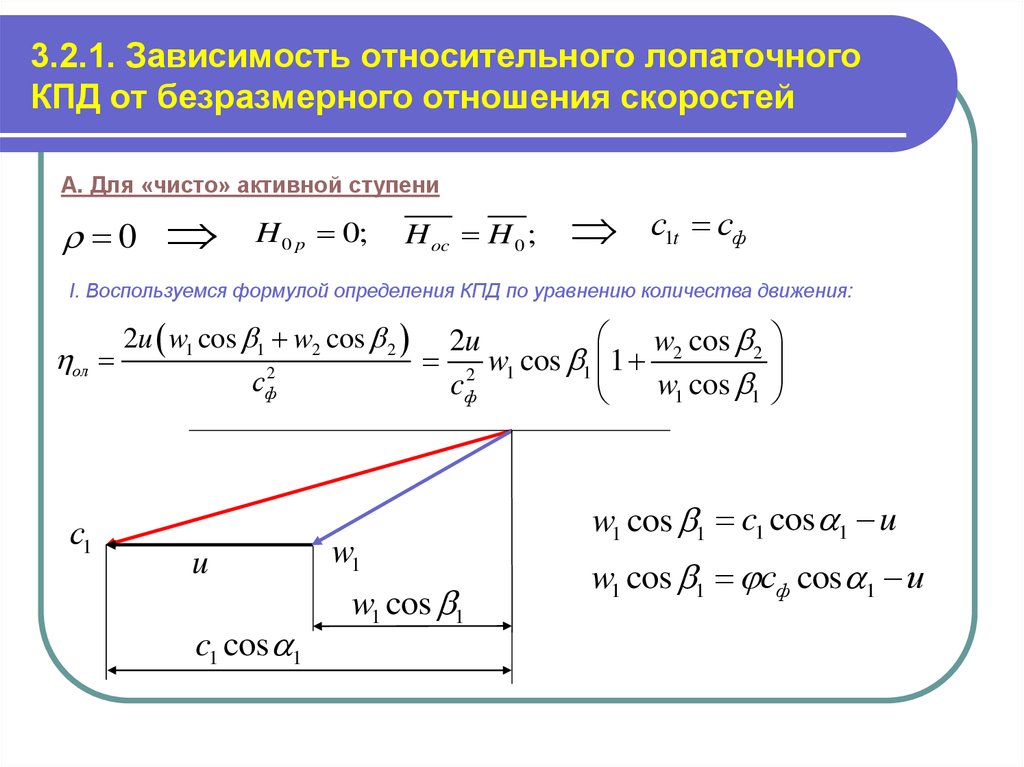
7. 3.2.1. Зависимость относительного лопаточного КПД от безразмерного отношения скоростей

А. Для «чисто» активной ступени
0
H 0 p 0;
H oc H 0 ;
с1t cф
I. Воспользуемся формулой определения КПД по уравнению количества движения:
ол
с1
2u w1 cos 1 w2 cos 2
сф2
u
c1 cos 1
w2 cos 2
2u
2 w1 cos 1 1
cф
w
cos
1
1
w1
w1 cos 1
w1 cos 1 c1 cos 1 u
w1 cos 1 сф cos 1 u

8.

u
w2 cos 2
u 2 w2 cos 2
2u
ол 2 cф cos 1 u 1
2 c cos 1 c 2 1 w cos
cф
w1 cos 1
ф
1
1
ф
u
xф
cф
- безразмерное отношение скоростей
т.к. w2 w2t , а
ол 0
w2t w1,
то
0
w2
w1
cos 2
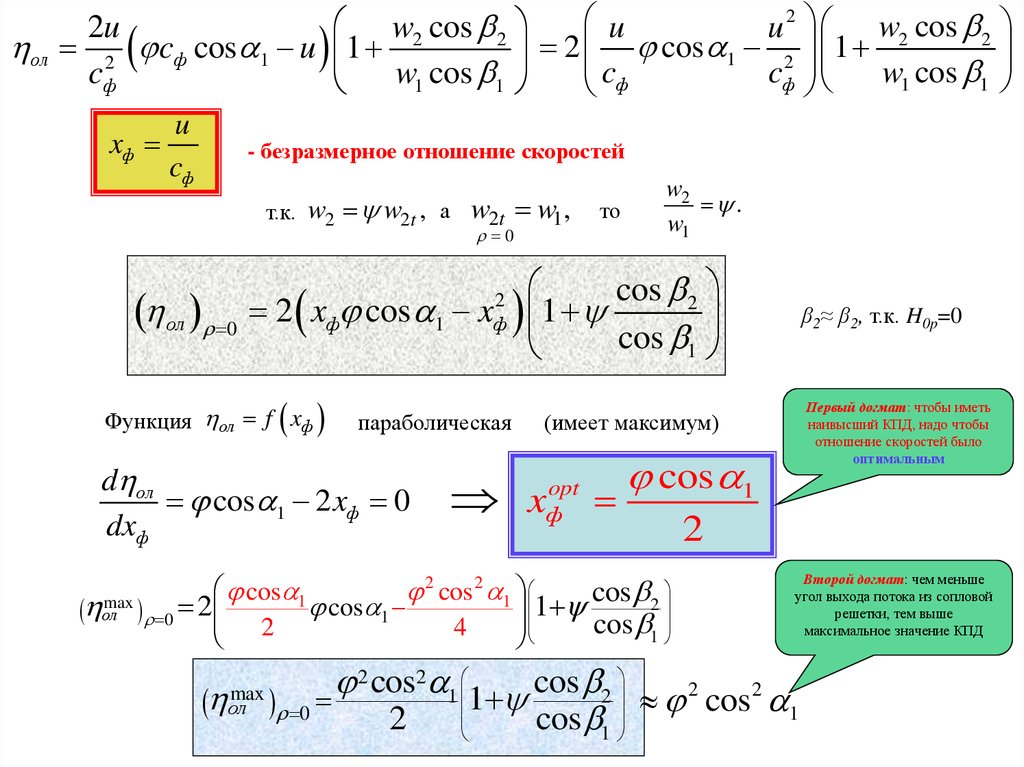
2 xф cos 1 x 1
cos
1
2
ф
Функция ол f xф
d ол
cos 1 2 xф 0
dxф
x
opt
ф
cos 1
cos 1
2 cos 2 1
cos
max
2
cos 1
ол 0 2
1 cos
2
4
1
max
ол
0
Первый догмат: чтобы
иметь наивысший КПД, надо
чтобы отношение скоростей
было оптимальным
параболическая (имеет максимум)
2
Второй догмат: чем
меньше угол выхода потока из
сопловой решетки, тем выше
максимальное значение КПД
2 cos2 1 1 cos 2
2
2
cos
1
2
cos 1

9.

u
w2 cos 2
u 2 w2 cos 2
2u
ол 2 cф cos 1 u 1
2 c cos 1 c 2 1 w cos
cф
w1 cos 1
ф
1
1
ф
u
xф
cф
- безразмерное отношение скоростей
т.к. w2 w2t , а
ол 0
w2t w1,
то
0
w2
.
w1
cos 2
2 xф cos 1 x 1
cos
1
2
ф
Функция ол f xф
параболическая
d ол
cos 1 2 xф 0
dxф
Первый догмат: чтобы иметь
наивысший КПД, надо чтобы
отношение скоростей было
оптимальным
(имеет максимум)
x
opt
ф
cos 1
cos 1
2 cos 2 1
cos
max
2
cos 1
ол 0 2
1 cos
2
4
1
max
ол
0
β2≈ β2, т.к. H0p=0
2
Второй догмат: чем меньше
угол выхода потока из сопловой
решетки, тем выше
максимальное значение КПД
2 cos2 1 1 cos 2
2
2
cos
1
2
cos 1

10.

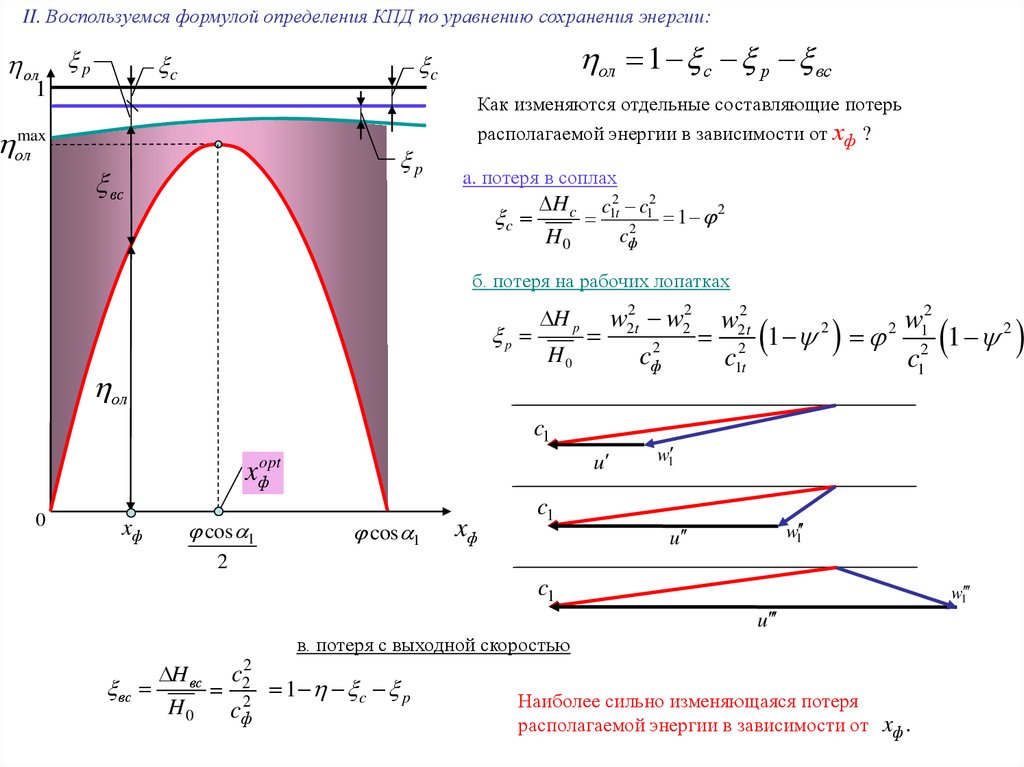
II. Воспользуемся формулой определения КПД по уравнению сохранения энергии:
ол
p
c
1
олmax
ол 1 c p вс
c
p
вс
Как изменяются отдельные составляющие потерь
располагаемой энергии в зависимости от хф ?
a. потеря в соплах
H c c12t c12
2
1
c
cф2
H0
б. потеря на рабочих лопатках
2
w22t w22 w22t
2
2 w1
2
p
1
1
H0
cф2
c12t
c12
H p
ол
c1
u
opt
ф
x
0
xф
cos 1
cos 1
xф
c1
w1
w1
u
2
c1
u
в. потеря с выходной скоростью
вс
H вс
H0
c22
cф2
1 c p
Наиболее сильно изменяющаяся потеря
располагаемой энергии в зависимости от xф .
w1

11.

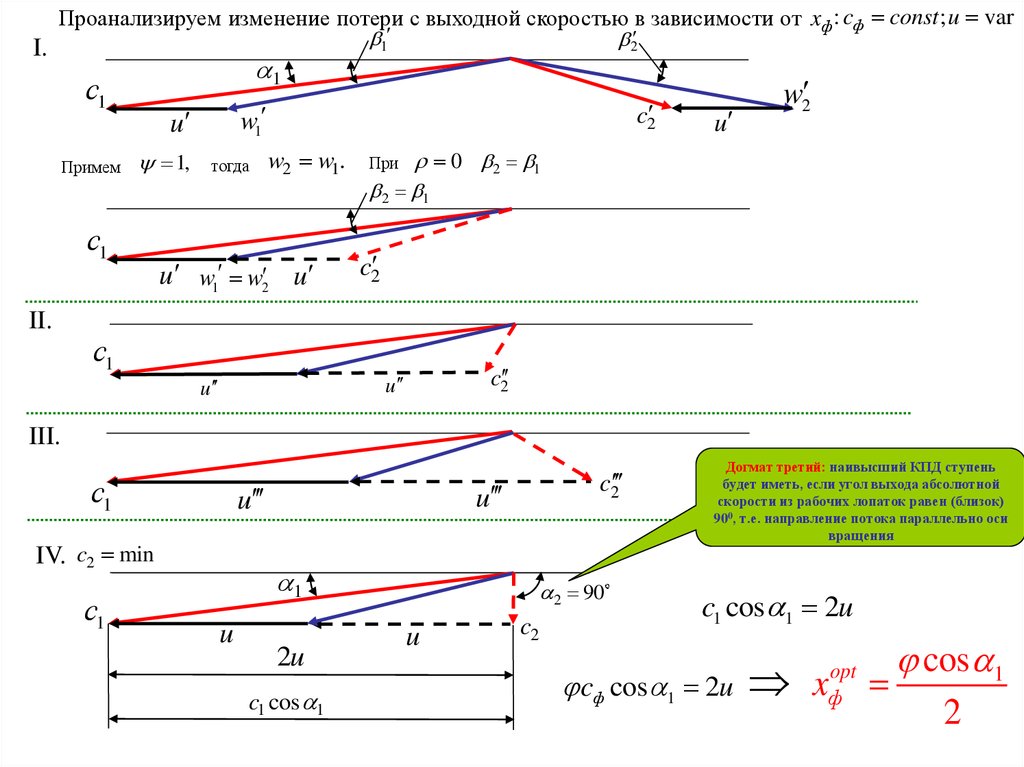
Проанализируем изменение потери с выходной скоростью в зависимости от xф : cф const ; u var
1
2
I.
1
с1
Примем
с1
II.
w1
u
1,
с1
c2
тогда
w2 w1.
u w1 w2 u
При
0 2 1
2 1
c2
c2
u
u
u
w2
III.
с1
IV. c2 min
с1
c2
u
u
1
u
2u
c1 cos 1
2 90
u
c2
Догмат третий: наивысший КПД ступень
будет иметь, если угол выхода абсолютной
скорости из рабочих лопаток равен (близок)
900, т.е. направление потока параллельно оси
вращения
c1 cos 1 2u
cф cos 1 2u
x
opt
ф
cos 1
2

12.

Б. Для ступени при любом значении степени реактивности:
ол 2 xф cos 1 1 xф cos 2 2 1 xф 2 xф cos 1 1
ол
1
олmax
p
0,5
c
opt
ф
x
cos 1
2 1
Потери:
a. потеря в соплах
вс
c12t
H c c12t c12
2 1 2 1 1 2
c
2
H0
cф
cф
c12t 2 1 H 0 ; cф2 2H 0
ол 0
б. потеря на рабочих лопатках
p
ол
H p
H0
w12
w22t
2
2 1 2 1 2
cф
cф
w22t 2 H0 w12
в. потеря с выходной скоростью
Минимальна при 2 90
x
opt
ф
0
xф
cos 1
cos 1
2
2 0,5
xфopt
x
x
opt
ф
xф
opt
ф
0,5
0
2

13. 3.2.2. Оптимальный располагаемый теплоперепад ступени

Задано: диаметр ступени и угловая скорость вращения ротора.
Определить: какой теплоперепад сработает ступень с наивысшим КПД.
H0
cф2
2
;
H0
opt
u2
2
H0
Частные случаи:
а)
H
H0
б)
opt
0
opt
0
0,5
2
u2
H0 2
2 xф
u
xф ;
cф
opt
xфopt
xфopt
2
cos 1
2 1
2 2 d 2 n2 1
2 cos2 1
0; _ n 50c 1; _ 1 13o ; _ 0,97
H0
opt
u dn
0
52,5d
2
в)
H
H0
opt
n 50
opt
0
n 25
4