Похожие презентации:
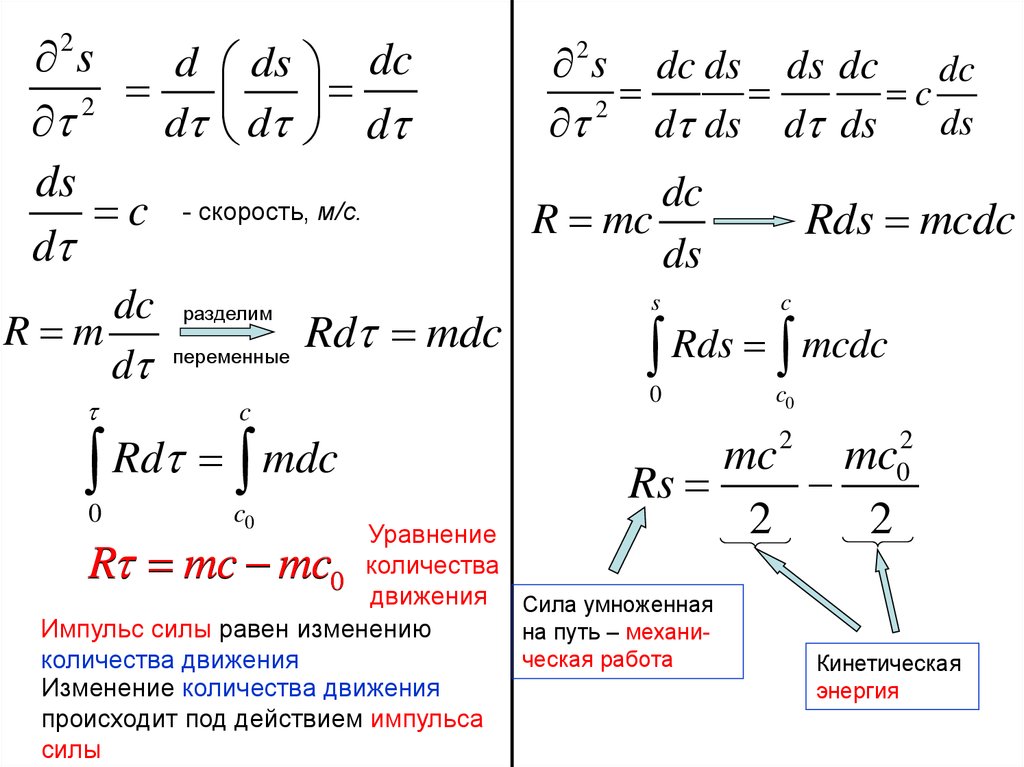
Уравнение количества движения
1.
2sd ds dc
2
d d d
ds
c - скорость, м/с.
d
dc
R m
d
разделим
переменные
Rd mdc
c
Rd mdc
0
c0
2 s dc ds ds dc dc
c
2
ds
d ds d ds
dc
R mc
ds
s
c
0
c0
Rds mcdc
2
2
0
mc mc
Rs
2
2
Уравнение
количества
0
движения Сила умноженная
Импульс силы равен изменению
на путь – механическая работа
количества движения
Изменение количества движения
происходит под действием импульса
силы
R mc mc
Rds mcdc
Кинетическая
энергия
2.
Б) Применение уравнения количества движения при движении жидкости (газа) вканале.
I. Феноменологический подход
Если известен секундный расход массы G массы[кг/с] и скорости потока на входе с1 [м/с]
и выходе канала с2 [м/с], то можно определить силу R [н], которая заставила измениться
количеству движения
R G c2 c1
Т.к. по третьему закону Ньютона сила действия равна силе противодействия, то можно
определить силу, с которой поток действует на стенки канала
R R G c1 c2
II. Проблема определения действительной скорости
3.
pdc
f 0 p0 f1 p0 dx dR dm
x
d
1
0
с0
p0
dR
с0+dc
p
p0 dx
x
dx
dR
f
0
1
0
где R
dR
dm
при dx 0 :
f
p
dc
dx dR dm
x
d
f1
f0 f1 f
: dm
fdx
p
dc
R
x
d
- сила сопротивления, отнесенная к 1кг массы протекающего газа.
Для установившегося режима
dp Rdx
dx
dc
d
dx
c
d
Интегрируя от 0-0 до 1-1
p dp
x dx
cdc dp Rdx
c12 c02
2
p0
x1
p1
x0
Уравнение количества
движения в одномерном
потоке
dp Rdx
4.
c12 c022
c02
2
p0
p0
p1
p1
dp
x1
p1
x0
dp Rdx
R x 0
* Теоретический процесс расширения
c12t
p0
dp lтехн h0 h1t
c12t c02
h0 h1t
2
** Действительный процесс расширения
R f x
Известно, что
R f ( , Re (c, , d ), кривизны канала, …)
в частности, возможностью
отрыва пограничного слоя при
диффузорном характере
течения
В теории турбин уравнение количества движения для потока в канале при
действительном течении заменяется экспериментальными данными.
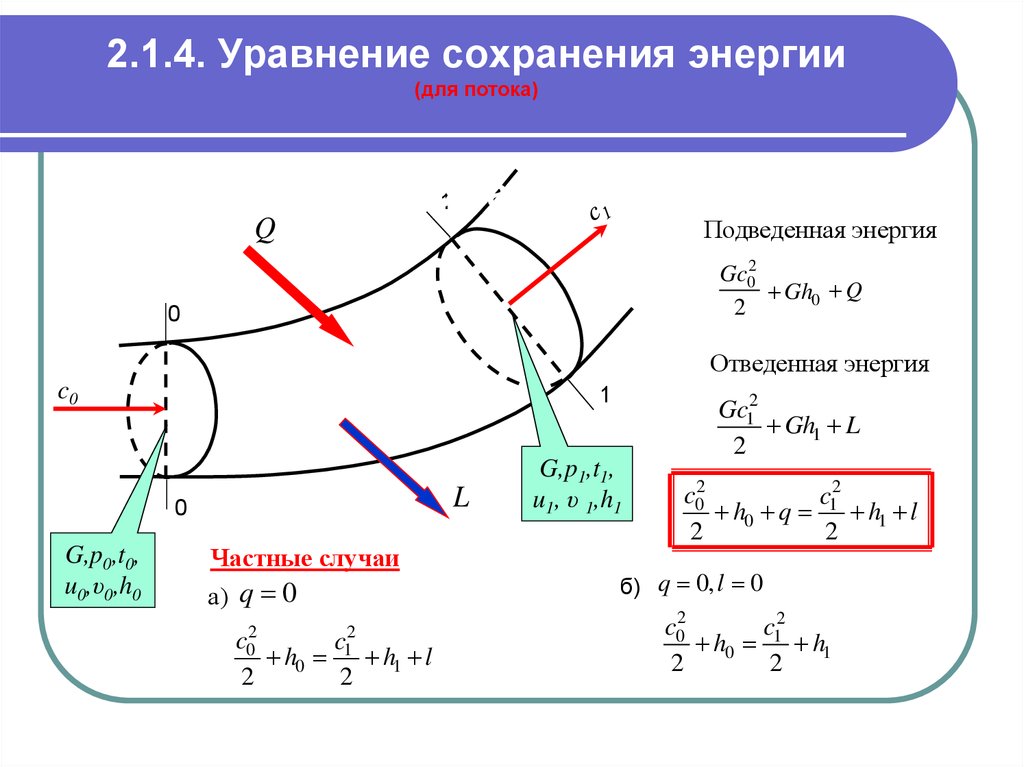
5. 2.1.4. Уравнение сохранения энергии (для потока)
2.1.4. Уравнение сохраненияэнергии
1
Подведенная энергия
Q
Gc02
Gh0 Q
2
0
Отведенная энергия
c0
1
L
0
G,p0,t0,
u0,υ0,h0
Частные случаи
а) q 0
c02
2
h0
c12
2
h1 l
G,p1,t1,
u1, υ 1,h1
Gc12
Gh1 L
2
c02
c12
h0 q h1 l
2
2
б) q 0, l 0
c02
c12
h0 h1
2
2
6.
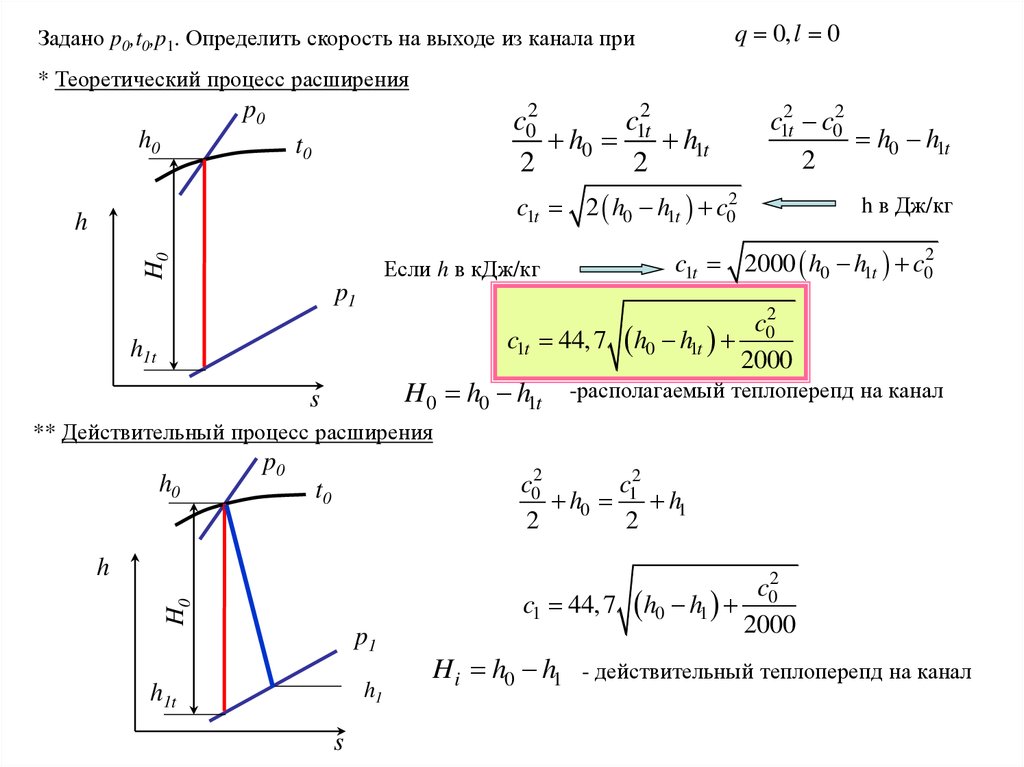
q 0, l 0Задано p0,t0,p1. Определить скорость на выходе из канала при
* Теоретический процесс расширения
p0
h0
c02
c12t
h0
h1t
2
2
t0
c12t c02
h0 h1t
2
c1t 2 h0 h1t c02
H0
h
Если h в кДж/кг
p1
h в Дж/кг
c1t 2000 h0 h1t c02
c02
c1t 44, 7 h0 h1t
2000
h1t
H 0 h0 h1t -располагаемый теплоперепд на канал
s
** Действительный процесс расширения
h0
p0
c02
c12
h0 h1
2
2
t0
H0
h
p1
h1
h1t
s
c02
c1 44, 7 h0 h1
2000
H i h0 h1 - действительный теплоперепд на канал
7.
Сравнение использования уравнений количества движения и сохранения энергииТеоретический процесс расширения
p0
h0
Уравнение количества
движения
t0
c12t
h
c02
c12t c02
h0 h1t
2
H0
2
h0 h1t
Уравнение сохранения
энергии
p1
c1t 2 h0 h1t c02
c1t 2 h0 h1t c02
h1t
s
Действительный процесс расширения
h0
p0
x1
c12 c02
h0 h1
2
p1
x0
c1 2 h0 h1 c02
Необходимо знать
термодинамический
процесс по длине
канала
Необходимо знать
начальное и конечное
состояние
p0
t0
c12 c02
2
H0
h
p1
h1
h1t
s
dp Rdx
8.
*** Ускорение потокаc12 c02
h0 h1
2
Если h1< h0 , то с1> с0 поток ускоряется (конфузорное течение)
Если h1> h0 , то с1< с0 поток замедляется (диффузорное течение)
9. 2.2. Характеристики потока при изоэнтропийном расширении газа в каналах
Канал, в котором поток плавно ускоряется, называется сопловым или простосоплом.
Канал, в котором поток плавно замедляется, называется диффузорным или
просто диффузором.
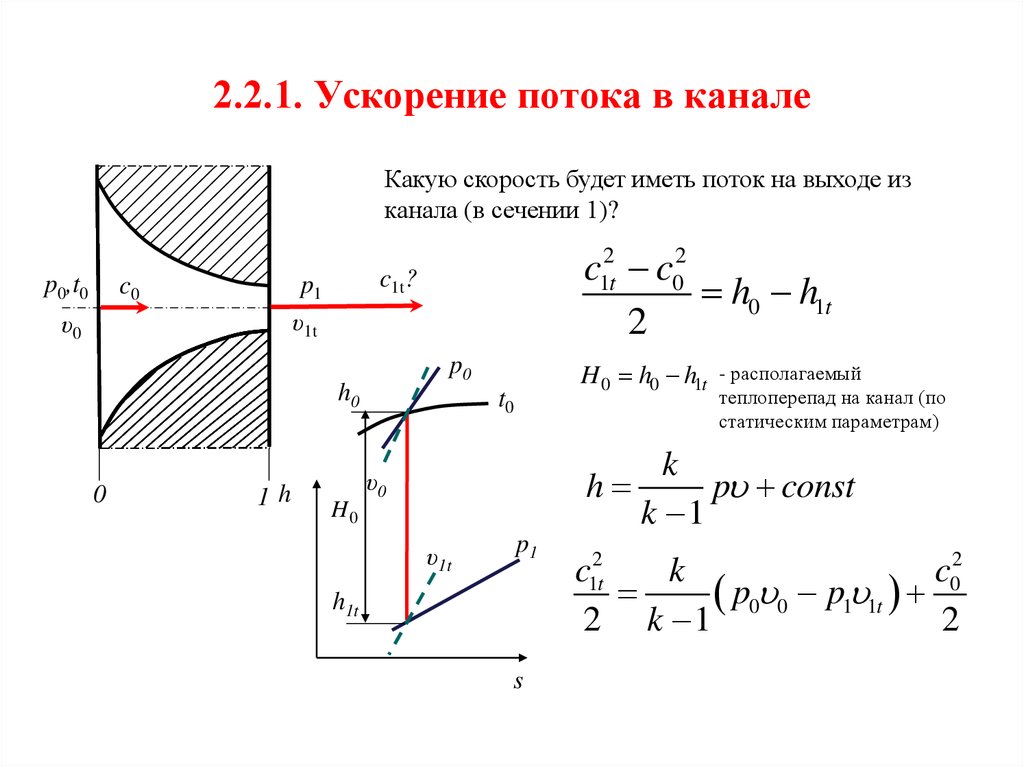
10. 2.2.1. Ускорение потока в канале
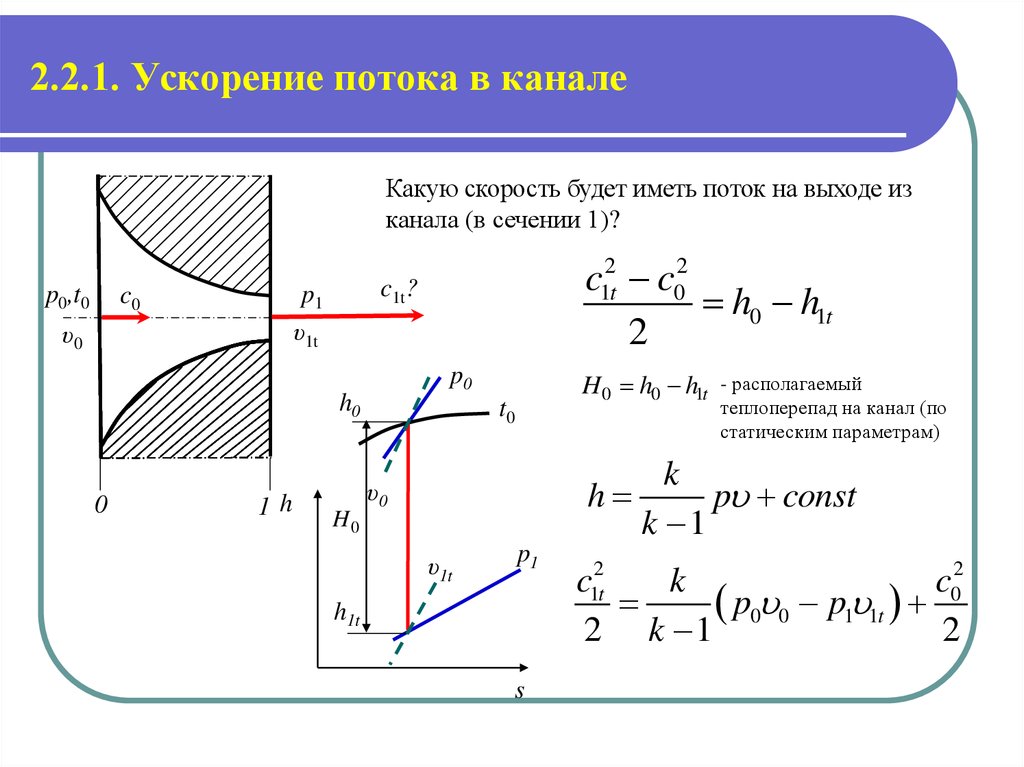
Какую скорость будет иметь поток на выходе изканала (в сечении 1)?
p0,t0
c1t?
p1
υ1t
c0
υ0
p0
h0
0
1h
c12t c02
h0 h1t
2
H 0 h0 h1t
t0
- располагаемый
теплоперепад на канал (по
статическим параметрам)
k
h
p const
k 1
υ0
H0
υ1t
p1
h1t
s
c12t
k
c02
p0 0 p1 1t
2 k 1
2
11. 2.2.1. Ускорение потока в канале
Какую скорость будет иметь поток на выходе изканала (в сечении 1)?
p0,t0
c1t?
p1
υ1t
c0
υ0
p0
h0
0
1h
c12t c02
h0 h1t
2
H0
H 0 h0 h1t
t0
- располагаемый
теплоперепад на канал (по
статическим параметрам)
k
h
p const
k 1
υ0
υ1t
p1
h1t
s
c12t
k
c02
p0 0 p1 1t
2 k 1
2
12.
c12tk
c02
p0 0 p1 1t
2 k 1
2
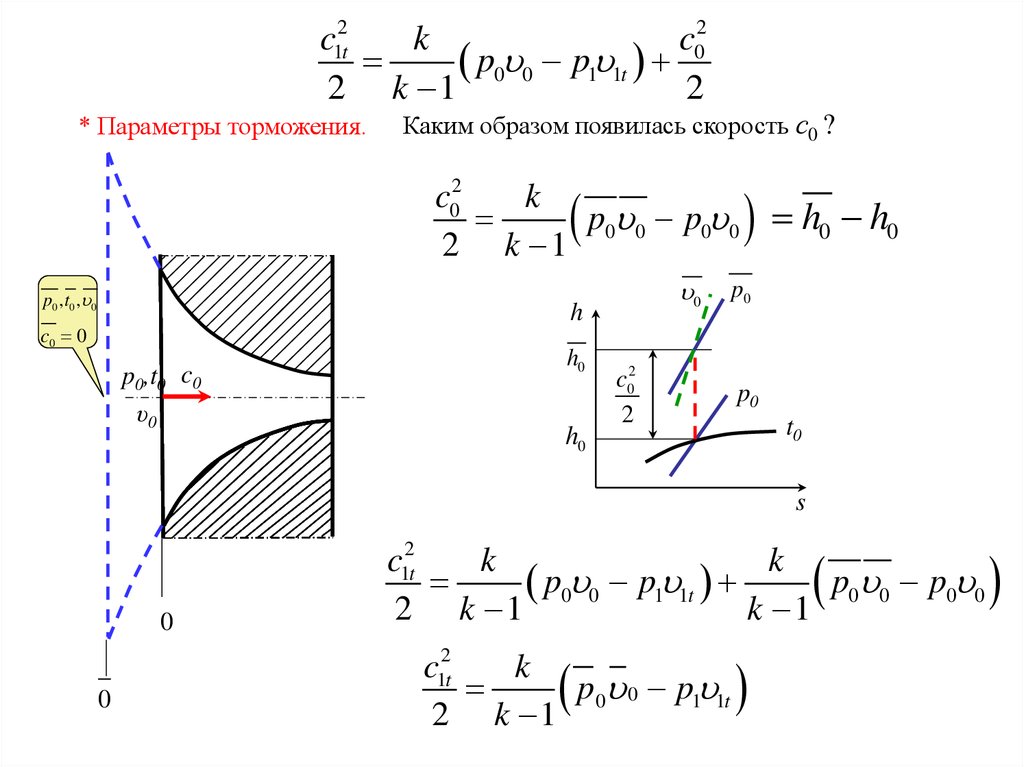
* Параметры торможения.
Каким образом появилась скорость с0 ?
c02
k
p0 0 p0 0 h0 h0
2 k 1
p0 , t0 , 0
0
h
c0 0
p0,t0 c0
υ0
h0
h0
c02
2
p0
p0
t0
s
0
_
0
c12t
k
k
p0 0 p0 0
p0 0 p1 1t
2 k 1
k 1
c12t
k
p0 0 p1 1t
2 k 1
13.
c12tk
p0 0 p1 1t h0 h1t
2 k 1
H h
c
k
p1 1t
p 0 0 1
2 k 1
p
0
0
0
0
h1t - располагаемый теплоперепад на
канал (по параметрам торможения на
2
1t
p1 p0
p1 1t
p 0 p1
p0 0
1
k
а) По уравнению изоэнтропы
1
k
c02
H0 H0
2
k 1
k
p k const имеем
1t p 0
0 p1
k
p0 0 p1 1kt
б) Обозначим
входе)
p1
p0
1
k
отношение давлений на канал (сопло)
k 1
c12t
k
k
p 0 0 1
2 k 1
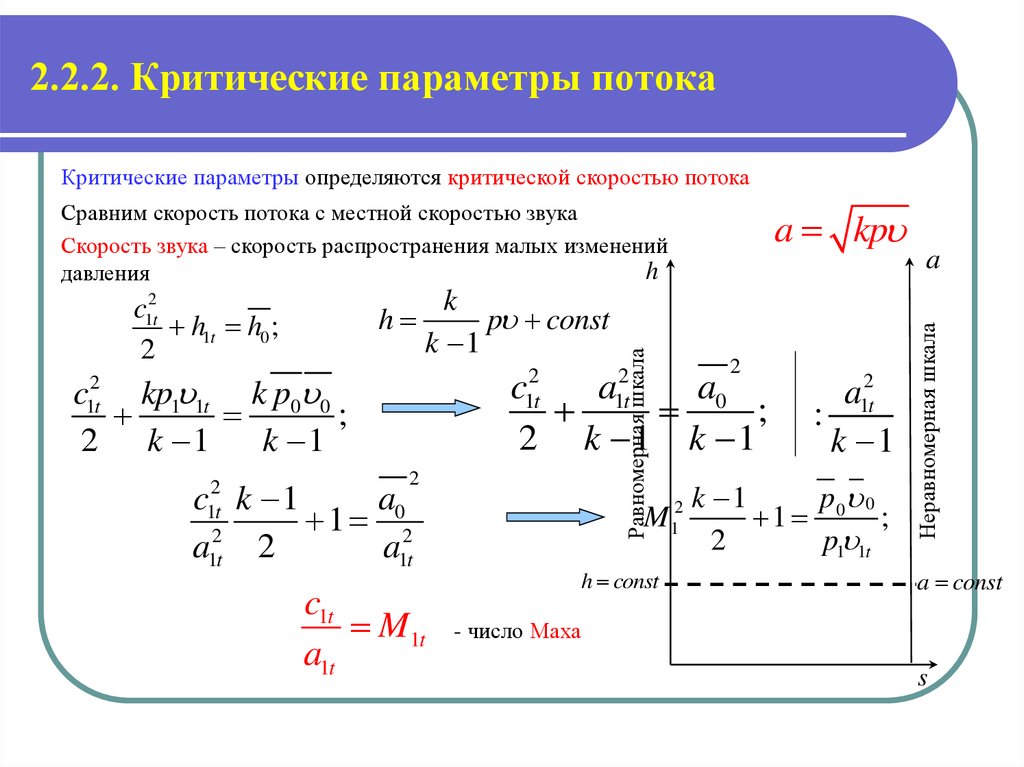
14. 2.2.2. Критические параметры потока
Критические параметры определяются критической скоростью потокаh
k
p const
k 1
2
1t
c
kp
kp
1 1t 0 0 ;
2 k 1
k 1
2
c
a
a0
;
2 k 1 k 1
2
1t
2
c k 1
a0
1 2
a 2
a1t
2
1t
2
1t
2
1t
a kp
c1t
M1t
a1t
M 12
h const
a12t
:
k 1
p 0
k 1
1 0 ;
2
p1 1t
a
Неравномерная шкала
c12t
h1t h0 ;
2
Равномерная шкала
Сравним скорость потока с местной скоростью звука
Скорость звука – скорость распространения малых изменений
h
давления
a const
- число Маха
s
15.
M 12p 0
k 1
1 0 ;
2
p1 1t
1 k
p 0 0
k
p1 1t
2 1 kk
M 1t
1
k 1
M 1t 1:
k 1
1
2
p1
*t
p0
1 k
k
t
c1t a1t a
k 1
2
1 k
k
t
2
t
k
1
k
k 1
- критическое отношение давлений
2
*t
k 1
k
k 1
Для:
перегретого пара k 1,3
t 0,546
влажного пара k 1,135
t 0,577
воздуха k 1,4
t 0,526
16.
Чем же особенны критические параметры?1. При критических параметрах скорость потока равна местной скорости звука.
2. Проанализируем такую задачу:
Заданы начальные параметры и расход пара через сопло.
Определить изменение площади выходного сечения сопла при изменения давления
на выходе
F1t G
1t
c1t
k 1
2k
k
c1t
p 0 0 1
k 1
p1
p0
h0 h1t
17.
p0p1
t0
H 01
F1t
1t c1t a1t
p1 p0
p11
p11
h
11
p12
p12
c1t aa1t1t
12
p1
p13
p12
F1min
1t
13
s
H 01
H 02
H 0
H 03
dF d dc
F
c
H0
18. 2.2.3.Расход пара (газа) через суживающееся сопло
Рассмотрим такую задачу.Как будет изменяться расход G через суживающееся сопло, площадью F1 ,
при постоянных параметрах торможения на входе p 0 const , t 0 const
и переменном давлении за соплом p1 ?
G F1t
F1
G ?
p0 , t0
c1t
1t
k 1
2k
c1t
p 0 0 1 k
k 1
p1 var
p1 c1t 1t
19.
GG
p1
p1
p1 p0
p
p0 , t0
p1 p1
p1 p0
p1
p0 , t0
p1 p1
p1
20.
Gp02
G 2
G 1
p01
p1 1 p01
p11 p01
p1 2 p02
p12 p02
p1
21.
* Практическое применение*
Заданы: p0 , p1 , т.е.
p1
.
p0
А. Выбор типа сопла:
- если * , то сопло должно быть расширяющимся
- если * , то сопло должно быть суживающимся
Б. Режим работы суживающегося сопла
- если * , то сопло работает в докритическом режиме и в выходном сечении сопла
давление будет равно давлению за соплом (р1)
- если * , то сопло работает в критическом режиме и в выходном сечении сопла
установится давление
p1* * p0
22.
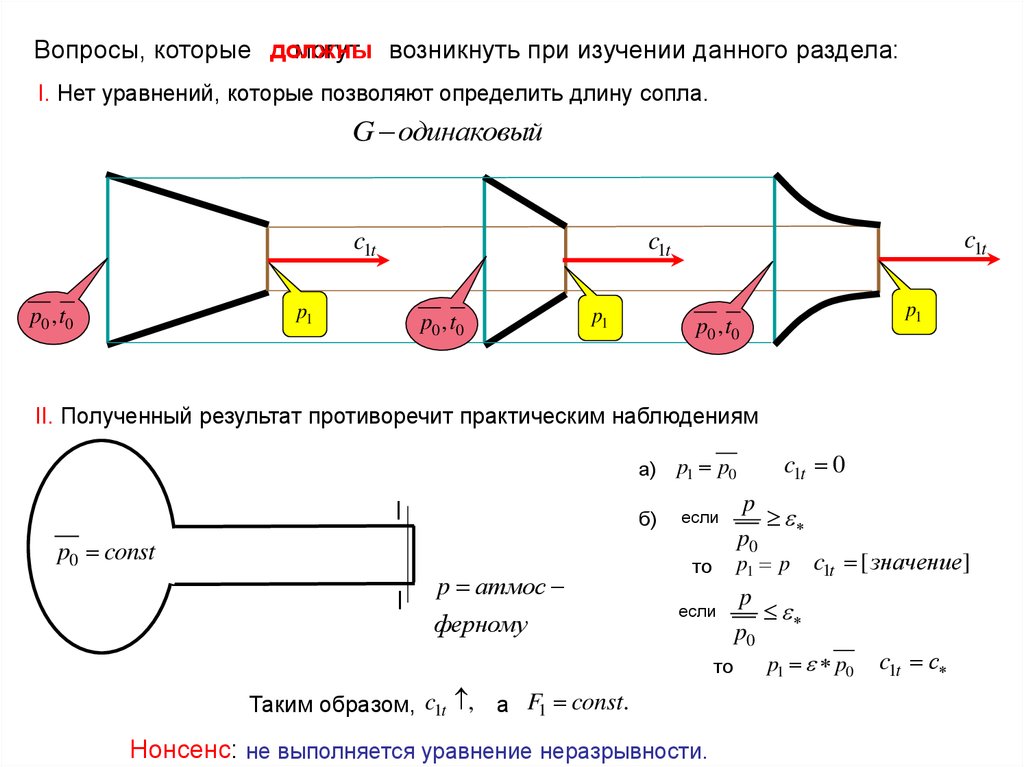
Вопросы, которые должнымогут возникнуть при изучении данного раздела:
I. Нет уравнений, которые позволяют определить длину сопла.
G одинаковый
p1
p0 , t0
c1t
c1t
c1t
p0 , t0
p1
p1
p0 , t0
II. Полученный результат противоречит практическим наблюдениям
I
p0 const
I
p атмос
ферному
а)
p1 p0
б)
если
c1t 0
p
p0
то
p1 p
если
p
p0
то
Таким образом, c1t , а F1 const.
Нонсенс: не выполняется уравнение неразрывности.
c1t [ значение]
p1 p0
c1t с
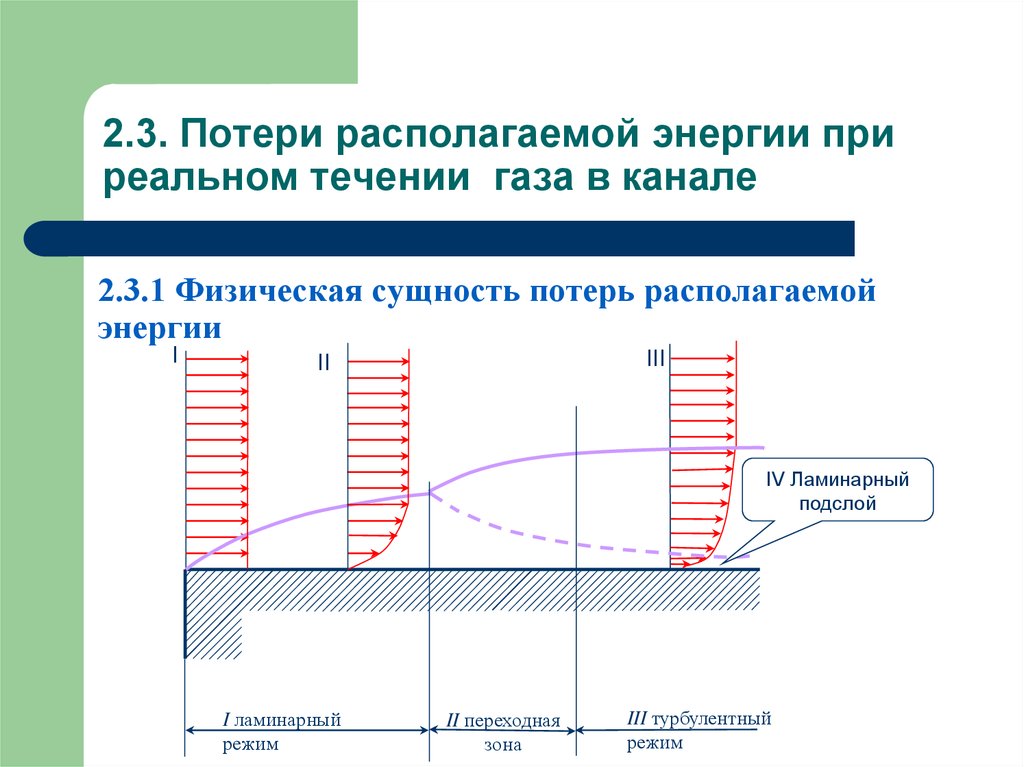
23. 2.3. Потери располагаемой энергии при реальном течении газа в канале
2.3.1 Физическая сущность потерь располагаемойэнергии
I
III
II
IV Ламинарный
подслой
I ламинарный
режим
II переходная
зона
III турбулентный
режим
24.
1с1ср
с1t
25. 2.3.2. Характеристики реального потока в соплах
А) Энергетические характеристикиУравнение сохранения энергии:
c12
h0 h1
- для реального потока
2
c12t
- для изоэнтропийного процесса
h0 h1t
2
Разность кинетических энергий теоретического и реального потоков:
c12t c12
H c h1 h1t
2 2
Потеря располагаемой
энергии
Относительная величина потери называется коэффициентом потерь
c
H c
H0
26.
p0h
c
c12t c12
2
H c 2 2
c1
1
c12t
H0
c1t
2
c12t
H0
2
c1
c1t
c12t c12
H c
2 2
H0
c02
h0 2
c или
(откуда)?
H c c H 0
h1 h1t H c
p1
H c
υ1t
t0
h1
h1t
1 c
p0
υ1
H0
- коэффициент скорости сопла
c 1 2
Известен
h0
s
27.
Б) Расходные характеристикиИзвестны:
площадь выходного сечения сопла (F1);
начальные параметры (p0, t0,c0);
конечное давление (p1).
Расход газа через сопло:
- при теоретическом процессе расширения
Gt
F1c1t
- при действительном процессе расширения
G
F1c1
Применение понятия
Знаем теоретический процесс
расширения
- коэффициент расхода сопла
F1c1 1t
1t
1 F1c1t
1
Какой в действительности пройдет расход
через сопло с заданной выходной
площадью?
h
G
1 1t
Справедливо только для
однофазной среды!!!
1t
Редко
встречающаяся
задача
G
Gt
1
F1c1t
1t
Какую выходную площадь должно
иметь сопло, чтобы пропустить
заданный расход
1
s
F1
G 1t
c1t
Основа
методики
расчета
турбинных
ступеней
1t
28.
В) Критическое отношение давленийp0 p1
h
h0
2
1t
c
2
2
*t
k 1
t0
c12
2 p p
1 t
t 0
p1 p0
h1
h1t
a const
s
k
k 1
k 1 1
1
k
1
1
k
k 1



















 Физика
Физика








