Похожие презентации:
Электроны в кристаллах
1. Презентация на тему: электроны в кристаллах
П О Д ГО ТО В И Л : С Т УД Е Н Т Г Р У П П Ы РТ - 11Д М И Т Р И Е В И Л ЬЯ
2.
ЭЛЕКТРОНЫ В КРИСТАЛЛАХОдноэлектронное приближение при котором вместо взаимодействия
данного электрона с остальными электронами по отдельности
рассматривается его движение в некотором результирующем
(самосогласованном) поле усредненного пространственного заряда
остальных электронов
2m
2 E W p We 0
В приближении сильной связи
предполагается, что во всем объеме
кристалла существует сильно
изменяющееся потенциальное поле
W p (r ) Wa W (r )
1
3.
ЭЛЕКТРОНЫ В КРИСТАЛЛАХРазрешенной зоной
называется интервал
значений энергии,
которой может обладать
электрон в кристалле
Запрещенные зоны
это энергетические
промежутки,
отделяющие
разрешенные зоны
друг от друга
2
4. ЭЛЕКТРОНЫ В КРИСТАЛЛАХ
ЭЛ
ЕКТРО
НЫ
ВКРИ
С
ТАЛ
ЛАХ
Свойство 1. Число квантовых состояний в разрешенной зоне равно
кратности вырождения атомного уровня энергии, из которого возникла
зона, умноженное на полное число атомов в кристалле
Свойство 2. Электроны являются фермионами и подчиняются
принципу Паули, два и более тождественных фермиона (частицы с
полуцелым спином) не могут одновременно находиться в одном и том
же квантовом состоянии, поэтому число электронов в разрешенной
зоне не может превзойти числа имеющихся в нем состояний,
называемых вакансиями.
Свойство 3. Низко расположенные уровни образуют узкие зоны, а
высоко расположенные – широкие.
Свойство 4. носителями заряда, создающими ток в кристалле могут
быть только электроны из обобществленной, частично заполненной
зоны. (проводимости) https://www.youtube.com/watch?v=qD7eLEvMHVI
3
5.
ЭЛЕКТРОНЫ В КРИСТАЛЛАХЗонная структура некоторых кристаллических
проводников и изоляторов
Пример 1. Кристаллы
одновалентных химических
элементов лития, натрия, калия,
меди (проводники) 1s 2 2s 1
Пример 2. Кристаллы
двухвалентных химических
элементов бериллия,
магния (проводники)
1s22s2
Пример 3. Кристалл
поваренной соли (изолятор)
Натрий 1s22s12p63s1
Хлор 1s22s22p63s23p5
4
6.
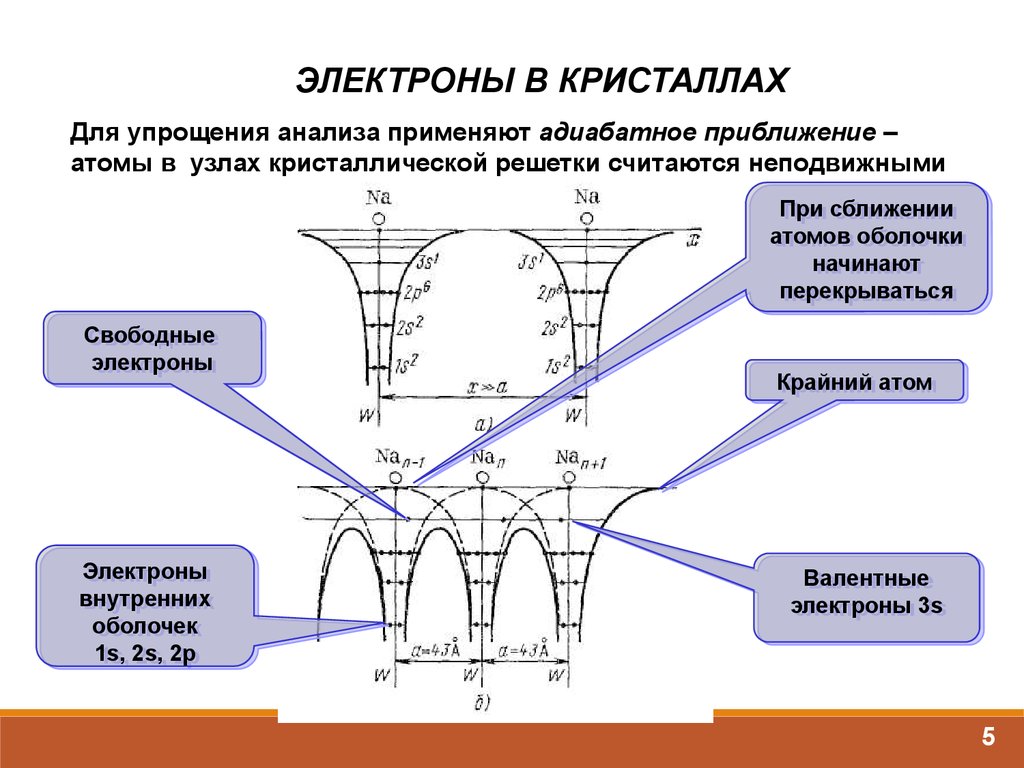
ЭЛЕКТРОНЫ В КРИСТАЛЛАХДля упрощения анализа применяют адиабатное приближение –
атомы в узлах кристаллической решетки считаются неподвижными
При
При сближении
сближении
атомов
атомов оболочки
оболочки
начинают
начинают
перекрываться
перекрываться
Свободные
Свободные
электроны
электроны
Электроны
Электроны
внутренних
внутренних
оболочек
оболочек
1s,
1s, 2s,
2s, 2p
2p
Крайний
Крайний атом
атом
Валентные
Валентные
электроны
электроны 3s
3s
5
7.
ЗАПОЛНЕНИЕ ЭЛЕКТРОНАМИЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ
ТВЕРДЫЕ
ТВЕРДЫЕ ТЕЛА
ТЕЛА
вещества
вещества сс неполным
неполным
заполнением
заполнением верхних
верхних
разрешенных
разрешенных зон
зон –– аа ии бб
(металлы)
(металлы)
вещества
вещества сс полным
полным
заполнением
заполнением валентной
валентной
зоны
зоны -- вв
Запрещенная
Запрещенная зона
зона относительно
относительно узкая
узкая -собственные
собственные полупроводники
полупроводники (0.5
(0.5 -1.2
-1.2 эВ)
эВ)
Запрещенная
Запрещенная зона
зона относительно
относительно широкая
широкая
-- диэлектрики
диэлектрики (4-5
(4-5 эВ)
эВ)
6
8.
ЭЛЕКТРОНЫ В КРИСТАЛЛАХ1.
1. Решение
Решение уравнения
уравнения
Шредингера
Шредингера сс учетом
учетом
периодичности
периодичности
потенциального
потенциального поля
поля вв
кристалле
кристалле имеет
имеет вид
вид волн
волн ––
волны
волны Блоха,
Блоха, волновая
волновая
функция
функция частицы
частицы
(обычно
(обычно электрона),
электрона),
расположенной
расположенной вв
периодическом
периодическом потенциале.
потенциале.
2
p
E
2m
3.
3. Закон–
Закон–
зависимос
зависимос
ть
ть ее
ее
энергии
энергии от
от
импульса
импульса
дисперсии
дисперсии
частицы
частицы
2.
2. В
В кристалле
кристалле многие
многие физические
физические
величины
величины являются
являются
периодическими
периодическими функциями
функциями
Например
Например квазиимпульс
квазиимпульс
k
a
a
2 hm
p
a
h
h
p
a
a
7
9.
ЭЛЕКТРОНЫ В КРИСТАЛЛАХПредставим скорость электронов в кристалле,
как групповую скорость распространения волн
де-Бройля
Волновой вектор
2 2 p p
k
h
1 dW
v vгр
dk
Энергия электрона, выраженная через
частоту, соответствующую волне деБройля
E h
F eE
На электрон во внешнем поле действует сила
Работа по перемещению
электрона приводит к изменению
энергии электрона
F dW
dW Fvгр dt
dt
dk
Сила, действующая
dvгр
1 d 2W dk
1 d 2W
a
2
F
на электрон
2
2
dk
F
dt
dt
dk
1
2
1 dW
mЭфф 2
2
dk
dt
dk
F
mЭфф
8
10.
ЭЛЕКТРОПРОВОДНОСТЬ КРИСТАЛЛОВeE
ma eE
a
m
eE
vср a
m
e 2 n
j envср
E
m
j E
e n
m
2
Удельная
Удельная
проводимость
проводимость
vср
E
en
9
11.
ТЕПЛОЕМКОСТЬ ЭЛЕКТРОННОГО ГАЗАne
1
e
E EF
kT
1
Полностью
Полностью
вырожденный
вырожденный
электронный
электронный
газ
газ
Распределение
Распределение
Ферми
Ферми
kT = EF
Условие
Условие
вырождения
вырождения
электронного
электронного газа
газа
3 h n
2 3
EF
2
3
2m
10
12.
ТЕПЛОЕМКОСТЬ ЭЛЕКТРОННОГО ГАЗАCкр CС
реш
2
e
Суммарная
Суммарная
тепловая
тепловая энергия
энергия
электрона
электрона
kT
U e 3n
2
-- доля
доля электронов,
электронов,
участвующих
участвующих вв
тепловом
тепловом движении
движении
3kT
2 EF
3kT kT 9nk T
U e 3n
2 EF 2
4 EF
dU e
Ce
dT
2
9 kT
Сe nk
2 EF
1.
1. При
При больших
больших температурах
температурах (больше
(больше температуры
температуры
Дебая)
Дебая) выполняется
выполняется закон
закон Дюлонга-Пти
Дюлонга-Пти
C реш 3nkС?
e
9
nk
2
kT
Cкр C реш
EF
2.
2. При
При малых
малых температурах
температурах
2 2 k 4T 3
CС
nk 3 3 =
реш
5 h Vs
e
9
2
kT
EF
CС
кр
e
11
13.
ЗАПОЛНЕНИЕ ЭЛЕКТРОНАМИЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ
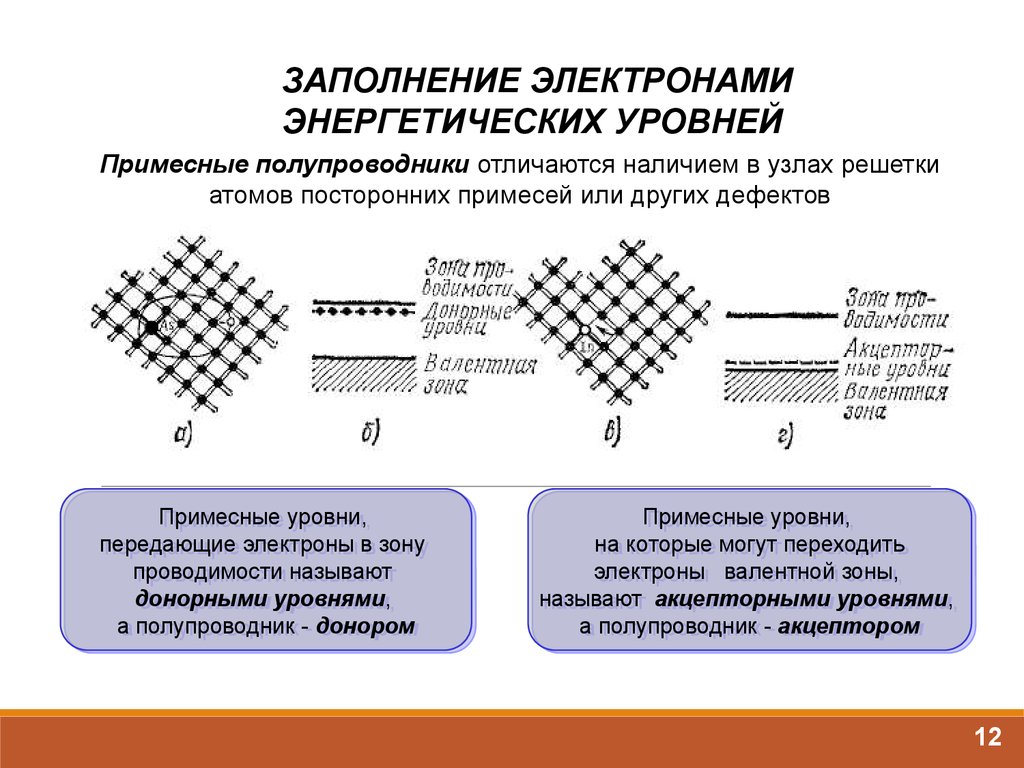
Примесные полупроводники отличаются наличием в узлах решетки
атомов посторонних примесей или других дефектов
Примесные
Примесные уровни,
уровни,
передающие
передающие электроны
электроны вв зону
зону
проводимости
проводимости называют
называют
донорными
донорными уровнями,
уровнями,
аа полупроводник
полупроводник -- донором
донором
Примесные
Примесные уровни,
уровни,
на
на которые
которые могут
могут переходить
переходить
электроны
электроны валентной
валентной зоны,
зоны,
называют
называют акцепторными
акцепторными уровнями,
уровнями,
аа полупроводник
полупроводник -- акцептором
акцептором
12
14.
СТАТИСТИКА ЭЛЕКТРОНОВ В ТВЕРДЫХ ТЕЛАХЕсли
Если число
число частиц
частиц N
N вв системе
системе
много
много меньше
меньше числа
числа возможных
возможных
состояний
состояний G,
G, то
то проблем
проблем
сс возможным
возможным заселением
заселением одного
одного
уровня
уровня несколькими
несколькими частицами
частицами
не
не существует
существует –– это
это
невырожденное
невырожденное состояние.
состояние.
Условие
Условие невырожденности
невырожденности
состояния
состояния системы
системы
N/G<<1
N/G<<1
Если
Если число
число частиц
частиц N
N вв системе
системе
сравнимо
сравнимо сс числом
числом возможных
возможных
состояний
состояний G,
G, то
то необходимы
необходимы правила
правила
заселением
заселением каждого
каждого уровня
уровня
несколькими
несколькими частицам
частицам –– это
это
вырожденное
вырожденное состояние.
состояние.
Условие
Условие вырожденности
вырожденности
состояния
состояния системы
системы
N/G
N/G ~~ 11
Концентрацию электронов в некотором диапазоне
энергий можно определить с помощью распределения
электронов по энергиям
Функция
Функция плотности
плотности
энергетических
энергетических состояний
состояний
4
f E 3 2m*
h
3
2
E
dne f E E ( E )dE
Энергия
Энергия электрона,
электрона,
отсчитанная
отсчитанная от
от
границы
границы зоны
зоны
13
15. Видеоролики
Термоэлектронная эмиссия https://youtu.be/O2-KQhmO5DMОпыт Штерна и Герлаха
https://youtu.be/2F-7uc0jTgo













 Физика
Физика








