Разработка и программная реализация в ПК «МВТУ» полной математической модели синхронного генератора в фазных координатах

1. Санкт-Петербургский государственный политехнический университет Кафедра «Системный анализ и управление»

Симаков И.П., Рябов Г.А.
РАЗРАБОТКА И ПРОГРАММНАЯ РЕАЛИЗАЦИЯ В ПК «МВТУ»
ПОЛНОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СИНХРОННОГО ГЕНЕРАТОРА
В ФАЗНЫХ КООРДИНАТАХ
И ИССЛЕДОВАНИЕ АВАРИЙНЫХ РЕЖИМОВ ЕГО РАБОТЫ
Санкт-Петербург
2016

2. ЦЕЛИ РАБОТЫ и ПОСТАНОВКА ЗАДАЧ ИССЛЕДОВАНИЯ

Разработка и компьютерная реализация полной
математической модели динамики СГ в фазных (в
статорных)
координатах
для
всестороннего
исследования переходных процессов в ЭЭС в аварийных
режимах (при коротких замыканиях всех возможных
видов и обрывах в статорных и роторных обмотках),
которые не могут быть рассчитаны с используемой
традиционно в теории электрических машин и ЭЭС
модели Парка-Горева в «виртуальных» (вращающихся с
ротором) координатах.

3. Задачи, подлежащие решению

1. Вывод полных (без упрощающих допущений!) уравнений электромагнитных и электромеханических
процессов в синхронном генераторе в фазных координатах - в неподвижных (статорных) осях и
процессов регулирования частоты и напряжения.
2. Преобразование полученной полной системы уравнений СГ к уравнениям в форме Парка-Горева .
3. Компьютерная реализация в ПК «МВТУ» модели СГ в форме Парка – Горева при работе на АИН
с проведением вычислительных экспериментов по пуску СГ на холостой ход, принятию нагрузки и
возникновению «металлических» коротких замыканий.
4. Разработка алгоритмов получения (пересчета) информации для уравнений СГ в фазных
координатах по справочных данным, приводимым, к сожалению, для обеспечения численного
решения уравнений Парка – Горева.
5. Компьютерная реализация в среде ПК «МВТУ» полной математической модели СГ в фазных
координатах с элементами анимации и визуализации для однофазных и трехфазных СГ.
6. Проведение вычислительных экспериментов на полной математической модели СГ в фазных
координатах для аварийных режимов, которые невозможно исследовать по уравнениям Парка –
Горева, в том числе при всех видах коротких замыканий в статорных цепях СГ, «глухих» или
«металлических», одной фазы на «землю», двух фаз на «землю», между фазами и при обрывах в
различных цепях СГ и регуляторах напряжения и частоты.

4.

Уравнения синхронного генератора в фазных
координатах (в статорных осях)
Основные допущения и предположения при математическом описании
•насыщение магнитных цепей отсутствует;
•отсутствие потерь в стали;
•кривые намагничивающих сил и индукций имеют синусоидальное распределение в
пространстве;
•индуктивные сопротивления рассеивания не зависят от положения ротора и от тока в
обмотках.
Дополнительно для принципиальной отработки компьютерной модели в работе не
учитывались (временно) демпферные обмотки.
Схема расположения обмоток генератора
B
А
ОВ
A
ОВ
C
Ea
ДО
В
Eb
Ec
С

5.

Связи между потокосцеплениями и токами
Уравнения балансов напряжений
в каждой из фаз статора:
d a
dt Ra I a U a U sa ,
d b
Rb I b U b U sb ,
dt
d c
dt Rc I c U c U sc ,
Уравнения балансов напряжений
в цепи возбуждения
d f
dt
a , b , c f
I a , Ib , Ic I f
a La I a M ab I b M ac I c M af I f ,
b M ba I a Lb I b M bc I c M bf I f ,
M I M I L I M I ,
ca
a
cb
b
c
c
cf
f
c
f M fa I a M fb I b M fc I c L f I f
Коэффициенты самоиндукции контуров фаз
статора La , Lb , Lc для явнополюсного СГ
являются периодическими функциями угла с
периодом
Rf I f U f
потокосцепления обмоток фаз статора и
обмотки возбуждения [Вб];
токи в соответствующих обмотках статора и
обмотке возбуждения [A];
La Lcp Lm cos 2 ,
2
2
Lb Lcp Lm cos 2
Lcp Lm cos 2
,
3
3
2
2
Lc Lcp Lm cos 2
Lcp Lm cos 2
,
3
3
Коэффициенты взаимной индукции обмоток
Ra , Rb , Rc R f активные сопротивления обмоток
статора и обмотки возбуждения [ ];
фаз статора
напряжения на зажимах фазных обмоток [B];
U a ,U b ,U c
Mab= Mba= Mcp + Lm Cos(2 -2 /3)
U sa ,U sb ,U sc - напряжения фаз сети
Mbc= Mcb= Mcp + Lm Cos 2
La , Lb , Lc коэффициенты самоиндукции фазных обмоток
статора
M = M = M + L Cos(2 +2 /3),
Уравнения моментов:
ca
ac
cp
m
Коэффициенты взаимной индукции обмотки
контура возбуждения и обмотками фаз
статора
где J – момент инерции всех вращающихся масс агрегата
J
d
M дв M c ,
dt
d
,
dt
в целом [кг м2]; Мдв - движущий (механический)
момент,приложенный к валу [н м];
Мс - момент сопротивления [н м];
M af M fa M afm Cos ,
M bf M fb M afm Cos ( 2 / 3),
M cf M fc M afm Cos ( 2 / 3),

6.

Электромагнитный момент, действующий на ротор машины
Mэ
Wэ
,
Wэ
1
( I a a I b b I c c I f f )
2
где Wэ – энергия магнитных полей машины

7.

Уравнений СГ в форме уравнений Парка-Горева
в физических единицах
Применение специального линейного преобразования, предложенного Р.
Парком (1929 г.), к исходным уравнениям в фазных координатах приводит к
дифференциальным уравнениям с постоянными коэффициентами
q
B
d
q
Ub
Uq
A
a
U
f
b
U
I
d
Uc
Ud
Uf
C
(а)
c
a
Взаимосвязь фазных координат и преобразованных во вращающиеся с ротором
координаты:
первая – неподвижная симметричная трёхфазная (a, b, c),
вторая - ортогональная система (d, q, O), вращающаяся с угловой
скоростью ротора d dt . ось q опережает ось d
d a
Ra I a U a ,
dt
I a I d cos I q sin ,
U a U d cos U q sin ,
a d cos q sin ,
d
( d cos q sin ) Ra ( I d cos I q sin )
dt
d d
d d q
d
cos d sin
sin q cos
Ra I d cos Ra I q sin .
dt
dt
dt
dt
d q
d d
d
d
q
Ra I d cos U q
d
Ra I q sin 0
U d
dt
dt
dt
dt
U d cos U q sin

8.

Преобразованные статорные уравнения
d d
dt q R I d U d U sd ,
d q R I U U ,
d
q
q
sq
dt
Уравнение ротора
d f
dt
Rf I f U f ,
Преобразованное уравнение моментов
J
d 2
3
M дв ( d I q q I d ).
2
dt
2
С математической точки зрения преобразование Парка для статорных уравнений заключается
во введении матрицы [А] специального вида:
Cos
2
A Sin
3
1
2
Cos ( 2 / 3)
Sin( 2 / 3) Sin( 2 / 3) ,
1
1
2
2
Cos ( 2 / 3)
связывающей вектор Y = (Ya, Yb, Yc)T фактических физических величин (напряжений (Ua, Ub, Uc)
или токов (Ia, Ib, Ic), или потокосцеплений ( a, b, c)) с вектором неких “фиктивных” величин
Y (Yd , Yq , Y0 ):
Ya Cos
2
Y Ya Sin
3
1
Ya
2
Yb Cos ( 2 / 3) Yc Cos ( 2 / 3)
Yb Sin( 2 / 3) Yc Sin( 2 / 3) ,
1
1
Yb
Yc
2
2

9.

дифференциальные уравнения статора в векторно- матричном виде:
T
где ( a , b , c ) ,
I ( I a , Ib , Ic )T ,
U (U a , Ub , Uc )T
d
R I U
dt
Умножим слева обе части уравнения на матрицу преобразования Парка:
Здесь:
A
d
R A I A U
dt
A U U (U d , U q , U o )T ,
A I I ( I d , I q , I o )T ,
A ( d , q , o )T .
преобразованные статорные
уравнения в развёрнутом виде
d
d d
R Id Ud ,
q
dt
dt
d d q
R Iq Uq ,
d
dt
dt
d o
R Io U o .
dt
преобразованные роторные
уравнения
d f
R f I f U f ;
dt
d rd
Rrd I rd 0;
dt
d rq
Rrq I rq 0
dt

10.

Связи между потокосцеплениями и токами
Статорная часть
Роторная часть
If
a
Ia
L I M I ,
b ss b sr rd
I rq
c
I c
f
If
Ia
rd M rs I b Lrr I rd ,
rq
I rq
I c
матрица индуктивностей статора :
La
Lss M ba
M ca
M ab
Lf
Lrr M rdf
O
M frd
матрица индуктивностей ротора
M af
M sr M bf
M cf
матрица взаимоиндуктивностей фазных обмоток
статора и обмоток роторных контуров
С учетом
Получим
A
1
Cos
Sin
1
Cos ( 2 / 3) Sin( 2 / 3) 1 ,
Cos ( 2 / 3) Sin( 2 / 3) 1
Lss I M sr I r ,
r M rs I Lrr I r ,
Ld Lср M ср 1.5Lm ,
Lq Lср M ср 1.5Lm
Lb
M cb
Lrd
O
M ard
M brd
M crd
M ac
M bc
Lc
O
O
Lrq
M arq
M brq
M crq
I A I
1
где
Ld
Lss 0
0
M afm
M sr 0
0
m
M ard
0
0
0
Lq
0
0
0 ,
Lo
0
m
M arq
,
0
Lf
Lrr M rdf
0
3 m
2 M af
3 m
M rs M ard
2
0
0
Lrd
0 ,
0
Lrq
0
0
0
0 .
3 m
M arq 0
2
M frd

11.

Преобразованные уравнения существенно отличаются от
уравнений в фазных координатах. Их отличие в следующем:
для идеализированной синхронной машины они являются
уравнениями с постоянными коэффициентами;
все коэффициенты самоиндукции и взаимоиндукции в
являются при принятых допущениях постоянными, не зависящими
от угла величинами;
имеет место меньшее число неизвестных переменных
(величин);
неизвестными величинами в них являются проекции
обобщённых векторов токов, напряжений и потокосцеплений, то
есть фиктивные величины.

12.

Уравнения синхронного генератора в форме уравнений Парка-Горева в
относительных единицах и натуральном времени
d d
q s r id s ud s usd ,
dt
d q r i u u ,
d
s
q
s
q
s
sq
dt
Уравнение цепи возбуждения в относительных единицах и
натуральном времени
Td
d eaf xd id ,
q xq iq ,
f
d = d / б, q = q / б, ud = Ud / Uб,
uq = Uq / Uб,id = Id / Iб, iq = Iq / Iб,
usd = Usd / Uб, usq = Usq / Uб, = d / dt, r = R / Zб.
I б I фн 2,
б
Z
б
Uб
б
,
U
I
б ,
б
dt
eaf u f ,
Td = Lf / R f - постоянная времени цепи возбуждения при
разомкнутой цепи статора
ds
TJ
mдв ( d iq q id ) ,
dt
x2
eaf ad id ,
xf
U б U фн 2 ,
d f
s = ( - s ) / s - скольжение ротора генератора
относительно синхронной скорости;
амплитуда номинального статорного напряжения
амплитуда номинального статорного тока
Уравнения СГ в форме уравнений Парка-Горева в
относительных единицах выраженные через токи и
напряжения
deaf
did
xq iq s r id s ud ,
dt
dt
di
(eaf xd id ) xq q s r iq s uq ,
dt
2
deaf xad
di
eaf Td
d uf ,
dt
x f dt
ds
TJ
mдв (eaf xd id ) iq xq iq id .
dt
xd

13.

Модель СГ, работающего на АИН
Математическая модель активно-индуктивной нагрузки (АИН)
LH
L
H
dI dH
d
LH I qH t RH I dH U Sd ,
dt
dt
dI qH
d
LH I dH t RH I qH U Sq .
dt
dt
или в эквивалентном виде:
didH
x
xH iqH s rH idH s usd ,
H
dt
x diqH x i r i u ,
H
dH
s
H
qH
s
sq
H dt
xH , rH - индуктивная и активная составляющие нагрузки в о.е..
С учетом уравнений нагрузки дифференциальные уравнения Парка-Горева в форме Коши имеют вид:
1
[ s (rc rн ) id ( xq xн ) iq (e u f )]
di
Td
d
,
2
( xd xн xad / x f )
dt
diq [( xd xн ) id s (rc rн ) iq e] ,
dt
( xq xн )
2
de
xad
1
id
s (rc rн )
2
( xd xн xad
/ x f )
xf
dt
2
xad
1
(
x
x
)
iq ( xd xн ) (e u f ) .
q
н
xf
Td
Напряжение на зажимах генератора
находим по формулам:
di
1 de
xd d xq iq s rc id ,
s dt
dt
diq
1
uq (e xd id ) s rc iq xq ,
s
dt
ud
u (ud2 uq2 ),

14.

Регулятор частоты вращения турбины
с учетом существенных нелинейностей ограничение скорости и динамической
нелинейности типа «упор»
F ( )
0
M
0
0
0
Управление
M0
M
0
Модель сервопривода в «арифметизованном» виде
dM
(1 f н ( M )) v( ) ( f н ( M ) f в ( M )) F ( ) ,
dt
1
f н ( M ) (1 Sign M )
;
2
1
f в ( M ) (1 Sign ( M M 0 ));
2
1
v( ) (1 Sign( ) ).
2
Модель автоматического регулятора частоты можно представить в виде блок
схемы:

15.

Модель регулятора напряжения с учетом ограничений
u f ( f )
u f max
0
u f max f
Структурная схема агрегата
0 u f umax

16.

17.

Для моделирования процессов использовался программный вычислительный
комплекс «Моделирование в технических устройствах» (ПК «МВТУ»),
созданный в МГТУ им. Н.Э.Баумана.
Процесс вывода агрегата на
номинальный режим
работы

18.

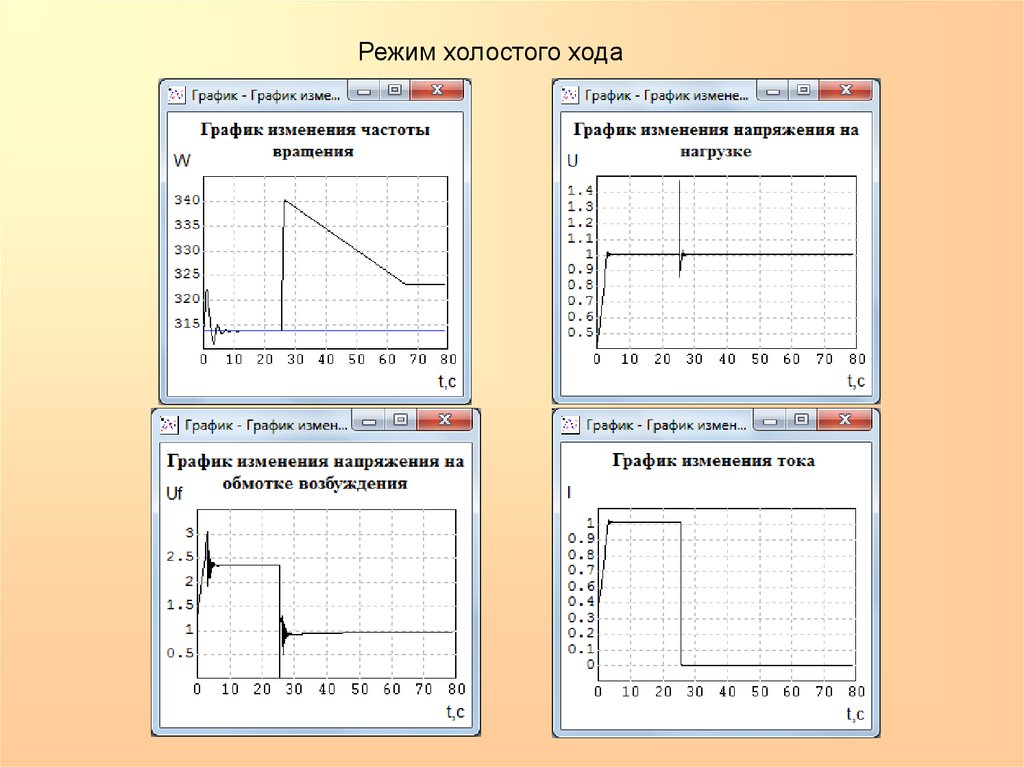
Режим холостого хода

19.

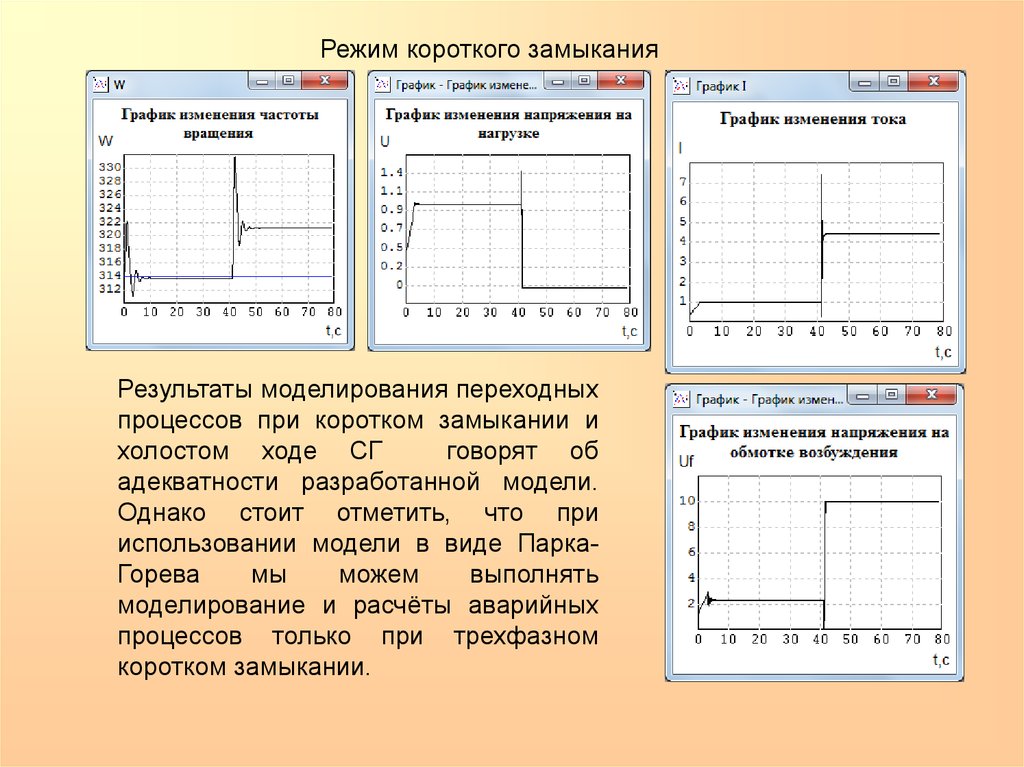
Режим короткого замыкания
Результаты моделирования переходных
процессов при коротком замыкании и
холостом ходе СГ
говорят об
адекватности разработанной модели.
Однако стоит отметить, что при
использовании модели в виде ПаркаГорева
мы
можем
выполнять
моделирование и расчёты аварийных
процессов только при трехфазном
коротком замыкании.

20.

Модель трехфазного СГ, работающего на активную нагрузку
в статорных осях
Формулы пересчета относительных единиц в физические:
R Ra Rb Rc r zб ,
M afm
xaf zб
s
X f x f zб ,
Lf
,
x f zб
Уравнение СГ в матричном виде:
La
M
M M ab
ac
M
af
M ab
M ac
Lb
M bc
M bc
Lc
M bf
M cf
M af
M bf
M cf
L f
s
,
M cp
Lcp
Lq Ld
4
Ld Lq
2
Lq
,
,
Lm
a U sa Ra
d b U sb 0
dt c U sc 0
f U f 0
xq zб
s
Ld Lq
2
0
0
Rb
0
0
Rc
0
0
,
Mm
Ld
xd zб
s
,
X af xaf zб ,
0 Ia
0 I b
,
0 Ic
R f I f
Ia
a
Ia
Ia
I
I
d b d
d
d Ib
b
b
M I M I M I ,
dt c dt
dt
dt
c
c
c
I f
f
I f
I f
d M d d M
d
M .
M
dt
d
dt
d
-2L msin(2 ),
2M msin(2 + /3),
-2L m cos(2 + /6),
d M 2M msin(2 + /3),
d
-2M m cos(2 + /6), -2M msin(2 ),
m
-M maf sin( + /3),
M af sin( ),
-2M m cos(2 + /6),
-2M msin(2 ),
2L msin(2 + /3),
M maf cos( + /6),
M maf sin( )
-M maf sin( + /3)
.
M maf cos( + /6)
0

21.

Уравнение СГ в фазных координатах с учетом АИН :
Ia
Ia
LН
I
M
d
d Ib
b
M
M
I I M Н
dt
dt
c
Н
c
I f
0
I f
MН
LН
MН
0
I a Ra Ran
MН 0
M Н 0 d I b 0
LН 0 dt I c 0
I f 0
0 0
0
0
Rb Rbn
0
0
Rc Rcn
0
0
Матричная форма записи уравнений СГ,
приведенная к нормальной форме, имеет вид:
Ia
I
1
d b
M M H M R
dt I c
I f
Уравнения регулятора
частоты
I a 0
I
b 0
I c 0
I f u f
f K ( s ),
1
2
(1 sign( f )),
Электромагнитный момент:
a
We
1
b
Me
I a I b I c I f
c
2
f
1
M e I a I b I c
2
Ia
1 I I I I M Ib
2 a b c f Ic
I f
Ia
I
b
I f M
Ic
I f
Уравнения регулятора напряжения:
0 I a 0
0 I b 0
.
0 I c 0
R f I f u f
U za I a Ran ,
1
U zv ( U za U zb U zc ),
3
dU zd
k (U zv U zd ),
dt
f u K u (U o U zd ),
Uf
1
fu fu U max U max ,
2
1
f H (1 sign( M g )),
2
1
f B (1 sign( M g M max )),
2
dM g
(1 f H ) ( f H f B ) f ,
dt
d
1
( M g M e ),
dt TM
d
.
dt

22.

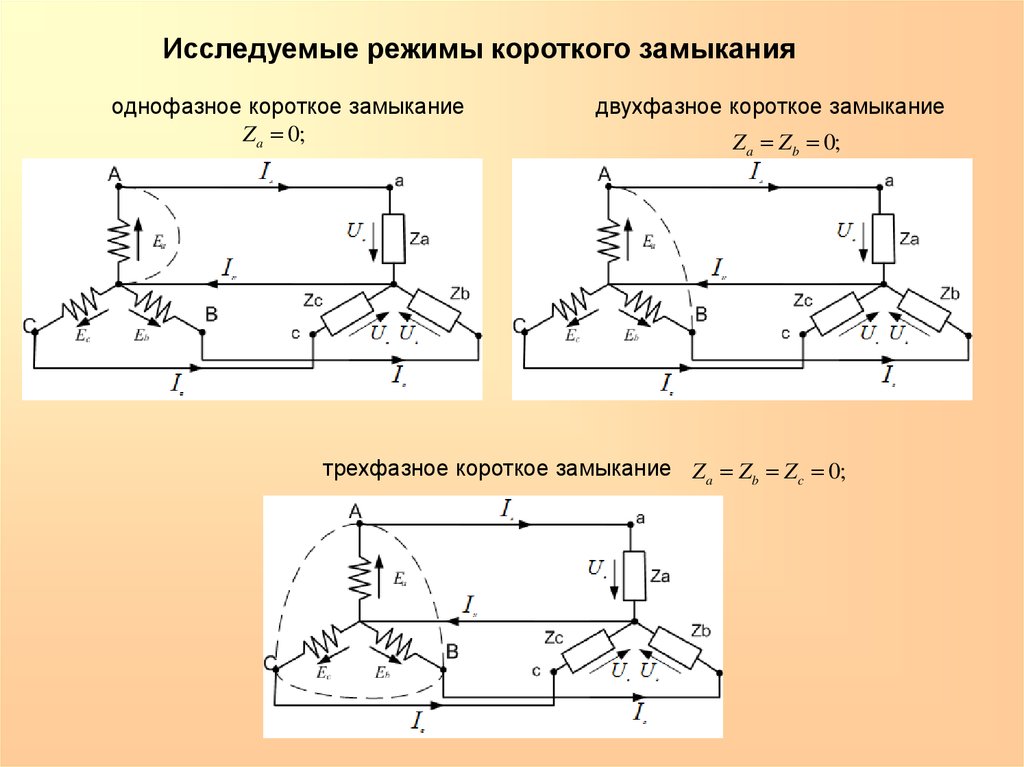
Исследуемые режимы короткого замыкания
однофазное короткое замыкание
Z a 0;
двухфазное короткое замыкание
Z a Zb 0;
трехфазное короткое замыкание Za Zb Zc 0;

23.

Переходные процессы при однофазном коротком замыкании

24.

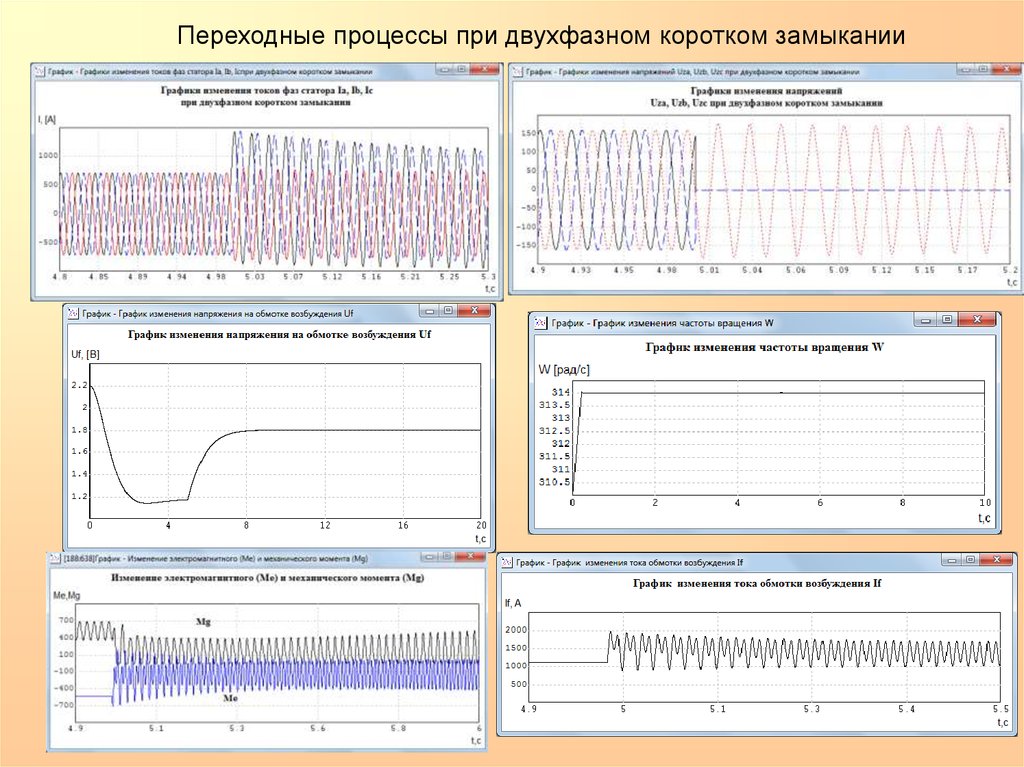
Переходные процессы при двухфазном коротком замыкании

25.

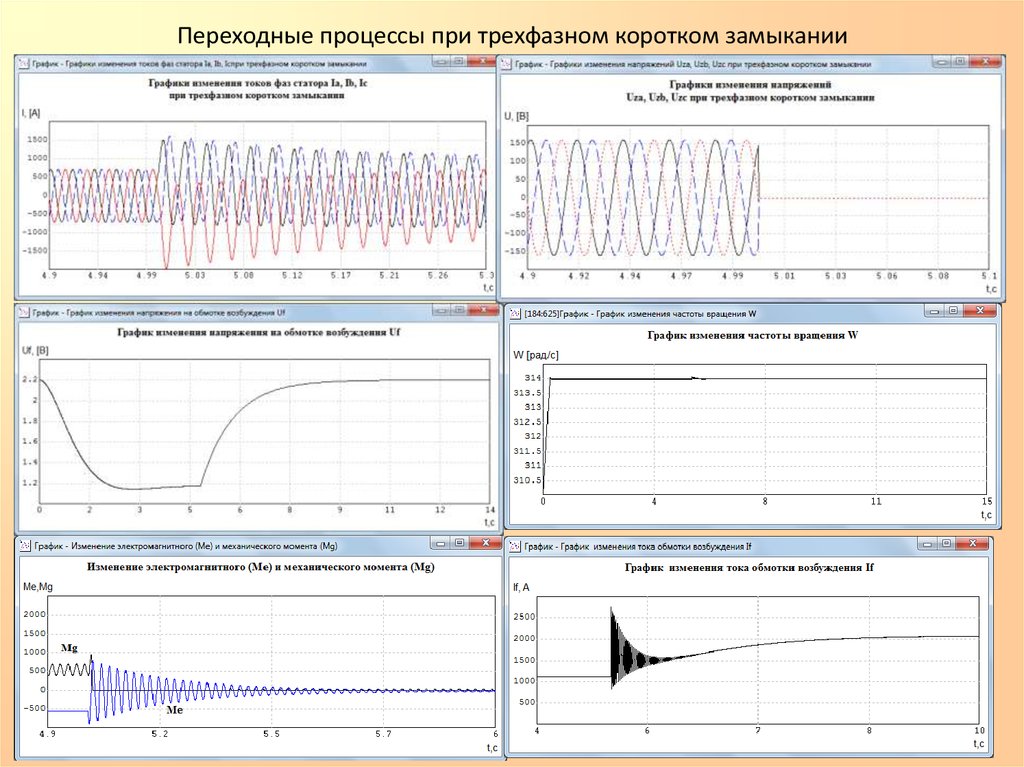
Переходные процессы при трехфазном коротком замыкании

26.

Научные и практические результаты.
Научные результаты.
1.
Разработана и программно реализована полная компьютерная математическая модель динамики СГ в
фазных координатах с автоматическими регуляторами напряжения и частоты вращения ротора и статической
АИН, предназначенная для исследования широкого набора аварийных режимов, которые невозможно
исследовать с использованием традиционных моделей Парка - Горева.
2.
Сделан подробный вывод полных уравнений динамики СГ в фазных координатах и способ их
приведения к форме Парка – Горева без пренебрежения динамикой электромагнитных процессов в
статорных обмотках генератора.
3.
Разработаны алгоритмы получения необходимых для реализации моделей СГ в фазных координатах
функциональных зависимостей индуктивностей и взаимных индуктивностей различных обмоток по
справочной информации о параметрах и характеристиках, приводимых для обеспечения расчетов динамики
по уравнениям Парка – Горева.
Практические результаты.
1.
Математическая модель СГ в фазных координатах практически реализована в среде отечественного
программного комплекса «Моделирование в технических устройствах» (ПК «МВТУ») с элементами анимации
и визуализации.
2.
Результаты проведенных на созданной компьютерной модели многочисленных вычислительных
экспериментов подтвердили ее практическую пригодность для расчетов динамики сложных аварийных
режимов. В частности, исследован ряд аварийных режимов работы СГ, включая все виды коротких
замыканий, которые не поддаются изучению по уравнениям Парка - Горева.
3.
Сформулированы направления дальнейших исследований с использованием моделей СГ в фазных
координатах в интересах расследования причин и хода развития каскадных аварий в ЭЭС и разработки
алгоритмов противоаварийного управления.

27.

Спасибо за внимание!