Похожие презентации:
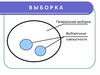
Генеральная совокупность и выборка
1. Генеральная совокупность и выборка
Выполнила: Буркеня Н.А.Учитель математики
МБОУ «Школа №17»
2.
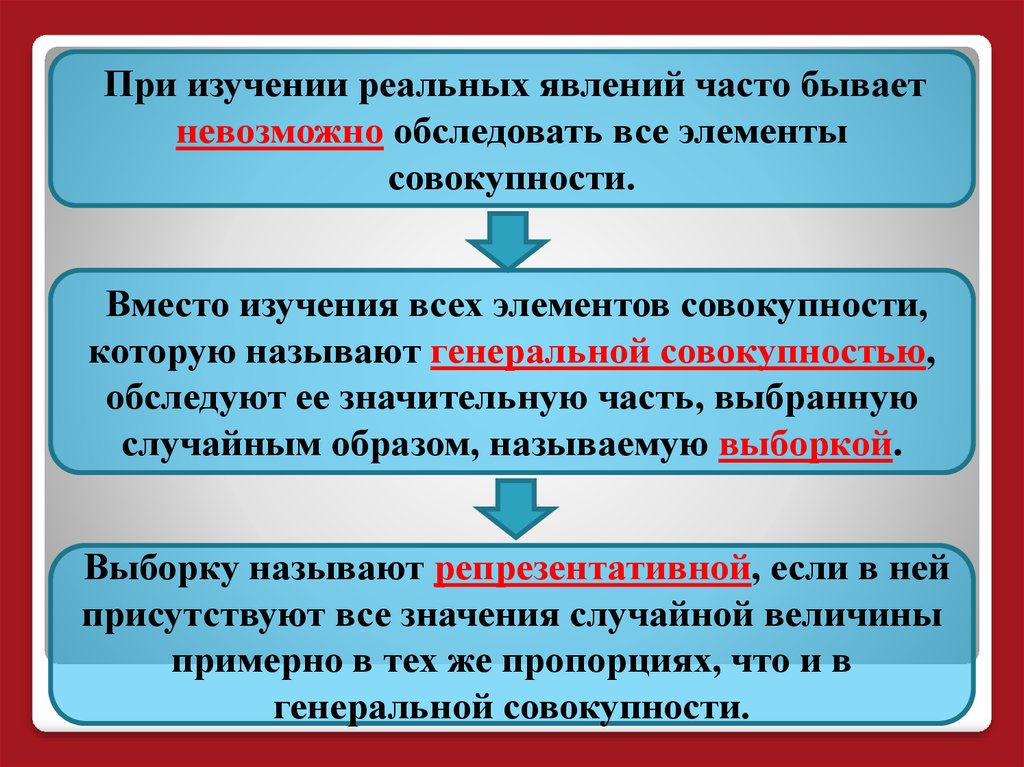
При изучении реальных явлений часто бываетневозможно обследовать все элементы
совокупности.
Вместо изучения всех элементов совокупности,
которую называют генеральной совокупностью,
обследуют ее значительную часть, выбранную
случайным образом, называемую выборкой.
Выборку называют репрезентативной, если в ней
присутствуют все значения случайной величины
примерно в тех же пропорциях, что и в
генеральной совокупности.
3.
SN
- объем генеральной совокупности
- объем репрезентативной выборки
M1 , M 2 ,..., M k - частоты
M N
S1 , S 2 ,..., S k
- частоты в генеральной
совокупности
S S
4.
Для идеально составленной репрезентативнойвыборки должно выполняться равенство:
Mi
Si
Wi ,
N
S
(1)
Где i – порядковый номер значения
признака (1≤i≤k).
Mi
Si S
или Si SWi ,
N
где 1 i k.
(2)
5. Пример 1
Фабрика резиновых изделий выиграла тендер наизготовление S 10000 армейских противогазов. Для
определения того, сколько противогазов каждого из
пяти существующих размеров следует изготовить,
были сделаны замеры у N=100 случайным образом
выбранных солдат ближайшей воинской части.
Распределение размеров противогазов X по частотам
M оказалось следующим:
X
M
0
5
1
21
2
47
3
22
Сколько противогазов каждого размера будет
изготавливать фабрика?
4
5
6.
N=100 солдат (объем репрезентативнойвыборки)
S 10000 - объем генеральной совокупности
Количество противогазов соответствующего
размера можно найти по формуле (2).
Размер (X)
0
1
2
3
4
Частота в
выборке (М)
5
21
47
22
5
Относительна
я частота
Количество
противогазов
7. Размах и центральные тенденции
РАЗМАХ И ЦЕНТРАЛЬНЫЕТЕНДЕНЦИИ
8. 1. Размах, мода и медиана
1. РАЗМАХ, МОДА И МЕДИАНАИмеются:
1) распределение случайной величины X — числа
прочитанных за каникулы книг десятью девочками по
частотам М;
2) распределение по частотам случайной величины У
— числа прочитанных за каникулы книг девятью
мальчиками того же класса.
X
M
3
3
4
2
5
3
8
1
Y
M
12
1
3
2
4
4
5
1
6
1
7
1
9.
Нужно сравнить интерес к чтению девочек имальчиков этого класса.
Для сравнения предложенных совокупностей
могут
быть
использованы
различные
характеристики. Перечислим некоторые из них.
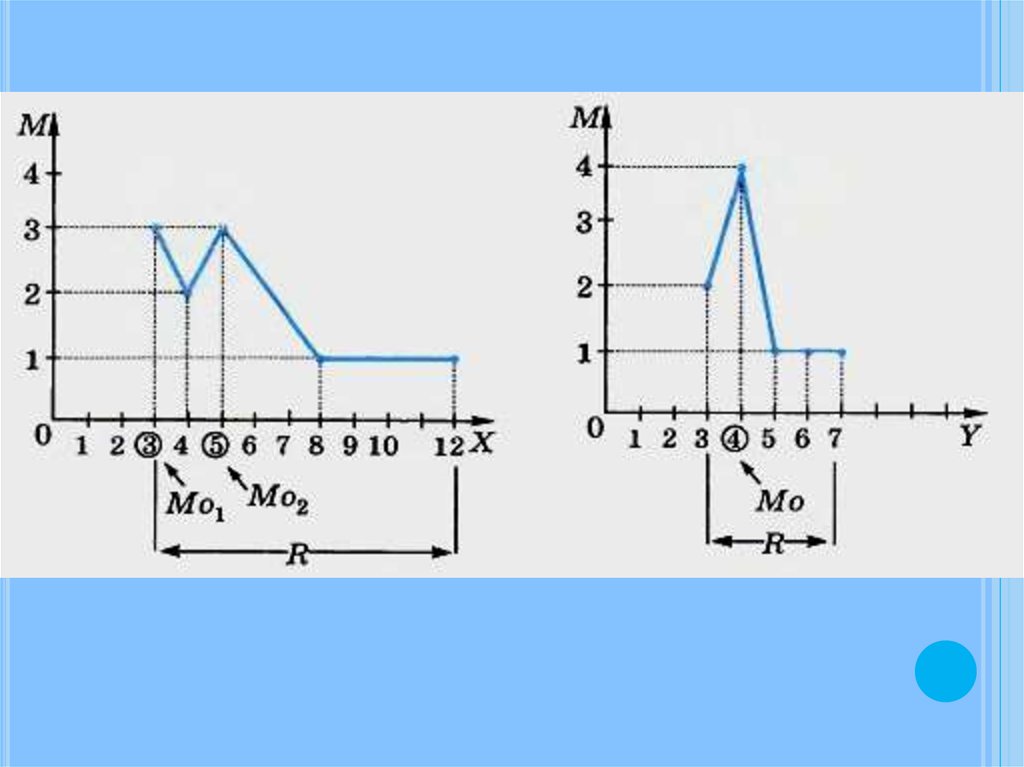
Выпишем последовательность:
3, 3, 3, 4, 4, 5, 5, 5, 8, 12
3, 3, 4, 4, 4, 4, 5, 6, 7.
10.
Размах (обозначается R) — разница междунаибольшим и наименьшим значениями случайной
величины.
Мода (обозначим Мо) — наиболее часто
встречающееся значение случайной величины.
Медиана (обозначим Me) — это так называемое
серединное значение упорядоченного ряда
значений случайной величины.
11.
12. Пример 1.
ПРИМЕР 1.Вычислить размах, моду и медиану для
последовательности:
-2, 3, 4, -3, 0, 1, 3, -2, -1, 2, -2, 1.
13.
2. СРЕДНЕЕ ЗНАЧЕНИЕСредним значением случайной величины X
(обозначается X ) называют среднее
арифметическое всех её значений.
Если все значения случайной величины X1,
Х2,…,ХN различны, то
X 1 X 2 ... X N
X
N
(3)
14.
Если значения случайной величины Xl,Х2,...,Xkимеют в совокупности соответственно
частоты М1,М2,…,Мk, то
X 1M 1 X 2 M 2 ... X k M k
X
M 1 M 2 ... M k
(4)
Зная, что М N , формулу (4) можно
переписать в виде
X 1M 1 X 2 M 2 ... X k M k
X
N
(4' )
15.
Меры центральнойтенденции
Мода
Медиана
Среднее
значение
Подчёркнем, что существует возможность измерить,
охарактеризовать совокупность одним числом, к
которому стремятся все её значения. Не для каждой
совокупности имеет смысл формально находить
центральные тенденции.













 Математика
Математика