Примеры расчета магнитных полей

1.

Кафедра физики
ЛЕКЦИЯ 2.
ПЛАН ЛЕКЦИИ
1. Примеры расчета магнитных полей:
- магнитное поле на оси кругового тока.
2. Поток вектора магнитной индукции.
Теорема Гаусса
Остроградского для вектора B.
3. Теорема о циркуляции вектора B.
4. Примеры расчета магнитных полей:
- магнитное поле соленоида.
- магнитное поле тороида (самостоятельно).
Общая физика. «Магнитостатика»
1

2.

Кафедра физики
Закон Био – Савара – Лапласа.
Примеры расчета магнитных полей
Магнитное поле на оси кругового тока
Пусть электрический ток силой
I течет по проводнику радиусом R .
Найдем магнитное поле на оси
А, находящейся на расстоянии
x тока в точке
a от центра
R
I
a
Общая физика. «Магнитостатика»
А
x
2

3.

Кафедра физики
Закон Био – Савара – Лапласа.
Примеры расчета магнитных полей
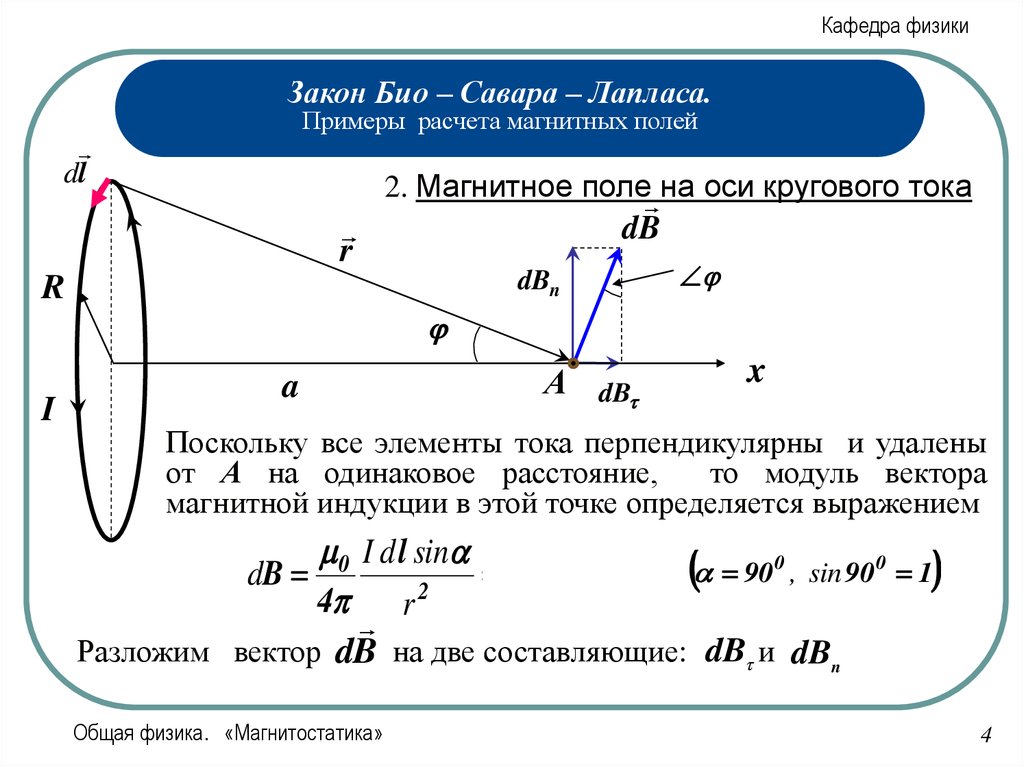
2. Магнитное поле на оси кругового тока
Разобьем круговой ток на элементы тока длиной
dl и проведем от
произвольного элемента тока радиус-вектор r в точку А.
dl
dB
r
R
I
a
А
x
Вектор dB направлен перпендикулярно
плоскости, в
которой располагаются вектора dl и r
Общая физика. «Магнитостатика»
3

4.

Кафедра физики
Закон Био – Савара – Лапласа.
Примеры расчета магнитных полей
dl
r
2. Магнитное поле на оси кругового тока
dB
dBn
R
I
a
А dB
x
Поскольку все элементы тока перпендикулярны и удалены
от А на одинаковое расстояние,
то модуль вектора
магнитной индукции в этой точке определяется выражением
0 I d l sin 0 I d l
90 0 , sin 90 0 1
dB
4 r 2
4 r 2
Разложим вектор dB на две составляющие: dB и dBn
Общая физика. «Магнитостатика»
4

5.

Кафедра физики
Закон Био – Савара – Лапласа.
Примеры расчета магнитных полей
dl
2. Магнитное поле на оси кругового тока
r
dB
Любые
два
противоположных
R
элемента
тока
создают
поле,
x
a
А dB
составляющие dBn
I
которых равны по
величине
и
противоположно
направлены.
Следовательно, эти составляющие уничтожают друг друга.
dBn
Поэтому вектор магнитной индукции можно определить,
просуммировав составляющие модулей вектора dB (этот вектор
направлен вдоль положительной нормали к контуру с током).
Общая физика. «Магнитостатика»
5

6.

Кафедра физики
Закон Био – Савара – Лапласа.
Примеры расчета магнитных полей
dl
2. Магнитное поле на оси кругового тока
r
dBn
R
dB
0 I d l
dB
4 r 2
I
А
a
x
dB
0 I
0 I
0 IR
B dB dB sin
sin dl
sin 2 R
sin
2
2
2
4 r
4 r
2 r
l
l
l
R
sin
,
Преобразуем полученное выражение, учитывая, что
r
2
2
2
r R a . После подстановки:
B
0 IR
2r
2
sin
0 IR
2 R a
2
Общая физика. «Магнитостатика»
2
R
R a
2
2
0 IR 2
2 R a
2
2
3
2
6

7.

Кафедра физики
Закон Био – Савара – Лапласа.
Примеры расчета магнитных полей
B
0 IR 2
2 R a
2
2
2. Магнитное поле на оси кругового тока
3
2
В центре кругового тока a 0,
индукция магнитного поля равна
Вдали от контура на оси x ( a R):
B
Если умножить числитель и знаменатель
этого выражения на , получим:
B0
0 I
2R
0 IR 2
2a 3
0 I R 2 0 IS
B
3
2 a
2 a 3
где S R 2 - площадь, охватываемая круговым током.
Общая физика. «Магнитостатика»
7

8.

Кафедра физики
Закон Био – Савара – Лапласа.
Примеры расчета магнитных полей
2. Магнитное поле на оси кругового тока
0 IS
B
2 a 3
IS - магнитный момент контура.
Принимая, что вдали от кругового тока a r , выражение для
индукции магнитного поля, созданного замкнутым круговым
током вдали от тока, запишется в виде:
0 pm
B
2 r 3
Общая физика. «Магнитостатика»
8

9.

Кафедра физики
Графическое изображение магнитного поля
кругового тока
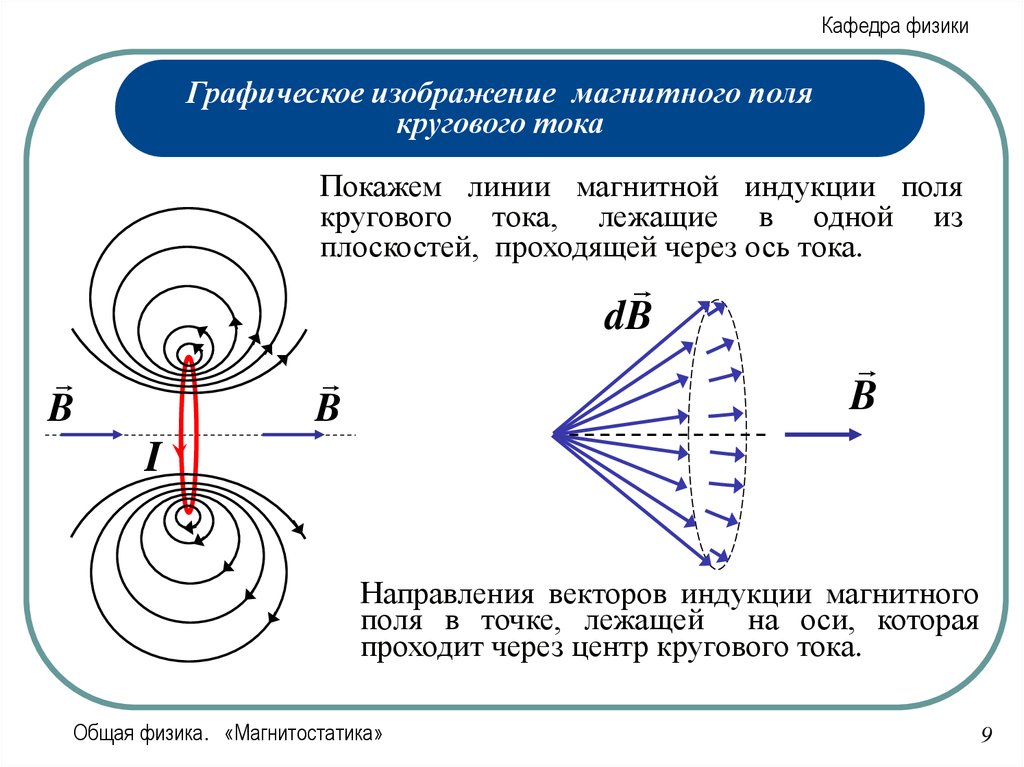
Покажем линии магнитной индукции поля
кругового тока, лежащие в одной из
плоскостей, проходящей через ось тока.
dB
B
B
B
I
Направления векторов индукции магнитного
поля в точке, лежащей на оси, которая
проходит через центр кругового тока.
Общая физика. «Магнитостатика»
9

10.

Кафедра физики
Поток вектора магнитной индукции. Теорема
Гаусса-Остроградского для вектора B
Магнитный поток через элемент dS поверхности S соответственно,
выражается формулой
dФ B ,dS BdS cos
0 0 B
dS dSn , n - орт вектора нормали.
Полный поток через поверхность S равен сумме потоков через
все элементы поверхности:
ФB B ,dS BdS cos BndS
и вектором магнитной
- угол между нормалью к площадке
индукции, Bn - проекция
вектора B на нормаль к площадке.
Магнитный поток B через площадку может быть как
положительным, так и отрицательным.
S
S
Для замкнутой поверхности:
S
ФB BndS
S
Общая физика. «Магнитостатика»
B , dS
S
10

11.

Кафедра физики
Поток вектора магнитной индукции. Теорема
Гаусса-Остроградского для вектора B
Силовые линии магнитного поля замкнуты. Следовательно, любая
линия пересекает замкнутую поверхность дважды (четное число
раз), причем один раз в положительном направлении, другой раз – в
отрицательном.
Поэтому
суммарный
магнитный
поток,
пронизывающий замкнутую поверхность S , всегда равен нулю:
ФB
B , dS 0
теорема Гаусса-Остроградского
для магнитного поля.
S
Поток вектора напряженности магнитного поля через любую
замкнутую поверхность равен нулю:
B , dS 0
S
Единица магнитного потока в СИ - вебер (Вб).
Общая физика. «Магнитостатика»
11

12.

Кафедра физики
Поток вектора магнитной индукции. Теорема
Гаусса-Остроградского для вектора B
Важное следствие
из теоремы Гаусса:
поток вектора B
через замкнутую
поверхность S не зависит от формы
этой поверхности.
Уравнение Гаусса в дифференциальной форме:
divB 0
Из векторного анализа: … дивергенция характеризует
интенсивность (обильность) истоков и стоков векторного поля.
divB 0 , следовательно магнитное поле не имеет стоков и истоков,
линии B замкнутые. Магнитное поле имеет соленоидальный или
вихревой характер.
Физическая причина соленоидальности магнитного поля - отсутствие
свободных магнитных зарядов, аналогичных электрическим зарядам.
Общая физика. «Магнитостатика»
12

13.

Кафедра физики
Теорема о циркуляции вектора
B
Циркуляцией вектора B по замкнутому контуру L называется
интеграл вида
B ,dl Bl dl
L
L
где dl- вектор элемента
длины
контура, Bl B cos , - угол
между векторами B и dl
Циркуляция вектора B по произвольному замкнутому контуру L
равна произведению 0 на алгебраическую сумму токов,
охватываемых контуром:
B ,dl 0 I
L
Это закон (теорема) о циркуляции вектора . Иначе:
B закон полного
тока для магнитного поля в вакууме.
Общая физика. «Магнитостатика»
13

14.

Кафедра физики
Теорема о циркуляции вектора
B ,dl 0 I
L
B
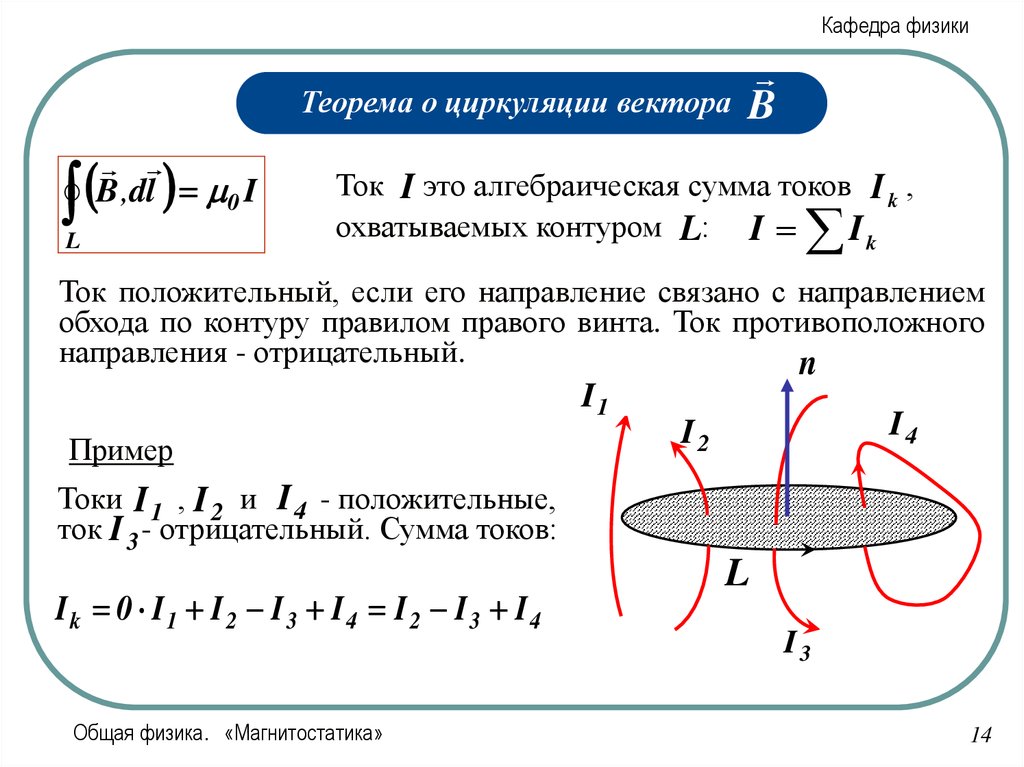
Ток I это алгебраическая сумма токов I k ,
охватываемых контуром L: I
Ik
Ток положительный, если его направление связано с направлением
обхода по контуру правилом правого винта. Ток противоположного
направления - отрицательный.
n
I1 0
Пример
I4 0
I2 0
Токи I 1 , I 2 и I 4 - положительные,
ток I 3 - отрицательный. Сумма токов:
Ik 0 I1 I 2 I 3 I4 I 2 I 3 I4
Общая физика. «Магнитостатика»
L
I3 0
14

15.

Кафедра физики
Теорема о циркуляции вектора
B
Если ток I распределен по объему, где расположен
контур L , то этот ток можно представить как
I j dS
Интеграл берется по произвольной поверхности S, «натянутой»
на контур L.
Общий вид теоремы о циркуляции вектора B:
B ,dl 0 j dS
L
Циркуляция вектора Bне равна нулю. Следовательно, магнитное
поле не потенциально.
Общая физика. «Магнитостатика»
15

16.

Кафедра физики
Теорема о циркуляции вектора
B
Применение теоремы.
Пример.
B
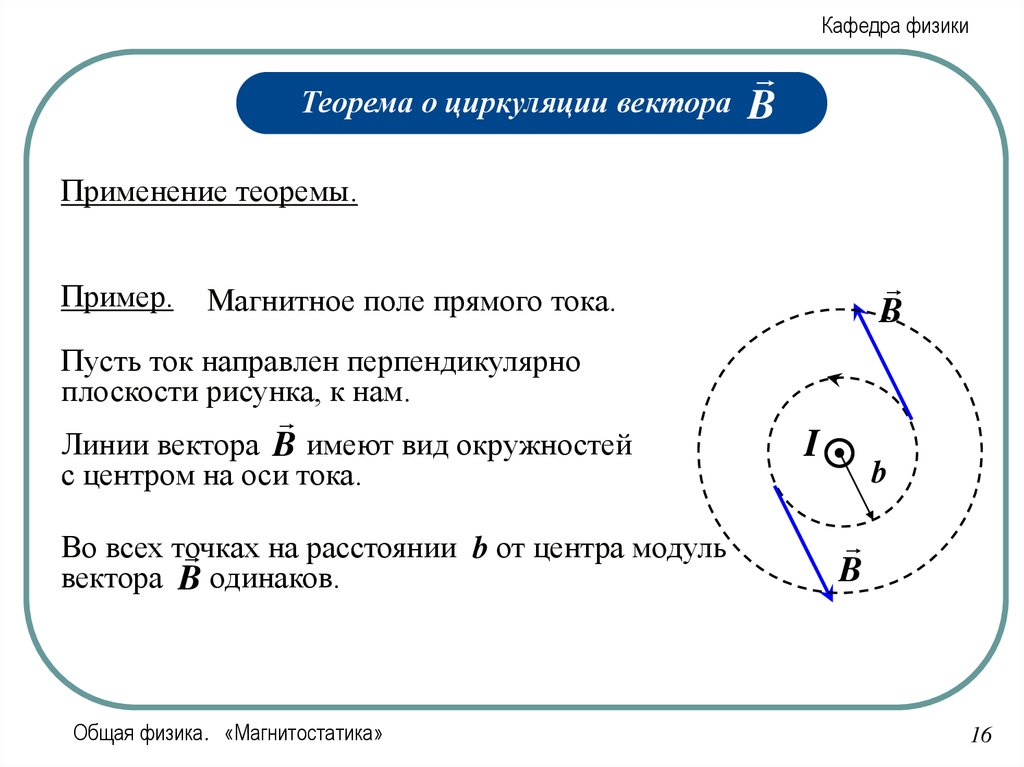
Магнитное поле прямого тока.
Пусть ток направлен перпендикулярно
плоскости рисунка, к нам.
Линии вектора B имеют вид окружностей
с центром на оси тока.
Во всех точках
на расстоянии b от центра модуль
вектора B одинаков.
Общая физика. «Магнитостатика»
I
b
B
16

17.

Кафедра физики
Теорема о циркуляции вектора
B
Применим теорему о циркуляции вектора B для
B
выбранного круглого контура L:
B , dl 0 I
L
L
I
b
B
B ,dl Bl dl Bdl B dl B 2 b 0 I
L
L
B 2 b 0 I ,
L
L
0 I
B
2 b
Формула совпадает с выражением, полученным в лекции 1.
Общая физика. «Магнитостатика»
17

18.

Кафедра физики
Примеры расчета магнитных полей
Самостоятельно:
расчет магнитного поля соленоида,
тороида.
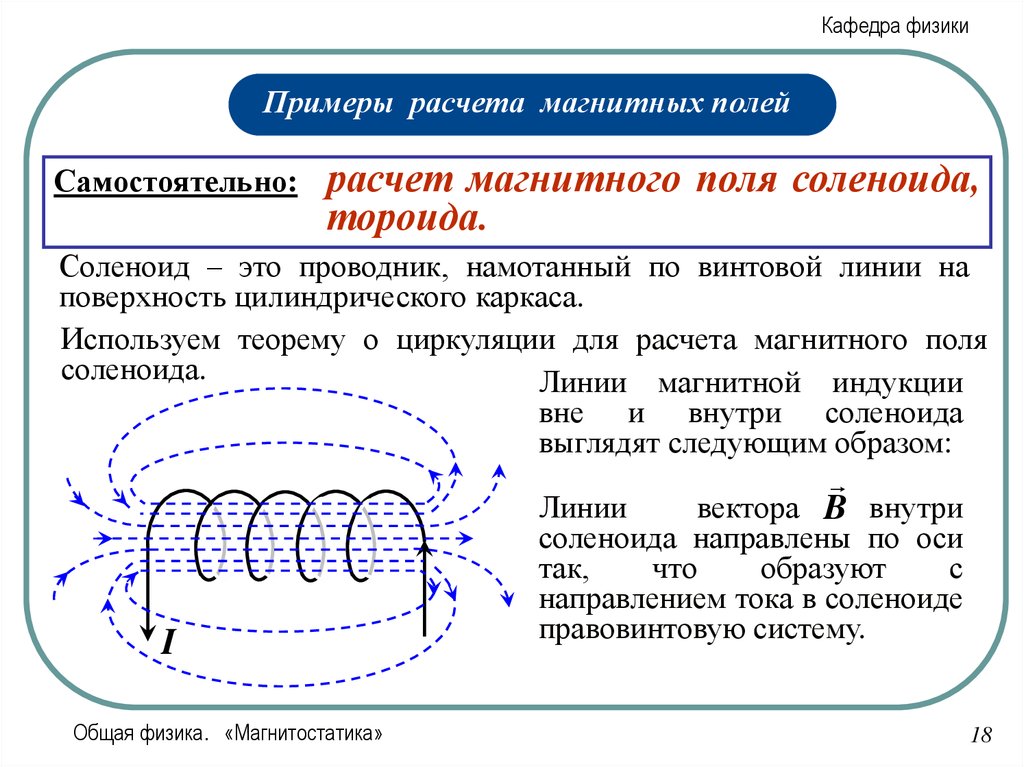
Соленоид – это проводник, намотанный по винтовой линии на
поверхность цилиндрического каркаса.
Используем теорему о циркуляции для расчета магнитного поля
соленоида.
Линии магнитной индукции
вне и внутри соленоида
выглядят следующим образом:
вектора B внутри
I
Общая физика. «Магнитостатика»
Линии
соленоида направлены по оси
так,
что
образуют
с
направлением тока в соленоиде
правовинтовую систему.
18

19.

Кафедра физики
Примеры расчета магнитных полей
Магнитное поле соленоида
Из опыта: чем длиннее соленоид, тем
меньше поле вне его. Поле бесконечно
длинного соленоида сосредоточено
внутри его, поле снаружи отсутствует.
I
Пусть длинный соленоид с током I
имеет n витков на единицу длины.
Если шаг винтовой линии мал, то каждый виток соленоида можно
заменить замкнутым витком.
Для расчета поля внутри соленоида выберем прямоугольный контур
и вычислим циркуляцию магнитного поля по этому контуру.
Общая физика. «Магнитостатика»
19

20.

Кафедра физики
Примеры расчета магнитных полей
Магнитное поле соленоида
Д
С
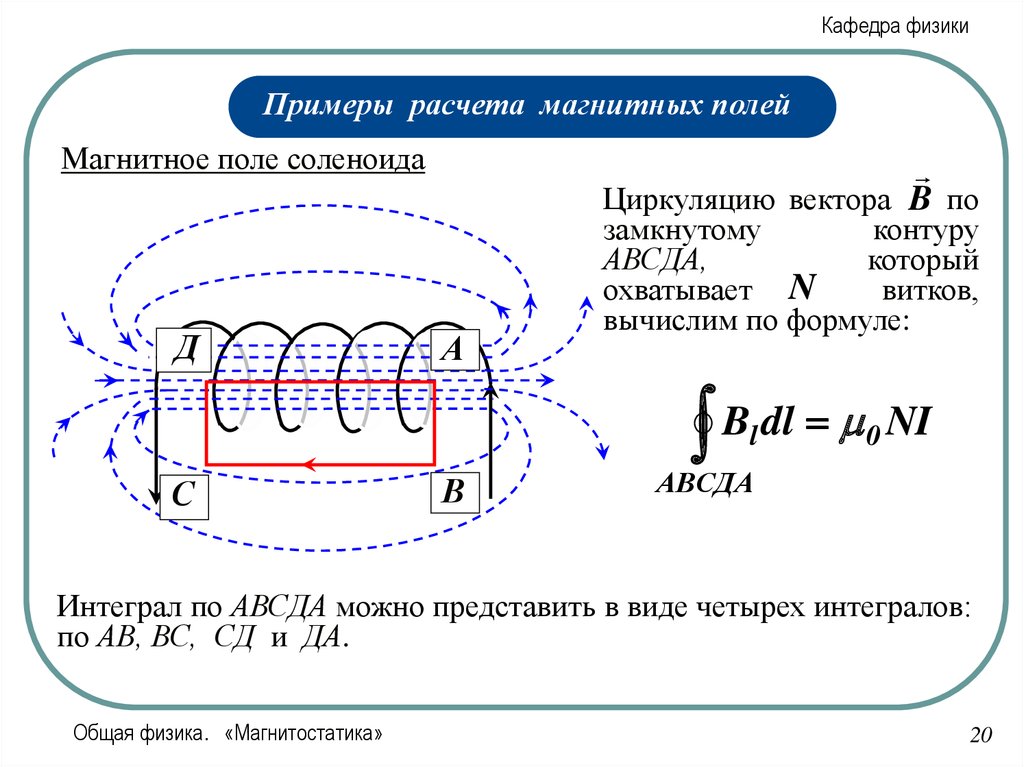
Циркуляцию вектора B по
А
В
замкнутому
контуру
АВСДА,
который
охватывает N
витков,
вычислим по формуле:
Bl dl 0 NI
АВСДА
Интеграл по АВСДА можно представить в виде четырех интегралов:
по АВ, ВС, СД и ДА.
Общая физика. «Магнитостатика»
20

21.

Кафедра физики
Примеры расчета магнитных полей
Магнитное поле соленоида
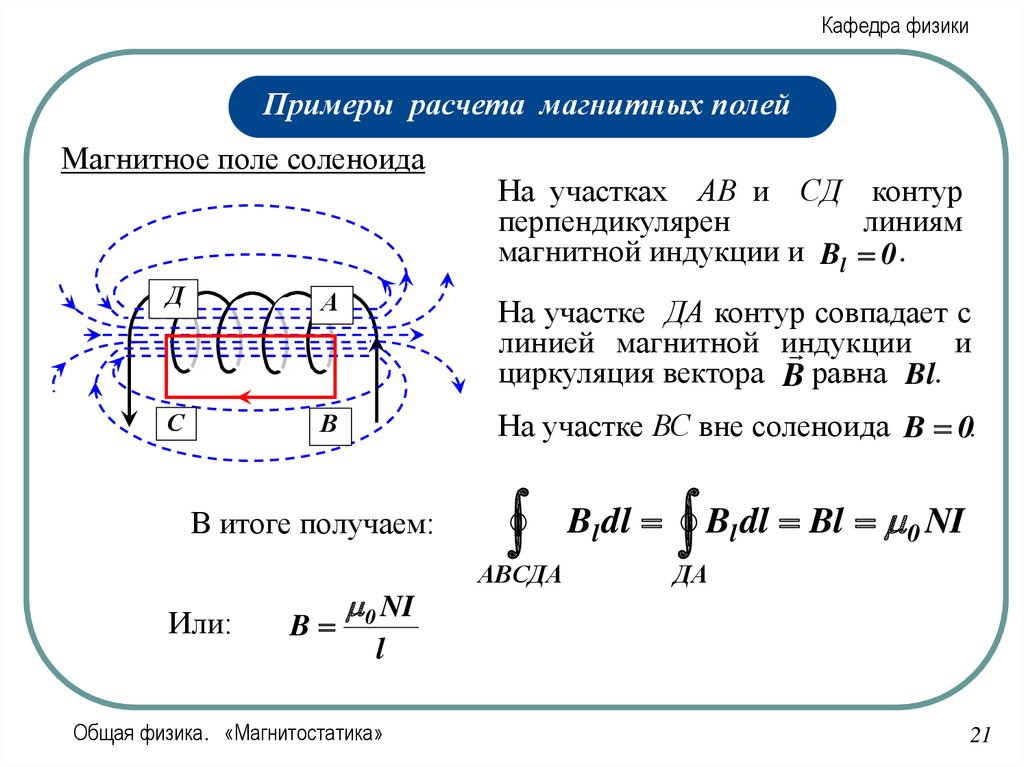
На участках АВ и СД контур
перпендикулярен
линиям
магнитной индукции и Bl 0 .
Д
А
На участке ДА контур совпадает с
линией магнитной индукции
и
циркуляция вектора B равна Bl.
С
В
На участке ВС вне соленоида B 0.
В итоге получаем:
Или:
B
0 NI
АВСДА
Bl dl
B dl Bl NI
l
0
ДА
l
Общая физика. «Магнитостатика»
21

22.

Кафедра физики
Примеры расчета магнитных полей
Магнитное поле соленоида
Поскольку N l n , то окончательно получим
B 0 nI
Таким образом, поле внутри соленоида однородно (краевыми
эффектами пренебрегаем). Произведение nI называется числом
ампервитков соленоида и относится к его характеристикам.
Д
А
С
В
Самостоятельно: расчет
Общая физика. «Магнитостатика»
Некорректность при выводе формулы:
интеграл по СВ принят равным нулю.
Строгий подход: линии магнитного
поля замкнуты и внешнее поле не
равно
нулю.
Однако,
это
некорректность принципиально на
результате не отражается.
магнитного поля тороида.
22