Похожие презентации:
Магнитное поле в вакууме
1. Магнитное поле в вакууме
Лекция 3 (продолжение)CEE
2.
ПланЗакон Био - Савара - Лапласа.
Магнитное поле прямого тока.
Магнитное поле в центре кругового проводника с
током.
Циркуляция вектора магнитной индукции.
Применение теоремы о циркуляции для
вычисления индукции магнитного поля.
Поток вектора магнитной индукции. Теорема
Гаусса для потока вектора магнитной индукции.
Работа магнитного поля по перемещению
проводника с током.
Работа при вращении контура с током в
однородном магнитном поле.
CEE
3.
Закон Био-Савара-ЛапласаБио, Савар и Лаплас установили закон, который позволяет
вычислить магнитную индукцию поля, созданного
элементом тока Idl на расстоянии r от него:
Т.е. индукция магнитного поля,
создаваемого элементом тока Idl
точке А на расстоянии r от него,
пропорциональна величине элемента
тока и синусу угла , равного углу
между направлениями элемента тока
Idl и r, а также обратно пропорциональна квадрату расстояния
между ними.
I
0 Idl sin
dB
2
4
r [1]
dl
r
A
dB
0 = 4π·10-7 Гн/м − магнитная постоянная
CEE
4.
Закон Био-Савара-ЛапласаЗакон Био - Савара - Лапласа в векторной
форме имеет вид:
0 I dl r
dB
3
4 r
[2]
Закон Био - Савара - Лапласа позволяет
вычислить магнитную индукцию поля любых
систем
токов,
используя
принцип
суперпозиции магнитных полей.
CEE
5.
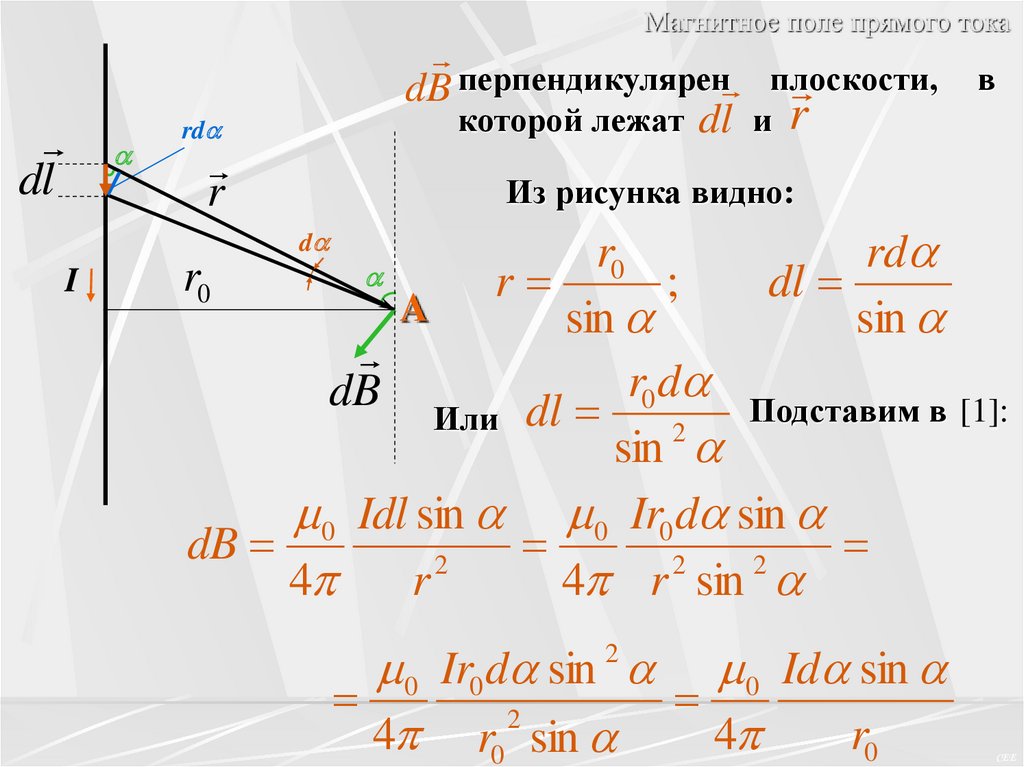
Магнитное поле прямого токаdl
в
dB перпендикулярен плоскости,
которой лежат dl и r
rd
r
Из рисунка видно:
r
rd
0
r0
r
;
dl
A
sin
sin
r0 d
dB
Подставим в [1]:
Или dl
2
sin
0 Idl sin 0 Ir0 d sin
dB
2
2
2
4
r
4 r sin
d
I
0 Ir0 d sin 2 0 Id sin
2
4 r0 sin
4
r0
CEE
6.
Магнитное поле прямого токаТогда, интегрируя последнее равенство, получим:
0 I
0 I
0 I
B dB
sin d
( cos ) 0
2
4 r0 0
4 r0
4 r0
Таким образом, магнитная индукция поля прямого
тока для вакуума:
0 I
B
2 r0
[3]
CEE
7.
Магнитное поле в центре кругового проводника с токомdl
R
I
Как следует
из рисунка, сложение
векторов dB можно заменить сложением
их модулей.
Кроме того, r = R, sin =1.
dB , B
Тогда, по закону Б-С-Л:
0 Idl sin
dB
4
R2
Модуль результирующего вектора В равен:
0 I
0 I
B dB
dl
2 R
2
2
4 R
4 R
или
B
0 I
[4]
2R
CEE
8.
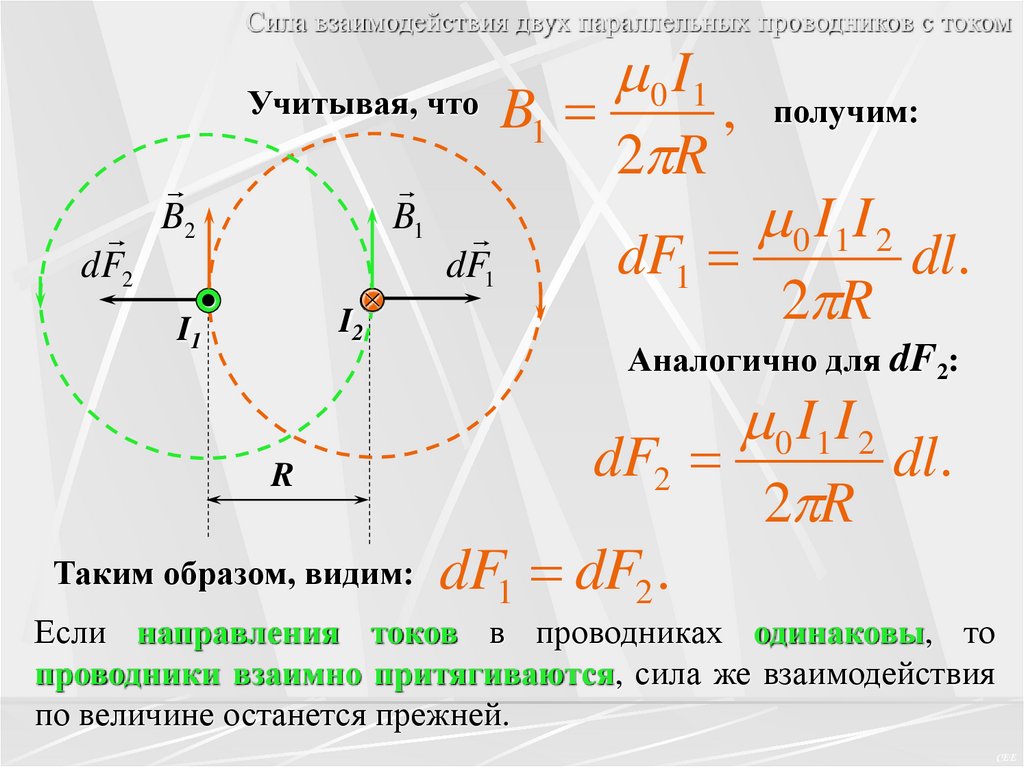
Сила взаимодействия двух параллельных проводников с токомПользуясь законом Био - Савара – Лапласа и законом
Ампера,
определим
силу
взаимодействия
двух
параллельных проводников с током.
Пусть токи имеют противоположное направление.
B2
dF2
B1
I2
I1
dF1 —
dF1
сила, с которой
магнитное поле B1 ,
созданное проводником
с
силой
тока
I1,
действует на участок dl
второго проводника.
Согласно закону Ампера
R
dF1 = В1I2dl
(т.к. α = 90°)
CEE
9.
Сила взаимодействия двух параллельных проводников с токомУчитывая, что
B2
dF2
B1
I2
I1
R
Таким образом, видим:
dF1
0 I1
B1
,
2 R
получим:
0 I1 I 2
dF1
dl.
2 R
Аналогично для dF2:
0 I1 I 2
dF2
dl.
2 R
dF1 dF2 .
Если направления токов в проводниках одинаковы, то
проводники взаимно притягиваются, сила же взаимодействия
по величине останется прежней.
CEE
10.
Циркуляция вектора магнитной индукции.Теорема о циркуляции вектора магнитной индукции
(закон полного тока для магнитного поля в вакууме):
Циркуляция вектора магнитной индукции по
произвольному
замкнутому
контуру
равна
произведению магнитной постоянной 0 на
алгебраическую сумму токов, охватываемых этим
контуром.
n
Bdl Bl dl 0 I k ,
L
L
k 1
где n — число проводников с токами, охватываемых
контуром L произвольной формы.
CEE
11.
Циркуляция вектора магнитной индукции.I2
I3
I5
I4
Ток считается положительным,
если его направление связано с
направлением обхода по контуру
правилом правого винта.
Для токов
записать:
I1
I1 – I5 можно
n
B
d
l
B
dl
I
(
0
I
I
l
0
k
0
1
2
L
L
k 1
I 3 I 4 I 4 0 I 5 ) 0 ( I 3 I 2 ).
Теорема о циркуляции вектора магнитной индукции справедлива только
для поля в вакууме.
CEE
12. Сравнение циркуляции векторов и
Сравнение циркуляциивекторов B и E
Edl El dl 0
L
L
Циркуляция вектора E
электростатического
поля всегда равна
нулю.
Электростатическое
поле потенциально.
n
Bdl Bl dl 0 I k
L
L
k 1
Циркуляция вектора B
магнитного поля не
равна нулю.
Магнитное поле
является вихревым.
CEE
13.
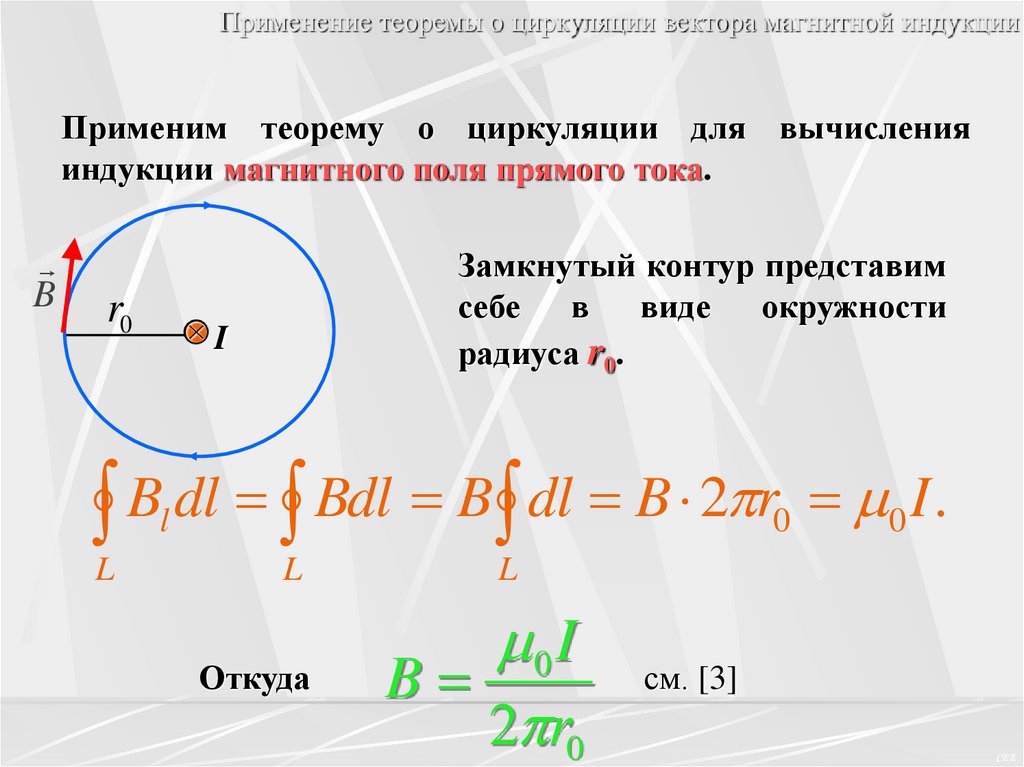
Применение теоремы о циркуляции вектора магнитной индукцииПрименим теорему о циркуляции для вычисления
индукции магнитного поля прямого тока.
B
r0
Замкнутый контур представим
себе в виде окружности
радиуса r0.
I
B
dl
Bdl
B
dl
B
2
r
I
.
l
0
0
L
L
Откуда
L
0 I
B
2 r0
см. [3]
CEE
14.
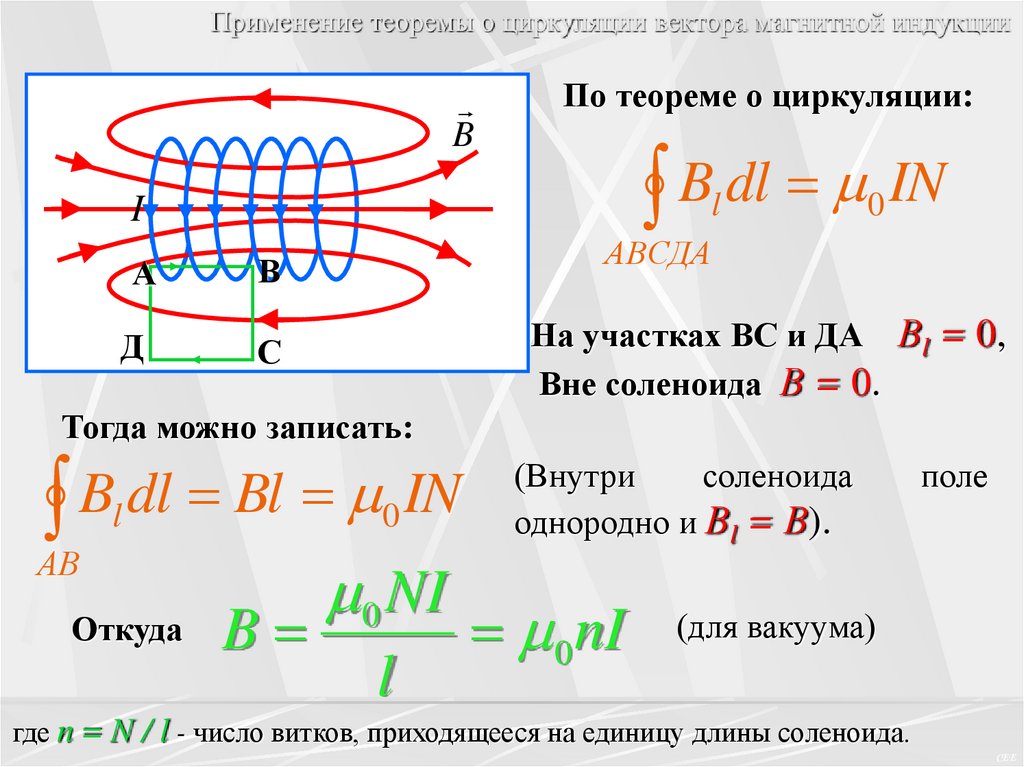
Применение теоремы о циркуляции вектора магнитной индукцииПрименим теорему о циркуляции для вычисления
индукции магнитного поля соленоида.
B
I
А
В
Рассмотрим соленоид длиной l,
имеющий N витков, по которому
течет ток I.
Д
С
Соленоидом называется цилиндрическая катушка, на
которую вплотную намотано большое число витков
провода. Поле внутри соленоида однородно.
Выберем замкнутый прямоугольный контур АВСДА.
CEE
15.
Применение теоремы о циркуляции вектора магнитной индукцииB
По теореме о циркуляции:
B
dl
IN
l
0
I
А
Д
АВСДА
В
На участках ВС и ДА Вl = 0,
Вне соленоида В = 0.
С
Тогда можно записать:
B
dl
Bl
IN
l
0
АВ
Откуда
B
0 NI
l
(Внутри
соленоида
однородно и Вl = В).
0 nI
поле
(для вакуума)
где n = N / l - число витков, приходящееся на единицу длины соленоида.
CEE
16.
Поток вектора магнитной индукцииdS
Магнитным потоком (потоком
вектора магнитной индукции)
через
малую
поверхность
площадью dS, которую можно
считать плоской и в пределах
которой магнитное поле можно
считать однородным, называется
скалярная физическая величина:
dΦB BdS Bn dS BdS cos
где Вn = Bcos α — проекция вектора В на нормаль к
плоскости контура.
CEE
17.
Поток вектора магнитной индукцииМагнитный поток сквозь произвольную поверхность
ΦB dΦB BdS Bn dS
S
S
Для однородного поля и плоской поверхности,
перпендикулярной вектору магнитной индукции:
ΦB BS
Магнитный поток выражается в веберах.
1 Вб = 1 Тл · 1 м2.
CEE
18.
Теорема Гаусса для потока вектора магнитной индукцииСледствием вихревого характера магнитного поля и
замкнутости силовых линий магнитной индукции является
выражение:
ΦB BdS Bn dS 0
S
S
Теорема Гаусса для потока
вектора магнитной индукции
Магнитный поток сквозь произвольную замкнутую
поверхность равен нулю.
В природе нет магнитных зарядов!
CEE
19.
ПотокосцеплениеОпределим
соленоид.
поток
вектора
магнитной
индукции
через
Индукция магнитного поля соленоида равна:
B
0 NI
l
0 nI
Поток магнитной индукции через один виток соленоида
площадью S равен:
ΦB BS
Тогда полный магнитный поток (потокосцепление) равен:
ΦB N
0 N IS
2
(для вакуума)
l
CEE
20.
Работа магнитного поля по перемещению проводника с токомСогласно закону Ампера на
проводник с током в
магнитном поле действует
сила F = IlВsin = IlВ,
которая направлена
вправо.
Если под действием этой силы проводник переместится на
dx, то
dA = Fdx = IBldx = IBdS = IdФ,
где dФ=Ф2−Ф1 — это изменение магнитного потока,
пронизывающего контур.
CEE
21.
Работа при вращении контура с током в однородном магнитном полеn
pm
B
n
B
pm
B
Φ1 BS BS cos BS
Φ2 BS BS cos 0 BS
Таким
образом,
Работа
при
вращении
контура
с
током
в
однородном
магнитном
поле из положения
1, в
котором векторы p m и B
направлены в противоположные стороны, в положение 2, в котором они
направлены одинаково:
A I (Φ2 Φ1 )
A I ( BS ( BS )) 2IBS 2 pm B
CEE














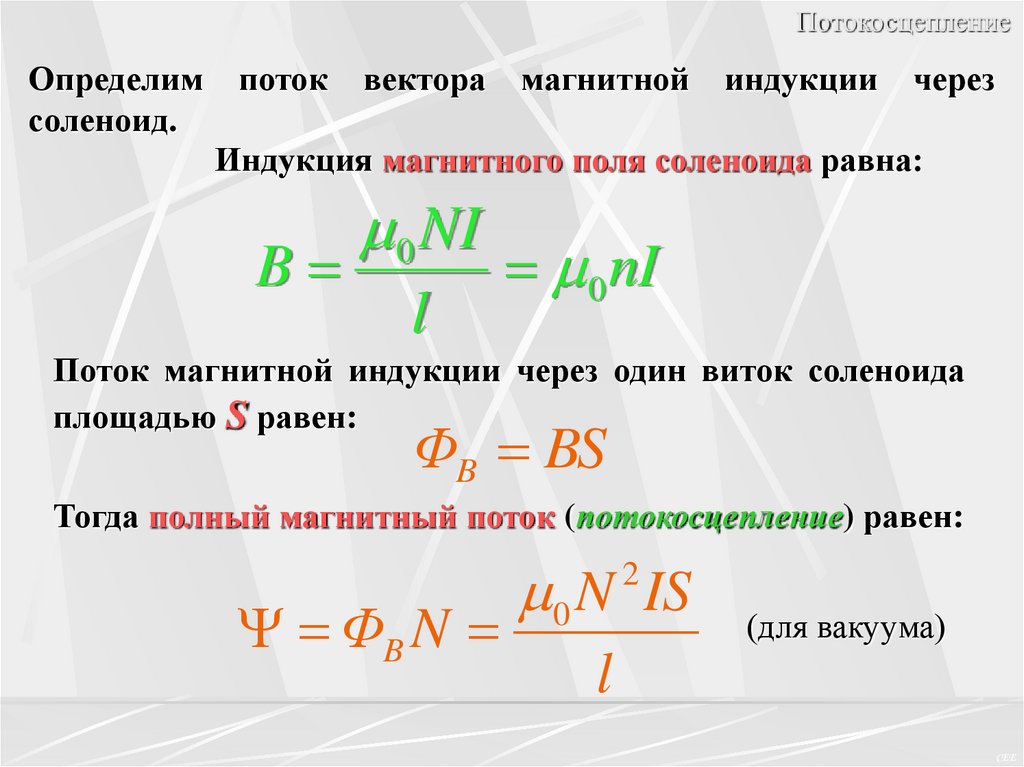


 Физика
Физика








