Множественная регрессия

1.

Тема 4. Множественная регрессия.
1. Модель с двумя независимыми переменными.
2. Оценка коэффициентов модели множественной
регрессии методом наименьших квадратов.
3. Парная и частная корреляция в модели
множественной регрессии.
4. Оценка
качества
модели
множественной
регрессии.
5. Мультиколлинеарность и методы ее устранения.
6. Интерпретация
коэффициентов
модели
множественной регрессии.

2.

Множественная регрессия – это уравнение
статистической
связи
с
несколькими
независимыми переменными:
y = f(x1, x2, …, xp)
где y – зависимая переменная (результативный
признак);
x1, x2, …, xp – независимые переменные
(факторы).

3.

Факторы, включаемые во множественную
регрессию, должны отвечать следующим
требованиям:
1. Они
должны
быть
количественно
измеримы. Если необходимо включить в
модель качественный фактор, не имеющий
количественного измерения, то ему нужно
придать количественную определенность.
2.
Факторы
не
должны
быть
интеркоррелированы и тем более находиться в
точной функциональной связи.

4.

Считается, что две переменные явно
коллинеарны, т.е. находятся между собой в
линейной зависимости, если
rxi x j 0,7
Если факторы явно коллинеарны, то они
дублируют друг друга и один из них
рекомендуется исключить из регрессии.

5.

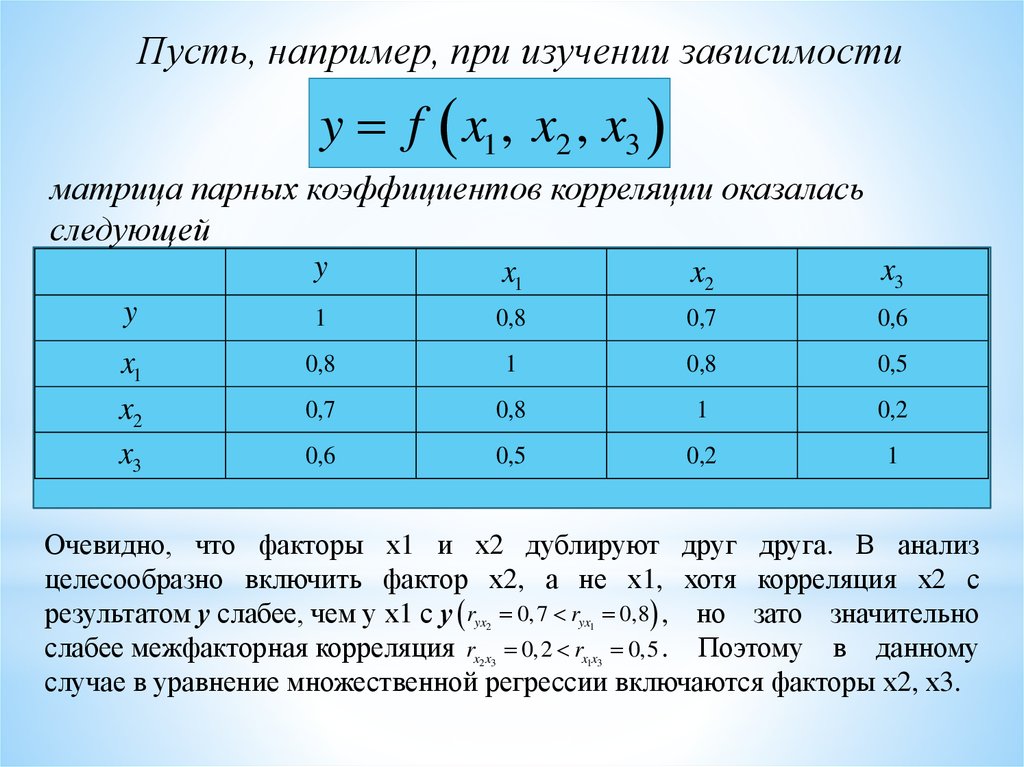
Пусть, например, при изучении зависимости
y f x1 , x2 , x3
матрица парных коэффициентов корреляции оказалась
следующей
y
x3
x2
x1
y
1
0,8
0,7
0,6
x1
x2
x3
0,8
1
0,8
0,5
0,7
0,8
1
0,2
0,6
0,5
0,2
1
Очевидно, что факторы х1 и х2 дублируют друг друга. В анализ
целесообразно включить фактор х2, а не х1, хотя корреляция х2 с
результатом у слабее, чем у х1 с у ryx 0,7 ryx 0,8 , но зато значительно
слабее межфакторная корреляция rx x 0,2 rx x 0,5 . Поэтому в данному
случае в уравнение множественной регрессии включаются факторы х2, х3.
2
1
2 3
1 3

6.

Включение в модель мультиколлинеарных факторов
нежелательно в силу следующих последствий:
1) Затрудняется интерпретация параметров множественной
регрессии как характеристик действия факторов в «чистом»
виде, ибо факторы коррелированы; параметры линейной
регрессии теряют экономический смысл.
2) Оценки параметров ненадежны, обнаруживают большие
стандартные ошибки и меняются с изменением объема
наблюдений (не только по величине, но и по знаку), что
делает модель непригодной для анализа и прогнозирования.

7.

Если бы факторы не коррелировали между собой, то
матрица парных коэффициентов корреляции между факторами
была бы единичной матрицей, поскольку все недиагональные
элементы
rxi x j
i j
были бы равны нулю.
Так, для уравнения,
переменных
включающего
три
объясняющих
y a b1 x1 b2 x2 b3 x3
матрица коэффициентов корреляции между факторами имела
бы определитель, равный единице:
rx1x1
rx1x2
rx1x3
1 0 0
Det R rx2 x1
rx2 x2
rx2 x3 0 1 0 1
rx3x1
rx3 x2
rx3 x3
0 0 1

8.

rx1x1
rx1x2
rx1x3
1 1 1
Det R rx2 x1
rx2 x2
rx2 x3 1 1 1 0
rx3x1
rx3x2
rx3x3
1 1 1
Одним из путей учета внутренней корреляции факторов
является переход к совмещенным уравнениям регрессии, т.е. к
уравнениям, которые отражают не только влияние факторов, но
и их взаимодействие. Так, если
y f x1 , x2 , x3
то возможно построение следующего совмещенного уравнения:
y a b1 x1 b2 x2 b3 x3 b12 x1 x2 b13 x1 x3 b23 x2 x3

9.

Наиболее широкое применение получили
следующие методы построения уравнения
множественной регрессии:
1) Метод исключения – отсев факторов из полного его
набора.
2) Метод включения – дополнительное введение фактора.
3) Шаговый регрессионный анализ – исключение ранее
введенного фактора.

10.

Метод наименьших квадратов (МНК).
Свойства оценок на основе МНК
В линейной множественной регрессии
y x a b1 x1 b2 x2 ... bm xm
параметры при Х называются коэффициентами «чистой»
регрессии.
Рассмотрим линейную модель множественной регрессии
y a b1 x1 b2 x2 ... bm xm
(1)
МНК позволяет получить такие оценки параметров, при
которых сумма квадратов отклонений фактических значений
результативного признака у от расчетных y минимальна:
y y
i
i
xi
2
min
(2)

11.

Имеем функцию m 1 аргумента:
S a, b1 , b2 , ..., bm y a b1 x1 b2 x2 ... bm xm
Находим частные производные первого порядка:
S
a 2 y a b1 x1 b2 x2 ... bm xm 0;
S 2 x y a b x b x ... b x 0;
1
1 1
2 2
m m
b
1
........................................................
S 2 x y a b x b x ... b x 0.
m
1 1
2 2
m m
bm
2

12.

После элементарных преобразований приходим к системе линейных
нормальных уравнений для нахождения параметров линейного уравнения
множественной регрессии (1):
na b1 x1 b2 x2 ... bm xm y,
2
a x1 b1 x1 b2 x1 x2 ... bm x1 xm yx1 ,
(3)
................................................................
2
a x b x x b
x
x
...
b
x
m
1
1 m
2
2 m
m
m yxm .
Для двухфакторной модели данная система будет иметь вид:
na
b1 x1 b2 x2 y,
2
a x1 b1 x1 b2 x1 x2 yx1 ,
2
a x2 b1 x1 x2 b2 x2 yx2 .

13.

МНК применим и к уравнению множественной регрессии
в стандартизированном масштабе:
t y 1t x1 2t x2 ... mt xm ,
(4)
где t y , t x1 , ..., t xm – стандартизированные переменные:
ty
y y
y
t xi
xi xi
xi
для которых среднее значение равно нулю:
ty txi 0
а среднее квадратическое отклонение равно единице:
t y txi 1
i
– стандартизированные коэффициенты регрессии.

14.

Применяя МНК к уравнению множественной регрессии
в стандартизированном
масштабе, получим
систему
нормальных уравнений вида
2 rx1x2 3rx1x3 ... m rx1xm ,
ryx1 1
3 rx1x3 ... m rx1xm ,
ryx2 1rx1x2 2
........................................................
ryx 1rx x 2 rx x 3 rx x ... m ,
1 m
2 m
3 m
m
ryxi
rxi x j
(5)
– коэффициенты парной и
межфакторной корреляции
Где
и

15.

Коэффициенты «чистой» регрессии bi связаны со
стандартизованными
коэффициентами i регрессии
следующим образом:
y
(6)
bi i
xi
Поэтому можно переходить от уравнения регрессии в
стандартизованном масштабе (4) к уравнению регрессии в
натуральном масштабе переменных (1), при этом параметр а
определяется как a y b x b x ... b x
1 1
2 2
m m
На основе линейного уравнения множественной регрессии
y a b1 x1 b2 x2 ... bm xm
(7)
могут быть найдены частные уравнения регрессии:
y x x , x ,..., x f x1 ,
1
2
3
m
y x2 x1 , x3 ,..., xm f x2 ,
.............................
y xm x1 , x2 ,..., xm 1 f xm ,
(8)

16.

При подстановке в эти уравнения средних значений
соответствующих факторов они принимают вид парных
уравнений линейной регрессии, т.е. имеем
y x1 x2 , x3 ,..., xm A1 b1 x1 ,
y x2 x1 , x3 ,..., xm A2 b2 x2 ,
................................
y x x , x ,..., x Am bm xm ,
m 1 2 m 1
где
A1 a b2 x2 b3 x3 ... bm xm ,
A a b x b x ... b x ,
2
1 1
3 3
m m
..............................................
Am a b1 x1 b2 x2 b3 x3 ... bm 1 xm 1.
(9)

17.

На основе частных уравнений регрессии определяются
частные коэффициенты эластичности:
Эyx bi
i
xi
(10)
y xi x1 , x2 ,... xi 1 , xi 1 ,..., xm
b
Где
– коэффициент регрессии для фактора Xi в уравнении
i
множественной регрессии,
y xi x1 , x2 ,... xi 1 , xi 1 ,..., xm
– частное уравнение регрессии.
Наряду с частными коэффициентами эластичности
могут быть найдены средние по совокупности показатели
эластичности:
xi
Эi bi
y xi
(11)