Построение эпюр внутренних усилий в консольной балке при изгибе. Подбор поперечного сечения

1. Побудова епюр M, Q та N у балках та рамах. Визначення розмірів перерізу.

2. Построение эпюр внутренних усилий в консольной балке при изгибе. Подбор поперечного сечения.

Для
заданной
консольной
балки
построить эпюры Mx и Qy и подобрать
поперечное сечение в виде двутавра,
двух швеллеров, прямоугольника (h=2b) и
круга.

3. 1. Определение внутренних усилий в консольной балке

z1 1
y
P =36 кН
1
1,5 м
z2
2
М =62 кНм
q =22 кН/м
2
2,4 м
q =22 кН/м
1,6 м
0 ≤ z1 ≤ 1,5м
Mx(z1) = – P∙z1;
z
Реакции для
консольной балки
можно не определять.
И выражения для Mx и
Qy записываем,
рассматривая в
равновесии левую
отсеченную часть.
Qy(z1) = – P= –36 (кН) – const;
Mx(0) = – 36∙0= 0;
Mx(1,5) = – 36∙1,5 = –54 (кНм);
0 ≤ z2 ≤ 2,4 м
Mx(z2) = – P∙(1,5+z2) + z2∙q∙z2/2 + M;
Mx(0) = – 36∙(1,5+0) + 0∙22∙0/2 +62= 8 (кНм);
Mx(2,4) = – 36∙(1,5+2,4) + 2,4∙22∙2,4/2 +62= – 15,04 (кНм);

4. Определение внутренних усилий Qy в консольной балке на втором участке

z1 1
y
P =36 кН
1
1,5 м
z2
2
М =62 кНм
q =22 кН/м
2
2,4 м
q =22 кН/м
Определение внутренних
усилий Qy в консольной
балке на втором участке
z
1,6 м
Qy(z2) = – P+ z2∙q;
Qy(0) = – 36+0 ∙ 22= – 36 (кН);
Qy(2,4) = – 36 + 2,4 ∙ 22= 16,8(кН);
dM x (z2 )
P 36
= – P + q Чz2 = 0; z 2,max = =
= 1.64 (м )
dz2
q 22
Mx, max (1,64) = – 36∙(1,5+1,64) + 1,64 ∙22∙1,64/2+62 = – 21,45 (кНм);

5.

z1 1
y
z2
P =36 кН
1
1,5 м
2
М =62 кНм
q =22 кН/м
2
2,4 м
z3
3
q =22 кН/м
Определение внутренних
усилий Mx и Qy в консольной
балке на третьем участке
z
3
1,6 м
0 ≤ z3 ≤ 1,6 м
Mx(z3) = – P∙(1,5+2,4+z3) + 2,4∙q∙(2,4/2+z3) + M – z3∙q∙z3/2;
Mx(0) = – 36∙(1,5+2,4) + 2,4∙22∙(1,2+0) +62 – 0∙22∙0/2 = – 15,04 (кНм);
Mx(1,6) = – 36∙(1,5+2,4+1,6) + 2,4∙22∙(1,2+1,6) +62– 1,6∙22∙1,6/2 =
= – 16,32 (кНм);
Qy(z3) = – P+ 2,4∙q – z3∙q;

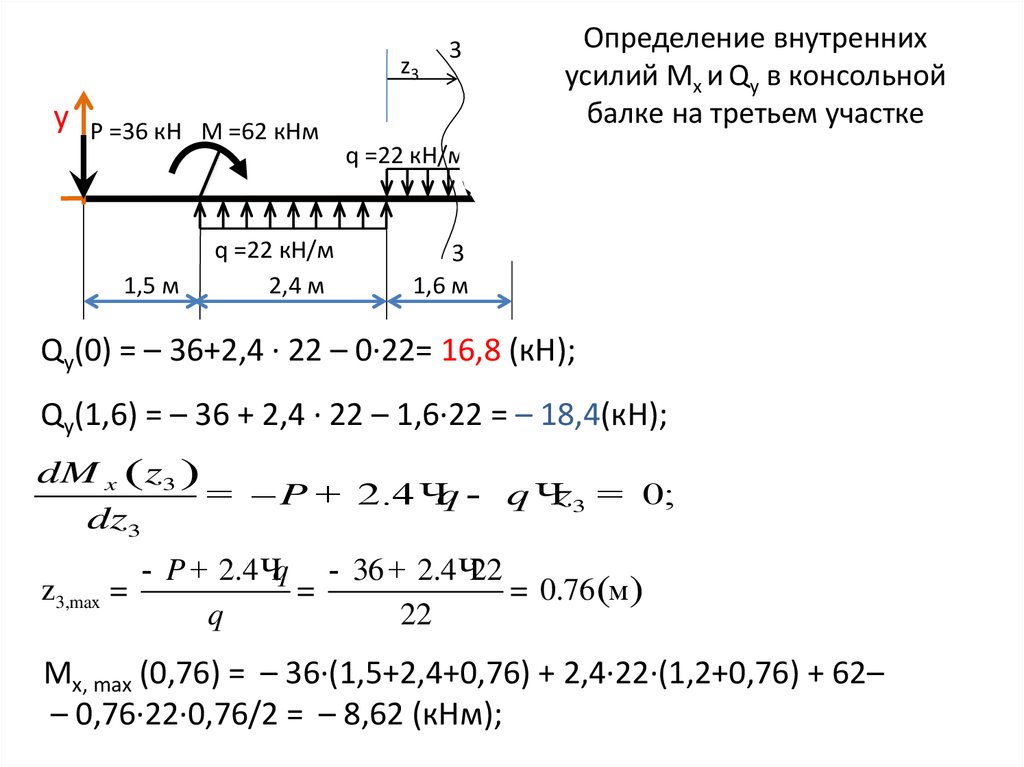
6. Определение внутренних усилий Mx и Qy в консольной балке на третьем участке

z3
y
P =36 кН М =62 кНм
1,5 м
q =22 кН/м
2,4 м
3
q =22 кН/м
Определение внутренних
усилий Mx и Qy в консольной
балке на третьем участке
z
3
1,6 м
Qy(0) = – 36+2,4 ∙ 22 – 0∙22= 16,8 (кН);
Qy(1,6) = – 36 + 2,4 ∙ 22 – 1,6∙22 = – 18,4(кН);
dM x (z3 )
= – P + 2.4 Чq - q Чz3 = 0;
dz3
- P + 2.4 Чq - 36 + 2.4 Ч22
z3,max =
=
= 0.76(м)
q
22
Mx, max (0,76) = – 36∙(1,5+2,4+0,76) + 2,4∙22∙(1,2+0,76) + 62–
– 0,76∙22∙0,76/2 = – 8,62 (кНм);

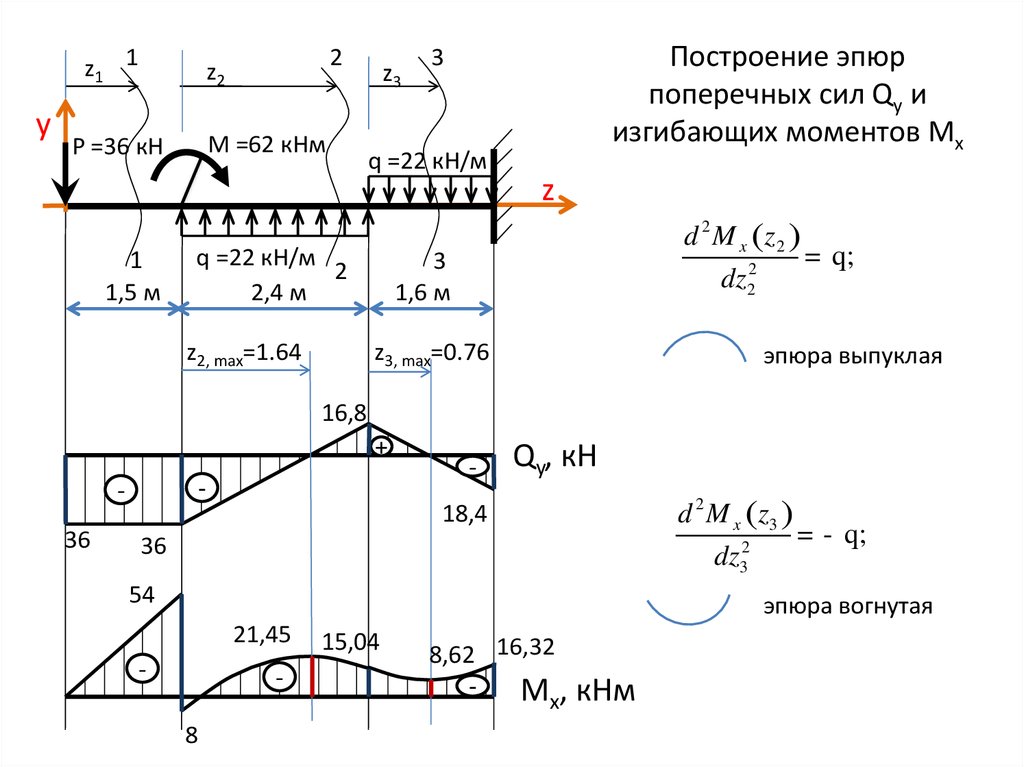
7. Построение эпюр поперечных сил Qy и изгибающих моментов Mx

z1 1
y
2
z2
М =62 кНм
P =36 кН
1
1,5 м
z3
q =22 кН/м
q =22 кН/м
2
2,4 м
z2, max=1.64
Построение эпюр
поперечных сил Qy и
изгибающих моментов Mx
3
z
d 2 M x (z2 )
= q;
2
dz2
3
1,6 м
z3, max=0.76
эпюра выпуклая
16,8
+
-
36
-
Qy, кН
d 2 M x (z3 )
= - q;
2
dz3
18,4
36
54
эпюра вогнутая
21,45
-
8
15,04
8,62 16,32
M , кНм
x

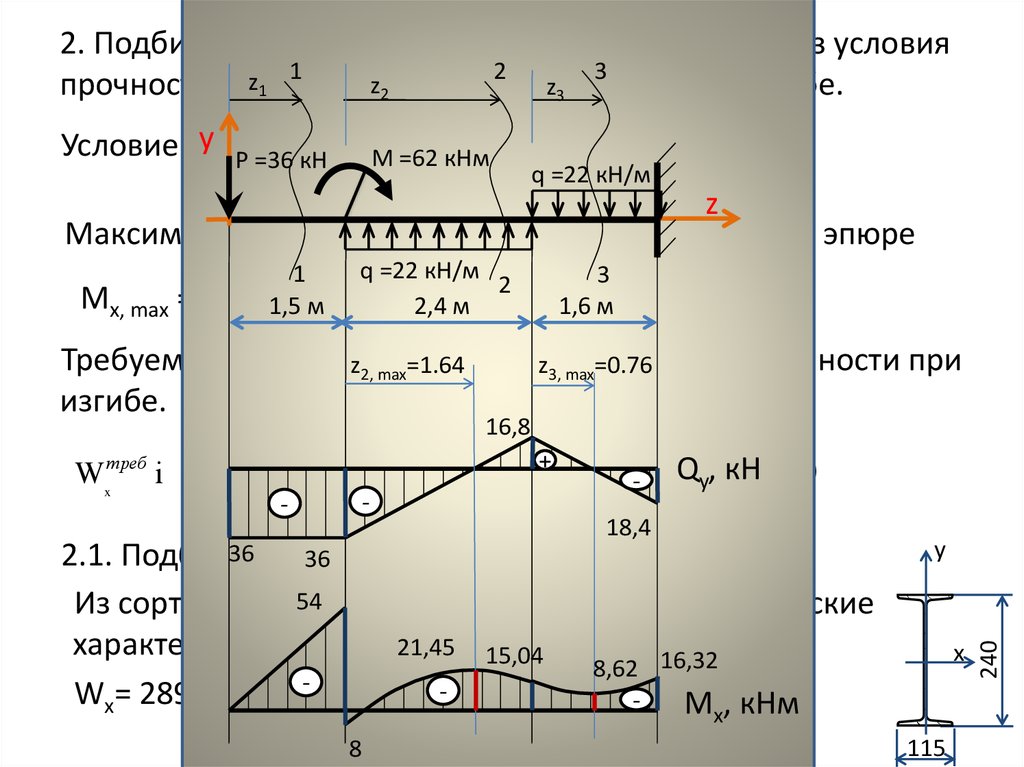
8. 2. Подбираем поперечные сечения балок, исходя из условия прочности по нормальным напряжениям при изгибе.

2. Подбираем поперечные сечения балок, исходя из условия
1
2
3
z2
прочности поz1нормальным
напряжениям
при изгибе.
z3
M x,max
y
Условие прочности
при
изгибе.
x=
Ј R
М =62 кНм
P =36 кН
q =22 кН/м
Wx
z
Максимальный по модулю изгибающий момент на эпюре
Mx, max =
q =22 кН/м
1
2
-54 (кНм)
1,5 м
2,4 м
3
1,6 м
Требуемый момент zсопротивления
условия прочности при
z3, maxиз
=0.76
2, max=1.64
изгибе.
Wx
і
M x,max
R
16,8
54 Ч10
3
+10- 3 м 3 =Q270
=
=
0.27
Ч
см
,
кН
(
)
(
)
y
6
200
- Ч10
18,4
36
2.1. Подбираем
сечение
в виде двутавра №24.
36
54
Из сортамента выписываем
основные геометрические
характеристики поперечного
сечения: 16,32
21,45 15,04
8,62
3
2
Wx= 289 см ; F = 34.8 см .M , кНм
y
x
x
8
115
240
треб
3

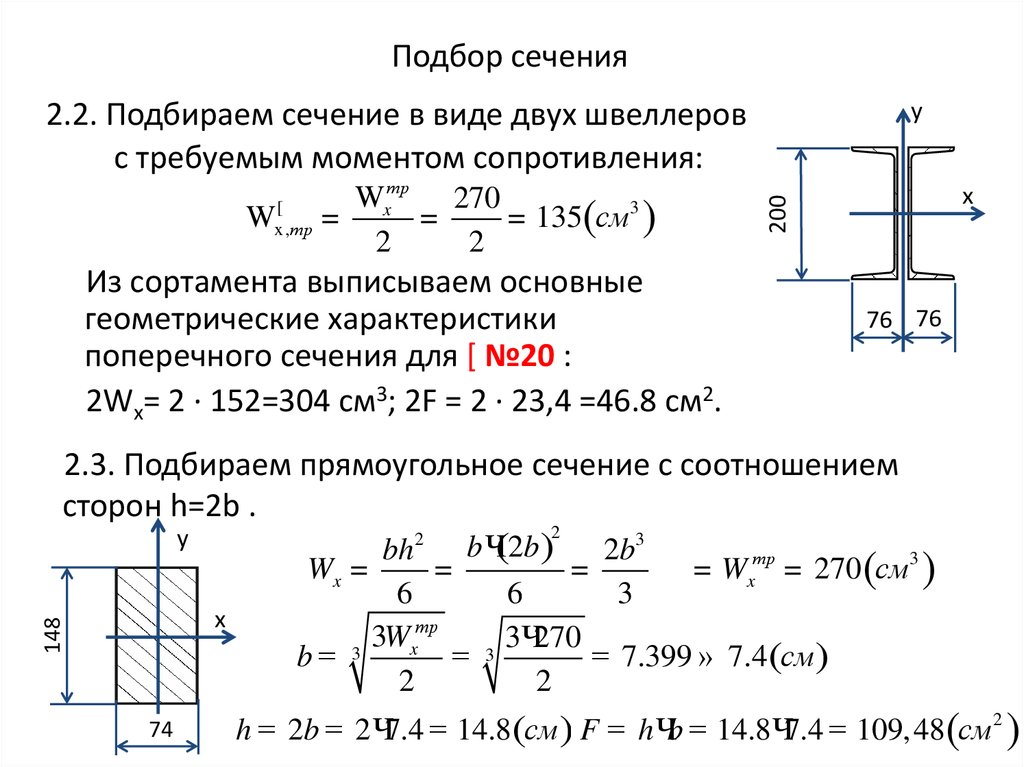
9. Подбор сечения

2.2. Подбираем сечение в виде двух швеллеров
с требуемым моментом сопротивления:
W
Wxтр 270
=
=
= 135(см3 )
2
2
Из сортамента выписываем основные
геометрические характеристики
поперечного сечения для [ №20 :
2Wx= 2 ∙ 152=304 см3; 2F = 2 ∙ 23,4 =46.8 см2.
x
200
[
x,тр
y
76 76
2.3. Подбираем прямоугольное сечение с соотношением
сторон h=2b .
y
148
x
74
2
b Ч(2b)
bh
2b3
= Wxтр = 270 (см3 )
Wx =
=
=
6
6
3
тр
3
W
3 Ч270
x
3
3
b=
=
= 7.399 » 7.4 (см)
2
2
2
h = 2b = 2 Ч7.4 = 14.8(см) F = h Чb = 14.8 Ч7.4 = 109, 48(см 2 )

10. Подбор сечения

2.4. Подбираем круглое сечение.
Wx,тр =
r=
3
r3
4
4Wxтр
тр
x
= W
=
3
= 270 (см
3
)
4 Ч270
= 7 (см)
3.14
F = r 2 = 3.14 Ч7 2 = 154.2 (см 2 )
y
x

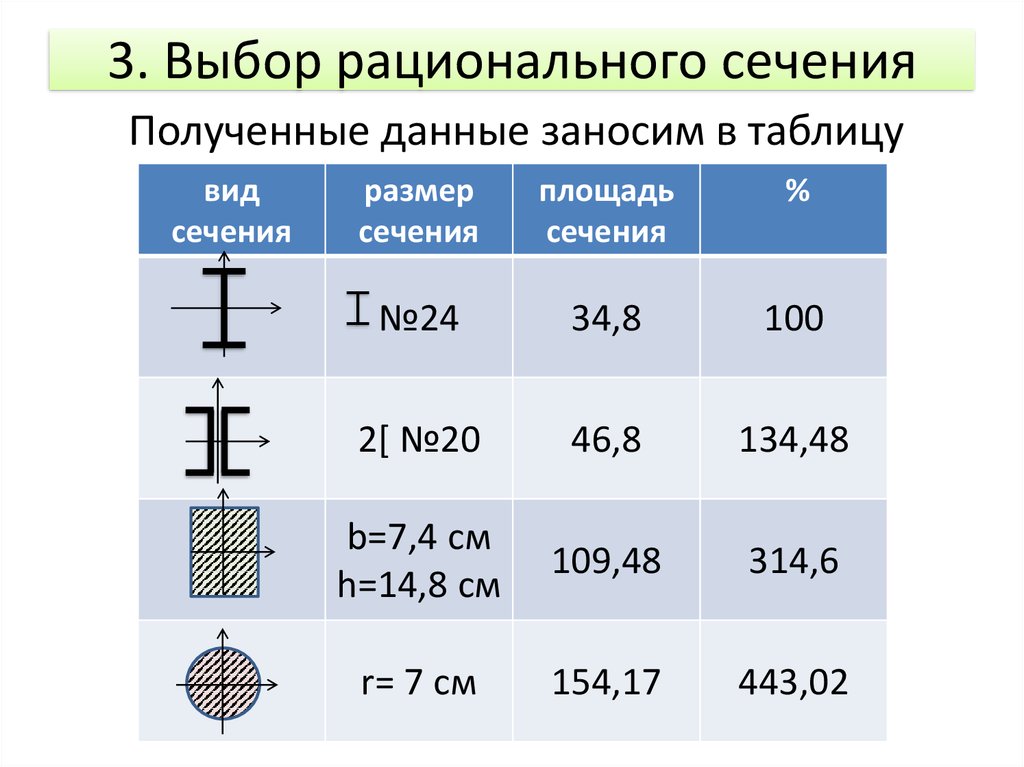
11. 3. Выбор рационального сечения

Полученные данные заносим в таблицу
вид
сечения
размер
сечения
площадь
сечения
%
№24
34,8
100
2[ №20
46,8
134,48
b=7,4 см
h=14,8 см
109,48
314,6
r= 7 см
154,17
443,02

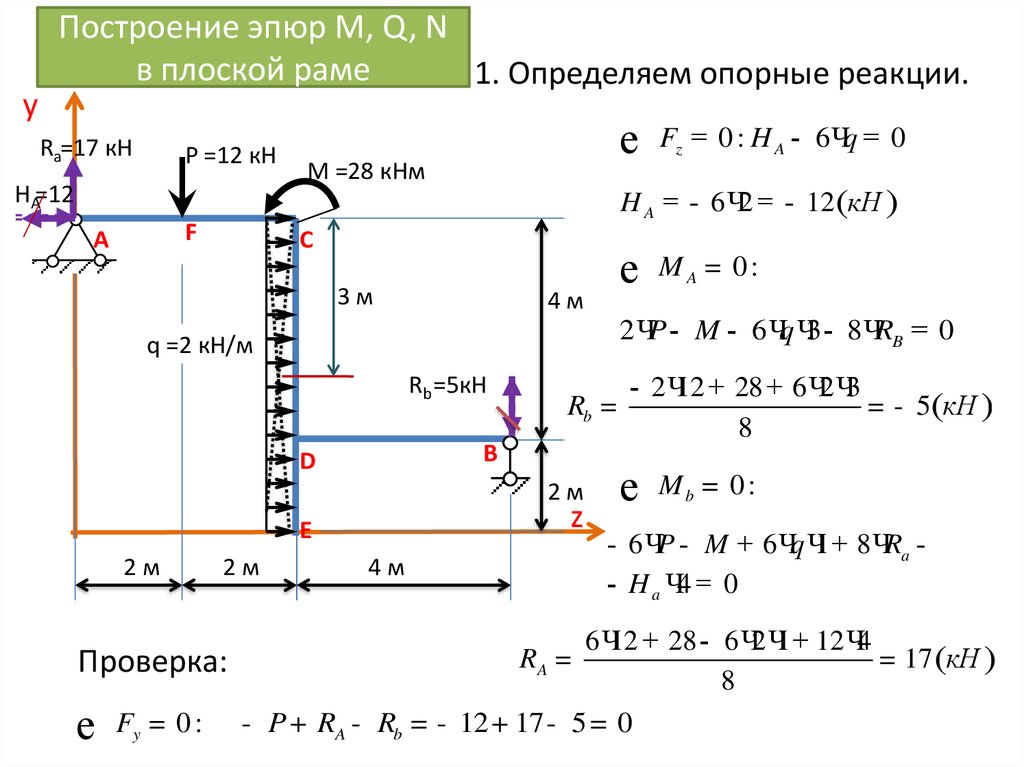
12. Построение эпюр М, Q, N в плоской раме

y
Построение эпюр М, Q, N
в плоской раме
1. Определяем опорные реакции.
Ra=17 кН
P =12 кН
HA=12
М =28 кНм
C
3м
е
4м
Rb =5кН
Rb =
B
D
2м
z
E
2м
Проверка:
е
Fy = 0 :
4м
MA = 0:
2 ЧP - M - 6 Чq Ч3 - 8ЧRB = 0
q =2 кН/м
2м
Fz = 0 : H A - 6 Чq = 0
H A = - 6 Ч2 = - 12(кН )
F
A
е
- 2 Ч12 + 28 + 6 Ч2 Ч3
= - 5(кН )
8
е
Mb = 0 :
- 6 ЧP - M + 6 Чq Ч1 + 8 ЧRa - H a Ч4 = 0
6 Ч12 + 28 - 6 Ч2 Ч1 + 12 Ч4
= 17 (кН )
8
- P + RA - Rb = - 12 + 17 - 5 = 0
RA =

13. 2. Определяем значения изгибающих моментов, поперечных и продольных сил.

0≤z ≤2м
1
1
y
Ra=17 кН
2
P =12 кН
HA=12
F
A
z1
Mx(z1) = Ra ∙z1; Mx(0) = 17∙0= 0;
Mx(2) = 17∙2 = 34(кНм);
М =28 кНм
Qy(z1) = Ra= 17 (кН) – const;
C
z2
Nz(z1) = Ha= 12 (кН) – const;
3м
2
1
q =2 кН/м
4м
Mx(z2) = Ra ∙(2+ z2) – P∙z2 ;
Rb =5кН
Mx(0) = 17 ∙(2+ 0) – 12∙0 =
= 34 (кНм);
B
D
2м
z
E
2м
2м
0 ≤ z2 ≤ 2 м
4м
Mx(2) = 17 ∙(2+ 2) – 12∙2 =
= 44 (кНм);
Qy(z2) = Ra – P = 17 – 12 =
= 5 (кН) – const;
Nz(z2) = Ha= 12 (кН) – const;

14.

2. Определяем значения изгибающих моментов, поперечных и
продольных сил. (продолжение)
0≤z ≤4м
3
1
y
Ra=17 кН
Mx(z3) = Ra ∙4 – P∙2 – М +
+ z3∙q∙z3/2 – Ha ∙z3;
2
P =12 кН
М =28 кНм
Mx(0) = 17 ∙4 – 12∙2 – 28 +
+ 0∙2∙0/2 – 12 ∙0 = 16 (кНм);
H=12
A
F
A
z1
C
z2
3м
2
1
q =2 кН/м
4м
z3
Qy(z3) = z3∙q – Ha;
Rb =5кН
3
3
Qy(0) = 0∙2 – 12= – 12(кН);
B
D
Mx(4) = 17 ∙4 – 12∙2 – 28 +
+ 4∙2∙4/2 – 12 ∙4 = – 16 (кНм);
2м
z Qy(4) = 4∙2 – 12= – 4(кН);
E
2м
2м
4м
Nz(z3) = Ra – P = 17 – 12 =
= 5 (кН) – const;

15.

2. Определяем значения изгибающих моментов, поперечных и
продольных сил. (продолжение)
0 ≤ z4 ≤ 4 м
Mx(z4) = – Rb ∙ z4;
1
y
Ra=17 кН
2
Mx(0) = – 5 ∙ 0 = 0 ;
P =12 кН
М =28 кНм
Mx(4) = – 5 ∙ 4 = –20 (кНм) ;
F
C
Qy(z4) = Rb = 5 (кН) – const
H=12
A
A
z1
z2
3м
2
1
q =2 кН/м
z3
3
3
D
5
E
2м
2м
4м
5
z5
4м
0 ≤ z5 ≤ 2 м
Rb =5кН
4
4
B
z4
Nz(z4) = 0;
Mx(z5) = z5∙q ∙ z5 /2;
2м
Mx(0) = 0∙q ∙ 0/2=0;
z Mx(2) = 2∙2 ∙ 2/2= 4 (кНм) ;
Qy(z5) = – z5∙q;
Qy(0) = – 0∙2 = 0;
Qy(2) = – 2∙2 = 4 (кН); Nz(z5) = 0;

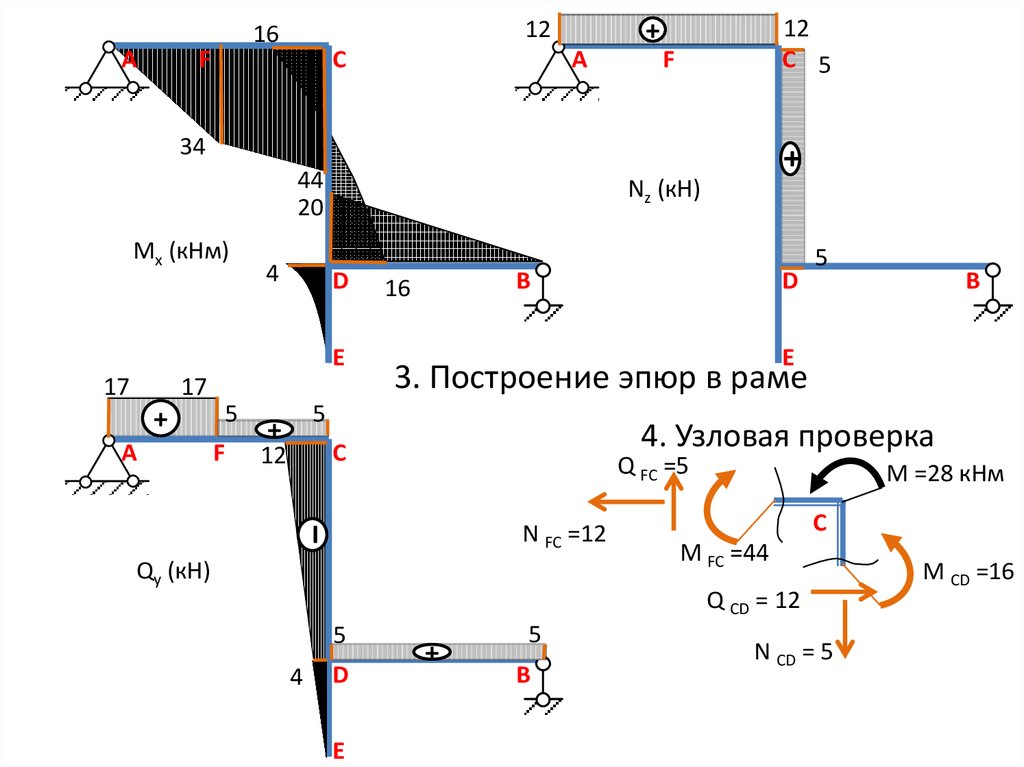
16. 3. Построение эпюр в раме

A
F
C
12
C 5
+
12
16
A
F
+
34
44
20
Mx (кНм)
4
Nz (кН)
D
E
17
17
+
F
4. Узловая проверка
C
12
Q FC =5
N FC =12
Qy (кН)
М =28 кНм
C
M FC =44
Q CD = 12
5
4
D
E
B
3. Построение эпюр в раме
5
+
D
E
̶
A
5
B
16
5
+
5
B
N CD = 5
M CD =16

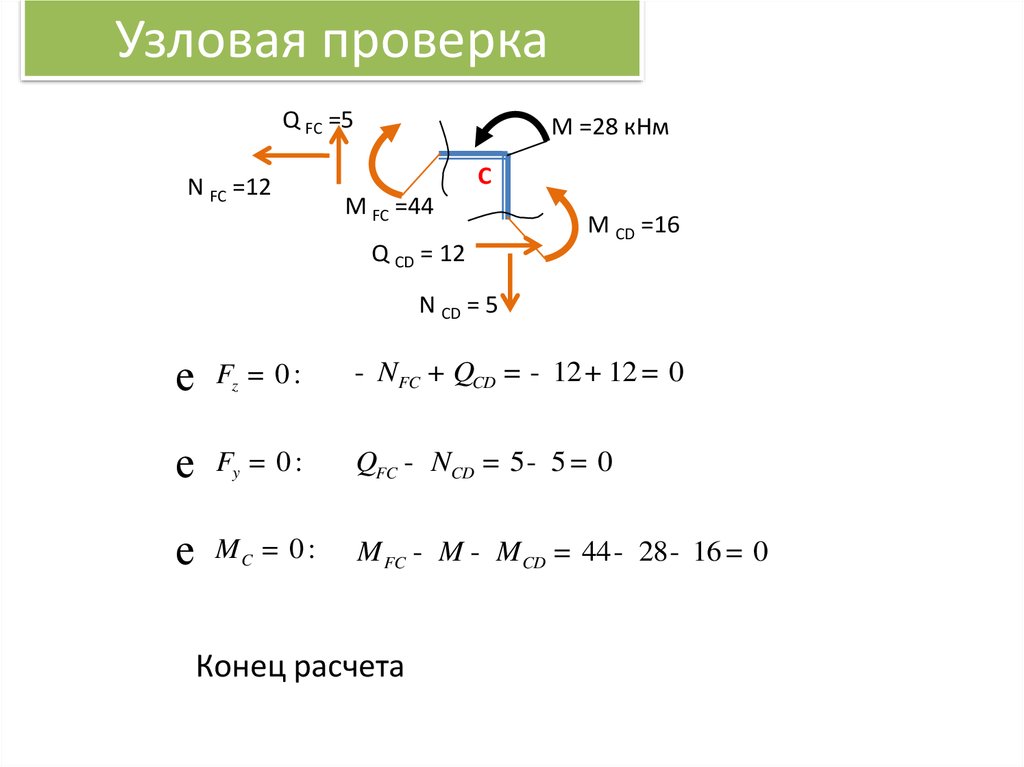
17. Узловая проверка

Q FC =5
N FC =12
М =28 кНм
C
M FC =44
Q CD = 12
M CD =16
N CD = 5
е
Fz = 0 :
- N FC + QCD = - 12 + 12 = 0
е
Fy = 0 :
QFC - NCD = 5 - 5 = 0
е
MC = 0 :
M FC - M - M CD = 44 - 28 - 16 = 0
Конец расчета