Похожие презентации:
Изгиб. Основные понятия и допущения
1. Изгиб
2.
ИЗГИБОсновные понятия и допущения
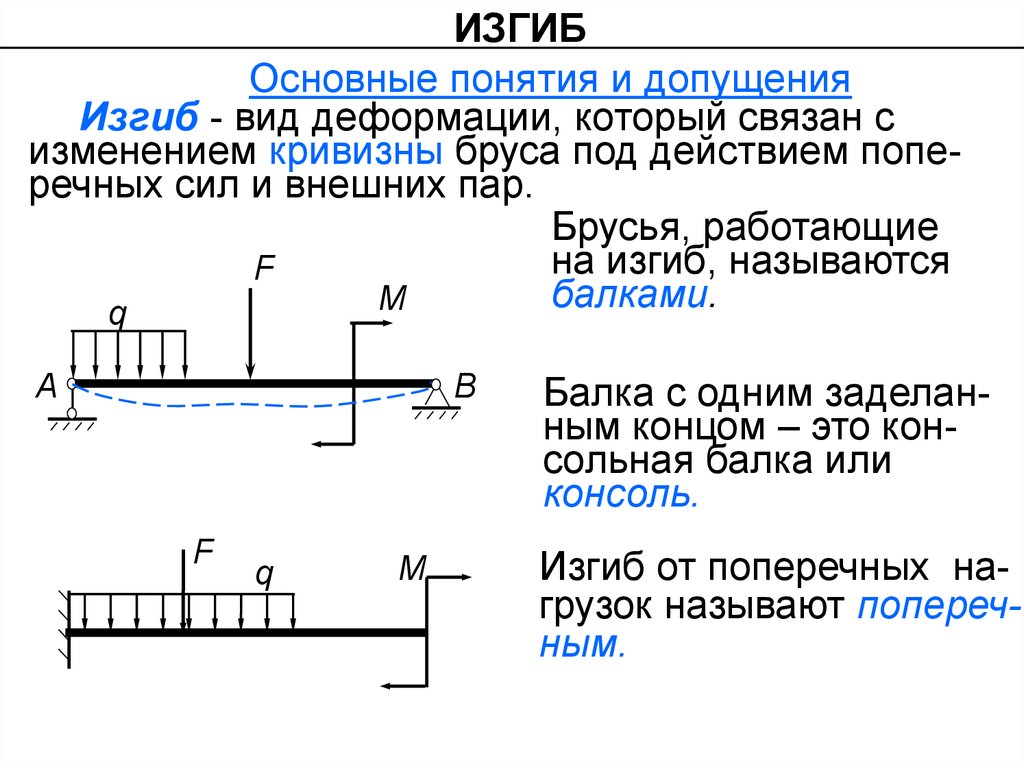
Изгиб - вид деформации, который связан с
изменением кривизны бруса под действием поперечных сил и внешних пар.
Брусья, работающие
на изгиб, называются
F
балками.
М
q
А
B
F
q
М
Балка с одним заделанным концом – это консольная балка или
консоль.
Изгиб от поперечных нагрузок называют поперечным.
3.
Основные понятия и допущенияПоперечный изгиб может быть плоским прямым или
косым изгибом.
Плоский изгиб происходит в случае, когда силовая
плоскость (плоскость действия изгибающего момента
проходит через одну из главных осей инерции
yС
F
С
yС
xС
F
xС
Если в поперечном сечении действует только изгибающий момент, деформация называется чистый
изгиб.
4.
Определение реакцийПри изгибе для закрепления балки, в основном, используются
1. шарнирно-неподвижная опора(цилиндрический
шарнир),
2. шарнирно-подвижная опора (стержень с
шарнирами на концах)
3. жесткая заделка.
Прежде чем приступить к расчету необходимо
составить расчетную схему, определить опорные
реакции.
5.
Определение реакцийДля плоской системы сил достаточно 3-х уравнений
статики.
Так как все силы действуют перпендикулярно продольной оси балки, горизонтальная составляющая
реакции равна нулю.
Поэтому из условий равновесия для определения
реакций применяют два следующих уравнения
статики :
ΣМ(А) = 0;
ΣМ (В) = 0
Третье уравнение используют для проверки правильности определения реакций:
ΣFky=0
Чаще записывается проще
ΣY=0
6.
Определение реакцийу YA
А
YB
q
F
М
B
z
ΣМ(А) = 0;
ΣМ (В) = 0
ΣY = 0
7.
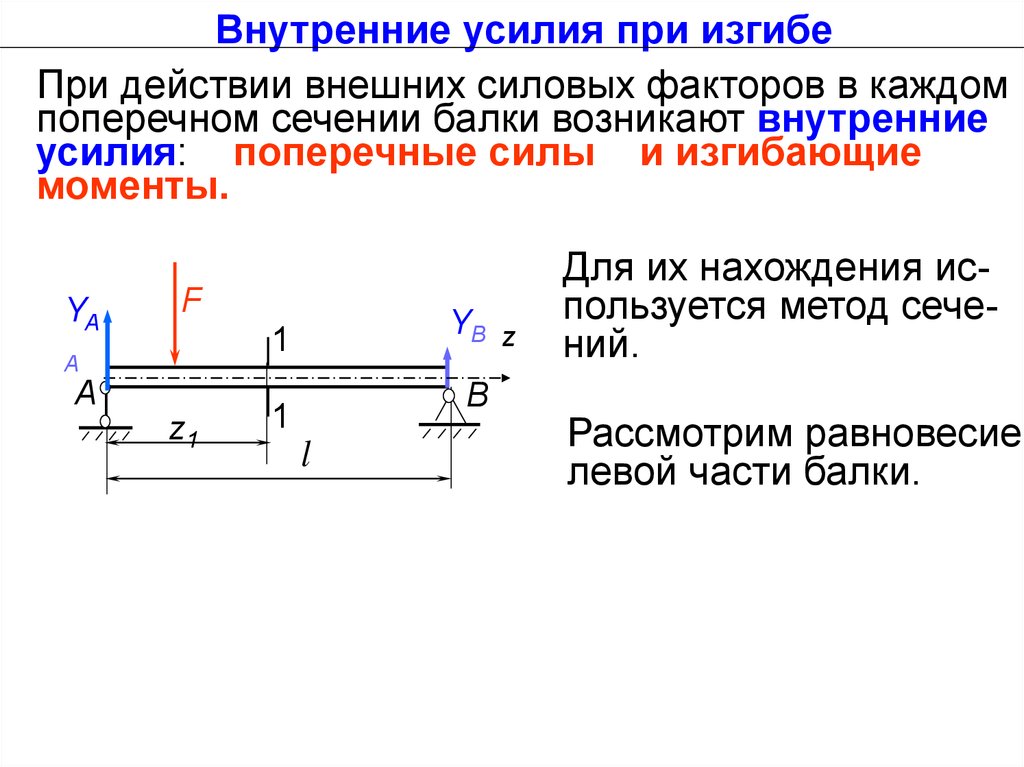
Внутренние усилия при изгибеПри действии внешних силовых факторов в каждом
поперечном сечении балки возникают внутренние
усилия: поперечные силы и изгибающие
моменты.
YA
F
YB z
1
A
А
z1
B
1
l
Для их нахождения используется метод сечений.
Рассмотрим равновесие
левой части балки.
8.
Внутренние усилия при изгибеВыполним приведение системы сил к центру сечения
О.
В соответствие с леммой Пуансо, силу, действующую на тело, можно переносить параллельно
самой себе, добавляя при этом пару, момент которой равен моменту данной силы относительно
новой точки приложения
Выполним это для каждой силы
F
YA
a
1
А
z1
1 O
z
9.
Внутренние усилия при изгибеF
YA
А
a
z1
O
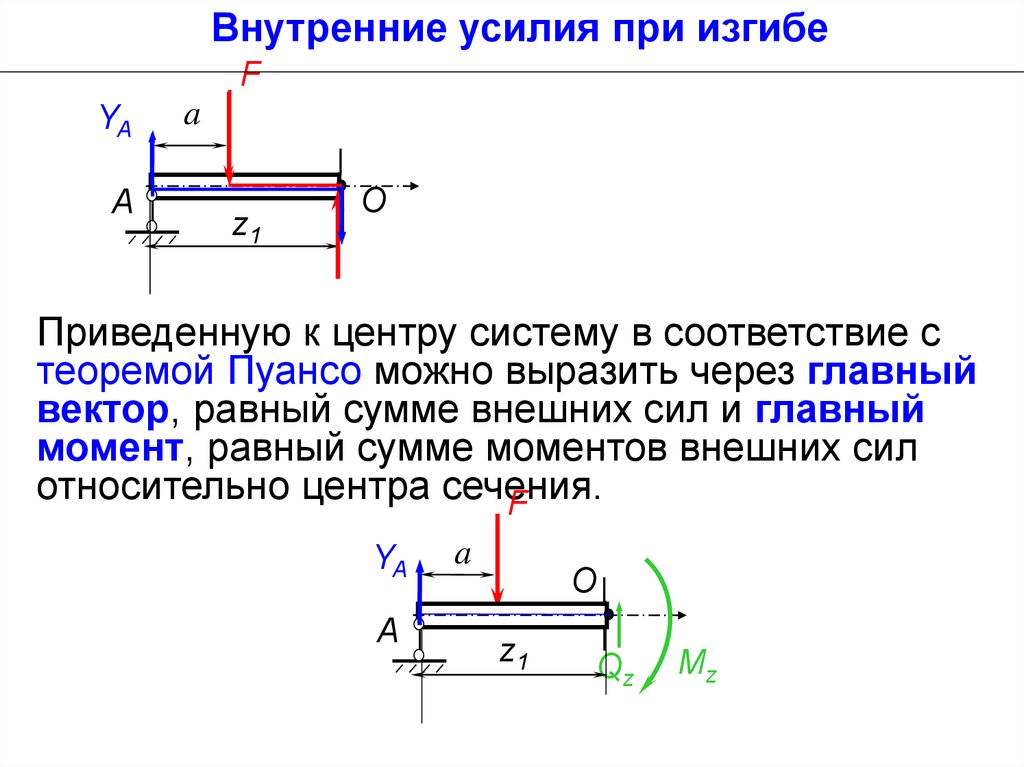
Приведенную к центру систему в соответствие с
теоремой Пуансо можно выразить через главный
вектор, равный сумме внешних сил и главный
момент, равный сумме моментов внешних сил
относительно центра сечения.
F
YA
А
a
O
z1
Qz
Mz
10.
Внутренние усилия при изгибеF
YA a
А
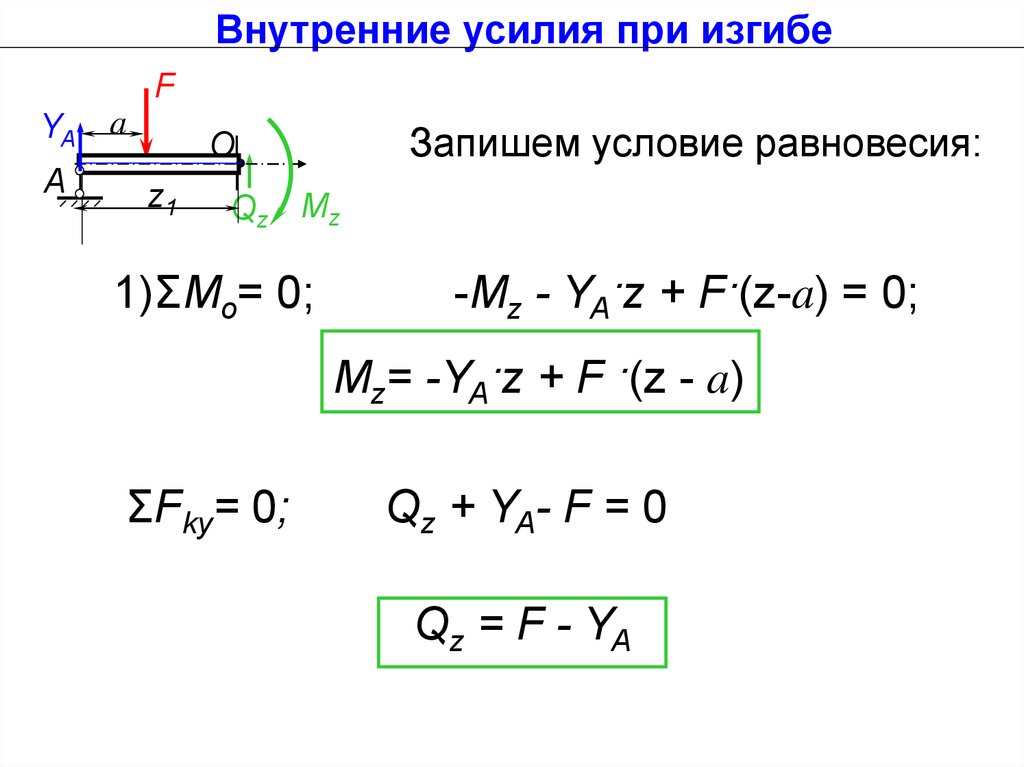
Запишем условие равновесия:
O
z1
Qz M z
1)ΣМо= 0;
-Мz - YA·z + F·(z-a) = 0;
Мz= -YA·z + F ·(z - a)
ΣFky= 0;
Qz + YA- F = 0
Qz = F - YA
11.
Внутренние усилия при изгибеИзгибающий момент Мz в любом сечении равен
алгебраической сумме моментов всех сил, действующих по одну сторону от сечения балки относительно центра тяжести сечения.
Поперечная сила Qz в любом сечении равна алгебраической сумме проекций всех внешних сил,
приложенных с одной стороны от сечения, на ось в
плоскости сечения, перпендикулярную к продольной
оси балки.
12.
Правило знаковy
+ Qz
y
F
z
F
- Qz
F
F
z
Поперечная сила считается положительной, если
она сдвигает левую часть балки от сечения вверх, а
правую - вниз
В противном случае поперечная сила отрицательна.
13.
Правило знаков+ Mz
M
M
- Mz
Изгибающий момент в
сечении считается
M положительным, если
он изгибает балку выпуклостью вниз
M
При изгибе балки выпуклостью вверх изгибающий
момент считается отрицательным.
14.
Порядок построения эпюр1. Балка вычерчивается в выбранном масштабе
с указанием размеров и нагрузок;
2. Определяются реакции с обязательной последующей проверкой;
3. Балка разбивается на отдельные участки со своим законом изменения нагрузки;
4. Для каждого участка записываются уравнения
для определения Qz и Мz;
5. Вычисляют ординаты Qz и Мz по составленным
для участков уравнениям;
6. Строят в принятом масштабе эпюры Qz и Мz,
откладывая вверх от оси балки положительные
значения, вниз - отрицательные.
15.
ИЗГИБy
ΣМ(А)=0; YB·l- q· l
ql
YA
YB
q
B
A
l
2
ΣМ(B)=0; -YAl· +q· l
z
(3)
ΣY= 0;
l
(1)
(2)
l
(1)
2 = 0;
l
(2)
2 = 0;
ql
YB=
2
ql
YA=
2
Проверка
(3) YA+YB - q· l = 0
0=0
16.
ИЗГИБРазбиваем балку на участки
y
1
YA
1
YB
1 q
A
B
z1
1
z1=0; z1= l
Участок один, так как характер
нагрузки не меняется
z
y
l
YA
1
1 q
A
z
z1
ΣY= 0;
-Qz1- qz1+ YA= 0
z12
ΣМ(o)=0; -YA·z1+ q·
+Mz1 = 0;
2
z12
Qz1 = YA- qz1 Mz1 = YA·z1- q
2
17.
ИЗГИБy
1
1
1 q
YB
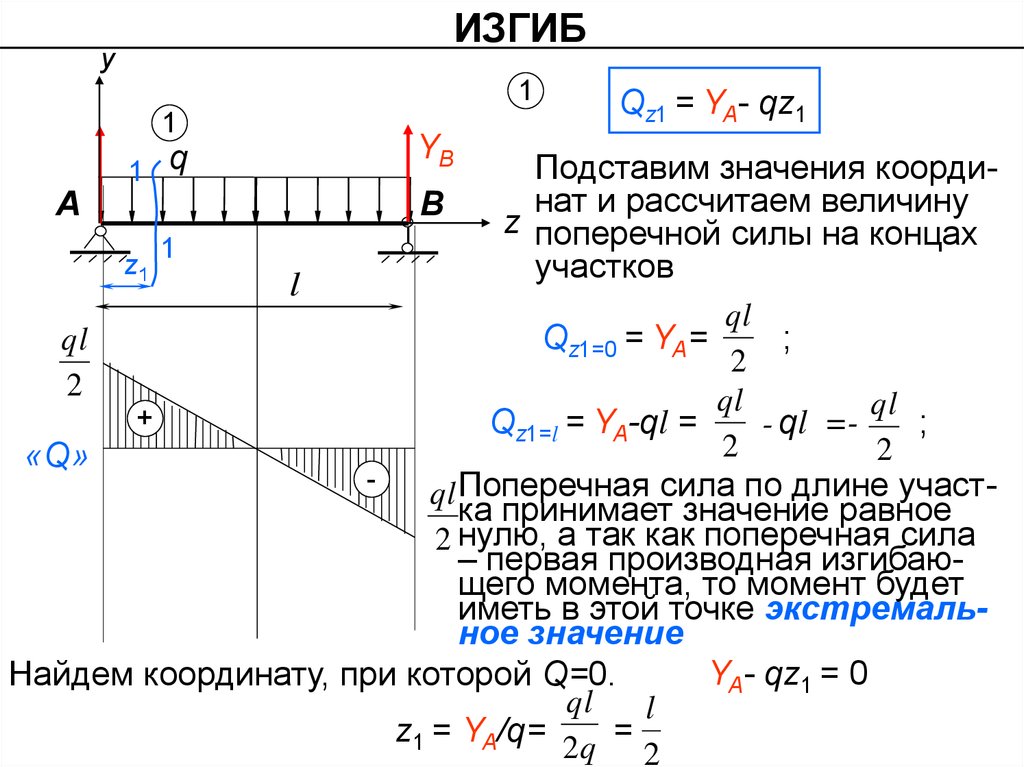
Qz1 = YA- qz1
Подставим значения координат и рассчитаем величину
A
B
z поперечной силы на концах
1
z1
участков
l
ql
Qz1=0 = YA=
;
ql
2
2
ql
ql
+
Qz1=l = YA-ql =
- ql =;
2
2
«Q»
ql Поперечная сила по длине участка принимает значение равное
2 нулю, а так как поперечная сила
– первая производная изгибающего момента, то момент будет
иметь в этой точке экстремальное значение
YA- qz1 = 0
Найдем координату, при которой Q=0.
ql
l
z1 = YA/q= 2q =
2
18.
ИЗГИБy
1
YB
1 q
A
B
z1
1
z
Mz1=0 =0
l2
ql
Mz1=l = ·l- q
=0
2
2
l
ql
2
M
+
«Q»
ql
2
8
«М»
Mz1
+
z12
= YA·z1- q
2
-
ql
2
ql 2
z 1= l
2
ql 2
ql l
=
8
8
22
Так как зависимость момента
от координаты квадратичная,
то линия, ограничивающая
эпюру моментов - парабола
Эпюра построена на сжатом волокне
19.
ИЗГИБy
YA
F
2
1
YB
B
A
l
l
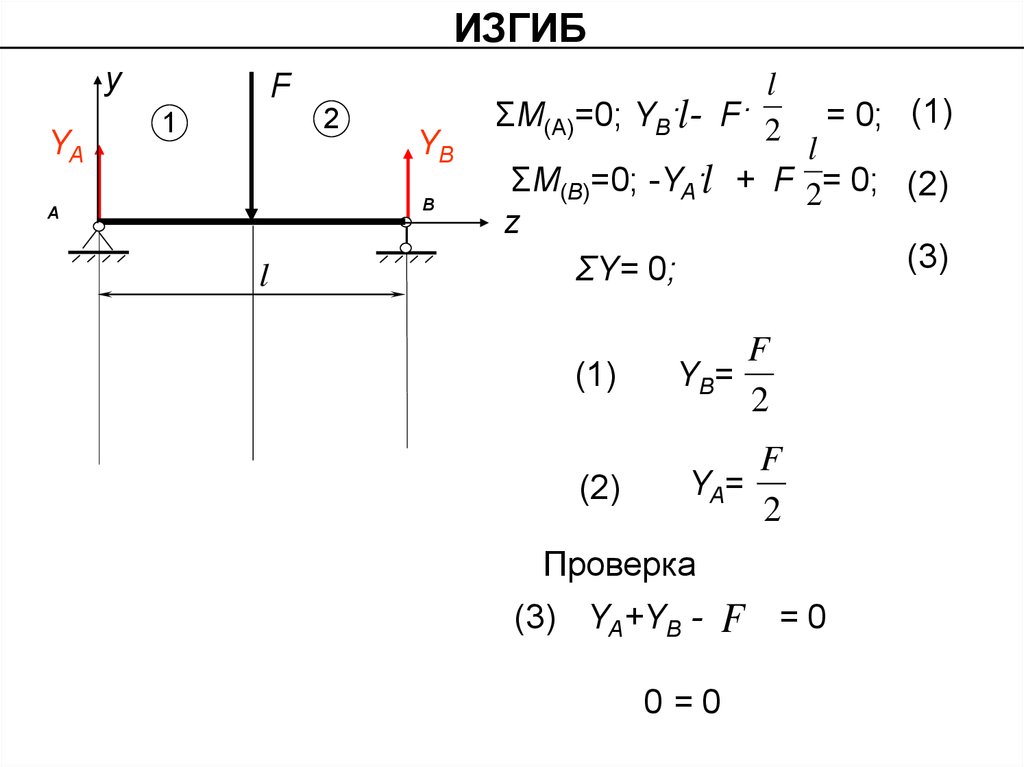
ΣМ(А)=0; YB·l- F· 2
= 0; (1)
l
ΣМ(B)=0; -YA·l + F 2= 0; (2)
z
(3)
ΣY= 0;
(1)
(2)
F
YB=
2
F
YA=
2
Проверка
(3) YA+YB -
F =0
0=0
20.
ИЗГИБYA
2
1
B
l
2
l
«Q»
Fl
4
«М»
YB
y
F
;
2
z YA
M
A
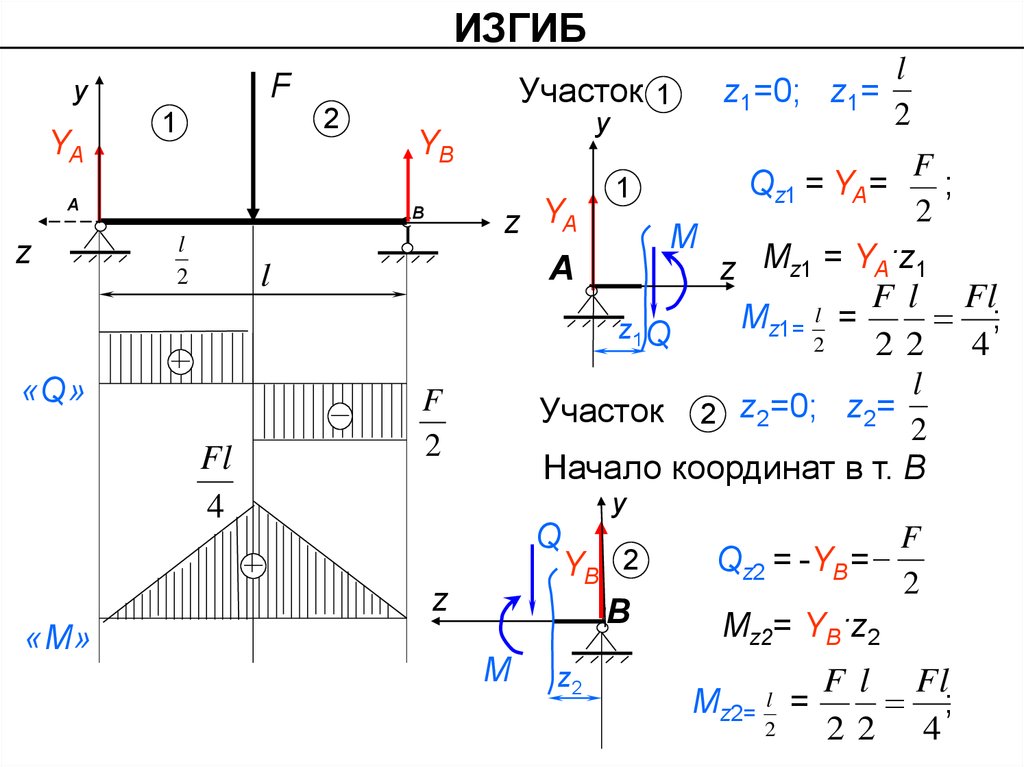
z Mz1 = YA·z1
F l Fl
l =
;
М
z1=
z1 Q
2
22 4
l
Участок 2 z2=0; z2=
2
Qz1 = YA=
1
A
z
l
z1=0; z1=
2
Участок 1
F
y
F
2
Начало координат в т. В
y
Q
z
M
YВ 2
В
z2
Qz2 = -YB=
F
2
Mz2= YB·z2
М
l
z2=
2
F l Fl
;
=
22 4
21.
ИЗГИБy
Определение реакций
F
YA
YB
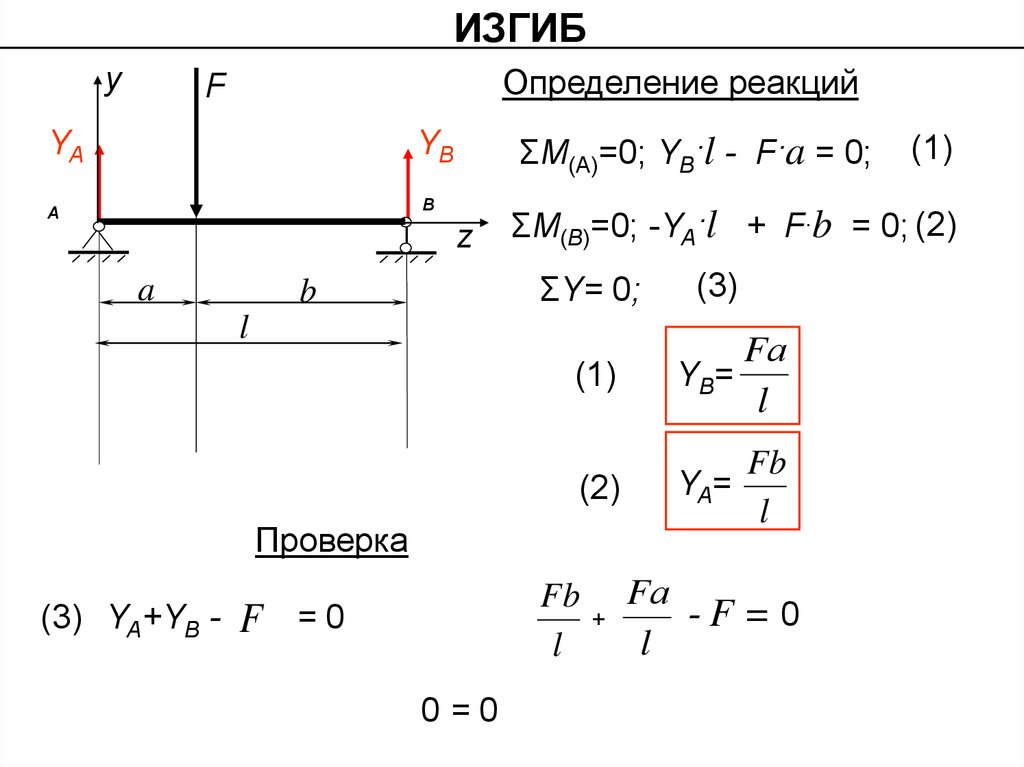
ΣМ(А)=0; YB·l - F·a = 0;
B
A
z
a
ΣМ(B)=0; -YA·l + F·b = 0; (2)
ΣY= 0;
b
l
(1)
(2)
Fb
YA=
l
Fb
l
F =0
0=0
(3)
Fа
YB=
l
Проверка
(3) YA+YB -
(1)
+
Fа
-F=0
l
22.
ИЗГИБy
YA
F
2
1
A
z1
a
l
Fb
l
«Q»
Fab
l
«М»
b
z2
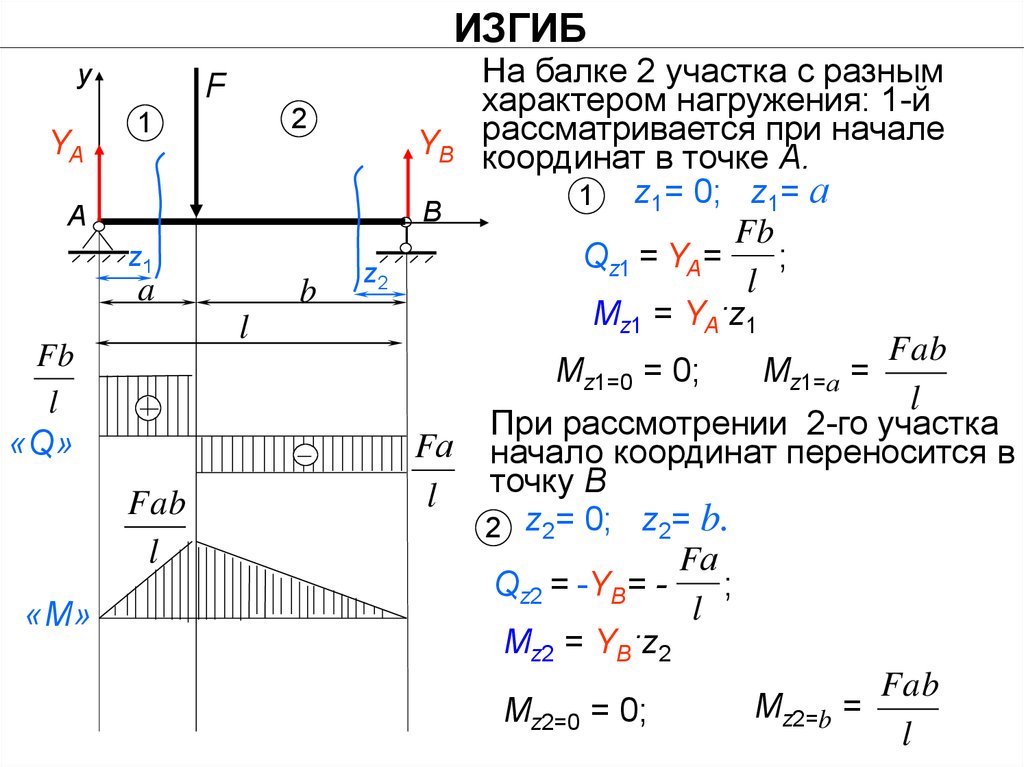
На балке 2 участка с разным
характером нагружения: 1-й
при начале
YB рассматривается
координат в точке А.
1 z1= 0; z1= а
B
Fb
Qz1 = YA=
;
l
Mz1 = YA·z1
Fab
Mz1=0 = 0;
Mz1=а =
l
При рассмотрении 2-го участка
Fа начало координат переносится в
точку В
l
2 z2= 0; z2= b.
Fа
Qz2 = -YВ= ;
l
Mz2 = YВ·z2
Fab
Mz2=b =
Mz2=0 = 0;
l
23.
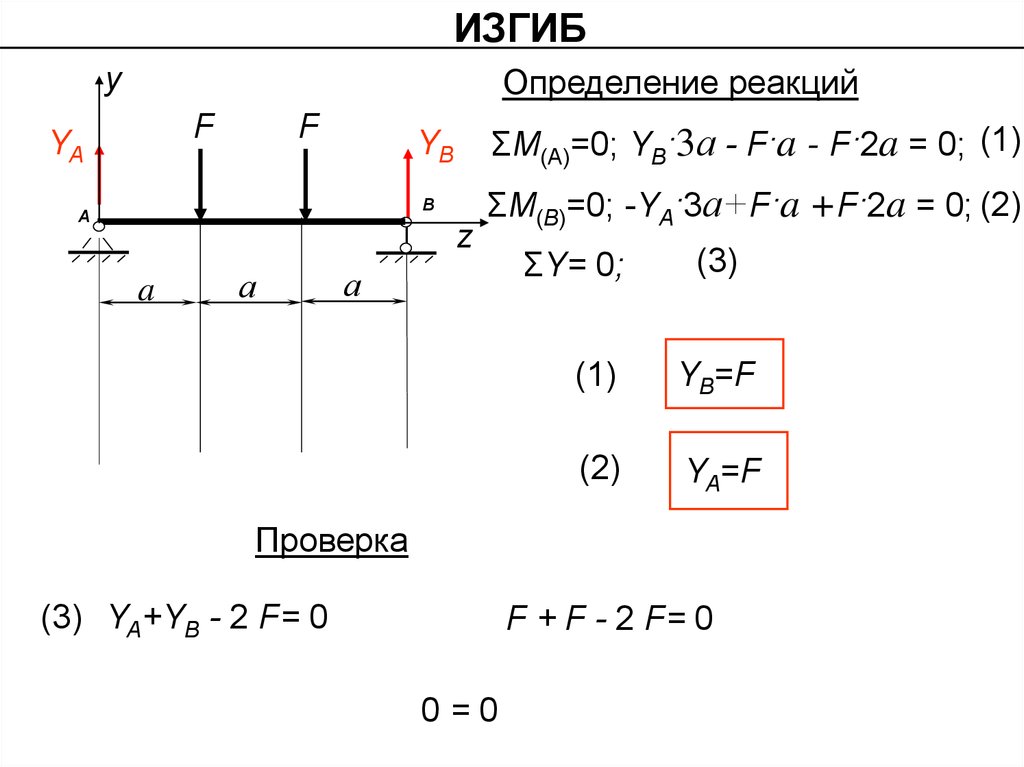
ИЗГИБОпределение реакций
y
F
YA
F
ΣМ(А)=0; YB·3а - F·a - F·2a = 0; (1)
YB
B
A
z
a
а
ΣМ(B)=0; -YА·3а+F·a +F·2a = 0; (2)
а
ΣY= 0;
(3)
(1)
YB=F
(2)
YA=F
Проверка
(3) YA+YB - 2 F= 0
F + F - 2 F= 0
0=0
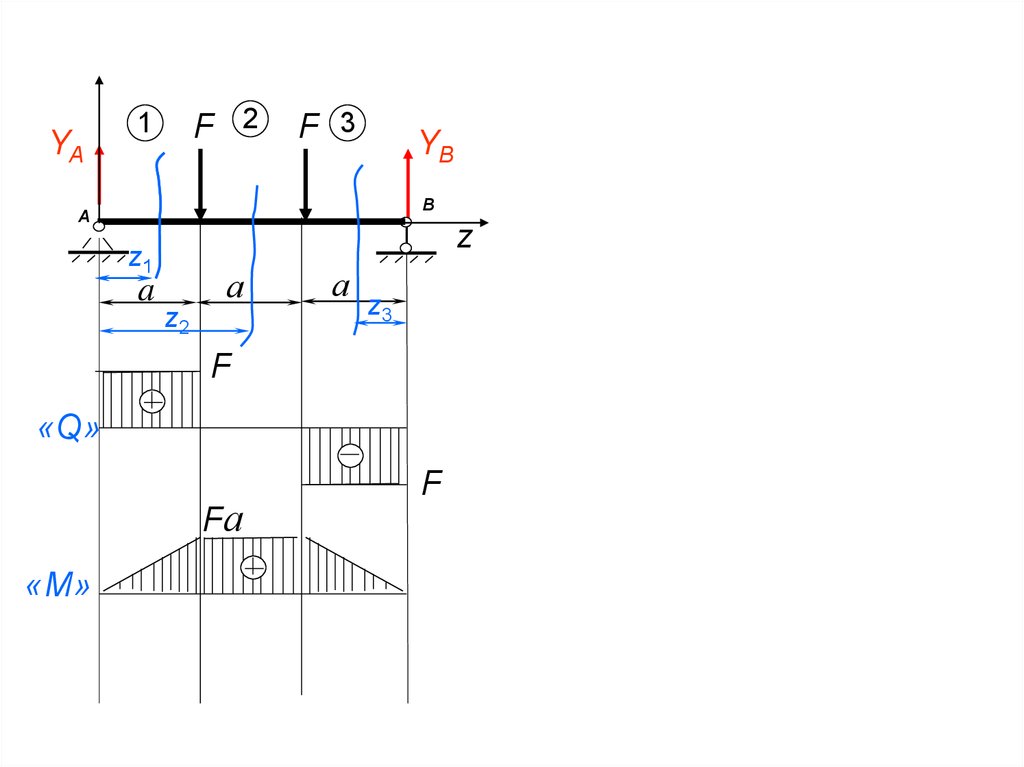
24.
YAF 2
1
F 3
YB
B
A
z
z1
a
а
z2
а
z3
F
«Q»
Fа
«М»
F
25.
FYA
2
1
М
B
A
z1
М
l
«Q»
a
b
l
Ма
l
Мb
l
z2 Y
B
26.
Контрольные правила для построения эпюрпоперечных сил и изгибающих моментов
1. На концевых шарнирных опорах Qz равны реакциям, а Мz равны нулю, если на опорах не приложены пары с моментами М.
2. На участках балки, где отсутствует распределенная нагрузка, поперечная сила постоянна, а изгибающий момент изменяется по линейному закону.
3. На участках, где приложена равномерно распределенная нагрузка, эпюра Qz изменяется по закону
прямой наклонной линии, а эпюра Мz - по закону
квадратичной параболы.
4.В том сечении, где эпюра Qz пересекается с
осевой линией, на эпюре Мz наблюдается
экстремальное значение момента (вершина
параболы)
5. В тех сечениях, где приложены сосредоточенные
силы (включая реакции), на эпюре Qz наблюдаются
скачки (перепады) на величину этих сил, а на эпюре
Мz - переломы смежных линий.
27.
Контрольные правила для построения эпюрпоперечных сил и изгибающих моментов
6. В тех сечениях, где приложены пары с моментами
М, на эпюре Мz наблюдаются скачки на величину
этих моментов.
7. На свободном конце консольной балки поперечная сила Qz равна нулю, если в этом месте не
приложена сосредоточенная сила; и изгибающий
момент Мz равен нулю, если в этом месте не
приложена внешняя пара с моментом М
8. В жесткой заделке консольной балки Qz равна
реакции, а изгибающий момент Мz равен реактивному моменту заделки.
28.
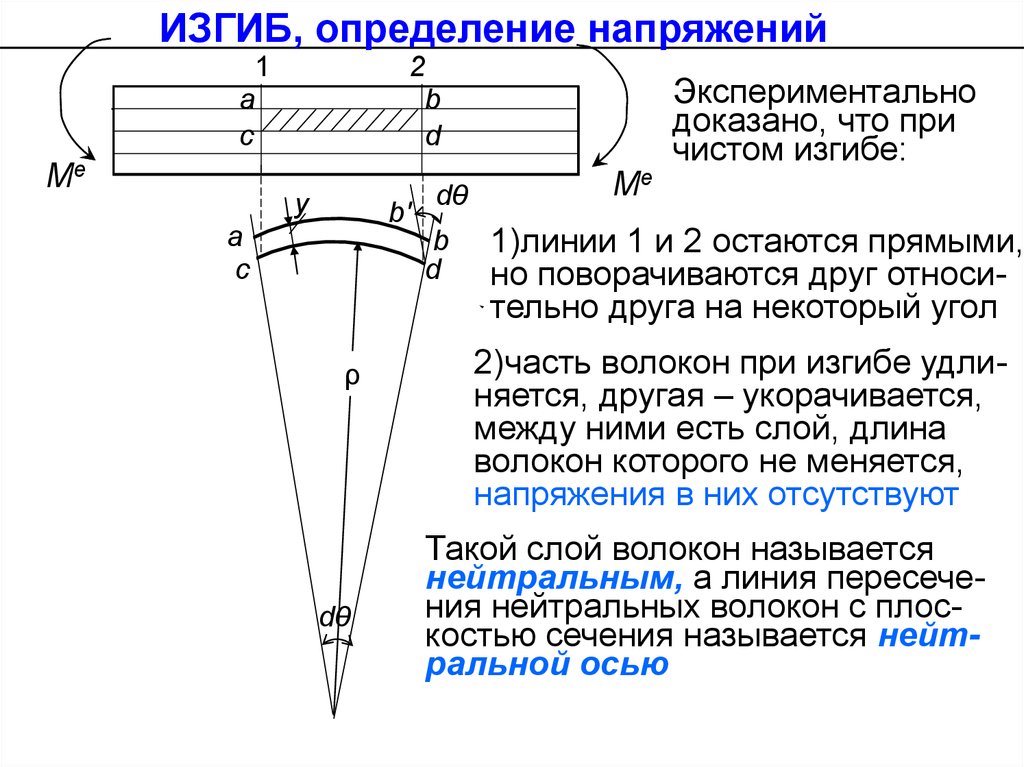
ИЗГИБ, определение напряжений1
2
a
c
Me
Экспериментально
доказано, что при
чистом изгибе:
b
d
y
b'
a
c
dθ
b
d
ρ
dθ
Me
1)линии 1 и 2 остаются прямыми,
но поворачиваются друг относительно друга на некоторый угол
2)часть волокон при изгибе удлиняется, другая – укорачивается,
между ними есть слой, длина
волокон которого не меняется,
напряжения в них отсутствуют
Такой слой волокон называется
нейтральным, а линия пересечения нейтральных волокон с плоскостью сечения называется нейтральной осью
29.
ИЗГИБ, определение напряженийy
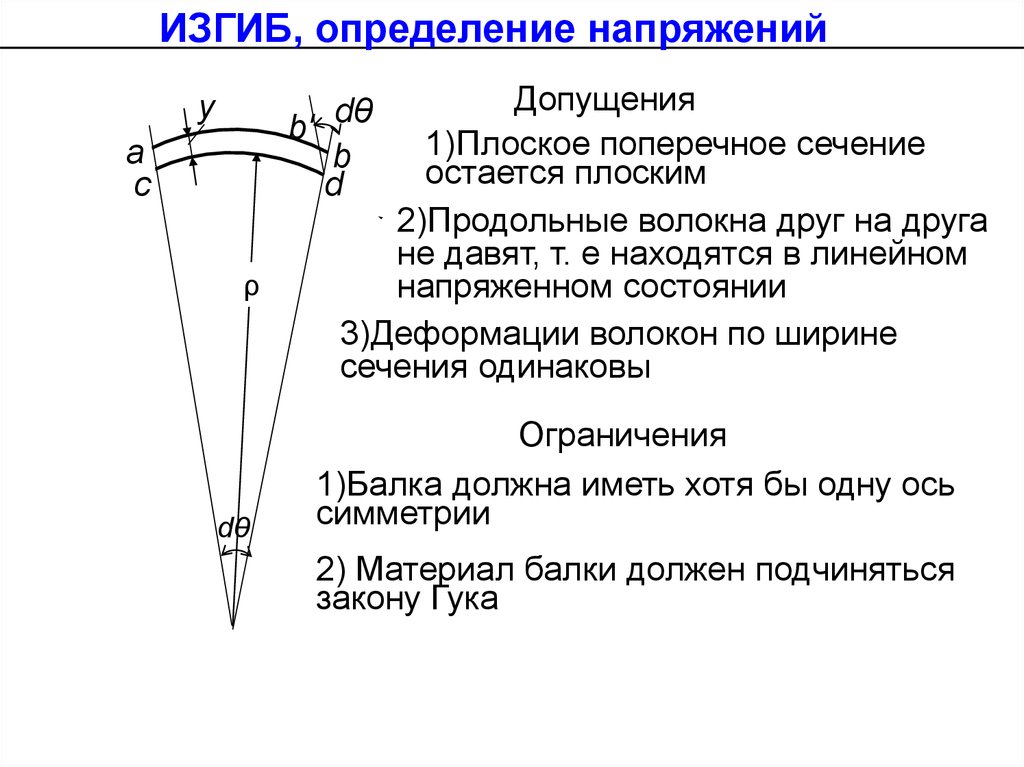
Допущения
1)Плоское поперечное сечение
остается плоским
2)Продольные волокна друг на друга
не давят, т. е находятся в линейном
напряженном состоянии
3)Деформации волокон по ширине
сечения одинаковы
b' dθ
b
d
a
c
ρ
dθ
Ограничения
1)Балка должна иметь хотя бы одну ось
симметрии
2) Материал балки должен подчиняться
закону Гука
30.
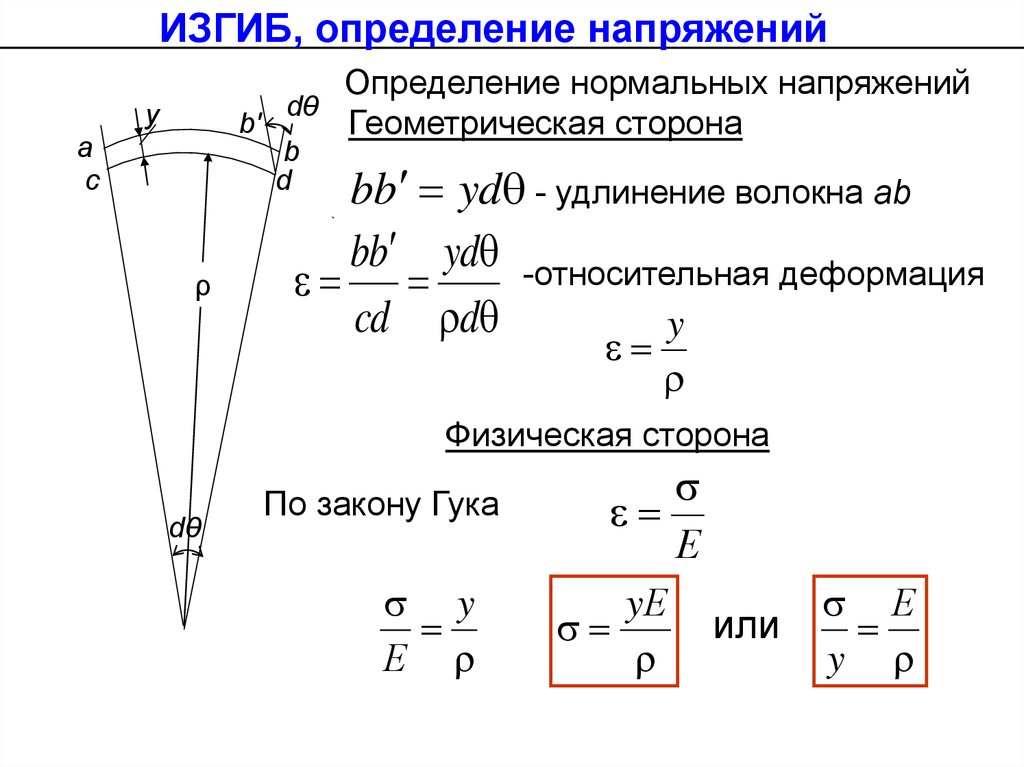
ИЗГИБ, определение напряженийОпределение нормальных напряжений
dθ
b'
Геометрическая сторона
y
a
c
b
d
ρ
bb yd - удлинение волокна ab
bb yd -относительная деформация
cd d
y
Физическая сторона
dθ
По закону Гука
y
Е
Е
yЕ
или
Е
y
31.
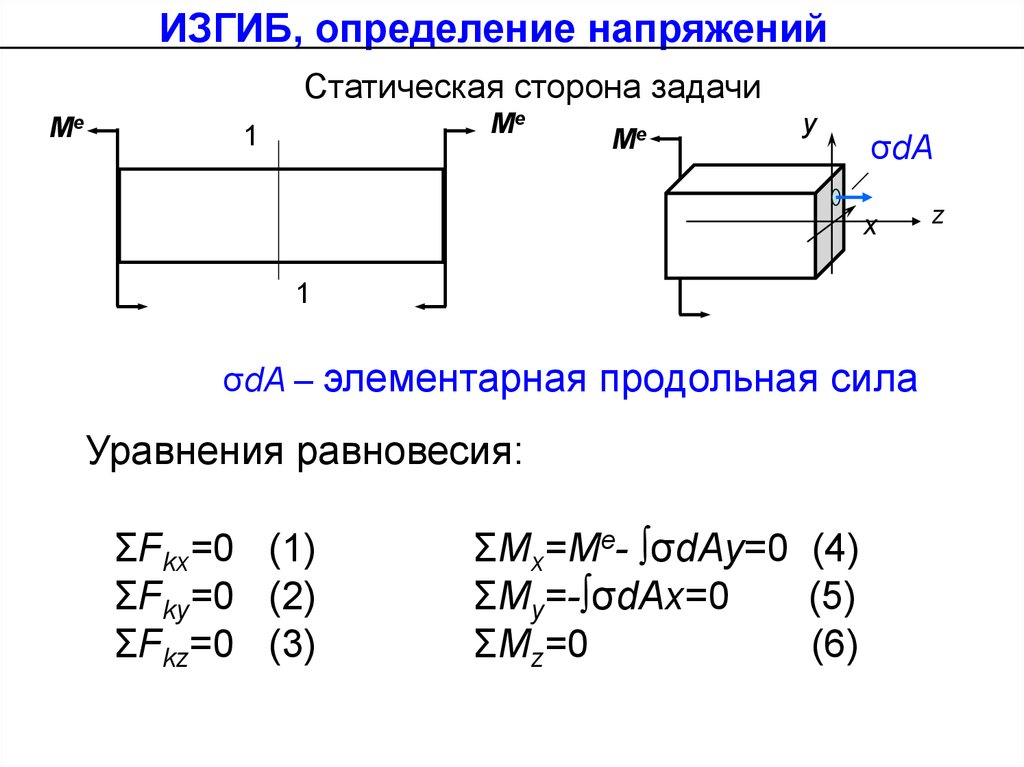
ИЗГИБ, определение напряженийСтатическая сторона задачи
Ме
Ме
1
Ме
y
σdA
x
1
σdA – элементарная продольная сила
Уравнения равновесия:
ΣFkx=0 (1)
ΣFky=0 (2)
ΣFkz=0 (3)
ΣMx=Me- ∫σdAy=0 (4)
ΣMy=-∫σdAx=0
(5)
ΣMz=0
(6)
z
32.
ИЗГИБ, определение напряженийИз (3) ∫σdA=0 , подставляя значение
получаем
Е
уdA 0
А
Е
0;
yЕ
,
уdA 0
А
S x уdA 0
А
Вывод: Статический момент относительно оси х
равен нулю, значит оси сечения являются центральными
33.
Из (5), подставляя значение σ, получаемЕ
уdAх 0
А
Е
0;
хуdA 0
А
I xy xуdA 0
А
Вывод: Центробежный момент инерции равен 0,
значит оси - главные
34.
ИЗГИБ, определение напряженийИз (4), подставляя значение σ, получаем
е
Ix М
y
е
М y
Ix
35.
Определение напряжений при изгибеПосле преобразований получены следующие выводы
1)Нейтральная ось проходит через центр сечения
2)Нейтральная ось является главной осью инерции
и перпендикулярна силовой плоскости
3)Нормальные напряжения определяются по формуле
M
y
Ix
или
max
M
Wx
4)Касательные напряжения определяются по формуле Журавского
I -осевой момент инерции;
отс
QS x
I xb
x
Wx-момент сопротивления;
Sxотс-статический момент отсеченной части;
b-ширина сечения
36.
ИЗГИБ Пример выполнения заданияРасчет балки на прочность
Для расчетной схемы балки необходимо:
1. Построить по длине балки эпюры изгибающих
моментов и поперечных сил.
2.Подобрать поперечное сечение балки
двутаврового профиля, материал Cталь 3
σadm = 160 МПa, τadm = 96 МПа.
37.
ИЗГИБ Пример выполнения задания1. Вычерчиваем балку в масштабе с указанием размеров и нагрузок
YА
YА=51,3кН
YВ=42,7кН
F=50кН
q=10кН/м
М=35кНм
В
А
4,4 м
1,1
1,1м
2.Определяем реакции опор из уравнений равновесия
ΣM(A)=0; M- q·4,4·2,2 - F·4,4 + YВ·6,6 = 0;
YВ =(- M + q·4,4·2,2 + F·4,4)/6,6 = 42,7 кН.
ΣM(В)=0; M + q ·4,4·4,4 + F·2,2 – YА·6,6 = 0;
YА =(M + q ·4,4·4,4 + F·2,2 )/6,6 = 51,3 кН.
Проверка
ΣY =0; YА + YВ - q·4,4 - F =0;
51,3 + 42,7 – 44 – 50 =0 0=0.
38.
ИЗГИБ Пример выполнения заданияу
YА
А
F=50кН
q=10кН/м
Закрыта отброшенная
М=35кНм YВ
часть
Характер нагружения: В
YA4,4имq
1,1м 1,1м
z
3.Определяем
количество
участков и их
границы.
39.
ИЗГИБ Пример выполнения заданияу
YА
F=50кН
q=10кН/м
YВ
М=35кНм
Изменился
1
А
4,4 м
характерz
В
нагружения,
1,1м добавилась
1,1м
сила
1
z1=0; z1=4,4 м;
40.
ИЗГИБ Пример выполнения заданияу
YА
F=50кН 2
q=10кН/м
М=35кНм YВ
1
z
А
В
4,4 м
1,1м
1,1м
1
2
z1=0; z1=4,4 м;
z2=4,4м; z2=5,5м;
41.
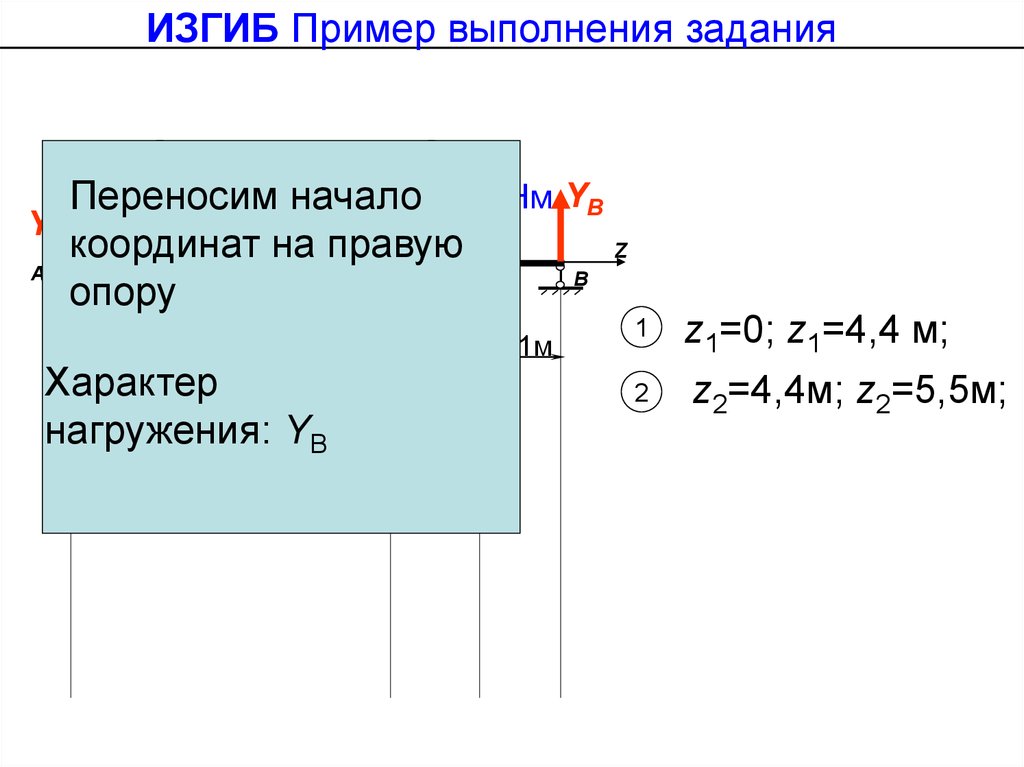
ИЗГИБ Пример выполнения заданияу
YА
А
F=50кН 2
q=10кН/м
Переносим
началоМ=35кНм YВ
1
координат на правую
опору
4,4 м
Характер
нагружения: YB
1,1м
z
В
1,1м
1
2
z1=0; z1=4,4 м;
z2=4,4м; z2=5,5м;
42.
F=50кНq=10кН/м
М=35кНм YВ
1
у
2
YА
А
z1
1
3
z2
2
4,4 м
1,1м
3 z
3
1,1м
z
В
1
2
3
z1=0; z1=4,4 м;
z2=4,4м; z2=5,5м;
z3=0; z3=1,1м;
Проводим сечения в
пределах участков
43.
ИЗГИБ Пример выполнения заданияНачало координат на левой стороне балки для сечений 1-1
и 2-2, для сечения 3-3 - на правой стороне.
Запишем аналитические выражения для Q в каждом
сечении и рассчитаем значения на концах сечений:
q=10кН/м
YА=51,3кН
А
М=35кНм
3
1
z1
F=50кН
1
z2
4,4 м
2
1,1
Qz1= YА - q·z1;
3z
Q
YВ=42,7кН
В
3
1,1м
Qz1=0=51,3 кН;
Qz1=4,4=7,3 кН.
Qz2= YА - q·4,4- F; Qz2=4,4=-42,7 кН. Qz2=5,5=-42,7кН.
Qz3= - YВ;
Qz3=0=-42,7кН;.
Qz3=1,1=-42,7кН.
44.
ИЗГИБ Пример выполнения заданияq=10кН/м
YА=51,3кН
А
М=35кНм
3
1
z1
M
F=50кН
1
z2
4,4 м
2
1,1
3z
YВ=42,7кН
В
3
1,1м
Определяем изгибающие
моменты:
Mz1= YА· z1 - q·z12/2;
Mz1=0=0;
Mz1=4,4=128,92 кНм.
Mz2= YА· z2 - q·4,4·(z2-2,2) –F(z2–4,4);
Mz2=4,4=51,3·4,4 - 10·4,4·2,2-50(4,4-4,4)=128,92 кНм;
Mz2=5,5=51,3·5,5 - 10·4,4·3,3-50(5, 5-4,4)= 81,95 кНм;
Mz3= YВz3
Mz3=0=0;
Mz3=1,1=46,95 кНм.
45.
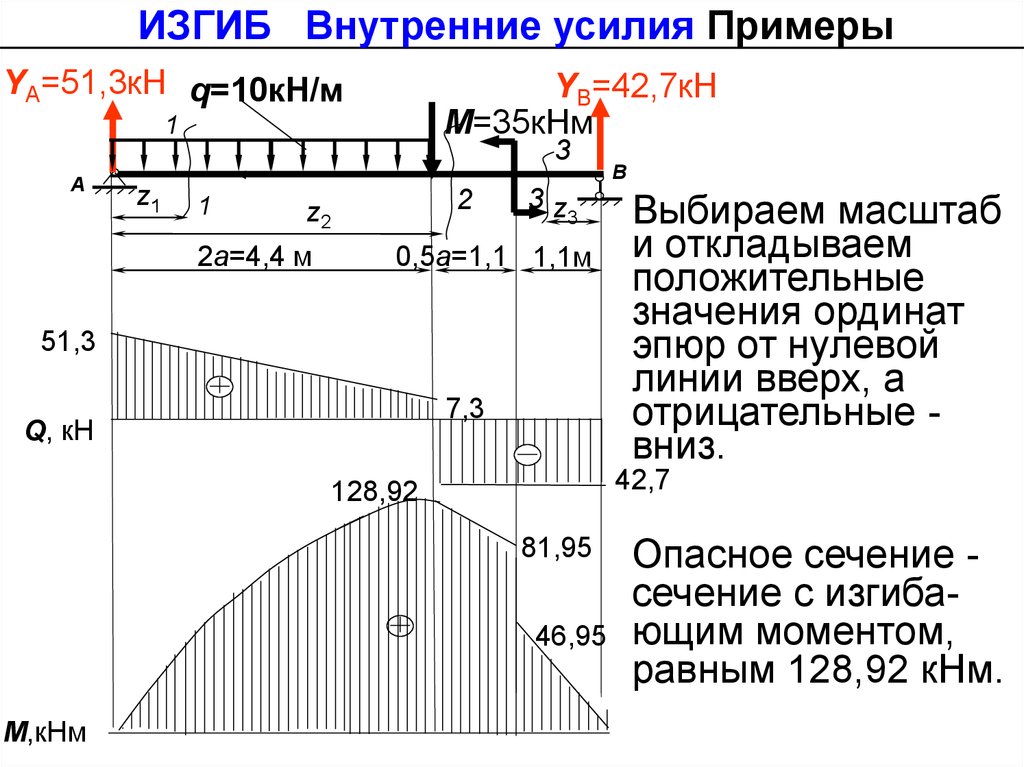
ИЗГИБ Внутренние усилия ПримерыYА=51,3кН q=10кН/м
YВ=42,7кН
М=35кНм
1
3
А
z1
1
2
z2
2а=4,4 м
3z
3
0,5а=1,1 1,1м
51,3
7,3
Q, кН
Выбираем масштаб
и откладываем
положительные
значения ординат
эпюр от нулевой
линии вверх, а
отрицательные вниз.
42,7
128,92
81,95
46,95
М,кНм
В
Опасное сечение сечение с изгибающим моментом,
равным 128,92 кНм.
46.
ИЗГИБ Пример выполнения заданияПодбор сечения двутаврового профиля выполняем
из условия прочности при изгибе
откуда
Mx
adm
Wн.о.
Wн.о.
Mx
adm
где Wн.о. – момент сопротивления относительно
нейтральной оси, которая в сечении балки совпадает
с осью х
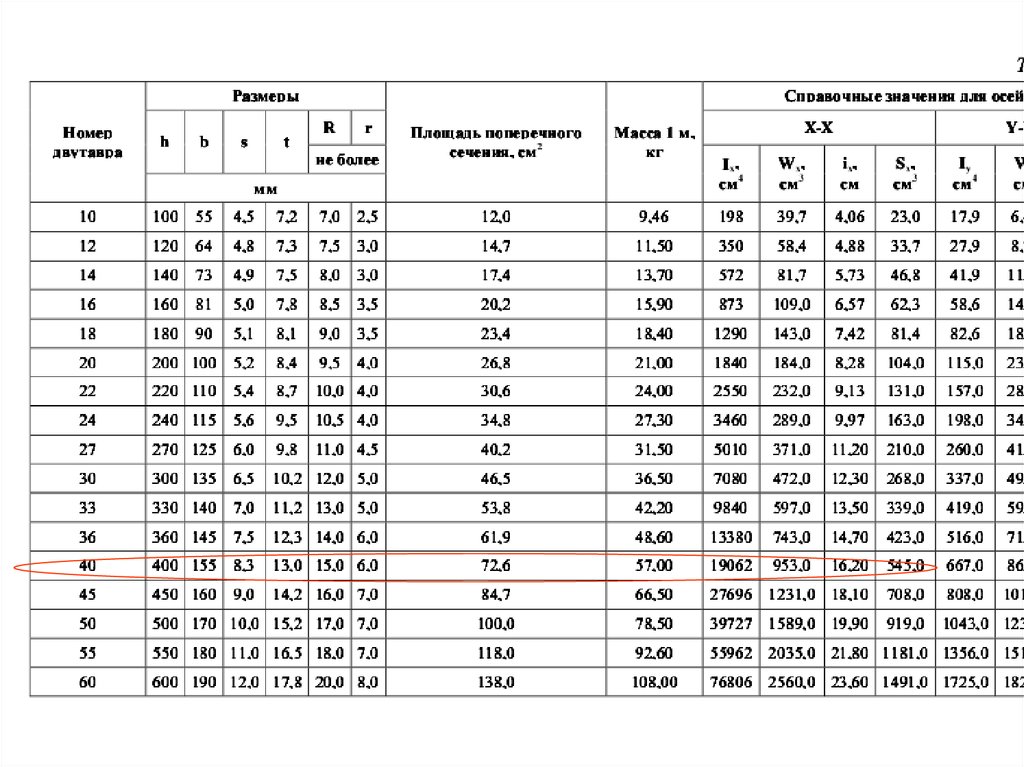
Wн.о.
128 ,92 10 3
8,05 10 4 м3 =805 см3
160
47.
48.
49.
ИЗГИБ Пример выполнения заданияа) Проверка по рабочим нормальным напряжениям:
M x 128 ,92 10 3
135
,
3
МПа
adm
6
Wн.о.
953 10
т. е. условие прочности выполняется.
50.
ИЗГИБ Пример выполнения заданияб) Проверка
напряжениям:
по
максимальным
касательным
отc
Qmax S н.о.
I н.о.b
Sx- статический момент отсеченной (верхней части)
относительно оси х в сечении;
Ix - момент инерции сечения,
b – толщина стенки, для двутавра b=s;
3
51,3 10 545 10
6
19062 10 8 8,3 10 3
17 ,7МПа <96 МПа
условие прочности по касательным напряжениям
также выполняется.
51.
Пример №2 решения задачи на изгибРасчет балки на прочность
Для расчетной схемы балки необходимо:
1. Построить по длине балки эпюры изгибающих моментов и
поперечных сил.
2.Подобрать поперечное сечение балки двутаврового
профиля, материал Cталь 3 при σadm = 160, τadm = 96 МПа.
3. Подобрать прямоугольное поперечное сечение балки,
материал – дерево, σadm = 10 МПa.
YА
М=20кНм
М=20кНм
YВ
q=40кН/м
В
А
1,0 м
1,0 м
1,0 м
z
52.
Пример решения задачи на изгиб1. Вычерчиваем балку в масштабе с указанием
размеров и нагрузок
YА
q=40кН/м
М=20кН
М=20к
YВ
м
Нм
В
А
1,0 м
1,0 м
1,0 м
z
53.
2. Определяем реакции, рассматривая условиеравновесия
ΣM(A)= 0; VВ·3 +M-M-q·1·1,5 = 0
VА
А
М=20кНм
М=20кНм
q=40кН/м
VВ
Rq
VВ = q·1·1,5/3=40·0,5=20кН.
VВ = 20 кН.
В
z
1,0 м
1,0 м
1,0 м
ΣM(В)= 0; -VА·3+M-M+q·1·1,5=0;
VА =20 кН
Балка симметричная, реакции
одинаковы.
Проверка
ΣУ =0; VА + VВ - q·1 = 0;
20 + 20 – 40 = 0;
0 = 0.
54.
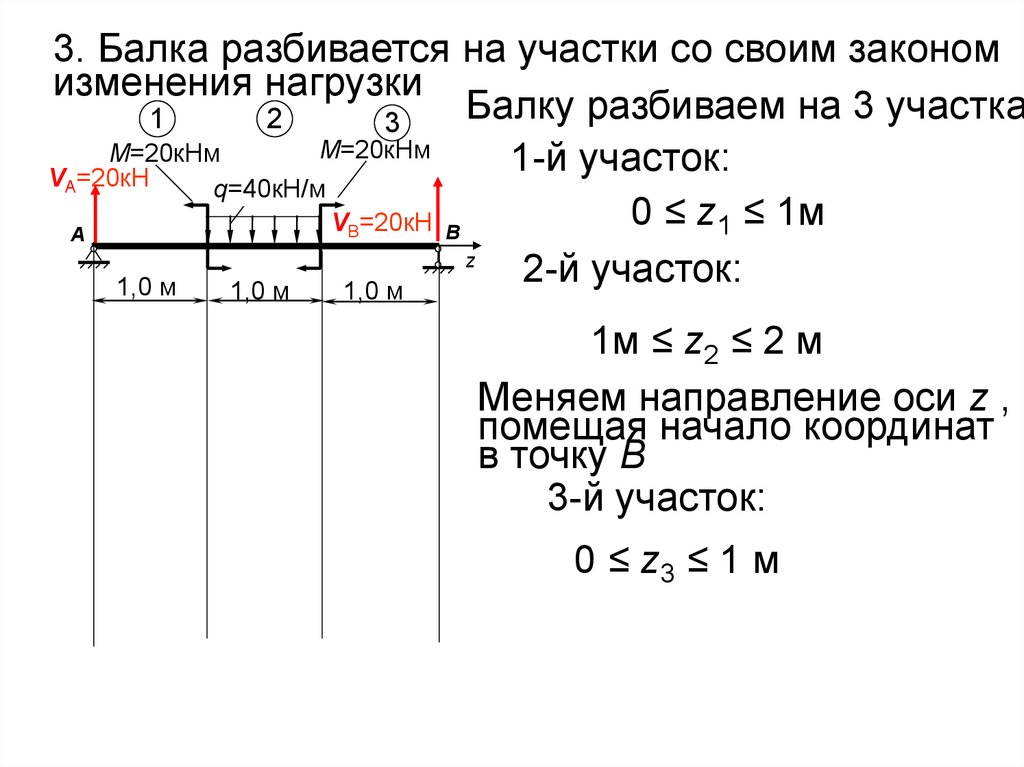
3. Балка разбивается на участки со своим закономизменения нагрузки
Балку разбиваем на 3 участка
1
2
3
М=20кНм
М=20кНм
1-й участок:
VА=20кН
q=40кН/м
0 ≤ z1 ≤ 1м
VВ=20кН В
А
z
2-й участок:
1,0 м
1,0 м
1,0 м
1м ≤ z2 ≤ 2 м
Меняем направление оси z ,
помещая начало координат
в точку В
3-й участок:
0 ≤ z3 ≤ 1 м
55.
4. В пределах каждого участка проводим сеченияЗаписываем уравнения для определения Qz и Мz,
М=20кНм
VА=20кН
q=40кН/м
А
2
1
z1 1
1,0 м
z2
1,0 м
2
М=20кНм
VВ=20кН
3
3 z3
1,0 м
20
Q, кН
При z2=1,5 м, Qz2=0.
учитывая правило знаков
M
Q
В
z
Аналитические выражения
для Q в каждом сечении и
значения для сечений на
концах участков :
Qz1= VА ;
Qz1=1=20 кН.
20 Qz1=0=20 кН;
Qz2= VА – q(z2-1);
Qz2=1=20 кН. Qz2=2= -20 кН.
Qz3= - VВ;
Qz3=0=-20 кН; Qz3=1=-20 кН.
Строим эпюру поперечных сил Q
56.
MVА=20кН
М=20кНм
q=40кН/м
2
А
М=20кНм
3
1
z1 1
z2
3
1,0 м 1,0 м
2
1,0 м
z3
VВ=20кН
В
Аналитические выражения
zдля М в каждом сечении и
значения для сечений на
концах участков :
20
Mz1= VА· z1;
Mz1=0=0; Mz1=1=20 кНм.
20
2/2);
20
20
M
=
V
·
z
q(z
-1)
z2
А
2
2
5,0
Mz2=1=20 кНм; Mz2=1,5=5 кНм;
М,кНм
Mz2=2=20 кНм;
Mz3= VВz3;
Mz3=0=0; Mz3=1=20 кНм.
Строим эпюру изгибающих моментов Mz
Q, кН
Опасные сечения - сечения с изгибающим моментом,
равным 20 кНм.
57.
Подбор сеченияПодбор сечения выполняем из условия прочности
при изгибе
откуда
где Wн.о. – момент сопротивления относительно
нейтральной оси, которая в сечении балки совпадает с осью х
м3= 125 см3.
58.
59.
Подбор сечения1) Двутавровый профиль, материал Сталь 3
Ближайшее к полученному значению момента
сопротивления соответствует двутавру № 18,
для которого Wн.о. = 143 см3 .
60.
Подбор сеченияПроверка по рабочим напряжениям:
а) нормальные напряжения
т. е. условие прочности выполняется.
б) максимальные касательные напряжения
где Sx- статический момент верхней части
относительно оси х;
Ix - момент инерции сечения;
b=s– толщина стенки
<96 МПа
61.
1) Прямоугольное сечение, материал дерево- момент сопротивления для прямоугольника относительно оси х
Учитывая заданное условие, имеем
h=2b
b
b x h = 144 x 288 мм2
Деревянное сечение по расходу материала весьма
не экономично.
62.
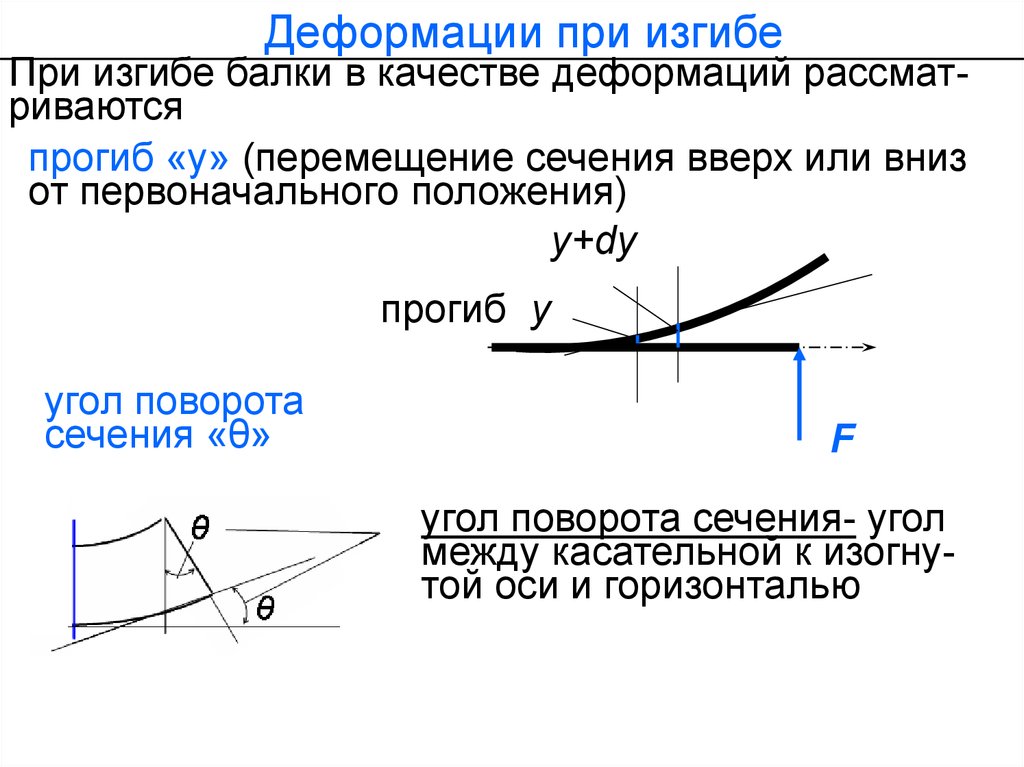
Деформации при изгибеПри изгибе балки в качестве деформаций рассматриваются
прогиб «у» (перемещение сечения вверх или вниз
от первоначального положения)
у+dy
прогиб у
угол поворота
сечения «θ»
F
угол поворота сечения- угол
между касательной к изогнутой оси и горизонталью
63.
Деформации при изгибеИз математики известно уравнение для определения кривизны линии
1
y
k
(1 ( y ) 2 )3/2
В области малых перемещений величиной
можно пренебречь и тогда
1
y
Еy
имеем
и, учитывая
EI x y M
2
(y )
M
y
Ix
уравнение изогнутой оси балки
64.
Деформации при изгибеили в виде
M
y
EI x
Интегрируя уравнение первый раз получают угол
поворота сечения, второй раз – прогиб
Но при интегрировании необходимо определять
постоянные интегрирования из граничных условий,
которыми являются условия закрепления балки
65.
Деформации при изгибеИз этих формул сформулированы различные методы определения деформаций
Для балок постоянной жесткости наиболее часто
используется метод начальных параметров, в
которых в качестве постоянных интегрирования
используется угол поворота в начале координат 0,
и прогиб в начале координат у0
При этом необходимо выполнять некоторые
приемы
66.
Деформации при изгибе1. Принимается единое начало координат, помещают его на левом конце балки
Растояния до точек
у
YB приложения момента,
F
силы и начала нагрузYA
q
b
М ки обозначаются соответственно: a, b, с.
B z
А
c
a
Если нагрузка заканчивается не доходя до рассматриваемого сечения, ее продлевают до сечения
На участке продления добавляют нагрузку противоположного знака
67.
Деформации при изгибеУниверсальные уравнения для определения
углов поворота
М( z а )
F( z b )
q( z с )
EIхθ= EI х 0
1!
2!
3!
2
прогибов
3
М ( z а )2
F ( z b )3
q( z с )4
EIхy= EI х y0 EI х 0 z
2!
3!
4!
,
где θ - угол поворота в исследуемом сечении;
у - прогиб в исследуемом сечении;
у0 - прогиб в начале координат;
θ0- угол поворота в начале кoоpдинат;
z- расстояние от начала координат до сечения,
где определяем перемещение;
68.
Пример определения деформаций при изгибеОпределим прогибы в
VА=20кН q=40кН/м
VВ=20кН точке С, где приложен
момент и в точке D
М
М=20кНм
посредине пролета.
C
В
А
Начало координат в
D
точке А
z
1,0 м 1,0 м 1,0 м
В точке А – опора,
поэтому
yА=y0=0
Но угол поворота на опоре не равен 0, поэтому,
чтобы определить θ0, используем второе условие
закрепления.
yВ=0.
69.
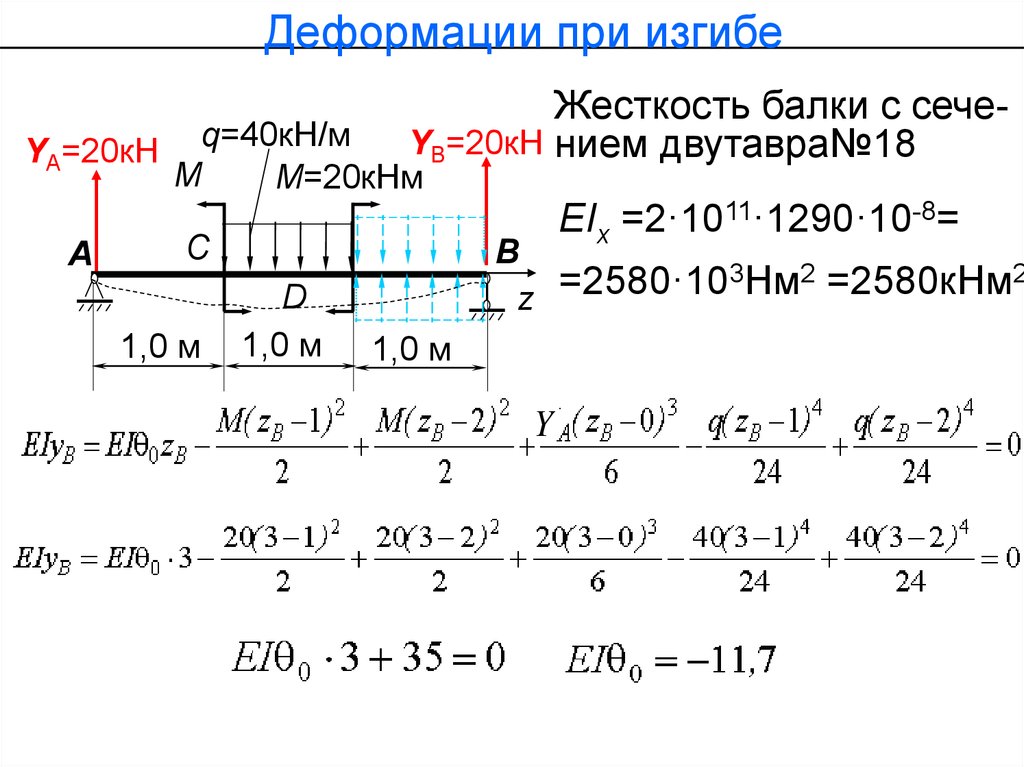
Деформации при изгибеYА=20кН
А
Жесткость балки с сечеYВ=20кН нием двутавра№18
q=40кН/м
М
М=20кНм
EIх =2·1011·1290·10-8=
В
3Нм2 =2580кНм2
=2580·10
z
C
1,0 м
D
1,0 м
1,0 м
Y
70.
Деформации при изгибеЕI y ЕI z
x C
x 0 C
YA (z C 0)3
6
zС =1м; EIyС=
м=-3 мм
ЕI y ЕI z
x D
x 0 D
Y A (z D 0)3
6
M (z D 1) 2
2
zD=1,5м
8,9
yD
0,0034 м =-3,4 мм
2580
q(z D 1) 4
24
71.
Деформации при изгибе18,26
уС
0,007м
2580
уС 0,7см


















































 Физика
Физика








