Технология компрессии изображений «Smart Compression of Images»

1.

Технология компрессии
изображений
«Smart Compression of Images»

2.

CONTENTS
•Objectives
• Smart Compression of Images Procedure
•Example 1. Lossy Compression Mode
•Third Step – the Core of General Algorithm
•Segments Comparison
•Example 2: Segments Comparison
•Minimal Basic Subset of Segments Selection
•Example 3: Minimal Basic Subset of Segments
Selection
•Smart Compression of Colored Images
•Main Features of Smart Compression
•Experiment 1: Smart Compression and JPG Comparison
•Experiment 2: probability of optimality for different
segment sizes as a function of size of an image
2

3.

Цели:
1. Высокая степень компрессии.
2. Возможность выбора режима компрессии:
• Компрессия без потерь качества изображения;
• Компрессия с контролируемой потерей
качества.
3. Гибкая адаптация к типу сжимаемого
изображения.
3

4.

Алгоритм «Smart Compression of Images»
Основной алгоритм компрессии вариабельными фрагментами
1. Выбор размеров квадратного фрагмента, на которые делится
изображение, не анализировавшегося ранее. Если таковых нет – переход
к шагу 7
2. Декомпозиция изображения на фрагменты.
3. Выделение минимального подмножества фрагментов, позволяющих
восстановить исходное изображение с заданным уровнем искажений с
помощью функций преобразования фрагментов.
4. Вычисление коэффициента компрессии “ ”. Если он больше
хранящегося в памяти, то переход к шагу 5, в противном случае – к шагу 6.
5. Прежнее значение коэффициента компрессии и соответствующий размер
фрагмента забываются, а новые – запоминаются.
6. Выбранный на шаге 1 последней итерации фрагмент считаем
анализировавшимся. Переход к шагу 1.
7.
Конец алгоритма.
4

5.

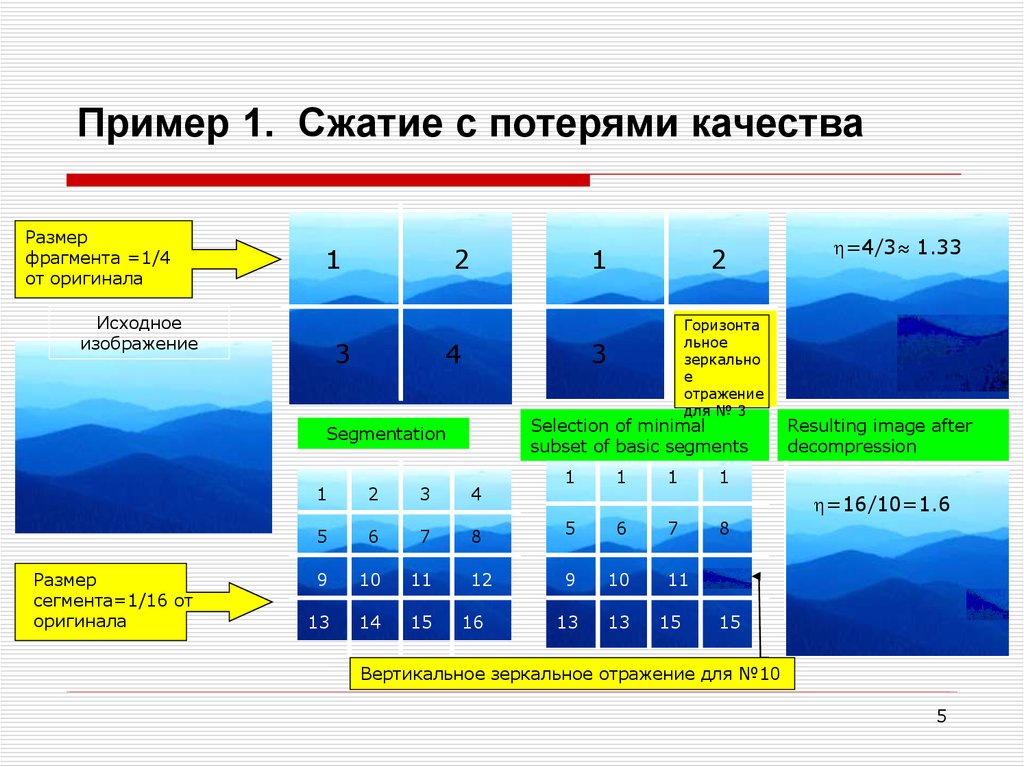
Пример 1. Сжатие с потерями качества
Размер
фрагмента =1/4
от оригинала
1
Исходное
изображение
2
3
1
4
Горизонта
льное
зеркально
е
отражение
для № 3
3
Selection of minimal
subset of basic segments
Segmentation
Размер
сегмента=1/16 от
оригинала
2
1
1
1
2
3
4
5
6
7
8
5
6
9
10
11
12
9
10
13
14
15
13
13
16
1
=4/3≈ 1.33
Resulting image after
decompression
1
=16/10=1.6
7
8
11
15
15
Вертикальное зеркальное отражение для №10
5

6. Пример2: Функции сравнения фрагментов

Сравниваются нижеприведенные фрагменты:
Исходные положения первого (Рис. 1a)
и второго (Рис. 1b) фрагментов.
a)
b)
Результат поворота второго фрагмента
на Х градусов, причем Х =:
Рис. 1
• 0 (Рис. 2a),
• ½π (Рис. 2b),
a)
b)
c)
d)
Рис. 2.
a)
b)
c)
Figure 3.
d)
• π (Рис. 2с),
• 1.5 π (Рис. 2d).
Зеркальные отражения второго
фрагмента(Рис. 3a) в сочетании с
приведенными выше углами
поворота. Сравнение Рис. 1a и Рис.
3c говорит о возможности
преобразовать второй фрагмент в
первый.
6

7.

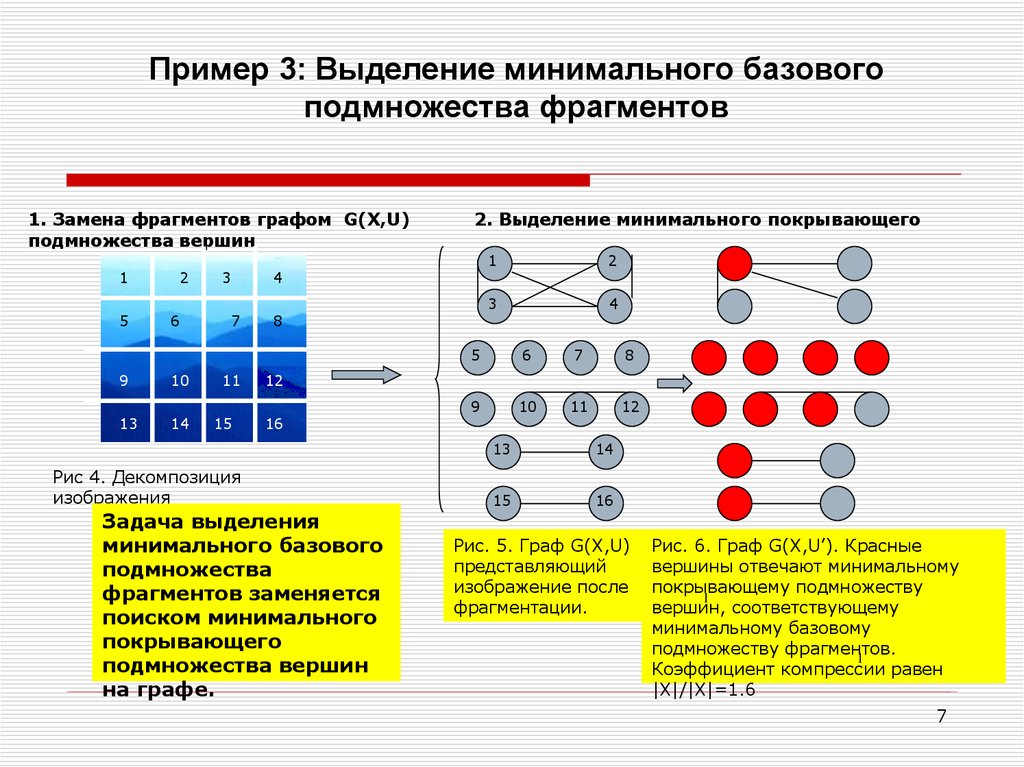
Пример 3: Выделение минимального базового
подмножества фрагментов
1. Замена фрагментов графом G(X,U)
подмножества вершин
1
5
2
6
9
10
13
14
3
7
11
15
2. Выделение минимального покрывающего
4
8
1
2
1
3
4
5
6
7
8
9
10
11
12
12
16
Рис 4. Декомпозиция
изображения
Задача выделения
минимального базового
подмножества
фрагментов заменяется
поиском минимального
покрывающего
подмножества вершин
на графе.
13
14
15
16
Рис. 5. Граф G(X,U)
представляющий
изображение после
фрагментации.
Рис. 6. Граф G(X,U’). Красные
вершины отвечают минимальному
покрывающему подмножеству
1
вершин, соответствующему
минимальному базовому
подмножеству фрагментов.
1
Коэффициент компрессии равен
|X|/|X|=1.6
7

8.

Компрессия цветных изображений
Smart Compression использует разложение на три цвета, каждый из которых
имеет градации яркости 0 – 256 each (Рис. 7).
Рис. 7.
Одним из способов использования вышеописанной технологии является
компрессия каждой монохромной картинки отдельно..
8

9.

Аналитические закономерности компрессии
статичных изображений вариабельными
фрагментами
Теорема 1. Оптимальное число квадратных фрагментов N,
разбиение на которое позволяет получить максимальный
коэффициент компрессии, в первом приближении равно:
Q
Nopt k
,
D
где: Q – размер оригинального изображения;
D – объем информации о каждом фрагменте,
хранимый в
памяти и достаточный для его восстановления;
k - коэффициент пропорциональности.
9

10.

Минимизация времени компрессии в однородных
вычислительных средах
Теорема 2.
Оптимальное число используемых однородных процессоров,
минимизирующее время сравнения фрагментов изображения,
равно:
m1,opt max 1; min P; 3g ,
Теорема 3.
Оптимальное число используемых однородных процессоров,
минимизирующее время выделения минимального базового
подмножества фрагментов изображения, равно:
m2 ,opt max 1; min P; k g
где: Р – число процессоров однородной
вычислительной среды; k - коэффициент
пропорциональности; g – пропускная способность
канала связи (Кб/сек)
10

11.

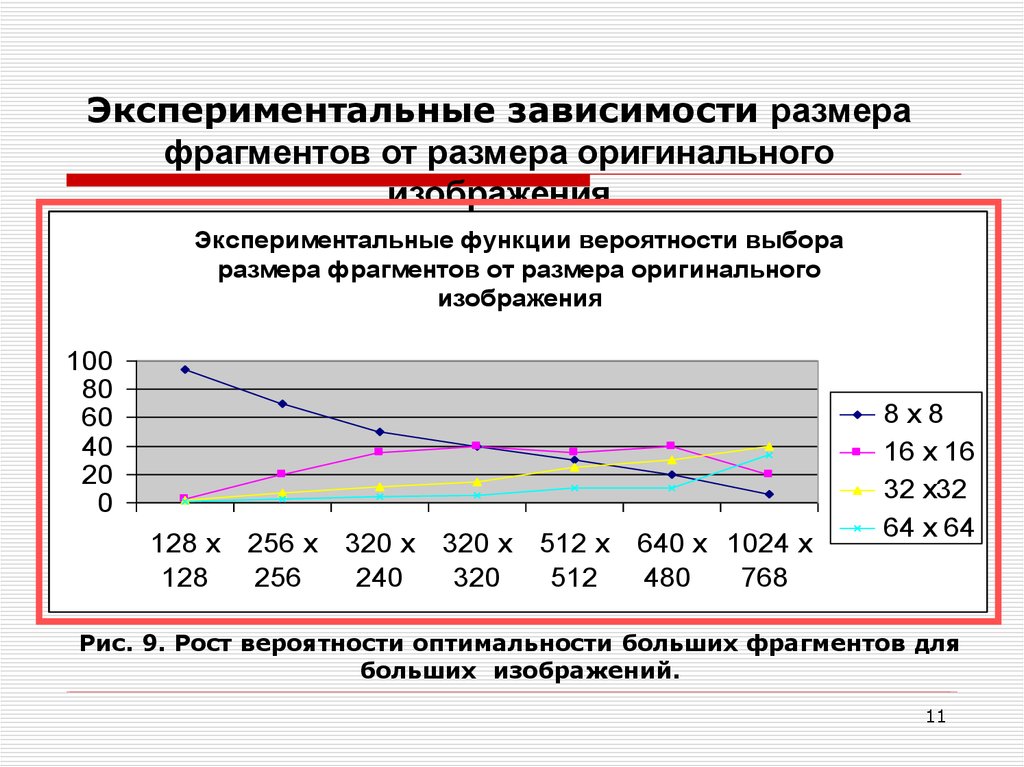
Экспериментальные зависимости размера
фрагментов от размера оригинального
изображения
Экспериментальные функции вероятности выбора
размера фрагментов от размера оригинального
изображения
100
80
60
40
20
0
128 x
128
256 x
256
320 x
240
320 x
320
512 x
512
640 x 1024 x
480
768
8x8
16 x 16
32 x32
64 x 64
Рис. 9. Рост вероятности оптимальности больших фрагментов для
больших изображений.
11