Похожие презентации:
Поиск решения задачи коммивояжера на взвешенных ориентированных сильносвязных графах методами типа ветвей и границ
1.
Лекция 14Поиск решения задачи
коммивояжера на
взвешенных
ориентированных
сильносвязных графах
методами типа ветвей и
границ
2. СОДЕРЖАНИЕ
1.Постановки задач коммивояжера.
2. Решение замкнутой задачи
коммивояжера методами типа
ветвей и границ.
3. Решение разомкнутой задачи
коммивояжера методами типа
ветвей и границ.
3. Часть 1
ЧАСТЬ 1Постановки задач
коммивояжера
4. Содержательные постановки «классических» задач коммивояжера
СОДЕРЖАТЕЛЬНЫЕ ПОСТАНОВКИ«КЛАССИЧЕСКИХ» ЗАДАЧ КОММИВОЯЖЕРА
1. Разомкнутая постановка задачи: коммивояжер
должен объехать все n городов, побывав в
каждом по одному разу, и затратив: - минимум
средств на путешествие либо
- минимум средств на максимальный переход.
2. Замкнутая постановка задачи: коммивояжер
должен объехать все n городов, побывав в
каждом по одному разу и вернуться в город из
которого стартовал, затратив:
-минимум средств на путешествие (аддитивная
задача коммивояжера)
- минимум средств на максимальный переход
(минимаксная задача коммивояжера).
4
5. Графовая интерпретация замкнутой задачи коммивояжера
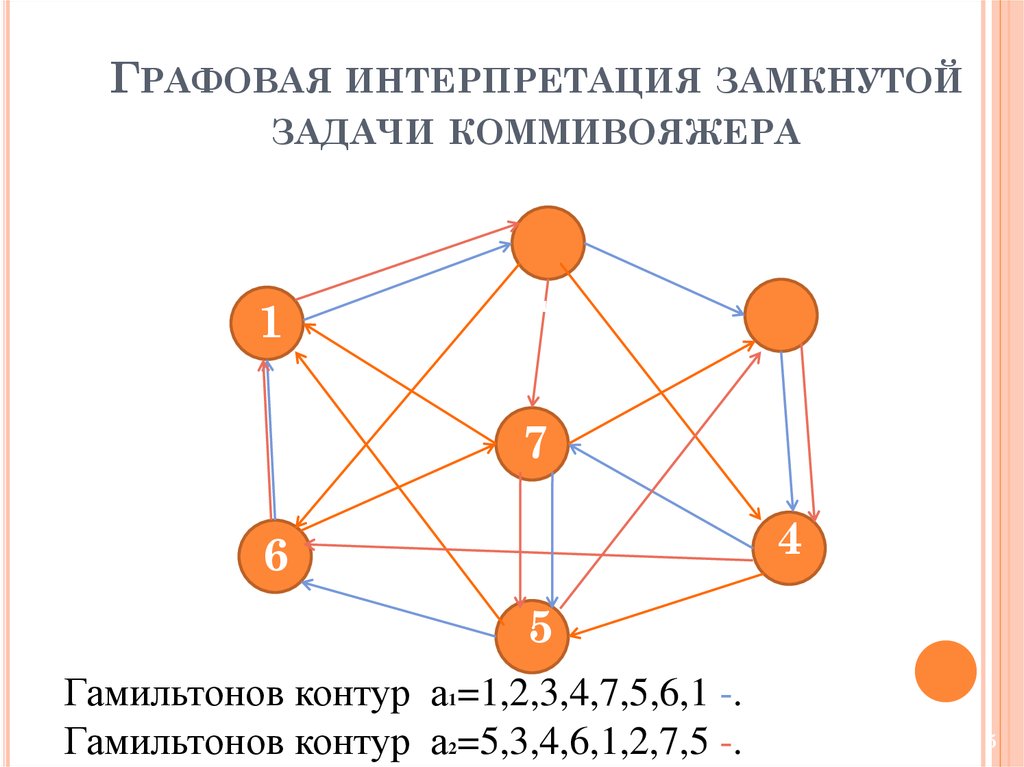
ГРАФОВАЯ ИНТЕРПРЕТАЦИЯ ЗАМКНУТОЙЗАДАЧИ КОММИВОЯЖЕРА
1
2
3
7
4
6
5
Гамильтонов контур а1=1,2,3,4,7,5,6,1 -.
Гамильтонов контур а2=5,3,4,6,1,2,7,5 -.
5
6. Обозначения и определения
ОБОЗНАЧЕНИЯ И ОПРЕДЕЛЕНИЯG ( X , U ) взвешенный орграф;
Х - множество вершин;
U - множество дуг;
A(G) - множество контуров графа;
a k k й контур множества A(G);
X(a k ) множество вершин k - го контура;
U(a k ) множество дуг k - го контура;
z(i, j) - булева переменная.
6
7. Формальная постановка аддитивной замкнутой задачи коммивояжера
ФОРМАЛЬНАЯ ПОСТАНОВКА АДДИТИВНОЙЗАМКНУТОЙ ЗАДАЧИ КОММИВОЯЖЕРА
min;
min;
rr((ii,, jj))zz((ii,, jj))
ii jj
a
A
(
G
)
:
X
(
a
)
X
z
(
i
,
j
)
0
;
a
A
(
G
)
:
X
(
a
)
X
z
(
i
,
j
)
0
;
k
k
k
k
U
U((aakk ))
((ii,, jj))
xxjj
X
X :: zz((ii,, jj)) 11;;
ii
xxqq
X
X :: zz((qq,,ii)) 11;;
ii
((ii,, jj))
U
U :: zz((ii,, jj)) 11,,00..
7
8. Формальная постановка аддитивной разомкнутой задачи коммивояжера
ФОРМАЛЬНАЯ ПОСТАНОВКА АДДИТИВНОЙРАЗОМКНУТОЙ ЗАДАЧИ КОММИВОЯЖЕРА
r (i, j ) z (i, j ) min;
i j
a k A(G ) : z (i, j ) 0;
( i , j ) U ( a k )
x j X \ ( xs xt ) : z (i, j )
i
z ( s, i ) 1;
i
z (i, t ) 1;
i
z (i, s ) z (t , k ) 0;
k
i
(i, j ) U : z (i, j ) 1,0.
z ( j , k ) 1;
k
8
9. Формальная постановка минимаксной разомкнутой задачи коммивояжера
ФОРМАЛЬНАЯ ПОСТАНОВКА МИНИМАКСНОЙРАЗОМКНУТОЙ ЗАДАЧИ КОММИВОЯЖЕРА
max max r (i, j ) z (i, j ) min;
j
i
a k A(G ) : z (i, j ) 0;
( i , j ) U ( a k )
x X \ ( x
j
s xt ) : z (i , j ) z ( j , k ) 1;
i
k
z ( s, i ) 1;
Самостоятельно:
i
дать формальную
z (i, t ) 1;
постановку
i
минимаксной
z (i, s ) z (t , k ) 0; замкнутой задачи
k
i
коммивояжера.
(i, j ) U : z (i, j ) 1,0.
9
10. Переменные для формальной постановки разомкнутой задачи коммивояжера как функции от перестановки
ПЕРЕМЕННЫЕДЛЯ ФОРМАЛЬНОЙ ПОСТАНОВКИ
РАЗОМКНУТОЙ ЗАДАЧИ КОММИВОЯЖЕРА КАК
ФУНКЦИИ ОТ ПЕРЕСТАНОВКИ
Пусть π = {i1, i2, …., in} – некоторая перестановка
вершин графа G(X,U), |X| = n, где ij – номер
вершины, стоящей на j-м месте в перестановке π.
Пусть переменная y(ij,i(j+1)) определена
следующим образом:
y(ij,i(j+1)) =
r(ij,i(j+1)), если дуга (ij. i(j+1)) принадлежит
множеству U;
∞ в противном случае.
11. формальные постановки задач коммивояжера как функции от перестановки
ФОРМАЛЬНЫЕ ПОСТАНОВКИ ЗАДАЧ КОММИВОЯЖЕРАКАК ФУНКЦИИ ОТ ПЕРЕСТАНОВКИ
Формальная постановка разомкнутой задачи
коммивояжера:
j n 1
R( ) y (i j , i j 1 );
j 1
R min R( ).
opt
Формальная постановка замкнутой задачи
коммивояжера:
j n 1
R( ) y (i j , i j 1 ) y (in , i1 );
j 1
R min R( ).
opt
12. Часть 2.
ЧАСТЬ 2.Методы типа ветвей и границ,
осуществляющие поиск
решения замкнутой задачи
коммивояжера на
сильносвязном взвешенном
ориентированном графе.
13. ПРОСТОЙ СПОСОБ ВЫЧИСЛЕНИЯ ОЦЕНКИ
Оценкой является суммарный вес удаленныхдуг.
Пусть I – подмножество удаленных дуг.
Тогда оценка Δ равна:
r(i, j ).
( i , j ) I
14. Простой способ вычисления оценки и фронтальный спуск
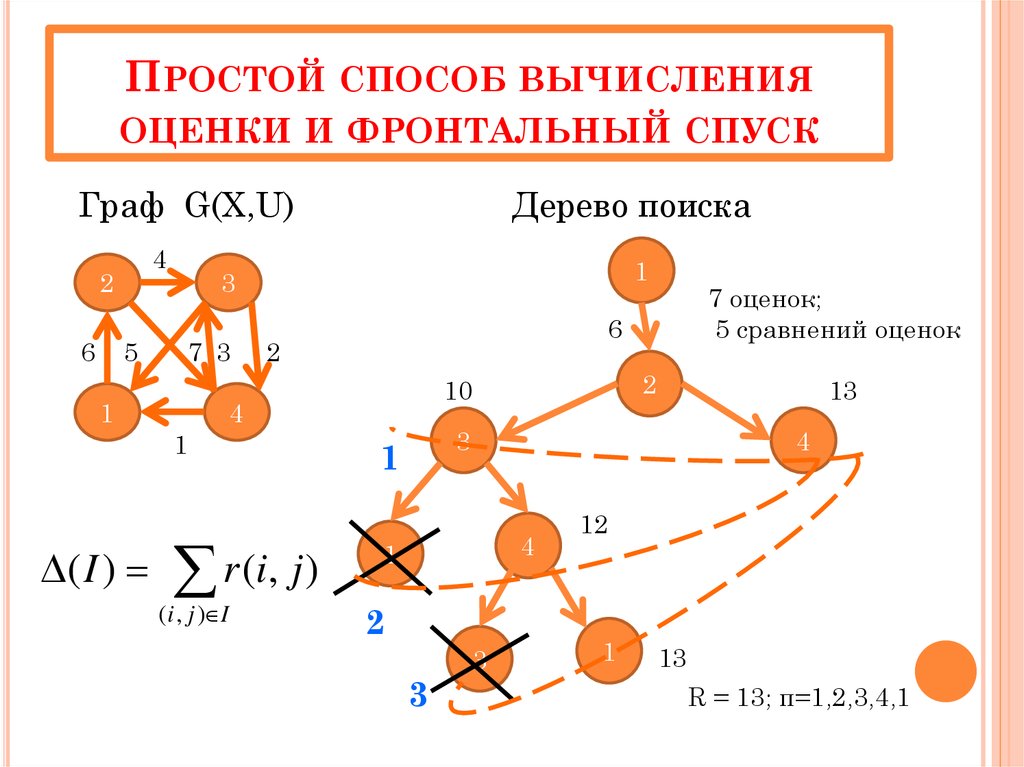
ПРОСТОЙ СПОСОБ ВЫЧИСЛЕНИЯОЦЕНКИ И ФРОНТАЛЬНЫЙ СПУСК
Граф G(X,U)
4
2
6
5
1
3
7 3
1
( i , j ) I
2
10
4
r (i, j )
7 оценок;
5 сравнений оценок
6
2
1
( I )
Дерево поиска
13
3
1
4
4
1
2
3
3
12
1
13
R = 13; π=1,2,3,4,1
15. Решить замкнутую задачу коммивояжера самостоятельно, пользуясь МВГ, реализующим фронтальный спуск по дереву ветвлений
РЕШИТЬ ЗАМКНУТУЮ ЗАДАЧУ КОММИВОЯЖЕРАСАМОСТОЯТЕЛЬНО, ПОЛЬЗУЯСЬ МВГ, РЕАЛИЗУЮЩИМ
ФРОНТАЛЬНЫЙ СПУСК ПО ДЕРЕВУ ВЕТВЛЕНИЙ
0
3
4
7
0
5
2
1
0
1
0
8
3
1
0
2
4
7
0
0
2
8
7
0
4
0
5
6
2
0
9
2
5
0
4
1
10
0
1
5
0
5
0
7
1
2
0
4
2
0
7
3
4
0
9
0
8
9
0
2
10
12
0
3
1
11
0
0
6
7
3
0
8
4
5
0
0
10
11
7
0
12
8
9
0
3
0
5
6
1
0
2
10
3
0
4
8
3
0
6
0
5
6
4
0
6
3
9
0
7
0
8
7
9
0
4
6
5
0
8
7
0
3
6
4
0
10
0
5
6
11
0
12
4
7
0
11
0
8
2
3
0
7
9
1
0
12
13
0
8
9
17
0
2
16
14
0
14
0
5
16
11
0
13
14
17
0
15
0
18
12
13
0
17
10
2
0
16
17
0
7
8
4
0
9
5
6
0
18
0
3
14
9
0
11
12
15
0
19
0
11
15
16
0
20
13
5
0
20
21
0
12
13
9
0
14
10
11
0
22
0
9
20
15
0
17
18
21
0
23
0
18
22
23
0
27
30
12
0
24
16. УТОЧНЕННЫЙ СПОСОБ ВЫЧИСЛЕНИЯ ОЦЕНКИ
Оценкой является сумма, включающаясуммарный вес удаленных дуг и суммарный
вес дуг с минимальным весом, заходящих в
вершины, соответствующие городам, в которые
коммивояжер еще не въезжал.
Пусть I – подмножество удаленных дуг, а J –
подмножество вершин, соответствующих
городам, в которые коммивояжер еще не
въезжал.
Тогда оценка Δ равна:
( i , j ) I
r (i, j ) min r (i, j ).
j J
i
17. ПРИМЕР ВЫЧИСЛЕНИЯ УТОЧНЕННОЙ ОЦЕНКИ
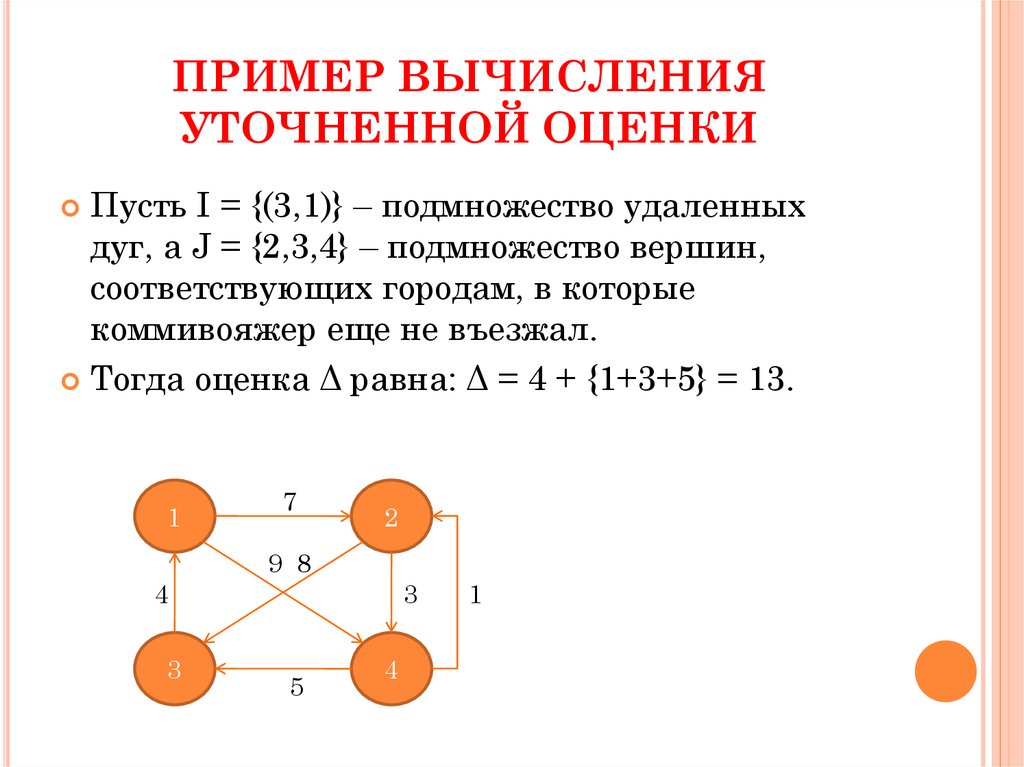
Пусть I = {(3,1)} – подмножество удаленныхдуг, а J = {2,3,4} – подмножество вершин,
соответствующих городам, в которые
коммивояжер еще не въезжал.
Тогда оценка Δ равна: Δ = 4 + {1+3+5} = 13.
1
7
2
9 8
4
3
3
5
4
1
18. Уточненный способ вычисления оценки и фронтальный спуск
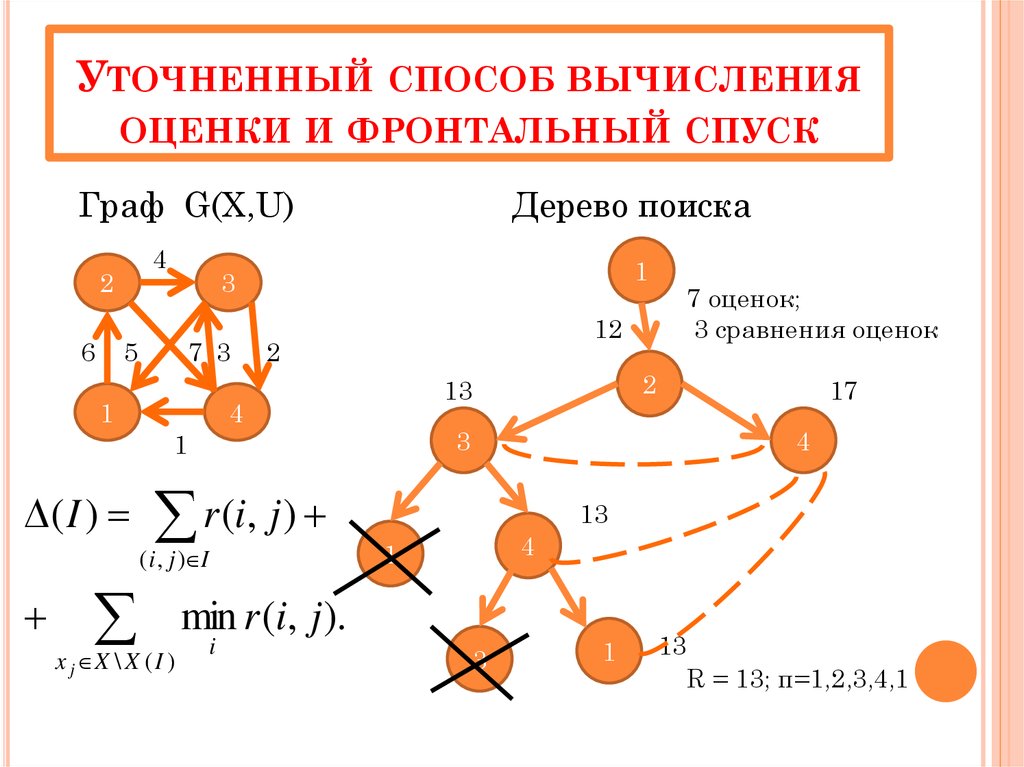
УТОЧНЕННЫЙ СПОСОБ ВЫЧИСЛЕНИЯОЦЕНКИ И ФРОНТАЛЬНЫЙ СПУСК
Граф G(X,U)
4
2
6
Дерево поиска
1
3
5
7 3
1
12
2
4
r (i, j )
( i , j ) I
x j X \ X ( I )
17
3
4
13
4
1
min r (i, j ).
i
2
13
1
( I )
7 оценок;
3 сравнения оценок
3
1
13
R = 13; π=1,2,3,4,1
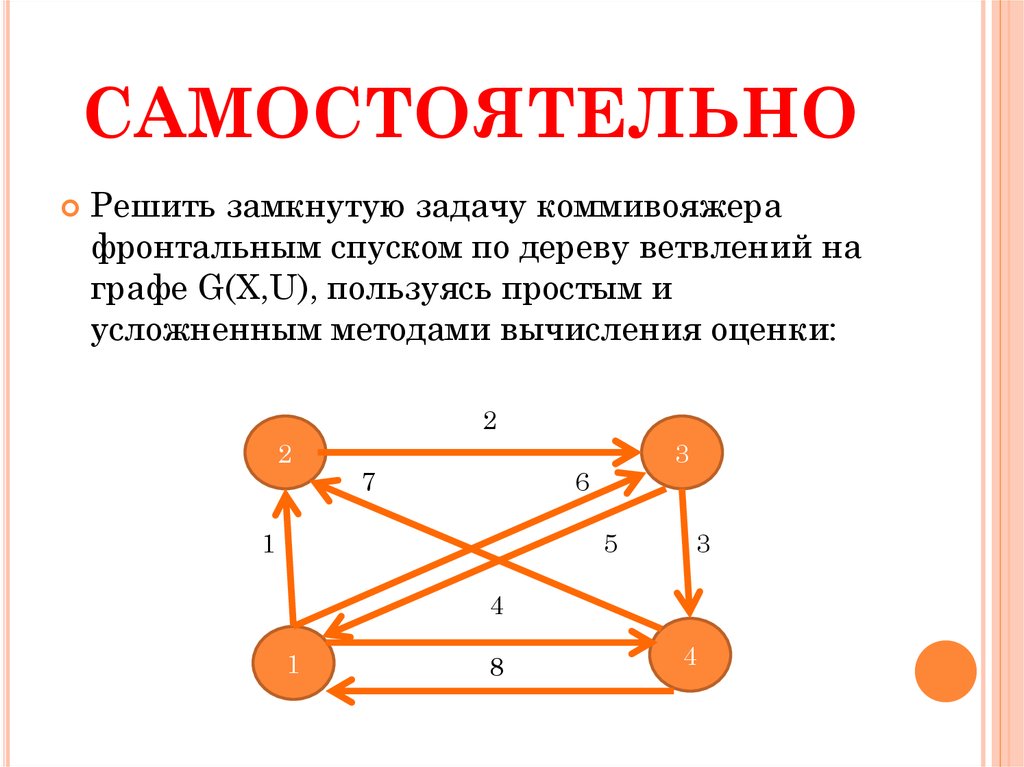
19. САМОСТОЯТЕЛЬНО
Решить замкнутую задачу коммивояжерафронтальным спуском по дереву ветвлений на
графе G(X,U), пользуясь простым и
усложненным методами вычисления оценки:
2
2
7
3
6
1
5
3
4
1
8
4
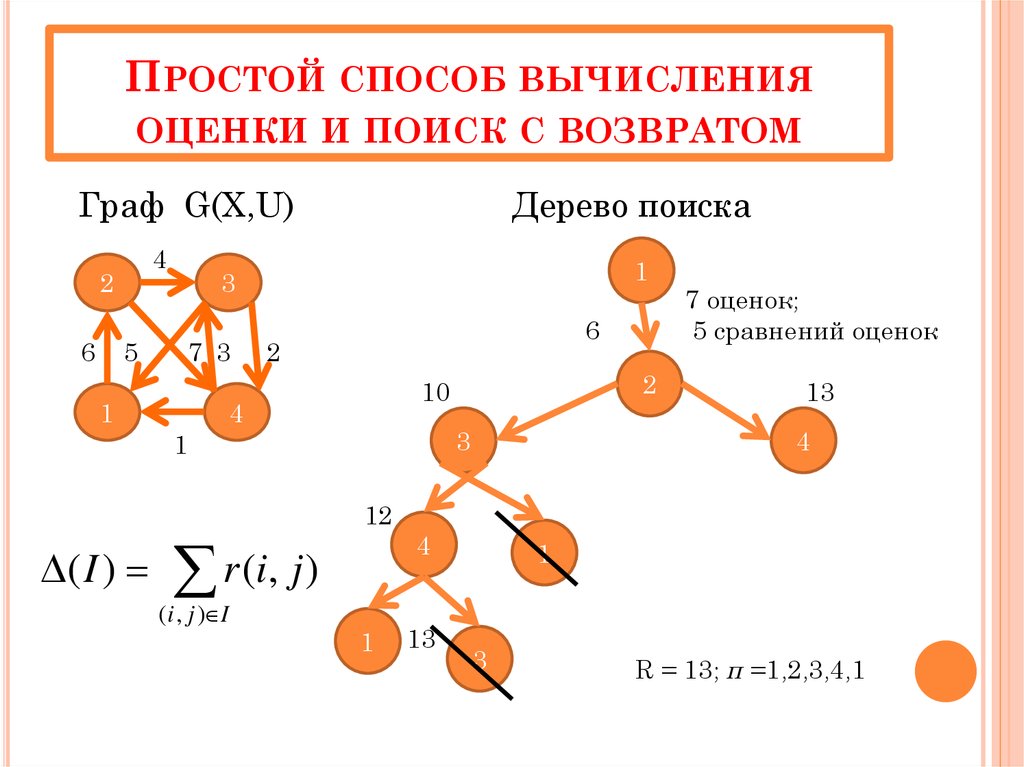
20. Простой способ вычисления оценки и поиск с возвратом
ПРОСТОЙ СПОСОБ ВЫЧИСЛЕНИЯОЦЕНКИ И ПОИСК С ВОЗВРАТОМ
Граф G(X,U)
4
2
6
5
Дерево поиска
1
3
7 3
1
6
2
4
3
1
12
( I )
r (i, j )
( i , j ) I
2
10
1
13
4
4
13
7 оценок;
5 сравнений оценок
1
3
R = 13; π =1,2,3,4,1
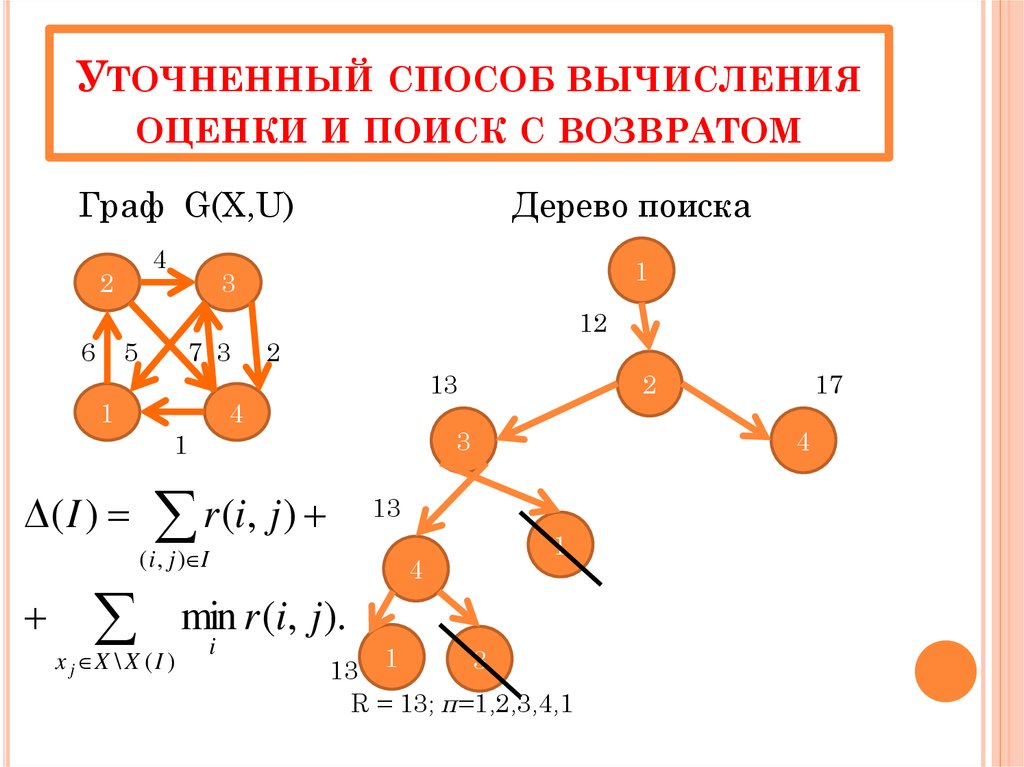
21. Уточненный способ вычисления оценки и поиск с возвратом
УТОЧНЕННЫЙ СПОСОБ ВЫЧИСЛЕНИЯОЦЕНКИ И ПОИСК С ВОЗВРАТОМ
Граф G(X,U)
4
2
6
Дерево поиска
1
3
5
7 3
1
12
2
13
4
3
1
( I )
r (i, j )
x j X \ X ( I )
4
1
min r (i, j ).
i
17
4
13
( i , j ) I
2
3
13 1
R = 13; π=1,2,3,4,1
22. САМОСТОЯТЕЛЬНО
Определить решение замкнутой задачикоммивояжера, осуществляя поиск с возвратом по
дереву ветвлений на графе G(X,U), и пользуясь
простым и усложненным методами вычисления
оценки.
2
2
7
3
6
1
5
3
4
1
8
4
23. ЧАСТЬ 3
РЕШЕНИЕРАЗОМКНУТОЙ
ЗАДАЧИ
КОММИВОЯЖЕРА
МЕТОДАМИ ТИПА
ВЕТВЕЙ И ГРАНИЦ
24. АЛГОРИТМ ПЕРЕХОДА ОТ РАЗОМКНУТОЙ «КЛАССИЧЕСКОЙ» ЗАДАЧИ КОММИВОЯЖЕРА К ЗАМКНУТОЙ
Пусть задан орграф G’(X’,U’) на которомследует решить разомкнутую задачу
коммивояжера при условии, что выделена
стартовая вершина xs и терминальная
вершина xt .
Преобразуем G’(X’,U,) в орграф G”(X’,U”)
добавлением дуги (t,s), обладающей нулевым
весом.
На орграфе G”(X’,U”) ищется оптимальное
решение замкнутой задачи коммивояжера.
Отбрасывая в полученном на предыдущем
шаге подмножестве дуг, дугу (t,s), получим
решение разомкнутой задачи коммивояжера.
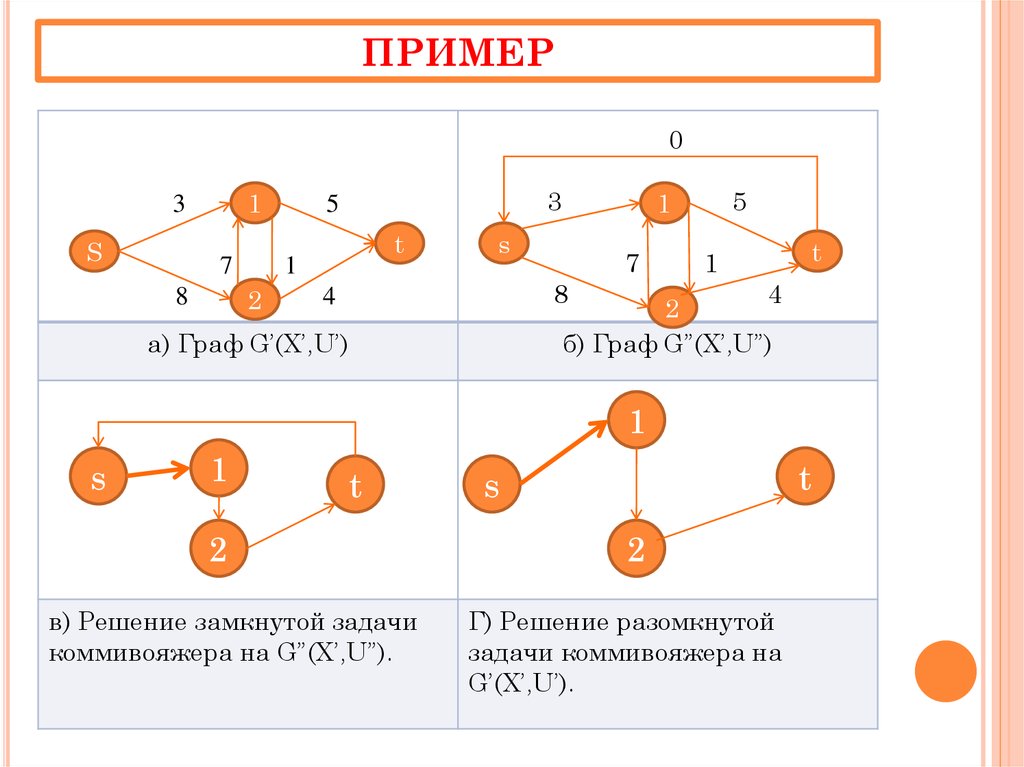
25. ПРИМЕР
01
3
S
7
t
1
2
8
3
5
5
1
s
7
t
1
8
4
2
б) Граф G”(X’,U”)
4
a) Граф G’(X’,U’)
1
s
1
t
2
в) Решение замкнутой задачи
коммивояжера на G”(X’,U”).
t
s
2
Г) Решение разомкнутой
задачи коммивояжера на
G’(X’,U’).
26. Эквивалентные преобразования графа, на котором решается разомкнутая задача коммивояжера
ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ ГРАФА, НА КОТОРОМРЕШАЕТСЯ РАЗОМКНУТАЯ ЗАДАЧА КОММИВОЯЖЕРА
1.
Если на исходном графе существует
дуга, ведущая из стартовой вершины в
терминальную, то она может быть
отброшена.
Если на исходном графе существуют
дуги, ведущие в стартовую вершину, то
они могут быть отброшены.
Если на исходном графе существуют
дуги, ведущие из терминальной
вершины, то они могут быть отброшены.
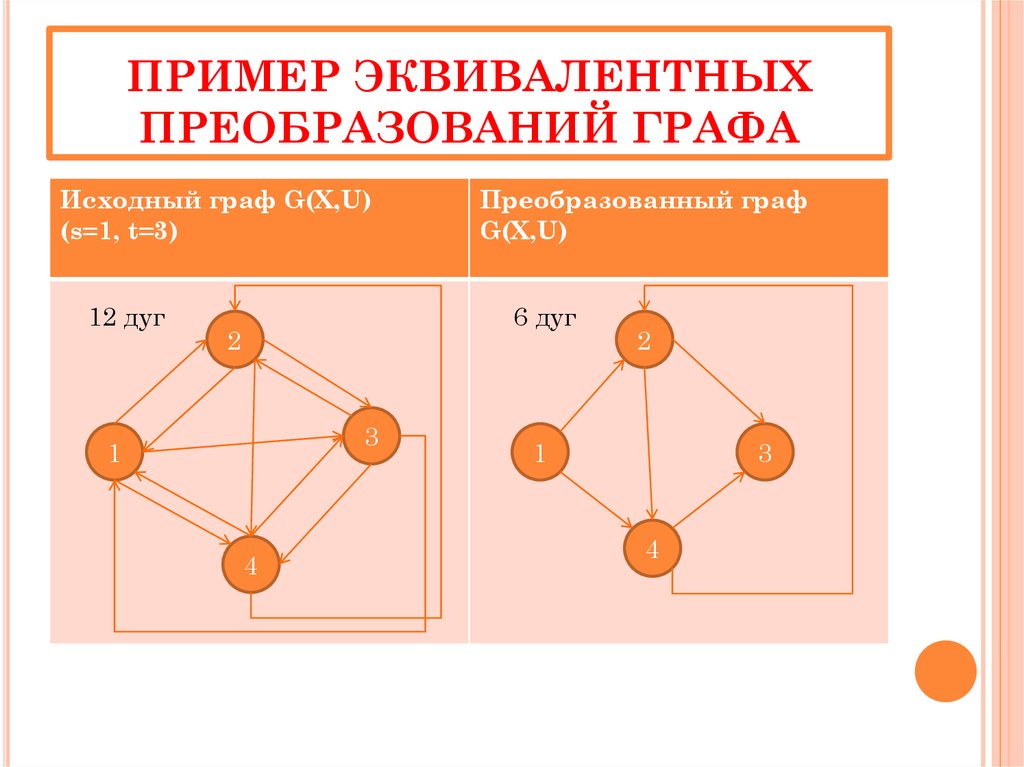
27. ПРИМЕР ЭКВИВАЛЕНТНЫХ ПРЕОБРАЗОВАНИЙ ГРАФА
Исходный граф G(X,U)(s=1, t=3)
12 дуг
Преобразованный граф
G(X,U)
6 дуг
2
3
1
4
2
1
3
4
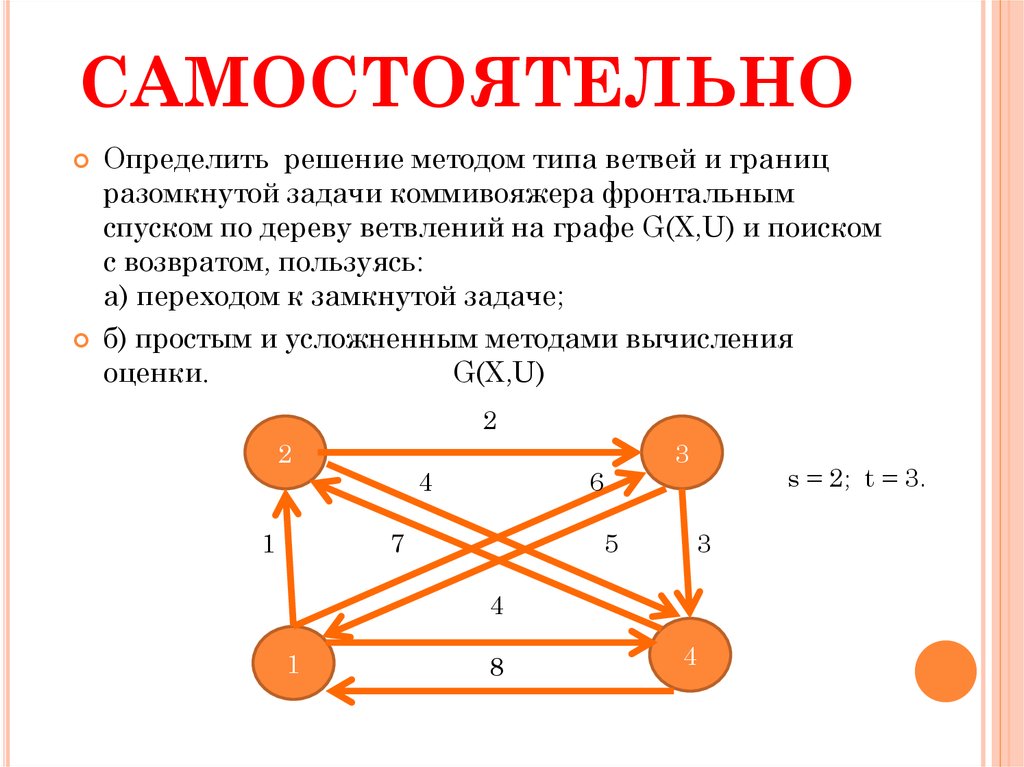
28. САМОСТОЯТЕЛЬНО
Определить решение методом типа ветвей и границразомкнутой задачи коммивояжера фронтальным
спуском по дереву ветвлений на графе G(X,U) и поиском
с возвратом, пользуясь:
а) переходом к замкнутой задаче;
б) простым и усложненным методами вычисления
оценки.
G(X,U)
2
2
1
4
3
6
7
5
s = 2; t = 3.
3
4
1
8
4
29. САМОСТОЯТЕЛЬНО
Предложите свой способрешения разомкнутой задачи
коммивояжера, опирающийся
на метод типа ветвей и границ
и не требующий перехода к
замкнутой задаче.



















 Программирование
Программирование








