Похожие презентации:
Методы типа ветвей и границ
1. Методы типа ветвей и границ
МЕТОДЫ ТИПА ВЕТВЕЙ И ГРАНИЦТПР
Лекция № 2-10
2. Содержание:
1. Задачи с булевыми переменными1.1. Фронтальный спуск по дереву ветвлений
1.2. Поиск с возвратом (алгоритм Балаша)
2. Многокритериальные задачи
2.1.Поиск величин эталонов методами типа
ветвей и границ.
2.2. Формальная постановка задачи.
2.3. Решение многокритериальной задачи
методом типа ветвей и границ.
3. ОБЩИЕ СВОЙСТВА МЕТОДОВ ТИПА ВЕТВЕЙ И ГРАНИЦ
1. Метод вычисления оценки таков, что помере спуска по дереву ветвлений оценка не
улучшается.
2. Спуск по дереву ветвлений прекращается,
если выбранная вершина обладает
следующими свойствами:
оценка этой вершины является наилучшей;
существует возможность определить
значения всех переменных, причем оценка
остается неизменной.
4. Часть 1
Решение задач сбулевыми
переменными
5.
1.1. Фронтальныйспуск по дереву
ветвлений
6. Содержательное описание алгоритма
Шаг 1. На построенной части дерева ветвленийвыбирается вершина с наилучшей оценкой,
принадлежащая i-у ярусу.
Шаг 2. Если i=n, где n – число переменных, то
перейти к шагу , в противном случае – к шагу 3.
Шаг 3. В базис частичного плана,
соответствующего выбранной вершине, вводится
(i+1)-я переменная и вычисляются
соответствующие оценки. Перейти к шагу 1.
Шаг 4. Конец алгоритма. Оценка выбранной на
предыдущем шаге вершины является
оптимальным значением целевой функции.
7. ПРИМЕР 1
Пусть задана задача о ранце вида:5 x1 3 x 2 10 x3 2 x 4 max
3 x1 7 x 2 8 x3 2 x 4 10
x 1,0; i 1,2,...,4
i
8. ДЕРЕВО ВЕТВЛЕНИЙ
XXopt = {0, 0, 1, 1}; R=12.9. Достоинства и недостатки фронтального спуска по дереву ветвлений:
Достоинства: шанс на неполный перебор,первый же полный допустимый план
является глобально оптимальным.
Недостатки: по мере спуска по дереву
ветвлений растет число оценок, хранимых
в памяти и затраты времени на их
сравнение при выборе направления
спуска.
10. САМОСТОЯТЕЛЬНО
Пользуясь фронтальным спуском решитьзадачу вида:
5 x1 3 x2 10 x3 2 x4 max;
3 x 7 x 8 x 2 x 10;
1
2
3
4
6
x
3
x
2
x
5
x
8
;
1
2
3
4
xi 1,0; i 1,2,...,4.
11.
1.2. Поиск с возвратом12. Содержательное описание алгоритма
Шаг 1. R = плохое значениеШаг 2. i = 1
Шаг 3. xi = 1
Шаг 4. Вычисляется оценка рекорда F
Шаг 5. Если F R, то перейти к шагу 6, нет –
к шагу 9
Шаг 6. Если все ограничения удовлетворяют, то
перейти к шагу 7, нет к шагу 9
Шаг 7. Если i = n, то перейти к шагу 8, нет –
к шагу 13
Шаг 8. R = F, печать R и вектора
Шаг 9. Если xi = 1, то перейти к шагу 10, нет –
к шагу 13
Шаг 10. xi = 0, перейти к шагу 4
Шаг 11. Если i = 1, то перейти к шагу 14, нет к шагу 12.
Шаг 12. i = i - 1, перейти к шагу 9.
Шаг 13. i = i + 1, перейти к шагу 3.
Шаг 14. Конец алгоритма. Последние выданные на печать значения R и , оптимальны.
13. ПРИМЕР 2
5 x1 3 x 2 10 x3 2 x 4 max;3 x1 7 x 2 8 x3 2 x 4 10;
x 1,0; i 1,2,3,4.
i
14. Построение дерева ветвлений
15. САМОСТОЯТЕЛЬНО
Пользуясь методом типа ветвей и границ,реализующим поиск с возвратом, решить
задачу вида:
5 x1 3 x2 10 x3 2 x4 max;
3 x 7 x 8 x 2 x 10;
1
2
3
4
6
x
3
x
2
x
5
x
8
;
1
2
3
4
xi 1,0; i 1,2,...,4.
16.
ЧАСТЬ 2Решение многокритериальных
задач методами типа ветвей и
границ
17. Основные положения
1. Свертка критериев с помощью эталоновпозволяет получить новую целевую функцию
вида:
Fi Fi min
zi
Fi max Fi min
i
2
,
где Fi - i– я целевая функция, zi = 1, если Fi
и zi = 0, если Fi min.
max,
18. ПРИМЕР 2
Пользуясь описанным выше методомсвертки, решить многокритериальную
задачу с булевыми переменными вида:
F1 7 x1 2 x2 5 x3 3 x4 max;
F 3 x 4 x 2 x 5 x min;
1
2
3
4
2
(1)
4 x1 3 x2 2 x3 6 x4 8;
5 x 7 x 4 x 8 x 8;
2
3
4
1
i : xi 1,0.
19. Условия свертки
Для того, чтобыпреобразовать (1) в
однокритериальную задачу,
следует определить
максимальные и
минимальные значения F1 и
F2.
20. Поиск максимальной величины F1
F1 7 x1 2 x2 5 x3 3 x4 max;4 x 3 x 2 x 6 x 8;
1
2
3
4
( 2)
5 x1 7 x2 4 x3 8 x4 8;
i : xi 1,0.
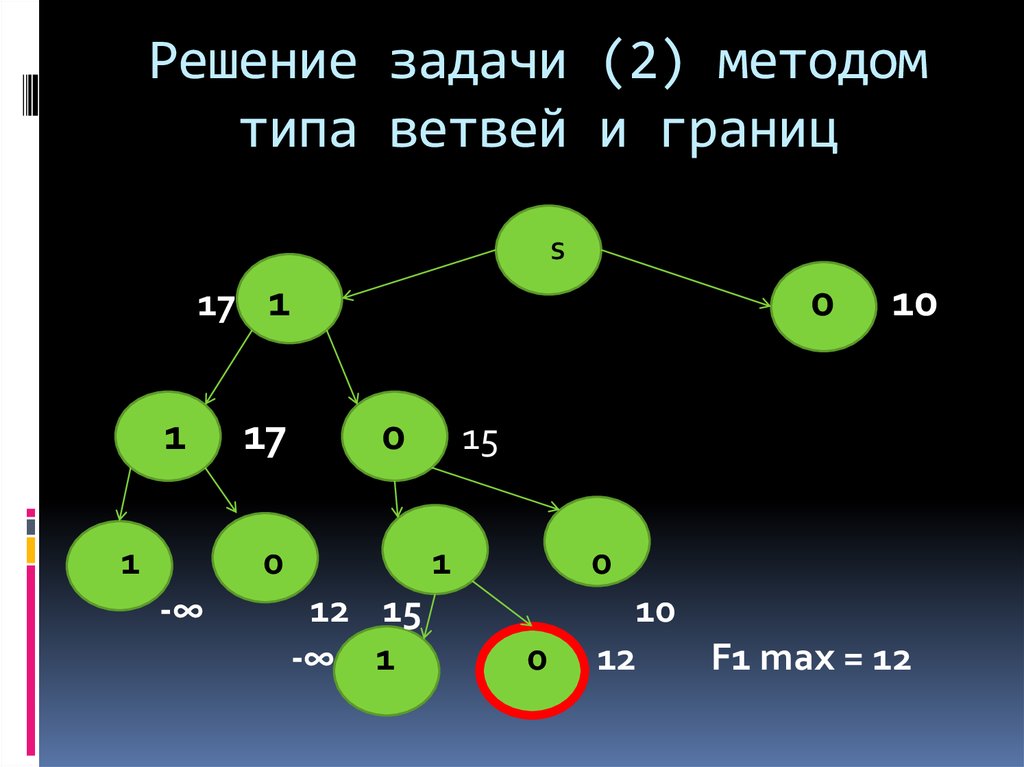
21. Решение задачи (2) методом типа ветвей и границ
S17 1
1
1
17
0
0
0
-∞
15
1
12 15
-∞ 1
10
0
0
10
12
F1 max = 12
22. Поиск минимальной величины F1 сводится к решению задачи (3):
F1 7 x1 2 x2 5 x3 3 x4 min;4 x 3 x 2 x 6 x 8;
1
2
3
4
(3)
5 x1 7 x2 4 x3 8 x4 8;
i : xi 1,0.
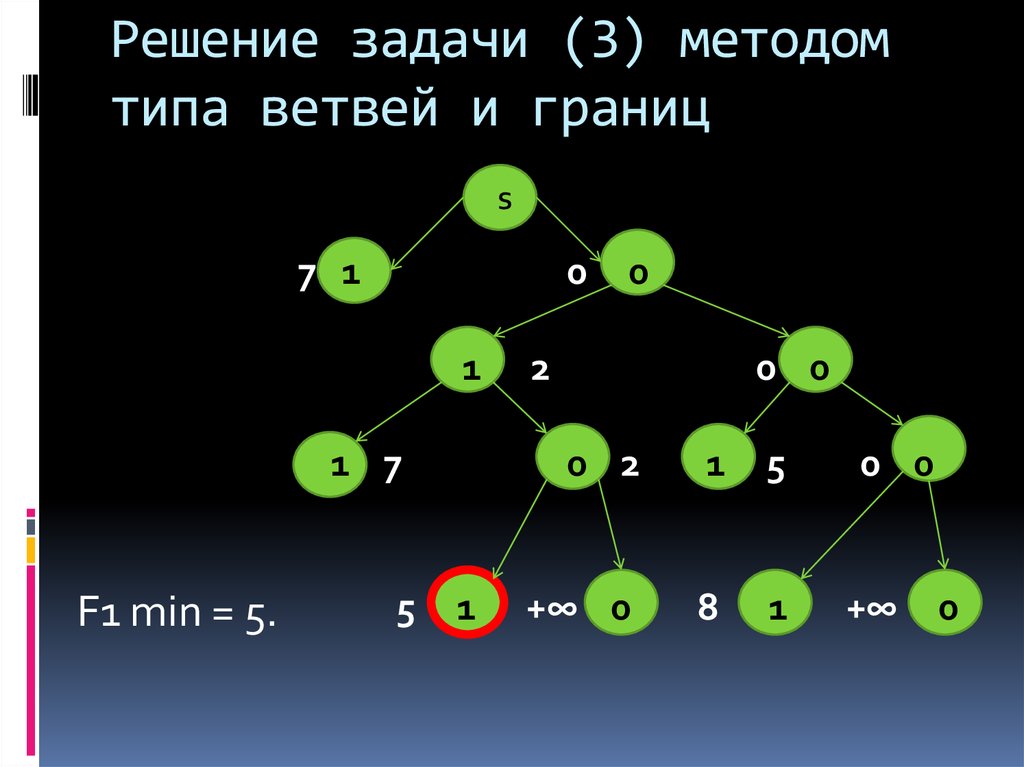
23. Решение задачи (3) методом типа ветвей и границ
S7 1
0
1
1 7
F1 min = 5.
5
1
0
2
0 0
0 2
1
5
+∞ 0
8
1
0 0
+∞
0
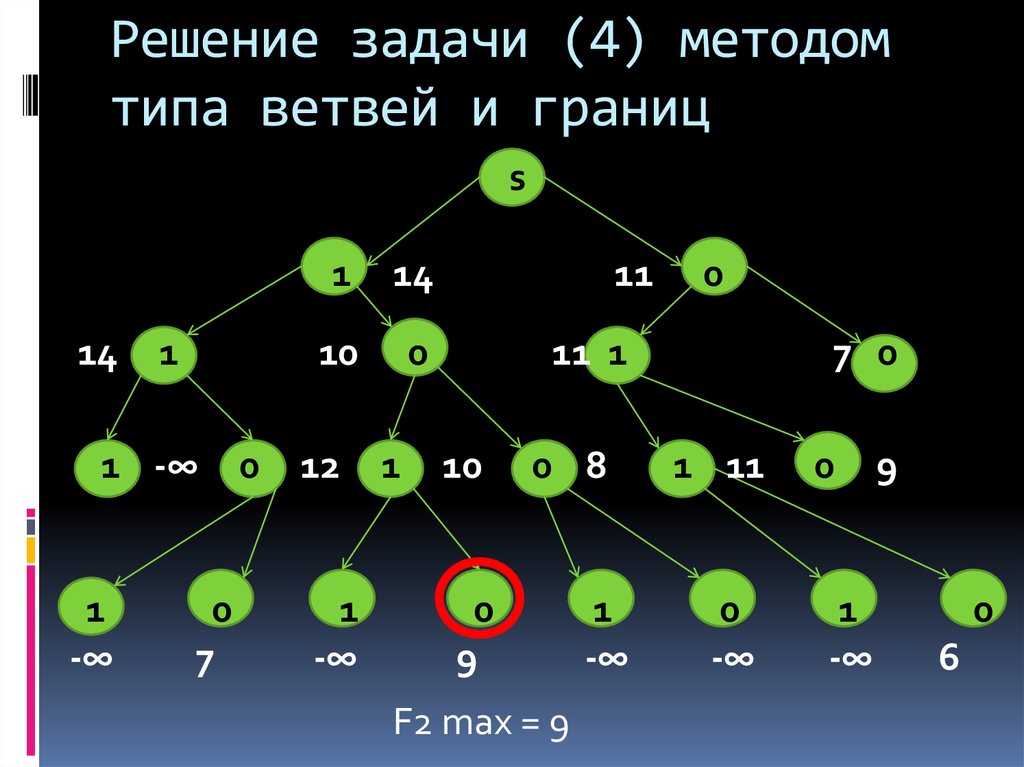
24. Поиск максимальной величины F2
F2 3 x1 4 x2 2 x3 5 x4 max;4 x 3 x 2 x 6 x 8;
1
2
3
4
( 4)
5 x1 7 x2 4 x3 8 x4 8;
i : xi 1,0.
25. Решение задачи (4) методом типа ветвей и границ
s14
1
1 -∞
1
-∞
0
7
0
1
14
10
0
12
1
-∞
1
11
0
11 1
10
0 8
0
9
F2 max = 9
1
-∞
7 0
1 11
0
-∞
0
1
-∞
9
0
6
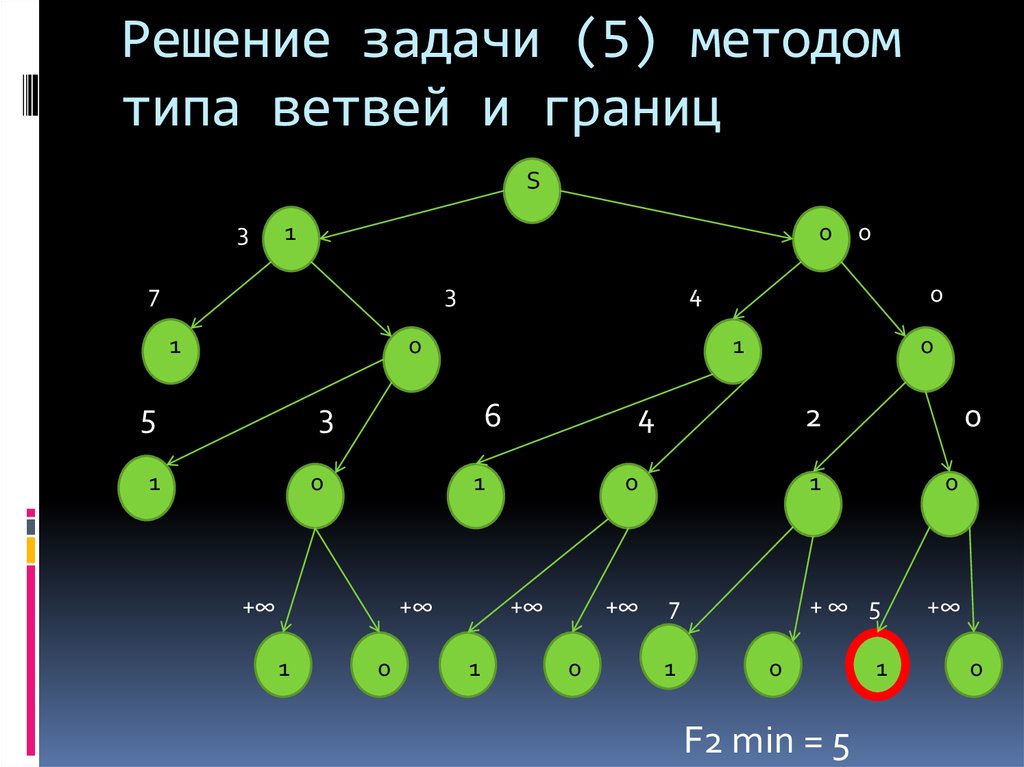
26. Поиск минимальной величины F2
F2 3x1 4 x2 2 x3 5 x4 min;4 x 3x 2 x 6 x 8;
1
2
3
4
(5)
5 x1 7 x2 4 x3 8 x4 8;
i : xi 1,0.
27. Решение задачи (5) методом типа ветвей и границ
S3
1
0
7
3
1
4
0
5
6
0
+∞
1
0
2
0
+∞
1
0
4
1
+∞
0
1
3
1
0
+∞
0
0
1
7
1
0
+∞ 5
0
F2 min = 5
1
+∞
0
28. Использование эталонов для преобразования(1) в однокритериальную задачу
22
F1 5
F2 5
0
min;
1
9 5
12 5
F1 7 x1 2 x2 5 x3 3x4 ;
(6)
F2 3x1 4 x2 2 x3 5 x4 ;
4 x 3x 2 x 6 x 8;
2
3
4
1
5 x1 7 x2 4 x3 8 x4 8;
i : xi 1,0.
29. Вид системы (6) после преобразований
22
12 F1 F2 5
min;
7 4
F1 7 x1 2 x2 5 x3 3x4 ;
( 7)
F2 3x1 4 x2 2 x3 5 x4 ;
4 x 3x 2 x 6 x 8;
2
3
4
1
5 x1 7 x2 4 x3 8 x4 8;
i : xi 1,0.
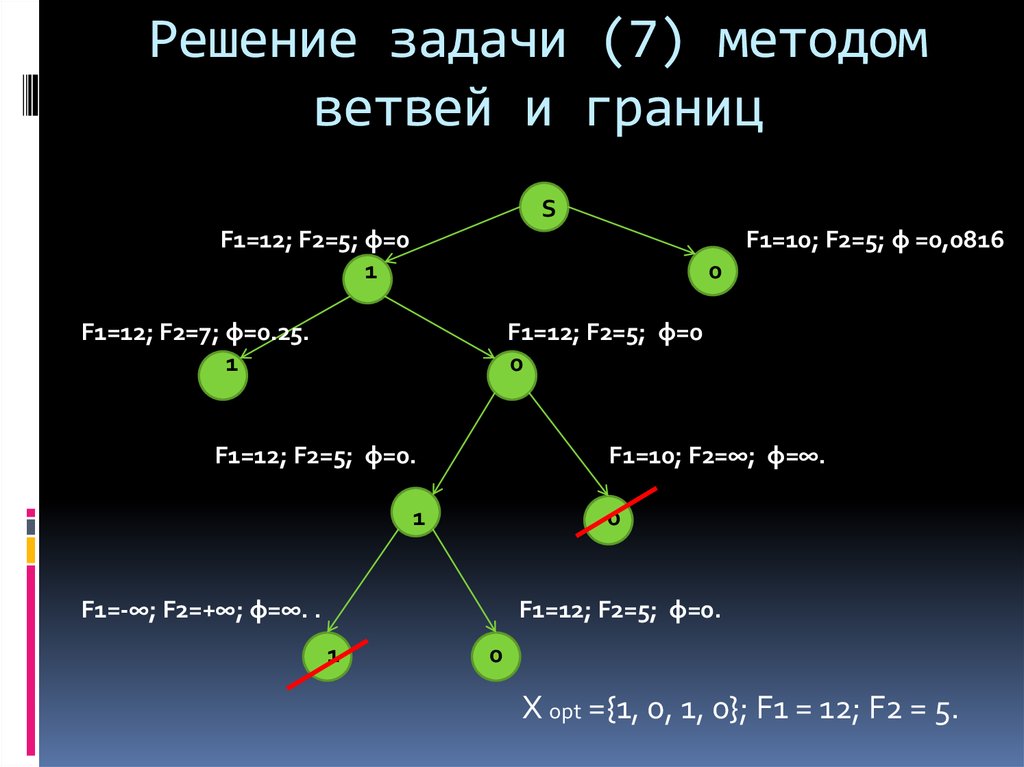
30. Решение задачи (7) методом ветвей и границ
SF1=12; F2=5; φ=0
1
F1=10; F2=5; φ =0,0816
0
F1=12; F2=7; φ=0.25.
1
F1=12; F2=5; φ=0
0
F1=12; F2=5; φ=0.
F1=10; F2=∞; φ=∞.
1
0
F1=-∞; F2=+∞; φ=∞. .
F1=12; F2=5; φ=0.
1
0
X opt ={1, 0, 1, 0}; F1 = 12; F2 = 5.
31. САМОСТОЯТЕЛЬНО
Решить, пользуясь рассмотренной вышетехнологией, систему вида:
F1 4 x1 2 x2 7 x3 max;
F 8 x 3x 2 x min;
1
2
3
2
(8)
4 x1 3x2 2 x3 8;
5 x 7 x 4 x 8;
2
3
1
i : xi 1,0.


























 Программирование
Программирование








