Похожие презентации:
Обобщенные задачи коммивояжера и планарные графы
1. ОБОБЩЕННЫЕ ЗАДАЧИ КОММИВОЯЖЕРА и планарные графы
Лекция 15ОБОБЩЕННЫЕ ЗАДАЧИ
КОММИВОЯЖЕРА И
ПЛАНАРНЫЕ ГРАФЫ
2. СОДЕРЖАНИЕ
1. Обобщенные задачикоммивояжера и их решение
перебором.
2. Связь обобщенной задачи
коммивояжера и задачи о
максимальной циркуляции.
2
3. ЧАСТЬ 1
ОБОБЩЕННЫЕ ЗАДАЧИКОММИВОЯЖЕРА
3
4. Содержательные постановки обобщенных задач коммивояжера
1. Разомкнутая постановка задачи:коммивояжер должен объехать заданное
подмножество городов, затратив минимум
средств на путешествие либо минимум
средств на максимальный переход.
2. Замкнутая постановка задачи:
коммивояжер должен объехать заданное
подмножество городов вернуться в город
из которого стартовал, затратив минимум
средств на путешествие либо минимум
средств на максимальный переход.
4
5. Основные отличия от «классических» постановок
1. К посещениюкоммивояжером обязательны
только вершины заданного
подмножества.
2. Отсутствует ограничение на
число посещений каждой
вершины.
5
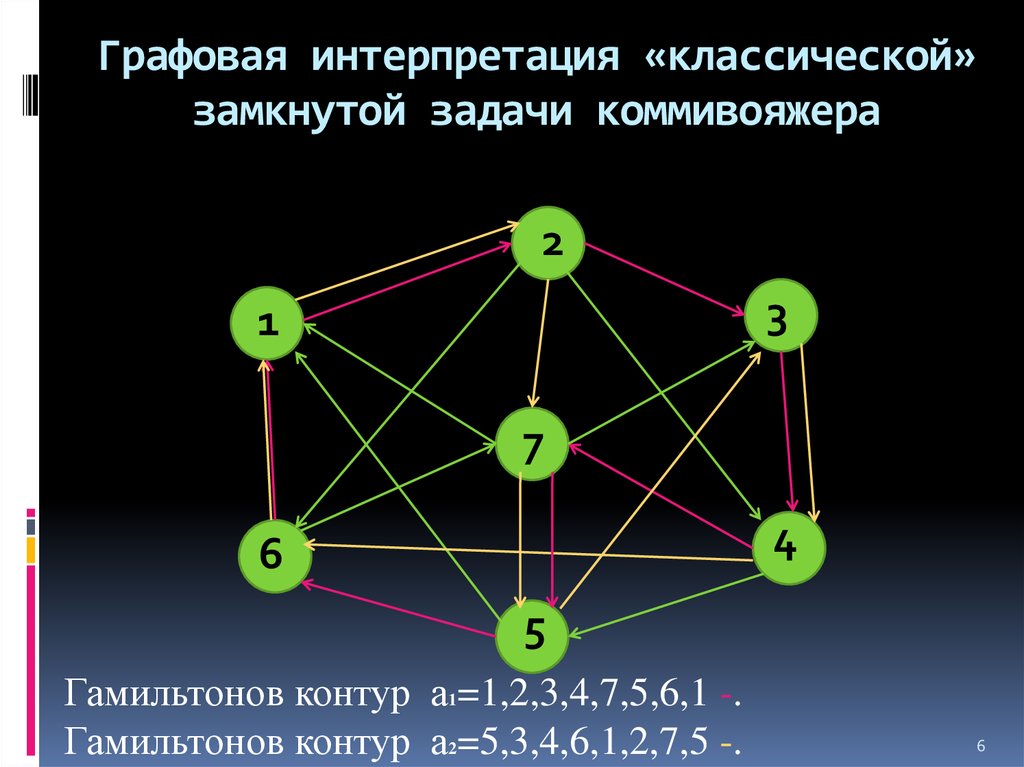
6. Графовая интерпретация «классической» замкнутой задачи коммивояжера
23
1
7
4
6
5
Гамильтонов контур а1=1,2,3,4,7,5,6,1 -.
Гамильтонов контур а2=5,3,4,6,1,2,7,5 -.
6
7.
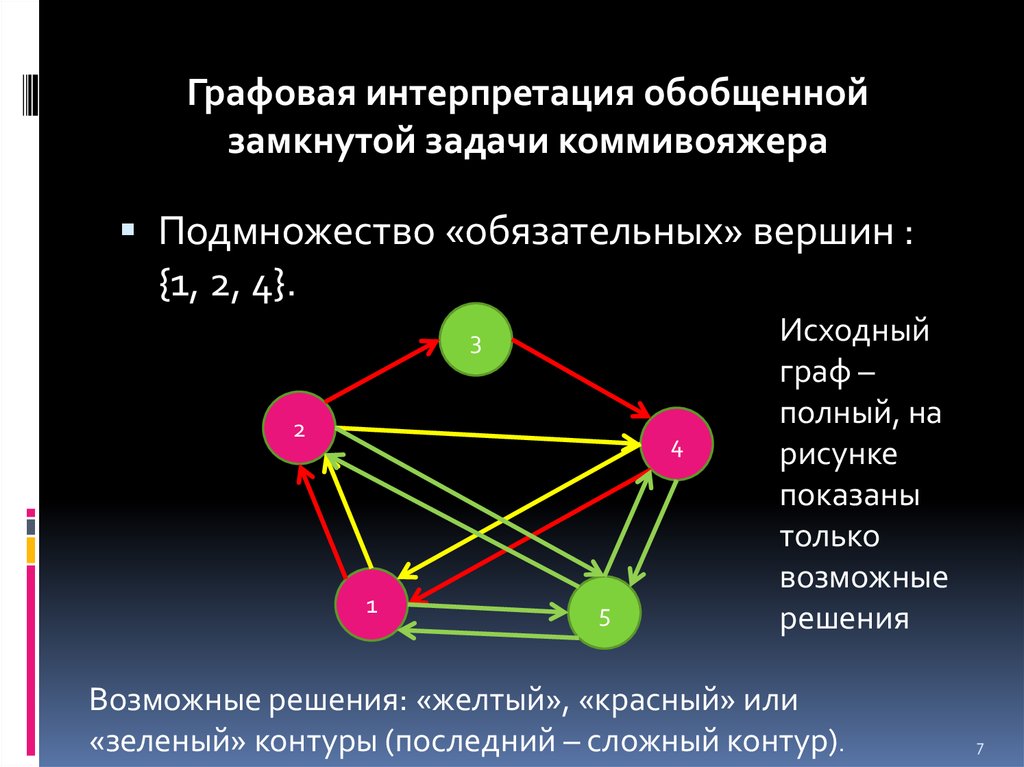
Графовая интерпретация обобщеннойзамкнутой задачи коммивояжера
Подмножество «обязательных» вершин :
{1, 2, 4}.
3
2
4
1
5
Исходный
граф –
полный, на
рисунке
показаны
только
возможные
решения
Возможные решения: «желтый», «красный» или
«зеленый» контуры (последний – сложный контур).
7
8. Обозначения и определения
G ( X ,U ) взвешенный орграф;Х - множество вершин;
U - множество дуг;
A(G) - множество контуров графа;
a k k й контур множества A(G);
X(a k ) множество вершин k - го контура;
U(a k ) множество дуг k - го контура;
X1 X подмножество " обязательн ых" вершин;
Ld ( q, p ) d й путь из q - й вершины в р - ю;
z(i, j) - булева переменная.
8
9. Формальная постановка «классической» аддитивной замкнутой задачи коммивояжера
j)min;
r (ir, (ji),zj()iz, (ji),
min;
i i j j
z (iz, (ji), j )0 ; 0;
(G
A()G: )X: (Xa k()a k ) X
X
a k a k A
( i , j )( iU
aU
, j ()
k )( a k )
xj X
:X
:
z (iz, (ji), j )1 ; 1;
x j
i i
x
xq X
:X
:
z ( qz,(iq), i )1 ; 1;
q
i i
(i, j ) U : z (i, j ) 1,0.
(
i
,
j
)
U
:
z
(
i
,
j
)
1
,
0
.
9
10. Формальная постановка обобщенной аддитивной замкнутой задачи коммивояжера
r (i , j ) z (i , j ) min;i j
z (i , j ) 1;
x p X 1 , xq X 1 :
d ( i , j ) Ld ( p ,q )
x j X 1 : z (i , j ) 1;
i
x X :
q
1 z ( q, i ) 1;
i
xq X : z ( q, i ) z (i , q);
i
i
(i , j ) U : z (i , j ) 1,0.
10
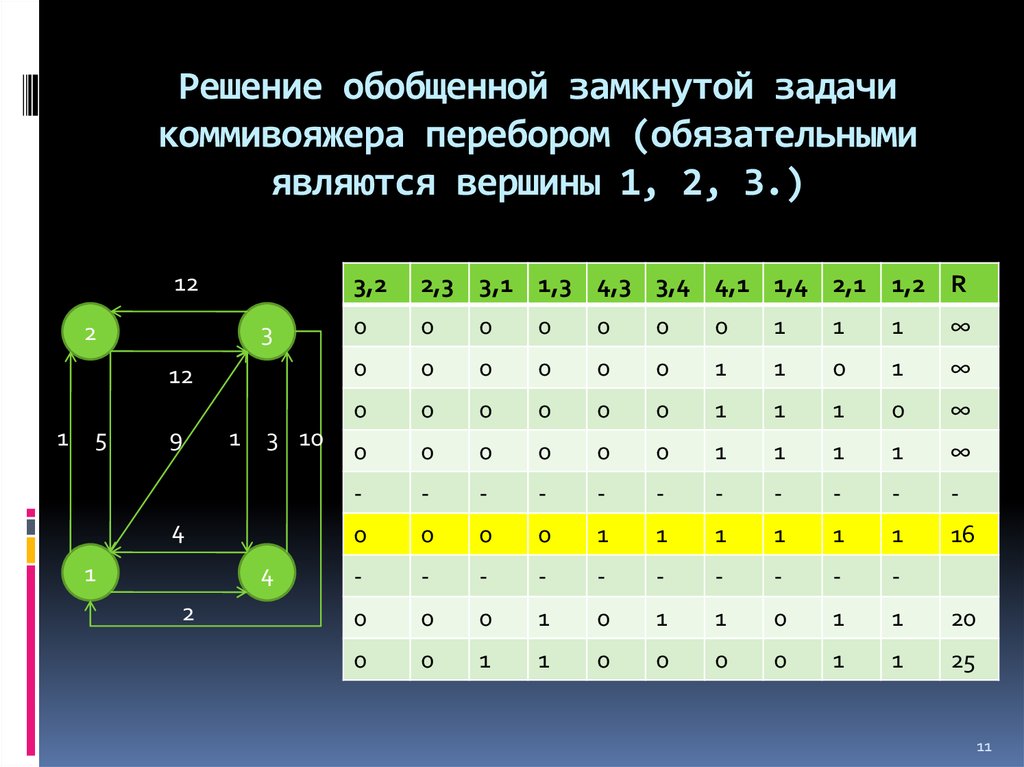
11. Решение обобщенной замкнутой задачи коммивояжера перебором (обязательными являются вершины 1, 2, 3.)
122
3
12
1
1
5
2
9
3 10
4
1
3
1
4
2
3,2
2,3 3,1 1,3 4,3 3,4 4,1 1,4 2,1 1,2 R
0
0
0
0
0
0
0
1
1
1
∞
0
0
0
0
0
0
1
1
0
1
∞
0
0
0
0
0
0
1
1
1
0
∞
0
0
0
0
0
0
1
1
1
1
∞
-
-
-
-
-
-
-
-
-
-
-
0
0
0
0
1
1
1
1
1
1
16
-
-
-
-
-
-
-
-
-
-
0
0
0
1
0
1
1
0
1
1
20
0
0
1
1
0
0
0
0
1
1
25
11
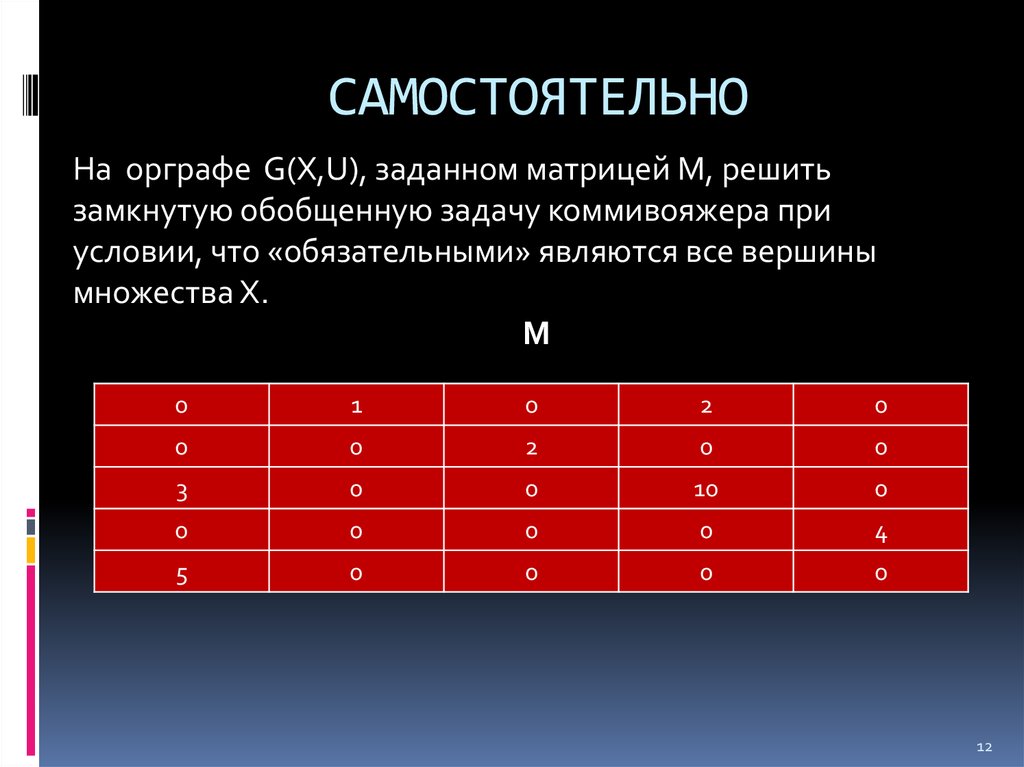
12. САМОСТОЯТЕЛЬНО
На орграфе G(X,U), заданном матрицей М, решитьзамкнутую обобщенную задачу коммивояжера при
условии, что «обязательными» являются все вершины
множества Х.
М
0
1
0
2
0
0
0
2
0
0
3
0
0
10
0
0
0
0
0
4
5
0
0
0
0
12
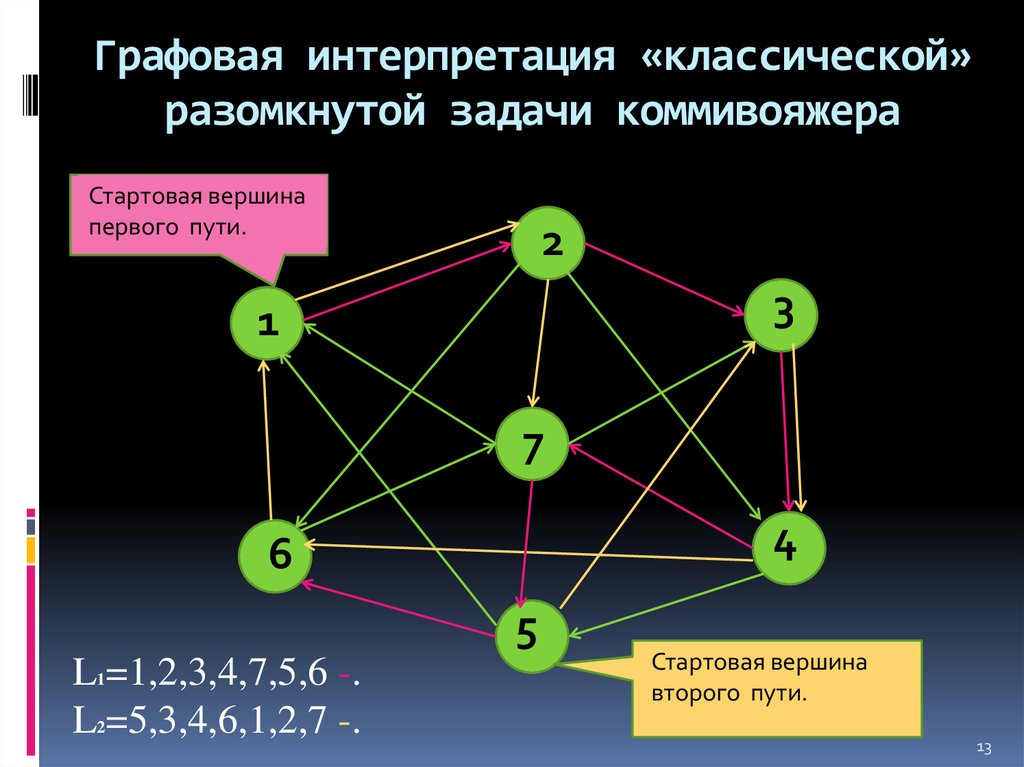
13. Графовая интерпретация «классической» разомкнутой задачи коммивояжера
Стартовая вершинапервого пути.
2
3
1
7
4
6
5
L1=1,2,3,4,7,5,6 -.
L2=5,3,4,6,1,2,7 -.
Стартовая вершина
второго пути.
13
14. Формальная постановка «классической» аддитивной разомкнутой задачи коммивояжера
r (i, j ) z (i, j ) min;i j
a k A(G ) : z (i, j ) 0;
( i , j ) U ( a k )
x j X \ ( xs xt ) : z (i, j )
i
z ( s, i ) 1;
i
z (i, t ) 1;
i
z (i, s ) z (t , k ) 0;
k
i
(i, j ) U : z (i, j ) 1,0.
z ( j , k ) 1;
k
14
15.
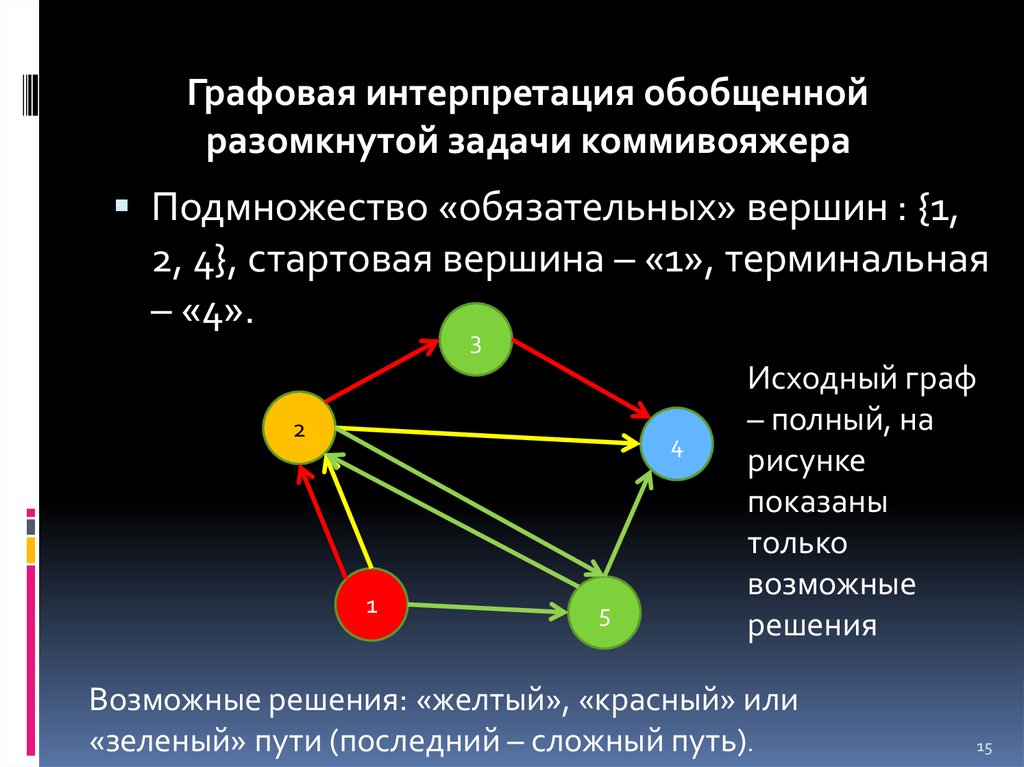
Графовая интерпретация обобщеннойразомкнутой задачи коммивояжера
Подмножество «обязательных» вершин : {1,
2, 4}, стартовая вершина – «1», терминальная
– «4».
3
2
4
1
5
Исходный граф
– полный, на
рисунке
показаны
только
возможные
решения
Возможные решения: «желтый», «красный» или
«зеленый» пути (последний – сложный путь).
15
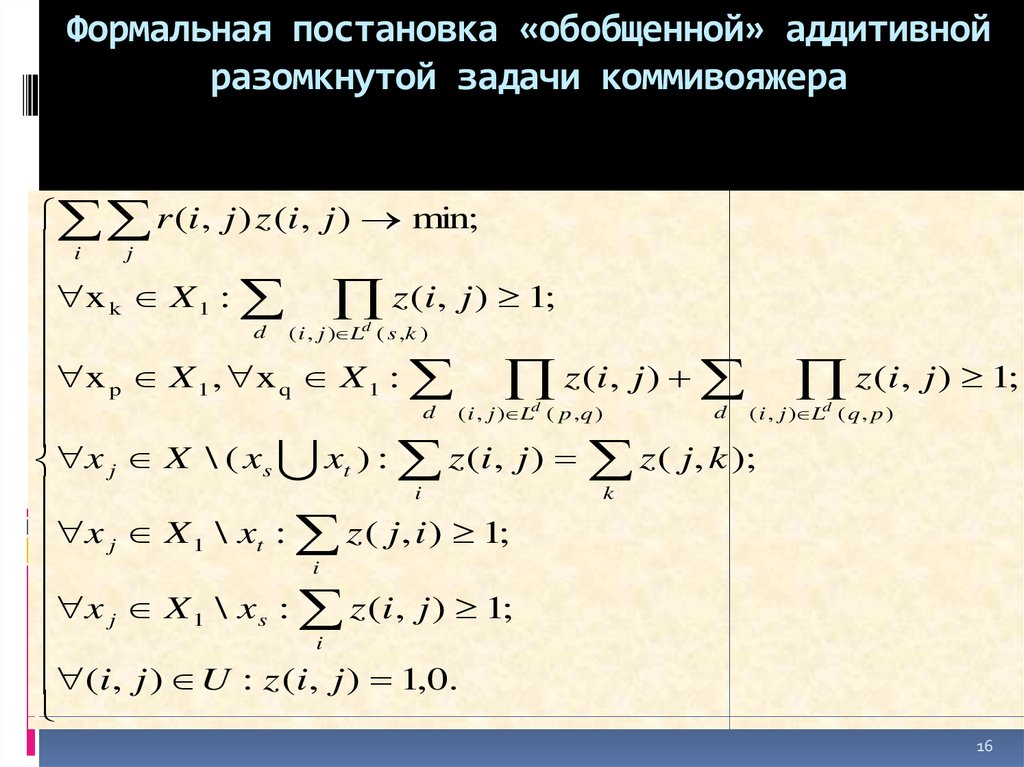
16. Формальная постановка «обобщенной» аддитивной разомкнутой задачи коммивояжера
r (i , j ) z (i , j ) min;i j
z (i , j ) 1;
x k X 1 :
d ( i , j ) Ld ( s ,k )
x p X 1 , x q X 1 :
z (i , j )
z (i , j ) 1;
d ( i , j ) Ld ( p , q )
d ( i , j ) Ld ( q , p )
x j X \ ( xs xt ) : z (i , j ) z ( j , k );
i
k
x j X 1 \ xt : z ( j , i ) 1;
i
x j X 1 \ xs : z (i , j ) 1;
i
(i , j ) U : z (i , j ) 1,0.
16
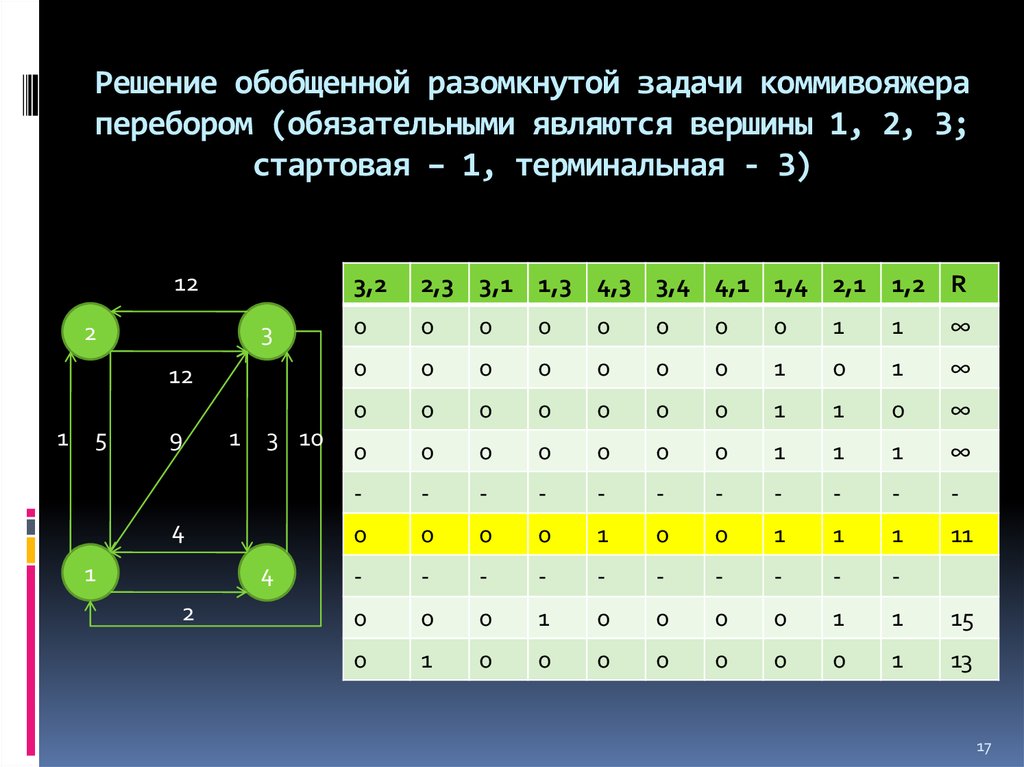
17. Решение обобщенной разомкнутой задачи коммивояжера перебором (обязательными являются вершины 1, 2, 3; стартовая – 1, терминальная - 3)
122
3
12
1
1
5
2
9
3 10
4
1
3
1
4
2
3,2
2,3 3,1 1,3 4,3 3,4 4,1 1,4 2,1 1,2 R
0
0
0
0
0
0
0
0
1
1
∞
0
0
0
0
0
0
0
1
0
1
∞
0
0
0
0
0
0
0
1
1
0
∞
0
0
0
0
0
0
0
1
1
1
∞
-
-
-
-
-
-
-
-
-
-
-
0
0
0
0
1
0
0
1
1
1
11
-
-
-
-
-
-
-
-
-
-
0
0
0
1
0
0
0
0
1
1
15
0
1
0
0
0
0
0
0
0
1
13
17
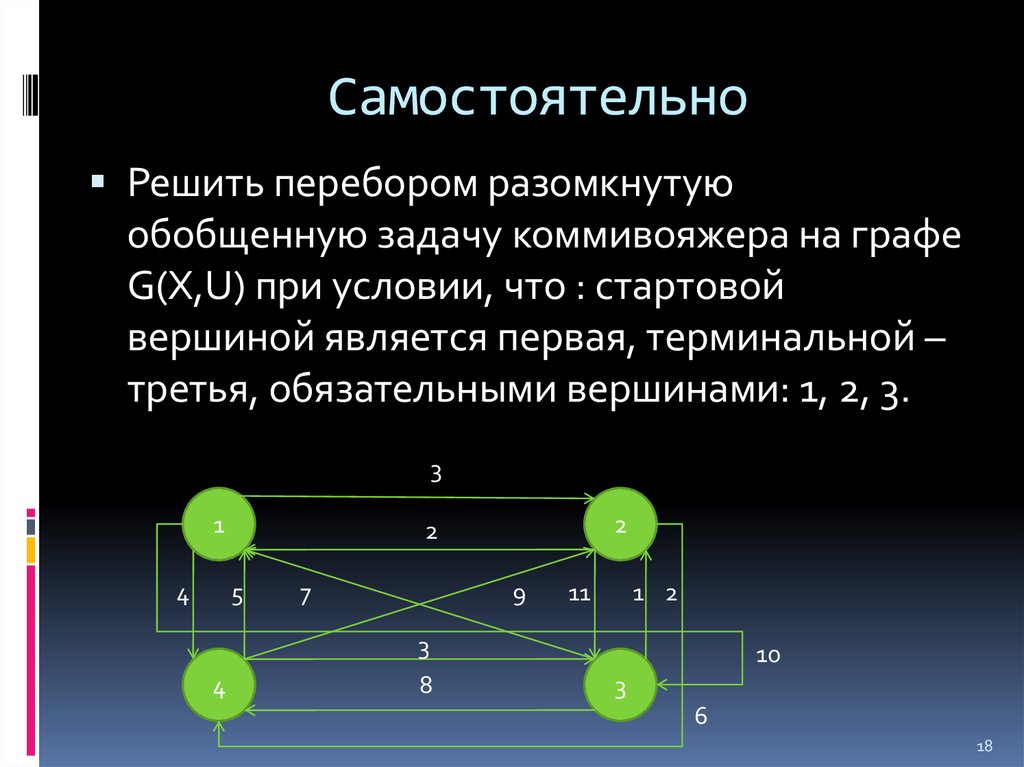
18. Самостоятельно
Решить перебором разомкнутуюобобщенную задачу коммивояжера на графе
G(X,U) при условии, что : стартовой
вершиной является первая, терминальной –
третья, обязательными вершинами: 1, 2, 3.
3
1
4
2
2
5
7
9
11
1 2
3
4
8
10
3
6
18
19. ЧАСТЬ 2
Связь задачи на разрывконтуров в сильносвязном
орграфе и обобщенной
задачи коммивояжера
19
20. Алгоритм 1
Шаг 1. На сильносвязном планарном взвешенноморграфе G(X,U) определить величину минимального
разреза R или максимальной циркуляции S.
Шаг 2. Построить орграф G’(X’,U’), двойственный графу
G(X,U).
Шаг 3. Модифицировать G’(X’,U’), добавив к каждой дуге
множества U’ параллельную и встречно
ориентированную дугу с нулевым весом. Полученный
орграф обозначить G”(X”,U”).
Шаг 4. На G”(X”,U”) решить обобщенную замкнутую
задачу коммивояжера при условии, что множество
обязательных вершин равно Х”. Длину пути
коммивояжера обозначить R1.
Шаг 5. Сравнить величины R, S, и R1.
20
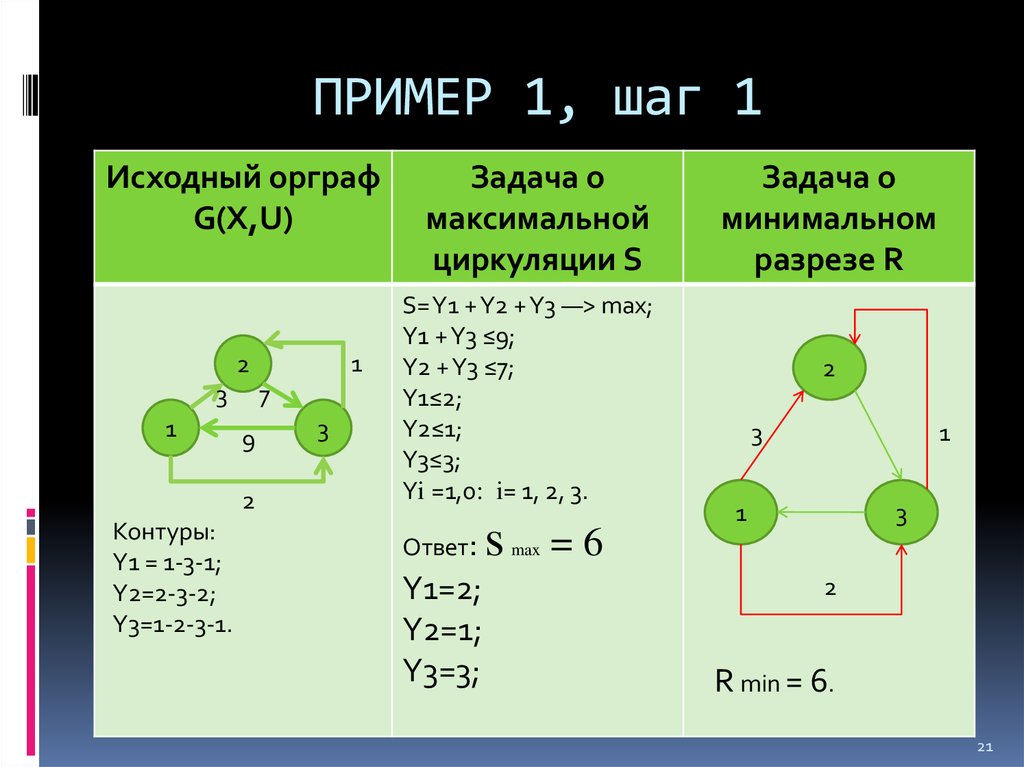
21. ПРИМЕР 1, шаг 1
Исходный орграфG(X,U)
1
2
3
1
7
9
2
Контуры:
Y1 = 1-3-1;
Y2=2-3-2;
Y3=1-2-3-1.
3
Задача о
максимальной
циркуляции S
S= Y1 + Y2 + Y3 ―> max;
Y1 + Y3 ≤9;
Y2 + Y3 ≤7;
Y1≤2;
Y2≤1;
Y3≤3;
Yi =1,0: i= 1, 2, 3.
Ответ:
Y1=2;
Y2=1;
Y3=3;
s
max
Задача о
минимальном
разрезе R
2
3
1
1
3
=6
2
R min = 6.
21
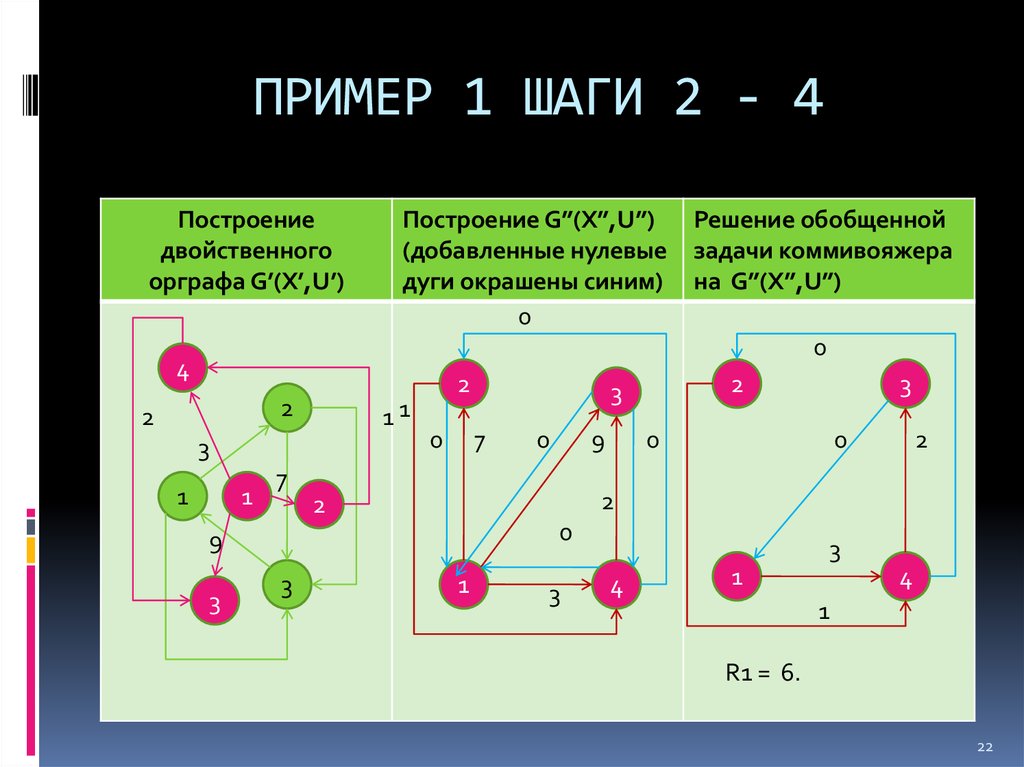
22. ПРИМЕР 1 ШАГИ 2 - 4
Построениедвойственного
орграфа G’(X’,U’)
Построение G”(X”,U”)
(добавленные нулевые
дуги окрашены синим)
0
Решение обобщенной
задачи коммивояжера
на G”(X”,U”)
0
4
2
2
11
3
1
1
2
0
7
0
9
7
0
0
0
3
3
2
2
2
9
3
2
3
1
3
3
4
1
4
1
R1 = 6.
22
23. САМОСТОЯТЕЛЬНО
Пользуясь приведенной ниже матрицей Мпостроить граф G(X,U), определить на нем
максимальную циркуляцию S и минимальный
разрез R, затем построить двойственный ему
орграф G’(X’,U’), преобразовать его в G”(X”,U”), и на
этом графе решить обобщенную задачу
коммивояжера. Ответ R1 сравнить с S и R.
M
0
0
0
1
9
0
0
0
3
2
0
0
0
1
7
0
23












 Программирование
Программирование








