Похожие презентации:
Олимпиадная физика
1.
колесоудар
Олимпиадная
физика
Задача 2 тел
продолжение
моделирование
N
Власов
Анатолий Иванович
vlasovai@bk.ru
N
2.
Олимпиаднаяфизика
Власов
Анатолий Иванович
vlasovai@bk.ru
3.
4.
5.
6.
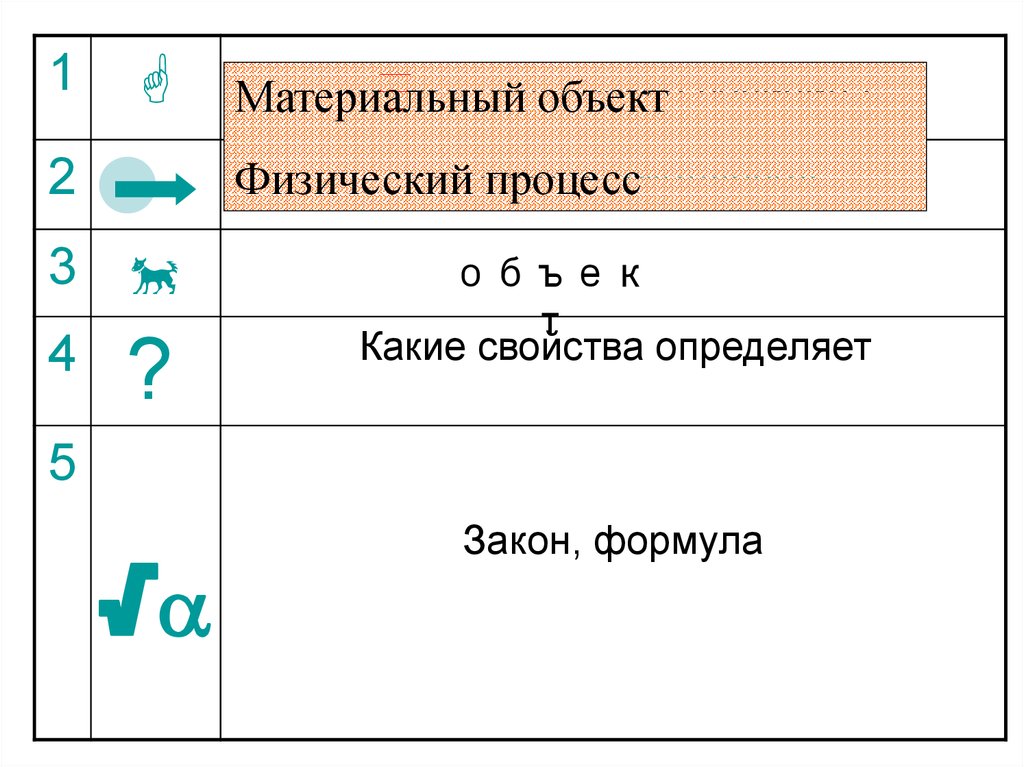
физическаявеличина
7.
1☻– физическая
Материальный
объект величина
векторная,
Физический
процессскалярная
2
3
4
?
объек
т
Какие свойства определяет
5
Закон, формула
√
8.
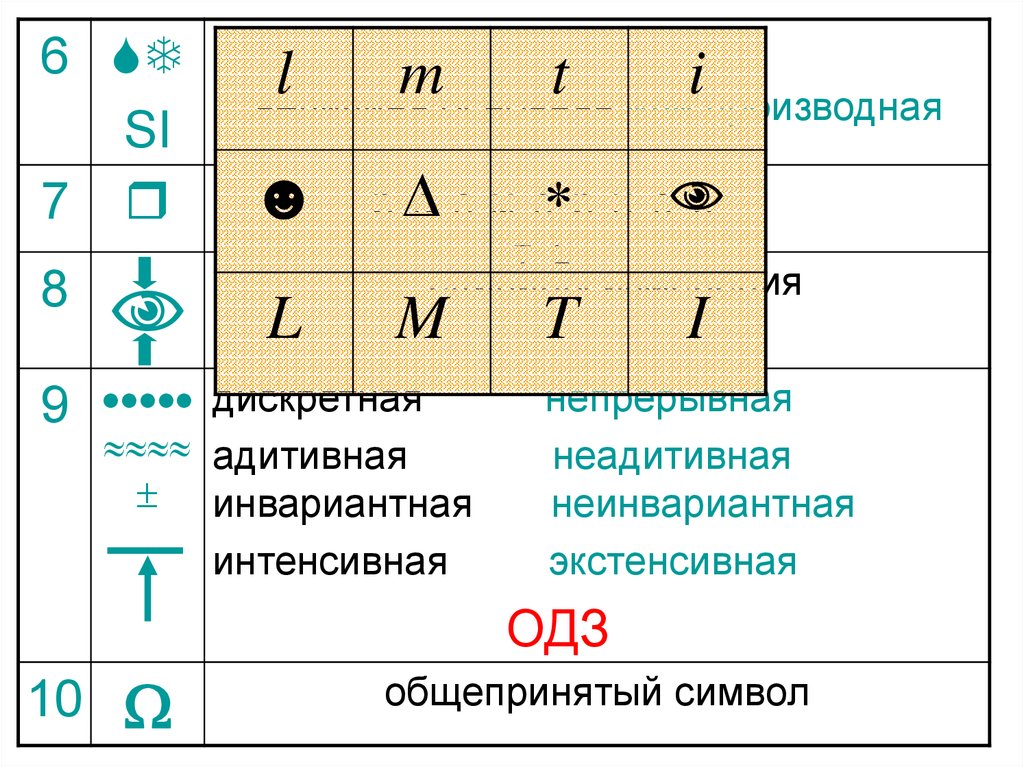
6SI
7
l
m
t
i
величина основная или производная
☻
размернос
ть
единицы измерения
8
9
дискретная
адитивная
инвариантная
интенсивная
L
M
T
I
непрерывная
неадитивная
неинвариантная
экстенсивная
ОДЗ
10
общепринятый символ
9.
1векторная
2
3
4
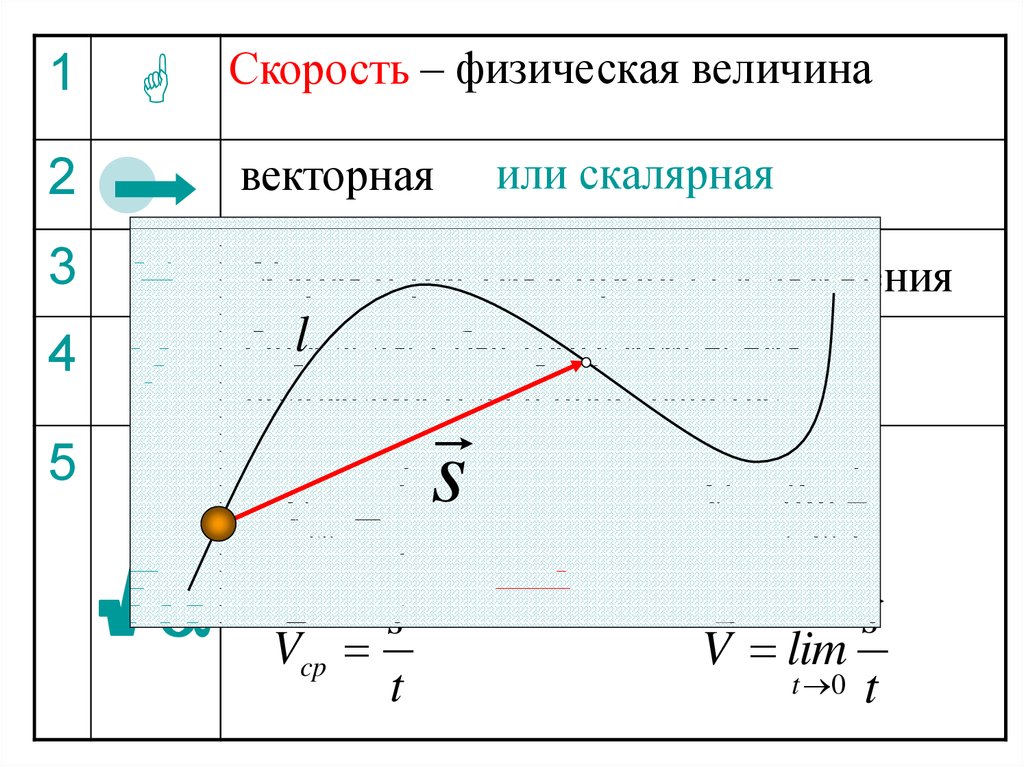
Скорость – физическая величина
или скалярная
Характеристика процесса движения
?
l
Определяет
быстроту изменения
положения тела в пространстве
5
Vcp
√
l s
t
s
Vcp
t
l
V lim
t 0 t
s
V lim
t 0 t
10.
6SI
7
8
9
величина производная
L
T
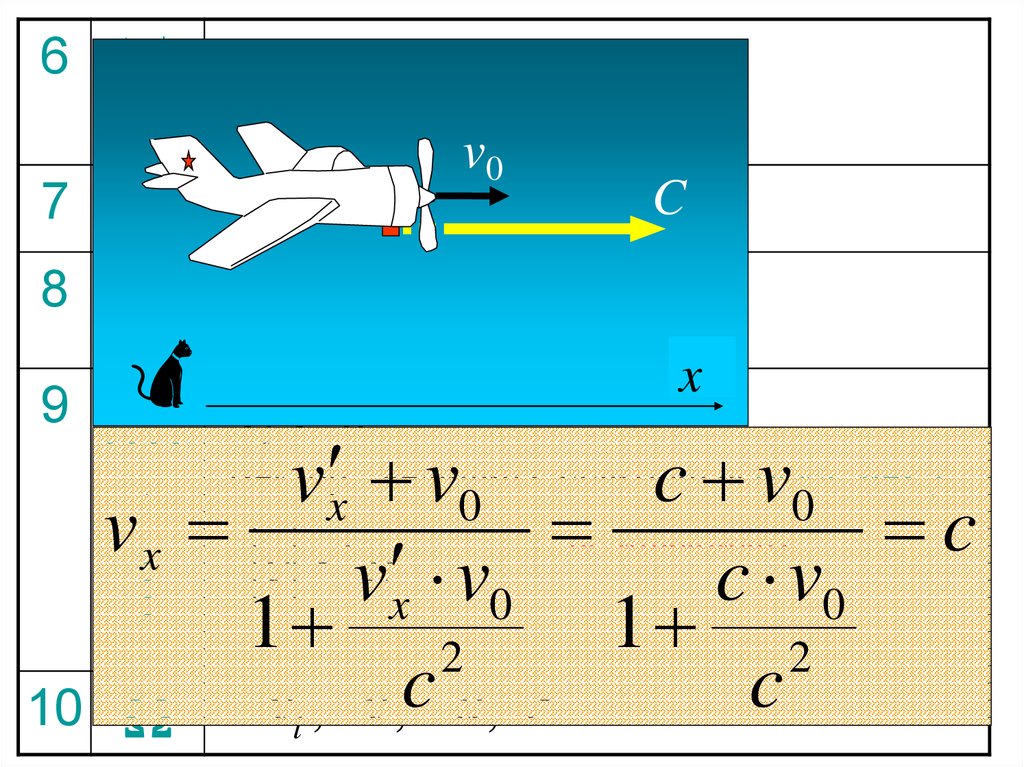
v0
C
м/с
v 0
x
l
Вектор
величина
аддитивная
(в
кл.
мех.)
x
0
0
не инвариант
x
v v
c v
v v c
c
v x v0
c v0
1 2
1 2
c
c
vl , v , u, c
10
11.
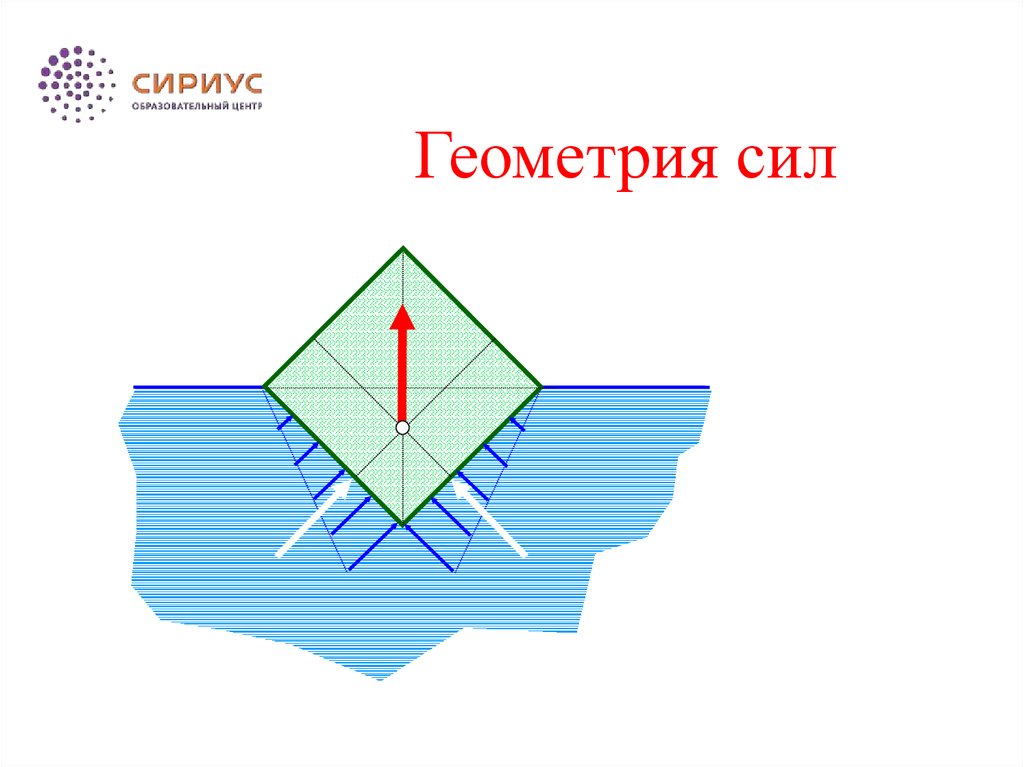
Геометрия сил12.
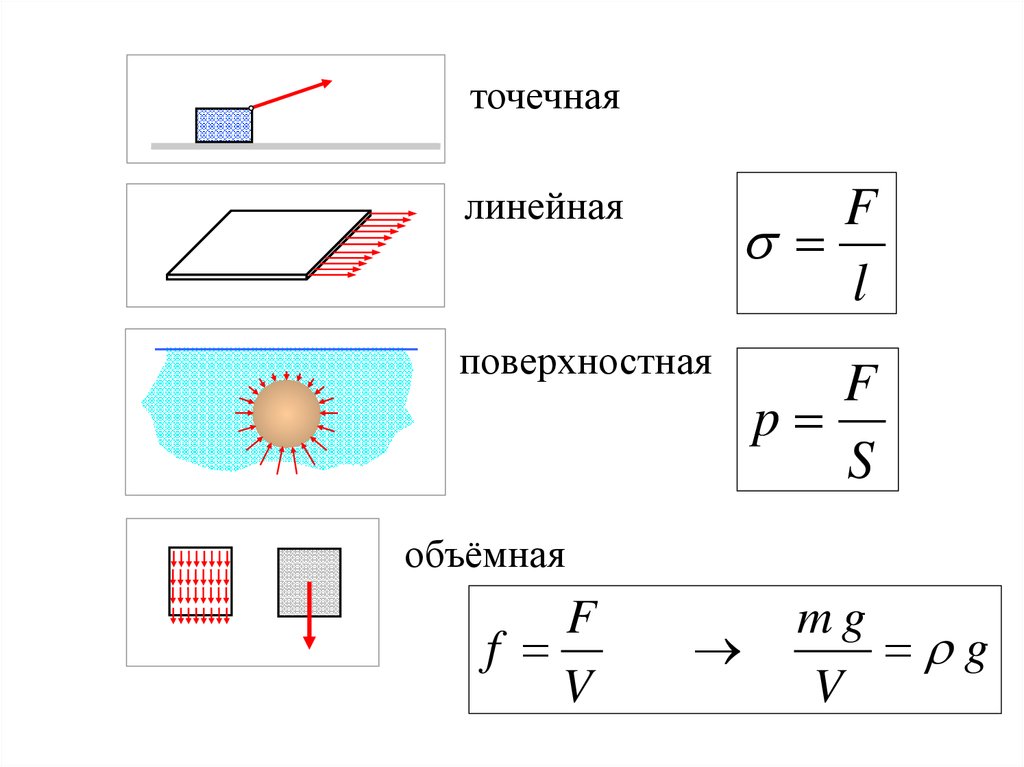
точечнаялинейная
F
l
поверхностная
F
p
S
объёмная
F
f
V
mg
g
V
13.
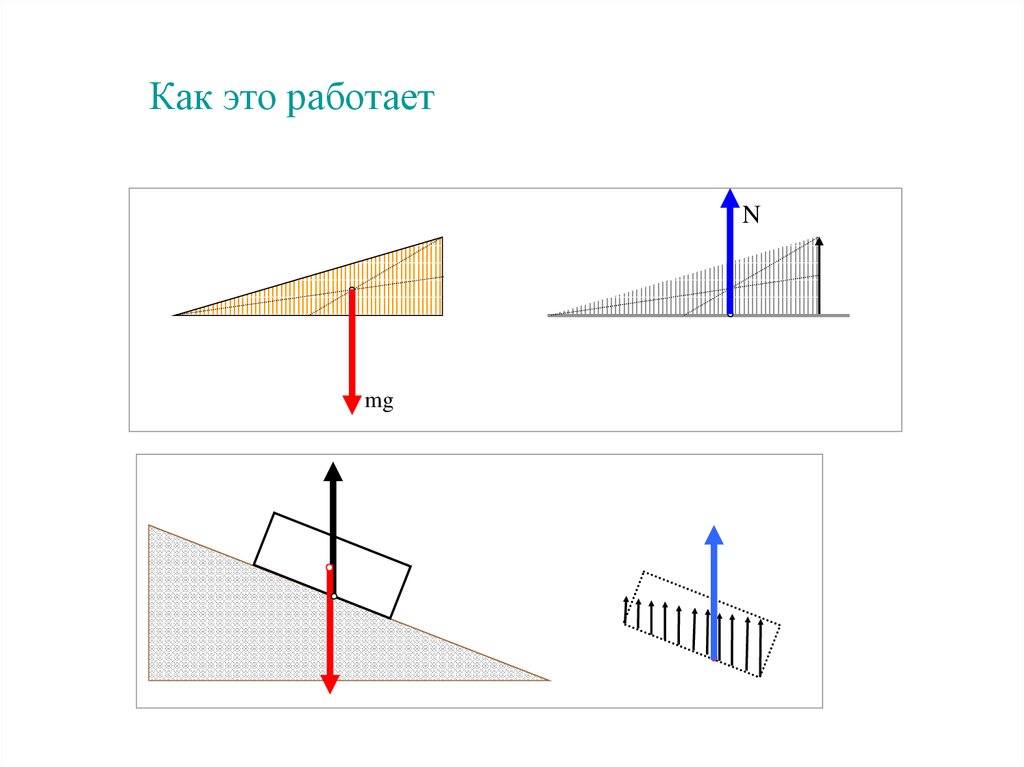
Как это работаетN
mg
14.
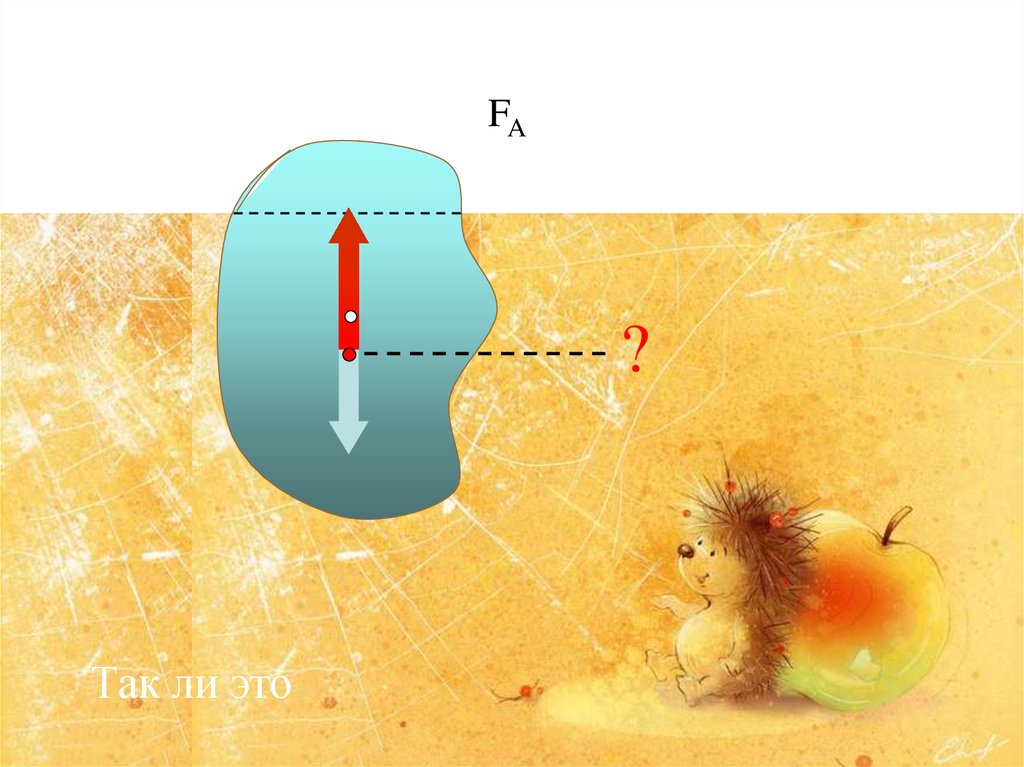
FA?
Так ли это
15.
Проблемы силы Архимеда16.
Явление Архимеда, закон.Простота и сложность.
z
F P dS P dV
S
V
k g dV m g
17.
ЯвлениеКто виноват (причина)
Закон
Почему именно так, а не иначе
?
18.
Явлениепоявление силы, направленной вверх
Кто виноват
неоднородность давления
Закон
F=-
m
g
Почему именно так, а не иначе
P= gh
∇ P=- g
19.
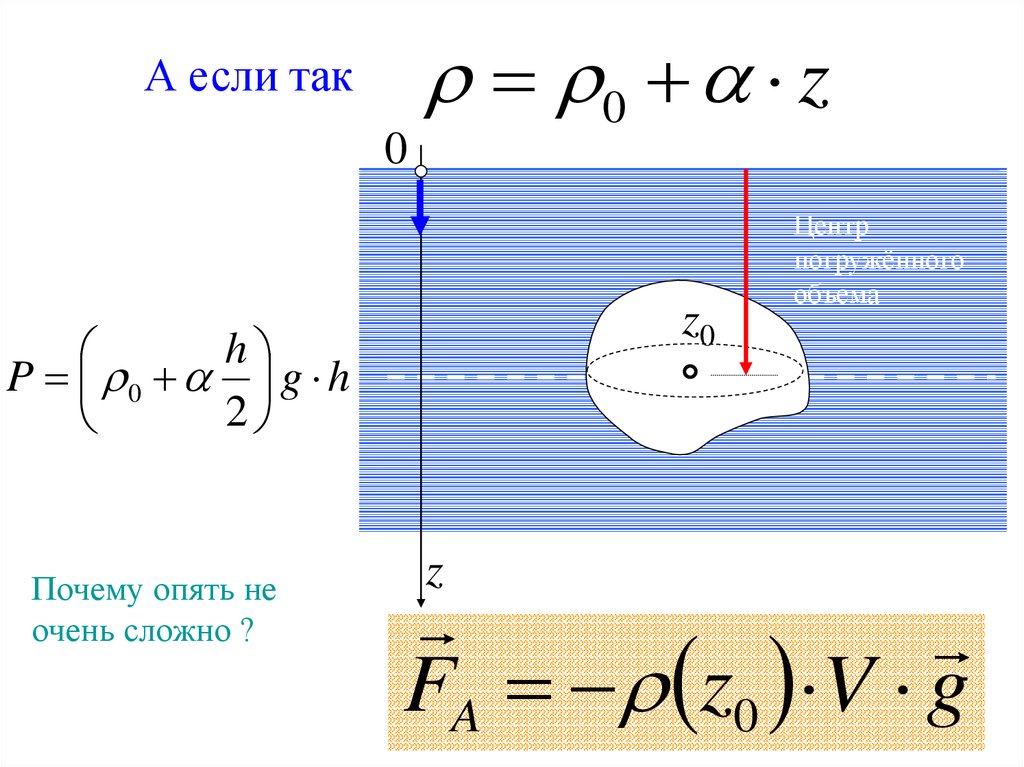
0 zА если так
0
z0
h
P 0 g h
2
Почему опять не
очень сложно ?
z
Центр
погружённого
объема
FA z0 V g
20.
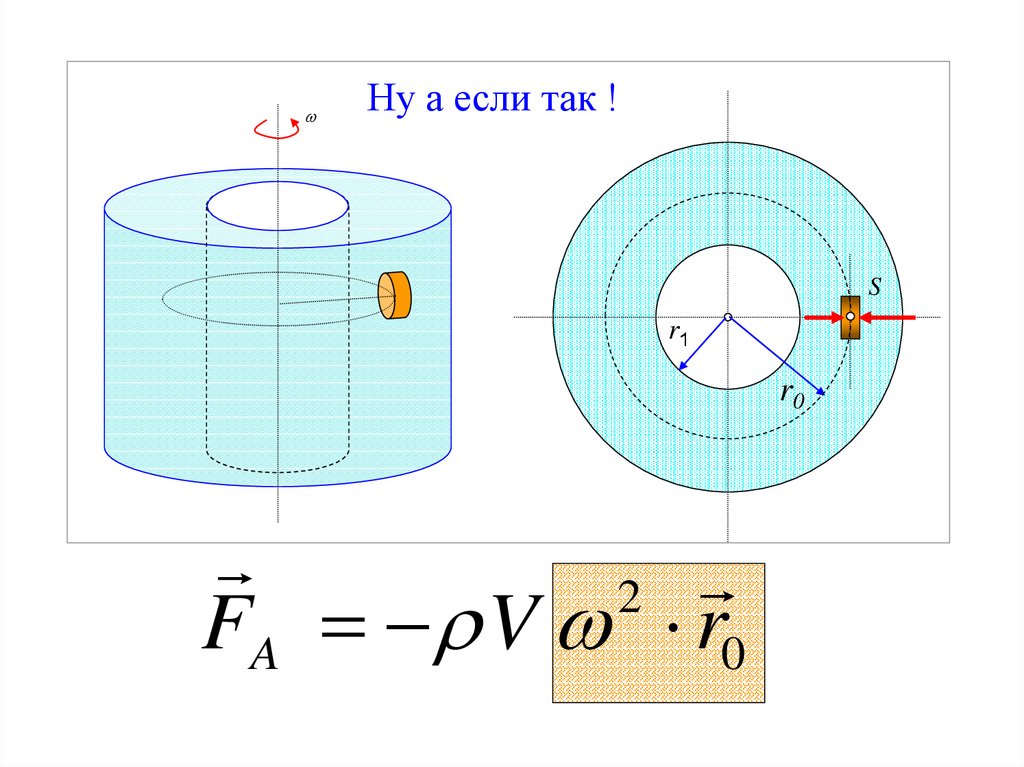
Ну а если так !S
r1
r0
2
FA V r0
21.
Удар22.
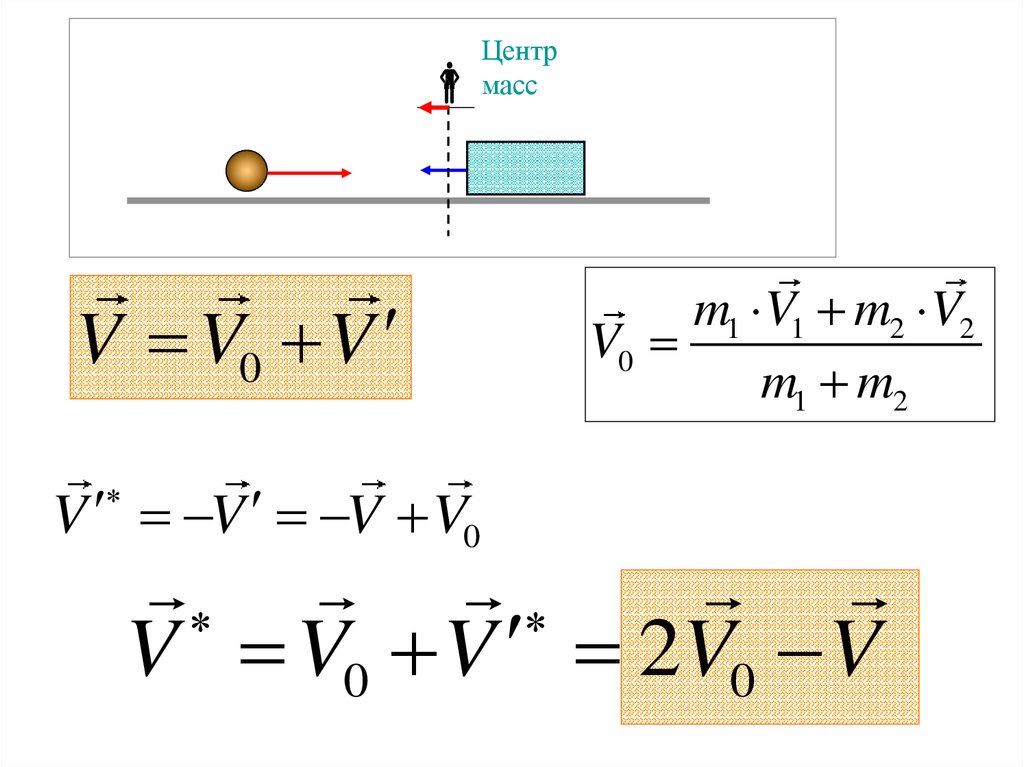
V V0 VV V V V0
Центр
масс
m1 V1 m2 V2
V0
m1 m2
V V0 V 2V0 V
23.
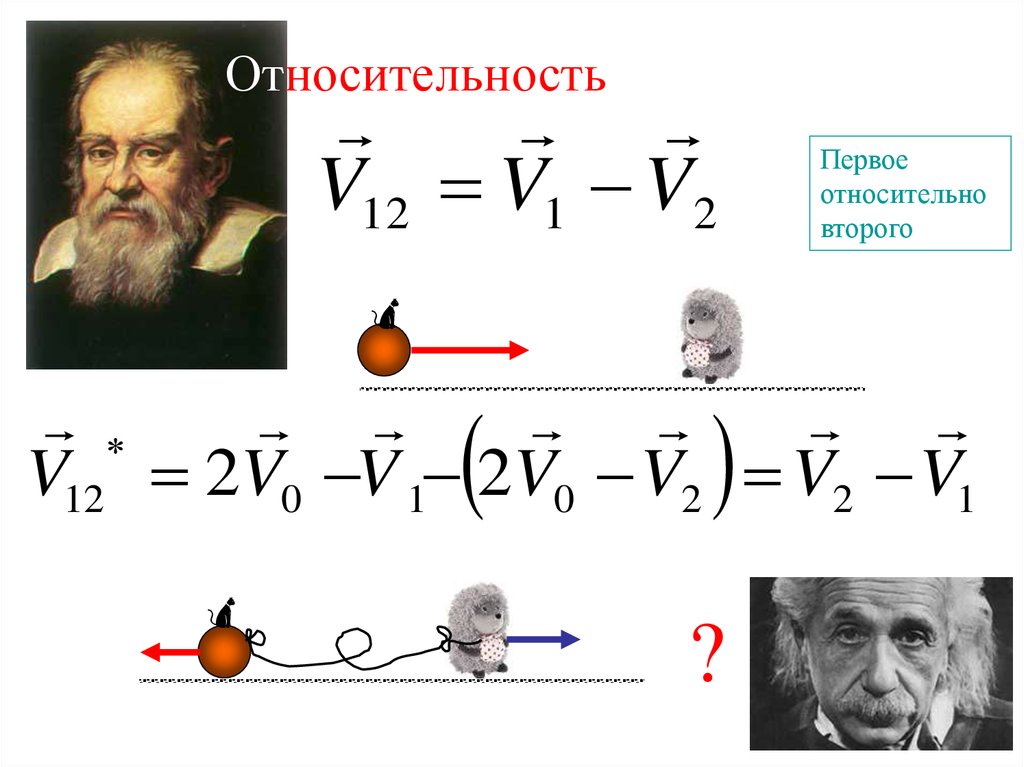
ОтносительностьV12 V1 V2
Первое
относительно
второго
V12 2V0 V 1 2V0 V2 V2 V1
?
24.
Удар ещё удар1
V 2 V0 V1
V2 2 V0
1
V
2 V0 2 V0 V1 V1
V2 2 V0 2 V 0
25.
задачаm
M
s ?
a
t
V1
m V1 a
a
m
S V2 t 2V0 2
2a
V1
m M V1
m M
a
t0 3
V1
26.
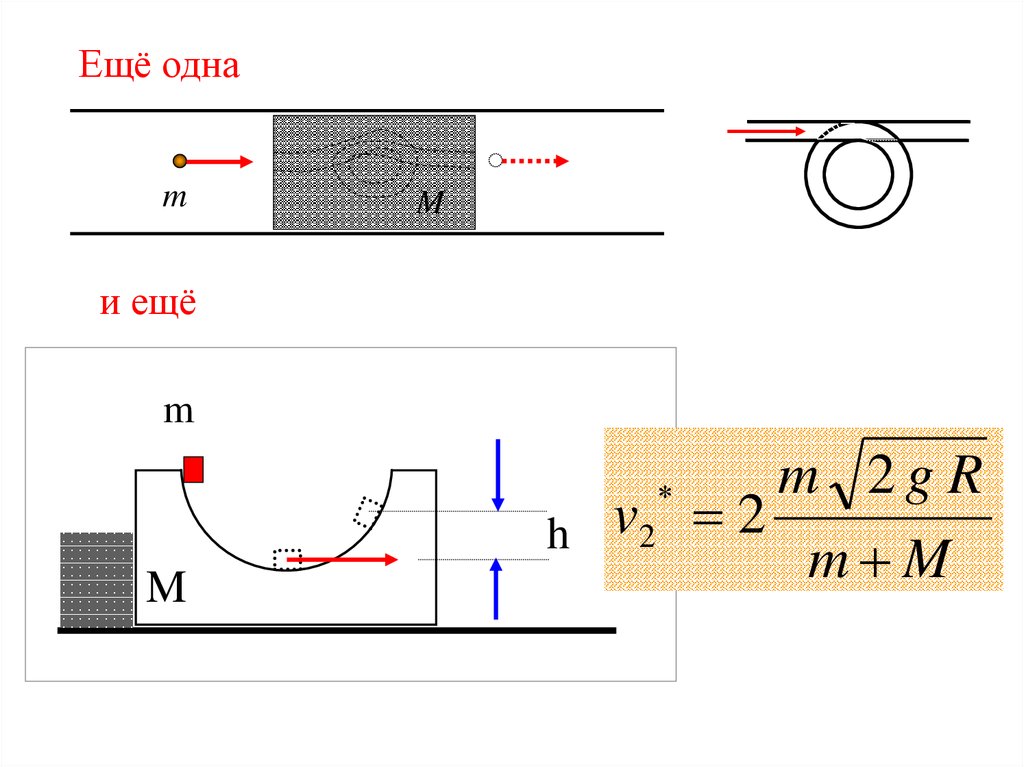
Ещё однаm
M
и ещё
m
m 2g R
h v2 2
m M
M
27.
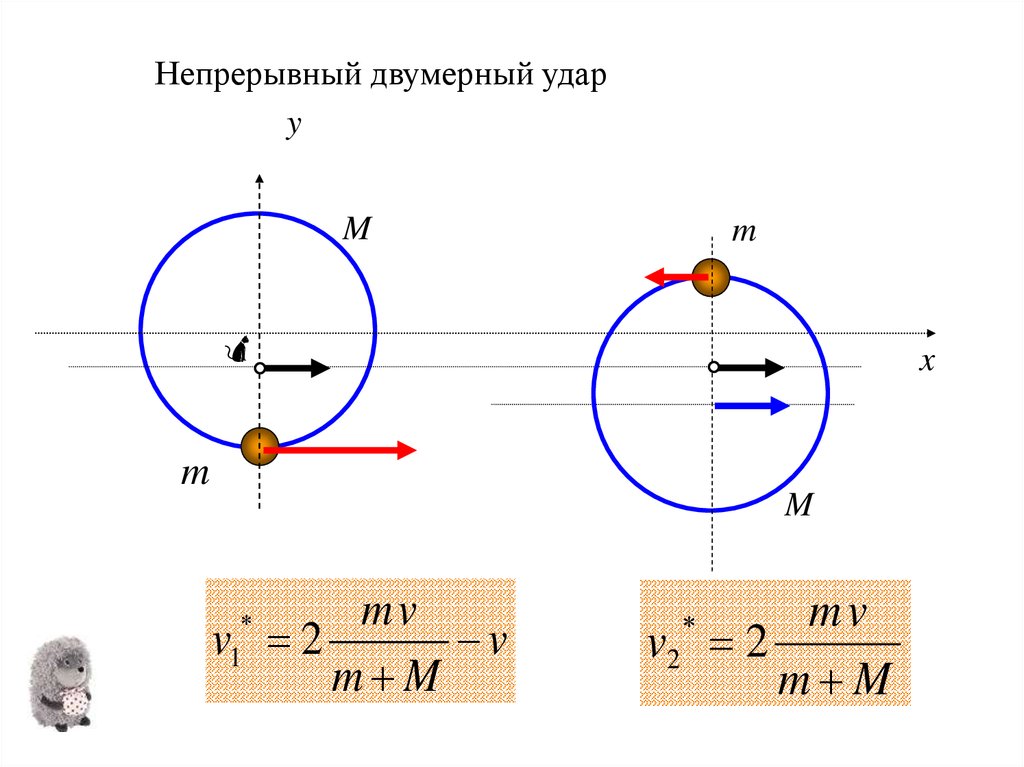
Непрерывный двумерный ударy
M
m
x
m
M
mv
v 2
v
m M
1
mv
v2 2
m M
28.
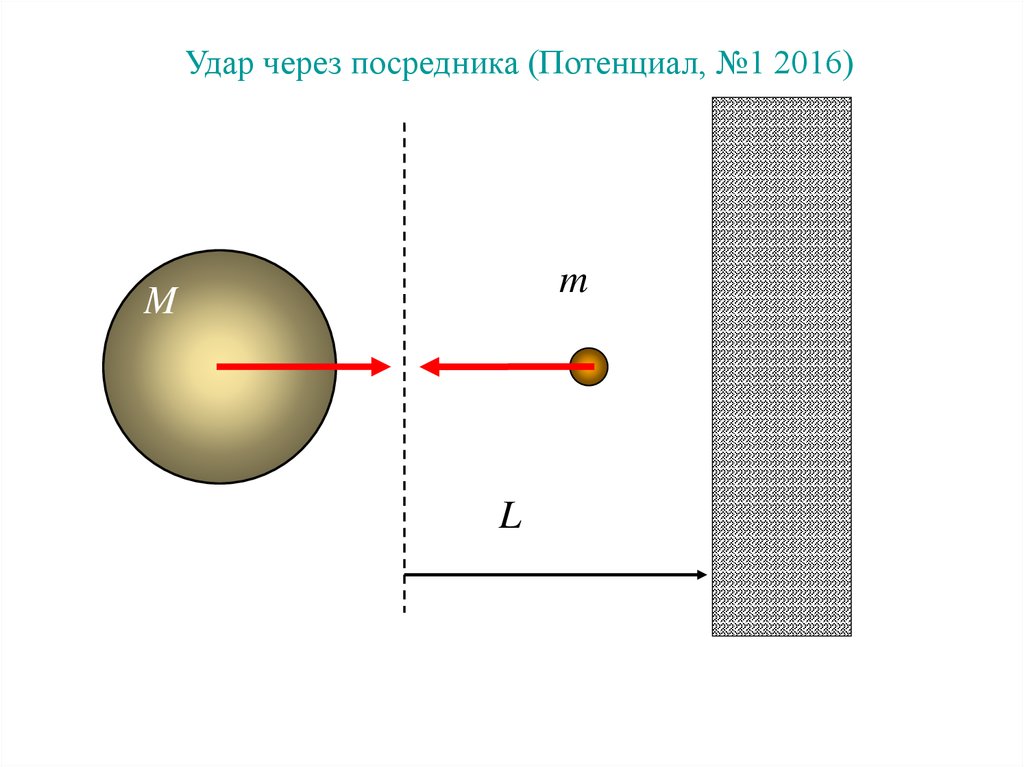
Удар через посредника (Потенциал, №1 2016)m
M
L
29.
Задача двух телэнергетика
30.
Рисункиматематика
Анатолий
Тимофеевич
Фоменко (р. 13
марта 1945,
Сталино (теперь Донецк),
Украинская ССР,
СССР) —
советский и
российский
учёныйматематик,
специалист по
топологии и ряду
других
направлений,
доктор физикоматематических
наук, а также
художник.
31.
Пространственнаязадача тел в
небесной
механике.
32.
33.
ТОПОЛОГИЧЕСКАЯ ЗАДАЧА "ОРАСЦЕПЛЕНИИ ЗАЦЕПЛЕННЫХ ПАЛЬЦЕВ"
Изображены этапы решения задачи: как
расцепить посредством гомеоморфизма
человеческого тела пальцы рук,
зацепленные как показано на начальном
рисунке? При этом разрешаются
произвольные непрерывные деформации
фигуры (гомеоморфизмы). Необходимая
последовательность деформаций
(изотопия) показана на рисунках. Впрочем,
здесь следует отметить одну тонкость.
Успешное решение задачи, показанное нами,
возможно лишь в том случае, когда человек
"обнажен по пояс". Если, например, у него
на руке надеты часы, то в конце описанной
деформации пальцы рук, конечно,
расцепятся, однако "завяжется" ремешок
часов
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
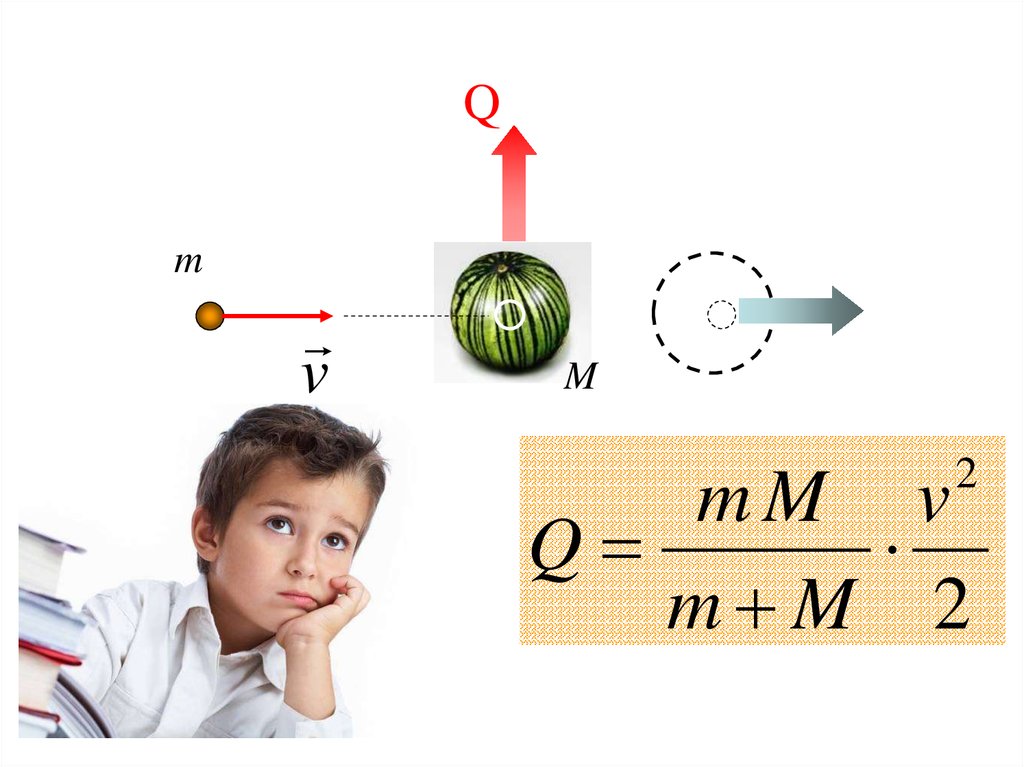
Qm
v
M
2
mM v
Q
m M 2
47.
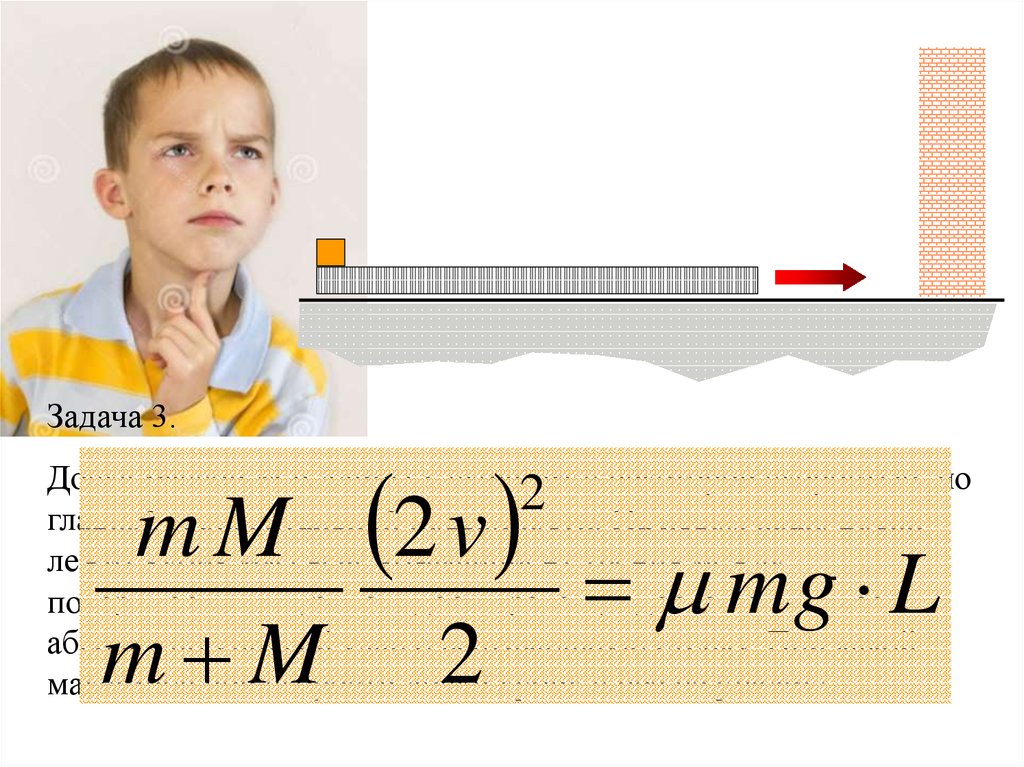
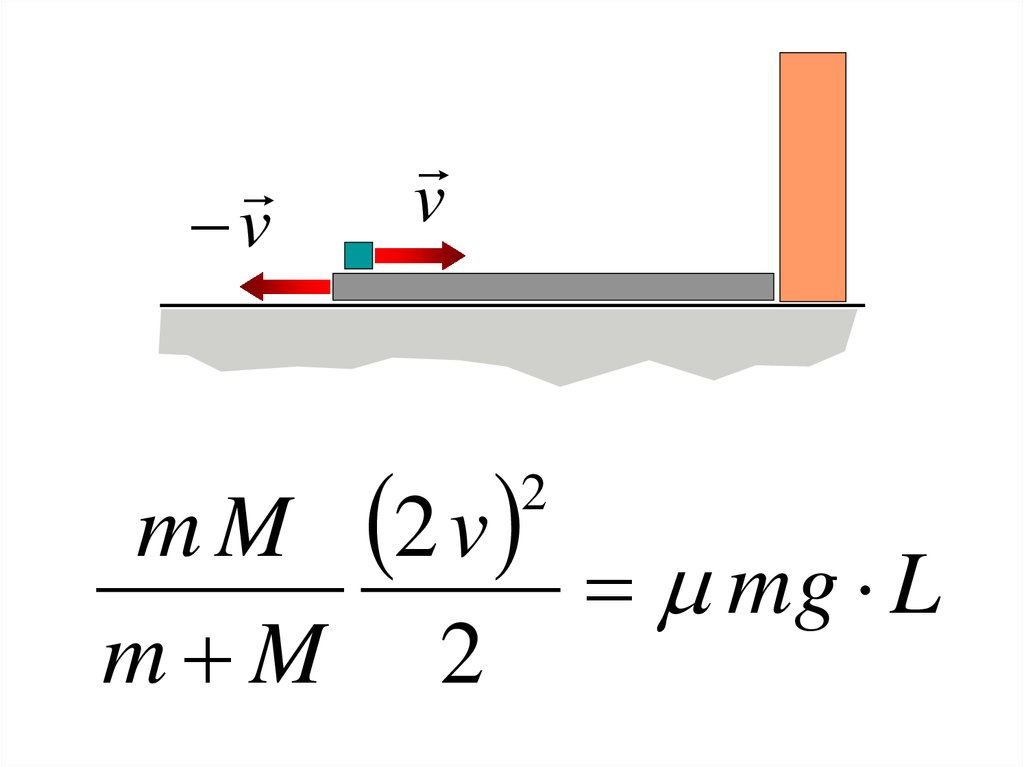
Задача 3.m M 2 v
mg L
m M 2
Доска массой M и длины L скользит с некоторой скоростью по
2
гладкой горизонтальной поверхности. На левом краю доски
лежит кубик массы m. коэффициент трения между
поверхностями кубика и доски равен . доска испытывает
абсолютно упругий удар о вертикальную стенку. При какой
максимальной скорости доски кубик с неё не упадет?
48.
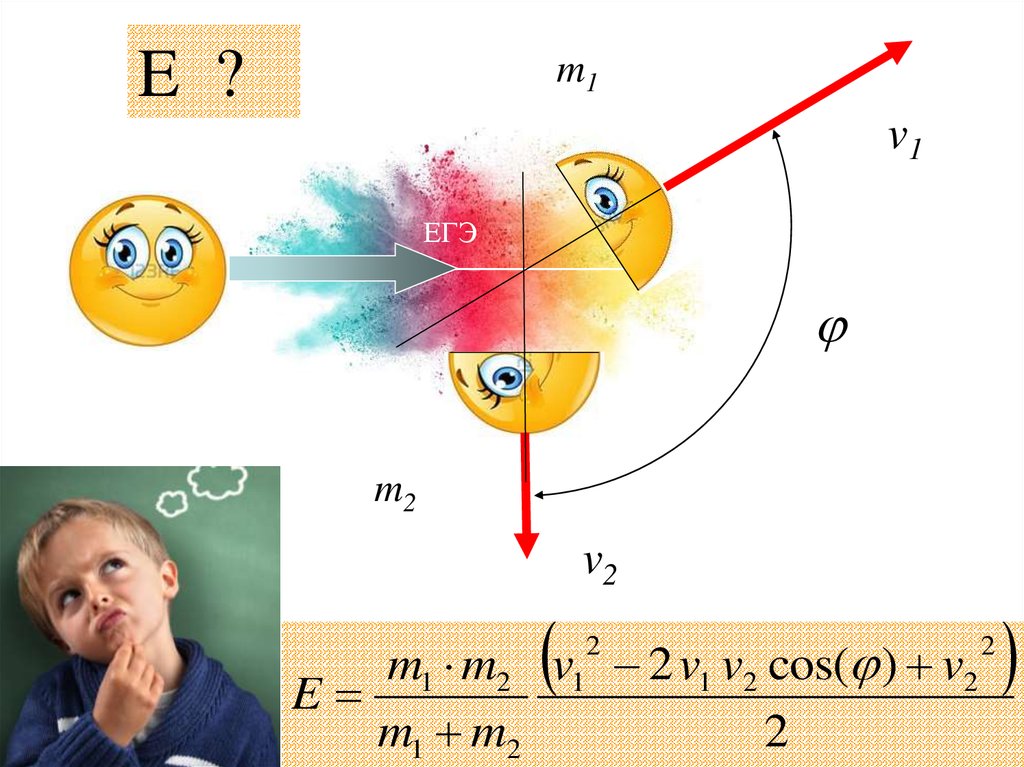
E ?m1
v1
ЕГЭ
m2
v2
m1 m2 v1 2 v1 v2 cos( ) v2
E
m1 m2
2
2
2
49.
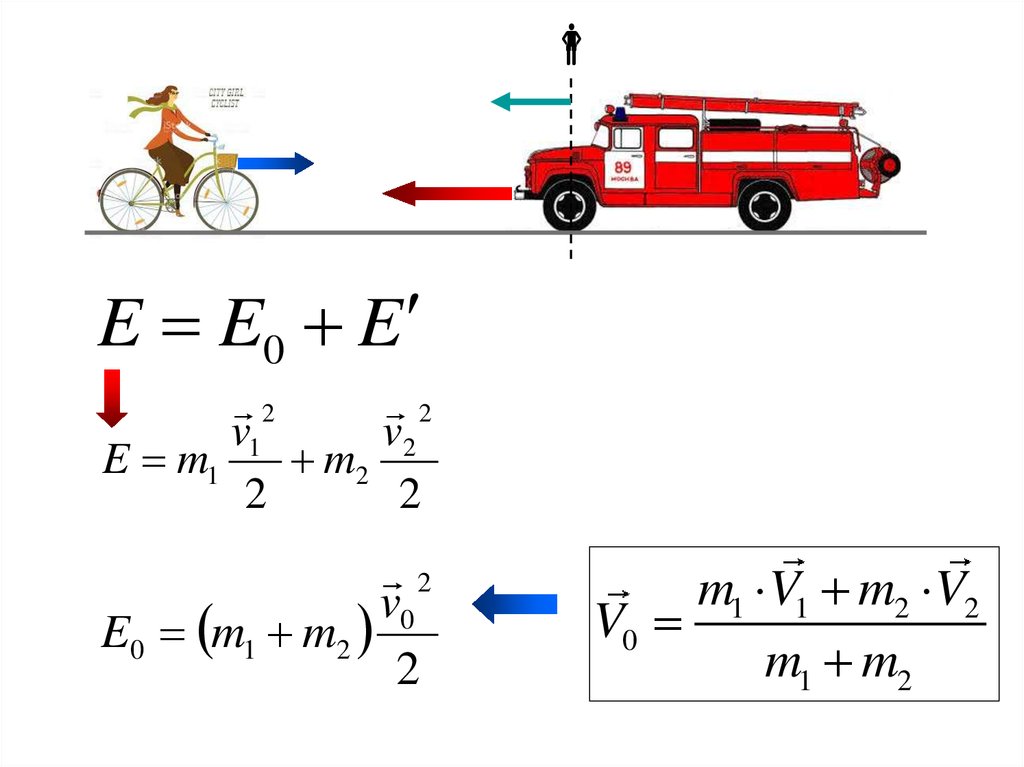
E E0 E2
2
v1
v2
E m1
m2
2
2
2
v0
E0 m1 m2
2
m1 V1 m2 V2
V0
m1 m2
50.
2m1 m2 v1 v2
E
m1 m2
2
51.
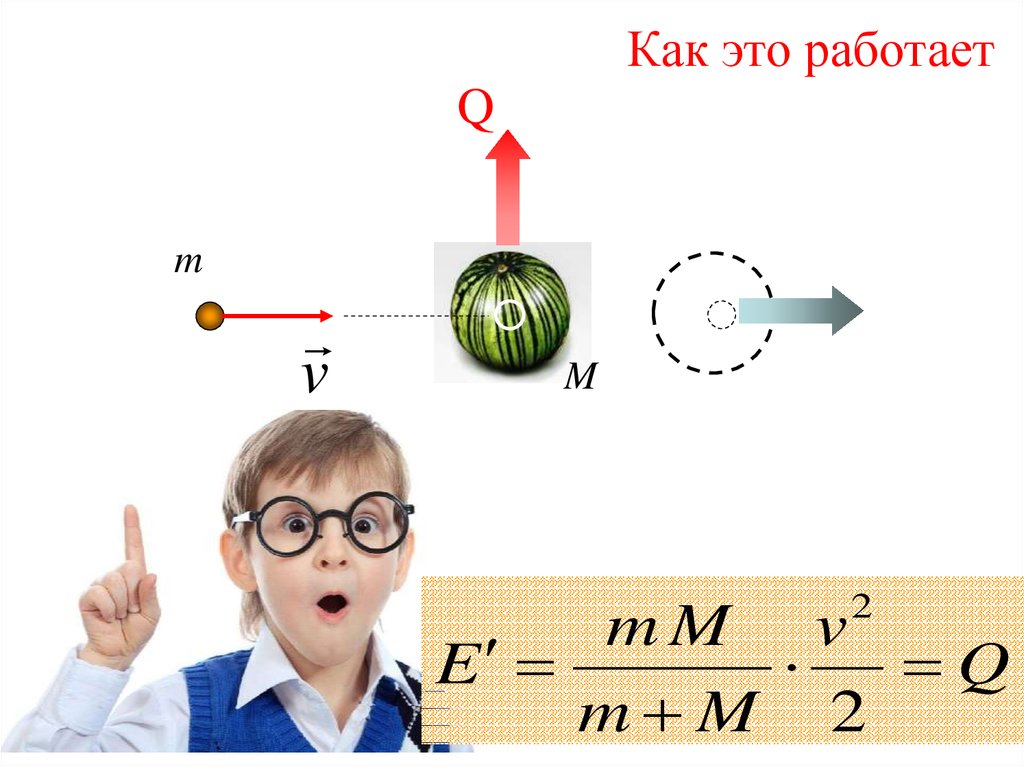
Как это работаетQ
m
v
M
2
mM v
E
Q
m M 2
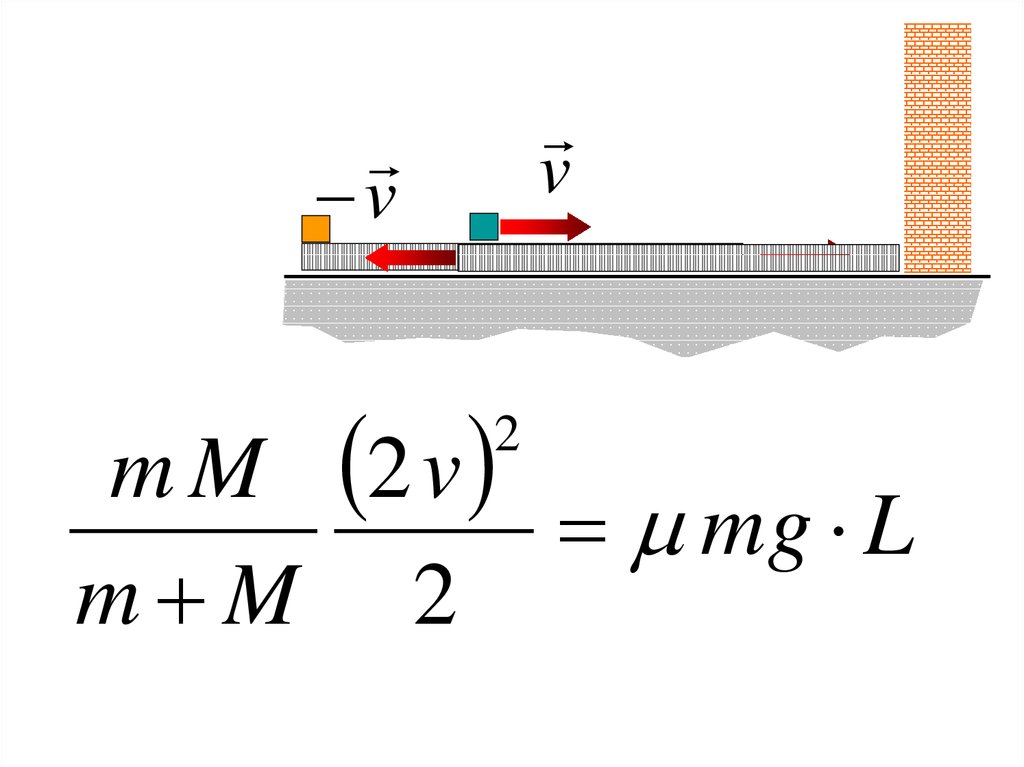
52.
vv
m M 2 v
mg L
m M 2
2
53.
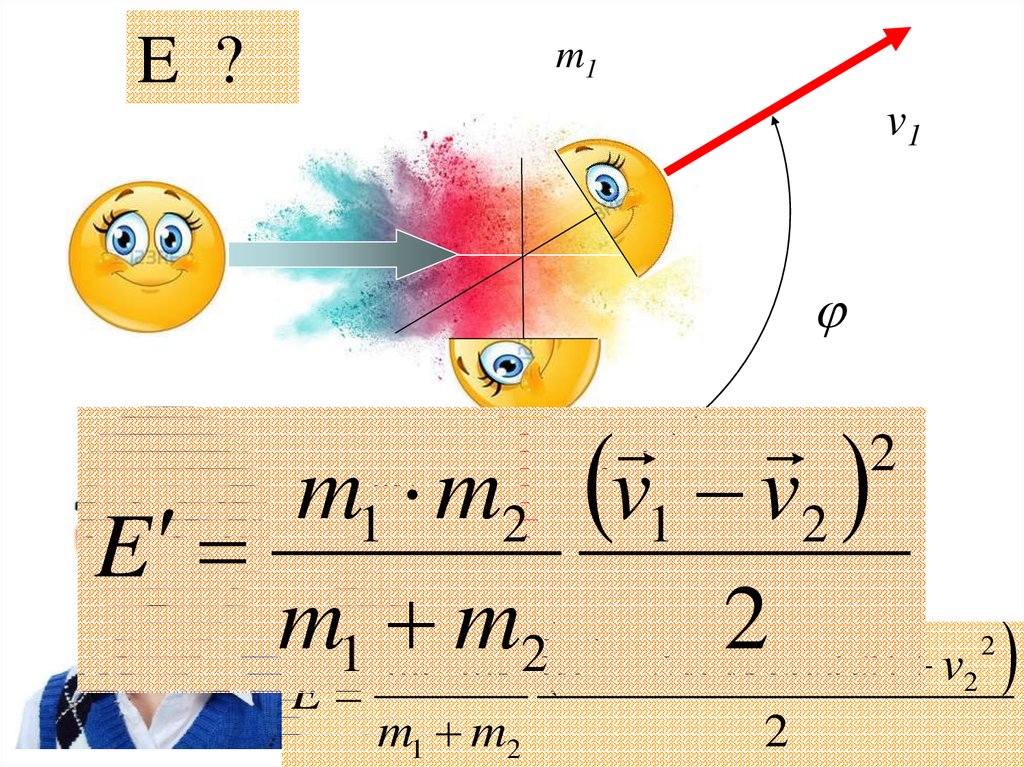
E ?m1
v1
2
m
m1 m2 v v1 v2
E
m1
m
2
m m 2 v 2 v v cos( ) v
E
2
2
2
1
2
m1 m2
1
2
1
2
2
2
54.
mM
h
mM 2g R m M
mgh
m M
2
h R
m M
v 2g R
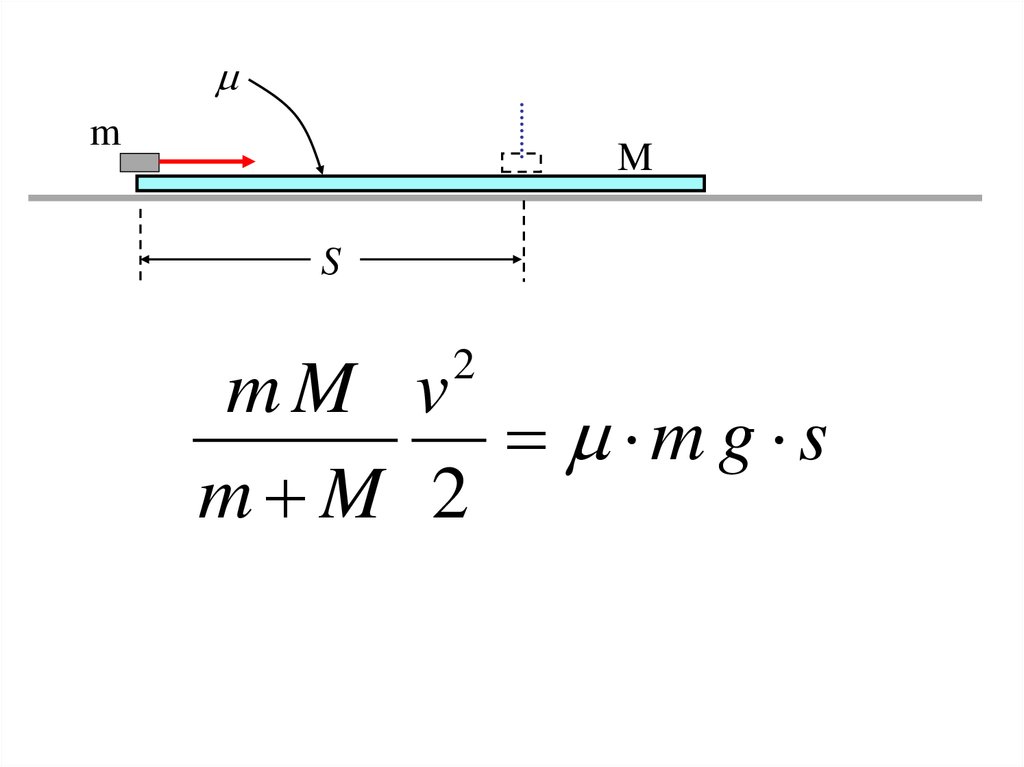
55.
mM
S
2
mM v
m g s
m M 2
56.
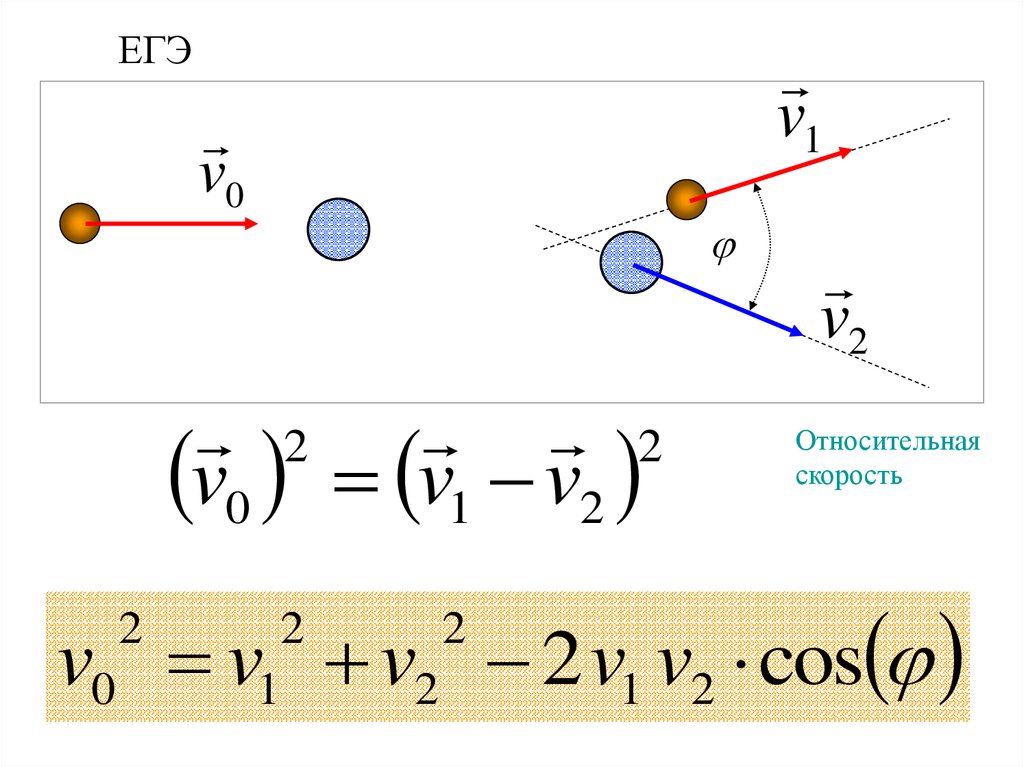
ЕГЭv1
v0
2 2
v0 v1 v2
v2
Относительная
скорость
v0 v v2 2 v1 v2 cos
2
2
1
2
57.
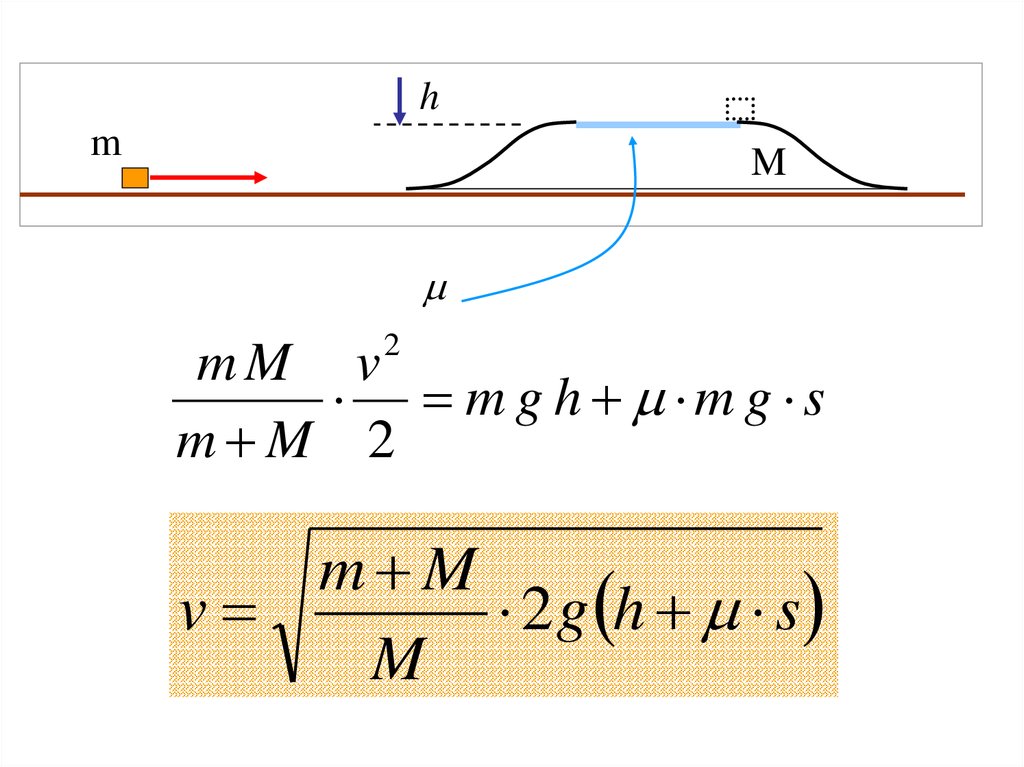
hm
M
2
mM v
m g h m g s
m M 2
m M
v
2 g h s
M
58.
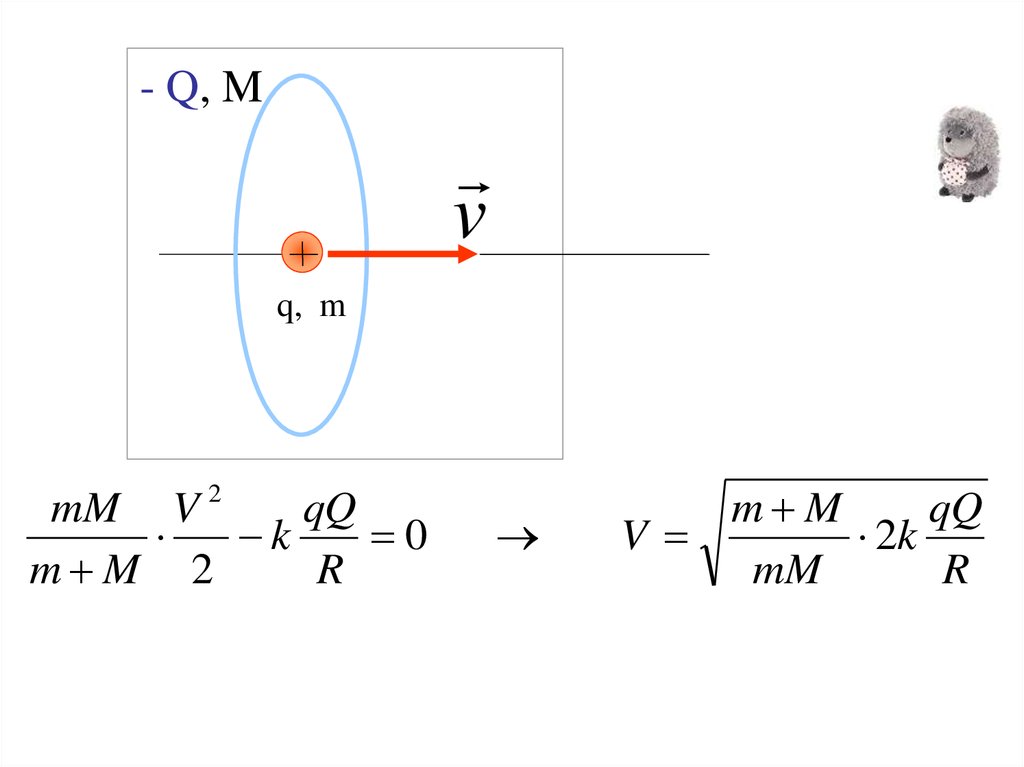
- Q, Mv
q, m
mM V 2
k
0
m M 2
R
m M
V
2k
mM
R
59.
m1m2
k
2
2
m M vx
x
k
m M 2
2
mM
T 2
m M k
2
2
v
x
m k
2
2
T 2
m
k
60.
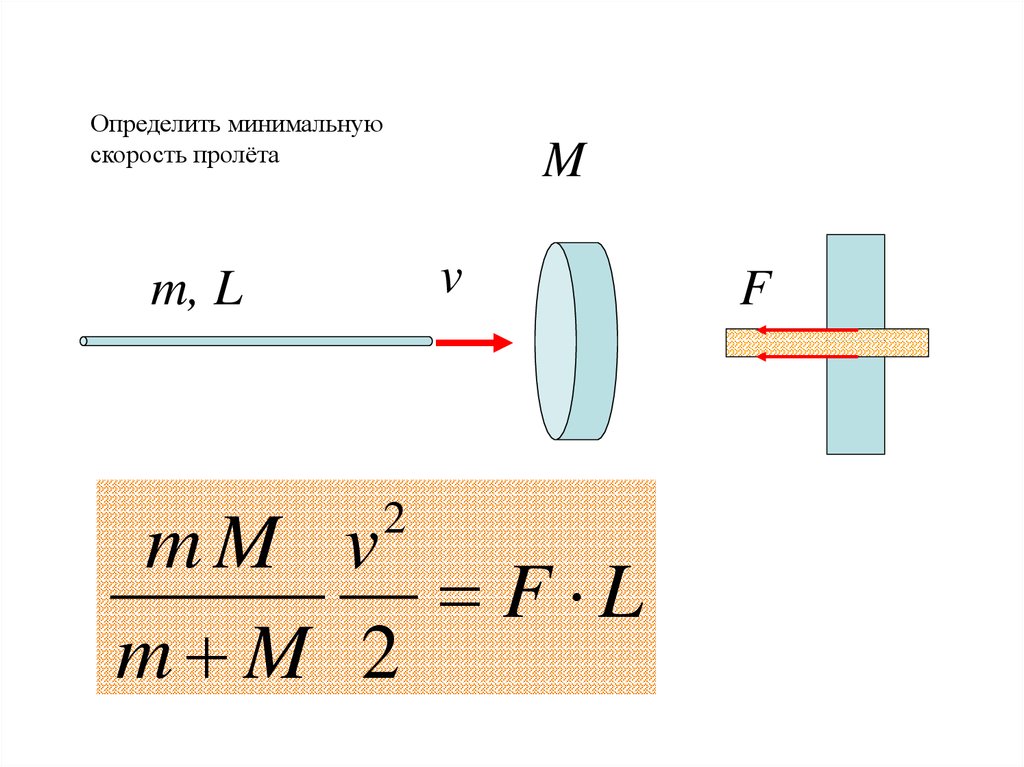
Определить минимальнуюскорость пролёта
M
v
m, L
2
mM v
F L
m M 2
F
61.
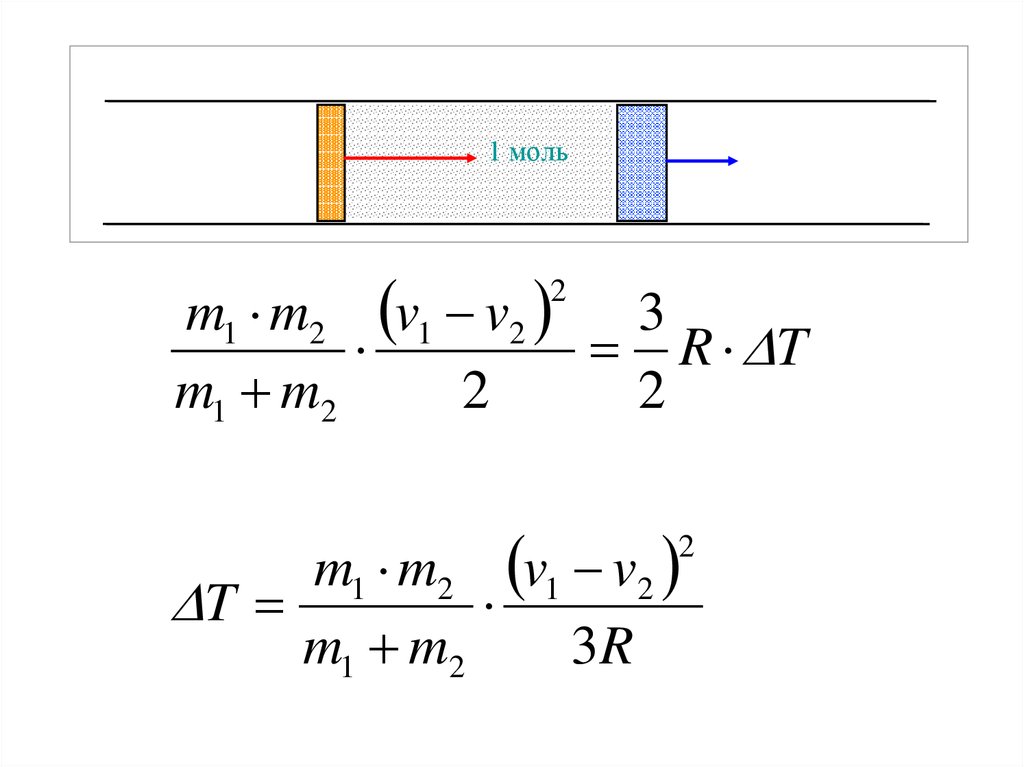
1 мольm1 m2 v1 v2
3
R T
m1 m2
2
2
2
m1 m2 v1 v2
T
m1 m2
3R
2
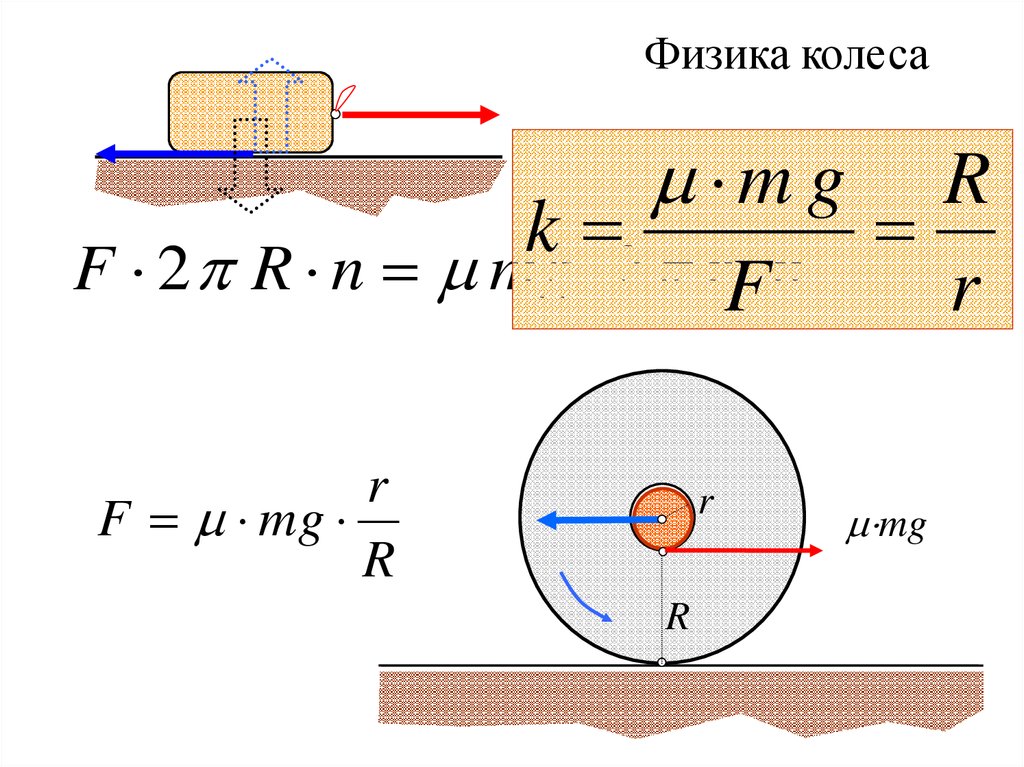
62.
Физика колесаm g
R
k
F 2 R n mg 2 rF n
r
r
F mg
R
r
R
mg
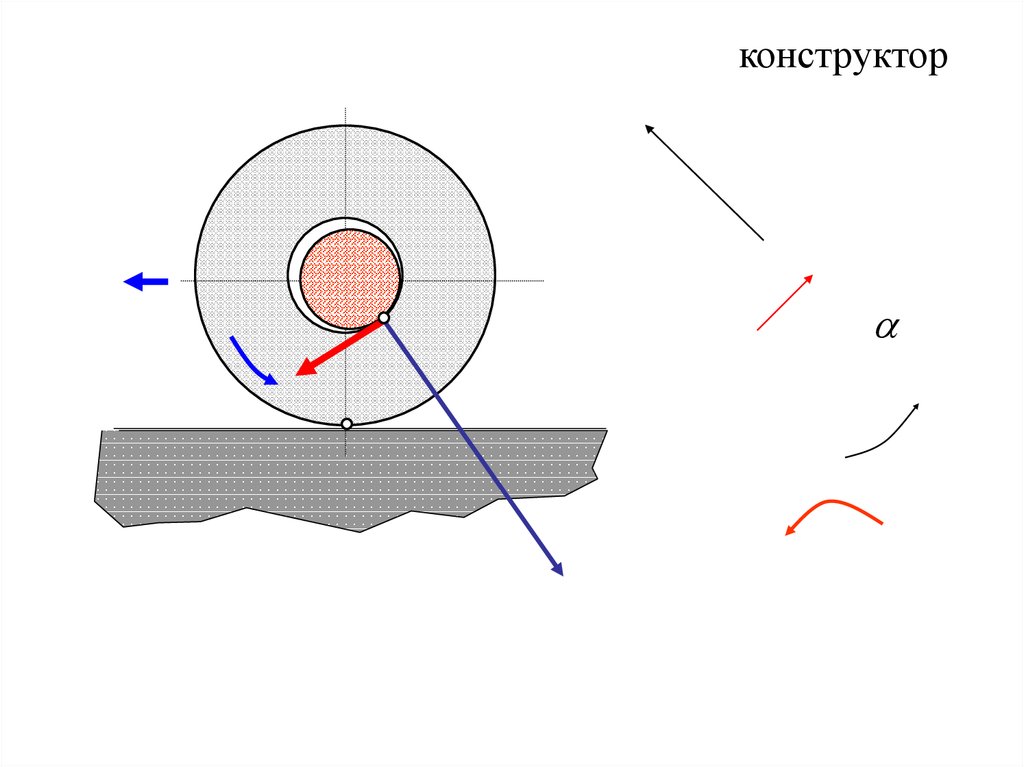
63.
конструктор64.
a 1 a2
x
N
N
1 a
2
2
x tg
r
a
R
N R Sin N R Cos r
1 a x
2
2
2 x a 0
2
2
65.
tgF mg
1 tg
F N Sin N Cos 0
N Cos N Sin m g 0
66.
a 1 a2
x
1 a
2
2
a 1
tg
F mg
1 tg
r
F mmg
g
R
2
k
R
1
F
r 1
2
2
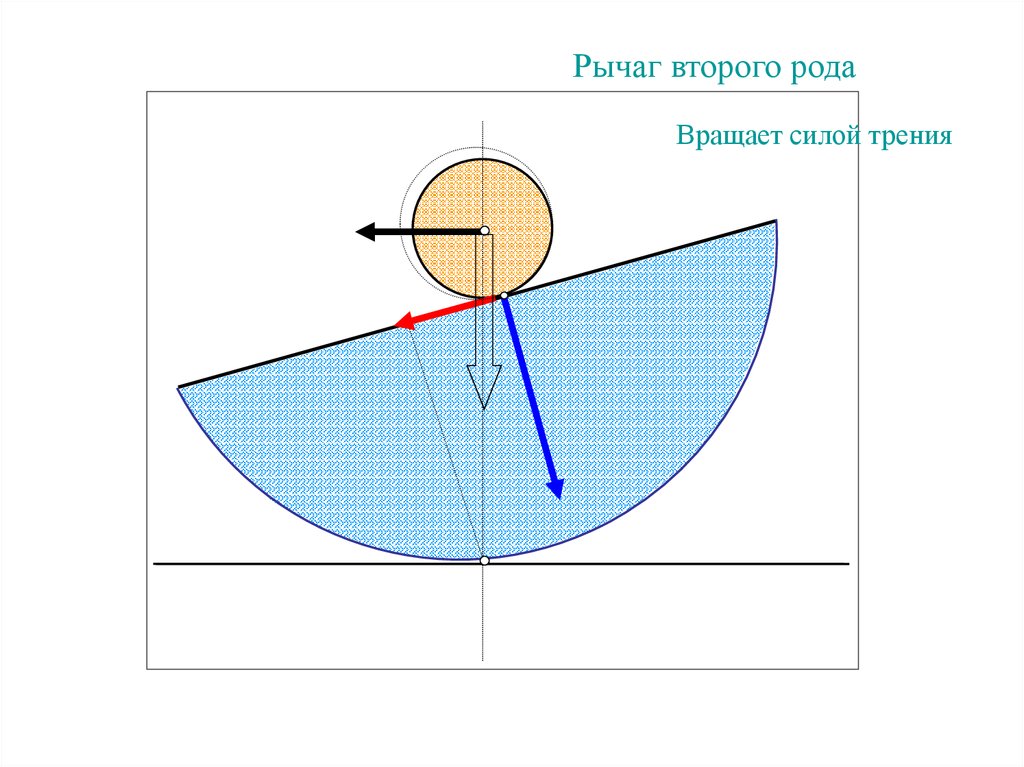
67.
Рычаг второго родаВращает силой трения
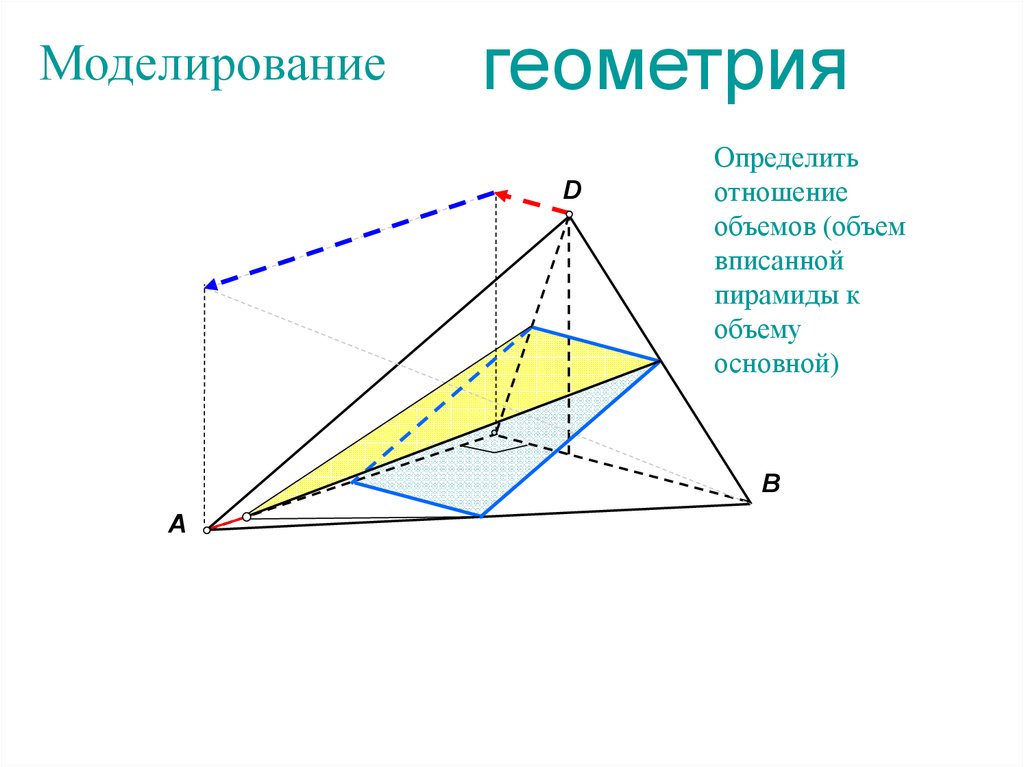
68.
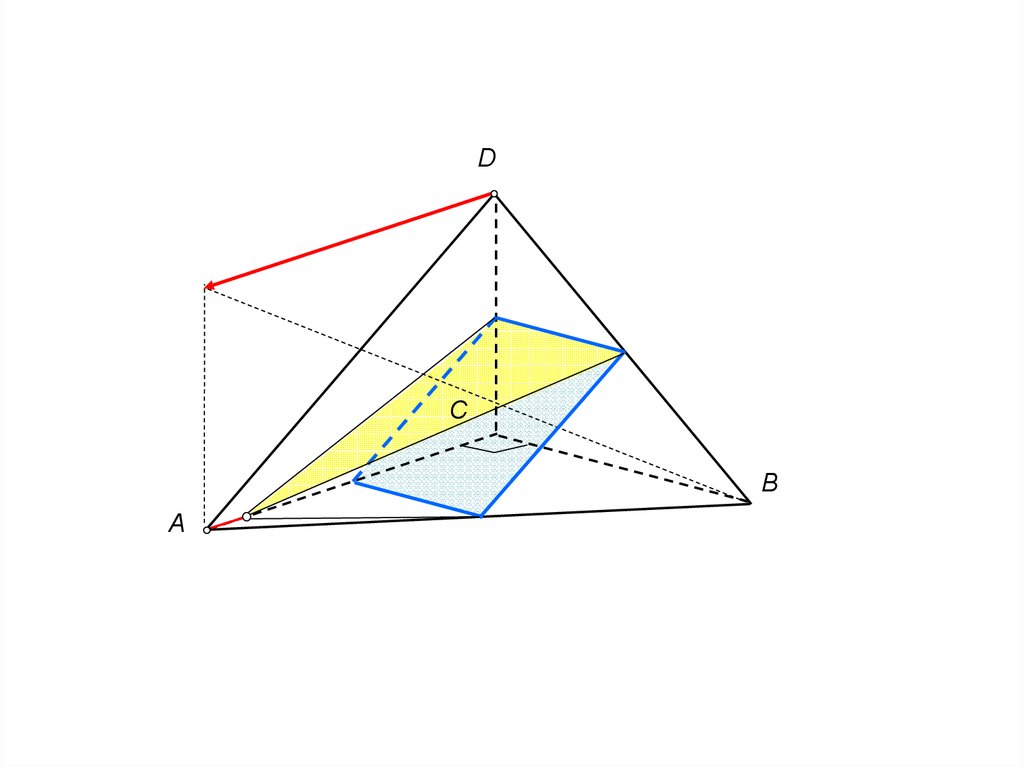
Моделированиегеометрия
D
Определить
отношение
объемов (объем
вписанной
пирамиды к
объему
основной)
B
A
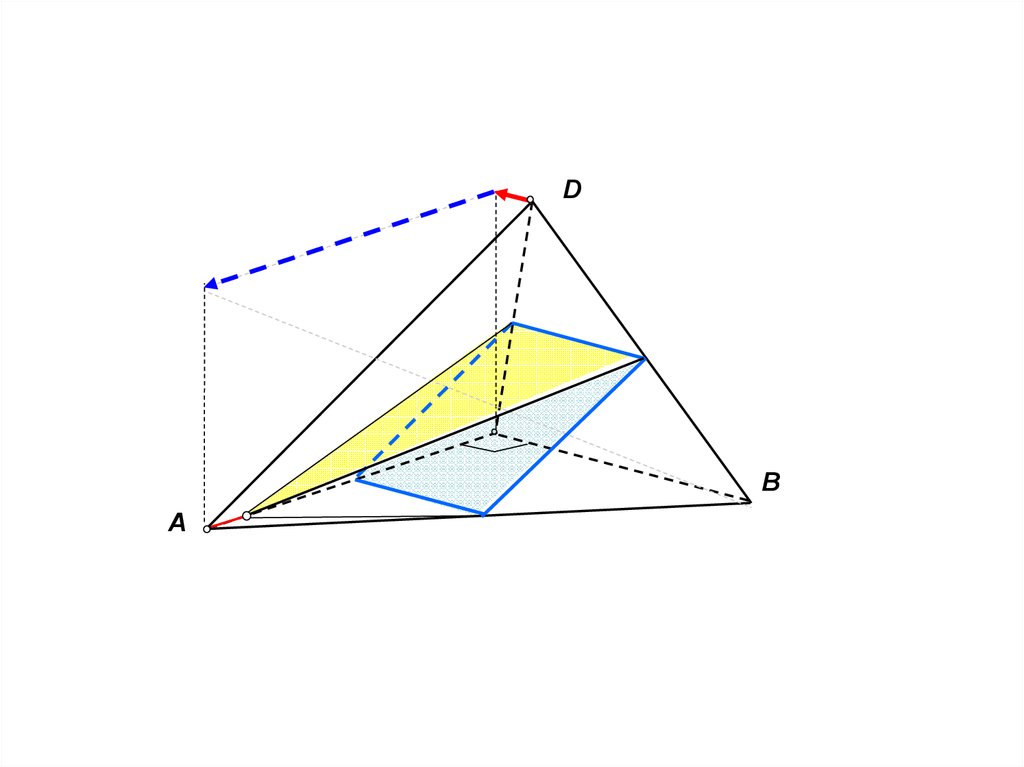
69.
DB
A
70.
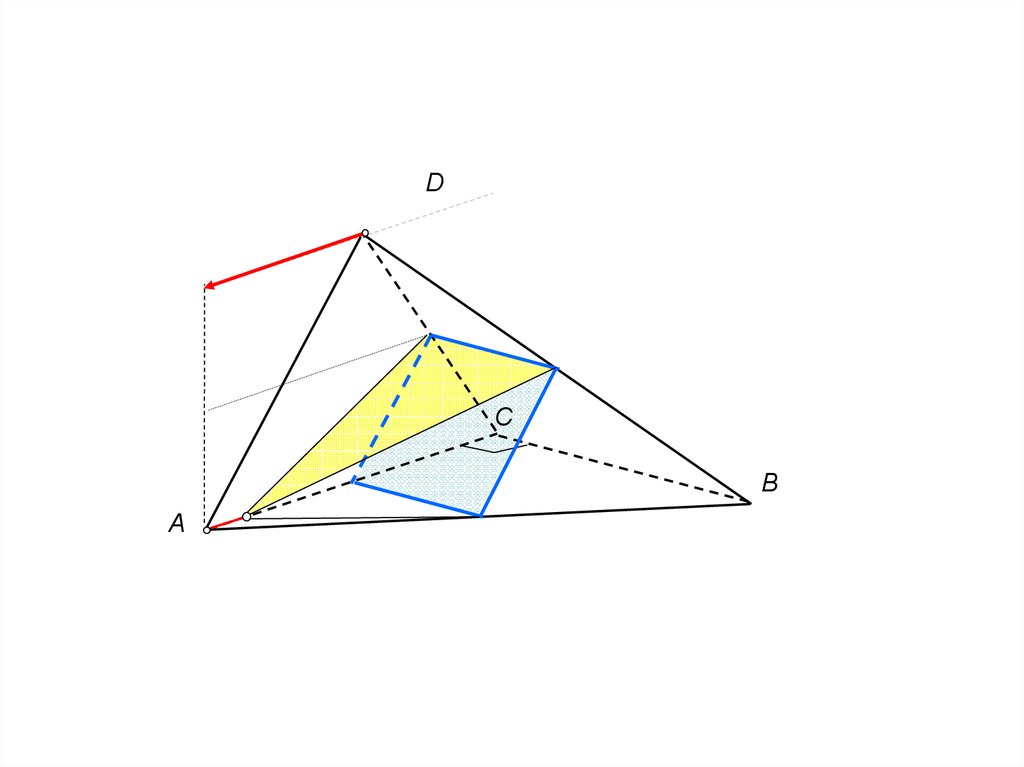
DC
B
A
71.
DB
A
72.
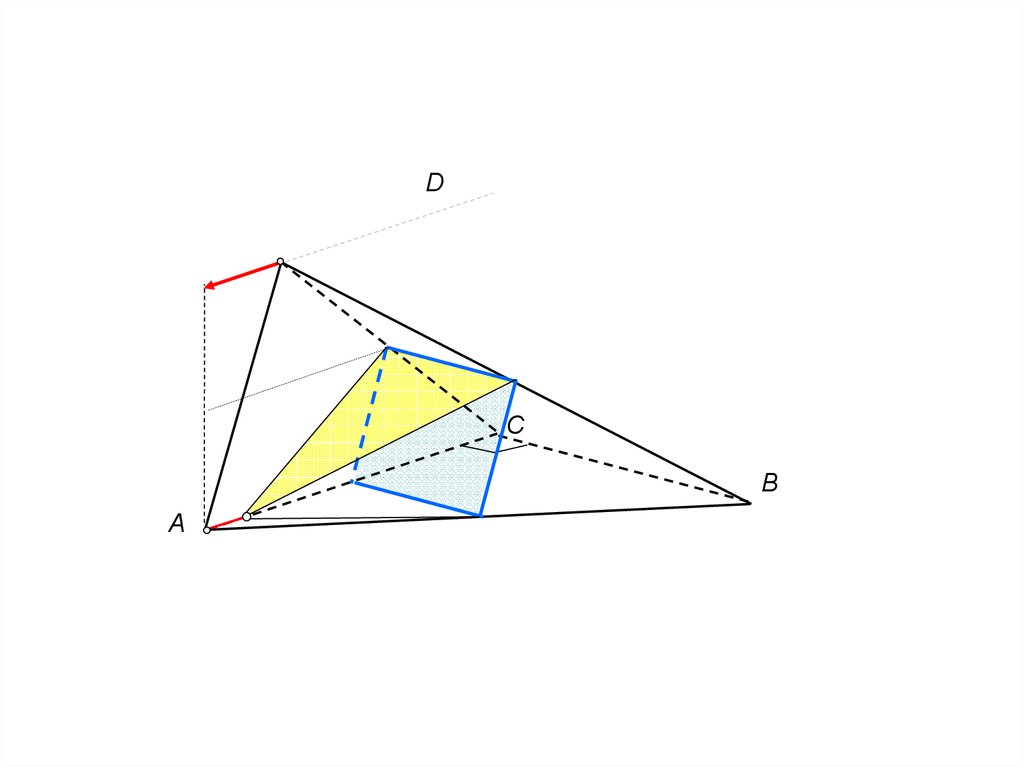
DC
B
A
73.
DC
B
A
74.
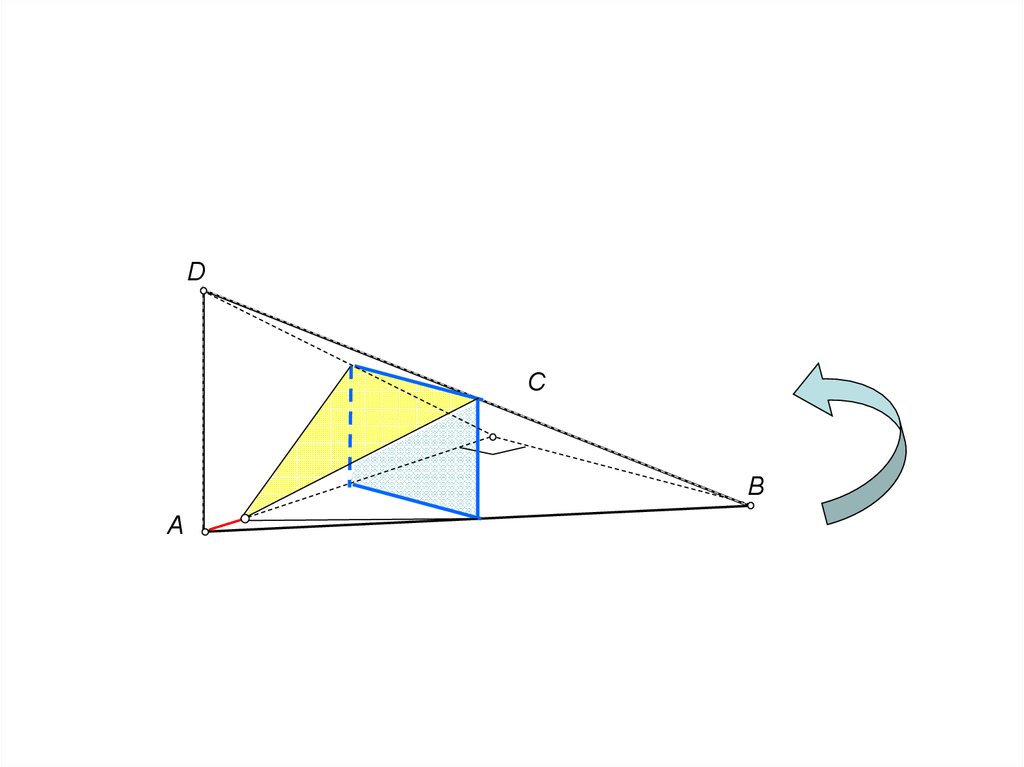
DC
B
A
75.
1 14 1
2
4 2
5 5
B
C
A
D
76.
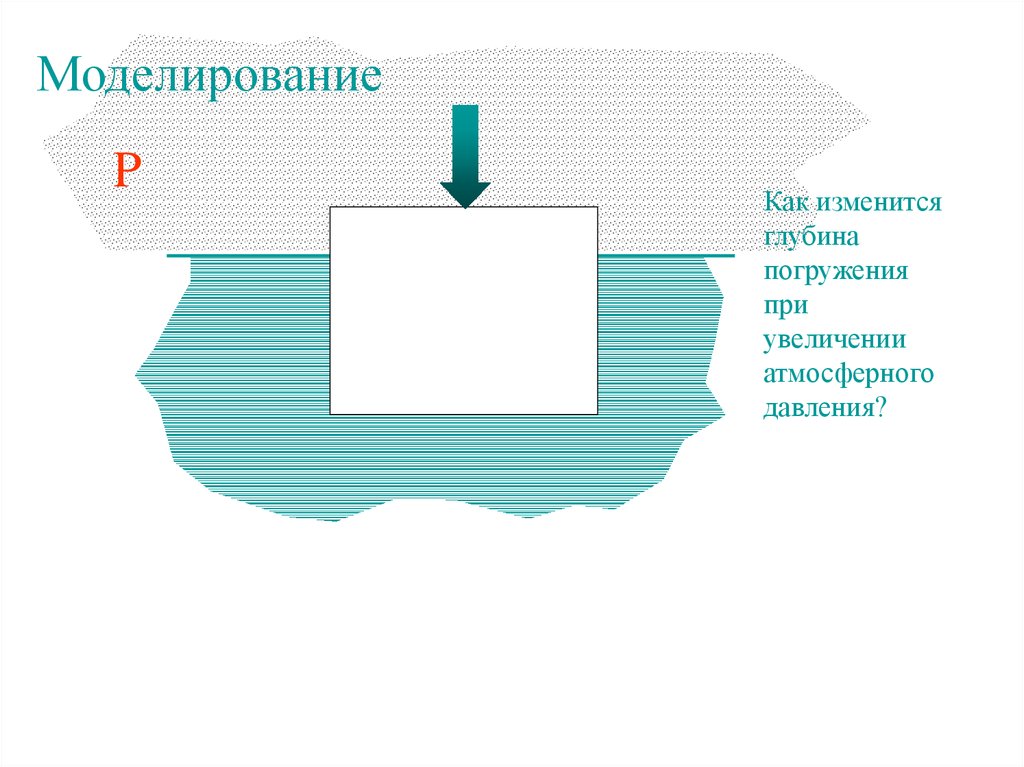
МоделированиеP
Как изменится
глубина
погружения
при
увеличении
атмосферного
давления?
77.
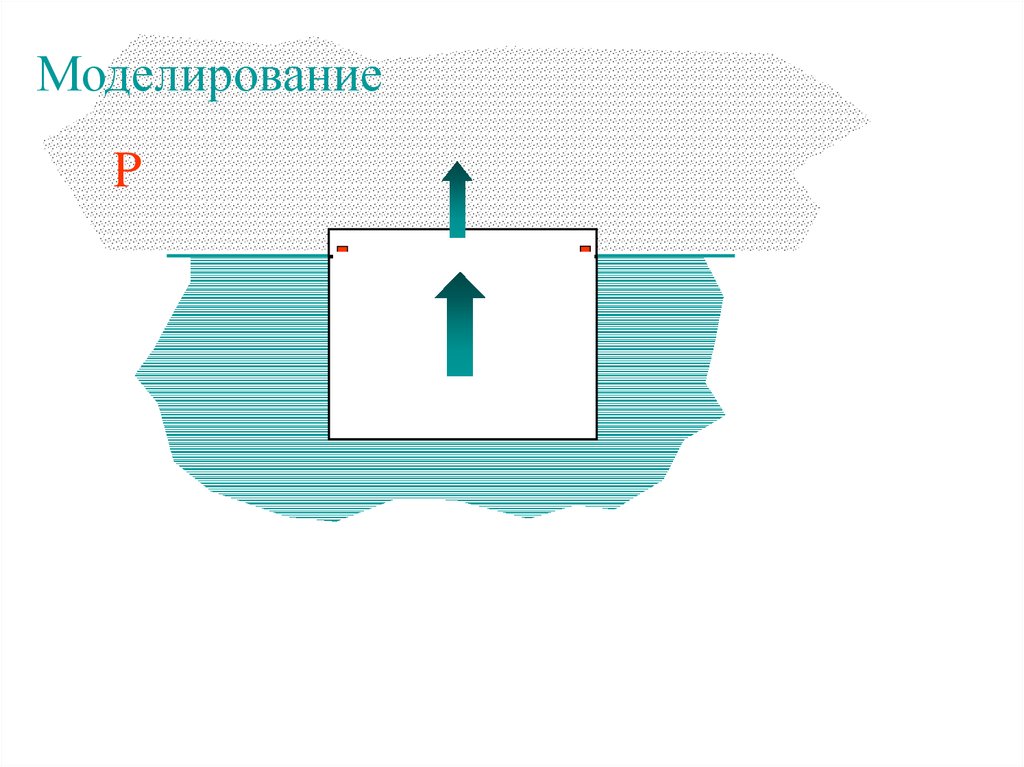
МоделированиеP
78.
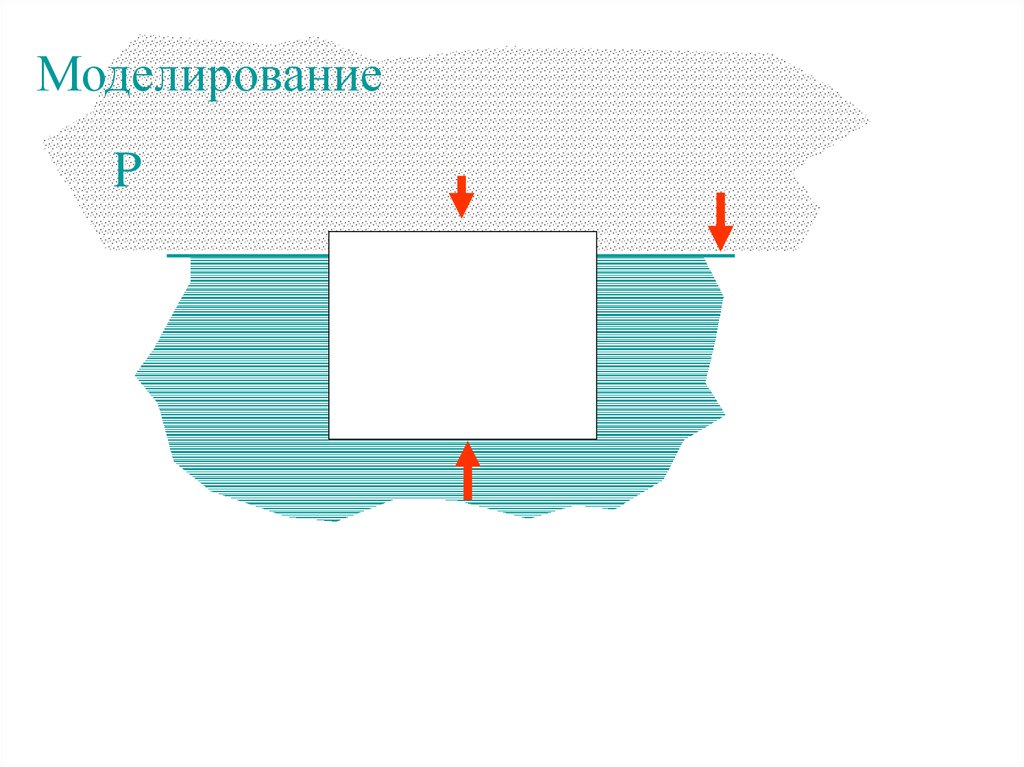
МоделированиеP
79.
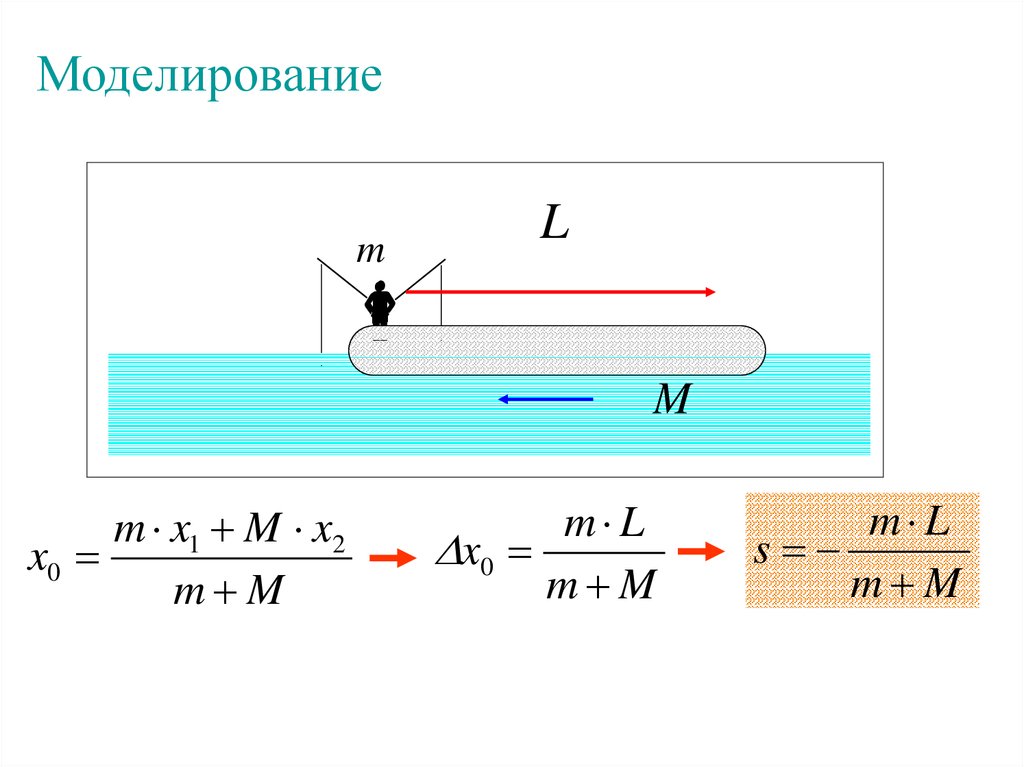
Моделированиеm
L
M
m x1 M x2
x0
m M
m L
x0
m M
m L
s
m M
80.
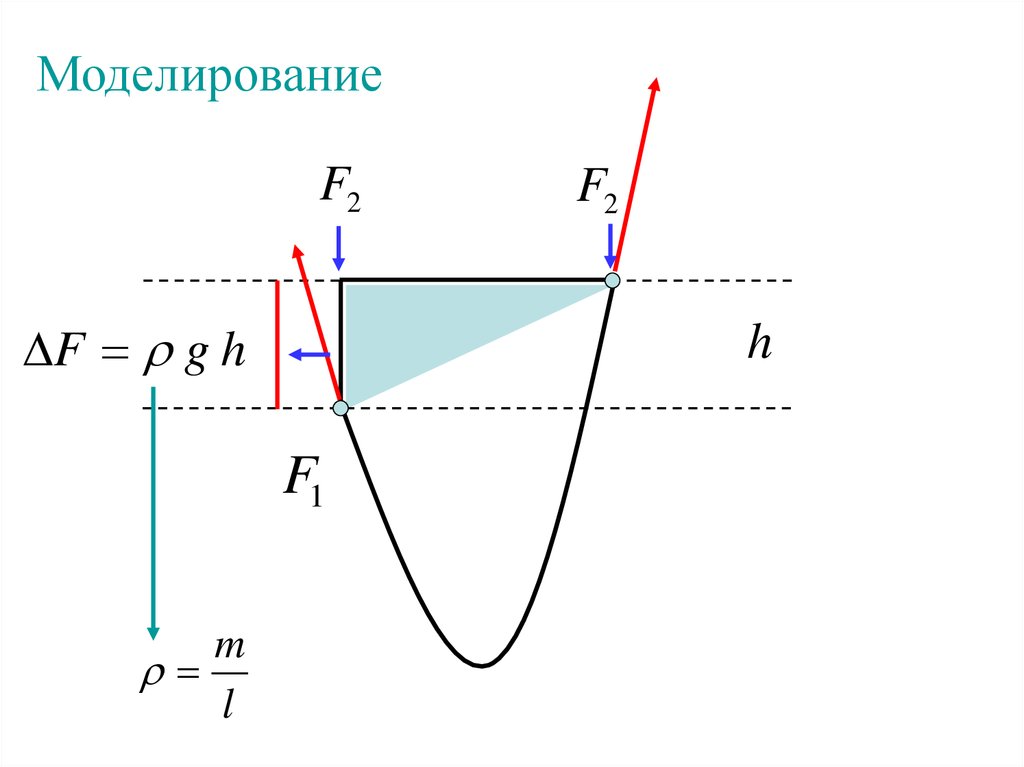
МоделированиеF2
F g h
h
F1
m
l
F2
81.
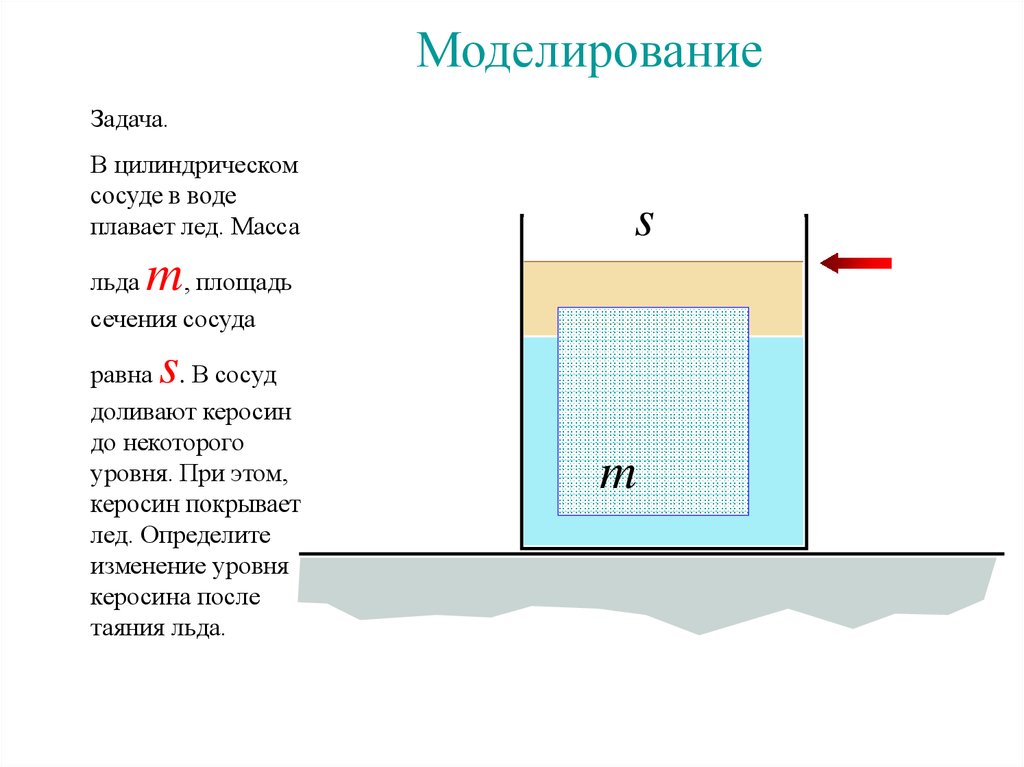
МоделированиеЗадача.
В цилиндрическом
сосуде в воде
плавает лед. Масса
s
m
льда
, площадь
сечения сосуда
s
равна . В сосуд
доливают керосин
до некоторого
уровня. При этом,
керосин покрывает
лед. Определите
изменение уровня
керосина после
таяния льда.
m
82.
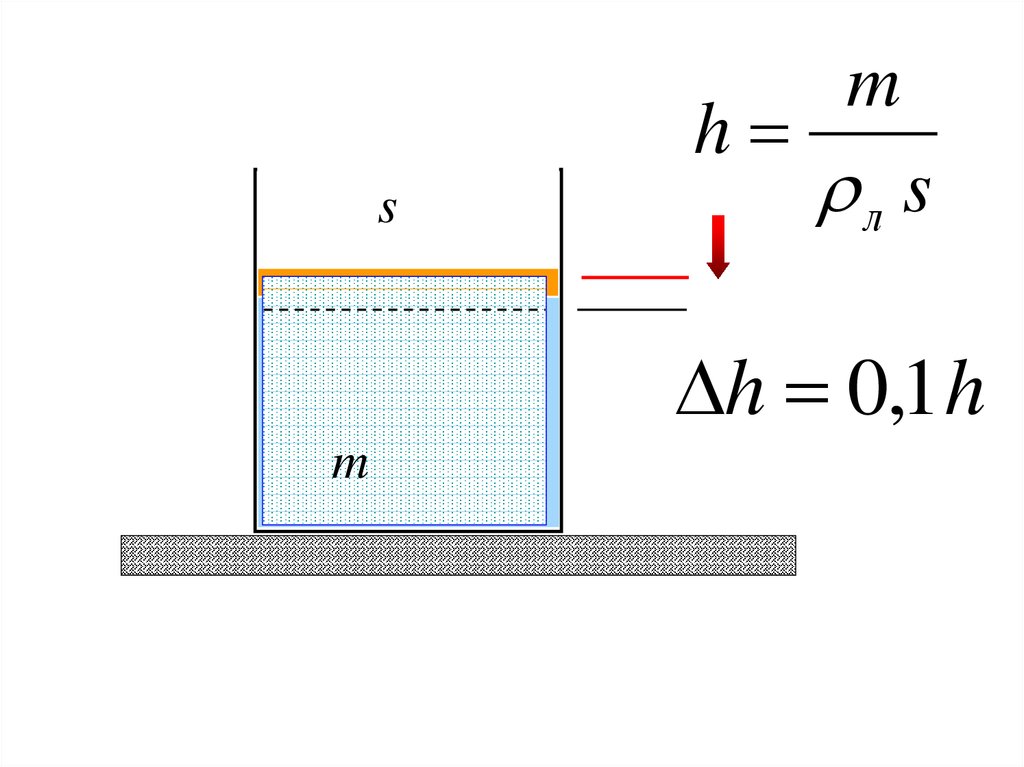
hs
m
л s
h 0,1 h
m
83.
Задача 1 (11 класс, олимпиада 2012)Пусть стеклянная бутылка плавает в
цилиндрическом сосуде с водой.
Внутренняя площадь дна сосуда
S = 250 см2. Из чайника в бутылку
медленно наливают воду и, когда
масса воды достигнет m = 300 г,
бутылка начинает тонуть. Оказалось,
что когда весь воздух из бутылки
вышел, уровень воды в сосуде
изменился на h = 0,60 см по
сравнению с тем моментом, когда в
бутылку начали наливать воду.
Вычислите вместимость бутылки.
84.
h85.
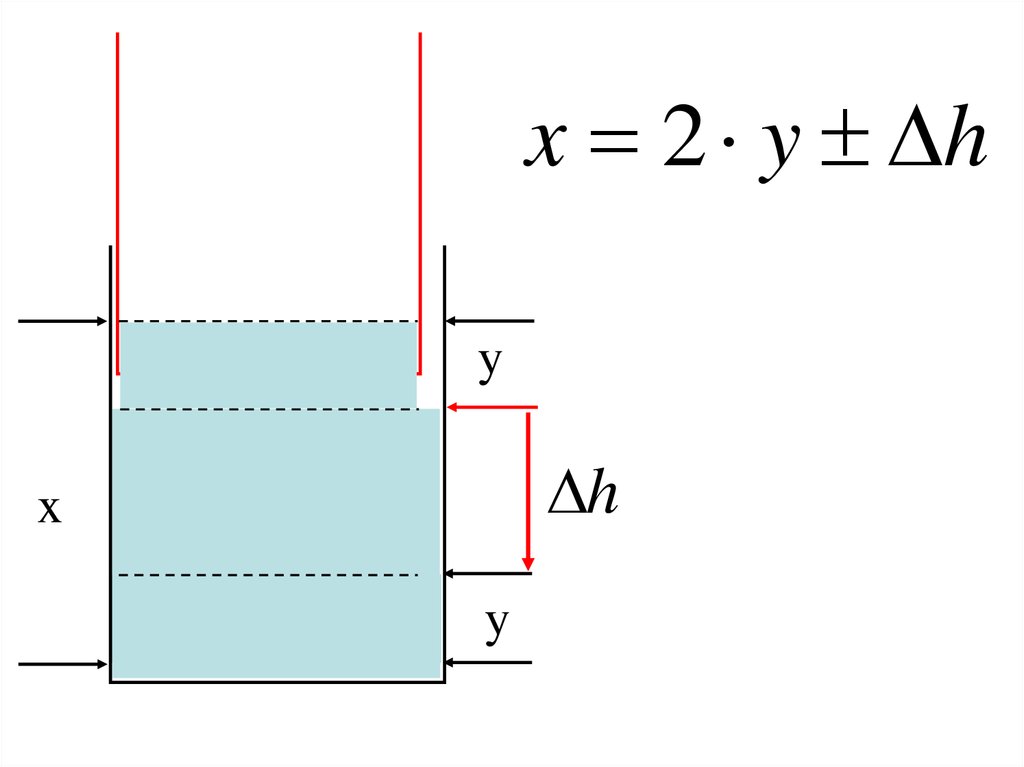
x 2 y hy
h
x
y
86.
Цилиндрический сосуд заполненводой. В него опускают
льдинку, внутри которой
находится золотое украшение.
Льдинка тонет, и уровень воды
в сосуде повышается на
величину h. После того, как
лед растаял, уровень воды в
сосуде изменился на величину
h. Определите:
знак изменения уровня воды в
сосуде после таяния льда
объем золотого украшения
силу давления льдинки на дно
сосуда в начале опыта.
Считать известными следующие
величины: (площадь сечения
сосуда, первое изменение
уровня, второе изменение
уровня, плотность воды,
плотность льда, плотность
золота, ускорение свободного
падения).
S 16 см 2 , h 5,2 см , h 0,5 см ,
в 1 г / см 3 , л 0,9 г / см 3 ,
з 19,3 г / см 3 , g 10 м/с 2
87.
88.
lh
l
z=h-l z
l 0,1 l
l 10 l
z h 10 h
89.
S 16 см , h 5,2 см , h 0,5 см ,2
в 1 г / см , л 0,9 г / см ,
3
3
з 19,3 г / см , g 10 м/с
3
2
Vз S h 10 h 16 5,2 10 0,5 3,2 см
3
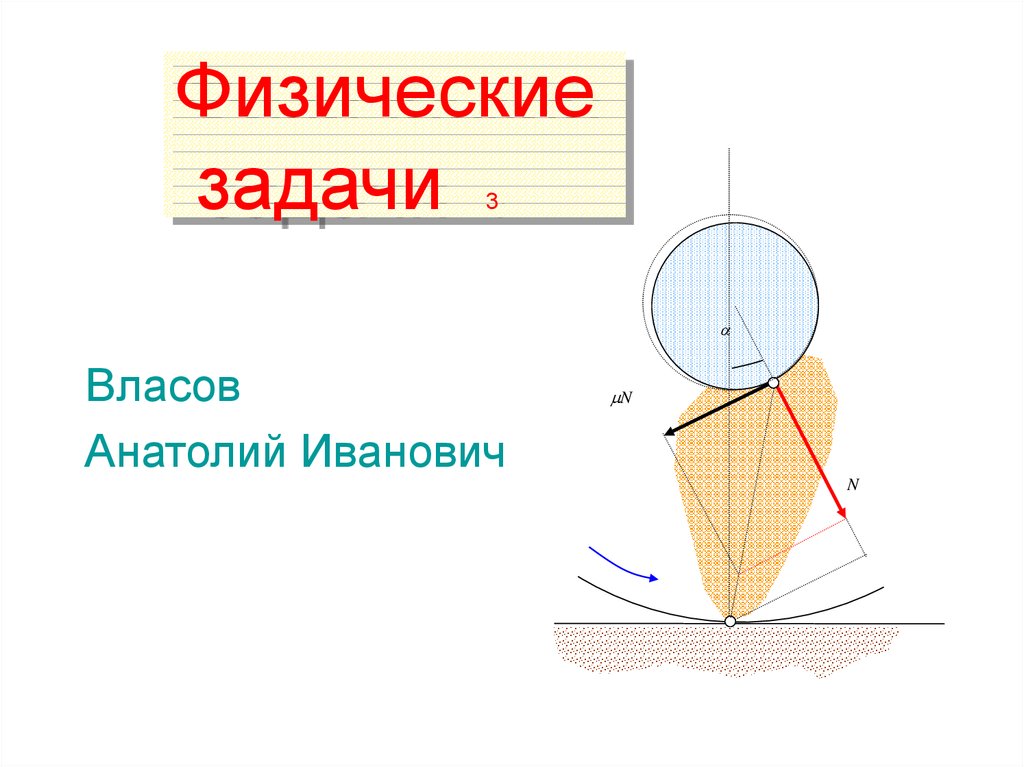
90. Физические задачи 3
ВласовАнатолий Иванович
N
N
91.
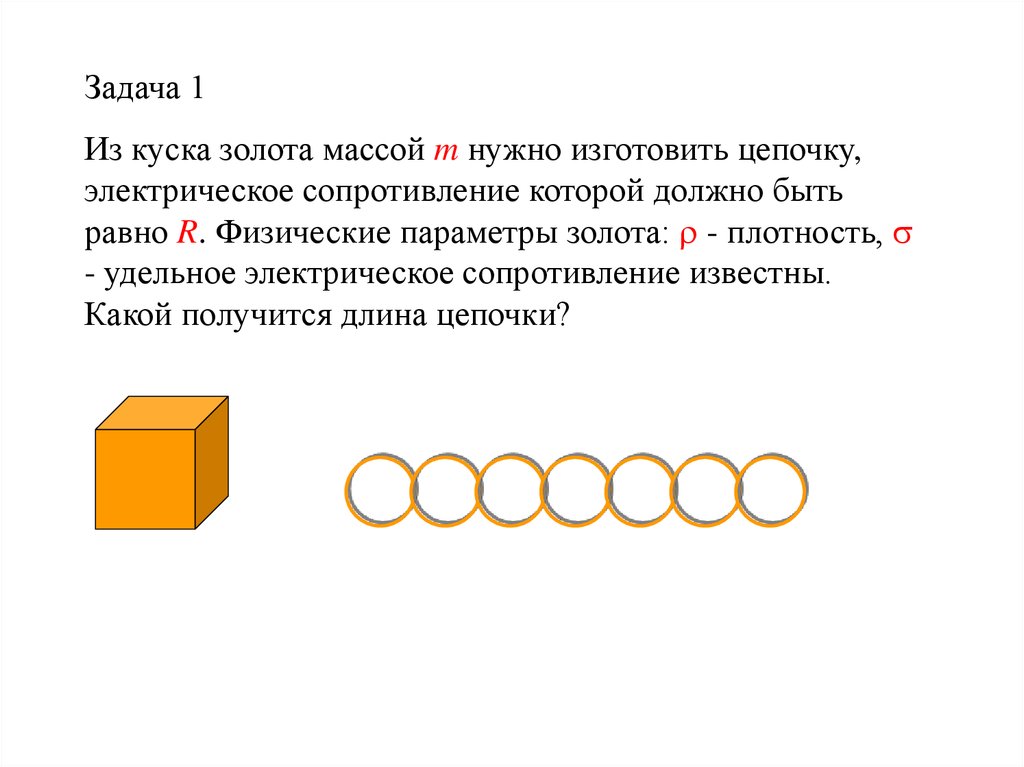
Задача 1Из куска золота массой m нужно изготовить цепочку,
электрическое сопротивление которой должно быть
равно R. Физические параметры золота: - плотность,
- удельное электрическое сопротивление известны.
Какой получится длина цепочки?
92.
геометрия2 r n 2 R
nr R
93.
94.
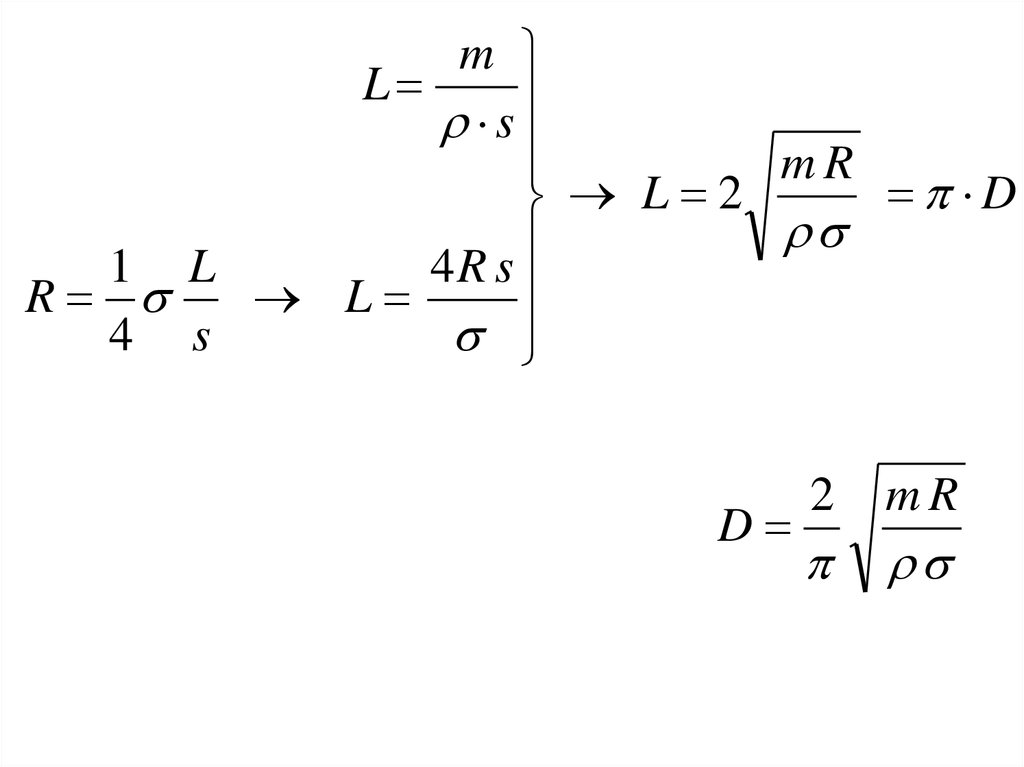
mL
s
mR
D
L 2
1 L
4R s
R
L
4 s
D
2
mR
95.
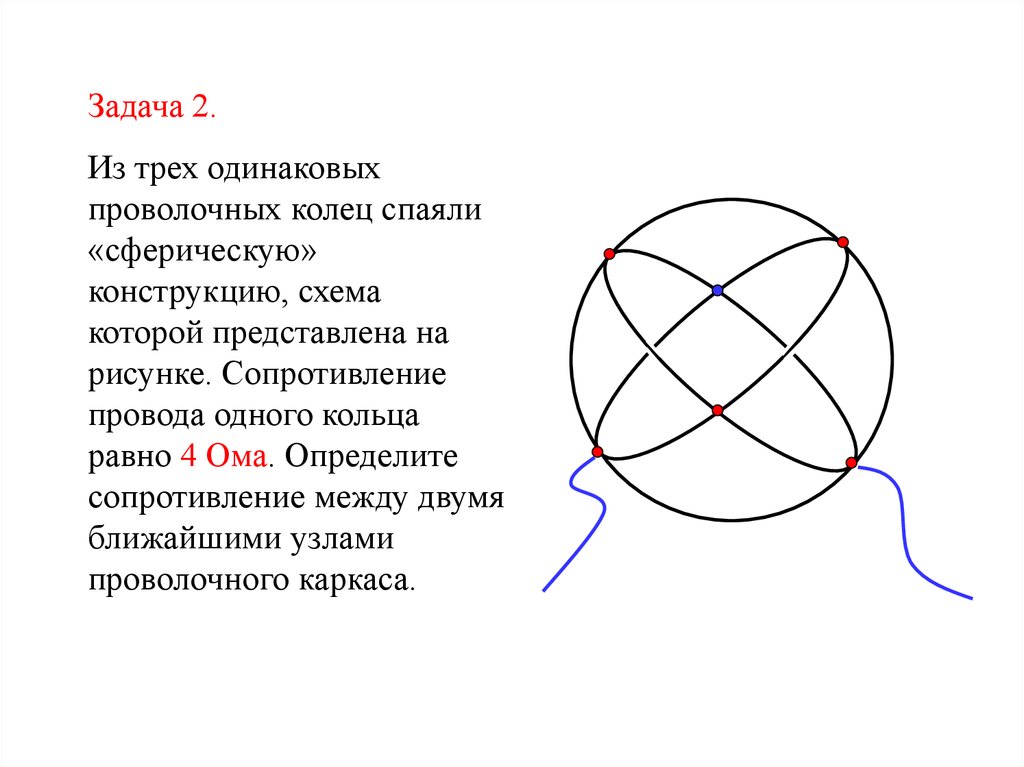
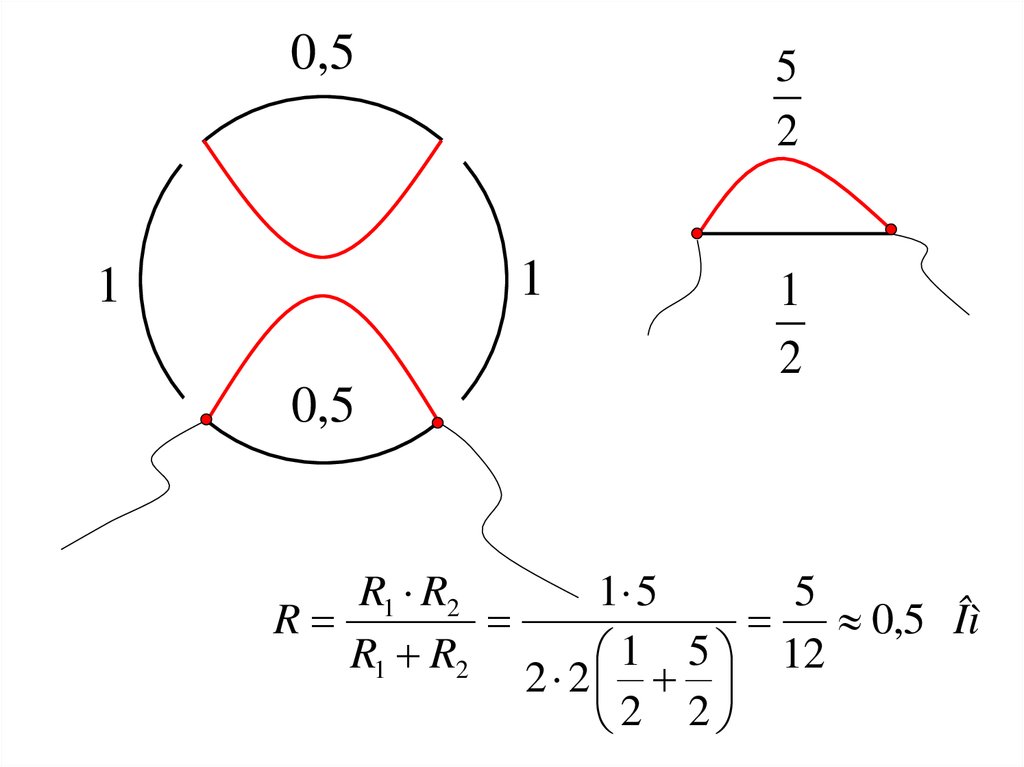
Задача 2.Из трех одинаковых
проволочных колец спаяли
«сферическую»
конструкцию, схема
которой представлена на
рисунке. Сопротивление
провода одного кольца
равно 4 Ома. Определите
сопротивление между двумя
ближайшими узлами
проволочного каркаса.
96.
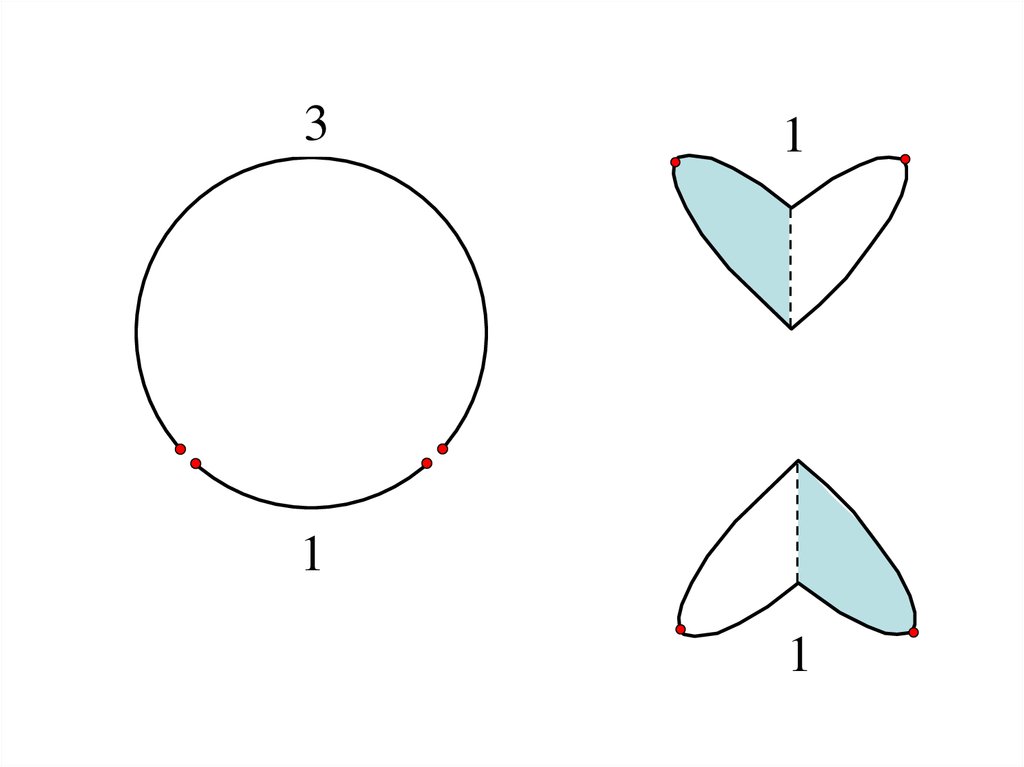
31
1
1
97.
0,55
2
1
1
1
2
0,5
R1 R2
R
R1 R2
1 5
5
0,5 Îì
1 5 12
2 2
2 2
98.
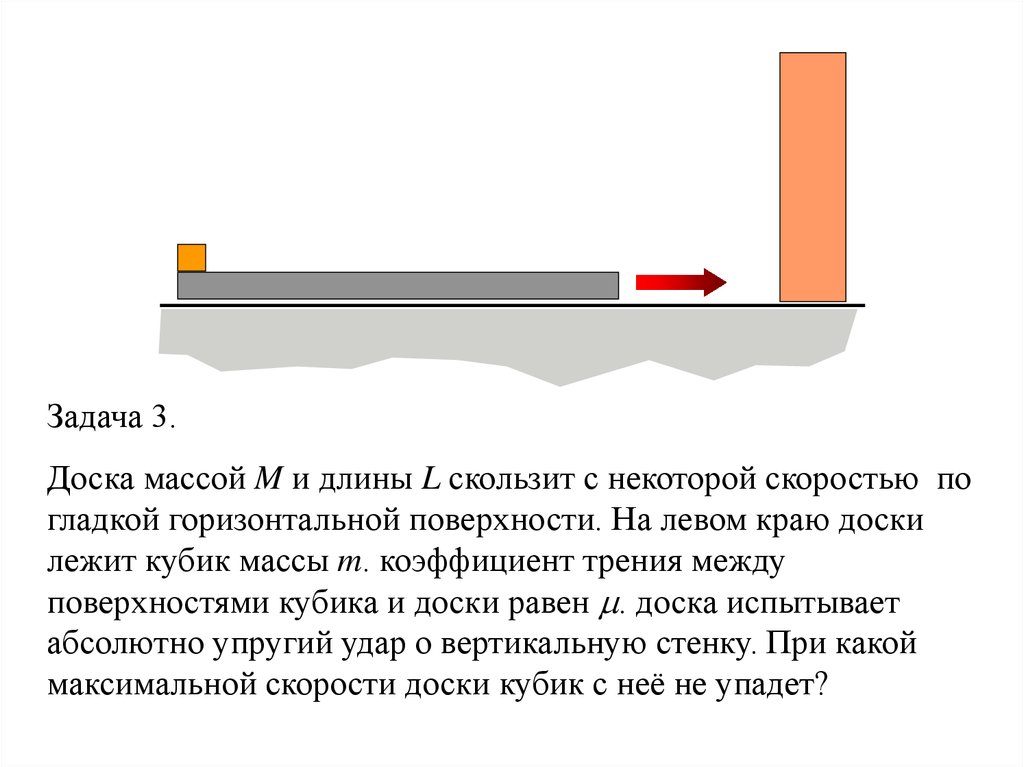
Задача 3.Доска массой M и длины L скользит с некоторой скоростью по
гладкой горизонтальной поверхности. На левом краю доски
лежит кубик массы m. коэффициент трения между
поверхностями кубика и доски равен . доска испытывает
абсолютно упругий удар о вертикальную стенку. При какой
максимальной скорости доски кубик с неё не упадет?
99.
E E0 E2
2
v1
v2
E m
M
2
2
2
v0
E0 m M
2
100.
m v1 M v2v0
m M
2
m M v1 v2
E
m M
2
101.
vv
m M 2 v
mg L
m M 2
2
102.
v0Задача 4.
По гладкой плоскости скользит горка, на вершине которой
находится небольшое тело. Скорость системы тел равна v0.
Потеряв равновесие тело съезжает с горки. Определите
скорость тела на плоскости. Масса горки значительно
превосходит массу тела.
103.
m M v v0mgh
m M
2
2
v v0
2
2gh
v v0 2 g h
104.
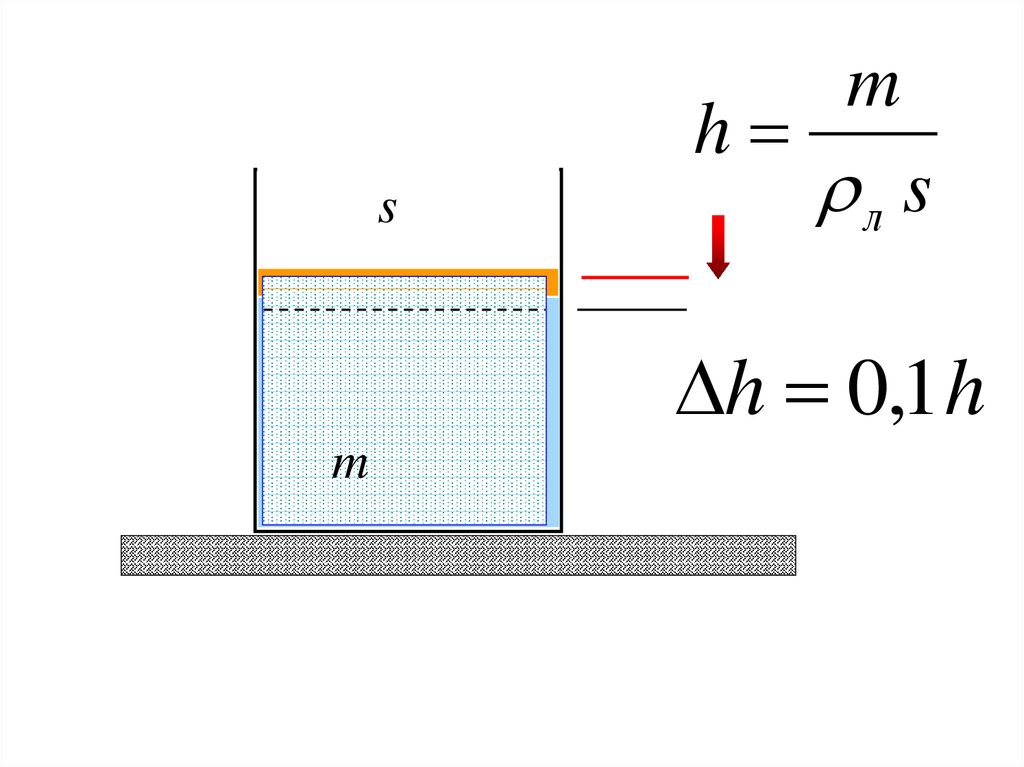
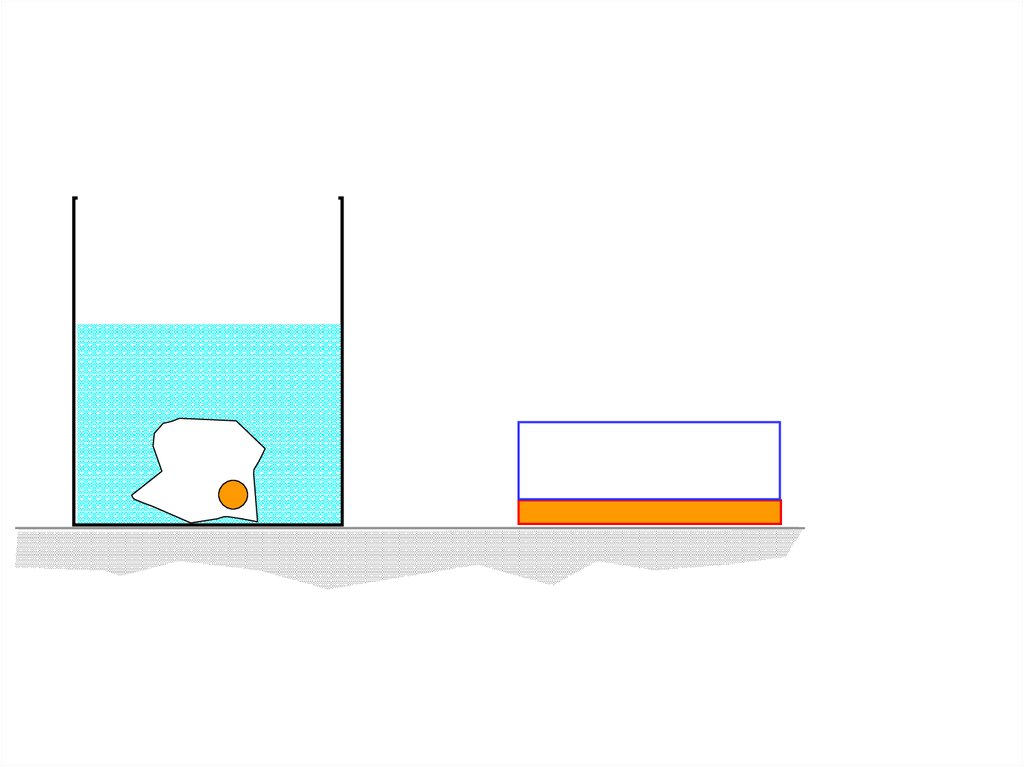
Задача.В цилиндрическом
сосуде в воде
плавает лед. Масса
s
m
льда
, площадь
сечения сосуда
s
равна . В сосуд
доливают керосин
до некоторого
уровня. При этом,
керосин покрывает
лед. Определите
изменение уровня
керосина после
таяния льда.
m
105.
hs
m
л s
h 0,1 h
m
106.
a g107.
l x2 x1 x1 x2 x3 x2 x3 x10
x4
x2
x1
x5
l x1 2 x3 x2
x3
a1 a2 2 a3 0
108.
l x3 x1 x3 x5l 2 x3 x1 x5
0
x4
x2
x1
x5
a5 2 a3 a1
x3
a4 a2
109.
mg T 2T m a4mg 2T T m a5
2 mg 4T 2 m a3
a1 a2 2 a3 0
a4 a2
a5 2 a3 a1
110.
a1 g3
a2 g
5
1
a3
5g
3
a4 g
5
7
a5 g
5
m x4 m x5 x4 x5
x0
m m
2
a4 a5 3 7 g
a0
g
2
5 5 2
111.
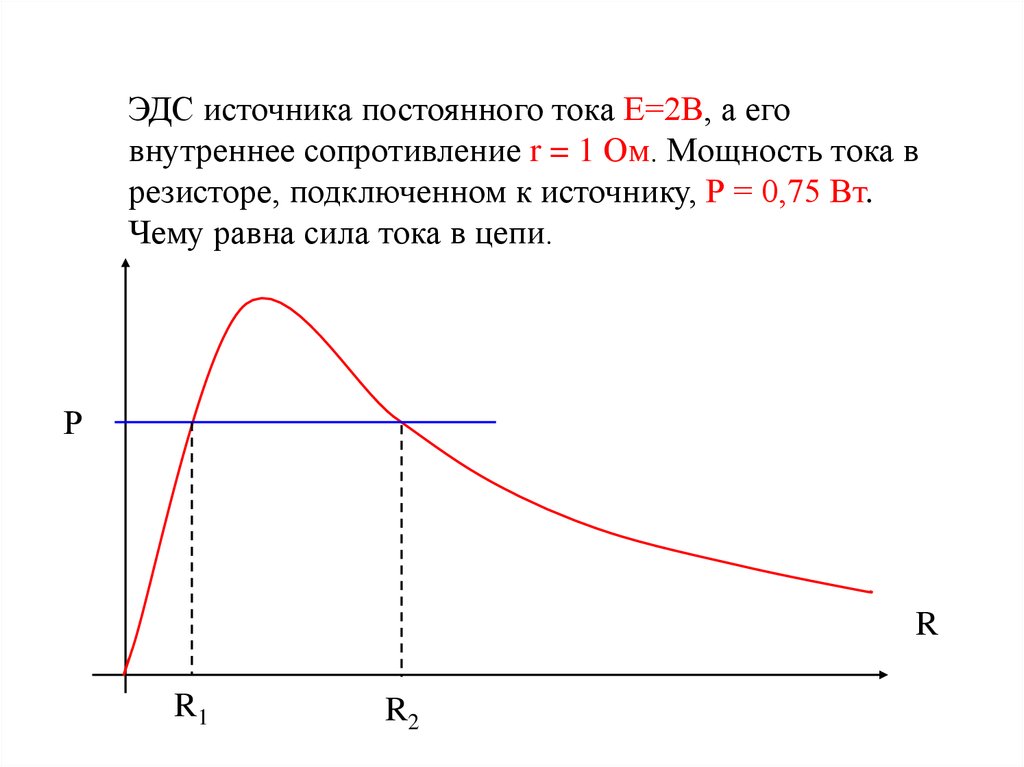
ЭДС источника постоянного тока Е=2В, а еговнутреннее сопротивление r = 1 Ом. Мощность тока в
резисторе, подключенном к источнику, Р = 0,75 Вт.
Чему равна сила тока в цепи.
Р
R
R1
R2
112.
E i P i r2
r i E i P 0
2
E E 4Pr
2r
2
i1, 2
2 4 4 0,75 2 1 1,5
A
2
2
0,5
113.
С помощью линзы с фокусным расстоянием F = 15 см.при различных положениях предмета были получены
изображения с пятикратным и двукратным увеличениями.
На сколько при этом изменялось расстояние между линзой
и экраном?
114.
Ff
y
f F
k
f F k 1
y
F
f F k 15 5 2 45 см
115.
Начальная скорость снаряда, выпущенного вертикальновверх, равна 200 м/с. В точке максимального подъема
снаряд разорвался на два одинаковых по массе осколка.
Первый осколок упал на Землю в точке выстрела имея
скорость в два раза больше начальной скорости снаряда.
Какую скорость имел второй осколок при падении на
Землю?
v2 400 м / с
116.
Задача 1 (11 класс, олимпиада 2012)Пусть стеклянная бутылка плавает в
цилиндрическом сосуде с водой.
Внутренняя площадь дна сосуда
S = 250 см2. Из чайника в бутылку
медленно наливают воду и, когда
масса воды достигнет m = 300 г,
бутылка начинает тонуть. Оказалось,
что когда весь воздух из бутылки
вышел, уровень воды в сосуде
изменился на h = 0,60 см по
сравнению с тем моментом, когда в
бутылку начали наливать воду.
Вычислите вместимость бутылки.
117.
h118.
x 2 y hy
h
x
y
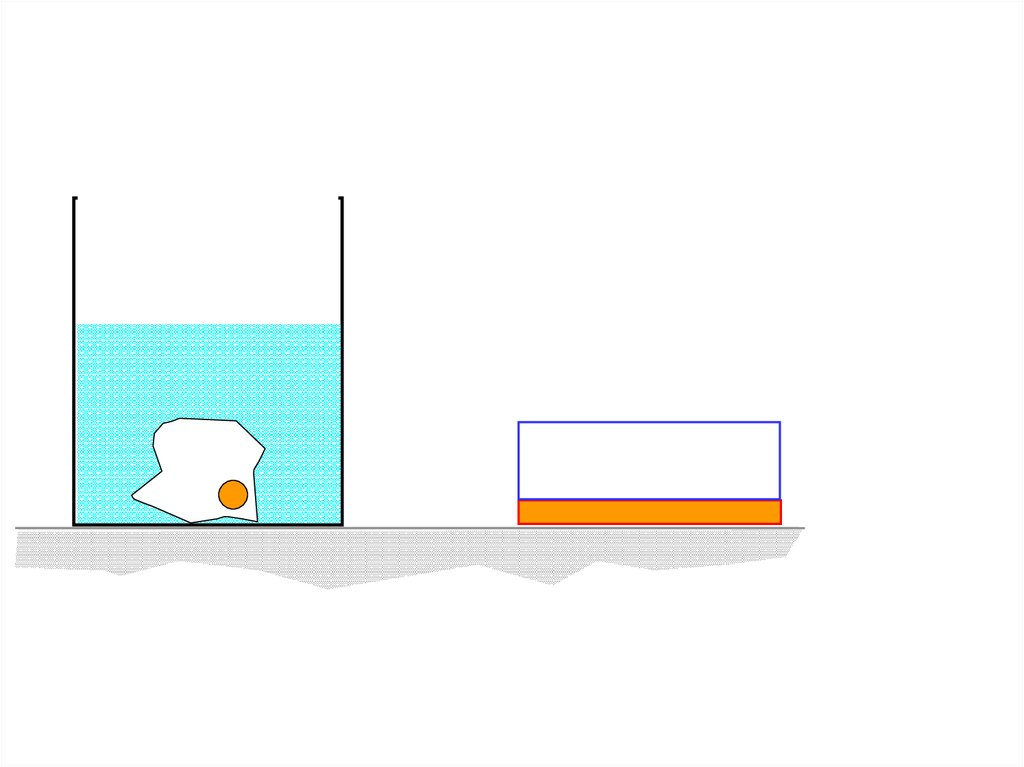
119.
Цилиндрический сосуд заполненводой. В него опускают
льдинку, внутри которой
находится золотое украшение.
Льдинка тонет, и уровень воды
в сосуде повышается на
величину h. После того, как
лед растаял, уровень воды в
сосуде изменился на величину
h. Определите:
знак изменения уровня воды в
сосуде после таяния льда
объем золотого украшения
силу давления льдинки на дно
сосуда в начале опыта.
Считать известными следующие
величины: (площадь сечения
сосуда, первое изменение
уровня, второе изменение
уровня, плотность воды,
плотность льда, плотность
золота, ускорение свободного
падения).
S 16 см 2 , h 5,2 см , h 0,5 см ,
в 1 г / см 3 , л 0,9 г / см 3 ,
з 19,3 г / см 3 , g 10 м/с 2
120.
121.
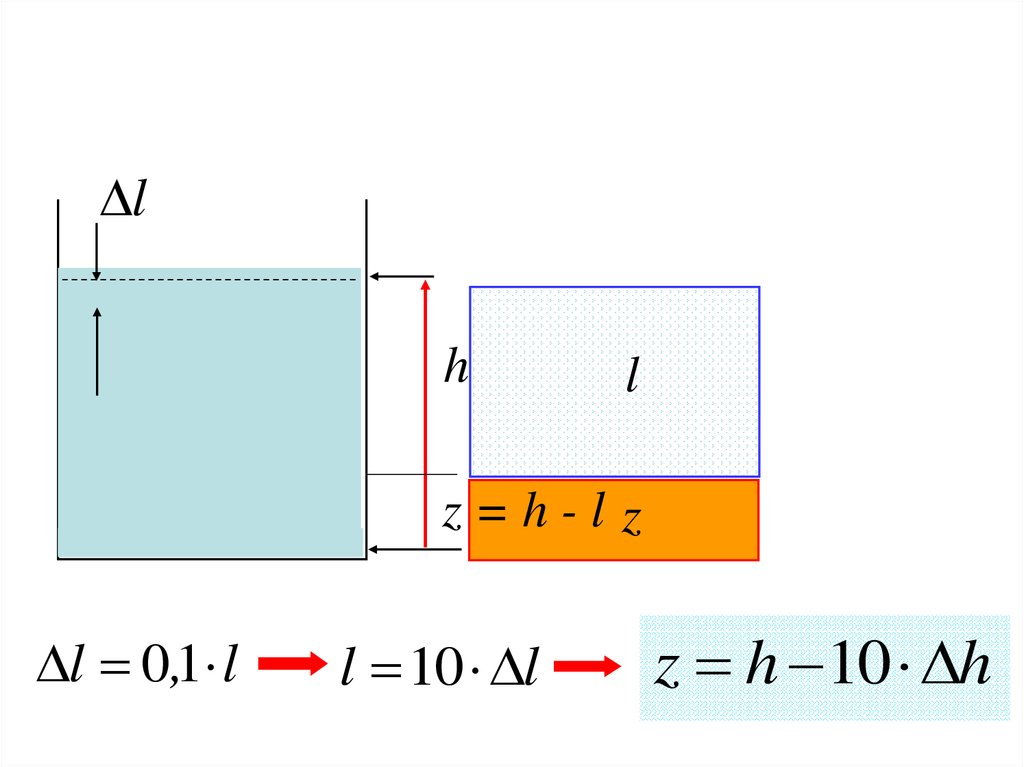
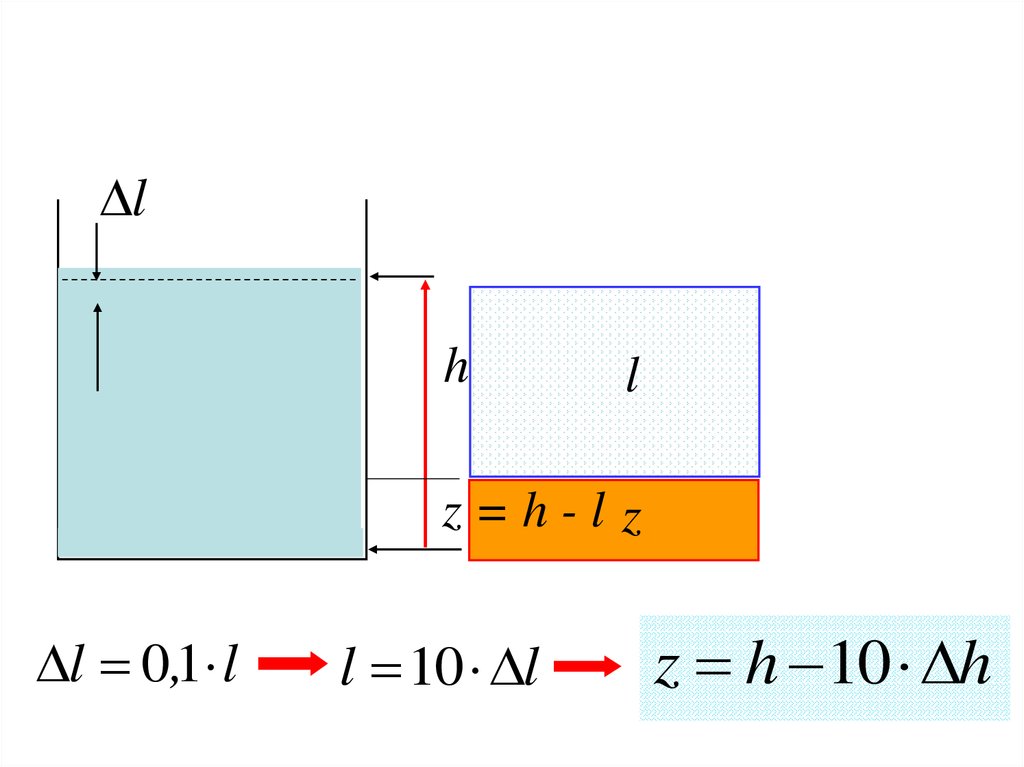
lh
l
z=h-l z
l 0,1 l
l 10 l
z h 10 h
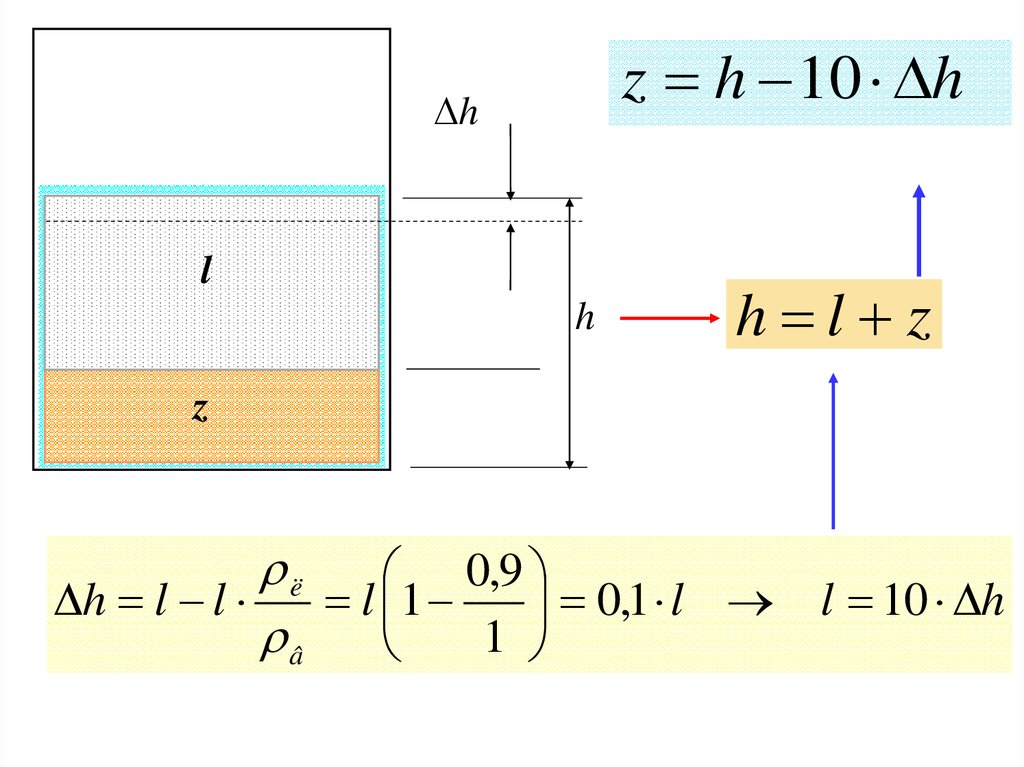
122.
z h 10 hh
l
h
h l z
z
ë
0,9
h l l
l 1
0,1 l l 10 h
â
1
123.
S 16 см , h 5,2 см , h 0,5 см ,2
в 1 г / см , л 0,9 г / см ,
3
3
з 19,3 г / см , g 10 м/с
3
2
Vз S h 10 h 16 5,2 10 0,5 3,2 см
3
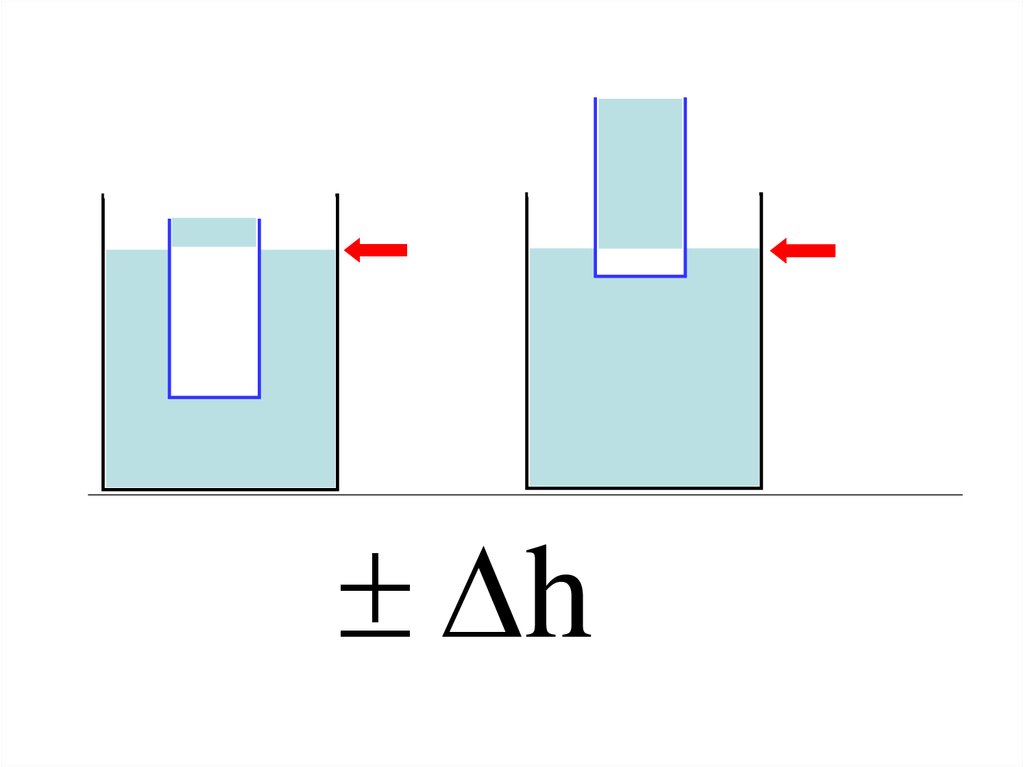
124.
F2F g h
h
F1
m
l
F2
125.
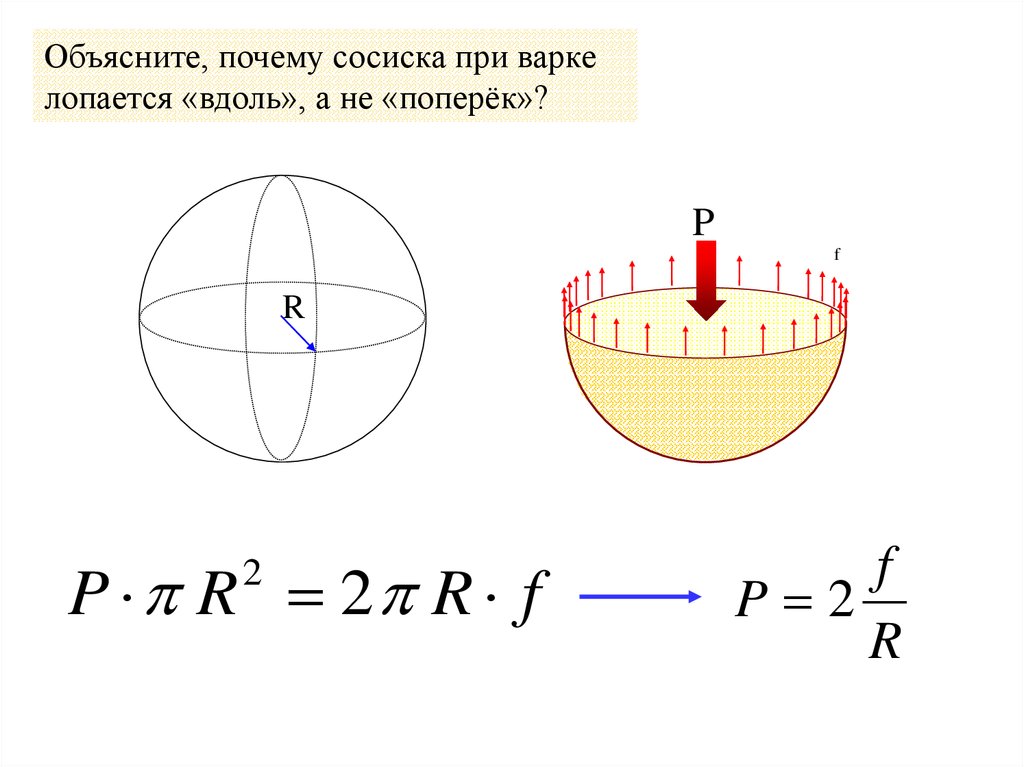
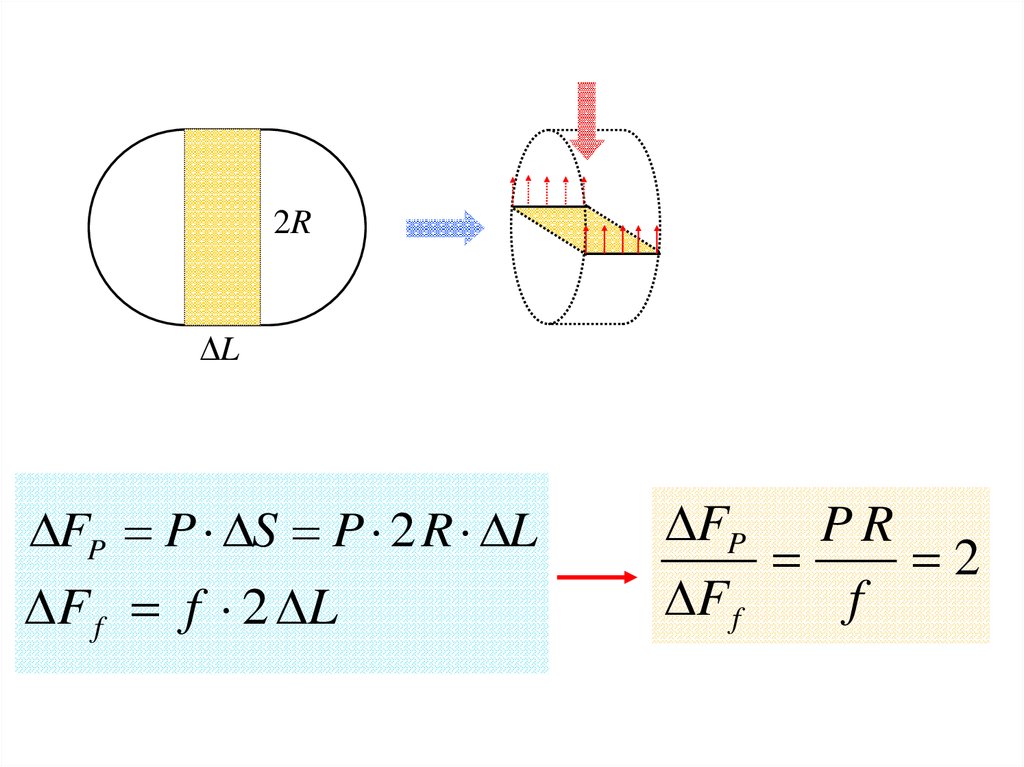
Объясните, почему сосиска при варкелопается «вдоль», а не «поперёк»?
P
f
R
P R 2 R f
2
f
P 2
R
126.
2RL
FP P S P 2 R L
F f f 2 L
FP P R
2
F f
f
127.
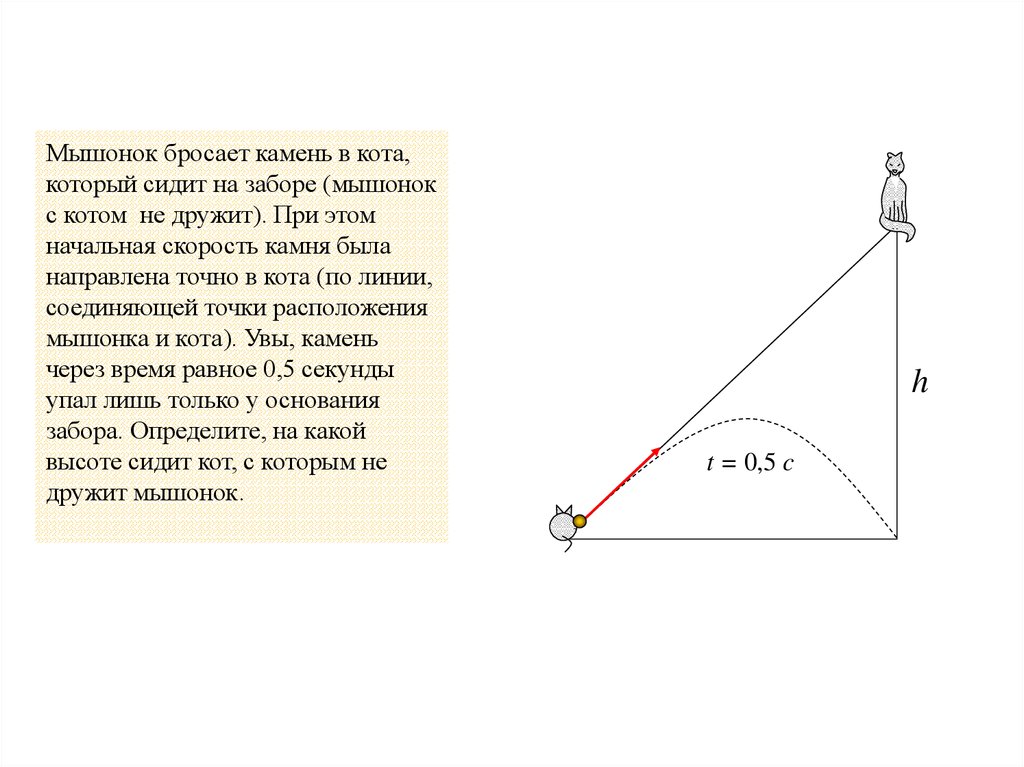
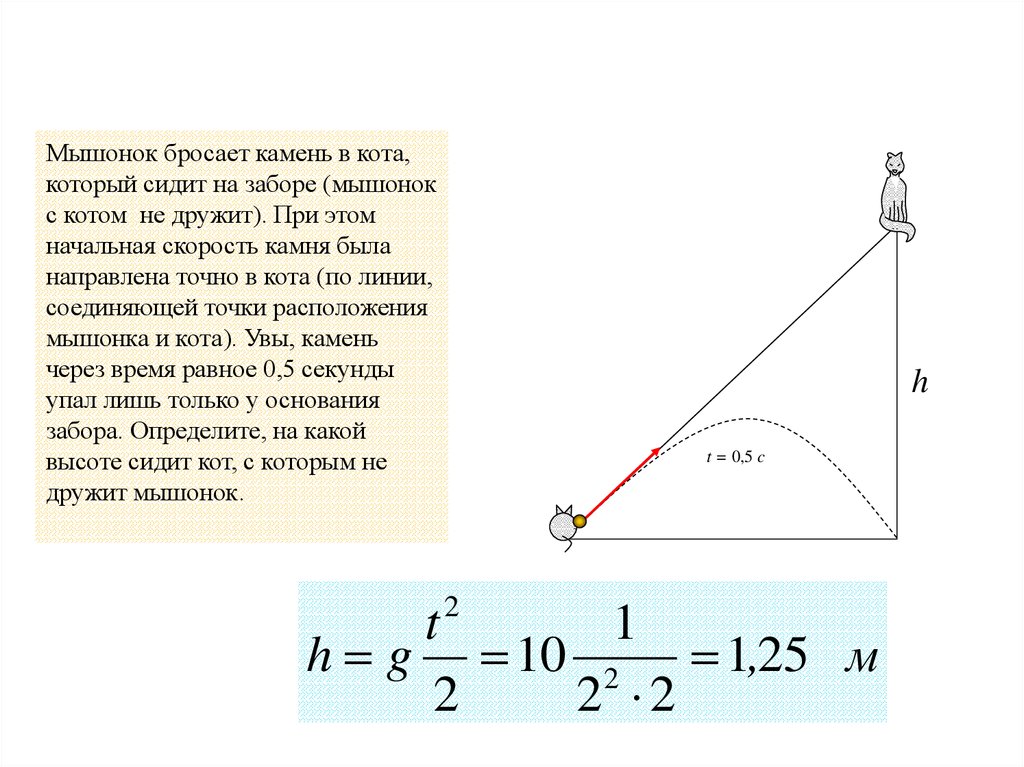
Мышонок бросает камень в кота,который сидит на заборе (мышонок
с котом не дружит). При этом
начальная скорость камня была
направлена точно в кота (по линии,
соединяющей точки расположения
мышонка и кота). Увы, камень
через время равное 0,5 секунды
упал лишь только у основания
забора. Определите, на какой
высоте сидит кот, с которым не
дружит мышонок.
h
t = 0,5 c
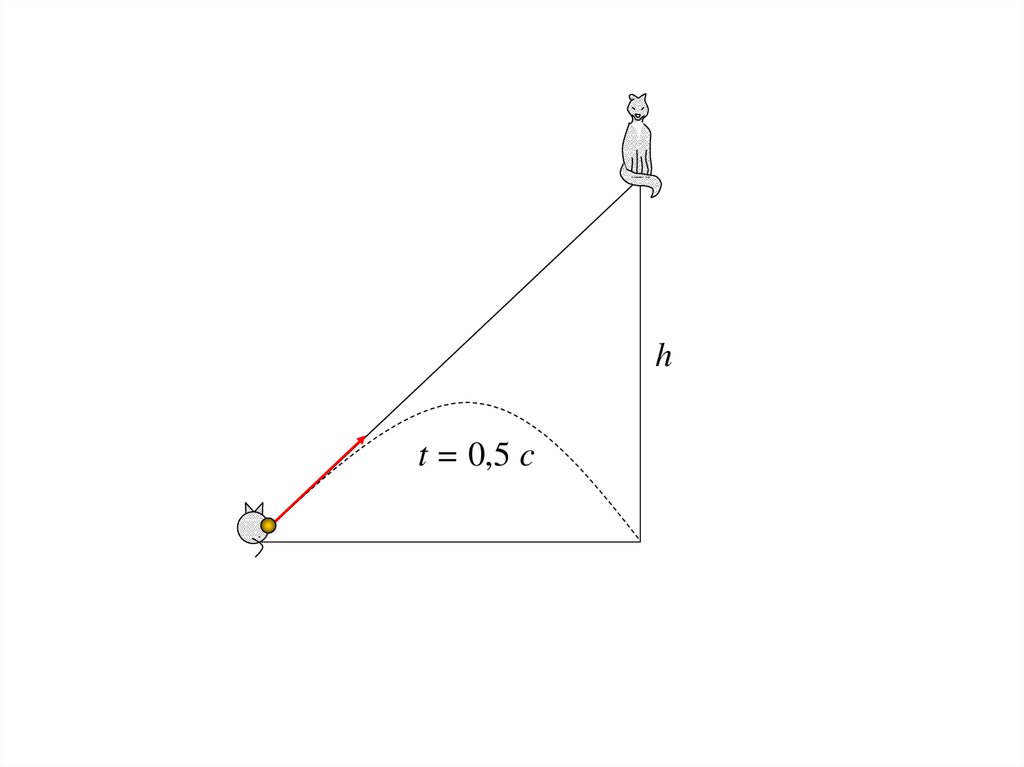
128.
ht = 0,5 c
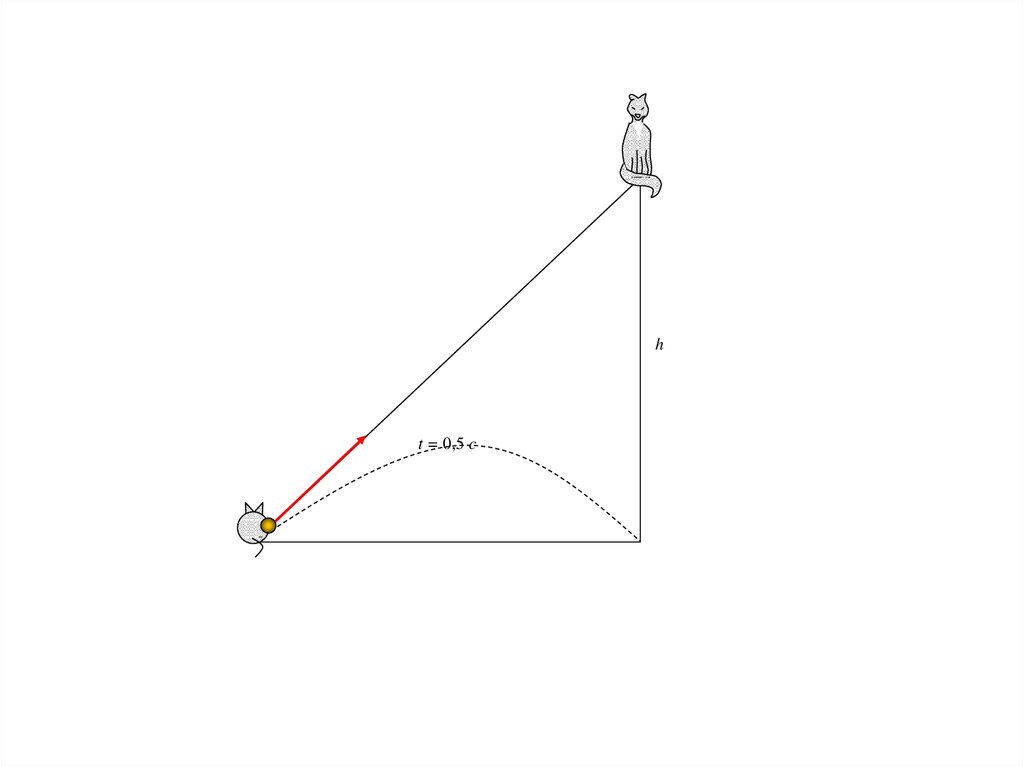
129.
ht = 0,5 c
130.
Мышонок бросает камень в кота,который сидит на заборе (мышонок
с котом не дружит). При этом
начальная скорость камня была
направлена точно в кота (по линии,
соединяющей точки расположения
мышонка и кота). Увы, камень
через время равное 0,5 секунды
упал лишь только у основания
забора. Определите, на какой
высоте сидит кот, с которым не
дружит мышонок.
h
t = 0,5 c
2
t
1
h g 10 2 1,25 м
2
2 2
131.
2t
S V0 t g
2
132.
На оси Ох в точке х1 = 0 находится оптический центр тонкойрассеивающей линзы с фокусным расстоянием F1=— 20 см, а в
точке х2 = 20 см — тонкой собирающей линзы с фокусным
расстоянием F2= З0 см. Главные оптические оси обеих линз лежат
на оси х. Свет от точечного источника S, расположенного в точке х<
0, пройдя данную оптическую систему, распространяется
параллельным пучком. Найдите координату х точечного источника.
d-?
133.
d = 140 см0
































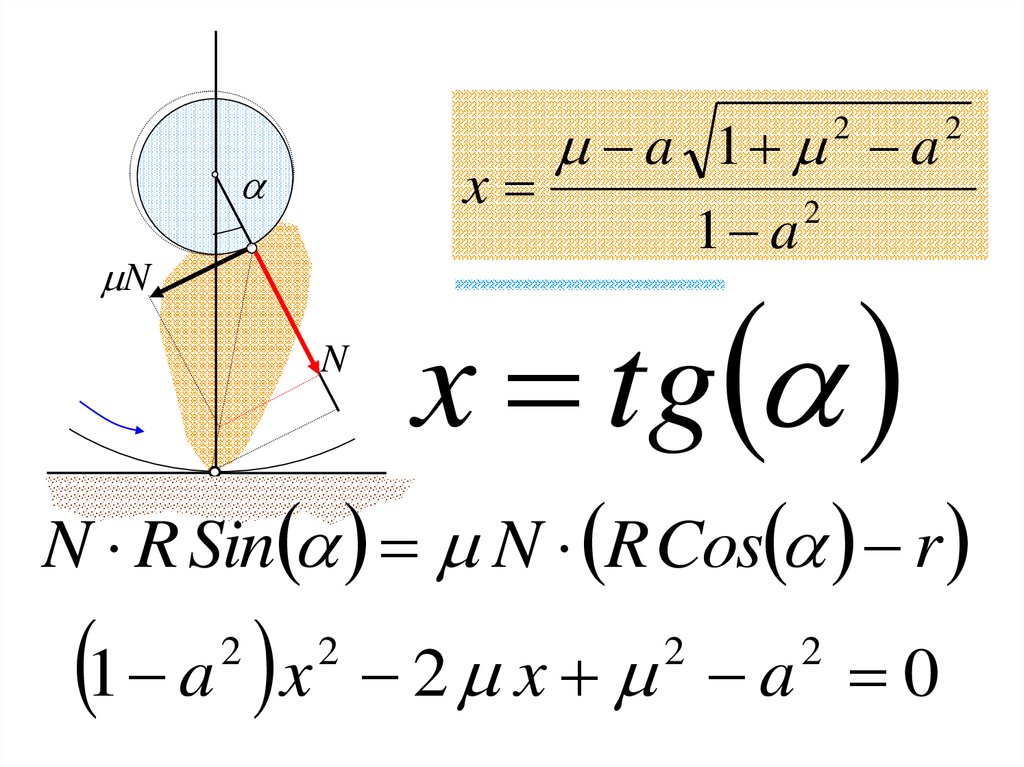

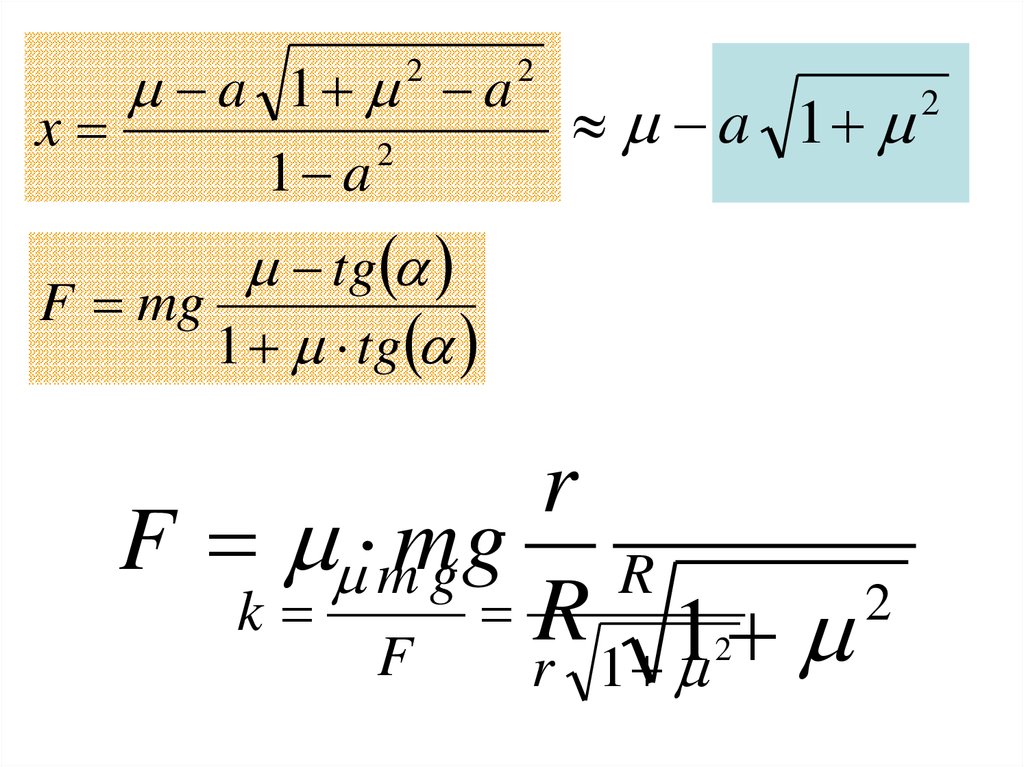





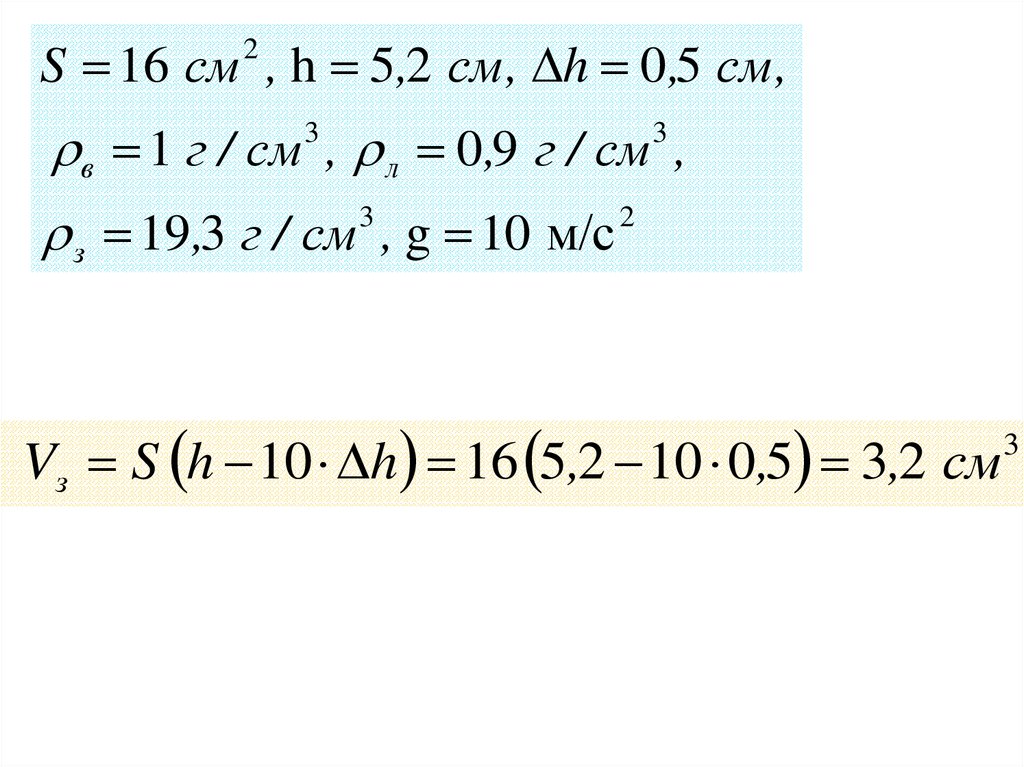


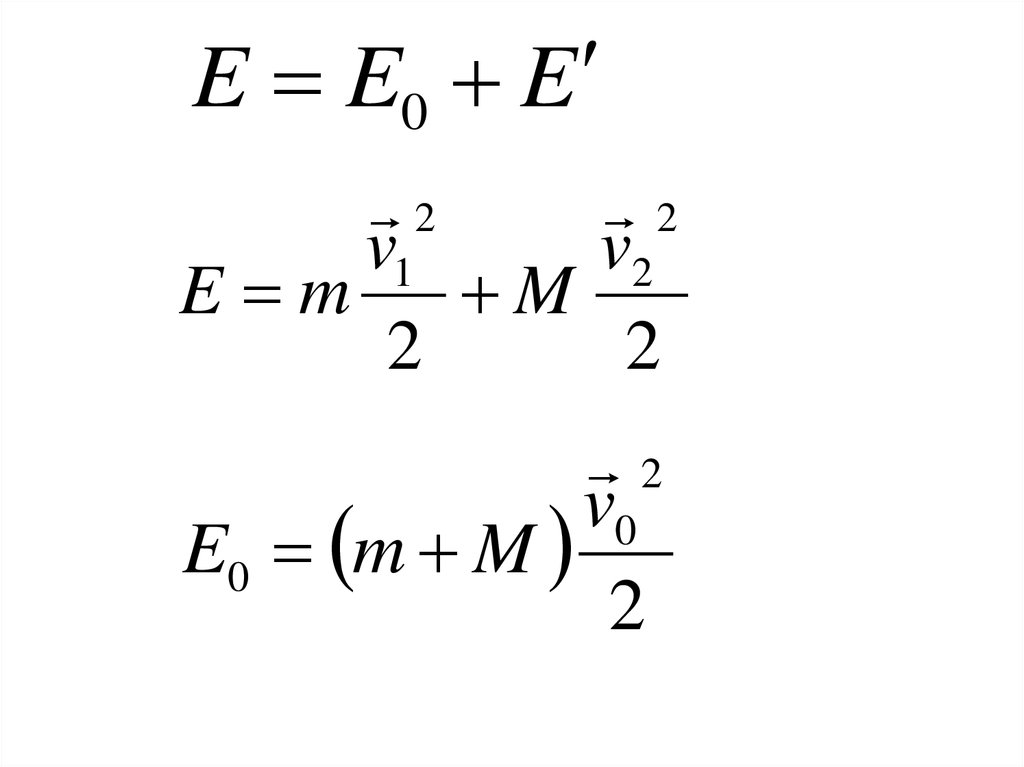
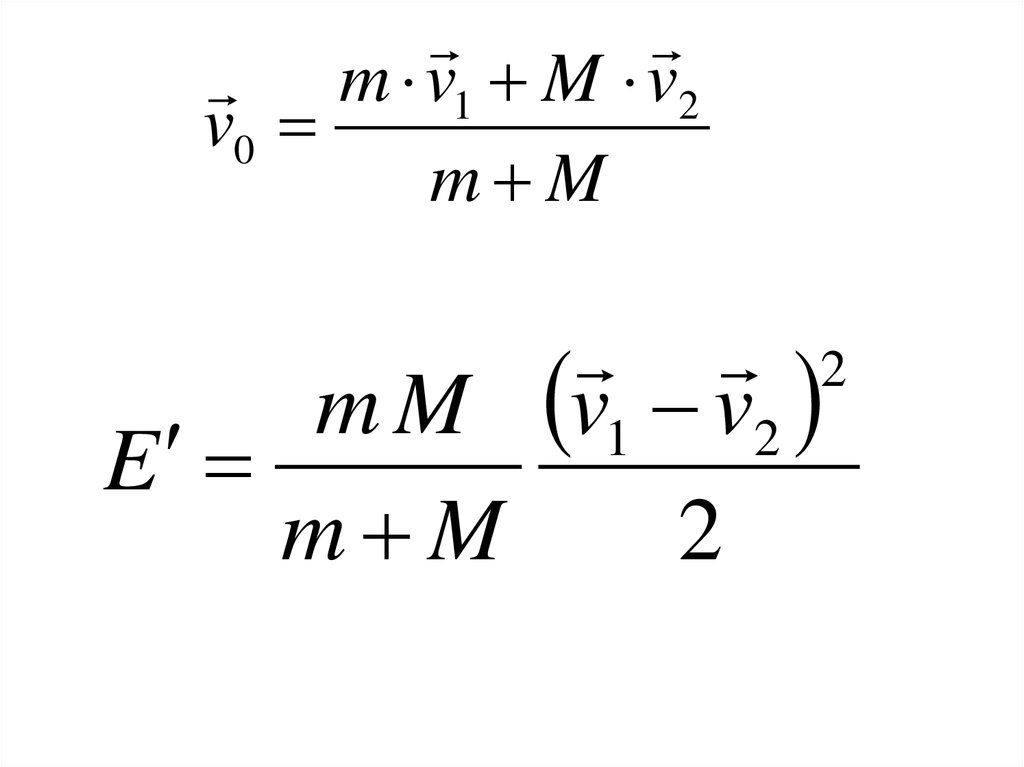

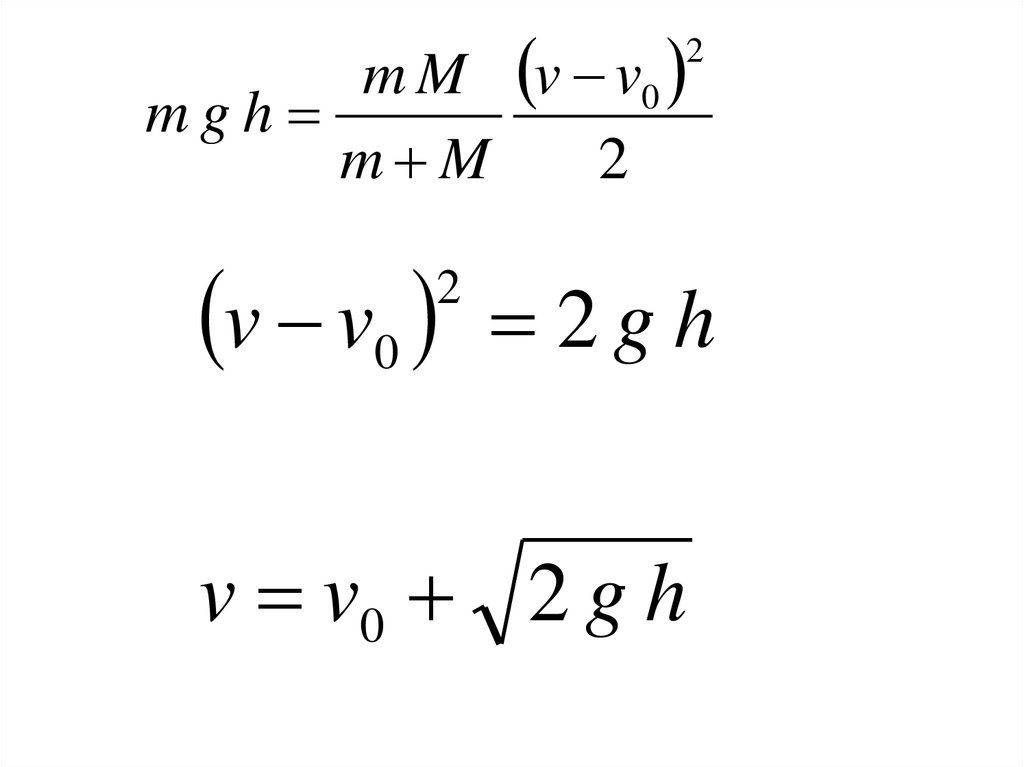


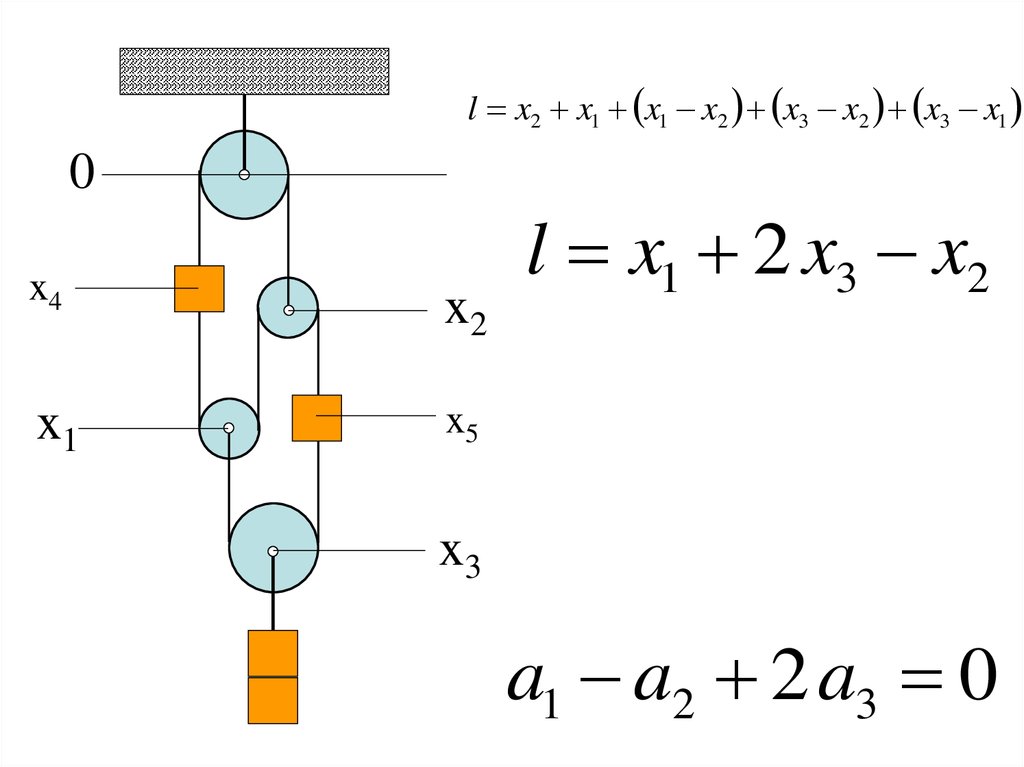


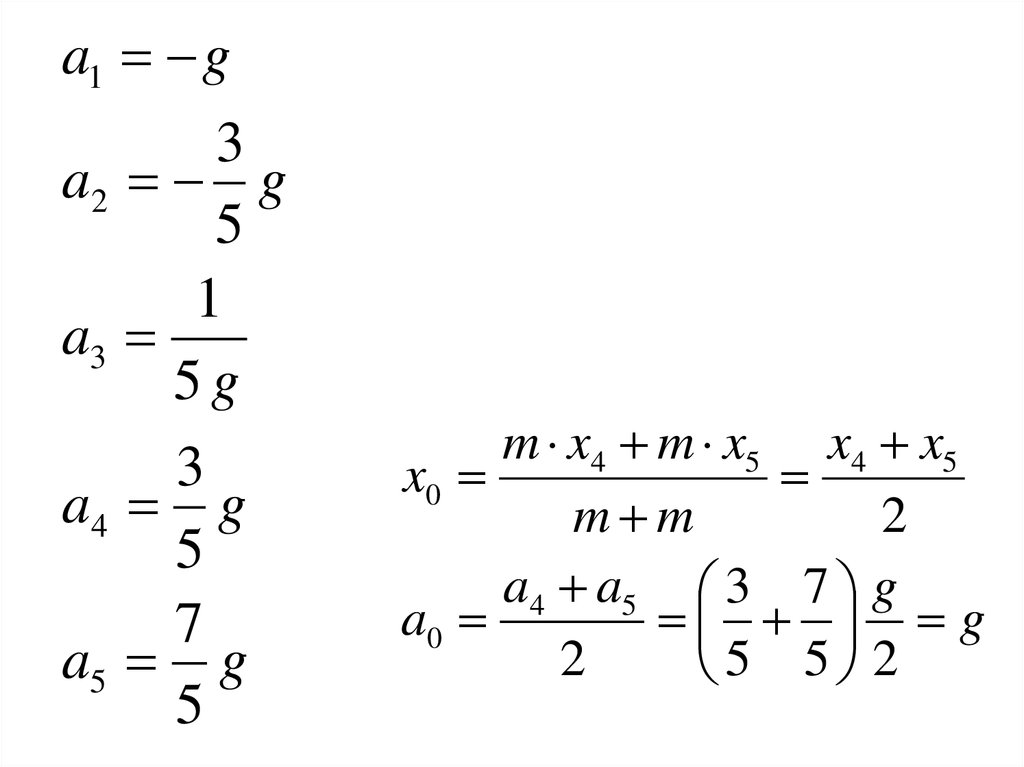
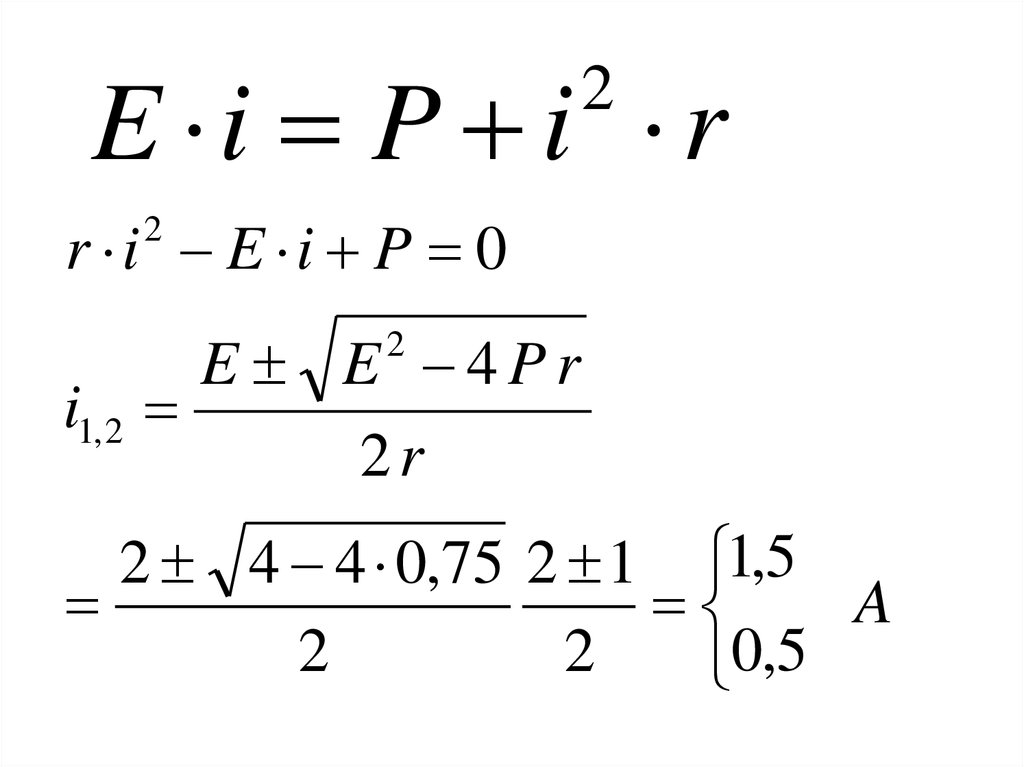








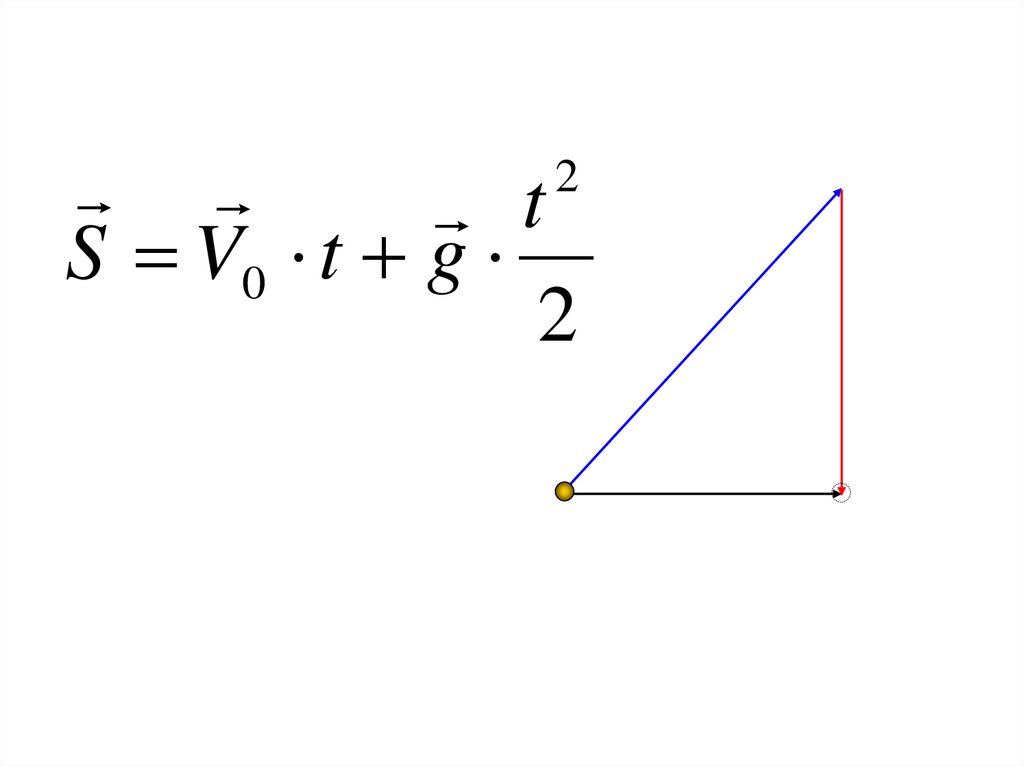


 Физика
Физика








