Похожие презентации:
Молекулярная физика. Механика. Лекция №1
1.
Лекция №1Механика
Молекулярная физика
2.
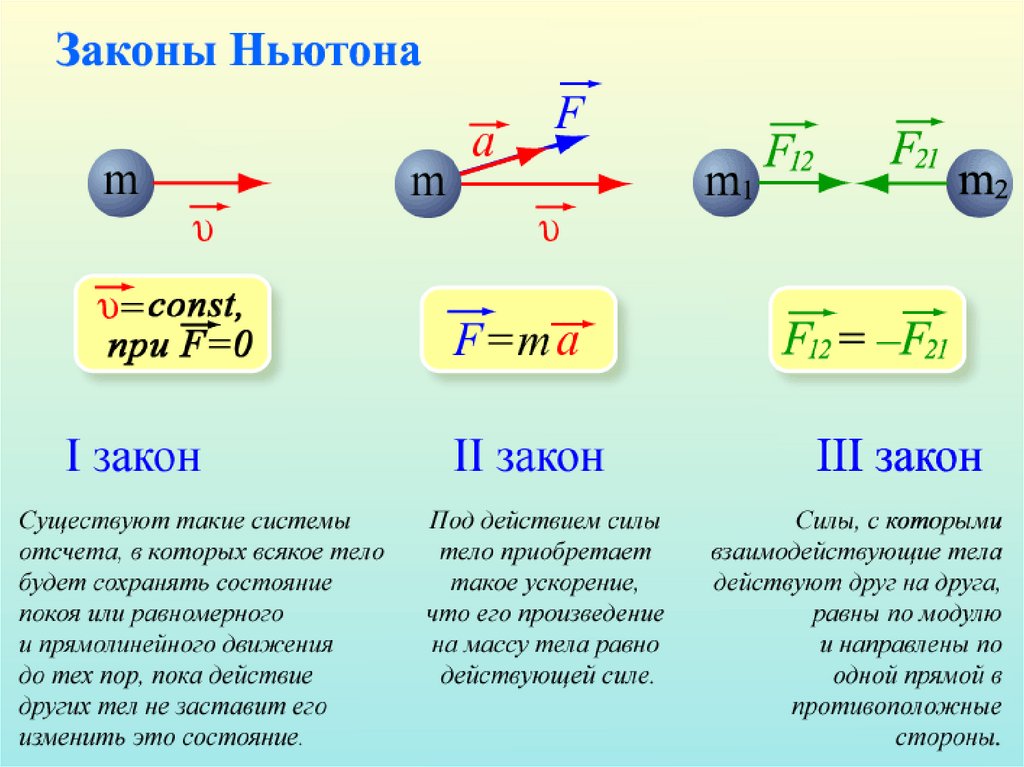
Классическая механикаНьютон
Область применимости классической механики – это
движение тел с большой (по сравнению с атомом)
массой, движущихся с малыми ( по сравнению со
скоростью света) скоростями.
Механика больших скоростей
(релятивистская механика)
Механика атомов
(квантовая механика)
Эйнштейн
Бор, Шредингер, Дирак, Планк и др
Уравнения релятивистской
механики в пределе малых ( по
сравнению со скоростью света)
скоростей переходят в
уравнения классической
механики
Уравнения квантовой механики
в пределе больших ( по
сравнению с массами атомов)
масс переходят в уравнения
классической механики
3. Структура механики
МеханикаМеханика
Кинематика
Материальной
точки
Динамика
Твёрдого тела
Статика
Сплошных сред
4.
–Кинематику называют геометриейчетырех измерений, так как она имеет
дело с тремя координатами
пространства и еще с четвертым
переменным,представляющим
собой время.
Скорости представляются первыми
производными от координаты по
времени,
ускорения - вторыми производными и
еще, кроме того, рассматриваются
производные от координат по времени
высших порядков, называемые
ускорениями высших порядков. С
аналитической точки зрения, вся
кинематика сводится к изучению
соотношений, существующих между
этими величинами.
5.
Векторы и скаляры.Величины, которые полностью определяются только числовыми
значениями, называются скалярами.
Величины, для полной характеристики которых нужно знать не
только их величину, но и направление – векторы.
В физике широко применяется векторная форма описания
движения. Положение точки задается радиус – вектором это
вектор, проведенный из начала координат в данную точку .
Для любого действия над произвольными векторами нужно
предварительно перенести один из векторов параллельно
самому себе так, чтобы векторы выходили из одной точки. Если
векторов несколько, действия производят попарно, или берут
проекции на две взаимно перпендикулярные оси (х и y).
6. Основные понятия механики
• Поступательное движение – такое, прикотором любая прямая, связанная с телом
перемещается параллельно самой себе
• Вращательное движение – такое, при
котором все точки тела движутся по
окружностям, центры которых лежат на одной
прямой, называемой осью вращения
6
7.
Рассмотрение любого движения начинают свыбора системы отсчета, включающей в себя:
тело отсчета,
систему координат и
приборы для исследования движения.
8.
Материальная точка - модель тела, размерами которого в рассматриваемыхусловиях можно пренебречь.
Траектория - линия, вдоль которой движется тело.
Путь - длина траектории.
Перемещение - вектор, соединяющий начальное и конечное положения
тела.
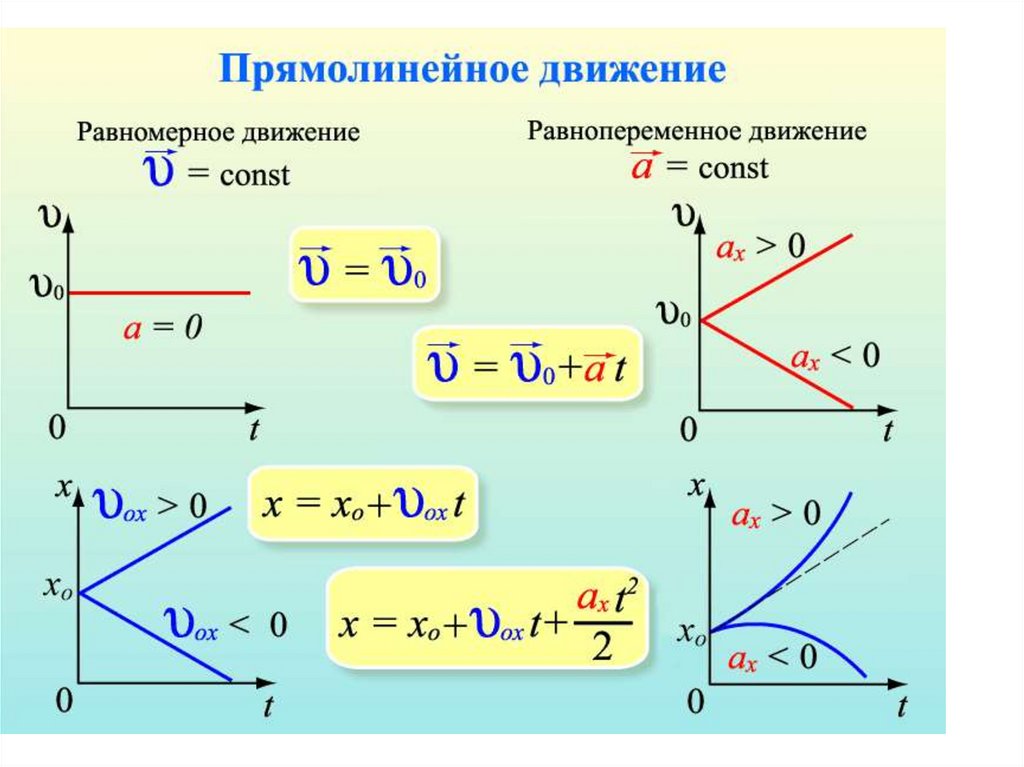
9.
Равномерное прямолинейное движение.Равномерное движение - движение при котором материальная
точка за любые равные промежутки времени совершает равные
перемещения.
При равномерном прямолинейном движении скорость тела
постоянна, ускорение равно нулю. Траектория равномерного
прямолинейного движения - прямая линия.
Для физических величин характеризующих движение имеем:
a=0
V=Const
Sx = Vx· t
x=x0+ Vx·t
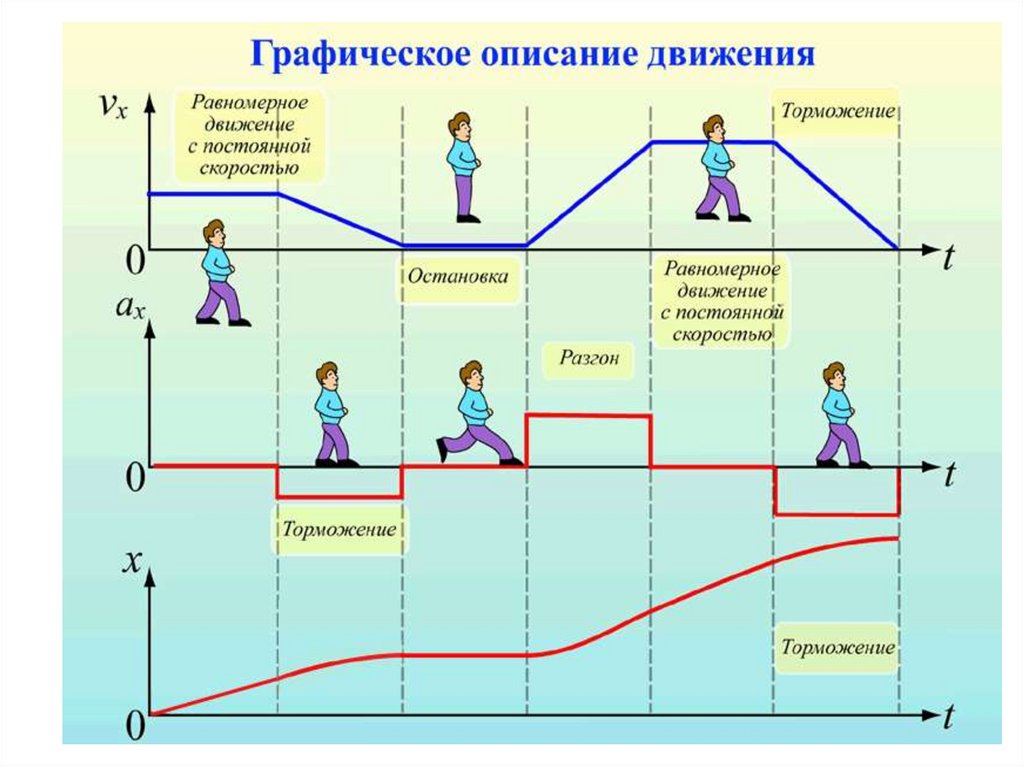
10.
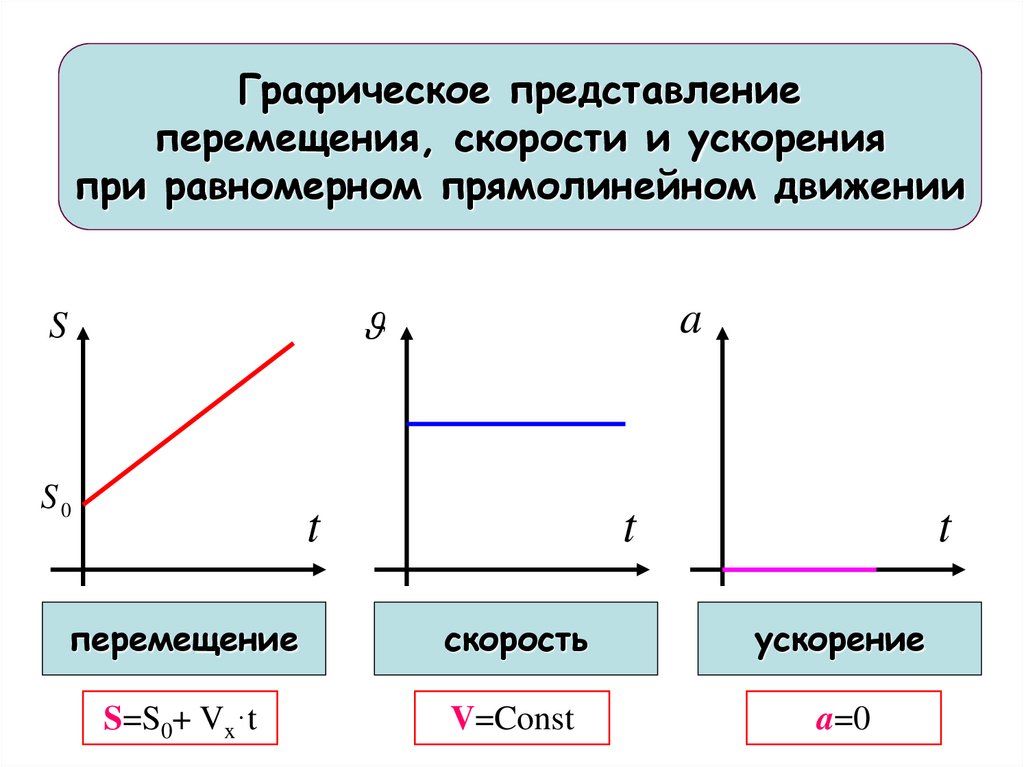
Графическое представлениеперемещения, скорости и ускорения
при равномерном прямолинейном движении
S
S0
a
t
t
t
перемещение
скорость
ускорение
S=S0+ Vx·t
V=Const
a=0
11. Неравномерное движение
Неравномерное движение• Движение, при котором за равные
промежутки времени тело совершает
неравные перемещения
называют неравномерным
или переменным.
12.
скоростьПо определению
v v0
a
t
тогда скорость равноускоренного
движения
v v0 at
При записи уравнения в проекции векторов на координатную ось ОХ имеем:
v x v0 x a x t
при a > 0
v x v0 x a x t
при a < 0
13. УСКОРЕНИЕ
– характеристика неравномерного движения,показывает на сколько изменилась скорость
за 1с.
v – конечная скорость
v v 0
v0 – начальная скорость
a
t
а – ускорение (м/с²)
а>0 движение равноускоренное, v увеличивается
a<0 движение равнозамедленное, v уменьшается
Направление вектора ускорения совпадает с направлением изменения
скорости.
14.
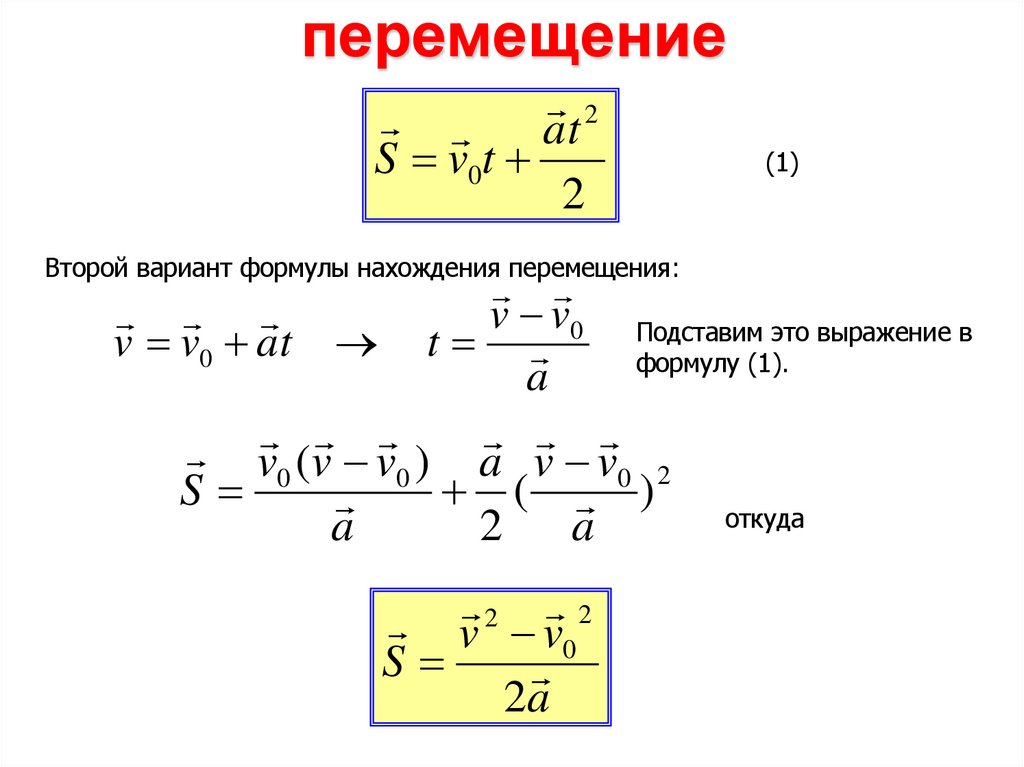
перемещение2
at
S v0t
2
Второй вариант формулы нахождения перемещения:
(1)
v v0 Подставим это выражение в
v v0 at t
формулу (1).
a
v 0 (v v 0 ) a v v 0 2
S
( )
откуда
a
2
a
v 2 v 0 2
S
2a
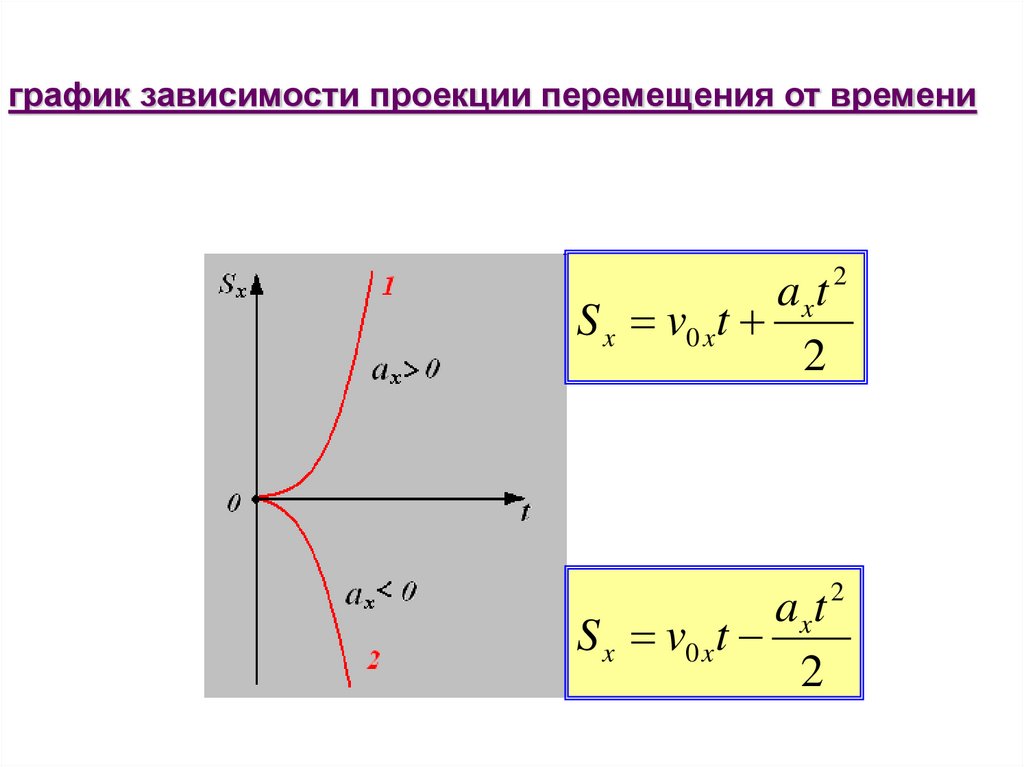
15.
график зависимости проекции перемещения от времениaxt 2
S x v0 x t
2
axt
S x v0 xt
2
2
16.
17.
18.
Классическая механикаНьютон
Область применимости классической механики – это
движение тел с большой (по сравнению с атомом)
массой, движущихся с малыми ( по сравнению со
скоростью света) скоростями.
Механика больших скоростей
(релятивистская механика)
Механика атомов
(квантовая механика)
Эйнштейн
Бор, Шредингер, Дирак, Планк и др
Уравнения релятивистской
механики в пределе малых ( по
сравнению со скоростью света)
скоростей переходят в
уравнения классической
механики
Уравнения квантовой механики
в пределе больших ( по
сравнению с массами атомов)
масс переходят в уравнения
классической механики
19.
Взаимодействие телСогласно явлению инерции, тело само не может изменить
скорость своего движения.
Для изменения скорости тела на него необходимо подействовать
другим телом.
Действие тел друг на друга называют взаимодействием.
В результате взаимодействия оба тела изменяют свою скорость.
1
2 0
20.
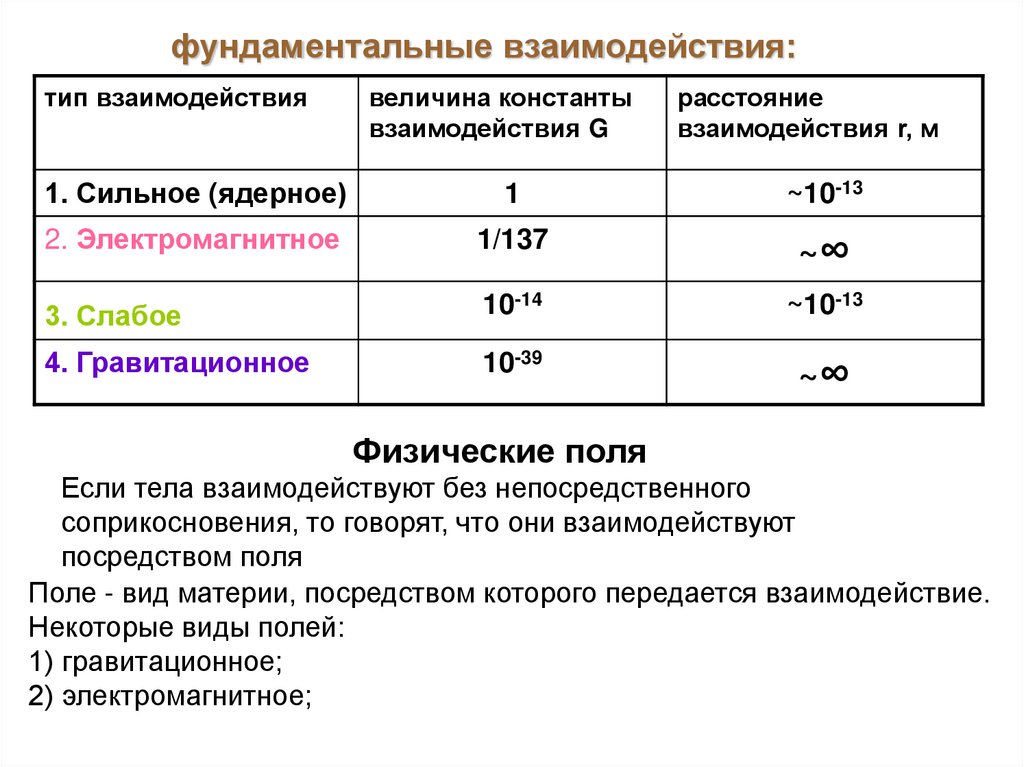
фундаментальные взаимодействия:тип взаимодействия
величина константы
взаимодействия G
расстояние
взаимодействия r, м
1. Сильное (ядерное)
1
~10-13
2. Электромагнитное
1/137
~∞
3. Слабое
10-14
~10-13
4. Гравитационное
10-39
~∞
Физические поля
Если тела взаимодействуют без непосредственного
соприкосновения, то говорят, что они взаимодействуют
посредством поля
Поле - вид материи, посредством которого передается взаимодействие.
Некоторые виды полей:
1) гравитационное;
2) электромагнитное;
21.
Силой называется всякое воздействие на данное тело,сообщающее ему ускорение или вызывающее его деформацию.
F – сила
Единица измерения –
Н (Ньютон)
Полная характеристика силы включает следующую
информацию:
1)природу взаимодействия;
2)тело, со стороны которого действует сила;
3)тело, на которое действует сила (точка приложения силы);
4)линия действия силы;
5)направление силы;
6)величина силы.
22.
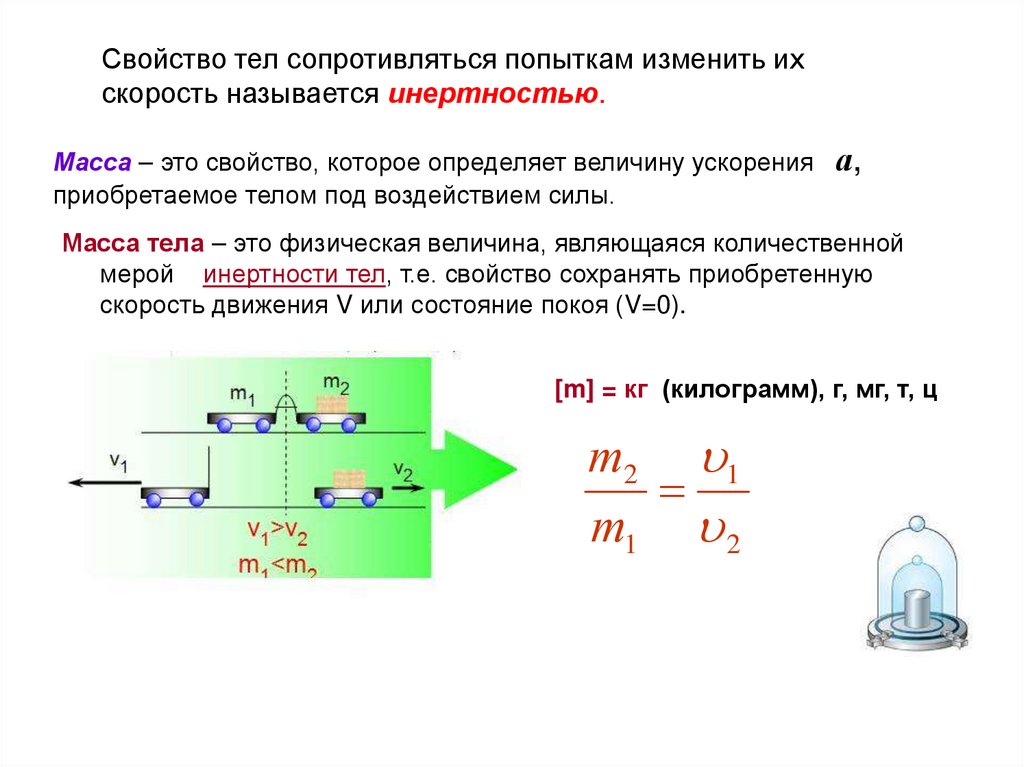
Свойство тел сопротивляться попыткам изменить ихскорость называется инертностью.
Масса – это свойство, которое определяет величину ускорения
приобретаемое телом под воздействием силы.
а,
Масса тела – это физическая величина, являющаяся количественной
мерой инертности тел, т.е. свойство сохранять приобретенную
скорость движения V или состояние покоя (V=0).
[m] = кг (килограмм), г, мг, т, ц
т 2 1
т1 2
23.
Импульс или количество движенияматериальной точки - вектор, равный
произведению массы точки на ее скорость:
p = mv.
Импульсом или количеством движения
системы материальных точек назовем
векторную сумму импульсов отдельных
материальных точек, из которых эта система
состоит.
Для системы из двух материальных точек
p = p1 + p2 = m1v1 + m2v2.
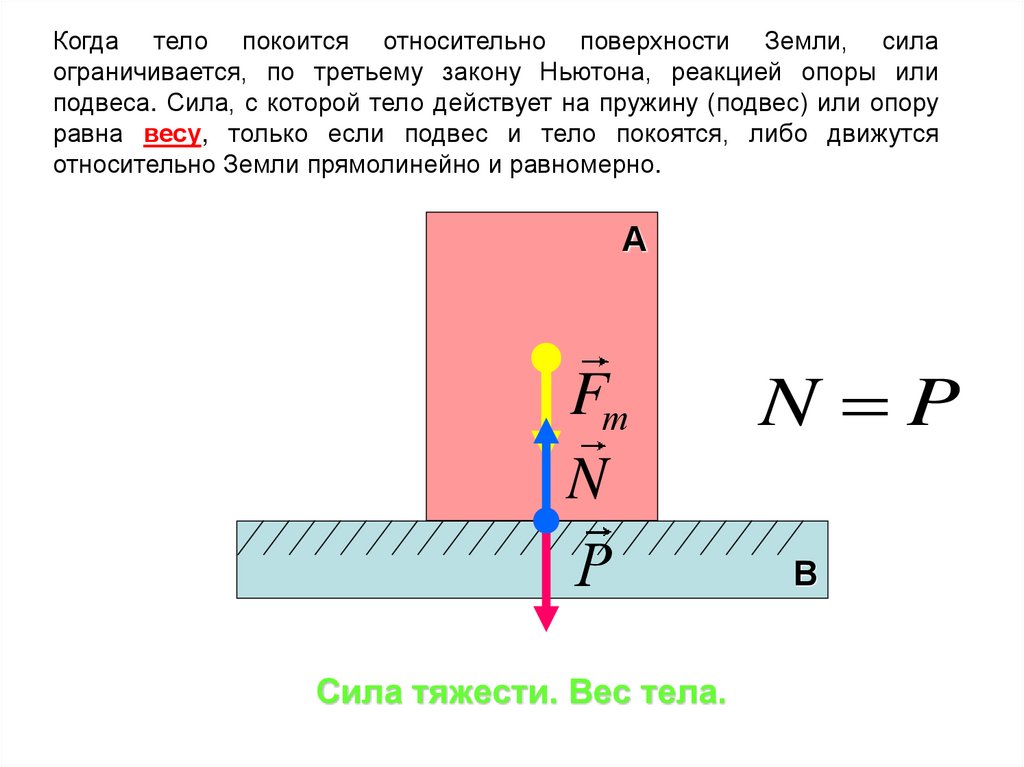
24. Сила тяжести. Вес тела.
Когда тело покоится относительно поверхности Земли, силаограничивается, по третьему закону Ньютона, реакцией опоры или
подвеса. Сила, с которой тело действует на пружину (подвес) или опору
равна весу, только если подвес и тело покоятся, либо движутся
относительно Земли прямолинейно и равномерно.
А
Fт
N
Р
Сила тяжести. Вес тела.
N P
В
25.
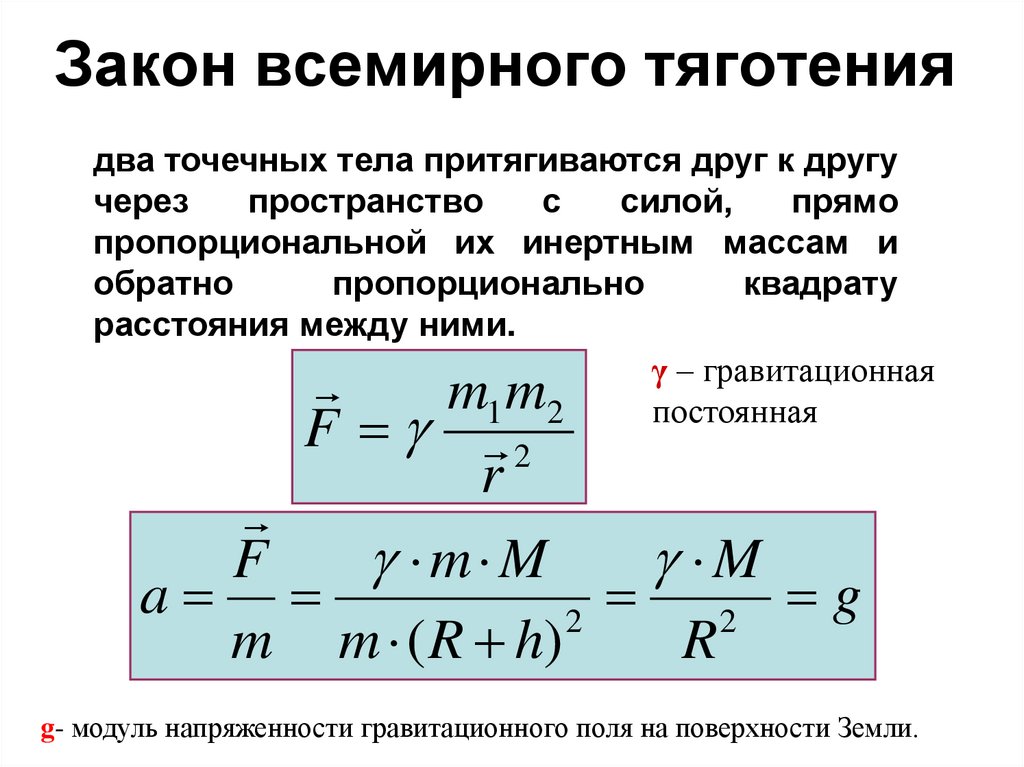
26. Закон всемирного тяготения
два точечных тела притягиваются друг к другучерез
пространство
с
силой,
прямо
пропорциональной их инертным массам и
обратно
пропорционально
квадрату
расстояния между ними.
γ – гравитационная
постоянная
1 2
2
mm
F
r
F
m M
M
a
g
2
2
m m ( R h)
R
g- модуль напряженности гравитационного поля на поверхности Земли.
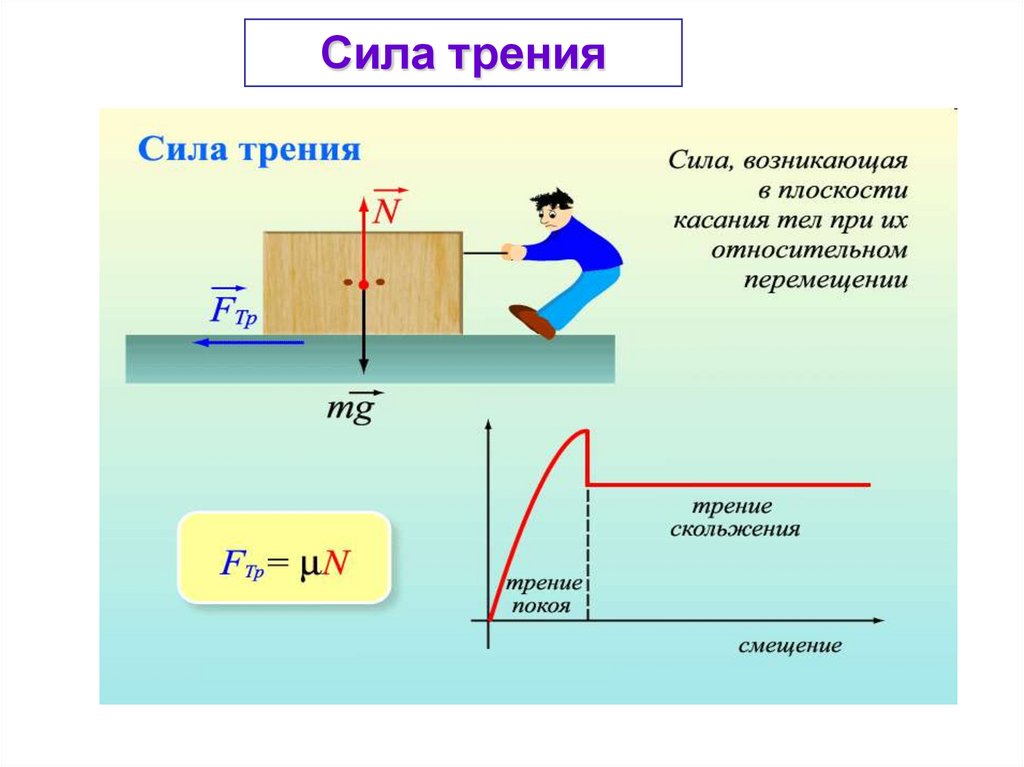
27.
Сила трения28.
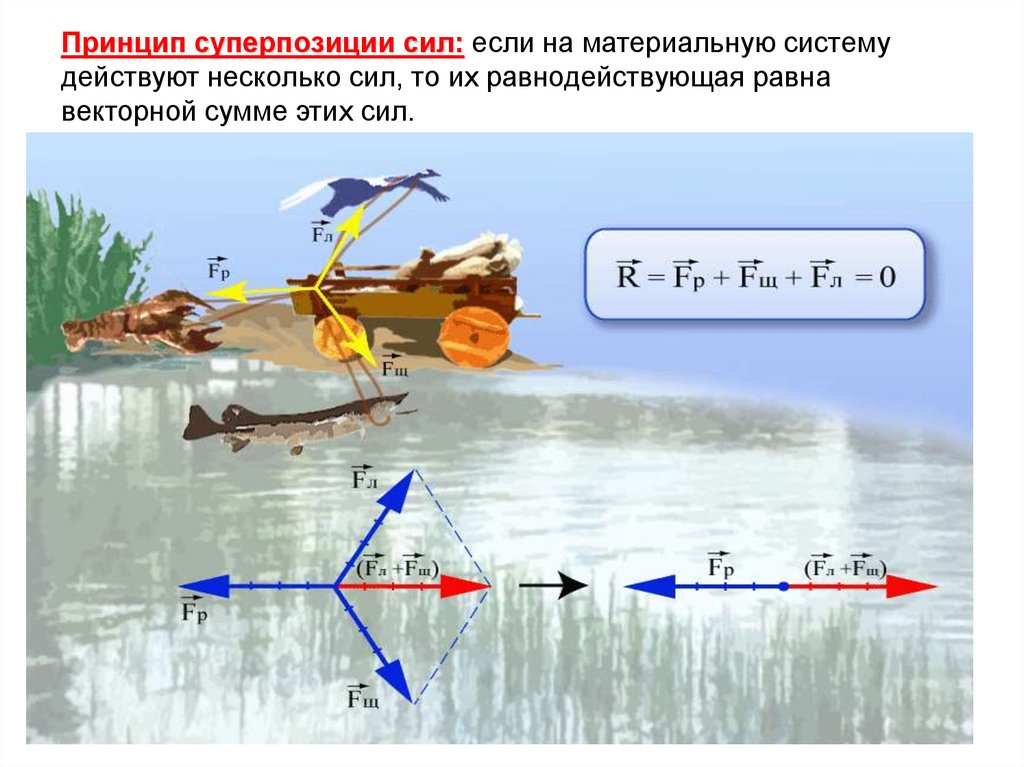
Принцип суперпозиции сил: если на материальную системудействуют несколько сил, то их равнодействующая равна
векторной сумме этих сил.
29.
РАБОТАFтяги
30.
Работа.работа – это скалярная
величина, равная скалярному
произведению
проекции силы f на направление перемещения r и пути, проходимого
точкой приложения силы:
s
A f r
1Дж=1Н·1м=1кг·м2/с2.
F
sF
A=fs·s=f·s·cosα, если α=const, то и fs=const
dr
α –острый, то cosα > 0, следовательно A > 0.
F
α – тупой, cosα < 0 и работа A < 0
α
s
Fц
α=π/2, cosα = 0, и работа A = 0
fs ≠ Const
fs
dA
dA lim f si si
si 0
A f s ds
s
Δsi
s
31.
Мощность.мощность – величина, показывающая какая работа совершается в
единицу времени и равная
dA F dr
W
F
dt
dt
1Дж/1сек=1Вт.
32. Энергия-
ЭнергияE•[ Дж ] - скалярная физическая величина,характеризующая способность тела
совершать работу.
33.
СУЩЕСТВУЕТ ДВА ВИДА МЕХАНИЧЕСКОЙЭНЕРГИИ: КИНЕТИЧЕСКАЯ И
ПОТЕНЦИАЛЬНАЯ, КОТОРЫЕ МОГУТ
ПРЕВРАЩАТЬСЯ ДРУГ В ДРУГА.
Потенциальная
энергия – это
энергия которой
обладают
предметы в
состоянии покоя.
Кинетическая
энергия – это
энергия тела
приобретенная
при движении.
34.
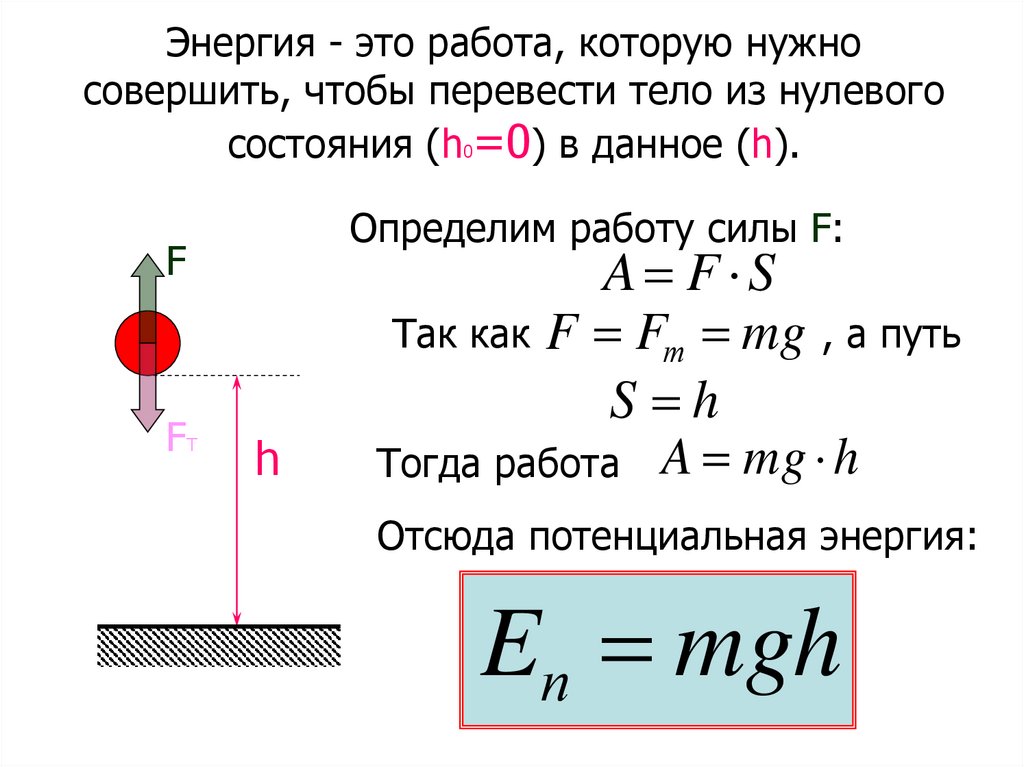
Энергия - это работа, которую нужносовершить, чтобы перевести тело из нулевого
состояния (h0=0) в данное (h).
Определим работу силы F:
F
FТ
h
A F S
Так как F Fт mg , а путь
S h
Тогда работа A mg h
Отсюда потенциальная энергия:
Eп mgh
Eп A mg h
35.
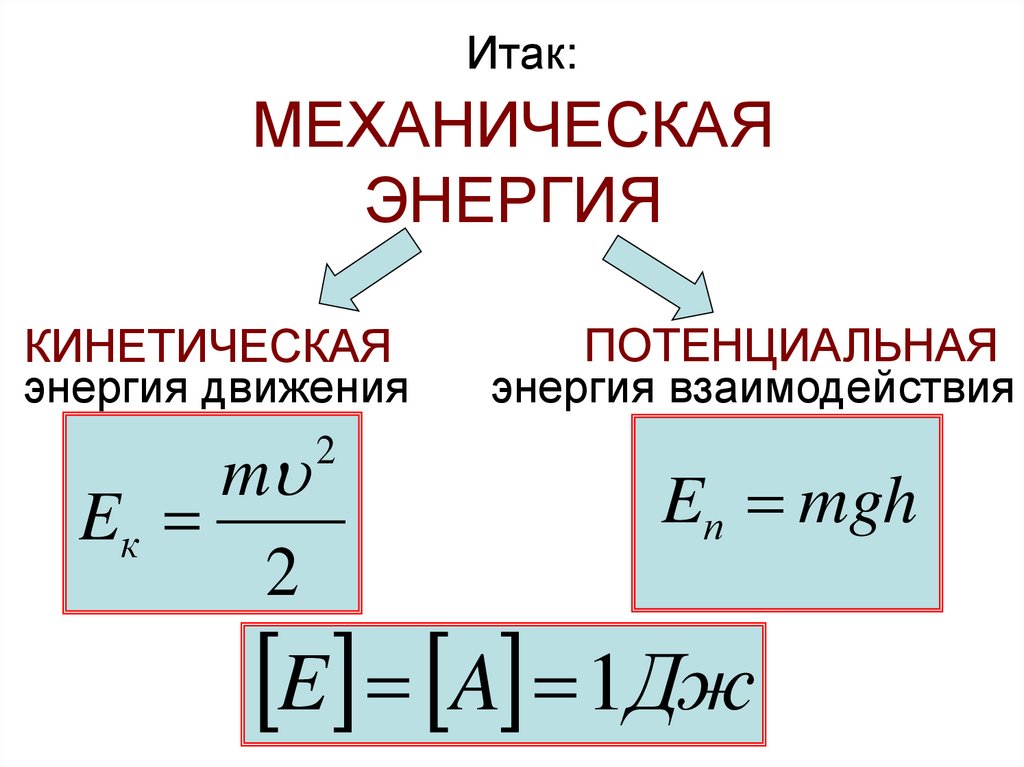
Итак:МЕХАНИЧЕСКАЯ
ЭНЕРГИЯ
КИНЕТИЧЕСКАЯ
энергия движения
m
Eк
2
2
ПОТЕНЦИАЛЬНАЯ
энергия взаимодействия
Eп mgh
E A 1Дж
36.
Превращение потенциальнойэнергии в кинетическую.
ПОДБРАСЫВАЯ ВВЕРХ МЯЧ, МЫ
СООБЩАЕМ ЕМУ ЭНЕРГИЮ ДВИЖЕНИЯ –
КИНЕТИЧЕСКУЮ ЭНЕРГИЮ.
ПОДНЯВШИСЬ, МЯЧ ОСТАНАВЛИВАЕТСЯ,
А ЗАТЕМ НАЧИНАЕТ ПАДАТЬ. В МОМЕНТ
ОСТАНОВКИ (В ВЕРХНЕЙ ТОЧКЕ) ВСЯ
КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ПОЛНОСТЬЮ
ПРЕВРАЩАЕТСЯ В ПОТЕНЦИАЛЬНУЮ.
ПРИ ДВИЖЕНИИ ТЕЛА ВНИЗ
ПРОИСХОДИТ ОБРАТНЫЙ ПРОЦЕСС.
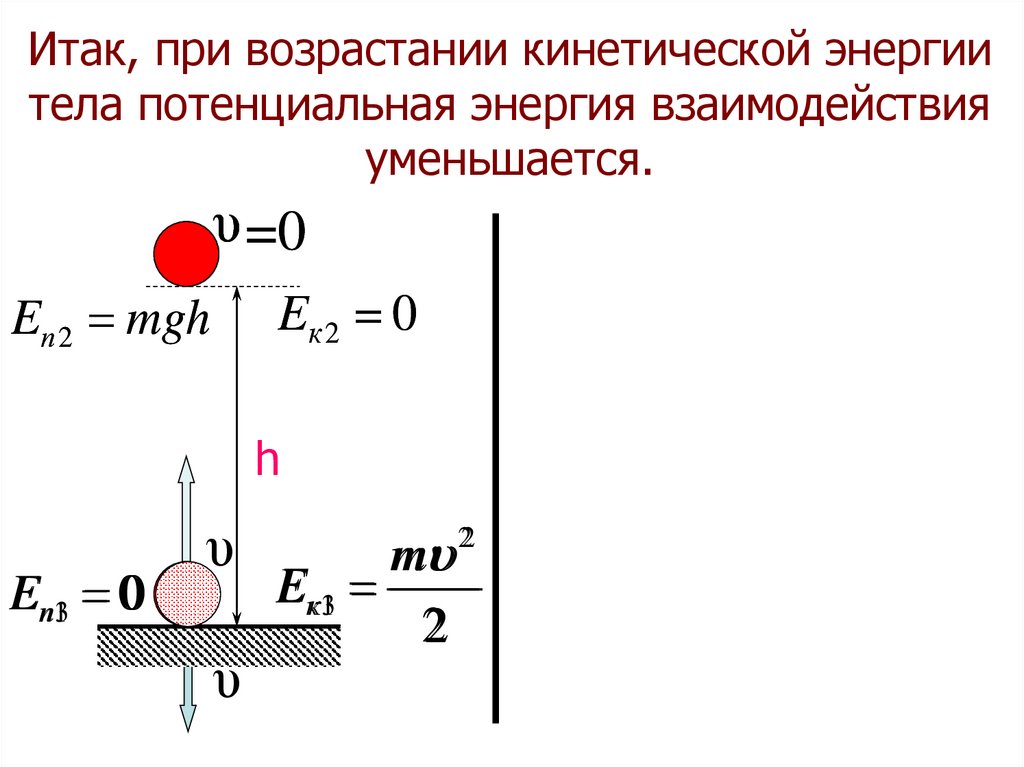
37.
Итак, при возрастании кинетической энергиитела потенциальная энергия взаимодействия
уменьшается.
υ =0
Eк 2 0
Eп 2 mgh
h
Eп13 0
υ
υ
m
E к13
2
22
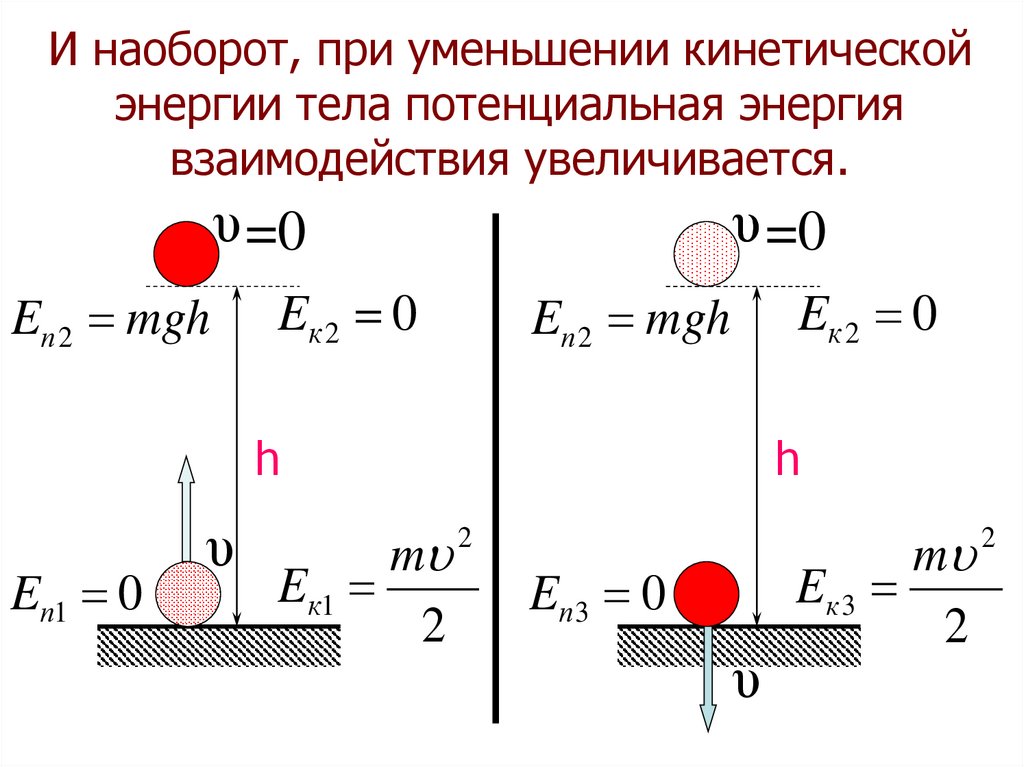
38.
И наоборот, при уменьшении кинетическойэнергии тела потенциальная энергия
взаимодействия увеличивается.
υ =0
Eп 2 mgh
υ =0
Eк 2 0
Eк 2 0
Eп 2 mgh
h
Eп1 0
υ
m
E к1
2
h
2
Eп 3 0
υ
m
Eк 3
2
2
39.
Рассмотрим систему тел, между которыми действуют толькоконсервативные силы . Изменение энергии тела происходит:
1) за счет внутренних сил равна изменению потенциальной энергии тела
Ep Ep1 Ep2
2) За счет внешних сил, работа которых равна А
Полная работа равна изменению кинетической энергии тела:
Ep1 Ep2 A Ek 2 Ek1
( Ep2 Ek 2 ) ( Ep1 Ek1 ) A
Eполн2 Eполн1 A
40.
Eполн2 Eполн1 AПриращение полной энергии системы тел, между которыми
действуют только консервативные силы, равно работе внешних сил,
приложенных к телам системы.
Если система замкнута, то А=0, тогда ΔЕполн=0,
Еполн = const
Полная механическая энергия замкнутой системы тел,
между которыми действуют только консервативные
силы, остается постоянной
Неконсерватевные силы рассматриваются как внешние (трение)
Общий закон
В замкнутой системе, изолированной от внешних воздействий, остается
постоянной сумма всех видов энергии
41. Динамика вращательного движения абсолютно твердого тела
42. Абсолютно твердое тело
Под твердым телом будем подразумевать абсолютнотвердое тело, в котором расстояния между любыми
двумя точками неизменны. Твердое тело можно
представить как совокупность большого количества
очень малых масс m i , которые можно считать МТ.
Теорема о движении центра масс твердого тела:
центр масс твердого тела движется так, как двигалась
бы материальная точка с массой, равной массе тела, и к
которой приложены все внешние силы, действующие на
тело.
Т.е. раньше мы говорили о МТ и о систем МТ и ее
центре масс теперь еще и об абсолютно твердом
теле.
43. Момент силы
Моментом силы N относительно точки О называетсявекторное произведение радиус-вектора направленного из
точки О в точку приложения силы :
N = rF
Величина вектора определяется,
выражением:
как и для любого векторного произведения,
N = rFsin α
где альфа– угол между векторами
r F
и
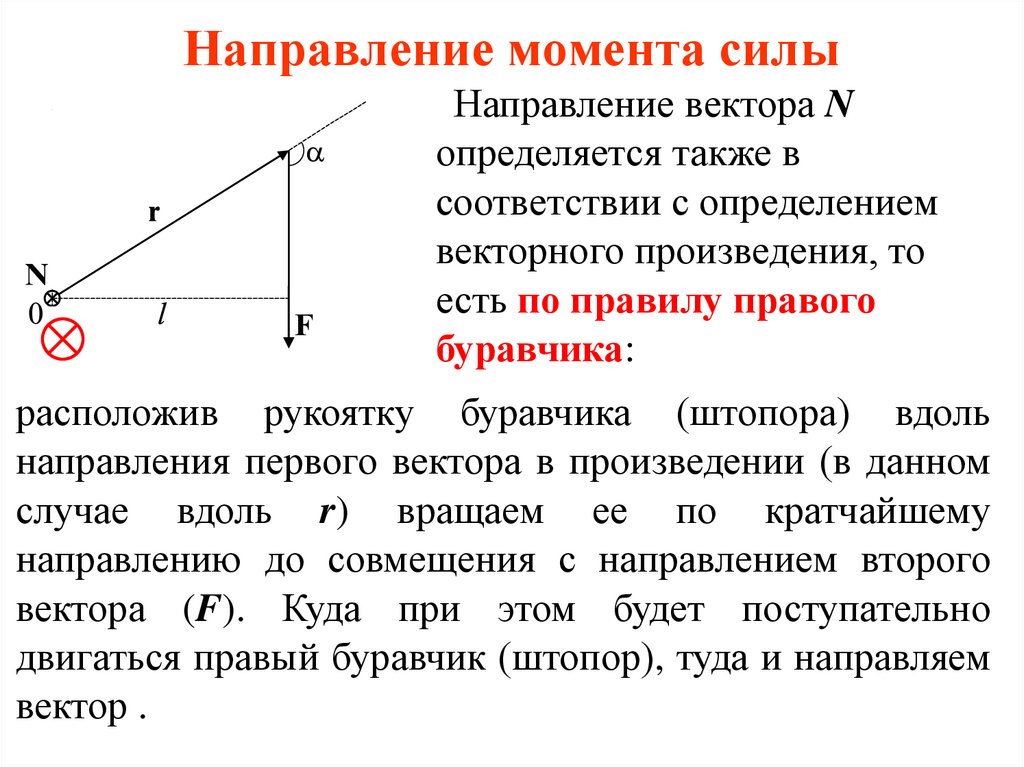
44. Направление момента силы
Направление вектора Nопределяется также в
соответствии с определением
векторного произведения, то
есть по правилу правого
буравчика:
расположив рукоятку буравчика (штопора) вдоль
направления первого вектора в произведении (в данном
случае вдоль r) вращаем ее по кратчайшему
направлению до совмещения с направлением второго
вектора (F). Куда при этом будет поступательно
двигаться правый буравчик (штопор), туда и направляем
вектор .
45. Момент импульса
Для МТ, моментом импульса относительно точки Оназывается вектор
L=[r, р] = [r,mV]
Моментом импульса МТ относительно оси называется
проекция вектора L на эту ось:
LZ=[r, р]Z
L системы материальных точек относительно какойлибо точки (или оси) называется сумма моментов
импульсов относительно этой точки (или оси) всех
материальных точек системы:
L= ∑ Li
i
46. Закон изменения и сохранения момента импульса
Производная по времени момента импульса системы(относительно какой-либо точки или оси) равна сумме
моментов (относительно той же точки или оси) всех внешних
сил, действующих на точки системы.
dL
= Nвнеш
dt
i
Это и есть закон изменения момента импульса или уравнение
моментов. В каждый Niвнеш входит произведение трех величин ri, Fiвнеш и sin I . Если
одна из них =0 то данный член вклада не дает. Один из возможных вариантов, если все
Fiвнеш =0 т.е. система замкнута , то dL/dt = 0
и L = const
Закон сохранения момента импульса: если сумма моментов внешних сил равна
нулю, то момент импульса системы не изменяется с течением времени (верно как
относительно точки, так и оси).
47. Момент инерции твердого тела
Твердое тело можно представить как систему МТ, удерживаемых внутренними силамина неизменных расстояниях друг от друга и по аналогии с МТ записать:
dL
N внеш
dt
Пусть Li момент импульса i-й частицы , ri — радиус окружности, по которой
движется МТ m i относительно оси вращения тела. Направление Li всех точек тела
относительно оси вращения одинаковое, так как в каждый момент времени
направление и величина угловых скоростей всех точек одинаковы (тело твердое).
L Li ω mi ri Iω
2
Величина I mi ri 2
называется моментом инерции твердого тела
относительно данной оси. Направление векторов L и совпадают только в случае
симметричного тела.
48. Момент инерции полого цилиндра
Найдем момент инерции полого цилиндра относительно его осисимметрии ОО.
I Δmi ri2 R 2 Δmi R 2m mR 2
где m — масса цилиндра.
Итак, момент инерции полого цилиндра (обруч, кольцо) прямо не зависит от высоты
этого цилиндра (косвенно зависит так как чем больше высота тем больше масса).
Момент инерции тела- аналог массы при вращательном движении. Он
характеризует не только инертность тела, но и распределение
массы относительно оси вращения. Для одного и того же тела
момент инерции относительно разных осей различен.
49. Момент инерции сложных тел
2I
Δm
r
Для определения момента инерции более сложных тел выражение
ii
следует уточнить, устремив элемент mi к нулю и найдя соответствующий предел:
I lim r Δmi
Δm 0
2
i
Как известно, такой предел называется интегралом:
I r dm ρ r dV
2
2
Интегрирование производится по всему объему тела V. Если плотность тела постоянна,
то можно вынести из под знака интегрирования.
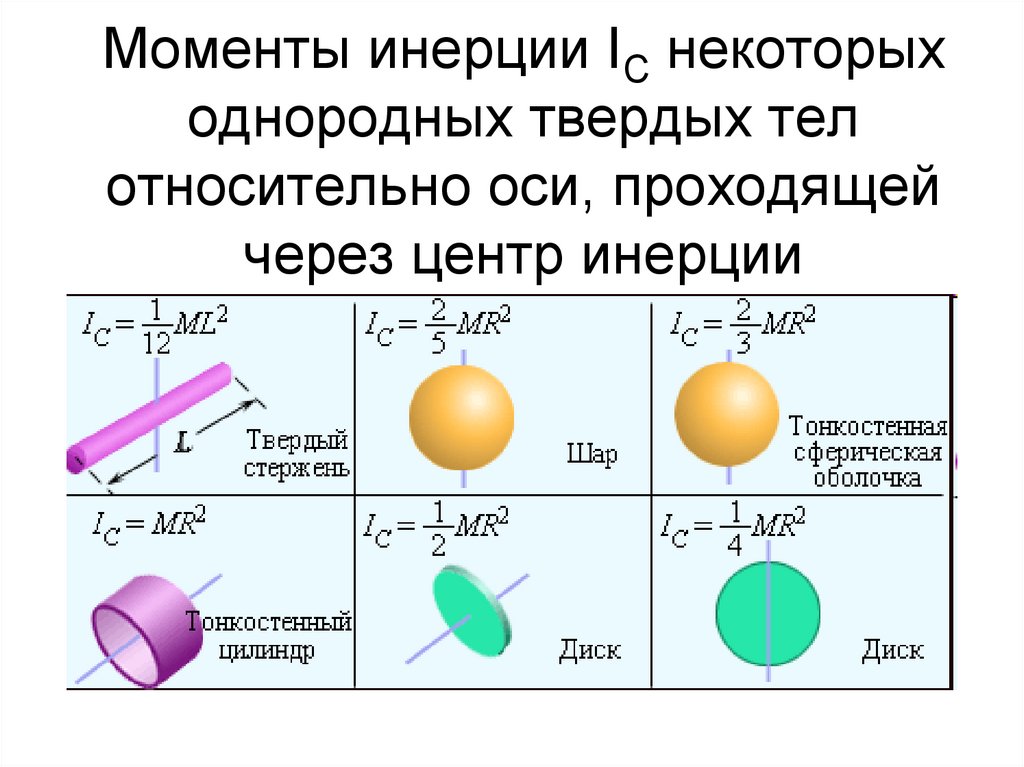
50. Моменты инерции IС некоторых однородных твердых тел относительно оси, проходящей через центр инерции
51. Теорема Штейнера
Зная момент инерции телаотносительно оси, проходящей через
центр масс, момент инерции
относительно произвольной оси
вычисляют по теореме Штейнера:
момент инерции относительно произвольной оси I
равен сумме момента инерции Ic относительно оси,
параллельной данной и проходящей через центр масс
тела, и произведения массы тела на квадрат расстояния
между осями d.
I I c md
2
52.
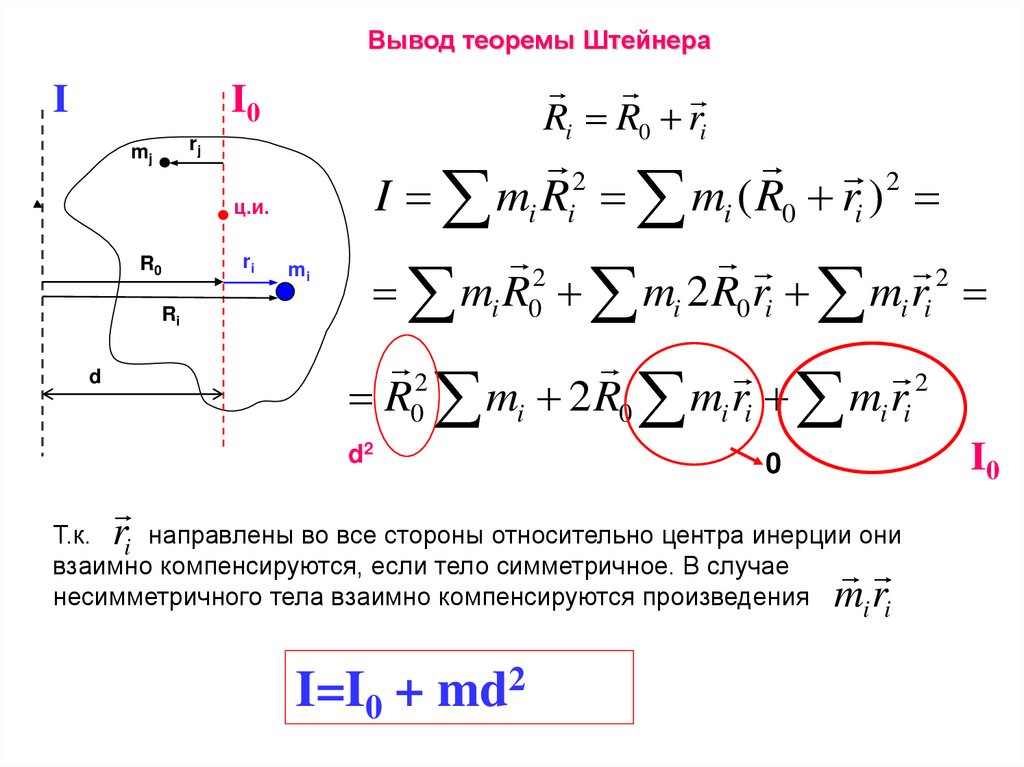
Вывод теоремы ШтейнераI
Ri R0 ri
I0
rj
mj
ц.и.
R0
Ri
d
ri
mi
2
2
I mi Ri mi ( R0 ri )
2
2
mi R0 mi 2 R0 ri mi ri
2
2
R0 mi 2 R0 mi ri mi ri
d2
0
Т.к. ri направлены во все стороны относительно центра инерции они
взаимно компенсируются, если тело симметричное. В случае
несимметричного тела взаимно компенсируются произведения mi ri
I=I0 + md2
I0
53.
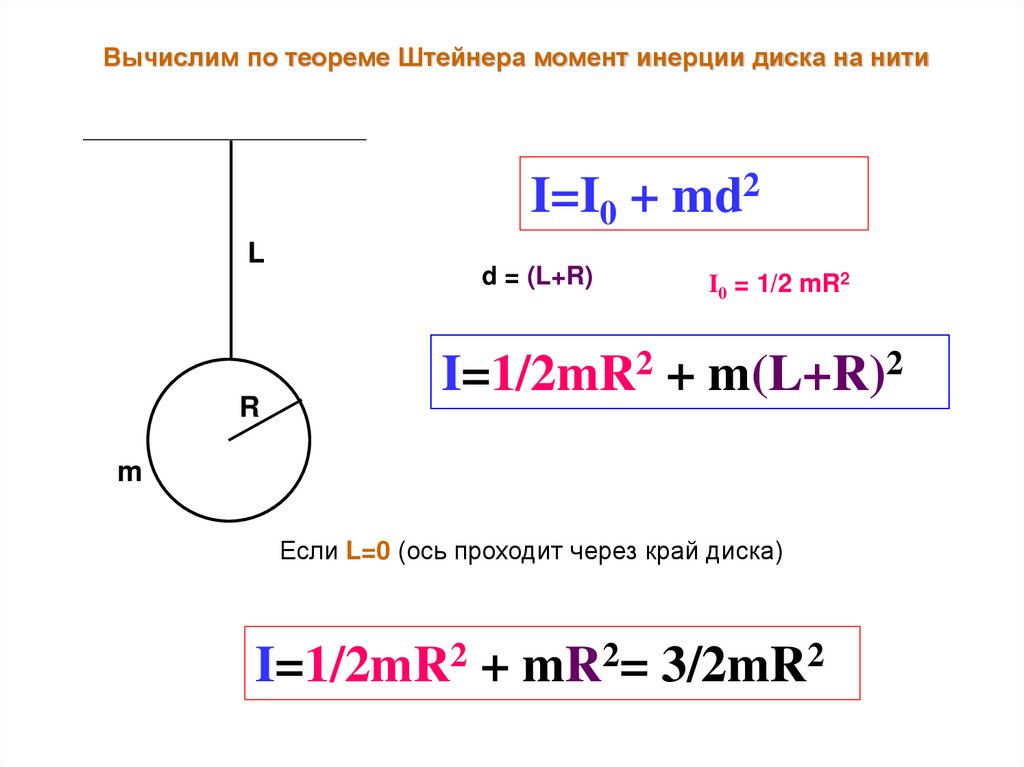
Вычислим по теореме Штейнера момент инерции диска на нитиI=I0 + md2
L
R
d = (L+R)
I0 = 1/2 mR2
I=1/2mR2 + m(L+R)2
m
Если L=0 (ось проходит через край диска)
I=1/2mR2 + mR2= 3/2mR2
54. Уравнение моментов для материальной точки
Как уже говорилось момент импульса МТ, двигающейсяпо окружности:
L mR ω Iω
2
Производная по времени равна:
dL
dω
I
Iβ
dt
dt
В соответствии с законом изменения момента импульса
для МТ получаем:
Iβ N iвнеш
i
55. Уравнение моментов
mv 2T
2
Заменив в выражении для кинетической энергии
массу на момент инерции I, а скорость v на угловую скорость получим
кинетическую энергию вращающегося вокруг неподвижной оси тела или
просто подставив v= R:
1 2
T Iω
2
Подставим момент импульса тела
L Iω
dL
Iβ N внеш
dt
Это закон изменения момента импульса твердого тела или основной закон динамики для
вращения твердого тела вокруг неподвижной оси. Как и в случае с МТ можно сопоставить
все величины для поступательного и вращательного движения.
56. Механика поступательного и вращательно движения относительно неподвижной оси
Все выражения для поступательного и вращательного движения внешне оченьпохожи. 2-й закон Ньютона:
dp
ma Fi
dt
dL
Iβ N iвнеш
dt
i
Аналогами также являются:
координата
х
- угол ,
линейная скорость
v
- угловая скорость ,
линейное ускорение a
- угловое ускорение ,
масса
m
- момент инерции I,
сила
F
момент силы N,
импульс
р
- момент
импульса L,
кинетическая энергия mv2/2 - кинетическая
энергия I 2/2,
работа
dA=Fsds
- работа dA=N d
мощность
P=Fvv
- P=N
-
57.
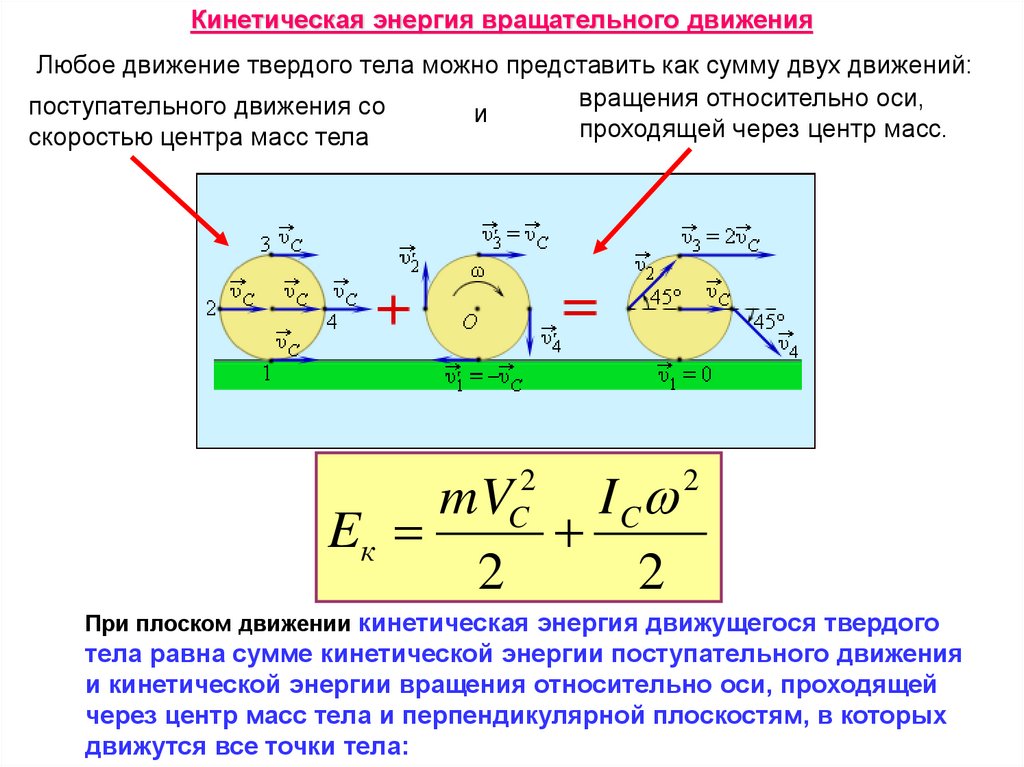
Кинетическая энергия вращательного движенияЛюбое движение твердого тела можно представить как сумму двух движений:
вращения относительно оси,
поступательного движения со
и
проходящей через центр масс.
скоростью центра масс тела
mV
I C
Eк
2
2
2
C
2
При плоском движении кинетическая энергия движущегося твердого
тела равна сумме кинетической энергии поступательного движения
и кинетической энергии вращения относительно оси, проходящей
через центр масс тела и перпендикулярной плоскостям, в которых
движутся все точки тела:
58.
Основные законымолекулярной физики
59.
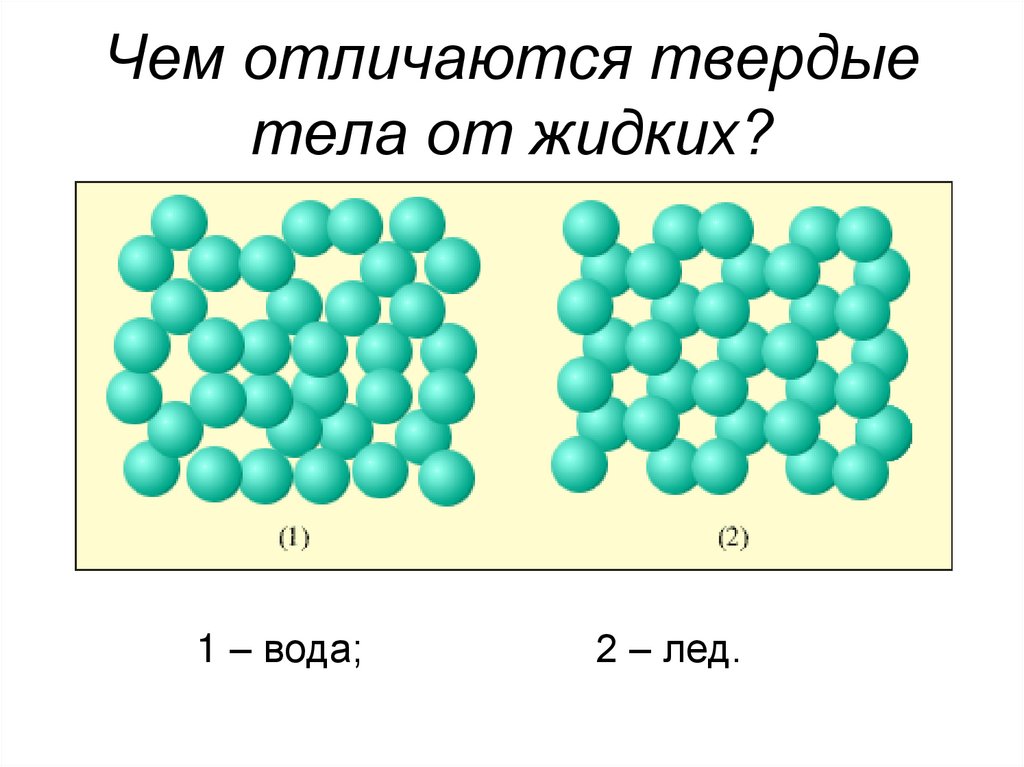
Жидкое состояниеКристаллы характеризуются наличием дальнего
порядка – упорядоченное расположение частиц по
отношению к любой частице наблюдается в пределах
значительного объема.
Газы имеют полностью разупорядоченное (хаотическое )
расположение частиц.
Жидкости обладают ближним порядком. По отношению
к любой частице расположение ближайших к ней соседей
является упорядоченным. Но по мере удаления от данной
частицы, расположение по отношению к ней других частиц
становится все менее упорядоченным.
60. Чем отличаются твердые тела от жидких?
1 – вода;2 – лед.
61. Чем отличаются газообразное состояние от жидкого?
1 - водяной пар2 - вода
62.
63. Какие силы действуют на молекулы внутри жидкости?
Поверхностное натяжениеКакие силы действуют на
молекулы внутри жидкости?
64.
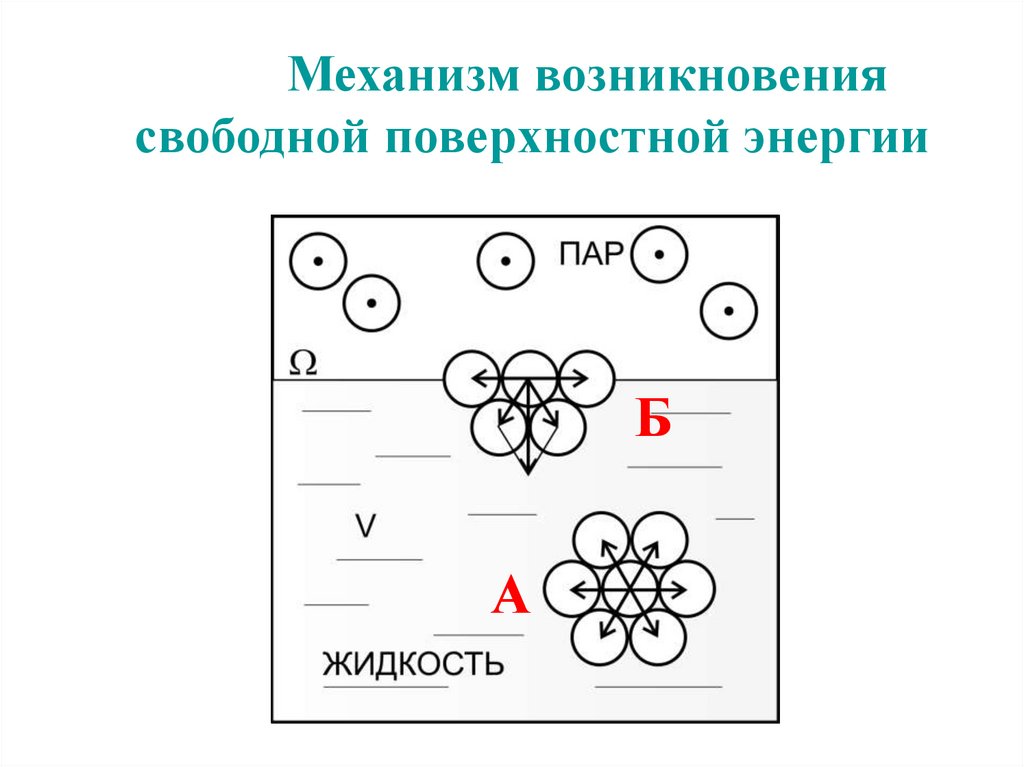
Механизм возникновениясвободной поверхностной энергии
Б
А
65.
Поверхностное натяжениеМолекулы
жидкости
располагаются
близко друг к другу, поэтому силы притяжения
между
ними
имеют значительную величину.
Взаимодействие
между
молекулами
быстро убывает с расстоянием, начиная с
некоторого
расстояния
r
(радиус
молекулярного действия) силами притяжения
между молекулами можно пренебречь.
Радиус r имеет величину порядка 10-9 м,
то есть нескольких эффективных диаметров
молекулы.
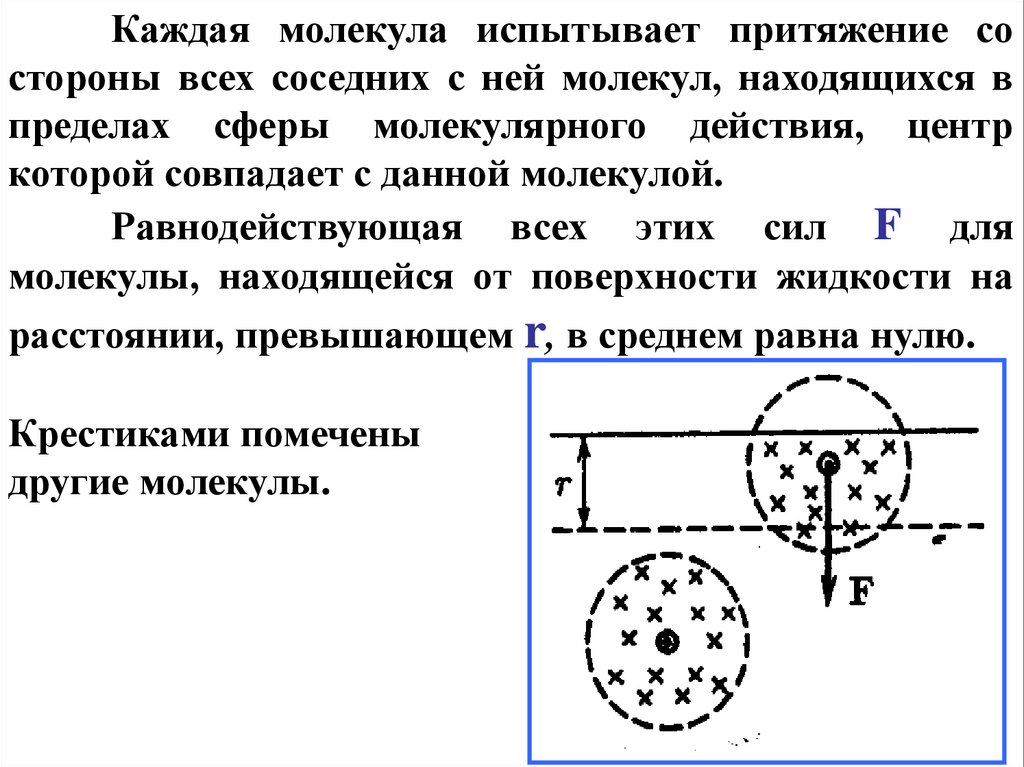
66.
Каждая молекула испытывает притяжение состороны всех соседних с ней молекул, находящихся в
пределах сферы молекулярного действия, центр
которой совпадает с данной молекулой.
Равнодействующая всех этих сил F для
молекулы, находящейся от поверхности жидкости на
расстоянии, превышающем r, в среднем равна нулю.
Крестиками помечены
другие молекулы.
67.
Для перехода молекулы из глубины жидкости вповерхностный слой она должна совершить работу
против действующих в поверхностном слое сил. Эта
работа совершается молекулой за счет запаса ее
кинетической энергии теплового движения и идет на
увеличение потенциальной энергии молекулы.
При обратном переходе молекулы в глубь
жидкости потенциальная энергия, которой обладала
молекула в поверхностном слое, переходит в
кинетическую энергию молекулы.
68. Чтобы вытащить некоторое количество молекул из глубины жидкости на поверхность, надо затратить положительную работу внешних сил
Поверхностное натяжениеЧтобы вытащить некоторое количество молекул из
глубины жидкости на поверхность, надо затратить
положительную работу внешних сил
пропорциональную изменению площади поверхности.
∆
Авнеш=σ∆S
σ-коэффициент поверхностного
натяжения
[1 Н/м = 1 Дж/м2 ]
69.
Поверхностное натяжение зависит:1. Природы жидкости;
2. Температуры; ↓ , Т↑
3. Давления; ↓ , р↑
4. Природы и концентрации растворенных
веществ (могут ↓ , ↑ и не влиять).
70.
ВеществоВода
Поверхностное
натяжения,
мДж/м2
72,8
Ртуть
436
Этанол
22,3
71.
Механизм удаления грязи спомощью мыльной воды
Прямыми измерениями установлено, что поверхностное
натяжение воды понижается в два с половиной раза при
добавлении мыла:
от 7*10-2 до 3*10-2 Дж/м2
72.
Теплоемкостьидеального газа
Изопроцессы
73.
Закон сохранения энергии для систем, в которыхсущественную роль играют тепловые процессы,
называется первым началом термодинамики:
Q U A
Q dU A
74.
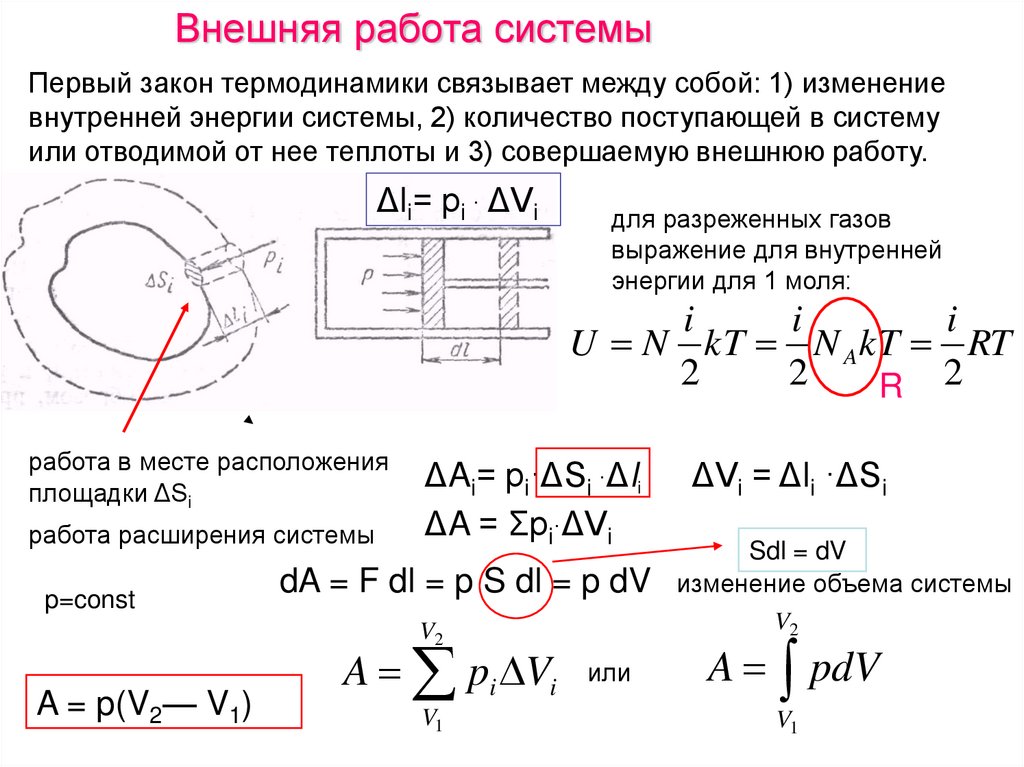
Внешняя работа системыПервый закон термодинамики связывает между собой: 1) изменение
внутренней энергии системы, 2) количество поступающей в систему
или отводимой от нее теплоты и 3) совершаемую внешнюю работу.
Δli= рi · ΔVi
для разреженных газов
выражение для внутренней
энергии для 1 моля:
i
i
i
U N kT N A kT RT
2
2
R 2
работа в месте расположения
площадки ΔSi
работа расширения системы
p=const
ΔAi= рi·ΔSi ·Δli
ΔA = Σpi·ΔVi
dA = F dl = p S dl = p dV
V2
A = p(V2— V1)
A pi Vi
V1
или
ΔVi = Δli ·ΔSi
Sdl = dV
изменение объема системы
V2
A pdV
V1
75.
Внутренняя энергия и теплоемкость идеального газаСредняя энергия одной молекулы
Т.к. молекулы идеального газа на
расстоянии не взаимодействую,
внутренняя энергия газа равна сумме
внутренних энергий всех молекул
i
U kT
2
Для 1 моля, где N=NA
i
i
U N AU N A kT RT
2
2
Внутренняя энергия произвольной массы m
m
mi
U Um
RT
2
Внутренняя энергия
идеального газа зависит
только от температуры
76.
ТеплоемкостьТеплоёмкость тела величина, равная количеству
теплоты, которую надо сообщить телу, чтобы
повысить его температуру на 1 градус:
dQ cmdT
если m=1кг
dQ
C
dT
Дж
К
77.
Теплоёмкость термодинамической системызависит от того, как изменяется состояние
системы при нагревании.
Наибольший
интерес
представляет
теплоемкость для случаев, когда нагревание
происходит при условии
V=Const (cV)
p=Const (cp) .
78.
V=Const (CV)Если газ нагревать при постоянном объёме,
то всё подводимое тепло идёт на нагревание
газа, то есть изменение его внутренней энергии.
Работы над другими телами не совершается.
A = p(V2— V1)=0
dQV = dU
Т.к. для 1 моля
(dА = 0)
dQ dU
CV
dT
dT
i
U RT
2
i
CV R
2
Т.о. CV не зависит от температуры, а зависит только от числа
степеней свободы i, т.е. от числа атомов в молекуле газа.
79.
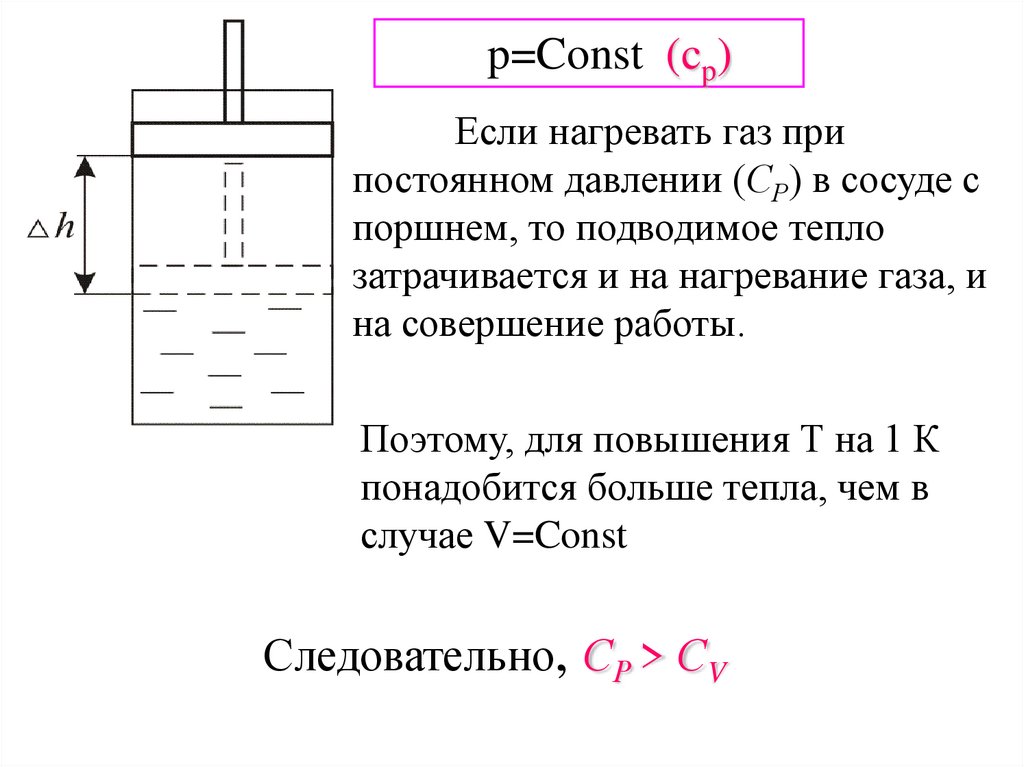
p=Const (cp)Если нагревать газ при
постоянном давлении (СР) в сосуде с
поршнем, то подводимое тепло
затрачивается и на нагревание газа, и
на совершение работы.
Поэтому, для повышения Т на 1 К
понадобится больше тепла, чем в
случае V=Const
Следовательно, СР > СV
80.
Запишем I начало ТД для 1 моля газаразделим на dT
Cp
dQ p
dT
dU
dQ p dU pdV
CV
dT
p(
dV
dT
) p CV R
Из уравнения Клапейрона-Менделеева имеем:
pVμ=RT
Vμ=RT/p
Т.о. работа, которую совершает 1 моль идеального газа при повышении
температуры на 1К равна газовой постоянной R.
отношение Cp/Cv есть постоянная для каждого газа величина
i
Cp 2 R R
2 i 2
1
i
CV
i
i
R
2
81.
Число степеней свободы, проявляющееся в теплоемкости зависит оттемпературы.
На рисунке показана качественная зависимость молярной
теплоемкости СV от температуры для одноатомного газа аргона (Ar) и
двухатомного газа водорода (H2)
Поступательное + вращательное + колебательное
Поступательное +
вращательное
Поступательное
Формулы для CV и Cp верны для определенных температурных
интервалов, причем каждому интервалу соответствует свое число
степеней свободы.
82.
Применение первого начала термодинамики кизопроцессам
Изопроцесс – процесс, проходящий при постоянном значении
одного из основных термодинамических параметров – P, V или Т.
1) изохорический процесс, при котором объем системы
остается постоянным (V = const).
2) изобарический процесс, при котором давление,
оказываемое со стороны системы на окружающие тела,
остается постоянным (р = const).
3) изотермический процесс, при котором температура
системы остается постоянной (Т = const).
4) адиабатический процесс, при котором на протяжении
всего процесса теплообмен с окружающей средой
отсутствует (dQ = 0; Q = 0)
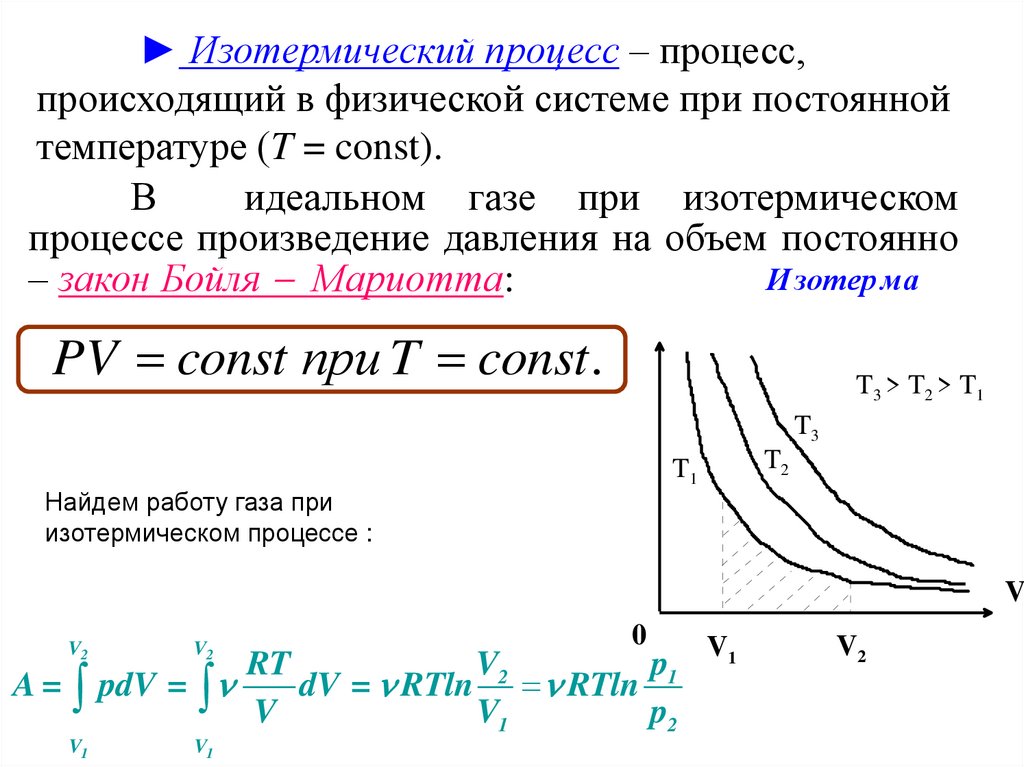
83.
► Изотермический процесс – процесс,происходящий в физической системе при постоянной
температуре (T = const).
В
идеальном газе при изотермическом
процессе произведение давления на объем постоянно
И зотер ма
– закон Бойля Мариотта:
PV const при T const. P
T 3 > T 2 > T1
T3
T2
T1
Найдем работу газа при
изотермическом процессе :
V
V2
V2
V1
V1
0
RT
V2
p1
A = pdV =
dV = RTln RTln
V
V1
p2
V1
V2
84.
Используя формулу U = сVT ,получаем
dU = сV dT = 0
Следовательно,
внутренняя
изотермическом процессе не меняется .
Поэтому
энергия
газа
при
Q A
Значит, при изотермическом процессе вся теплота,
сообщаемая газу, идет на совершение им работы над внешними
телами.
Поэтому
m
p1
Q = A = RTln
M
p2
Чтобы при расширении газа его температура не понижалась, к
газу необходимо подводить количество теплоты, равное его
работе над внешними телами.
85.
► Изохорический процесс – процесс,происходящий в физической системе при постоянном
объеме (V = const).
P const при V const
T
- закон Шарля
При изохорическом процессе механическая
работа газом не совершается.
Q U
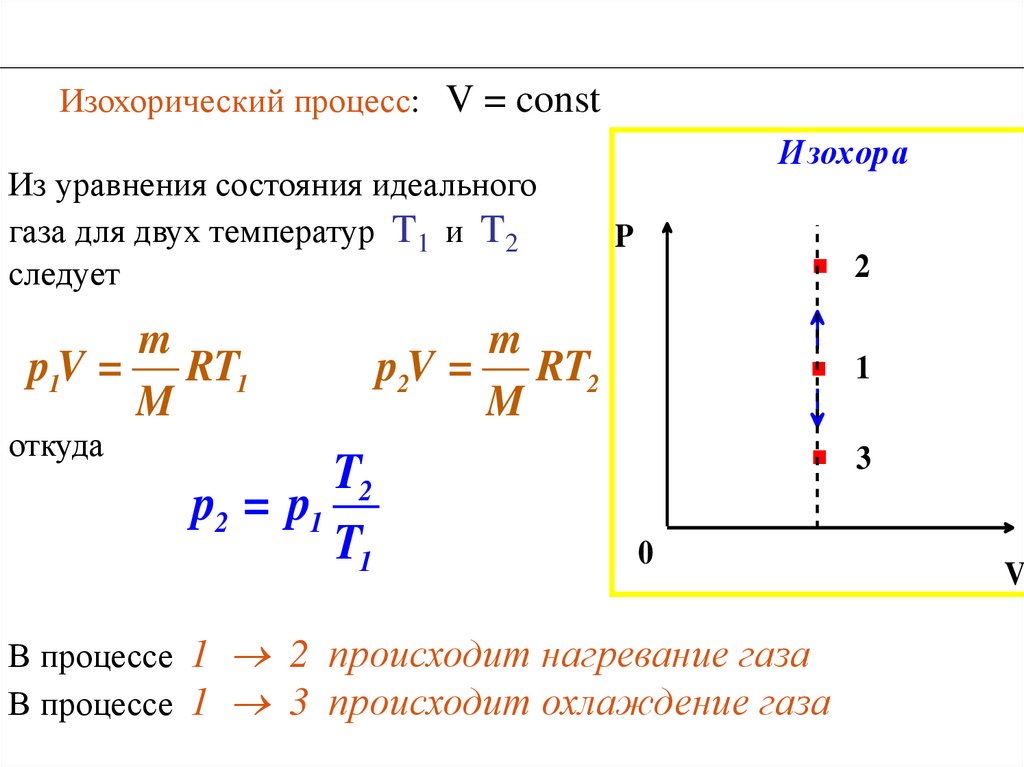
86.
Изохорический процесс: V = constИз уравнения состояния идеального
газа для двух температур T1 и T2
следует
m
p1V = RT1
M
откуда
T2
p2 = p1
T1
Изохор а
.
.
.
P
m
p2V = RT2
M
0
В процессе 1 2 происходит нагревание газа
В процессе 1 3 происходит охлаждение газа
2
1
3
V
87.
Пусть начальное состояние газа отвечает состоянию принормальных условиях Т0 = 0°С = 273.15 °К, р0 = 1 атм, тогда для
произвольной температуры Т давление в изохорическом процессе
находится из уравнения
T
p = p0
T0
Давление газа пропорционально его температуре - Закон Шарля
Поскольку
dA = pdV = 0 , то при изохорическом процессе
газ не совершает работу над внешними телами.
При этом переданная газу теплота равна
dQ = dА + dU = dU
То есть при изохорическом процессе вся теплота,
передаваемая газу, идет на увеличение его внутренней энергии.
m
d'Q = dU = cV dT
M
88.
► Изобарический процесс – процесс,происходящий в физической системе при
постоянном давлении (P = const).
V
T
const при P const
Q U А
- закон ГейЛюссака
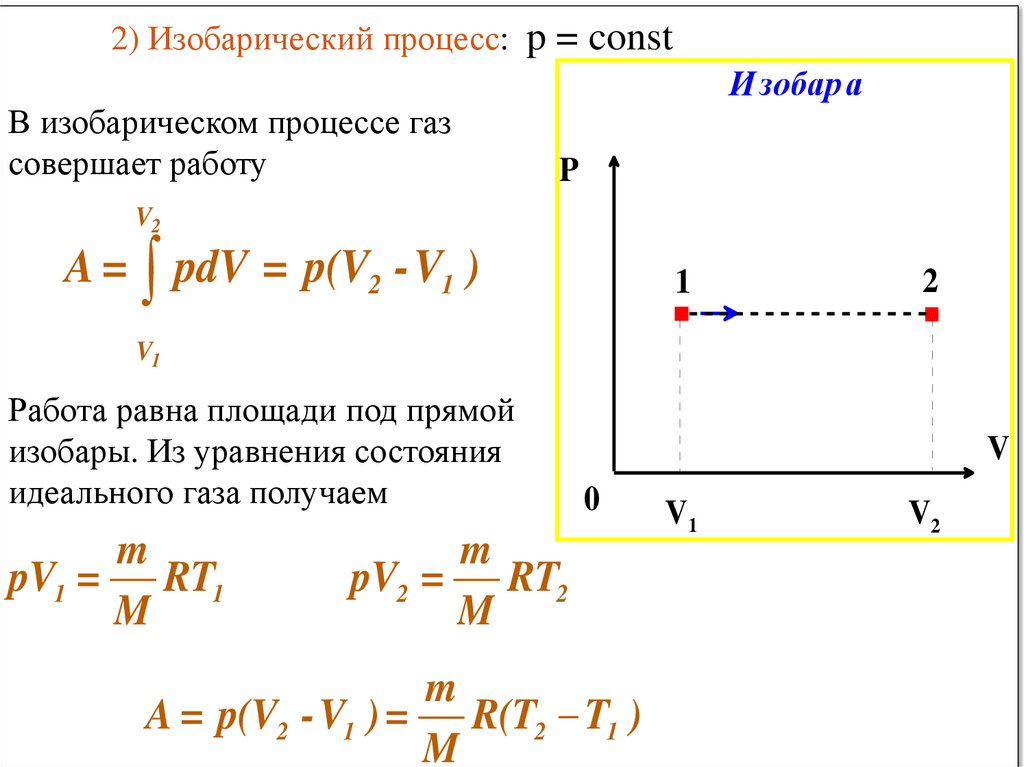
89.
2) Изобарический процесс: p = constВ изобарическом процессе газ
совершает работу
Изобар а
P
V2
.
A = pdV = p(V2 -V1 )
1
V1
Работа равна площади под прямой
изобары. Из уравнения состояния
идеального газа получаем
m
pV1 = RT1
M
.
2
V
0
m
pV2 = RT2
M
m
A = p(V2 -V1 ) = R(T2 T1 )
M
V1
V2
90.
Перепишем последнее соотношение в видеA
R=
ν(T2 - T1 )
Это равенство раскрывает физический смысл газовой постоянной R
- она равна работе 1 моля идеального газа, совершаемой им при
нагревании на 1 К в условиях изобарного расширения.
Возьмем в качестве начального состояния - состояние
идеального газа при нормальных условиях (Т0, V0), тогда объем
газа V при произвольной температуре Т в изобарическом процессе
равен
T
V = V0
T
0
постоянном давлении
Объем газа при
температуре - закон Гей-Люссака.
пропорционален его
91.
► Адиабатный процесс – процесс, происходящий вфизической системе без теплообмена с окружающей
средой (Q = 0).
PV const
уравнение Пуассона.
CP i 2
CV
i
γ – показатель адиабаты.
А U
92.
4) Адиабатический процесс : dQ = 0При адиабатическом процессе теплообмен между газом и
окружающей
средой
отсутствует.
Из
первого
начала
термодинамики получаем
dA = - dU
Поэтому в адиабатическом процессе работа газа над
внешними телами совершается за счет убыли его внутренней
энергии.
Используя
dU = сVdT ; dA = рdV
находим
рdV = - сV dT
С другой стороны, из уравнения состояния идеального газа следует
d(рV) = pdV + Vdp = RdT
93.
ИсключаяdT , получаем
рdV = - сV (pdV + vdp)/R
Откуда
dp
R dV
dV
= -( 1 + )
= -γ
p
cV V
V
Интегрируя, находим
p2
V2
dp
dV
=
-γ
p p V V
1
1
p2
V2
ln( ) = -γln( )
p1
V1
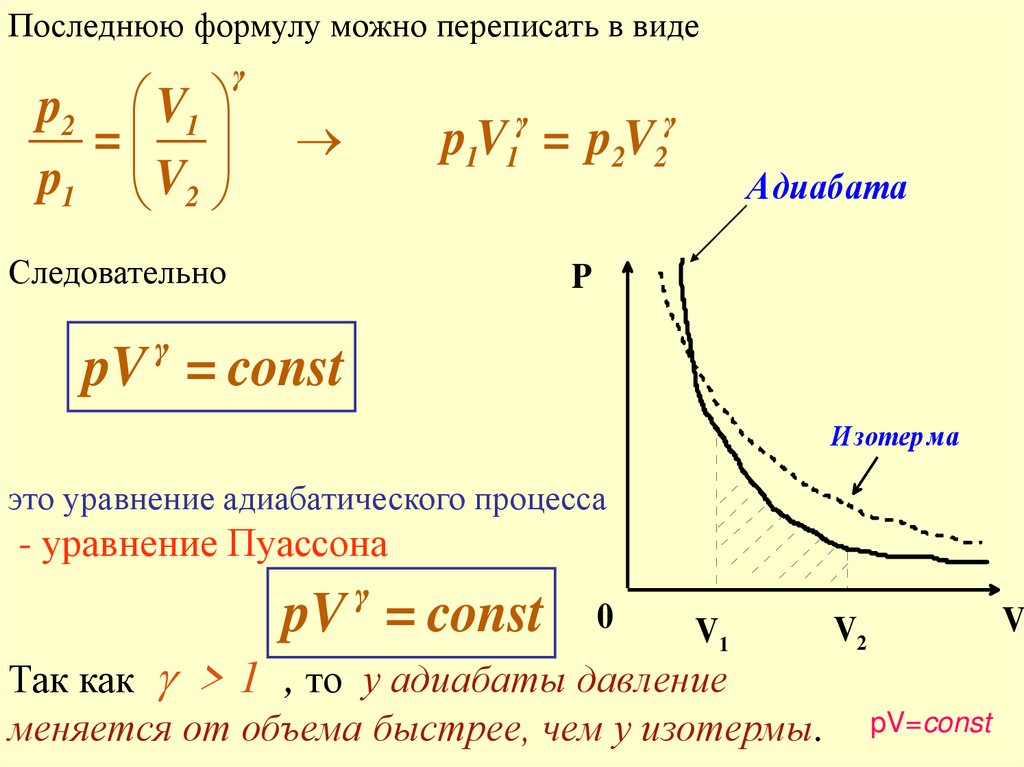
94.
Последнюю формулу можно переписать в видеp2 V1
=
p1 V2
γ
γ
1 1
γ
2 2
pV = pV
Следовательно
Адиабата
P
γ
pV = const
Изотер ма
это уравнение адиабатического процесса
- уравнение Пуассона
γ
pV = const
0
V1
Так как > 1 , то у адиабаты давление
меняется от объема быстрее, чем у изотермы.
V
V2
pV=const
95.
Используяуравнение
состояния
преобразуем уравнение Пуассона к виду
pV = νRT
Значит
или
TV
p
νRTV
(γ -1)
(1-γ)
(γ -1)
идеального
газа,
= const
= const
γ
T = const
При адиабатическом расширении идеальный газ
охлаждается, а при сжатии – нагревается.
96.
Политропический процессПолитропический
процесс
–
процесс,
протекающий при постоянной теплоёмкости,
cm = const.
где cm – молярная теплоемкость.
pV const , n
n
c cp
c cV
где n - показатель политропы.
,
97.
Найдем уравнение политропы для идеального газа.Из первого начала термодинамики следует
d'Q = dU + pdV = νcm dT
dU = νdU m = νcV dT
откуда получаем
ν(cm - cV )dT = pdV
98.
С другой стороны, из уравнения состояния идеального газаd(νRT)
Поэтомуd(pV)
можно=
записать
pdV +Vdp = νRdT
(cm - cV )(pdV + VdP) = pRdV
(c - ccV =-cR)pdV
+ (cm - cV )Vdp = 0
+ R то
Поскольку m
P
V
dV
dp
(cm - cP )
+ (cm - cV ) = 0
V
p
99.
cm - c PОбозначим n =
cm - cV
Интегрируем
Следовательно
, получим
dV dp
n
+ =0
V
p
V2
p1
nln = ln
V1
p2
p2V2n = p1V1n
n
pV = const
- уравнение политропы,
n - показатель политропы.
100.
Все изопроцессы являются частным случаемполитропического процесса:
pV const , n адиабата.
pV const , n 1 изотерма .
p const , n 0 изобара .
1
n
pV const , p V const ,
n V const изохора.
n
101.
ЭнтропияАдиабатические процессы в термодинамических системах могут
быть равновесными и неравновесными. Для характеристики
равновесного адиабатического процесса можно ввести некоторую
физическую величину, которая оставалась бы постоянной в
течение всего процесса; ее назвали энтропией S.
Энтропия есть такая функция состояния системы, элементарное
изменение которой при равновесном переходе системы из одного
состояния в другое равно полученному или отданному количеству
теплоты, деленному на температуру, при которой произошел этот
процесс
для бесконечно малого изменения состояния системы
dQ cmdT
dS
T
T
102.
Следовательно, S = const, адиабатный процесс по другомуназывают – изоэнтропийным процессом.
Во всех случаях, когда система получает извне теплоту, то Q —
положительно, следовательно, S2 > S1 и энтропия системы
увеличивается.
Если же система отдаст теплоту, то Q имеет отрицательный знак
и, следовательно, S2 < S1; энтропия системы уменьшается.
Энтропия системы пропорциональна массе (или числу частиц) этой
системы
Q=c m ΔT
Масса системы представляется в виде суммы масс ее составных
частей, поэтому энтропия всей системы будет равна сумме
энтропии ее составных частей, т. е. энтропия есть аддитивная
величина.
103.
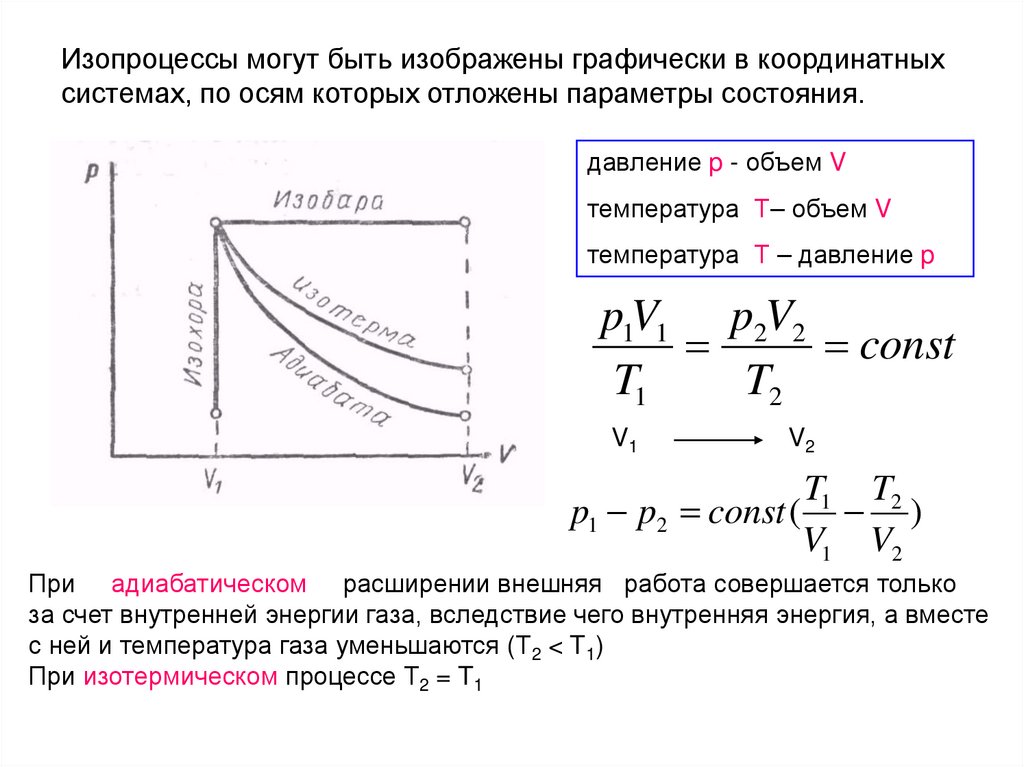
Изопроцессы могут быть изображены графически в координатныхсистемах, по осям которых отложены параметры состояния.
давление p - объем V
температура Т– объем V
температура Т – давление p
p1V1 p2V2
const
T1
T2
V1
V2
T1 T2
p1 p2 const ( )
V1 V2
При адиабатическом расширении внешняя работа совершается только
за счет внутренней энергии газа, вследствие чего внутренняя энергия, а вместе
с ней и температура газа уменьшаются (Т2 < T1)
При изотермическом процессе Т2 = T1
104.
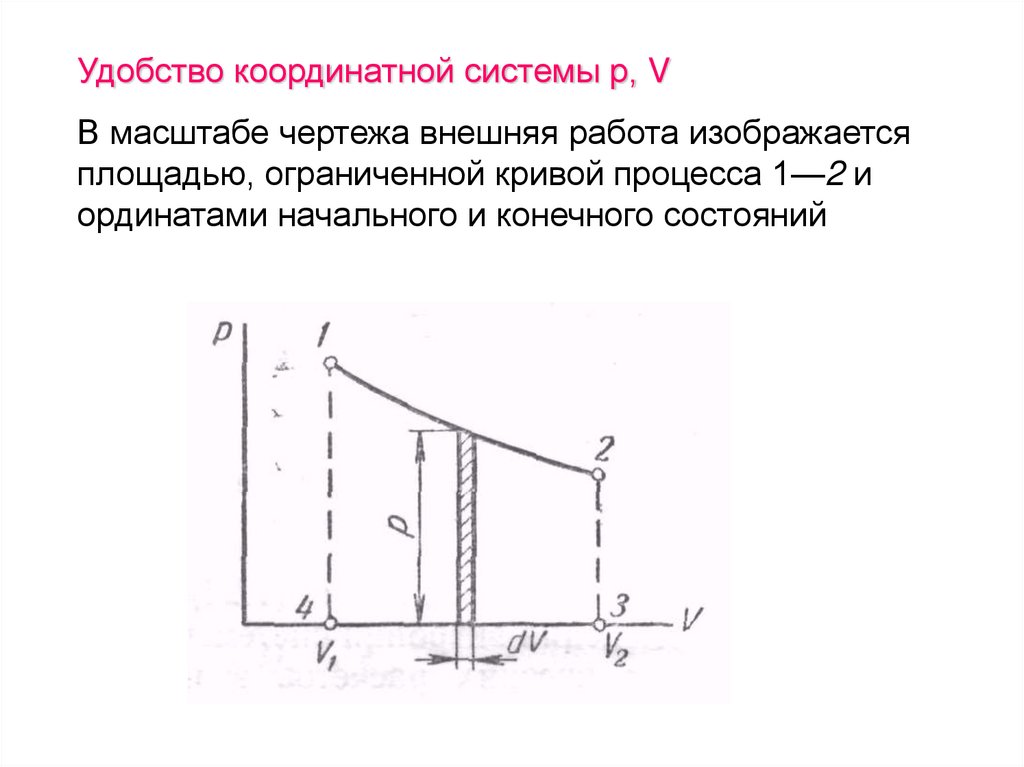
Удобство координатной системы р, VВ масштабе чертежа внешняя работа изображается
площадью, ограниченной кривой процесса 1—2 и
ординатами начального и конечного состояний
105.
Круговые (замкнутые) процессыСовокупность термодинамических процессов, в
результате которых система возвращается в исходное
состояние, называется круговым процессом (циклом).
Прямой цикл – работа за
цикл
A pdV 0
Обратный цикл – работа
за цикл
A pdV 0
106.
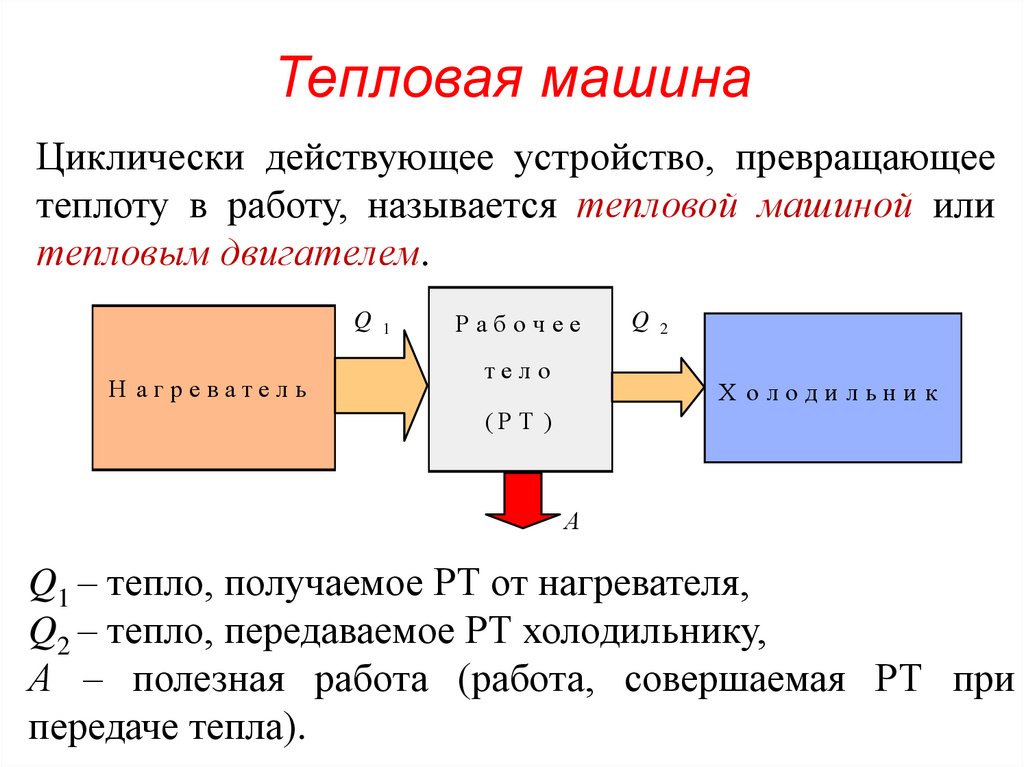
Тепловая машинаЦиклически действующее устройство, превращающее
теплоту в работу, называется тепловой машиной или
тепловым двигателем.
Q 1
Н агреватель
Рабочее
тело
Q 2
Х олодильни к
(Р Т )
А
Q1 – тепло, получаемое РТ от нагревателя,
Q2 – тепло, передаваемое РТ холодильнику,
А – полезная работа (работа, совершаемая РТ при
передаче тепла).
107.
22
1
1
Q 1
p
2
a
1
b
-Q 2
Q 1
-Q 2
0
V
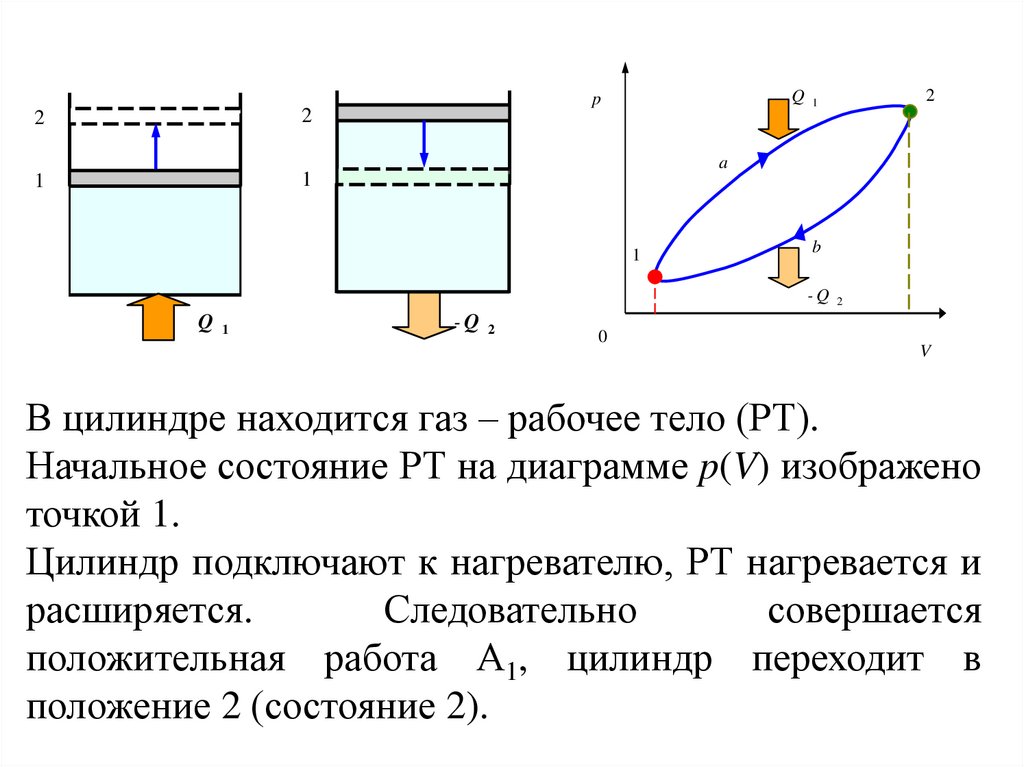
В цилиндре находится газ – рабочее тело (РТ).
Начальное состояние РТ на диаграмме p(V) изображено
точкой 1.
Цилиндр подключают к нагревателю, РТ нагревается и
расширяется.
Следовательно
совершается
положительная работа А1, цилиндр переходит в
положение 2 (состояние 2).
108.
Процесс 1–2: –Q 1
p
2
Q1 U 2 U 1 A1
a
1
первое начало термодинамики.
b
-Q 2
0
V
Работа А1 равна площади под кривой 1a2.
Чтобы поршень цилиндра вернуть в исходное
состояние 1, необходимо сжать рабочее тело,
затратив при этом работу – А2.
109.
Q 1p
2
a
1
b
-Q 2
0
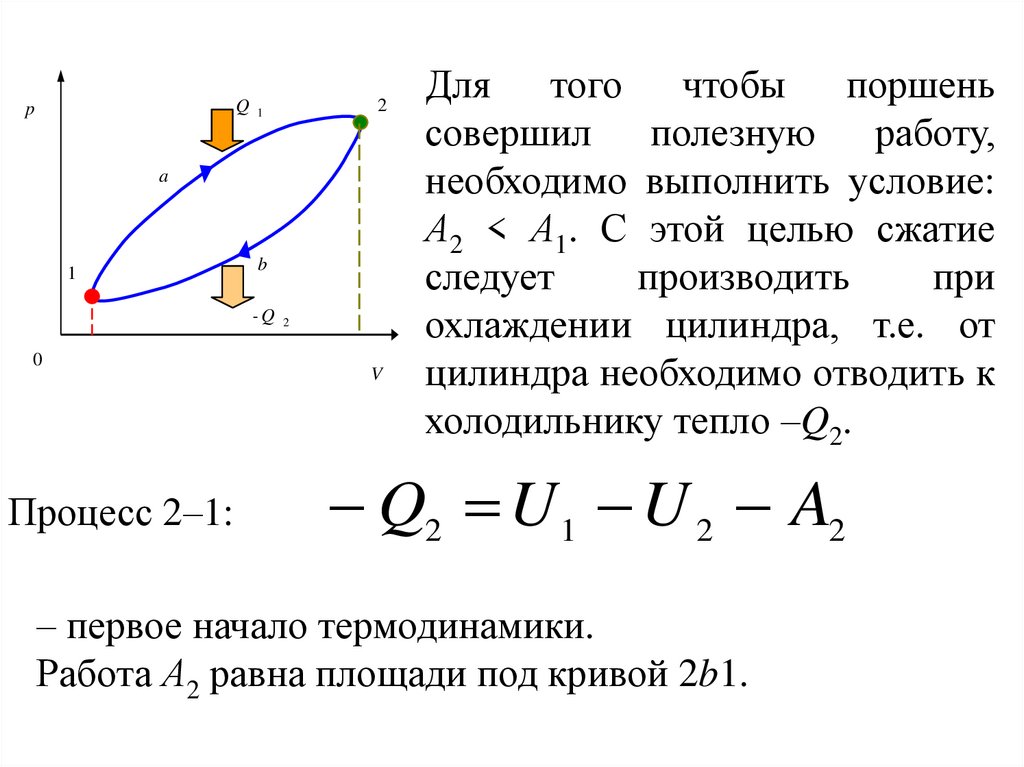
Процесс 2–1:
V
Для того чтобы поршень
совершил полезную работу,
необходимо выполнить условие:
А2 < А1. С этой целью сжатие
следует
производить
при
охлаждении цилиндра, т.е. от
цилиндра необходимо отводить к
холодильнику тепло –Q2.
Q2 U 1 U 2 A2
– первое начало термодинамики.
Работа А2 равна площади под кривой 2b1.
110.
Q 1p
a
2
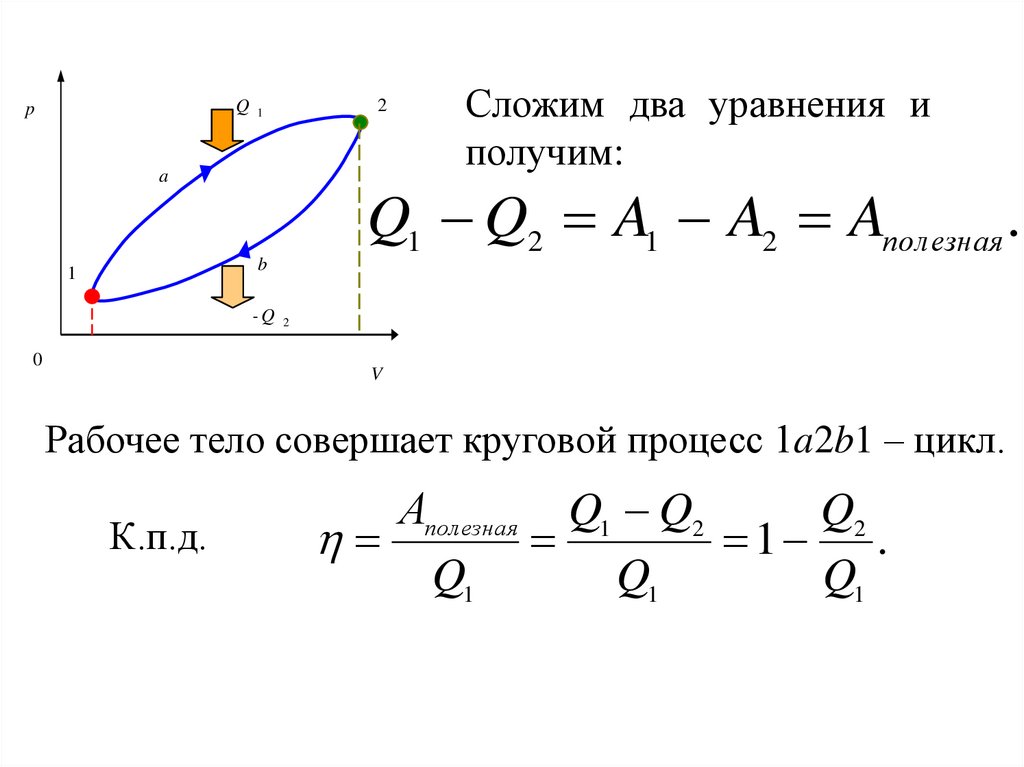
Сложим два уравнения и
получим:
Q1 Q2 A1 A2 Aпол езная .
b
1
-Q 2
0
V
Рабочее тело совершает круговой процесс 1a2b1 – цикл.
К.п.д.
Аполезная Q1 Q2
Q2
1 .
Q1
Q1
Q1
111.
Q 1p
2
a
m
M
pV RT T pV
;
M
Rm
1
b
-Q 2
0
V
при V const , pнагревателя p холодильника Т н Т х .
Процесс возвращения рабочего тела в исходное
состояние происходит при более низкой температуре.
Следовательно, для работы тепловой машины
холодильник принципиально необходим.
112.
Цикл КарноНикола Леонард Сади Карно –
французский офицер инженерных
войск, в 1824 г. опубликовал
сочинение «Размышления о
движущей силе огня и о машинах
способных развить эту силу».
Ввел понятие кругового и обратимого
процессов, идеального цикла тепловых машин,
заложил тем самым основы их теории. Пришел к
понятию механического эквивалента теплоты.
113.
Карно вывел теорему, носящую теперь егоимя:
из всех периодически действующих тепловых
машин, имеющих одинаковые температуры
нагревателей и холодильников, наибольшим КПД
обладают обратимые машины. Причем КПД
обратимых машин, работающих при одинаковых
температурах нагревателей и холодильников,
равны друг другу и не зависят от конструкции
машины. При этом КПД меньше единицы.
114.
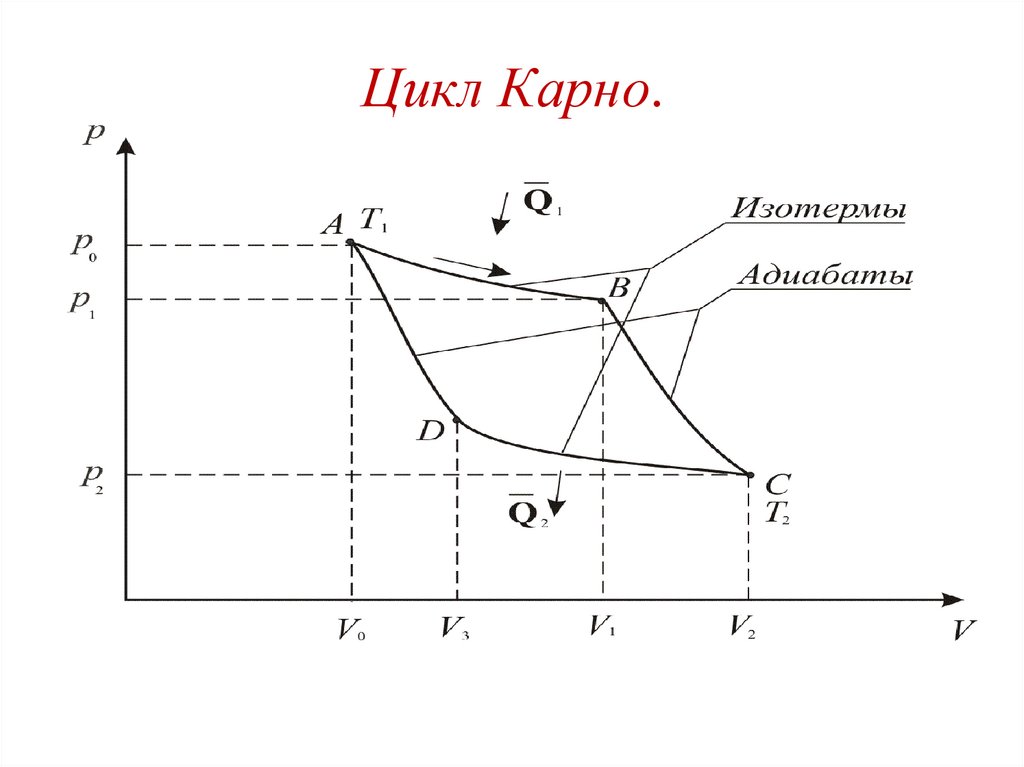
Цикл Карно.115.
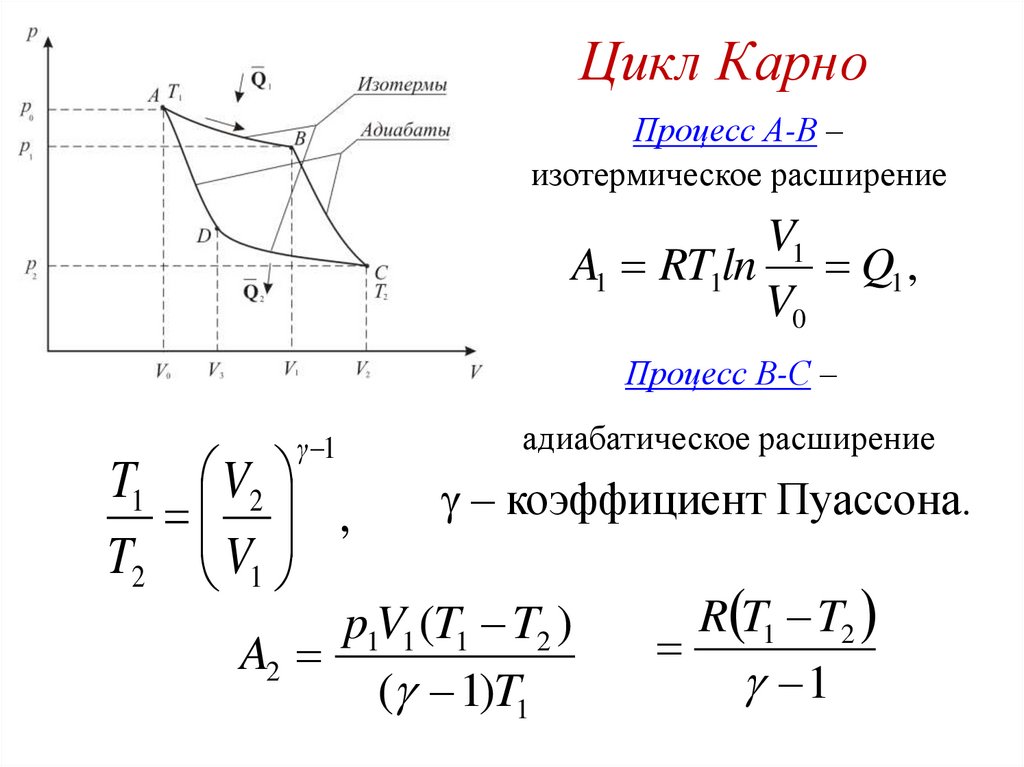
Цикл КарноПроцесс А-В –
изотермическое расширение
V1
A1 RT1ln Q1 ,
V0
Процесс В-С –
γ 1
T1 V2
,
T2 V1
адиабатическое расширение
– коэффициент Пуассона.
p1V1 (T1 T2 )
A2
( 1)T1
R T1 T2
1
116.
Цикл КарноПроцесс С-D –
изотермическое сжатие
V3
A3 RT2ln Q2
V2
Процесс D-A –
адиабатическое сжатие
V3
V0
γ 1
T1
T2
R
A4
(T1 T2 )
1
117.
V1 R (T1 T2 )A RT1 ln
V0
1
V3 R(T1 T2 )
RT2 ln
V2
1
A Q1 Q2
Q2
T2
1 1
Q1
Q1
Q1
T1
118.
T21
T1
Если Т2 = 0, то η = 1, что невозможно, т.к.
абсолютный нуль температуры не существует.
Если Т1 = ∞, то η = 1, что невозможно, т.к.
бесконечная температура не достижима.
КПД цикла Карно η < 1 и зависит от
разности температур между нагревателем и
холодильником (и не зависит от конструкции
машины и рода рабочего тела).
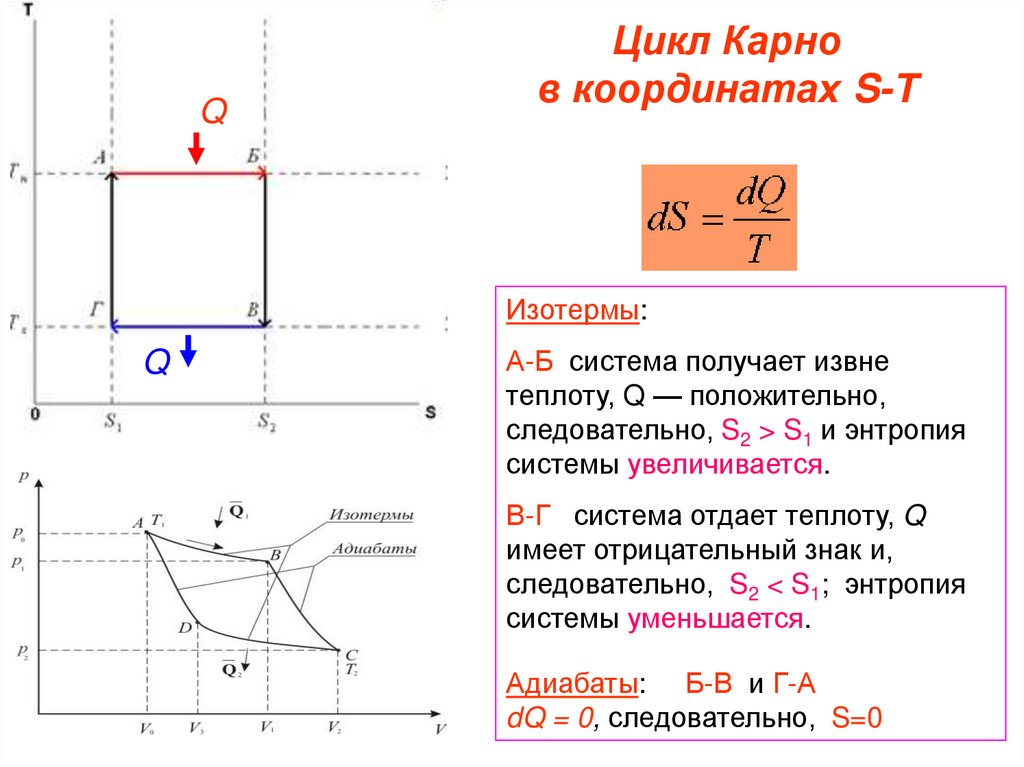
119. Цикл Карно в координатах S-T
QЦикл Карно
в координатах S-T
Изотермы:
Q
А-Б система получает извне
теплоту, Q — положительно,
следовательно, S2 > S1 и энтропия
системы увеличивается.
В-Г система отдает теплоту, Q
имеет отрицательный знак и,
следовательно, S2 < S1; энтропия
системы уменьшается.
Адиабаты: Б-В и Г-А
dQ = 0, следовательно, S=0
120.
Теоремы Карно.1. К.п.д. η обратимой идеальной тепловой
машины Карно не зависит от рабочего
вещества.
2. К.п.д. необратимой машины Карно не может
быть больше к.п.д. обратимой машины Карно.
121.
ВТОРОЕНАЧАЛО
ТЕРМОДИНАМИКИ
122.
Второе начало термодинамики1) невозможны круговые процессы, в результате которых система
только получала бы извне теплоту Q1 и совершала эквивалентную
положительную внешнюю работу А = Q1
2) круговые процессы, совершаемые любыми термодинамическими
системами, сопровождаются получением некоторого количества
теплоты Q1 от тел, имеющих высокие температуры, обязательной
отдачей части этой теплоты Q2 телам, имеющим низкие температуры, и
превращением разности Q1 — Q2 в механическую работу.
теплота связана с беспорядочным движением частиц системы, а
механическая работа обусловлена упорядоченным движением этих частиц.
Можно утверждать, что превращение теплоты в механическую работу есть
переход энергии беспорядочного движения молекул системы в энергию
упорядоченного движения. В связи с этим второй закон термодинамики
можно понимать иначе:
3) при помощи круговых процессов, совершаемых какой-нибудь
термодинамической системой, невозможно полностью превратить
энергию беспорядочного теплового движения частиц окружающих тел
в энергию упорядоченного движения самих этих тел
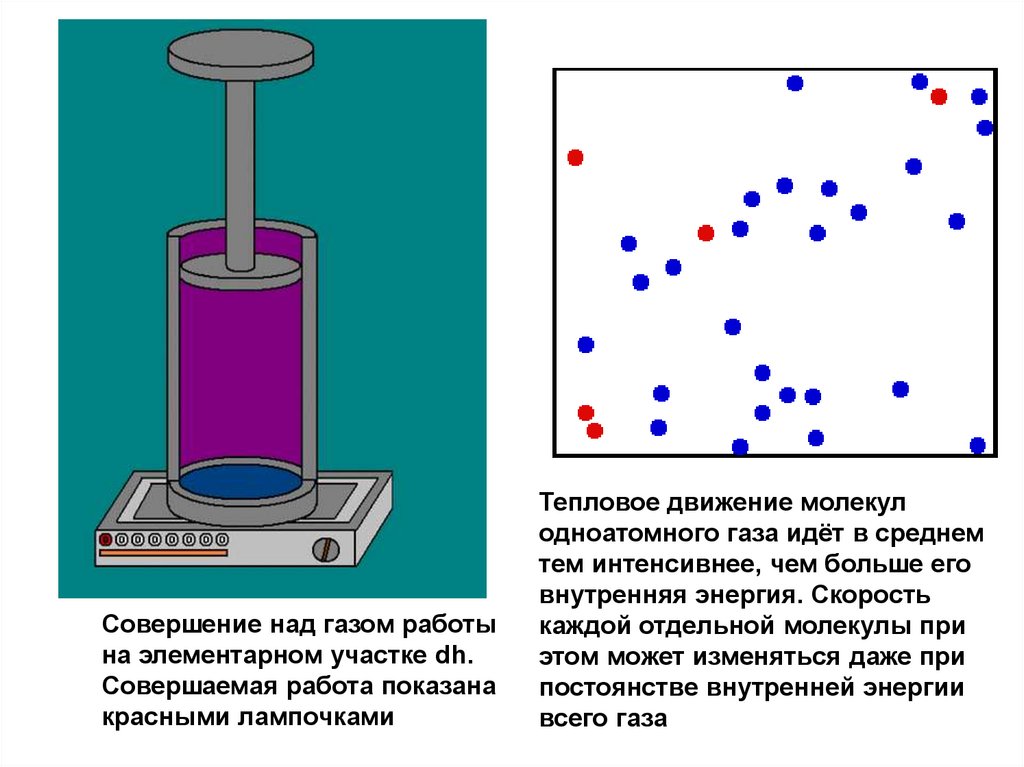
123.
Совершение над газом работына элементарном участке dh.
Совершаемая работа показана
красными лампочками
Тепловое движение молекул
одноатомного газа идёт в среднем
тем интенсивнее, чем больше его
внутренняя энергия. Скорость
каждой отдельной молекулы при
этом может изменяться даже при
постоянстве внутренней энергии
всего газа
124.
U2-U1=Q - AПрименяя это соотношение к круговым процессам, полагали U1= U2, и поэтому
Q = А. При этом считалось очевидным, что, возвращаясь в исходное
состояние, система приобретает в точности то же самое значение внутренней
энергии, которое она имела вначале.
внутренняя энергия термодинамических
систем есть однозначная функция
состояния этих систем.
I начало термодинамики
при равновесном круговом процессе суммарное изменение энтропии
термодинамических систем равно нулю, т. е., возвращаясь в исходное
состояние, система приобретает в точности то же самое значение своей
энтропии, которую она имела вначале.
II начало термодинамики
4) энтропия термодинамической системы, находящейся в
равновесном состоянии, есть однозначная функция этого
состояния.
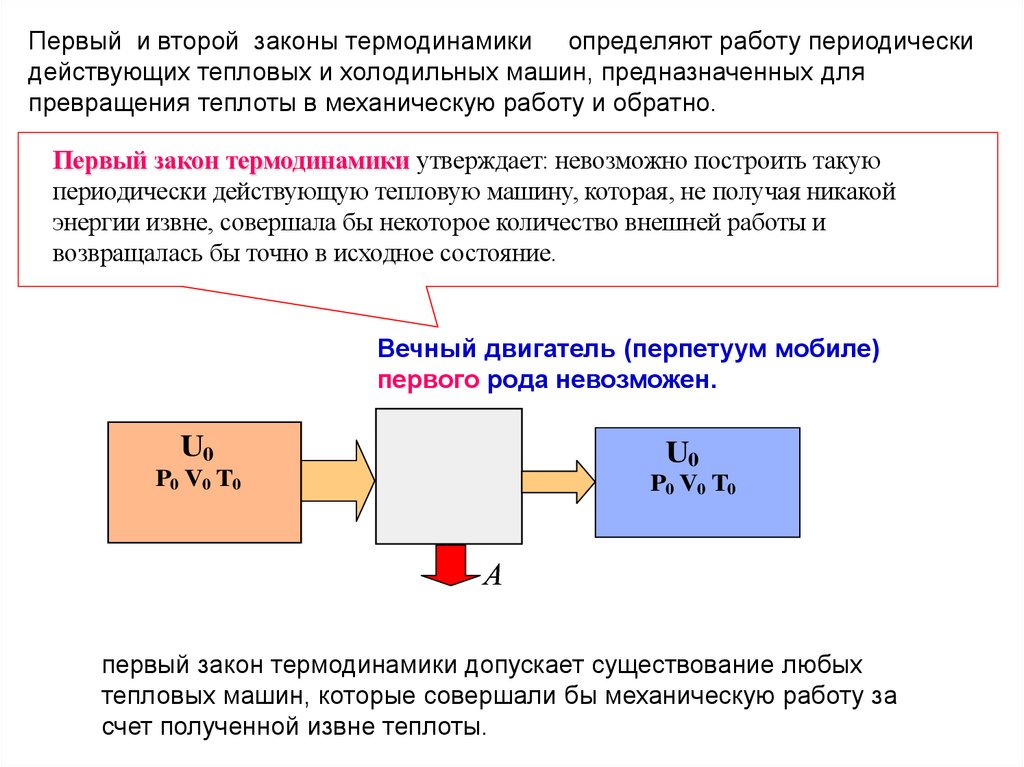
125.
Первый и второй законы термодинамики определяют работу периодическидействующих тепловых и холодильных машин, предназначенных для
превращения теплоты в механическую работу и обратно.
Первый закон термодинамики утверждает: невозможно построить такую
периодически действующую тепловую машину, которая, не получая никакой
энергии извне, совершала бы некоторое количество внешней работы и
возвращалась бы точно в исходное состояние.
Вечный двигатель (перпетуум мобиле)
первого рода невозможен.
U0
U0
P0 V0 T0
P0 V0 T0
А
первый закон термодинамики допускает существование любых
тепловых машин, которые совершали бы механическую работу за
счет полученной извне теплоты.
126.
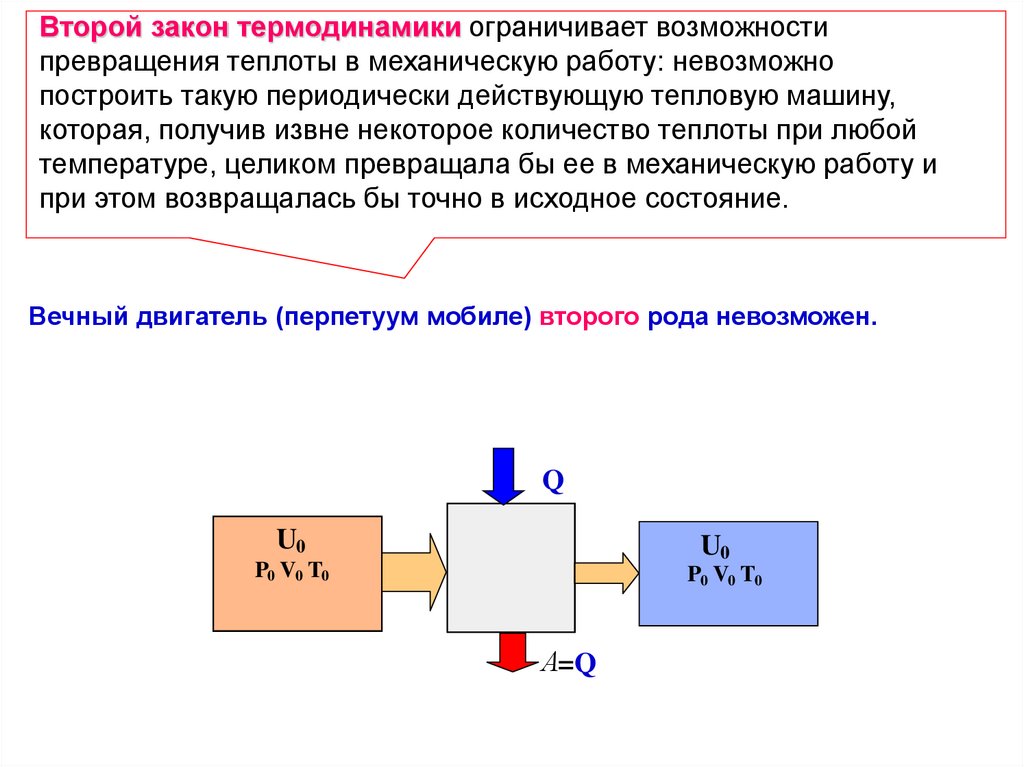
Второй закон термодинамики ограничивает возможностипревращения теплоты в механическую работу: невозможно
построить такую периодически действующую тепловую машину,
которая, получив извне некоторое количество теплоты при любой
температуре, целиком превращала бы ее в механическую работу и
при этом возвращалась бы точно в исходное состояние.
Вечный двигатель (перпетуум мобиле) второго рода невозможен.
Q
U0
U0
P0 V0 T0
P0 V0 T0
А=Q
127. Примеры конструкций вечного двигателя
Колесо Да Винчи128.
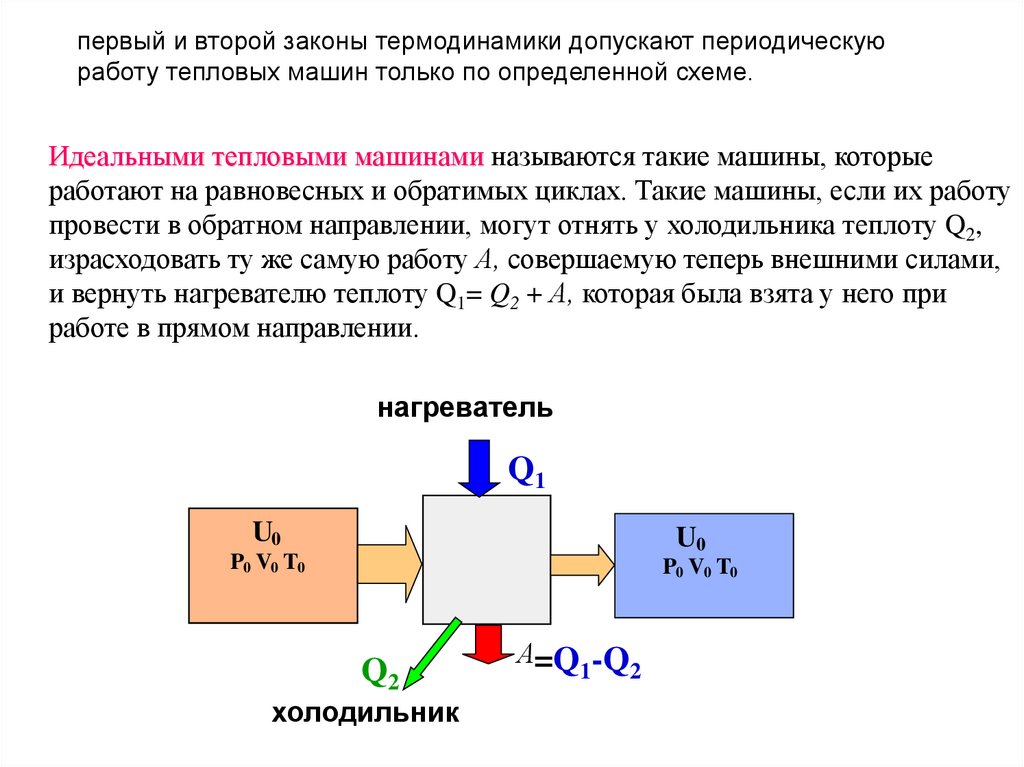
первый и второй законы термодинамики допускают периодическуюработу тепловых машин только по определенной схеме.
Идеальными тепловыми машинами называются такие машины, которые
работают на равновесных и обратимых циклах. Такие машины, если их работу
провести в обратном направлении, могут отнять у холодильника теплоту Q2,
израсходовать ту же самую работу А, совершаемую теперь внешними силами,
и вернуть нагревателю теплоту Q1= Q2 + А, которая была взята у него при
работе в прямом направлении.
нагреватель
Q1
U0
U0
P0 V0 T0
P0 V0 T0
Q2
холодильник
А=Q -Q
1
2
129.
Можно показать, что при заданных температурах источника теплоты Т1 ихолодильника Т2 коэффициент полезного действия КПД всех идеальных
тепловых машин, работающих как в прямом, так и в обратном
направлениях, независимо от их конструкции, состава рабочего вещества
и характера совершаемого в машине цикла, одинаков и равен:
Аполезная Q1 Q2 T1 T2
.
Q1
Q1
T1
130.
Идеальныйгаз
131.
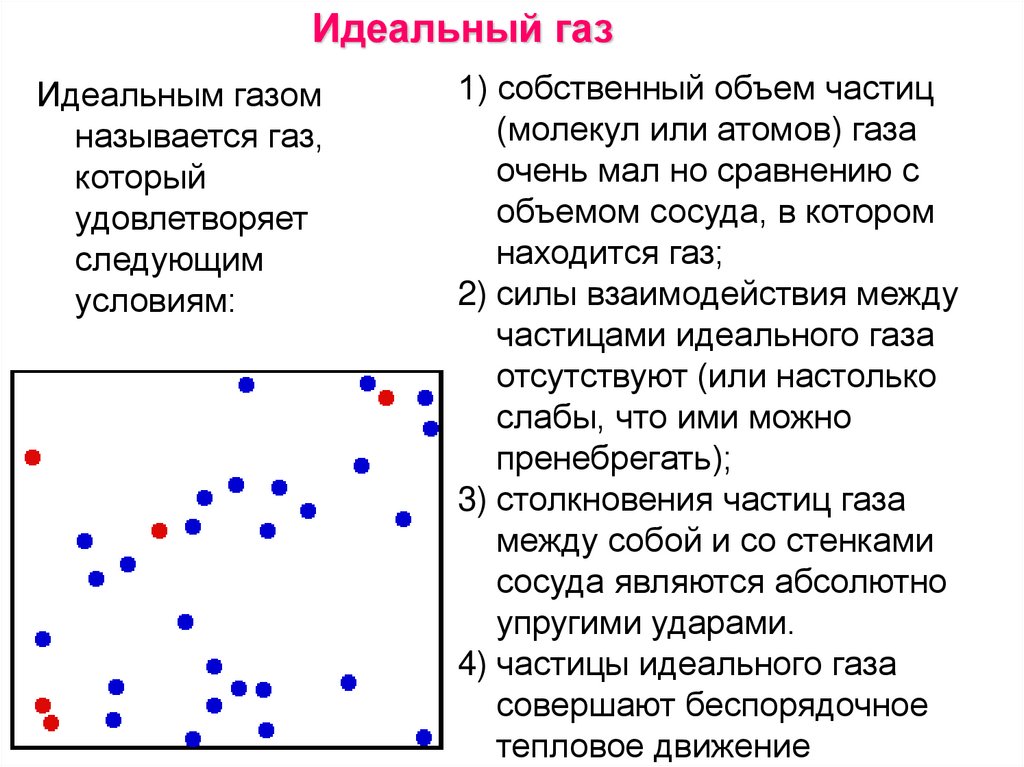
Идеальный газИдеальным газом
называется газ,
который
удовлетворяет
следующим
условиям:
1) собственный объем частиц
(молекул или атомов) газа
очень мал но сравнению с
объемом сосуда, в котором
находится газ;
2) силы взаимодействия между
частицами идеального газа
отсутствуют (или настолько
слабы, что ими можно
пренебрегать);
3) столкновения частиц газа
между собой и со стенками
сосуда являются абсолютно
упругими ударами.
4) частицы идеального газа
совершают беспорядочное
тепловое движение
132.
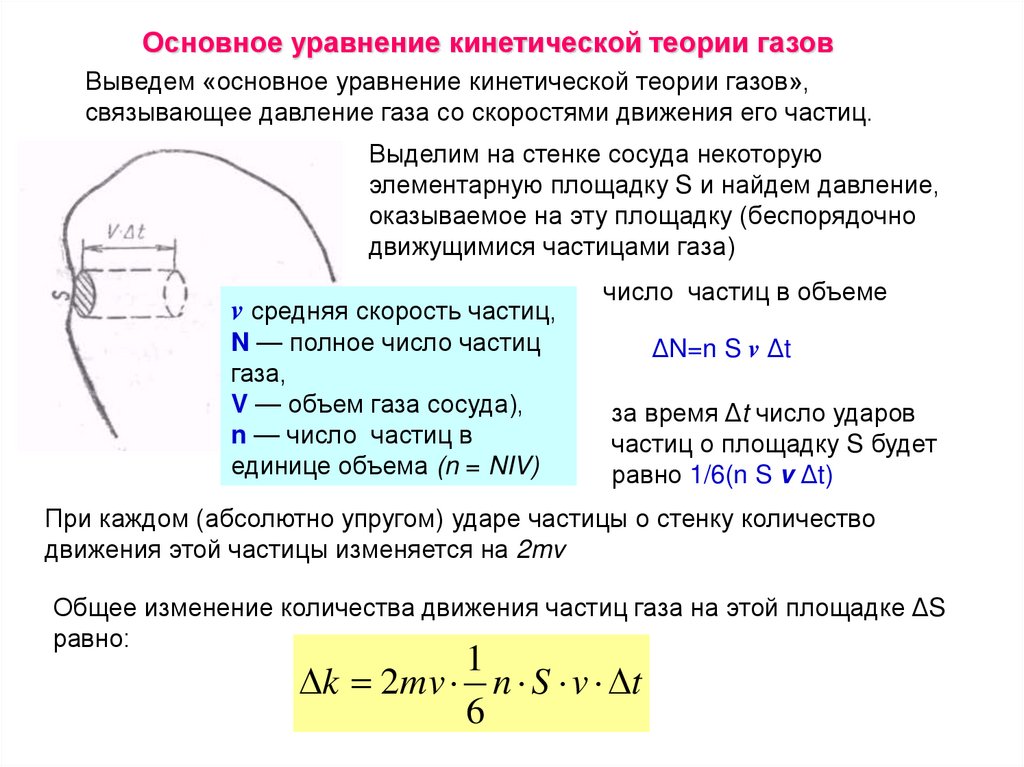
Основное уравнение кинетической теории газовВыведем «основное уравнение кинетической теории газов»,
связывающее давление газа со скоростями движения его частиц.
Выделим на стенке сосуда некоторую
элементарную площадку S и найдем давление,
оказываемое на эту площадку (беспорядочно
движущимися частицами газа)
v средняя скорость частиц,
N — полное число частиц
газа,
V — объем газа сосуда),
n — число частиц в
единице объема (n = NIV)
число частиц в объеме
ΔN=n S v Δt
за время Δt число ударов
частиц о площадку S будет
равно 1/6(n S v Δt)
При каждом (абсолютно упругом) ударе частицы о стенку количество
движения этой частицы изменяется на 2mv
Общее изменение количества движения частиц газа на этой площадке ΔS
равно:
1
k 2mv n S v t
6
133.
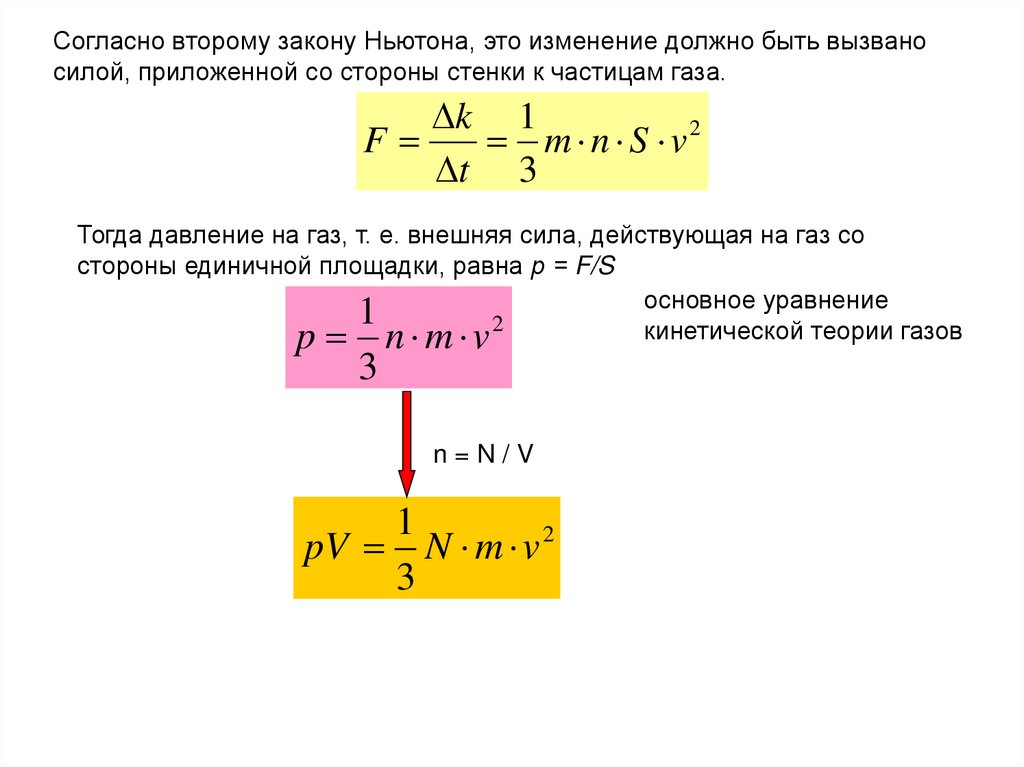
Согласно второму закону Ньютона, это изменение должно быть вызваносилой, приложенной со стороны стенки к частицам газа.
k 1
F
m n S v2
t 3
Тогда давление на газ, т. е. внешняя сила, действующая на газ со
стороны единичной площадки, равна р = F/S
основное уравнение
1
кинетической теории газов
p n m v2
3
n=N/V
1
pV N m v 2
3
134.
Мы предполагали, что скорости молекул одинаковы; если же в газеимеются молекулы с разными скоростями
1
1
1
1
2
2
2
2
pV ( N1 m1 v1 N 2 m2 v2 ...) m N i vi m N vкв
3
3
3
3
vкв называется средней квадратичной скоростью молекул газа;
она отличается от средней арифметической скорости
N 1 v 1 N 2 v 2 . N n v n
N
2
vкв
2
2
Теоретическое вычисление скоростей молекул основано на двух
предположениях:
1) в газе не существует даже двух молекул, имеющих в точности
одинаковые скорости;
2) число молекул ΔN, скорости которых лежат в узких пределах между v и
v + Δv (например, от 100 до 101 м/с или от 500 до 501 м/с), прямо
пропорционально общему числу молекул N, ширине интервала Δv и
зависит от величины скорости и.
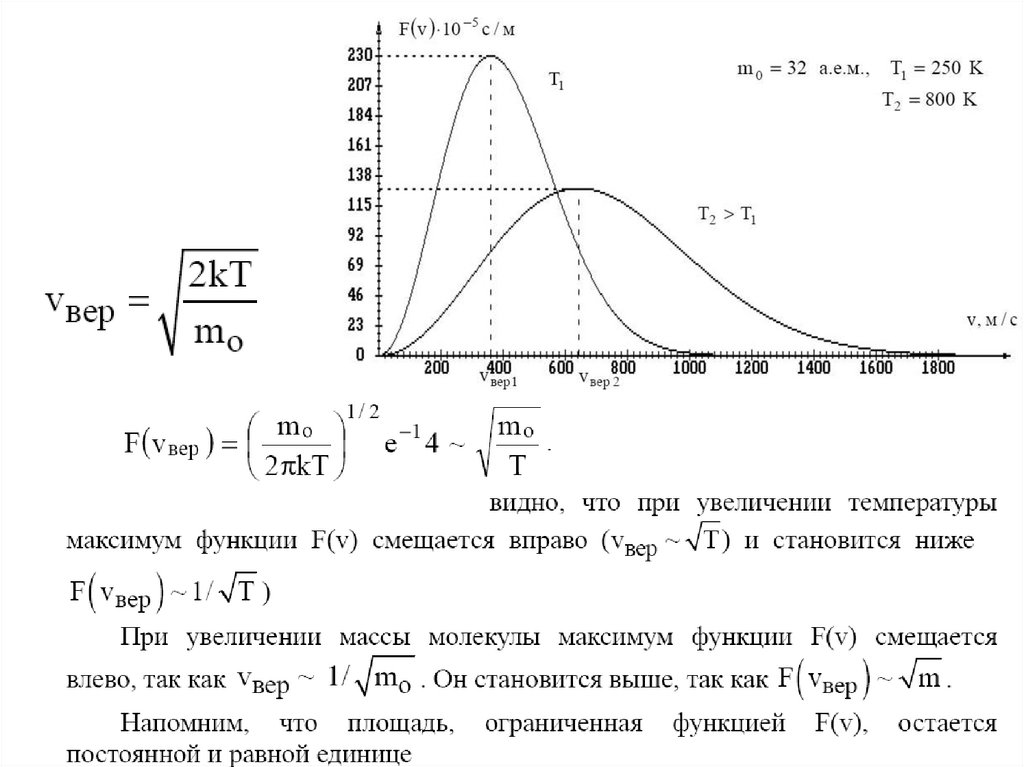
135.
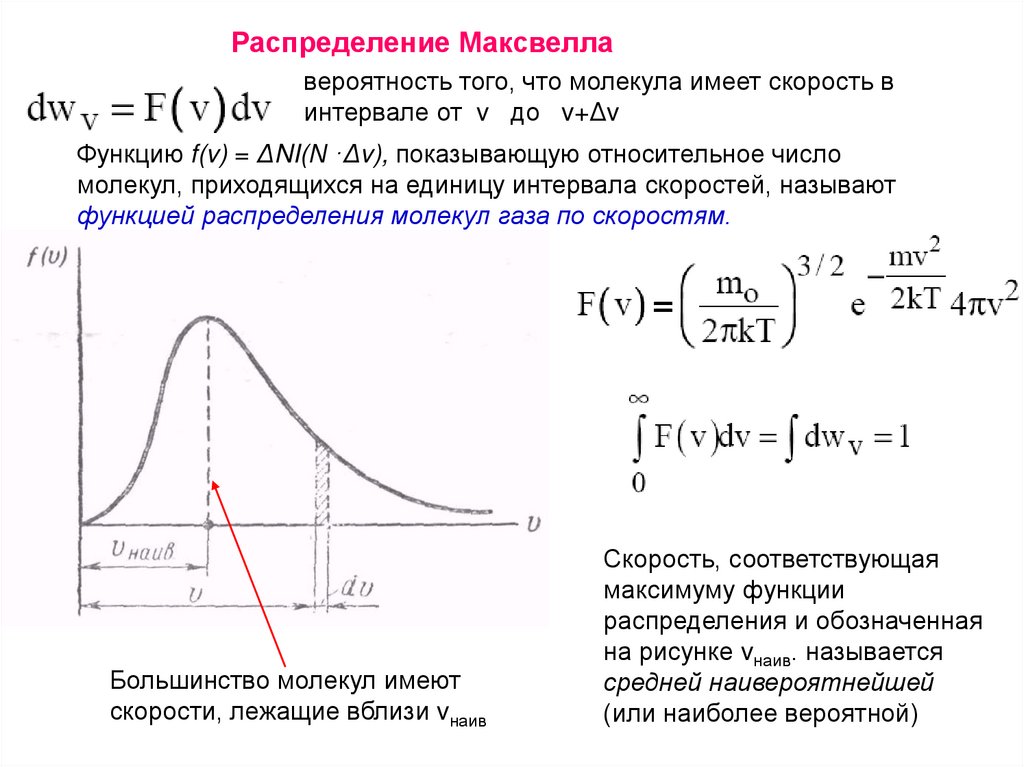
Распределение Максвеллавероятность того, что молекула имеет скорость в
интервале от v до v+Δv
Функцию f(v) = ΔNI(N ·Δv), показывающую относительное число
молекул, приходящихся на единицу интервала скоростей, называют
функцией распределения молекул газа по скоростям.
Большинство молекул имеют
скорости, лежащие вблизи vнаив
Скорость, соответствующая
максимуму функции
распределения и обозначенная
на рисунке vнаив. называется
средней наивероятнейшей
(или наиболее вероятной)
136.
137.
Идеальныйи
реальный
газ
138.
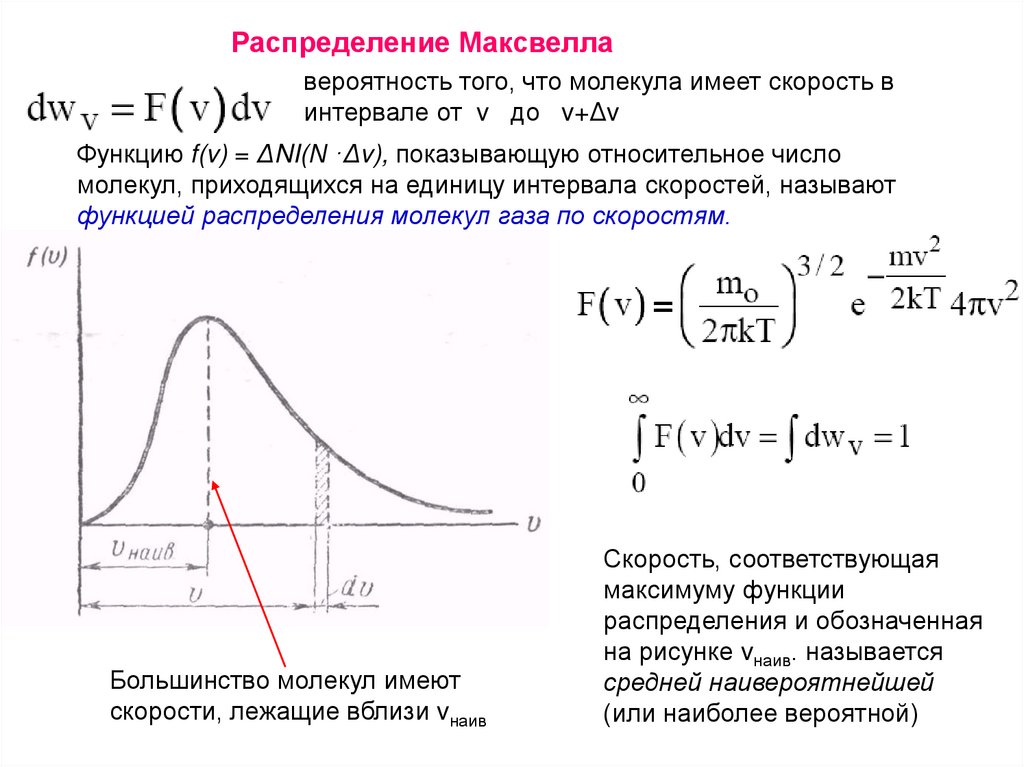
Распределение Максвеллавероятность того, что молекула имеет скорость в
интервале от v до v+Δv
Функцию f(v) = ΔNI(N ·Δv), показывающую относительное число
молекул, приходящихся на единицу интервала скоростей, называют
функцией распределения молекул газа по скоростям.
Большинство молекул имеют
скорости, лежащие вблизи vнаив
Скорость, соответствующая
максимуму функции
распределения и обозначенная
на рисунке vнаив. называется
средней наивероятнейшей
(или наиболее вероятной)
139.
140.
Уравнение состояния идеального газаПусть в объеме V при давлении р и температуре Т находятся N молекул газа.
М = Nm
Число молекул в газе
Количество газа
N N 0 N 0
M
M
Объем газа V (м2), давление p (Н/м2), температура T— по абсолютной шкале
Кельвина
Измерения показали, что у газов при равновесных переходах из одного
состояния в другое изменения параметров р, V и Т с некоторым
приближением удовлетворяют объединенному закону Бойля—Мариотта и
Гей-Люссака: для данной массы газа отношение произведения объема газа
на его давление к абсолютной температуре сохраняется постоянным при
переходе газа из одного равновесного состояния в другое:
pV
const
T
идеальный газ определяется как такой газ, который в точности подчиняется
законам Бойля—Мариотта и Гей-Люссака, а следовательно, объединенному
закону
141.
при данном р и ТV~М~N
k – коффициент
пропорциональности
k
pV
T
pV
1,38 10 23 Дж / К
TN
pV
k N
T
pV=NkT
p V = N k T= kN0
уравнение состояния идеального
газа (Клапейрона—Менделеева)
pV=NkT
N
p kT
V
~ N, тогда
M
T R
pV
M
M
T
RT
разделим обе части на объем
p n k T
давление газа прямо
пропорционально числу молекул в
единице объема и температуре
газа.
142.
Сравним уравнениеpV N k T
с основным уравнением кинетической теории газов
1
2
NkT m N vкв
3
1
2
pV m N vкв
3
2
mvкв
3
kT
2
2
выражение для средней квадратичной скорости молекул в зависимости от
температуры газа.
M
3kT
3RT
RT
vкв
1,73
m
N
N0
для 1 молекулы
m
N0
143.
Явленияпереноса
144.
Переход идеального газа из неравновесных состояний вравновесное происходит благодаря так называемым явлениям
переноса — 1)диффузии, 2) теплопроводности и 3)
внутреннему трению.
Благодаря этим явлениям происходит непрерывное
выравнивание плотности, давления и температуры в пределах
объема газа. Это выравнивание происходит как при наличии,
так и при отсутствии внешнего воздействия на газ.
средняя длина свободного пробега молекул λ –
среднее расстояние, которое проходит молекула от
одного столкновения до другого.
d
Минимальное расстояние на которое
сближаются при столкновении центры
молекул, называется эффективным
диаметром молекулы d.
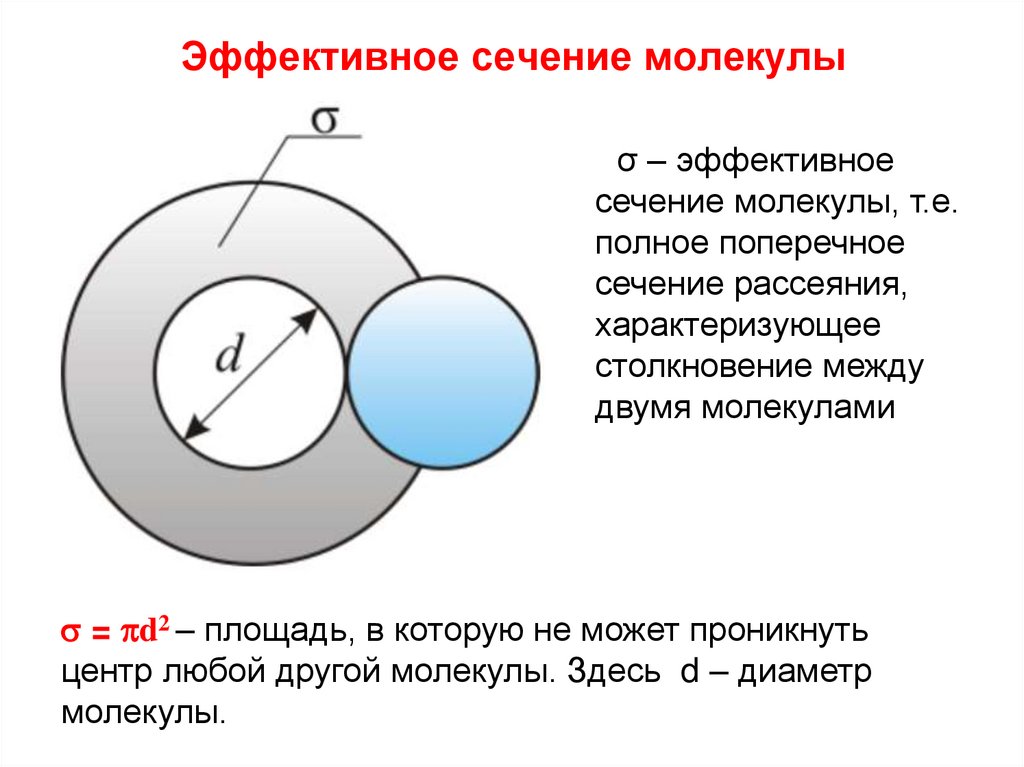
145. Эффективное сечение молекулы
σ – эффективноесечение молекулы, т.е.
полное поперечное
сечение рассеяния,
характеризующее
столкновение между
двумя молекулами
= pd2 – площадь, в которую не может проникнуть
центр любой другой молекулы. Здесь d – диаметр
молекулы.
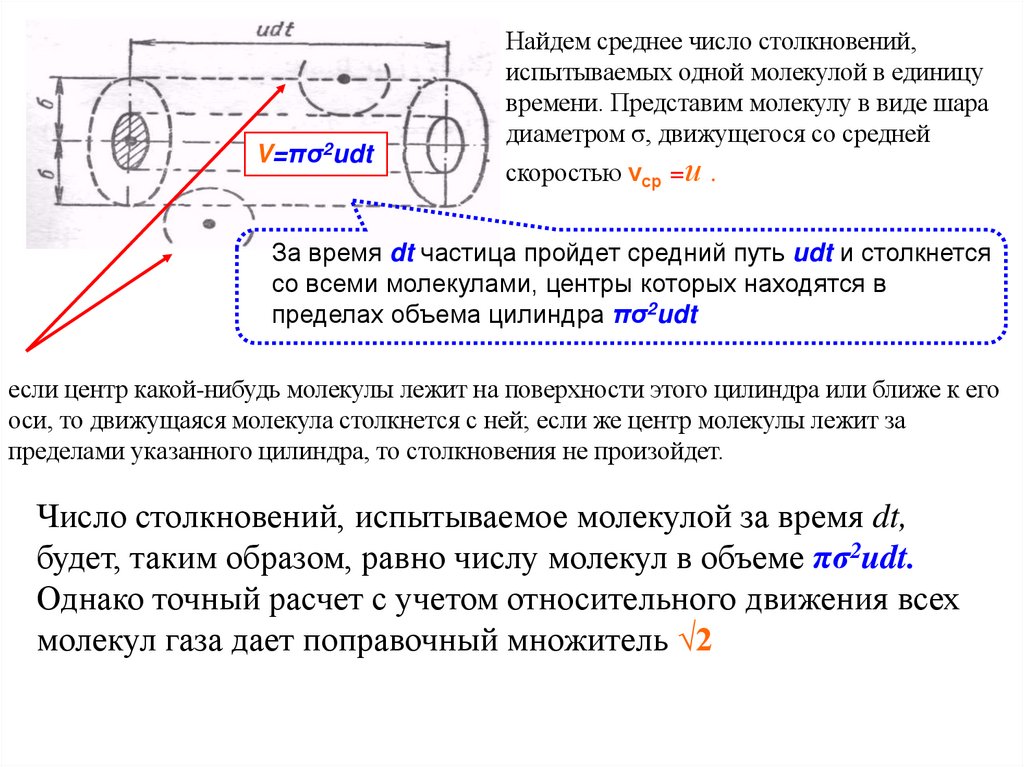
146.
V=πσ2udtНайдем среднее число столкновений,
испытываемых одной молекулой в единицу
времени. Представим молекулу в виде шара
диаметром σ, движущегося со средней
скоростью νср =и .
За время dt частица пройдет средний путь udt и столкнется
со всеми молекулами, центры которых находятся в
пределах объема цилиндра πσ2udt
если центр какой-нибудь молекулы лежит на поверхности этого цилиндра или ближе к его
оси, то движущаяся молекула столкнется с ней; если же центр молекулы лежит за
пределами указанного цилиндра, то столкновения не произойдет.
Число столкновений, испытываемое молекулой за время dt,
будет, таким образом, равно числу молекул в объеме πσ2udt.
Однако точный расчет с учетом относительного движения всех
молекул газа дает поправочный множитель √2
147.
2p 2 nudt2p 2 nu
dt
Число столкновений
в единицу времени
n – число частиц в единице объема
Тепловые скорости ~ нескольких сот м/с. Однако из-за большое
числа соударений молекула не перемещается за малое время на
большие расстояния
длина свободного пробега равна отношению среднего пути,
проходимого молекулой за единицу времени (т.е. скорости и) к
числу испытываемых за это время столкновений
u
1
2p 2 n
Обычно <λ> ~ 10-7м, что в 100 раз
больше, чем среднее расстояние
между молекулами (у газов).
Вакуум – степень разрежения газа при которой средняя длина
свободного пробега молекул имеет тот же порядок величины, что и
размеры сосуда, в котором находится газ
148.
Явления переноса в газахМолекулы газа при хаотическом движении, взаимодействуют друг с
другом, перемещаются на значительные расстояния. Такие
микропроцессы приводят либо к непосредственному переносу массы
вещества молекулами, либо к постепенной , от молекулы к молекуле,
передаче энергии и импульса в определенном направлении.
Явления переноса – это группа явлений обусловленных
хаотическим движением молекул и приводящих при этом
к направленному переносу
массы (диффузия),
кинетической энергии (теплопроводность) и
импульса (внутреннее трение)
На основе молекулярно-кинетической теории можно получить общее
уравнение переноса, описывающее все перечисленные явления
149.
l << <λ>S
1
2
В каждом объеме n·S·l молекул.
В направлении ┴ площадке S
перемещается 1/6 (n·S·l) молекул слева и
столько же справа. Т. к. объем находится
на расстоянии <λ> от S, то все молекулы
достигнут площадки S без соударений.
l
λ
λ
Каждая молекула способна переносить некоторую величину Z (масса,
импульс, кинетическая энергия), а все молекулы переносят 1/6 (n·S·l) Z или
1/6 S·l·H ,где Н = n· Z –физическая величина, переносимая молекулами,
заключенными в единичном объеме. В результате через площадку S из
объемов 1 и 2 за промежуток времени Δτ переносится величина
1/6 S·l·H1 - 1/6 S·l·H2 = 1/6 S·l·(H1-Н2)
Чтобы определить время Δτ, предположим, что все молекулы движутся с
одинаковыми средними скоростями <ν> Тогда молекулы из объемов 1 или 2
пересекают площадку в течение времени Δτ = l/ <ν>
150.
Т.о. за единицу времени переносится величина1 Sl ( H1 H 2 ) 1 Sl ( H1 H 2 )
1
S ( H1 H 2 ) (1)
6
6
l
6
Изменение величины Н на единице длины dx (dH/dx) называется градиентом
величины Н. Т.к. (H1-Н2) это изменение величины Н на расстоянии 2 <λ> ,то
dH ( H1 H 2 )
dx
2
или
dH
( H1 H 2 ) 2
dx
Подставив полученные выражения в (1) и умножив на Δt, получим поток G
переносимой величины Н за промежуток Δt сквозь площадку S.
1
dH
G
S t
3
dx
Общее уравнение переноса
151.
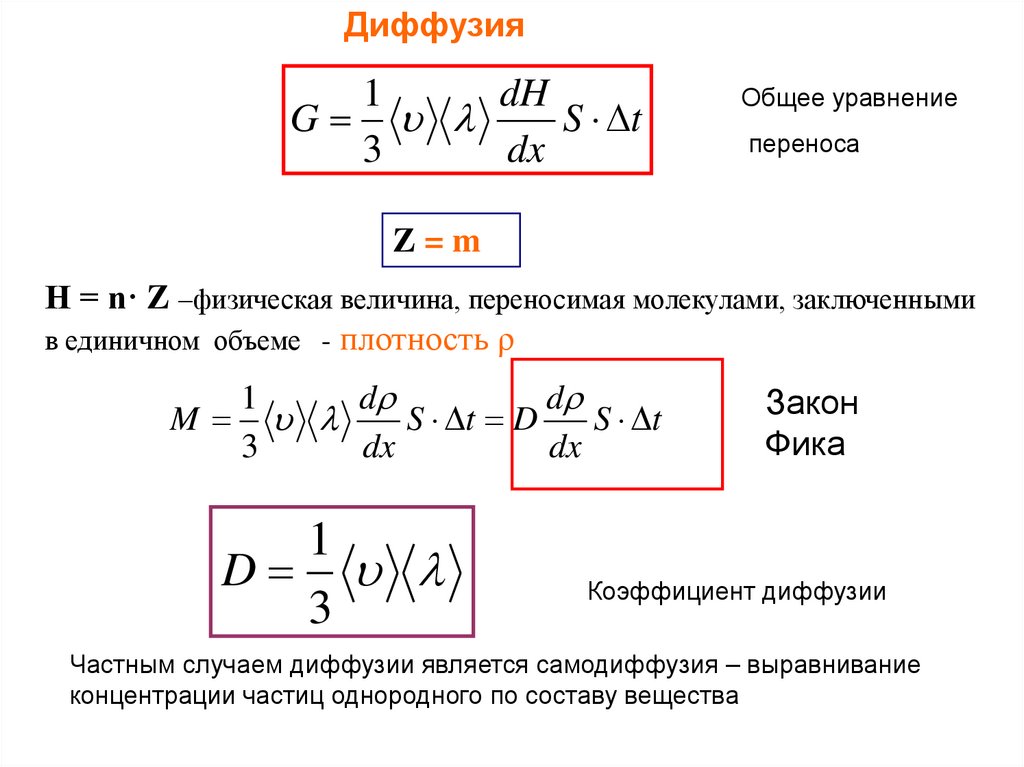
Диффузия1
dH
G
S t
3
dx
Общее уравнение
переноса
Z=m
Н = n· Z –физическая величина, переносимая молекулами, заключенными
в единичном объеме - плотность ρ
1
d
d
M
S t D
S t
3
dx
dx
1
D
3
Закон
Фика
Коэффициент диффузии
Частным случаем диффузии является самодиффузия – выравнивание
концентрации частиц однородного по составу вещества
152.
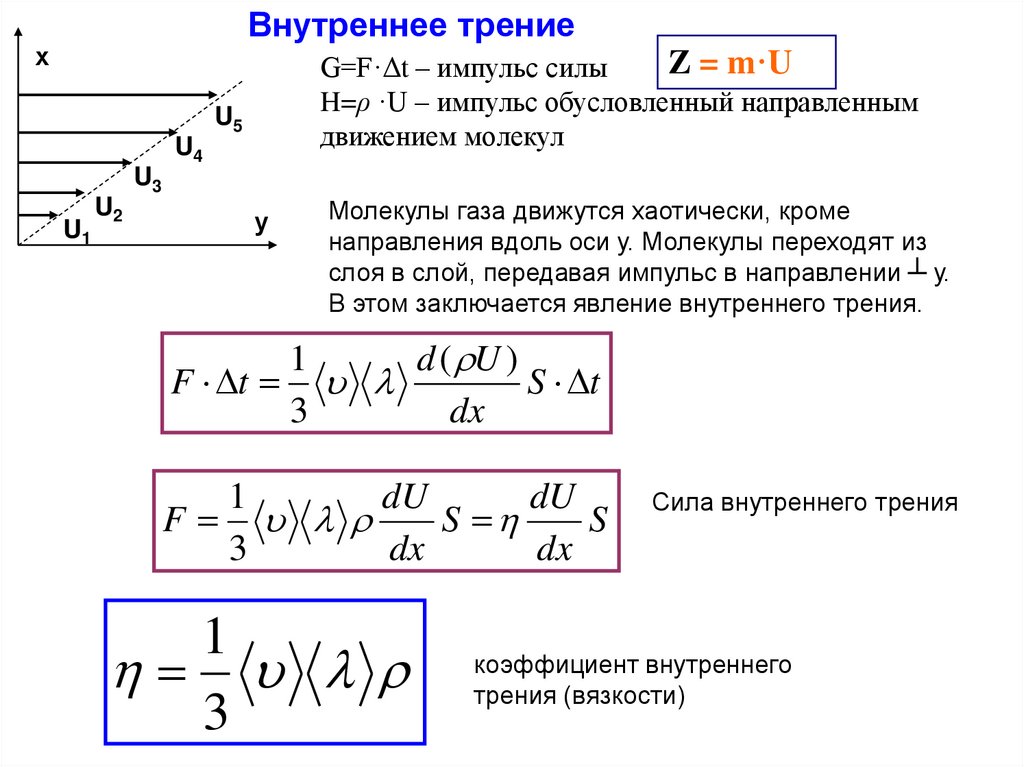
Внутреннее трениех
Z = m·U
G=F·Δt – импульс силы
H=ρ ·U – импульс обусловленный направленным
движением молекул
U5
U4
U3
U1
U2
у
Молекулы газа движутся хаотически, кроме
направления вдоль оси у. Молекулы переходят из
слоя в слой, передавая импульс в направлении ┴ у.
В этом заключается явление внутреннего трения.
1
d ( U )
F t
S t
3
dx
1
dU
dU
F
S
S
3
dx
dx
1
3
Сила внутреннего трения
коэффициент внутреннего
трения (вязкости)
153.
ТеплопроводностьТеплопроводность газов согласно молекулярно-кинетической теории – это
процесс направленной передачи кинетической энергии при соударениях.
G = количество переданной теплоты
Z = i/2 kT
Н = кинетическая энергия молекул, находящихся в единичном объеме
Q
H=i/2 nkT
d i
3
( nkT ) S t
dx 2
k = R/NA, n=ρ/m0, μ=m0NA
или
Q
i
3
dT
nk
S t
2
dx
CV
i
cV
R
2
i
i R
i
kn
R cV
2
2 N A m0 2
1
dT
Q cV
S t
3
dx
Уравнение
теплопроводности
154.
Однако опытным путем для теплопроводности получено уравнение ФурьеdT
Q
S t
dx
1
dT
Q cV
S t
3
dx
Cравнивая уравнение Фурье и уравнение переноса,
получаем выражение для теплопроводности Λ
1
cV
3
ср.арифм ет
8RT
p
Зависимость внутреннего трения η и теплопроводности Λ
от давления р имеет особенности.
155.
η,Λ1
cV
3
λ~1/n, ρ~n .
Сосуд Дьюара
для хранения
сжиженых
газов 1881 г.
р
< λ> ·ρ не изменяется с концентрацией, а значит и
при уменьшении давления (p=nkT).
Это сохраняется до тех пор, пока <λ> не станет
равной размерам сосуда, после чего при
уменьшении давления плотность ρ продолжает
уменьшаться, а длина свободного пробега λ не
изменяется, т.к. не может стать > размеров сосуда. В
этом случае внутреннее трение η и
теплопроводность Λ изменяются ~ р, что
используют в термосах и сосудах Дьюара.
Первые сосуды Дьюара для коммерческого использования были
произведены в 1904 году, когда была основана немецкая компания
Термос (нем. Thermos GmbH).
1906 г.
Burger, R., U.S. Patent 872 795, «Double walled vessel with a
space for a vacuum between the walls», December 3, 1907.
156.
Реальныйгаз
157.
Измерения показывают, что соотношения, полученные в предыдущейглаве для идеального газа, в частности — уравнение равновесного
состояния
pV
M
RT
могут быть применимы и к реальным газам, но только при небольших
давлениях и высоких температурах. Например, у азота при температуре 0° С
произведение pV отличается от М/μ RT для интервала давлений от 1 до 100
атм не более, чем на 0,5%, а для давлений, близких к 1000 атм, это отличие
доходит до 100%.
Такое расхождение объясняется главным образом действием молекулярных
сил.
158.
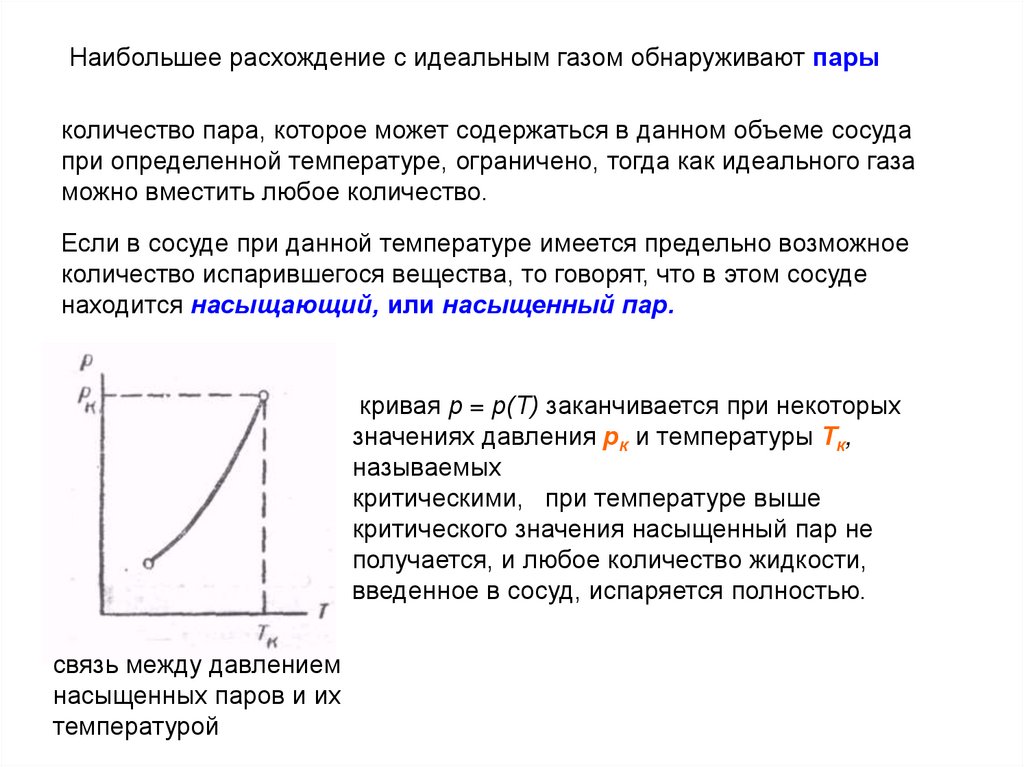
Наибольшее расхождение с идеальным газом обнаруживают парыколичество пара, которое может содержаться в данном объеме сосуда
при определенной температуре, ограничено, тогда как идеального газа
можно вместить любое количество.
Если в сосуде при данной температуре имеется предельно возможное
количество испарившегося вещества, то говорят, что в этом сосуде
находится насыщающий, или насыщенный пар.
кривая р = р(Т) заканчивается при некоторых
значениях давления рк и температуры Тк,
называемых
критическими, при температуре выше
критического значения насыщенный пар не
получается, и любое количество жидкости,
введенное в сосуд, испаряется полностью.
связь между давлением
насыщенных паров и их
температурой
159.
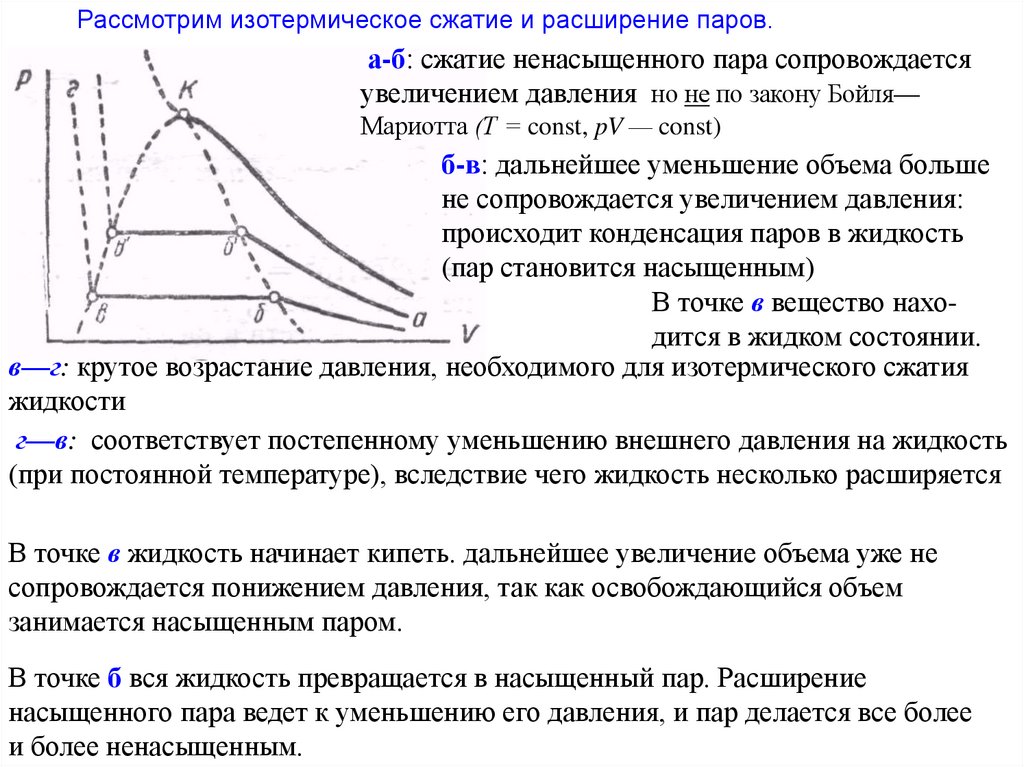
Рассмотрим изотермическое сжатие и расширение паров.а-б: сжатие ненасыщенного пара сопровождается
увеличением давления но не по закону Бойля—
Мариотта (Т = const, pV — const)
б-в: дальнейшее уменьшение объема больше
не сопровождается увеличением давления:
происходит конденсация паров в жидкость
(пар становится насыщенным)
В точке в вещество находится в жидком состоянии.
в—г: крутое возрастание давления, необходимого для изотермического сжатия
жидкости
г—в: соответствует постепенному уменьшению внешнего давления на жидкость
(при постоянной температуре), вследствие чего жидкость несколько расширяется
В точке в жидкость начинает кипеть. дальнейшее увеличение объема уже не
сопровождается понижением давления, так как освобождающийся объем
занимается насыщенным паром.
В точке б вся жидкость превращается в насыщенный пар. Расширение
насыщенного пара ведет к уменьшению его давления, и пар делается все более
и более ненасыщенным.
160.
Если провести изотермическое сжатие того же количествапара при более высокой температуре, то состояние
насыщения наступает при меньшем объеме и большем
давлении (точка б‘ ).
Жидкое состояние при тех же
значениях температуры и давления
(точка в‘ ) характеризуется большим
объемом; при переходе от в к в'
уменьшение объема жидкости от
повышения давления меньше, чем
увеличение объема от повышения
температуры.
с увеличением температуры вещества точки б и в сближаются, т. е. удельный
объем насыщенного пара приближается к удельному объему жидкости.
Состояние вещества (обозначенное на рис. буквой К), при
котором плотность жидкости и плотность насыщенного пара,
находящегося в равновесии с ним, равны, называется
критическим состоянием вещества.
Критическое состояние для каждого1 вещества характеризуется
определенными значениями давления рк, температуры Тк и удельного объема
Vк.
161.
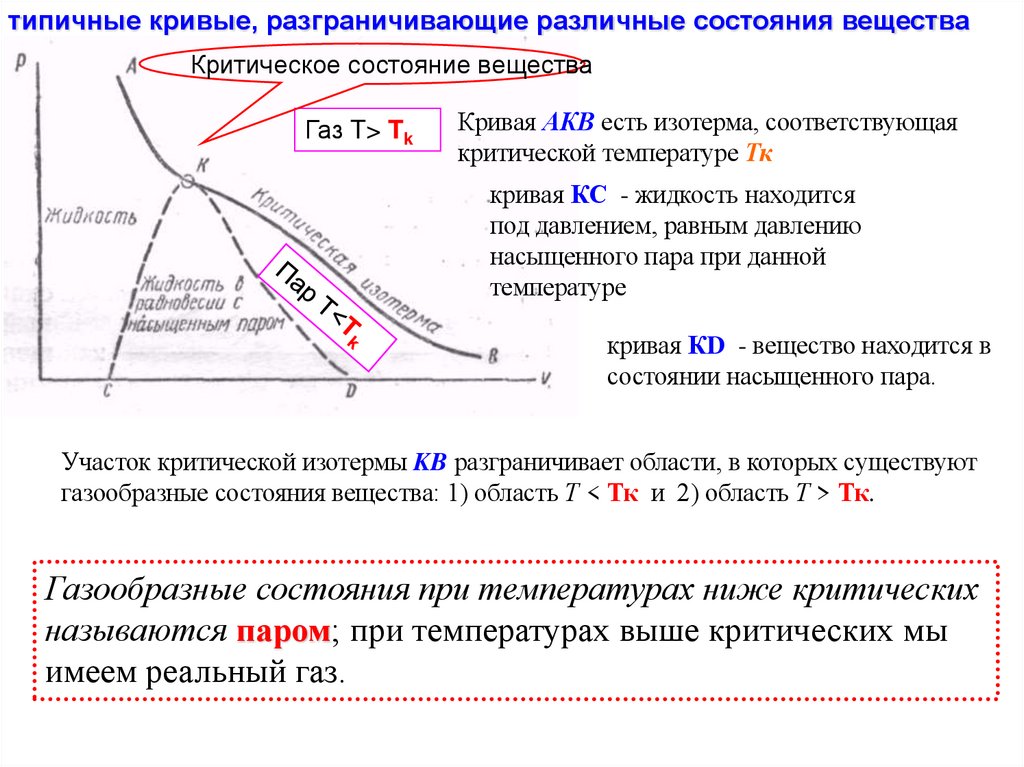
типичные кривые, разграничивающие различные состояния веществаКритическое состояние вещества
Газ T> Tk
Кривая АКВ есть изотерма, соответствующая
критической температуре Тк
кривая КС - жидкость находится
под давлением, равным давлению
насыщенного пара при данной
температуре
кривая КD - вещество находится в
состоянии насыщенного пара.
Участок критической изотермы KB разграничивает области, в которых существуют
газообразные состояния вещества: 1) область Т < Тк и 2) область Т > Тк.
Газообразные состояния при температурах ниже критических
называются паром; при температурах выше критических мы
имеем реальный газ.
162.
Рассмотрим изохорические, изобарические и изотермическиепроцессы, при которых вещество переходит из одного
состояния в другое
1→2: изобарическое сжатие,
сопровождаемое охлаждением. Вещество
переходит из газообразного состояния
«сразу» в жидкое, как только Т станет
меньше критической
1→3: изохорическое охлаждение.
Вещество также скачком переходит из
газообразного состояния в жидкое.
4→5: если изобарическое сжатие производить при давлении, меньшем
критического, то газ сначала переходит в ненасыщенный пар, затем
становится насыщенным, а при дальнейшем сжатии (и охлаждении)
постепенно конденсируется в жидкость.
4→6: изохорическое охлаждение. В отличие от 1→3 производится при
удельном объеме, большем, чем критический удельный объем; охлаждаемый
газ проходит через область ненасыщенного пара, превращается в
насыщенный и затем частично конденсируется.
163.
7→8 →9 →10: изотермический процесс.7 имеется ненасыщенный пар
8 насыщенное состояние, в которое путем
сжатия переводится пар
9 окончание постепенной конденсации,
9 → 10: изотермическое сжатие жидкости.
11 → 12: изотермический процесс протекающий при температуре выше критической.
Вещество все время остается в газообразном состоянии; таким образом, путем
изотермического сжатия нельзя превратить газ в жидкость, если температура этого
процесса выше критического значения.
Для сжижения газа совершенно необходимо охладить его до температуры ниже
критической.
Если изотермический процесс 7→8 →9 →10: производить с тщательно очищенным
веществом, лишенным всяких посторонних примесей, и сам процесс вести
достаточно медленно, то можно наблюдать так называемые метастабильные
состояния
164.
Уравнение Ван-дер-Ваальса.При выводе уравнения состояния идеального газа, которое для 1 моля имеет вид
pV=RT
были сделаны два существенно важных предположения:
1) молекулы газа не взаимодействуют между собой; только во время
столкновений на короткое время появляются силы отталкивания;
2) собственный объем молекул очень мал по сравнению с объемом сосуда,
в котором находится газ.
Для реальных газов, а тем более для жидкостей, эти предположения не могут
быть использованы.
Из всех предложенных уравнений для реального вещества наибольшей
известностью пользуется уравнение Ван-дер-Ваальса: для 1 моля
a
( p 2 )(V b) RT
V
а и b — постоянные для данного вещества величины
165.
«поправки», внесенные в уравнение состояния идеального газа:а/V2 – величина, учитывающая взаимодействие молекул
и обратно пропорциональным квадрату удельного объема (объема одного
моля газа)
b- величина, учитывающая собственный объем молекул. Как показывают
расчеты она должна равняться 4Vi (Vi - собственный объем молекул)
Величины а и b уравнения Ван-дер-Ваальса имеют различные значения для
различных газов; их можно найти, измеряя объем, давление и температуру данного
газа в различных состояниях.
Для вещества, имеющего массу М, это уравнение Ван-дер-Ваальса.
запишется в следующем виде:
M
2
a
M
( p 2 2 )(V b) RT
V
166. Критические параметры газа
Критическими параметрами газа называются значения его макропараметров(давления, объёма и температуры) в критической точке, т.е. в таком состоянии,
когда жидкая и газообразная фазы вещества неразличимы. Найдем эти
параметры для газа Ван-дер-Ваальса, для чего преобразуем уравнение
состояния:
Умножим обе части на V2/p
Мы получили уравнение третьей степени относительно V.
В критической точке все три корня уравнения сливаются в один, поэтому
предыдущее уравнение эквивалентно следующему:
167. Критические параметры газа
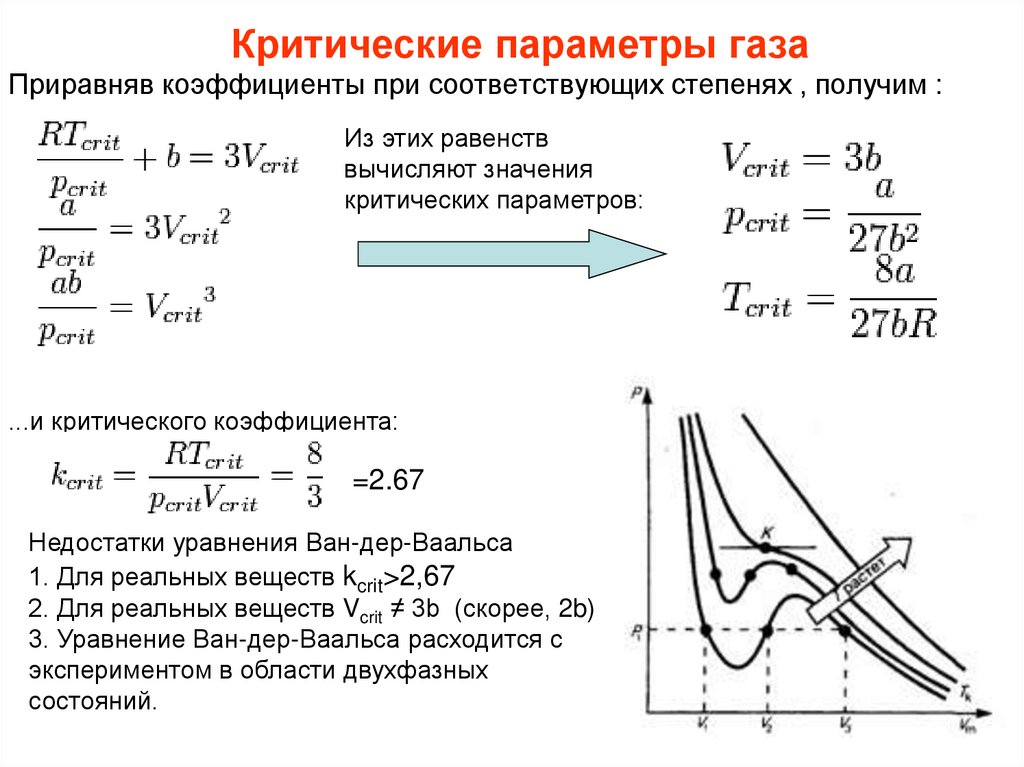
Приравняв коэффициенты при соответствующих степенях , получим :Из этих равенств
вычисляют значения
критических параметров:
...и критического коэффициента:
=2.67
Недостатки уравнения Ван-дер-Ваальса
1. Для реальных веществ kcrit>2,67
2. Для реальных веществ Vcrit ≠ 3b (скорее, 2b)
3. Уравнение Ван-дер-Ваальса расходится с
экспериментом в области двухфазных
состояний.
168.
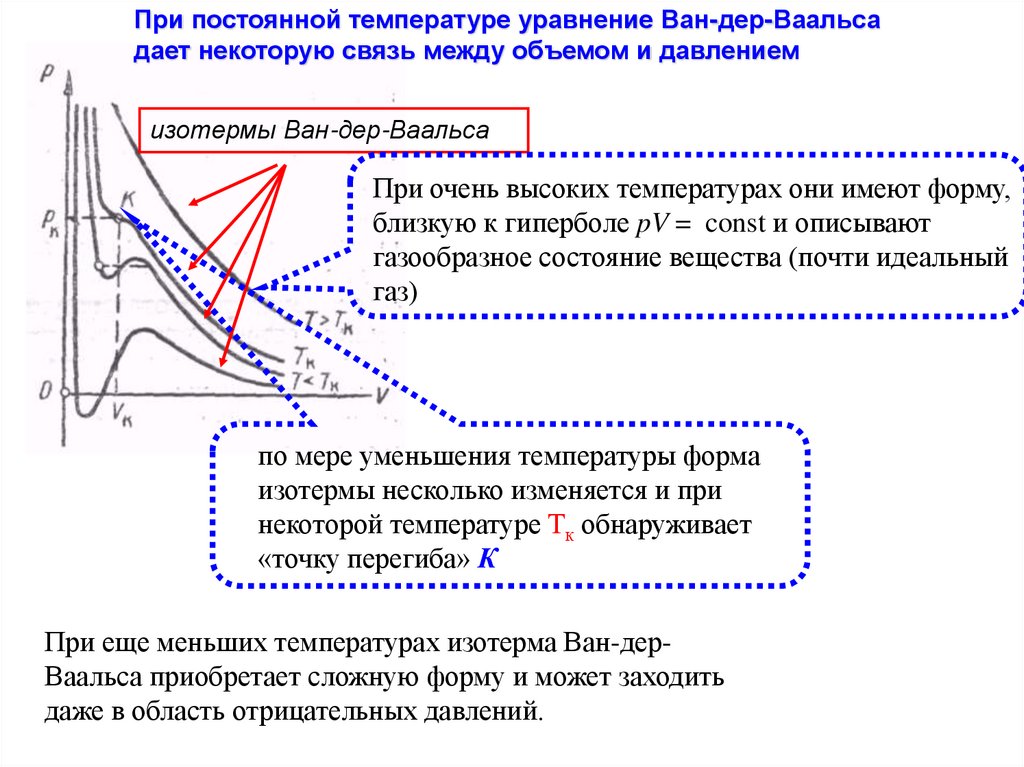
При постоянной температуре уравнение Ван-дер-Ваальсадает некоторую связь между объемом и давлением
изотермы Ван-дер-Ваальса
При очень высоких температурах они имеют форму,
близкую к гиперболе pV = const и описывают
газообразное состояние вещества (почти идеальный
газ)
по мере уменьшения температуры форма
изотермы несколько изменяется и при
некоторой температуре Тк обнаруживает
«точку перегиба» К
При еще меньших температурах изотерма Ван-дерВаальса приобретает сложную форму и может заходить
даже в область отрицательных давлений.
169.
изотермы, соответствующие низким температурамИзмерения показывают, что изотермы реального вещества приближаются к
изотермам Ван-дер-Ваальса на участках
1—2 соответствующих жидким состояниям,
5—6 соответствующих парообразным состояниям вещества;
однако в средней части реальная
изотерма идет не по кривой 2—3—4—5,
как этого требует уравнение Ван-дерВаальса, а по изобаре 2—5 (в точке 2
имеется только «кипящая жидкость», а в
точке 5 — только насыщенный пар)
если опыты провести с очень чистым Ееществом, а сжатие, расширение, подвод и отвод
теплоты производить достаточно медленно, то можно обнаружить состояния,
соответствующие участкам:
2—3 (перегретая жидкость) и
5—4 (пересыщенный пар)
участок 3—4; - часть изотермы соответствует неустойчивым состояниям вещества:
при сжатии давление не увеличивается, а уменьшается, т. е. вещество не только не
оказывает «сопротивление» сжатию, но, наоборот, само «способствует» этому.
170.
Изотермы реального газаСиние — изотермы при температуре ниже
критической. Зелёные участки на них —
метастабильные состояния.
Участок левее точки F — нормальная
жидкость.
Точка F — точка кипения.
Прямая FG — равновесие жидкой и
газообразной фазы.
Участок FA — перегретая жидкость.
Участок F′A — растянутая жидкость (p<0).
Участок AC — аналитическое продолжение
изотермы, физически невозможен.
Участок CG — переохлаждённый пар.
Точка G — точка росы.
Участок правее точки G — нормальный газ.
Красная — критическая изотерма.
K — критическая точка.
Голубые — сверхкритические изотермы












































































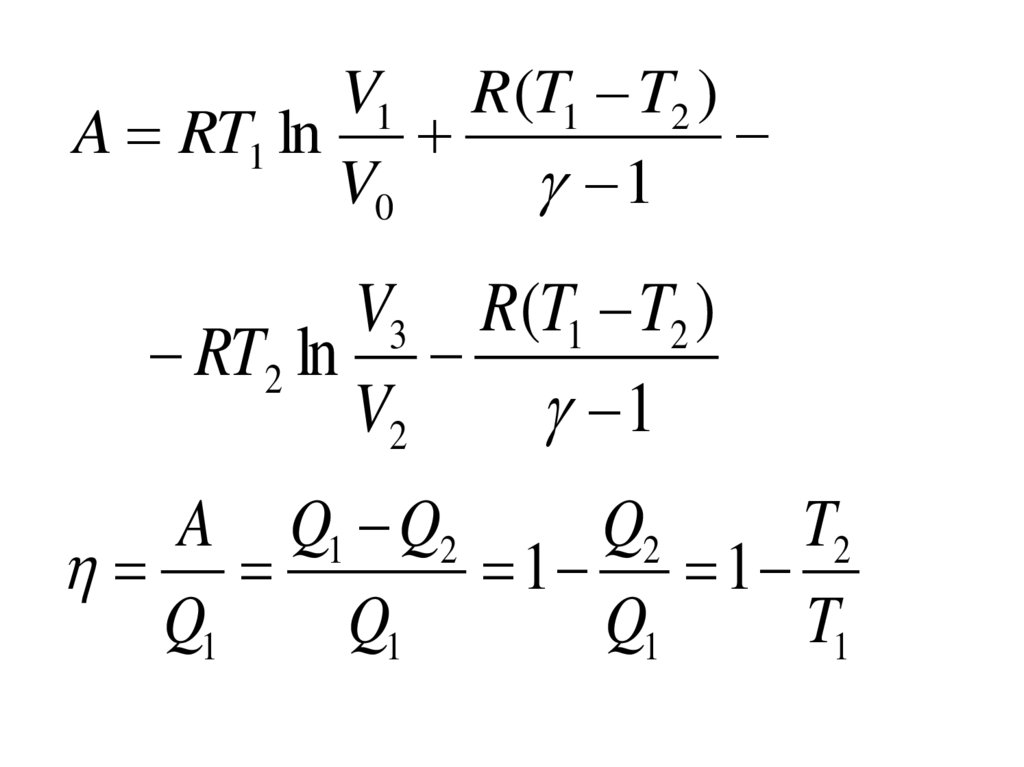
































 Физика
Физика








