Консультация по физике

1.

КОНСУЛЬТАЦИЯ
ПО ФИЗИКЕ
Лубенченко О. И., кафедра физики им. В. А. Фабриканта
НИУ «МЭИ», 2021 г.

2.

Задача 1
Один моль азота расширился при постоянной температуре 300 К от объёма 2 л
до объёма 5 л. Найти работу и изменение внутренней энергии газа, а также
количество теплоты, переданное газу.
РЕШЕНИЕ
Q ΔU A
p
p1
ΔU 0
1
pV const
V1
V2
V2
V2
V1
V1
A p V dV p1V1
2
0
pV p1V1
V
p1V1
p V
V
V
dV
p1V1 ln 2
V
V1

3.

Задача 1
p1V1 νRT1
V2
A νRT1 ln
V1
V2
Q νRT1 ln
V1
ЧИСЛЕННЫЙ РАСЧЁТ
5
Q A 1 8,31 300ln 2,28 103 Дж
2

4.

Задача 2
Два моля двухатомного идеального газа претерпели адиабатный процесс.
Начальная температура 300 К, конечная — 350 К. Найти работу и изменение
внутренней энергии газа, а также количество теплоты, переданное газу.
РЕШЕНИЕ
Q 0
p
2
i
ΔU νR T2 T1
2
1
0
0 ΔU A
ЧИСЛЕННЫЙ РАСЧЁТ
V
I=5
A ΔU
i
A νR T1 T2
2
5
ΔU 2 8,31 350 300 2,1 103 Дж
2
A 2,1 103 Дж

5.

Задача 3
На рисунке изображён график процесса, происходящего с идеальным газом.
Найти работу газа. Газ — аргон; V1 = 1,0 л; V2 = 3V1; p1 = 0,10 МПа; p2 = 2p1.
РЕШЕНИЕ
A A12 A23
A12 p1 V2 V1 2p1V1
A 2p1V1
ЧИСЛЕННЫЙ РАСЧЁТ
A 2 1,0 105 1,0 10 3 200 Дж
A23 0

6.

Задача 4
На рисунке изображён график процесса, происходящего с идеальным газом.
Найти количество теплоты, переданное газу. Газ — метан, V1 = 1,0 л; V2 = 4V1;
p1 = 1,0 МПа; p2 = 3p1.
РЕШЕНИЕ
Q ΔU A
i
p1V1 νRT1
p2V2 νRT3
ΔU νR T3 T1
2
i
i
11i
ΔU p2V2 p1V1 3p1 4V1 p1V1
p1V1
2
2
2
A A12 A23 A12 0 A23 p2 V2 V1 3p1 3V1 9p1V1

7.

Задача 4
11i
Q
p1V1 9p1V1
2
11i
Q
9 p1V1
2
ЧИСЛЕННЫЙ РАСЧЁТ
I=6
11 6
Q
9 1,0 106 1,0 10 3 4,2 104 Дж
2

8.

Задача 5
На рисунке изображён график процесса, происходящего с идеальным газом.
Найти изменение внутренней энергии газа. Газ – гелий; V1 = 15 л; V2 = V1/2;
p1 = 0,40 МПа. Процесс 1-2 — адиабатный.
РЕШЕНИЕ
3-1: V1 V2
T1
T3
p1V1 νRT1
i
ΔU νR T3 T1
2
V2
V2
i
T3 T1
ΔU νRT1 1
V1
2
V1
V2
i
i
ΔU p1V1 1 p1 V2 V1
2
V1
2

9.

Задача 5
i
ΔU p1V1
4
ЧИСЛЕННЫЙ РАСЧЁТ
I=3
3
ΔU 4,0 105 1,5 10 2 4,5 103 Дж
4

10.

Задача 6
В сосуде имеется смесь двух газов (массы m1 и m2, молярные массы μ1 и μ2).
Объём сосуда равен V, температура смеси T. Найти давление в сосуде.
РЕШЕНИЕ
З-н Дальтона: p p1 p2
m1
p1V μ RT
1
p V m2 RT
2
μ2
m1 m2 RT
p
μ
μ
2 V
1

11.

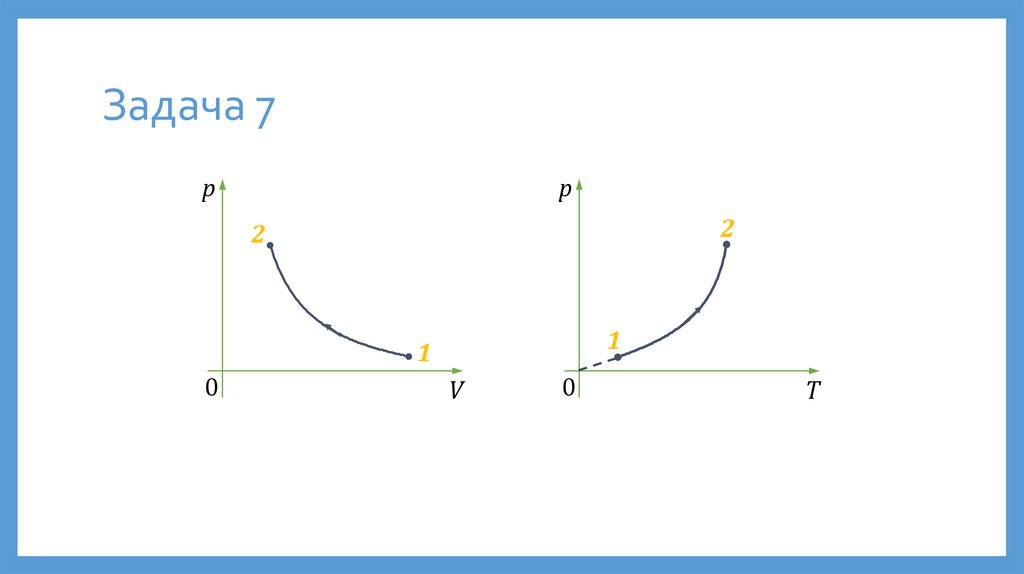
Задача 7
Давление газа при нагревании изменяется по закону p = αT2, где α —
положительная константа. Построить графики этого процесса в координатах
(p, V), (p, T).
РЕШЕНИЕ
pV νRT
2
p
αT
pV
p α
νR
2
ν 2R 2
p
αV 2

12.

Задача 7
p
p
2
2
1
1
0
V
0
T

13.

Задача 8
Тонкий обруч скатывается без проскальзывания с наклонной плоскости с
высоты 0,20 м. Найти скорость центра обруча в нижней точке плоскости.
РЕШЕНИЕ
m
R
h
1
Объект исследования: обруч — ТТ
ИСО — лабораторная
t
C
2
⊗ω
C
vC
Wп 0
ЗСМЭ: W const
Aнп 0
ΔWк ΔWп 0
mvC2 Iω2
ΔWк Wк2 Wк1
0
2
2

14.

Задача 8
ΔWп Wп2 Wп1 0 mgh
mvC2 Iω2
mgh 0
2
2
vC
ω
(качение без проскальзывания) I mR 2
R
mvC2 mR 2 vC2
vC gh
mgh 0
2
2
2R
ЧИСЛЕННЫЙ РАСЧЁТ
м
vC 9,8 2,0 10 1 1,4
с

15.

Задача 9
На рисунке изображена система грузов на невесомых нерастяжимых нитях,
намотанных на массивный блок, момент инерции которого равен I, радиусы
шкивов R и 2R. Блок может вращаться вокруг своей оси без трения, нити не
проскальзывают по блоку. Массы грузов указаны на рисунке. Найти ускорения
грузов и натяжения нитей.
РЕШЕНИЕ
Объект исследования: блок — ТТ, груз 1 — МТ, груз 2 — МТ
ИСО — лабораторная
II закон Ньютона (для груза 1): ma1 Fт T1
II закон Ньютона (для груза 2): ma2 Fт T2

16.

Задача 9
N
⊙ M T2
t
R2
y : ma1 Fт Т 1
⊙ε
y : ma2 Fт Т 2
⊗ MT
z : Iε T2 R2 T1 R1
R
O ⊙z 1
T1
T2
1
Дополнительные соотношения:
Fт mg (закон всемирного тяготения)
Fт
T2
T1
m
m
Fт
Fт
a2
y
ОУДВД (для блока): Iε M Fт M N M T1 M T2
a1
T1 T1
(нити невесомы)
T2 T2
a1 εR1 (нити нерастяжимы и не проскальзывают по
блоку)
a2 εR2

17.

Задача 9
mRε mg Т 1
2mRε mg Т 2 (R1 = R, R2 = 2R)
Iε 2T R T R
2
1
Т 1 mg mRε
Т 2 mg 2mRε
Iε 2T R T R
2
1
Iε 4mR 2ε mR 2ε 2mgR mgR
mgR 2
a1
I 5mR 2
Iε 2 mg 2mRε R mg mRε R
ε
mgR
I 5mR 2
2mgR 2
a2
I 5mR 2
mR 2
Т 1 mg ma1 mg 1
2
I
5
mR
I 6mR 2
Т 1 mg
I 5mR 2
4mR 2
I mR 2
Т 2 mg 2ma2 mg 1
Т 2 mg
2
I
5
mR
I 5mR 2

18.

Задача 10
Камень бросают вертикально вверх со скоростью v0. Через время τ из той же
точки с такой же скоростью бросают второй камень. На какой высоте камни
столкнутся?
РЕШЕНИЕ
y
h
0
t = t*
v0
v0
1
2
t=0
t=τ
Объект исследования: камень 1 — МТ, камень 2 — МТ
ИСО — земля
gt 2
g Кинематический закон (для камня 1): r t r v t
1
0
0
2
Кинематический закон (для камня 2):
r2 t r0 v0 t τ
g t τ
2
2

19.

Задача 10
gt 2
y1 t v0t
2
y2 t v0 t τ
g t τ
2
2
При t = t*
y1 t * y2 t * h
g t * τ
gt
*
v0t
v0 t τ
2
2
*
*2
*2
*2
2
gt
gt
gτ
v0t *
v0t * v0τ
gτt *
2
2
2
2
v0 τ
t
g 2
*

20.

Задача 10
2
2
2
2
v
v
v
v
τ
v
v
τ
gt
τ
g
τ
gτ
h v0t *
v0 0 0 0 0 0 0
2
g
2 2g 2
8
g 2 2 g 2
*2
v02 gτ 2
h
2g
8

21.

Задача 11
Два тела массами 2,0 кг и 4,0 кг движутся в одну сторону вдоль одной прямой
со скоростями, по модулю соответственно равными 5,0 м/с и 2,5 м/с, и
испытывают абсолютно неупругий удар. Найти скорости тел после удара.
РЕШЕНИЕ
Объект исследования: механическая система — тело 1
(МТ) + тело 2 (МТ)
ИСО — лабораторная
t
m1 v1
m2 v2
m1 + m2 u
x
ЗСИ: P const
удар
m1 v1 m2 v2 m1 m2 u
x : m1 v1 m2 v2 m1 m2 u
m1 v1 m2 v2
u
m1 m2

22.

Задача 11
ЧИСЛЕННЫЙ РАСЧЁТ
2,0 5,0 4,0 2,5
м
u
1,67
2,0 4,0
с

23.

Задача 12
Зная уравнение движения материальной точки, записанное в СИ:
x(t) = 3t2 + t + 8, найти скорость и ускорение точки через время 3 с после начала
движения.
РЕШЕНИЕ
dx
6t 1
dt
d vx
ax
6
dt
vx
v 6t 1 i
a 6i
ЧИСЛЕННЫЙ РАСЧЁТ
м
v 6 3 1 19
с
a 6
м
с2

24.

Задача 13
Однородный стержень длиной l может свободно вращаться вокруг
горизонтальной оси, проходящей через один из его концов. Какую
минимальную скорость нужно сообщить нижнему концу стержня, чтобы он
сделал полный оборот в вертикальной плоскости?
РЕШЕНИЕ
Объект исследования: стержень — ТТ
ИСО — лабораторная
1
z⊙
l
m
⊙
ωmin
v min
z⊙
t
2
ЗСМЭ: W const
Aнп 0
ΔWк ΔWп 0
2
Iωmin
ΔWп Wп2 Wп1 mgl 0
ΔWк Wк2 Wк1 0
2
Wп 0

25.

Задача 13
2
Iωmin
mgl 0
2
ml 2
I
3
vmin ωmin l
vmin
ωmin
2mgl 3
l
ml 2
2mgl
I
vmin 6gl

26.

Задача 14
Два тела одинаковой массы m движутся по взаимно перпендикулярным
прямым со скоростью v и испытывают абсолютно неупругий удар. Найти
скорость и кинетическую энергию системы после удара.
РЕШЕНИЕ
u
m
α
v1
2m
v2
m
t
y
Объект исследования: механическая система — тело
1 (МТ) + тело 2 (МТ)
ИСО — лабораторная
ЗСИ: P const
x
F
внеш
0, удар
mv1 mv2 2mu
x : mv 2mu cos α
y : mv 2mu sin α

27.

Задача 14
π
α
4
mv
tg α
1
mv
2m v 2m u cos α sin α
2 2
2
2
2
2
2mu2
m
v
Wк
mu2
2
2
2
u
mv2
Wк
2
v
2

28.

Задача 15
Пушка массы M стоит на гладкой горизонтальной поверхности. Пушка
выстреливает снарядом массы m под углом α к горизонту. Скорость пушки
после выстрела равна u. Найти скорость снаряда при выстреле.
РЕШЕНИЕ
t
u
M
v
α
m
x
Объект исследования: механическая система
— пушка (ТТ) + снаряд (МТ)
ИСО — лабораторная
ЗСИ: Px const
внеш
F
x 0
0 mv cos α Mu
Mu
v
m cos α

29.

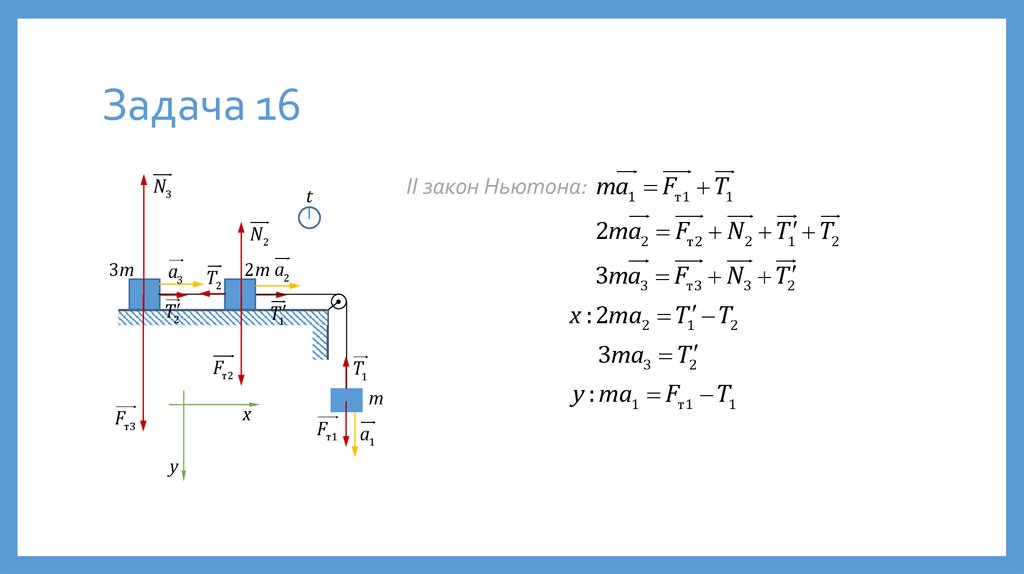
Задача 16
На рисунке изображена система тел, соединённых невесомыми
нерастяжимыми нитями. Массы тел указаны на рисунке. Блок невесом и может
вращаться вокруг своей оси без трения. Найти модуль ускорения тел и силу
натяжения всех нитей. Трением пренебречь.
РЕШЕНИЕ
Объект исследования: груз 1 (МТ), груз 2 (МТ), груз 3
(МТ)
ИСО — лабораторная

30.

Задача 16
m N3
3m
a3
II закон Ньютона: ma1 Fт1 T1
t
T2
N2
2ma2 Fт2 N2 T1 T2
2m a2
3ma3 Fт3 N3 T2
T2
x :2ma2 T1 T2
T1
Fт2
T1
x
Fт3
y
3ma3 T2
m
Fт1
a1
y : ma1 Fт1 T1

31.

Задача 16
Дополнительные соотношения:
(закон всемирного тяготения)
Fт1 mg
a1 a2 a3 a (нити нерастяжимы)
T1 T1 ,T2 T2 (нити невесомы)
2ma T1 T2
3ma T2
ma mg T
1
3mg
T2
6
2ma 3ma ma T1 T2 T2 mg T1 mg
mg
T2
2
mg
mg T1
6
5mg
T1
6
g
a
6

32.

Задача 17
На рисунке изображена система грузов, соединённых невесомыми
нерастяжимыми нитями, одна из которых перекинута через массивный блок —
сплошной цилиндр. Блок может вращаться вокруг своей оси без трения, нить
не проскальзывает по блоку. Массы грузов и блока указаны на рисунке. Найти
модули ускорений грузов и натяжение нити.
РЕШЕНИЕ
Объект исследования: груз 1 (МТ), груз 2 (МТ), блок (ТТ)
ИСО — лабораторная
m
2m
m

33.

Задача 17
N
⊙ M T1
m
t
R2
O ⊗z R
T1
⊗ε
T2 ⊗ M T2
Fт
a1 T1
m
T2
2m
Fт1
y F
т2
II закон Ньютона (для груза 1): ma1 Fт1 T1
II закон Ньютона (для груза 2): 2ma2 Fт2 T2
ОУДВД (для блока): Iε M Fт M N M T1 M T2
y : ma1 Fт1 Т 1
y :2ma2 Fт2 Т 2
z : Iε T R T R
2
1
Дополнительные соотношения:
a2
Fт1 mg , Fт2 2mg (закон всемирного тяготения)
(нить невесома)
T1 T1 , T2 T2

34.

Задача 17
a1 a2 a εR (нить нерастяжима и не проскальзывает по блоку)
mR 2
I
2
ma mg Т 1
Т 1 mg ma
7ma
Т
2
mg
2
ma
2
ma
2
mg
Т
mg
2
2
2
ma
2
mR a T2R T1R
2mg 2ma mg ma
2
2 R
2
9
10
a g T1 mg T2 mg
7
7
7