Аксиомы стереометрии и их применение

1.

2.

C
B
A
B a
A
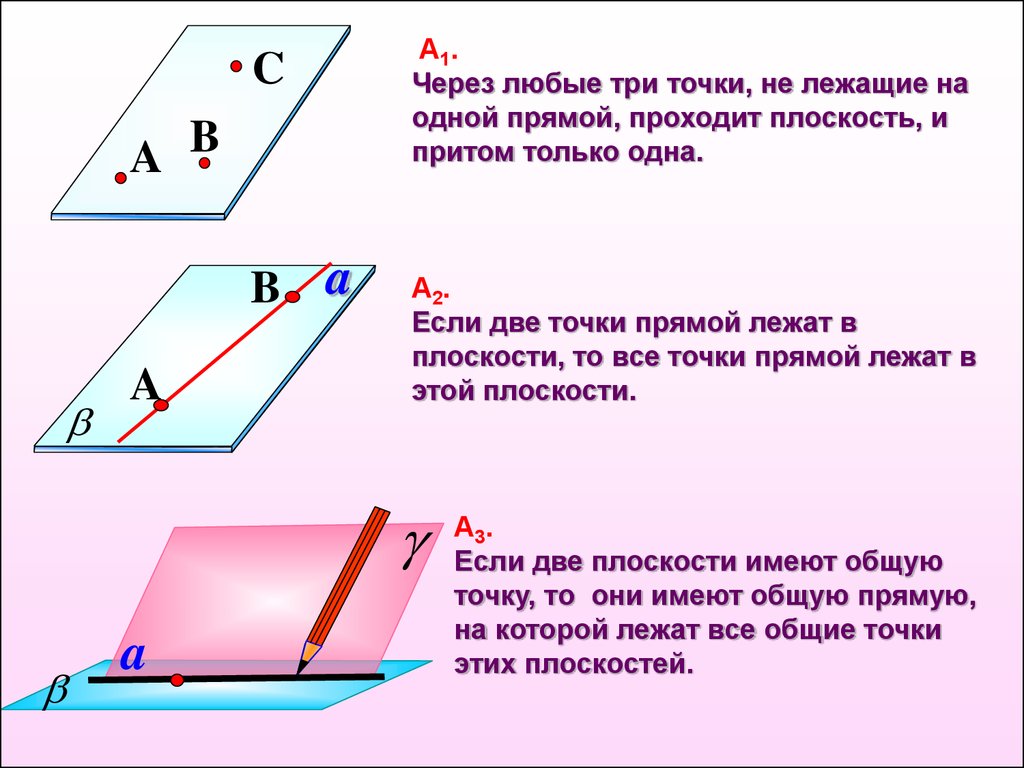
А 1.
Через любые три точки, не лежащие на
одной прямой, проходит плоскость, и
притом только одна.
А 2.
Если две точки прямой лежат в
плоскости, то все точки прямой лежат в
этой плоскости.
a
А 3.
Если две плоскости имеют общую
точку, то они имеют общую прямую,
на которой лежат все общие точки
этих плоскостей.

3.

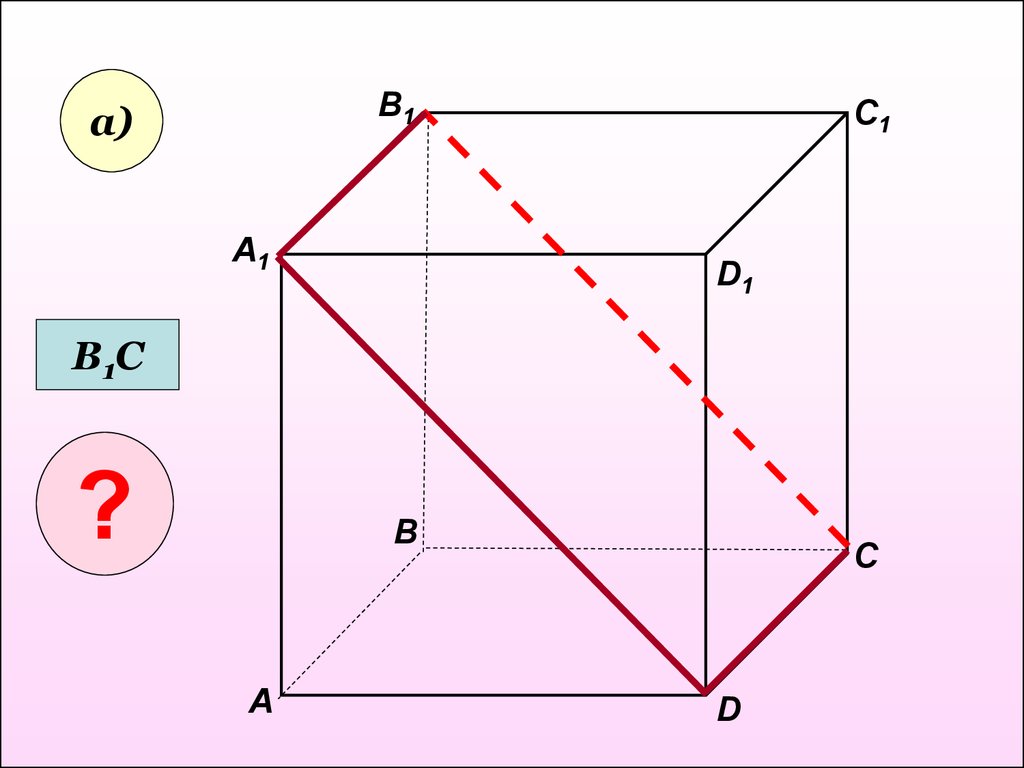
• Пользуясь данным
рисунком, назовите:
• а) три плоскости,
содержащие прямую В1С; A1
B1
C1
D1
B
A
C
D

4.

В1
а)
А1
C1
D1
В1С
?
В
А
С
D

5.

В1
а)
А1
C1
D1
В1С
?
В
А
С
D

6.

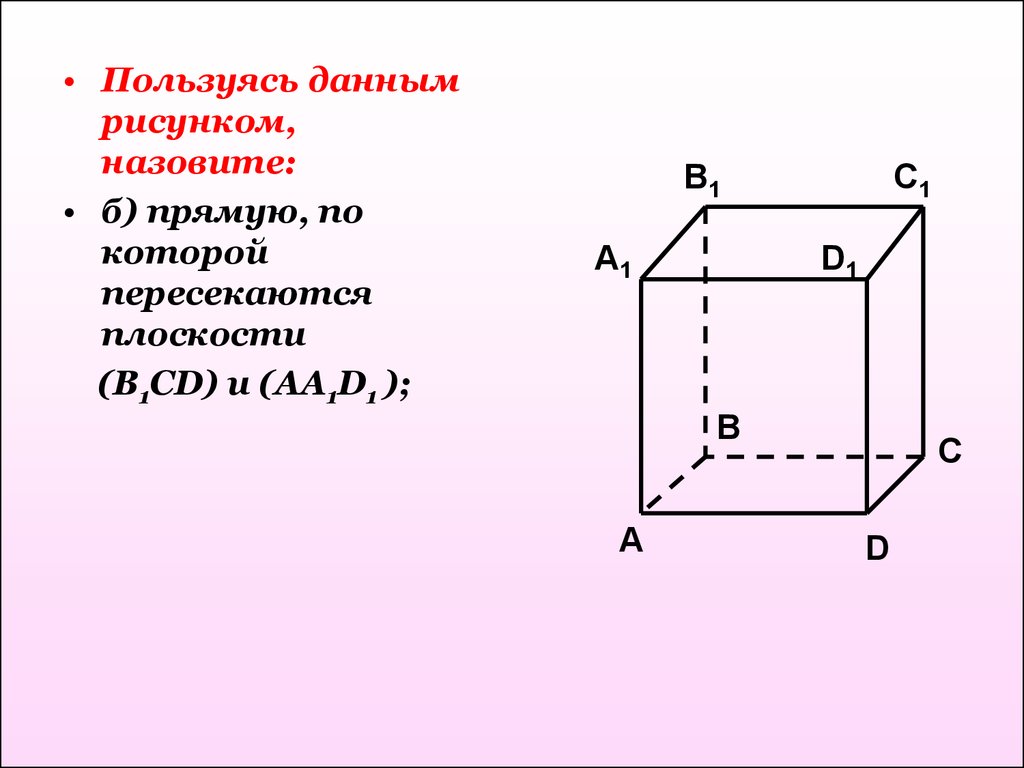
• Пользуясь данным
рисунком,
назовите:
• б) прямую, по
которой
пересекаются
плоскости
(B1CD) и (AA1D1 );
B1
A1
C1
D1
B
A
C
D

7.

( B1CD) ( AA1D1 ) A1D
В1
б)
А1
C1
D1
В
А
С
D

8.

• Пользуясь данным
рисунком, назовите:
B1
A1
• в) плоскость, не
пересекающуюся с
прямой CD1 ; с прямой
BC1
C1
D1
B
C
A
D

9.

D1
С1
M
А1
В1
N
D
С
K
А
В
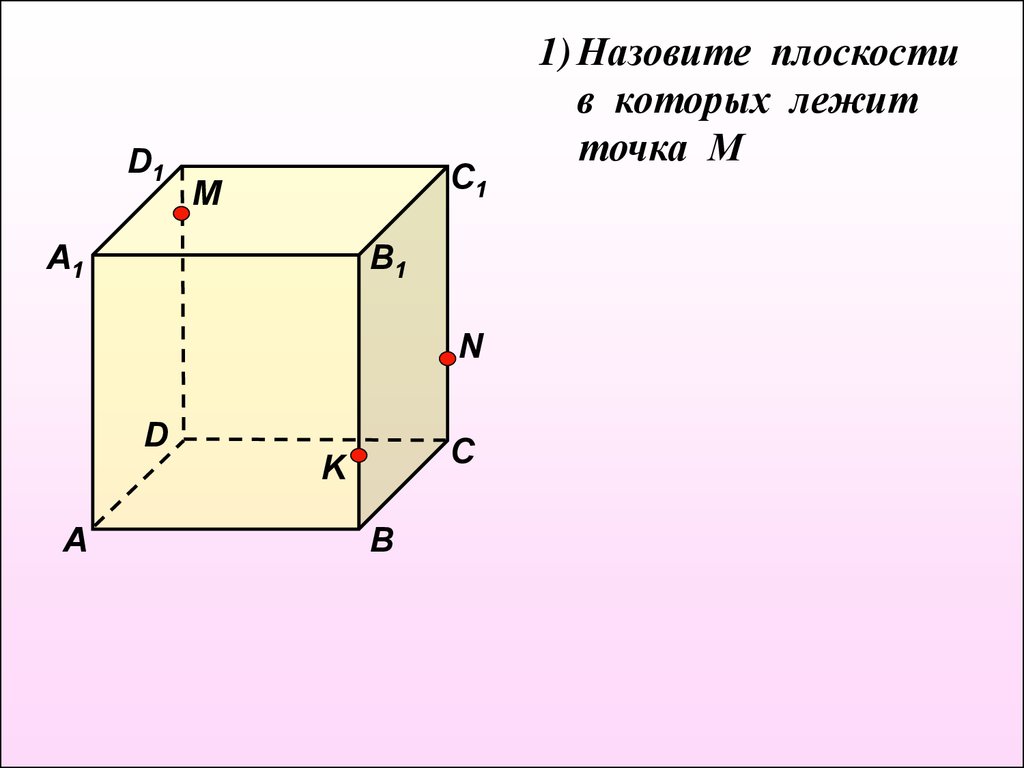
1) Назовите плоскости
в которых лежит
точка М

10.

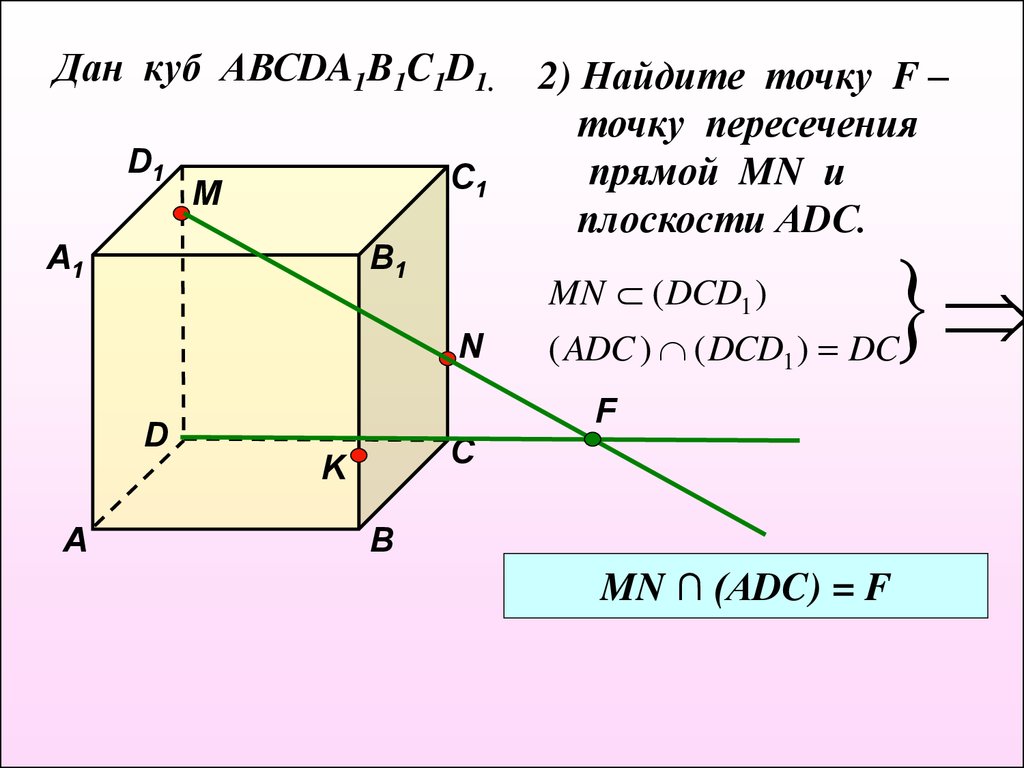
Дан куб АВСDA1B1C1D1.
D1
С1
M
А1
В1
MN ( DCD1 )
N
( ADC ) ( DCD1 ) DC
F
D
С
K
А
2) Найдите точку F –
точку пересечения
прямой MN и
плоскости АDС.
В
MN ∩ (АDC) = F

11.

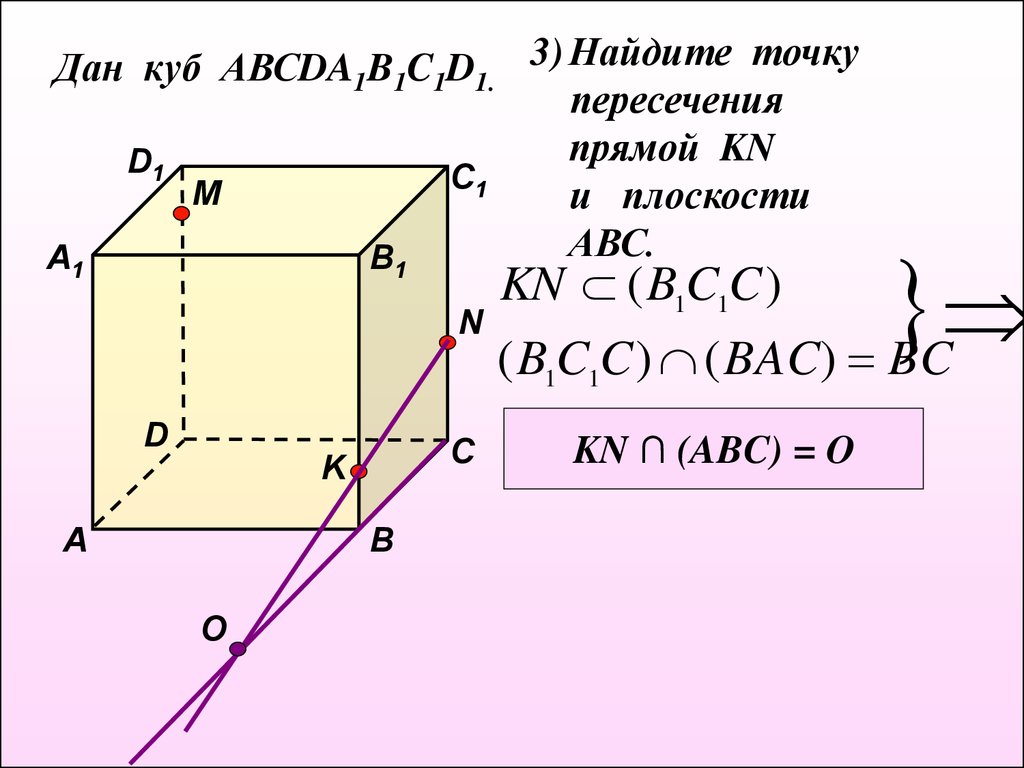
Дан куб АВСDA1B1C1D1. 3) Найдите точку
пересечения
прямой KN
D1
С1
M
и плоскости
АВС.
А
В
1
1
N
( B C C ) ( BAC) BC
KN ( B1C1C )
1
D
С
K
А
В
О
1
KN ∩ (ABC) = O

12.

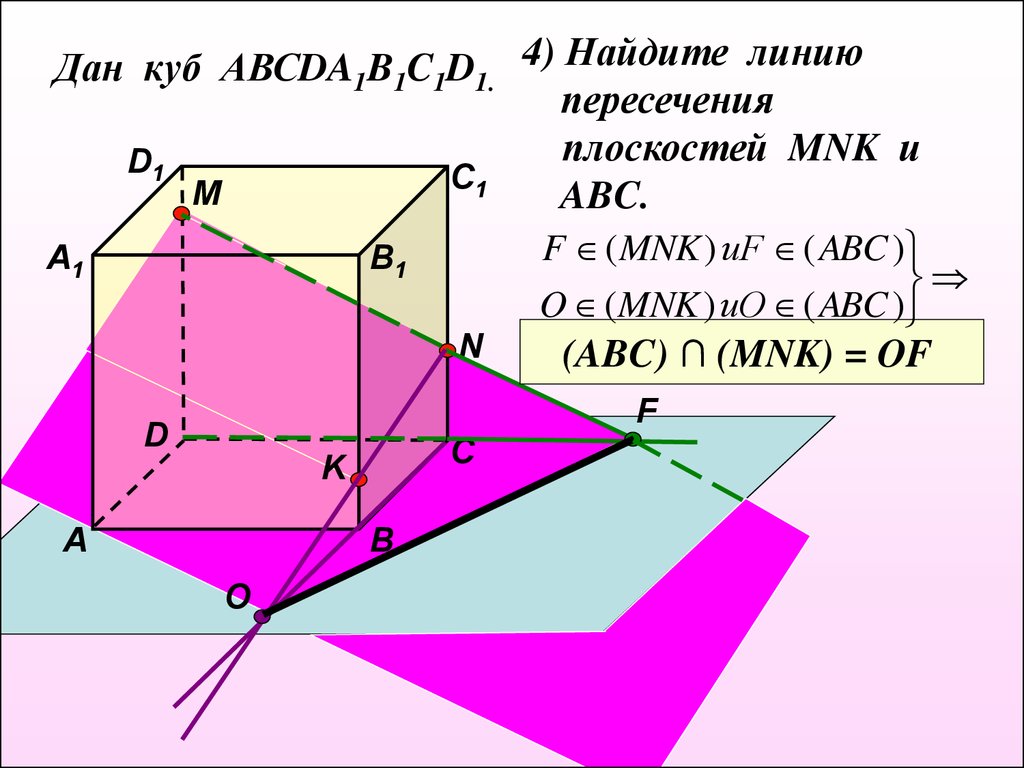
Дан куб АВСDA1B1C1D1. 4) Найдите линию
пересечения
плоскостей MNK и
D1
С1
M
ABC.
А1
F ( MNK ) иF ( ABC )
O ( MNK ) иO ( ABC )
В1
N
(ABC) ∩ (MNK) = OF
F
D
С
K
А
В
O